Формулы числовых характеристик статистического распределения
Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.
Индивидуальное задание 1
Вариант 11
Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моду;
- квантильное отклонение;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:
Эмпирическую функцию распределения определим по формуле
Здесь nx – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:
Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле
Выборочную дисперсию находим по формуле
Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу
Подправленную дисперсию вычисляем согласно формулы
Выборочное среднее квадратичное отклонение вычисляем по формуле
Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии
Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
Медиану находим по 2 формулам:
если число n — четное;
если число n — нечетное.
Здесь берем индексы в xi согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому
Мода – это варианта которая в вариационном ряду случается чаще всего, то есть
Квантильное отклонение находят по формуле
где – первый квантиль, – третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему
Коэффициент асимметрии находим по формуле
Здесь центральный эмпирический момент 3-го порядка,
Подставляем в формулу коэффициента асимметрии
Эксцессом статистического распределения выборки называется число, которое вычисляют по формуле:
Здесь m4центральный эмпирический момент 4-го порядка. Находим момент
а далее эксцесс
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
yukhym.com
Онлайн калькулятор: Показатели вариации
Пользователь Мария попросила написать такой калькулятор: Показатели вариации и анализ частотных распределений.
Расчеты не очень сложные, поэтому вот и он. Теория, по уже сложившейся традиции, под калькулятором.
addimport_exportmode_editdeleteИсследуемая совокупность
Размер страницы: 5102050100chevron_leftchevron_rightДля разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;50
Точность вычисленияЗнаков после запятой: 2
Среднее арифметическое
Размах вариации
Среднее линейное отклонение
Среднее квадратическое отклонение
Коэффициент осцилляции (проценты)
Относительное линейное отклонение (проценты)
Коэффициент вариации (проценты)
Сохранить share extension
Вариация — это различие индивидуальных значений какого-либо признака внутри изучаемой совокупности.
Ну, например, есть класс учеников — изучаемая совокупность, у них есть, скажем, годовая оценка по русскому языку. У кого-то она «5», у кого-то «4» ну и так далее. Набор этих оценок по всему классу, вместе с их частотой (т. е. встречаемостью, скажем, у 10 человек – «5», у 7 человек – «4», у 5 человек – «3») и есть вариация, по которой можно рассчитать массу показателей.
Этим мы сейчас и займемся.
Абсолютные показатели
Размах вариации — разность между максимальным и минимальным значениями признака
- Среднее линейное отклонение — среднее арифметическое отклонение индивидуальных значений от средней.
,
где — частота появления значения.
Если индивидуальных значений слишком много, для упрощения расчетов данные могут группировать, т. е. объединять в интервалы. Тогда имеет смысл середины i-го интервала, или среднего значения признака на i-том интервале
- Дисперсия — средняя из квадратов отклонений значений признаков от средней.
Дисперсию также можно рассчитать и таким способом:
, где
- Среднее квадратическое отклонение — , корень из дисперсии.
Относительные показатели
Абсолютные показатели измеряются в тех же величинах, что и сам признак, и показывают абсолютный размер отклонений, поэтому их неудобно применять для сравнения изменчивости разных признаков совокупности. Поэтому дополнительно рассчитывают относительные показатели вариации, которые обычно выражают в в процентах.
Коэффициент осцилляции — характеризует колеблемость крайних значений признака вокруг средней арифметической.
Относительное линейное отклонение или линейный коэффициент вариации — характеризует долю усредненного значения абсолютных отклонений от средней арифметической.
- Коэффициент вариации — характеризует степень однородности совокупности, наиболее часто применяемый показатель.
Совокупность считается однородной при значениях меньше 40%. При значениях больше 40% говорят о большой колеблемости признаков и совокупность считается неоднородной.
planetcalc.ru
Выборочное среднее
Выборочное среднее значение как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества.
Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, мы можем судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества.
Выборочное среднее определяется при помощи следующей формулы:
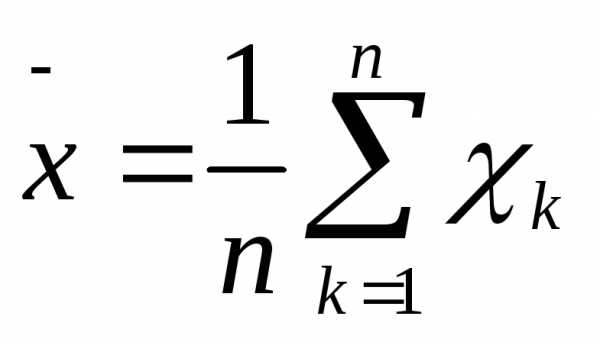
где
хср —выборочная средняя величина или среднее арифметическое значение по выборке;
п — количество испытуемых в выборке или частных психодиагностических показателей, на основе которых вычисляется средняя величина;
xk — частные значения показателей у отдельных испытуемых. Всего таких показателей п, поэтому индекс k данной переменной принимает значения от 1 до п;
∑ — принятый в математике знак суммирования величин тех переменных, которые находятся справа от этого знака.
Выражение 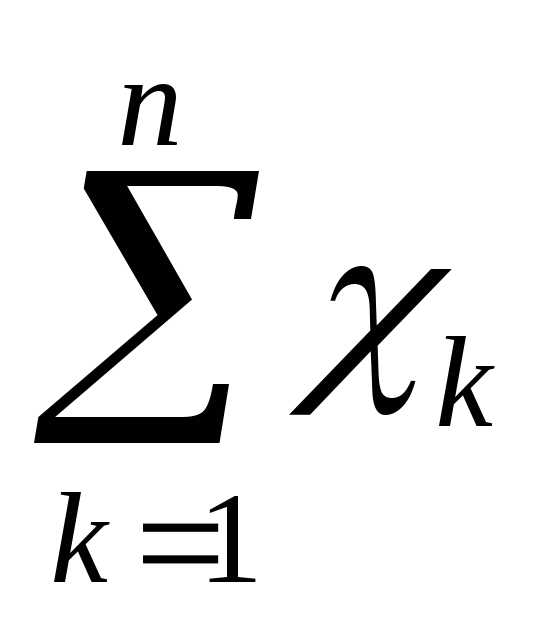
Пример. Допустим, что в результате применения психодиагностической методики для оценки некоторого психологического свойства у десяти испытуемых мы получили следующие частные показатели степени развитости данного свойства у отдельных испытуемых: х1= 5, х2 = 4, х3 = 5, х4 = 6, х5 = 7, х6 = 3, х7 = 6, х8= 2, х9= 8, х10 = 4. Следовательно, п = 10, а индекс k меняет свои значения от 1 до 10 в приведенной выше формуле. Для данной выборки среднее значение1
, вычисленное по этой формуле, будет равно:1 В дальнейшем, как это и принято в математической статистике, с целью сокращения текста мы будем опускать слова «выборочное» и «арифметическое» и просто говорить о «среднем» или «среднем значении».
В психодиагностике и в экспериментальных психолого-педагогических исследованиях среднее, как правило, не вычисляется с точностью, превышающей один, два знака после запятой, т.е. с большей, чем десятые или сотые доли единицы.
В психодиагностических обследованиях большая точность расчетов не требуется и не имеет смысла, если принять во внимание приблизительность тех оценок, которые в них получаются, и достаточность таких оценок для производства сравнительно точных расчетов.
Дисперсия
Дисперсия как статистическая, величина характеризует, насколько частные значения отклоняются от средней величины в
Чем больше дисперсия, тем больше отклонения или разброс данных. Прежде чем представлять формулу для расчетов дисперсии, рассмотрим пример. Воспользуемся теми первичными данными, которые были приведены ранее и на основе которых вычислялась в предыдущем примере средняя величина. Мы видим, что все они разные и отличаются не только друг от друга, но и от средней величины. Меру их общего отличия от средней величины и характеризует дисперсия. Ее определяют для того, чтобы можно было отличать друг от друга величины, имеющие одинаковую среднюю, но разный разброс.
Представим себе другую, отличную от предыдущей выборку первичных значений, например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко убедиться в том, что ее средняя величина также равна 5,0. Но в данной выборке ее отдельные частные значения отличаются от средней гораздо меньше, чем в первой выборке. Выразим степень этого отличия при помощи дисперсии, которая определяется по следующей формуле:
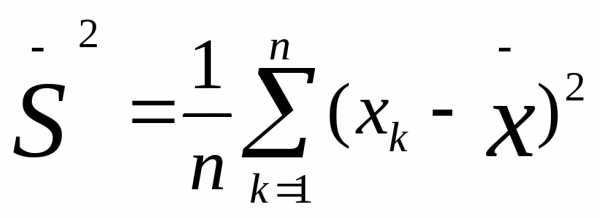
где 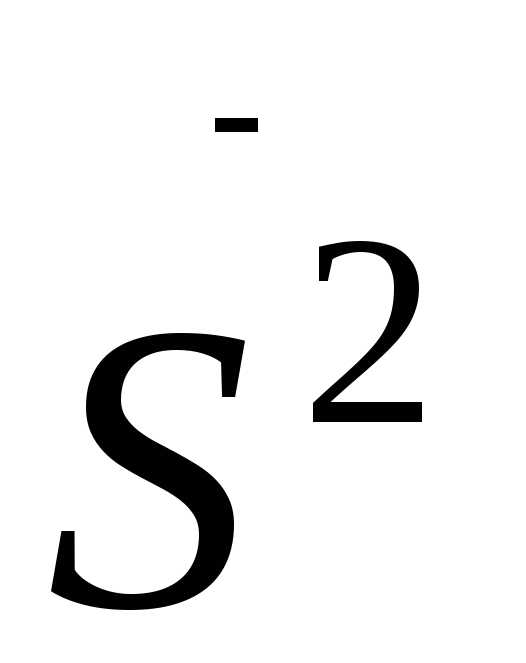 — выборочная
дисперсия, или просто дисперсия;
— выборочная
дисперсия, или просто дисперсия;
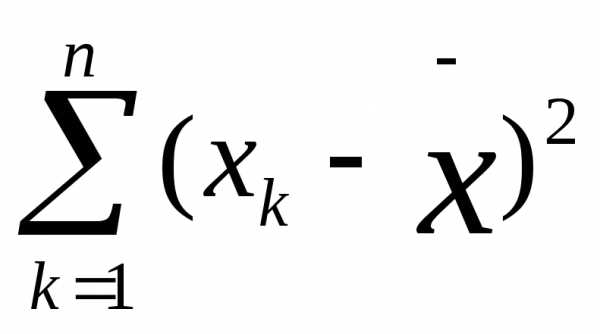 — выражение,
означающее, что для всех xk от
первого
до последнего в данной выборке необходимо
вычислить разности
между частными и средними значениями,
возвести эти разности
в квадрат и просуммировать;
— выражение,
означающее, что для всех xk от
первого
до последнего в данной выборке необходимо
вычислить разности
между частными и средними значениями,
возвести эти разности
в квадрат и просуммировать;
п — количество испытуемых в выборке или первичных значений, по которым вычисляется дисперсия.
Заметим, что во многих изданиях дисперсию принято обозначать как D(x).
Определим дисперсии для двух приведенных выше выборок частных значений, обозначив эти дисперсии соответственно индексами 1 и 2:
Мы видим, что дисперсия по второй выборке (0,4) значительно меньше дисперсии по первой выборке (3,0). Если бы не было дисперсии, то мы не в состоянии были бы различить данные выборки.
studfiles.net
Дисперсия: генеральная, выборочная, исправленная
Генеральная дисперсия
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.
Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:
С этим понятием также связано понятие генерального среднего квадратического отклонения.
Определение 3
Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
\[{\sigma }_г=\sqrt{D_г}\]Выборочная дисперсия
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 4
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 5
Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.
Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:
С этим понятием также связано понятие выборочного среднего квадратического отклонения.
Определение 6
Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
\[{\sigma }_в=\sqrt{D_в}\]Исправленная дисперсия
Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $\frac{n}{n-1}$, то есть
С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Пример задачи на нахождение дисперсии и среднего квадратического отклонения
Пример 1
Выборочная совокупность задана следующей таблицей распределения:
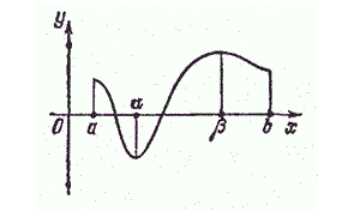
Рисунок 1.
Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Решение:
Для решения этой задачи для начала сделаем расчетную таблицу:
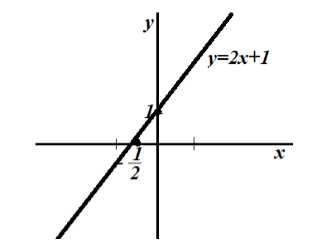
Рисунок 2.
Величина $\overline{x_в}$ (среднее выборочное) в таблице находится по формуле:
\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}\]То есть
\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}=\frac{305}{20}=15,25\]Найдем выборочную дисперсию по формуле:
\[D_в=\frac{\sum\limits^k_{i=1}{{{(x}_i-\overline{x_в})}^2n_i}}{n}=\frac{523,75}{20}=26,1875\]Выборочное среднее квадратическое отклонение:
\[{\sigma }_в=\sqrt{D_в}\approx 5,12\]Исправленная дисперсия:
\[{S^2=\frac{n}{n-1}D}_в=\frac{20}{19}\cdot 26,1875\approx 27,57\]Исправленное среднее квадратическое отклонение:
\[S=\sqrt{S^2}\approx 5,25\]spravochnick.ru
Характеристики выборки и генеральной совокупности
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использованию статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой. Число объектов N из генеральной совокупности и из выборки n называются соответственно объемом генеральной совокупности N и объемом выборки n.
Статистическое описание и вероятностные модели применяются к физическим, экономическим, социологическим, биологическим процессам, обладающим тем свойством, что хотя результат отдельного измерения физической величины X не может быть предсказан с достаточной точностью, но значение некоторой функции от множества результатов повторных измерений может быть предсказан с существенно лучшей точностью. Такая функция называется статистикой. Часто точность предсказания некоторой статистики возрастает с возрастанием объема выборки.
Наиболее известные статистики – относительная частота, выборочные средние, дисперсия. Когда возрастает объем выборки n, многие выборочные статистики сходятся по вероятности к соответствующим параметрам теоретического распределения величины X. Поэтому каждую выборку рассматривают как выборку из теоретически бесконечной генеральной совокупности, распределение признака в которой совпадает с теоретическим распределением вероятности случайной величины. Во многих случаях теоретическая генеральная совокупность есть идеализация действительной совокупности, из которой получена выборка.
Различные значения наблюдаемого признака, встречающегося в совокупности, называются вариантами. Частоты вариантов выражают доли (удельные веса) элементов совокупности с одинаковыми значениями признака. Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующим им частотами.
Значения, находящиеся в середине вариационного ряда, принято делить на собственно средние и структурные средние. Собственно среднее — это арифметическое среднее. Структурные средние — мода и медиана. Кроме того, чтобы охарактеризовать структуру вариационного ряда, используют квартили, квинтили, децили и процентили. Теперь обо всём по порядку.
Среднее арифметическое значение генеральной совокупности находят по формуле:
(1)
где
— число единиц генеральной совокупности,
— значение j-го наблюдения.
Если величина выборки X может принимать значения с вероятностями соответственно , то средним значением величины X для выборки (её математическим ожиданием E(x) ,будет
или
или же (2)
для негруппированных выборок и
(3)
для группированных выборок, где
— число единиц выборки,
— число классов,
— значение i-го класса,
— частота i-го класса.
Пример 1. В таблице даны значения средней температуры воздуха в населённом пункте N в 2014 году:
| Месяц | |
| 1 | -2,3 |
| 2 | -4,0 |
| 3 | 2,0 |
| 4 | 9,0 |
| 5 | 10,0 |
| 6 | 19,4 |
| 7 | 19,9 |
| 8 | 17,1 |
| 9 | 14,9 |
| 10 | 7,3 |
| 11 | 2,2 |
| 12 | -0,3 |
Найти среднюю температуру воздуха.
Решение. Найдём среднюю температуру воздуха как среднее значение для негруппированной выборки:
Пример 2. В таблице – данные о группировке сельских хозяйств по урожайности зерновых:
Урожайность зерновых в центнерах с га |
Число сельских хозяйств – абсолютное |
Удельный вес сельских хозяйств – в процентах |
до 5,0 |
4244 |
6,2 |
5,1-10,0 |
10446 |
15,2 |
10,1-15,0 |
18956 |
27,5 |
15,1-20,0 |
20207 |
29,3 |
20,1-25,0 |
8159 |
11,9 |
25,1-30,0 |
4145 |
6,0 |
30,1-35,0 |
1316 |
1,9 |
35,1-40,0 |
792 |
1,2 |
40,1-45,0 |
183 |
0,3 |
45,1-50,0 |
182 |
0,3 |
50,1-55,0 |
161 |
0,2 |
Всего |
68791 |
100,0 |
Найти среднюю урожайность зерновых.
Решение. Так как имеем только группированные данные и неизвестна средняя урожайность каждой группы, как приближенные значения к средней каждой группы примем центры интервалов:
Центры интервалов |
||
2,5 |
4222 |
10610,0 |
7,5 |
10446 |
78345,0 |
12,5 |
18956 |
236950,0 |
17,5 |
20207 |
363622,5 |
22,5 |
8159 |
183577,5 |
27,5 |
4145 |
113987,5 |
32,5 |
1316 |
42770,0 |
37,5 |
792 |
29700,0 |
42,5 |
183 |
7777,5 |
47,5 |
182 |
8645,0 |
52,5 |
161 |
8452,5 |
Всего |
68791 |
1074437,5 |
Найдём требуемую в условии задачи среднюю урожайности зерновых:
Итак, средняя урожайность по выборке составляет 15,6 центнеров с га.
Модой называют значение, которое в вариационном ряду встречается чаще других. Моду можно найти на гистограмме как самый высокий столбец.
Например, в выборке, значения которой 20, 50, 60, 70, 80, 20, 20, 75, 70, 20, 80, 20, 50, 60, модой является 20.
Медианой называют значение, которое находится в середине вариационного ряда. Первая половина элементов выборки меньше этого значения, а вторая половина — больше.
Если в выборке нечётное число элементов, то за медиану принимают собственно серединное значение. Например, в выборке, значения которой 14, 15, 18, 21, 27, медианой является 18.
Если в выборке чётное число элементов, то медиану находят, выбирая два значения, которые находятся в середине и вычисляя их среднее арифметическое. Например, есть выборка 11, 14, 15, 18, 21, 27. Медиану находят так: (15+18)/2 = 16,5.
По аналогии с медианой, которая делит значения выборки на две части, вводят понятие квартилей, которые делят вариационный ряд на 4 равные части.
Децили делят вариационный ряд уже на 10 одинаковых частей, а квинтили — на 5. Процентили делят вариационный ряд на 100 равных частей.
Дисперсией величины называется среднее значение квадрата отклонения величины от её среднего значения. Дисперсию генеральной совокупности рассчитывают по формуле:
(4)
Дисперсию выборки рассчитывают по формуле:
(5)
для негруппированных выборок и
(6)
для группированных выборок.
Пример 3. В таблице – данные о возрасте жителей административной территории Т в 2013 году. Не будем приводить эту таблицу из-за её громоздкости. Отметим лишь, что в таблице дана численность каждого из возрастов (по одному году, например, 33 года, 40 лет, 65 лет и т.д.) в группах от 0 лет по 94 года (включительно) и численность всей возрастной группы в интервале 95-99 лет, а также численность жителей старше 100 лет.
Требуется найти средний возраст жителей административной территории и дисперсию среднего возраста.
Решение. Найдём средний возраст. Так как данные в таблице являются данными генеральной совокупности, находим средний возраст генеральной совокупности:
В таблице – данные о числе жителей каждого возраста, исключение же – жители в возрасте 95-99 лет и старше 100 лет. Поэтому рассчитали центр интервала возрастной группы 95-99 лет: 97 лет и в расчётах использовали его.
Так как число жителей старше 100 лет относительно небольшое, чтобы упростить расчёты, нижнюю границу интервала приняли за значение признака.
Итак, средний возраст жителей административной территории Т – 38,2 года
Найдём теперь его дисперсию:
Пример 4. Найти дисперсию урожайности зерновых в сельских хозяйствах, используя данные примера 2.
Решение. Средняя урожайность по выборке составляет 15,6 центнеров с га. Чтобы найти дисперсию, создадим дополнительную таблицу.
Центры интервалов |
Число хозяйств |
|||
2,5 |
4244 |
-13,1 |
172,1 |
730412,3 |
7,5 |
10446 |
-8,1 |
65,9 |
688558,6 |
12,5 |
18956 |
-3,1 |
9,7 |
184391,3 |
17,5 |
20207 |
1,9 |
3,5 |
71505,7 |
22,5 |
8159 |
6,9 |
47,3 |
386328,5 |
27,5 |
4165 |
11,9 |
141,2 |
585113,6 |
32,5 |
1316 |
16,9 |
285,0 |
375024,0 |
37,5 |
792 |
21,9 |
478,8 |
379196,9 |
42,5 |
183 |
26,9 |
722,6 |
132234,9 |
47,5 |
182 |
31,9 |
1016,4 |
184986,0 |
52,5 |
161 |
36,9 |
1360,2 |
218995,1 |
Всего |
68791 |
— |
— |
393679,1 |
Теперь у нас есть всё, чтобы найти дисперсию:
Пример 5. Найти дисперсию температуры в населённом пункте N в 2009 году, используя данные примера 1.
Решение. Данная выборка – негруппированная, найдём дисперсию температуры для негруппированной выборки:
Стандартное отклонение равно положительному корню из дисперсии. Стандартное отклонение генеральной совокупности находят по формуле
(7)
Стандартное отклонение выборки находят по формуле
. (9)
для негруппированных выборок и
(10)
для группированных выборок.
Погрешности выборки характеризуют, насколько значительная ошибка допущена при замещении генеральной совокупности выборкой. Сколь бы тщательно ни подбирали выборку, параметр генеральной совокупности и оценка выборки Т всегда будут отличаться. Их разница является погрешность выборки .
Среднюю стандартную погрешность выборки находят по формуле
(11)
Средняя стандартная погрешность выборки характеризует рассеяние средних арифметических выборки по отношению к средним генеральной совокупности: чем больше погрешность, тем дальше среднее арифметическое выборки может находиться от среднего генеральной совокупности. В свою очередь, чем меньше погрешность, тем ближе к среднему генеральной совокупности находится среднее выборки. При увеличении числа наблюдений n стандартная погрешность уменьшается.
Стандартную погрешность называют также абсолютной погрешностью средней величины и нередко записывают .
Пример 6. Найти стандартную погрешность средней урожайности сельских хозяйств и интервал оценки, используя результаты примеров 2 и 4.
Решение. В примере 2 найдена средняя урожайность зерновых, равная 15,6 центнеров с га. В примере 4 найдена дисперсия урожайности, равная 57,2. Найдём стандартное отклонение урожайности:
Найдём теперь стандартную погрешность:
Интервал оценки средней урожайности:
Всё по теме «Математическая статистика»
function-x.ru
Найти моду, медиану, дисперсию может каждый!
Найти моду, медиану, дисперсию и другие характеристики учат в курсе теории вероятностей для анализа статистического распределения выборки. Если Вы имеете заготовленные формулы или методичку, то само по себе вычисления числовых характеристик статистических выборок не является сложным. Однако на контрольных, индивидуальных заданиях, а еще для заочников все всегда выглядит сложнее, чем есть на самом деле. Ниже приведены решения которые многие вещи из вероятности сделают для Вас простыми и понятными. Главное не спешите и в подобных примерах поступайте по аналогии.
Индивидуальное задание 1
Вариант 8
Задача 1. Составить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моде;
- квантильное отклонения;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана следующими значениями
4, 9, 7, 4, 7, 5, 6, 3, 4, 5, 7, 2, 3, 8, 5, 6, 7, 4, 3, 4.
Решение: Записываем выборку в виде вариационного ряда (в порядке возрастания):
2; 3; 3; 3; 4; 4; 4; 4; 4; 5; 5; 5; 6; 6; 7; 7; 7; 7; 8; 9.
Запишем статистическое распределение выборки в виде дискретного статистического распределения частот:
Значение эмпирической функции распределения определяем по формуле
где nx количество элементов выборки меньше х. Используя таблицу, а также учитывая, что объем выборки n=1+3+5+3+2+4+1+1=20, запишем эмпирическую функцию распределения:
Далее вычислим числовые характеристики статистического распределения выборки.
1. Выборочное среднее вычисляем по формуле
2. Выборочную дисперсию вычисляем по формуле
3. Подправленную дисперсию находим по формуле
4. Выборочное среднее квадратичное отклонение вычисляем по формуле
5. Подправленное среднее квадратичное отклонение находим по формуле
6. Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
7. Медиану вычисляют по формулам:
если число n — четное;
если число n — нечетное.
Здесь берем индексы в x[i] согласно нумерации вариант в вариационном ряду.
В нашем случае п=20, поэтому
8. Мода — это варианта которая в вариационном ряду случается чаще всего, то есть
9. Квантильное отклонение найдем по формуле
половины разницы – третьего и – первого квантилей.
Сами же квантили получаем искусственной разбивкой вариационного ряда на 4 равные части. В нашем случае
10. Коэффициент вариации вычисляем по формуле
11. Коэффициент асимметрии находим по формуле
Здесь m3 центральный эмпирический момент 3-го порядка,
Отсюда коэффициент асимметрии равен 0,3
12. Эксцессом статистического распределения выборки называется число которое находят по формуле:
В числителе имеем центральный эмпирический момент 4-го порядка
Момент и среднее квадратичное отклонение подставляем в формулу и определяем эксцесс
По тому как все доступно и понятно на практике выглядит делаем вывод, что найти моду, медиану и дисперсию должен уметь каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
yukhym.com
§ 9. Выборочная дисперсия
Для того чтобы охарактеризовать
рассеяние наблюдаемых значений
количественного признака выборки вокруг
своего среднего значения 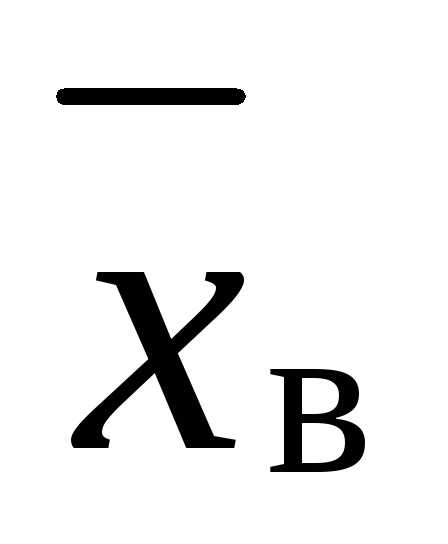 , вводят сводную
характеристику — выборочную дисперсию.
, вводят сводную
характеристику — выборочную дисперсию.
Выборочной дисперсией 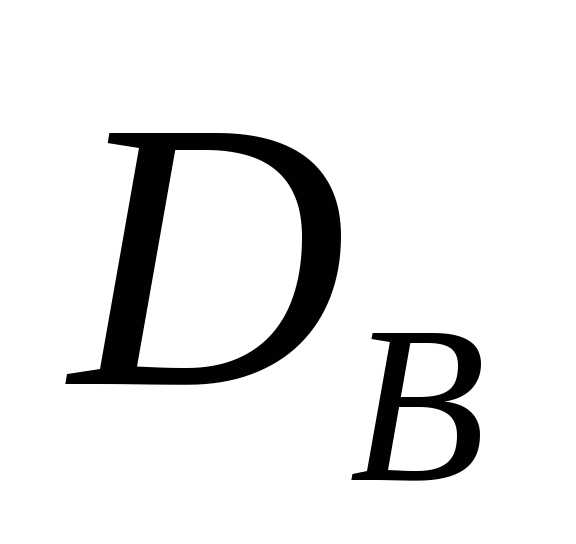 называют среднее
арифметическое квадратов отклонения
наблюдаемых значений признака от их
среднего значения
называют среднее
арифметическое квадратов отклонения
наблюдаемых значений признака от их
среднего значения 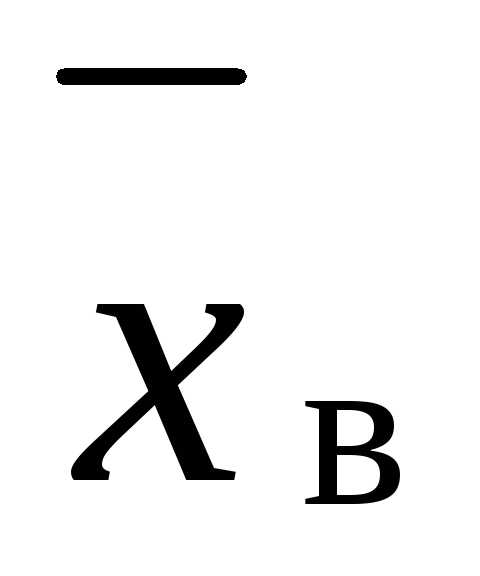 .
.
Если все значения x1, х2, …, xn признака выборки объема п различны, то
.
Если же значения признака x1, х2, …, xk имеют соответственно частоты п1, n2,…, nk, причем n1 + n2+…+nk = n, то
,
т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Пример. Выборочная совокупность задана таблицей распределения
xi 1 2 3 4
ni 20 15 10 5
Найти выборочную дисперсию.
Решение. Найдем выборочную среднюю (см. § 4):
.
Найдем выборочную дисперсию:
.
Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой-средним квадратическим отклонением.
Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
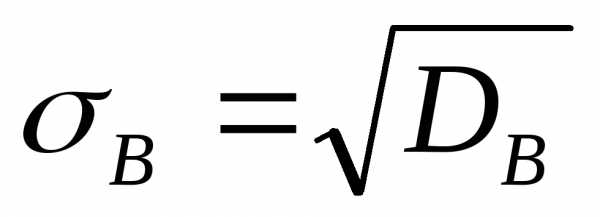 .
.
§ 10. Формула для вычисления дисперсии
Вычисление дисперсии, безразлично-выборочной или генеральной, можно упростить, используя следующую теорему.
Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:
.
Доказательство. Справедливость теоремы вытекает из преобразований:
.
Итак,
,
где ,.
Пример. Найти дисперсию по данному распределению
xi 1 2 3 4
ni 20 15 10 5
Решение. Найдем общую среднюю:
.
Найдем среднюю квадратов значений признака:
.
Искомая дисперсия
=5-22=1.
§11. Групповая, внутригрупповая, межгрупповая и общая дисперсии
Допустим, что все значения количественного признака X совокупности, безразлично-генеральной или выборочной, разбиты на k групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти групповую среднюю (см. § 6) и дисперсию значений признака, принадлежащих группе, относительно групповой средней.
Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней
,
где ni —
частота значения xi;
j —
номер группы; 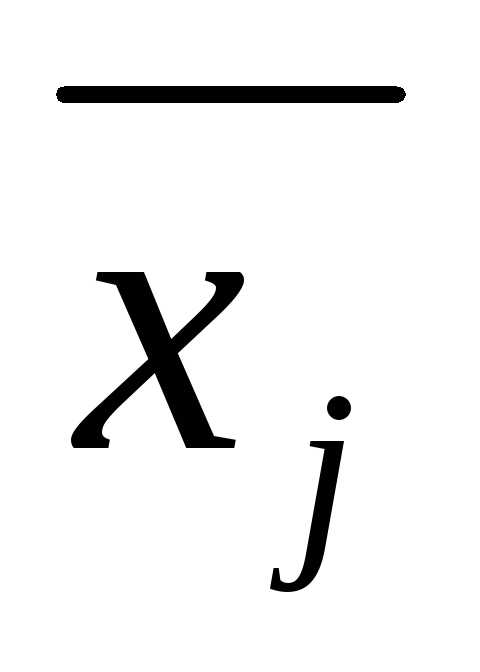 — групповая средняя
группы j;
— групповая средняя
группы j; 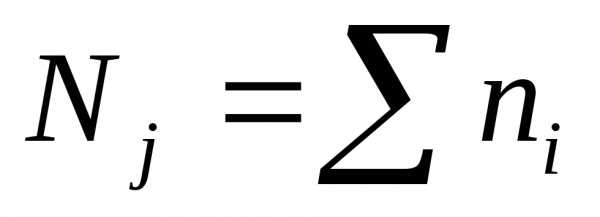 —
объем группыj.
—
объем группыj.
Пример 1. Найти групповые дисперсии совокупности, состоящей из следующих двух групп:
первая группа | вторая группа | ||||||||
xi | ni | xi | ni | ||||||
2 | 1 | 3 | 2 | ||||||
4 | 7 | 8 | 3 | ||||||
5 | 2 | ||||||||
Решение. Найдем групповые средние:
;
.
Найдем искомые групповые дисперсии:
;
.
Зная дисперсию каждой группы, можно найти их среднюю арифметическую.
Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп:
,
где Nj — объем группы j; п =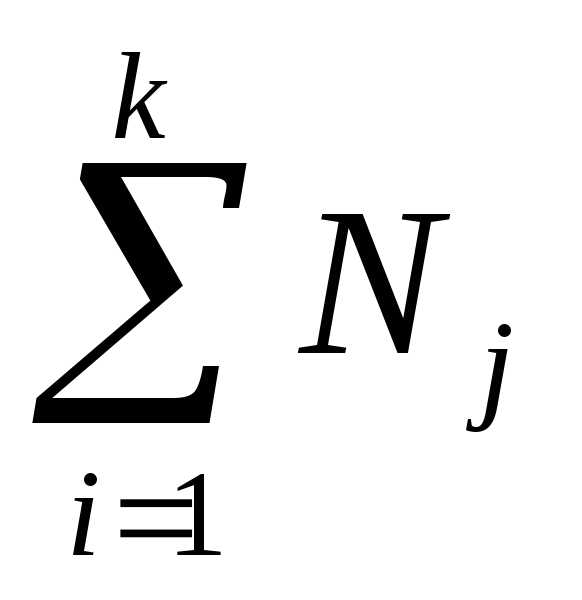 —
объем всей совокупности.
—
объем всей совокупности.
Пример 2. Найти внутригрупповую дисперсию по данным примера 1.
Решение. Искомая внутригрупповая дисперсия равна

Зная групповые средние и общую среднюю, можно найти дисперсию групповых средних относительно общей средней.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
,
где 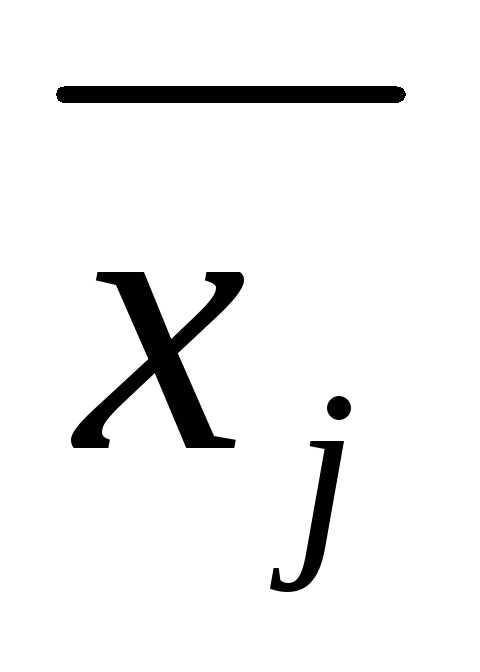 —
групповая средняя группыj; Nj — объем группы j;
—
групповая средняя группыj; Nj — объем группы j; 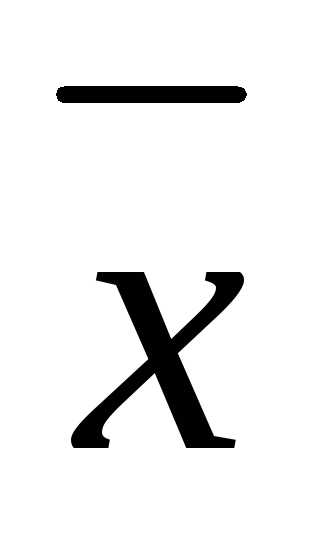 — общая средняя; n =
— общая средняя; n =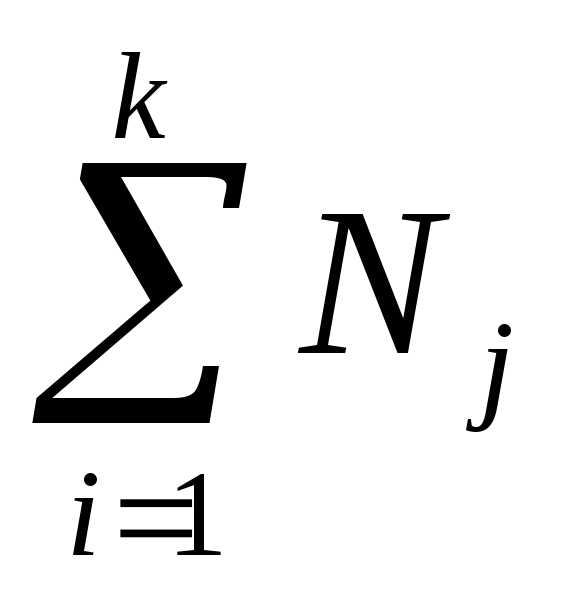 —
объем всей совокупности.
—
объем всей совокупности.
Пример 3. Найти межгрупповую дисперсию по данным примера 1.
Решение. Найдем общую среднюю:
.
Используя
вычисленные выше величины 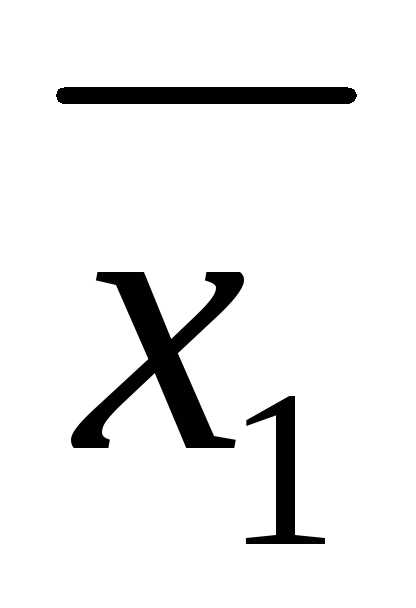 =
4,
=
4,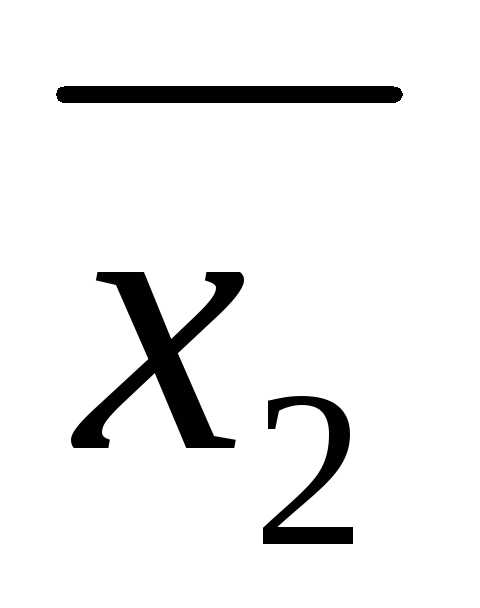 =
6, найдем искомую межгрупповую дисперсию:
=
6, найдем искомую межгрупповую дисперсию:
.
Теперь целесообразно ввести специальный термин для дисперсии всей совокупности.
Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:
,
где ni — частота значения xi ; 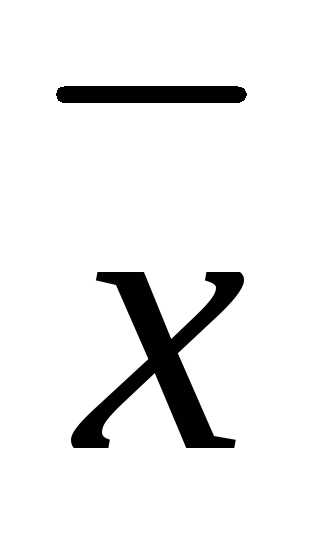 —
общая средняя; n — объем всей совокупности.
—
общая средняя; n — объем всей совокупности.
Пример 4. Найти общую дисперсию по данным примера 1.
Решение. Найдем искомую общую дисперсию, учитывая, что общая средняя равна 14/3:
Замечание. Найденная общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
Dобщ= 148/45;
Dвнгр + Dмежгр= 12/5 + 8/9= 148/45.
В следующем параграфе будет доказано, что такая закономерность справедлива для любой совокупности.
studfiles.net
