Кривые второго порядка. Эллипс: формулы и задачи
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Определение эллипса. Эллипсом называется множество
всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами,
есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и
(- a, О), а ось ординат — в точках (b, О) и
(- b, О). Эти четыре точки называются вершинами эллипса. Отрезок
между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат —
малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b, то уравнение эллипса принимает вид . Это уравнение окружности радиуса a, а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a, если сжать её в a/b раз вдоль оси Oy.
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса,
если его полуоси соответственно равны 5 и 4.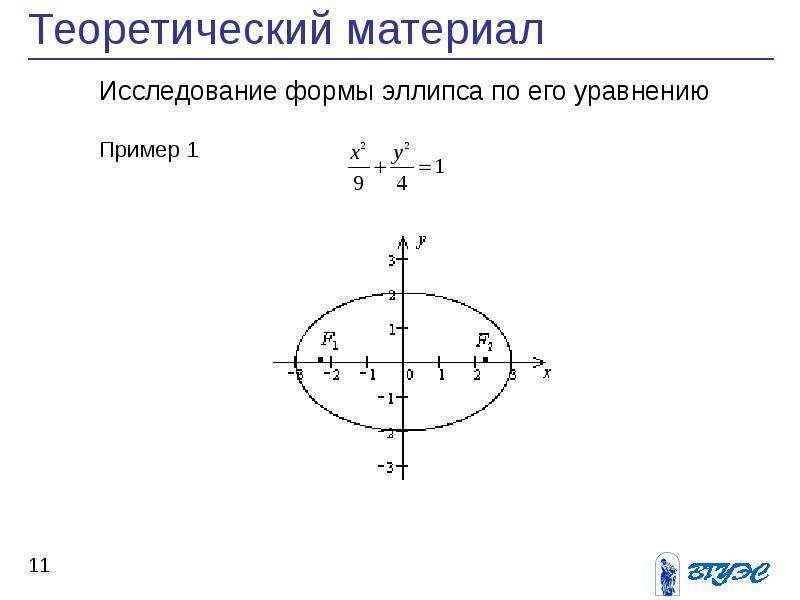
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5, меньшая полуось — это b = 4. Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
Число
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13. Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:.
Получаем фокусы эллипса:
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии
по краям).
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка
на эллипсе .
Если находится, найти расстояние от этой точки до фокусов эллипса.
Проверить, находится ли точка
на эллипсе .
Если находится, найти расстояние от этой точки до фокусов эллипса.Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов
должна быть равна 2
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
Как построить эллипс по уравнению
Эллипс – геометрическое место точек M(x;y), сумма расстояний которых до двух данных точек F1F2 имеет одно и то же значение 2a:
точки F1 и F2 – называются фокусами эллипса;
расстояние F1F2– фокусное расстояние и равно F1F2=2с;
a — большая полуось;
b — малая полуось;
c — фокальный радиус, то есть полу расстояние между фокусами;
p — фокальный параметр;
Rmin – минимальное расстояние от фокуса до точки на эллипсе;
Rmax— максимальное расстояние от фокуса до точки на эллипсе;
где
Длина малой оси эллипса 134 м.
Постройте кривую 4x 2 +9y 2 =36. Найдите фокусы, фокальный параметр и эксцентриситет.
Делим обе части на 36 и получаем каноническое уравнение эллипса
a=3, b=2
c 2 =a 2 -b 2 =3 2 -2 2 =9-4=5
Отсюда находим Фокусы F1(-2,2;0) F2(2,2;0)
Фокальный параметр находим следующим образом
Эксцентриситет эллипса
Пример 3
Постройте кривую . Найдите фокусы и эксцентриситет.
Решение
Уравнение запишем в виде
a=1, b=5
Это уравнение не является каноническим уравнением эллипса, так как b>a, а должно быть b c 2 =a 2 − b 2 =5 2 −1 2 =25 − 1=24
Следовательно, фокусы в системе координат (x’;y’) имеют координаты (-4,9;0) и (4,9;0), а в системе (x;y) координаты
Эксцентриситет эллипса равен
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F – числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) – длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат – в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат – малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность – частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия – эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось – это a = 5 , меньшая полуось – это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
– если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
– если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат – каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
Если – произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и – расстояния до этой точки от фокусов , то формулы для расстояний – следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже – красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и – расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9.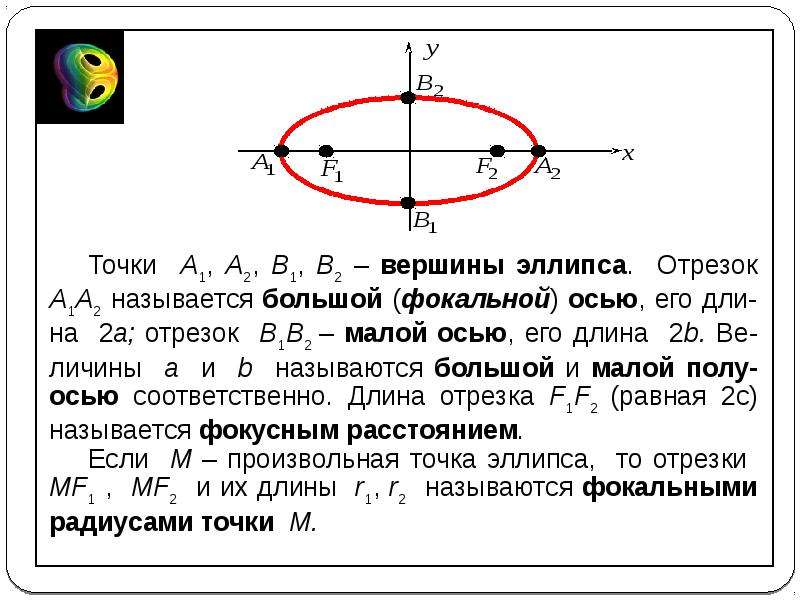 Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e – эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 – искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Определение 7.1. Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 есть заданная постоянная величина, называют эллипсом.
Определение эллипса дает следующий способ его геометрического построения. Фиксируем на плоскости две точки F1 и F2, а неотрицательную постоянную величину обозначим через 2а. Пусть расстояние между точками F1 и F2 равно 2c. Представим себе, что нерастяжимая нить длиной 2а закреплена в точках F1 и F2, например, при помощи двух иголок. Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
Итак, описываемое множество не пусто, если а ≥ с. При а = с эллипс представляет собой отрезок с концами F1 и F2, а при с = 0, т.е. если указанные в определении эллипса фиксированные точки совпадают, он является окружностью радиуса а. Отбрасывая эти вырожденные случаи, будем далее предполать, как правило, что а > с > 0.
Фиксированные точки F1 и F2 в определении 7.1 эллипса (см. рис. 7.1) называют фокусами эллипса, расстояние между ними, обозначенное через 2c, — фокальным расстоянием, а отрезки F1M и F2M, соединяющие произвольную точку M на эллипсе с его фокусами, — фокальными радиусами.
Вид эллипса полностью определяется фокальным расстоянием |F1F2| = 2с и параметром a, а его положение на плоскости — парой точек F1 и F2.
Из определения эллипса следует, что он симметричен относительно прямой, проходящей через фокусы F1 и F2, а также относительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 7.2, а). Эти прямые называют осями эллипса. Точка O их пересечения является центром симметрии эллипса, и ее называют центром эллипса, а точки пересечения эллипса с осями симметрии (точки A, B, C и D на рис. 7.2, а) — вершинами эллипса.
Число a называют большой полуосью эллипса, а b = √(a 2 — c 2 ) — его малой полуосью. Нетрудно заметить, что при c > 0 большая полуось a равна расстоянию от центра эллипса до тех его вершин, которые находятся на одной оси с фокусами эллипса (вершины A и B на рис. 7.2, а), а малая полуось b равна расстоянию от центра эллипса до двух других его вершин (вершины C и D на рис. 7.2, а).
Уравнение эллипса. Рассмотрим на плоскости некоторый эллипс с фокусами в точках F1 и F2, большой осью 2a. Пусть 2c — фокальное расстояние, 2c = |F1F2| 2 + y 2 ) + √((x + c) 2 + y 2 ) = 2a. (7.2)
Пусть 2c — фокальное расстояние, 2c = |F1F2| 2 + y 2 ) + √((x + c) 2 + y 2 ) = 2a. (7.2)
Это уравнение неудобно, так как в нем присутствуют два квадратных радикала. Поэтому преобразуем его. Перенесем в уравнении (7.2) второй радикал в правую часть и возведем в квадрат:
(x — c) 2 + y 2 = 4a 2 — 4a√((x + c) 2 + y 2 ) + (x + c) 2 + y 2 .
После раскрытия скобок и приведения подобных слагаемых получаем
√((x + c) 2 + y 2 ) = a + εx
где ε = c/a. Повторяем операцию возведения в квадрат, чтобы убрать и второй радикал: (x + c) 2 + y 2 = a 2 + 2εax + ε 2 x 2 , или, учитывая значение введенного параметра ε, (a 2 — c 2 ) x 2 /a 2 + y 2 = a 2 – c 2 . Так как a 2 — c 2 = b 2 > 0, то
x 2 /a 2 + y 2 /b 2 = 1, a > b > 0. (7.4)
Уравнению (7.4) удовлетворяют координаты всех точек, лежащих на эллипсе. Но при выводе этого уравнения использовались неэквивалентные преобразования исходного уравнения (7.2) — два возведения в квадрат, убирающие квадратные радикалы. Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли.
Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли.
Мы можем не проверять эквивалентность преобразований, если учтем следующее. Пара точек F1 и F2, |F1F2| = 2c, на плоскости определяет семейство эллипсов с фокусами в этих точках. Каждая точка плоскости, кроме точек отрезка F1F2, принадлежит какому-нибудь эллипсу указанного семейства. При этом никакие два эллипса не пересекаются, так как сумма фокальных радиусов однозначно определяет конкретный эллипс. Итак, описанное семейство эллипсов без пересечений покрывает всю плоскость, кроме точек отрезка F1F2. Рассмотрим множество точек, координаты которых удовлетворяют уравнению (7.4) с данным значением параметра a. Может ли это множество распределяться между несколькими эллипсами? Часть точек множества принадлежит эллипсу с большой полуосью a. Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению
Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению
т.е. уравнения (7.4) и (7.5) имеют общие решения. Однако легко убедиться, что система
при ã ≠ a решений не имеет. Для этого достаточно исключить, например, x из первого уравнения:
что после преобразований приводит к уравнению
не имеющему решений при ã ≠ a, поскольку . Итак, (7.4) есть уравнение эллипса с большой полуосью a > 0 и малой полуосью b =√(a 2 — c 2 ) > 0. Его называют каноническим уравнением эллипса.
Вид эллипса. Рассмотренный выше геометрический способ построения эллипса дает достаточное представление о внешнем виде эллипса. Но вид эллипса можно исследовать и с помощью его канонического уравнения (7.4). Например, можно, считая у ≥ 0, выразить у через x: y = b√( 1 — x 2 /a 2 ), и, исследовав эту функцию, построить ее график. Есть еще один способ построения эллипса. Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x 2 + y 2 = а 2 . Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат, то получится кривая, которая описывается уравнением x 2 + (ya/b) 2 = a 2 , т. е. эллипс.
Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x 2 + y 2 = а 2 . Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат, то получится кривая, которая описывается уравнением x 2 + (ya/b) 2 = a 2 , т. е. эллипс.
Замечание 7.1. Если ту же окружность сжать с коэффициентом a/b 2 — a 2 ), ε = 2c/2b = c/b.
При с =0, когда эллипс превращается в окружность, и ε = 0. В остальных случаях 0 2 — с 2 ), а с = εa = 4, то b = √(5 2 — 4 2 ) = 3. Значит каноническое уравнение имеет вид x 2 /5 2 + y 2 /3 2 = 1. Для построения эллипса удобно изобразить прямоугольник с центром в начале канонической системы координат, стороны которого параллельны осям симметрии эллипса и равны его соответствующим осям (рис. 7.4). Этот прямоугольник пересекается с
осями эллипса в его вершинах A(—5; 0), B(5; 0), C(0; -3), D(0; 3), причем сам эллипс вписан в него. На рис. 7.4 указаны также фокусы F1,2(±4; 0) эллипса.
Геометрические свойства эллипса. Перепишем первое уравнение в (7.6) в виде |F1M| = (а/ε — x)ε. Отметим, что величина а/ε — x при а > с положительна, так как фокус F1 не принадлежит эллипсу. Эта величина представляет собой расстояние до вертикальной прямой d: x = а/ε от точки M(x; у), лежащей левее этой прямой. Уравнение эллипса можно записать в виде
Оно означает, что этот эллипс состоит из тех точек M(x; у) плоскости, для которых отношение длины фокального радиуса F1M к расстоянию до прямой d есть величина постоянная, равная ε (рис. 7.5).
У прямой d есть » двойник » — вертикальная прямая d’, симметричная d относительно центра эллипса, которая задается уравнением x = —а/ε. Относительно d’ эллипс описывается так же, как и относительно d. Обе прямые d и d’ называют директрисами эллипса. Директрисы эллипса перпендикулярны той оси симметрии эллипса, на которой расположены его фокусы, и отстоят от центра эллипса на расстояние а/ε = а 2 /с (см. рис. 7.5).
рис. 7.5).
Расстояние p от директрисы до ближайшего к ней фокуса называют фокальным параметром эллипса. Этот параметр равен
p = a/ε – c = (a 2 – c 2 )/c = b 2 /c
Эллипс обладает еще одним важным геометрическим свойством: фокальные радиусы F1M и F2M составляют с касательной к эллипсу в точке M равные углы (рис. 7.6).
Это свойство имеет наглядный физический смысл. Если в фокусе F1 расположить источник света, то луч, выходящий из этого фокуса, после отражения от эллипса пойдет по второму фокальному радиусу, так как после отражения он будет находиться под тем же углом к кривой, что и до отражения. Таким образом, все лучи, выходящие из фокуса F1, сконцентрируются во втором фокусе F2, и наоборот. Исходя из данной интерпретации указанное свойство называют оптическим свойством эллипса.
Вывод уравнения эллипса
Введем
прямоугольную систему координат. Пусть
фокусы эллипса лежат на оси Х,
причем
т. Е.– межфокусное расстояние эллипса.
(чертеж
7.)
[8.С.467]
Пусть
фокусы эллипса лежат на оси Х,
причем
т. Е.– межфокусное расстояние эллипса.
(чертеж
7.)
[8.С.467]
Чертеж 7.
Пусть – произвольная точка эллипса. Величиныназываютсяфокальными радиусами точки М эллипса. По определению эллипса: r1 + r2 = 2a, а > c. Из прямоугольных треугольников, по теореме Пифагора, имеем:
(2)
Преобразуем уравнение, умножим уравнение (2) на , получим:
(3)
Сложим уравнения (2) и (3):
(4)
Возведем равенство(4) в квадрат, получим:
Пусть так как, откуда уравнение имеет вид:
где
(5)
каноническое уравнение эллипса
с центром в начале координат.
Соответственно, отсюда получаем уравнение:
где каноническое уравнение эллипса с центром в точке . Где числа а и b соответственно большая и малая полуоси эллипса. Заметим, что а >с Если а < , то фокусы эллипса будут лежать на осиОУ, если а = , то эллипс превращается в окружность.
Точки ,называютсявершинами эллипса. Отметим, что эллипс целиком расположен внутри прямоугольника, ограниченного прямыми
Исследование свойств эллипса по его уравнению
1) Пересечение эллипса с осями координат:
Найдем точки пересечения эллипса с осью ОХ: Пусть y=0, тогда уравнение эллипса имеет вид: , следовательно.
Отсюда следует, что точки (-a,0),(a,0) являются точками пересечения с осью ОХ.
Найдем точки пересечения эллипса с осью ОУ: Пусть х=0,отсюда имеем: , отсюда.

Следовательно, точки (-b,0),(b,0)являются точками пересечения с осью ОУ.
Отсюда заключаем, что границы эллипса , отображающие его схематичное построение. (чертеж 8.) [1.С. 105]
Чертеж 8.
Расстояние |A1A2| = 2a называется большой (фокальной) осью эллипса, расстояние |B1B2| = 2b называется малой осью эллипса. Расстояния от начала координат до вершин A2(a, 0), B2(0, b) называются соответственно большой и малой полуосями эллипса.
Вывод: Таким образом, заключаем, что эллипс вписан в прямоугольник с размерами 2a, 2b (чертеж 9.).
Чертеж 9.
2) Симметрия эллипса относительно координатных осей ox и oy:
Пусть принадлежит эллипсу, т. е- верное равенство.
Точка симметрична точкеотносительно оси ОХ
—
верное равенство.
Следовательно, принадлежит эллипсу, отсюда заключаем, что эллипс симметричен относительно ОХ
Точка симметрична точкеотносительно оси ОУ, следовательно, эллипс симметричен относительно оси ОУ.
Точка симметрична точкеотносительно О (центра), следовательно, эллипс симметричен относительно начала координат.[1.С.105-106]
3) Фокусы эллипса:
Пусть фокусы эллипса лежат на оси ОX. Межфокусное расстояние эллипса равно причем . Заметим, что
. [1.С.106]
4) Эксцентриситет эллипса:
Определение 2.2. Эксцентриситетом эллипса называют отношение межфокусного расстояния 2с к длине большой оси 2а.
.
Так как , следовательно,.
Если
стремится к нулю при постоянном значении,
тостремится к нулю. При этом величинастремится к.
В предельном случаи уравнение эллипса
принимает вид:.
Это уравнение окружности. Если,
то.
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
10.)
[1.С.106]
При этом величинастремится к.
В предельном случаи уравнение эллипса
принимает вид:.
Это уравнение окружности. Если,
то.
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
10.)
[1.С.106]
Чертеж 10.
5) Диаметры эллипса:
Всякая хорда, проходящая через центр эллипса, называется диаметром эллипса. В частности, диаметрами эллипса является его большая ось и малая ось. Всякий диаметр эллипса, не являющийся его осью, больше малой оси, но меньше большой оси (чертеж 11.). [1.С.106-107]
Чертеж 11.
6) Касательная к эллипсу:
Уравнение касательной к эллипсу где- координаты точки касания и соответственно большая и меньшая полуоси эллипса (чертеж 12.).
Чертеж 12.
7) Частный случай эллипса — окружность:
,
где
окружности.
8) Взаимное расположение точек и эллипса:
эллипсу, если верное равенство,
Если толежит внутри эллипса,
Если толежит вне эллипса. [1.С.100]
Изображение эллипса
Построение без использования ИКТ: Для построения эллипса построим прямоугольную систему координат с центром в точке О и единичный отрезок. Построим прямоугольник со сторонами 2a=14,2b=10 и впишем в него эллипс так, чтобы координаты точек (-7;0),(7;0),(0;-5),(0;5) принадлежали эллипсу.(чертеж 13.)
Чертеж 13.
С использованием ЭСО- Mathcad:
Полученное уравнение эллипса имеет вид: . Для построения линии второго порядка в программеMathcad приводим уравнение к виду: (чертеж 14.)
Чертеж
14.
Построение без использования ИКТ: Для построения эллипса построим прямоугольную систему координат с центром в точке О и единичный отрезок. Построим прямоугольник со сторонами 2a=8,2b=14 и впишем в него эллипс так, чтобы координаты точек (-4;0),(4;0),(0;-7),(0;7) принадлежали эллипсу.(чертеж 15.)
Чертеж 15.
С использованием ЭСО- Mathcad:
Для построения линии в Mathcad приведем ее к виду: ,.(чертеж 16.)
Чертеж 16.
ГИПЕРБОЛА
Определение 3.1. Гипербола — множество точек плоскости, модуль разности расстояний от которых до двух данных точек этой плоскости, называемых фокусами гиперболы, есть заданная постоянная величинаменьшая, чем расстояние между фокусами [8.С.510]
фокусное расстояние, уравнение, свойства и эксцентриситет фигуры
Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.
Что такое эллипс и фокусное расстояние
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и . Допустим, что расстояние = – фокусное расстояние.
Рис. 1
– фокусы .
; ,
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Теорема:
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью, (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, . Так как по определению сумма – постоянная величина, то приравнивая получается:
.
Уравнение эллипса
Уравнение элиппса бывает двух видов:
- Каноническое уравнение эллипса.

- Параметрическое уравнение эллипса.
Сначала рассмотрим каноническое уравнение эллипса:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:
Если центр эллипсa смещен в точку с координатами тогда уравнение:
Чтобы получить каноническое уравнение эллипса, разместим и на оси симметричной к началу координат. Тогда у фокусов будут такие координаты и (см. рис. 2).
Пусть – произвольная точка эллипса. Обозначим через и – расстояние от точки к фокусам. Согласно с определением эллипса:
(1)
Рис. 2
Подставим в (1) , и освободимся от иррациональности, подняв обе части к квадрату, получим:
(подносим к квадрату обе части): ,
Обозначим: , получаем каноническое уравнение эллипса:
(2)
Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из у нас получается . Так как , тогда , и поэтому .
Так как , тогда , и поэтому .
Для построения эллипса обратим внимание, что если точка принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки тоже удовлетворяют это уравнение: из
.
Точки – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.
Из уравнения (2) находим , для первой четверти .
Если , тогда . Если же , тогда . Точки и , а также симметричные с ними , – вершины эллипса, точка – центр эллипса, = большая ось, – малая ось эллипса.
Если первой четверти, тогда из получается, что при возрастании от к значение падает от к . (рис. 3)
Параметрическое уравнение выглядит так:
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом равен углу между касательной и фокальным радиусом .
2. Уравнение касательной к эллипсу в точке с координатами :
.
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами и у треугольника , тогда выполняется соотношение:
=
Эксцентриситет эллипса
ОпределениеЭксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначаетсяЗначения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:
Рис. 3
3
Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и , тогда вычислим – полуфокусное расстояние.
Строим фокусы и на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках и . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Примеры решения задач
Пример 1 Пример 2 Пример 3Найти оси, вершины и фокусы эллипса или . Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
, . Откуда находим оси эллипса: , и координаты вершин: , , , . Дальше из формулы:
. Значит, фокусами эллипса есть точки: и . Для построения эллипса отложим на осях и вершины соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении большей полуосью будет , тогда фокусы эллипса будут расположены на оси и тогда .
Эллипс – фокусное расстояние, уравнение, свойства и эксцентриситет фигуры обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру
Эллипс | matematicus.ru
Эллипс – геометрическое место точек M(x;y), сумма расстояний которых до двух данных точек F1F2 имеет одно и то же значение 2a:
F1M+F2M=2a
точки F1 и F2 – называются фокусами эллипса;
расстояние F1F2 – фокусное расстояние и равно F1F2=2с;
a — большая полуось;
b — малая полуось;
c — фокальный радиус, то есть полу расстояние между фокусами;
p — фокальный параметр;
Rmin – минимальное расстояние от фокуса до точки на эллипсе;
Rmax— максимальное расстояние от фокуса до точки на эллипсе;
где
Пример 1
Длина малой оси эллипса 134 м. Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Решение
Пример 2
Постройте кривую 4x2+9y2=36. Найдите фокусы, фокальный параметр и эксцентриситет.
Решение
Делим обе части на 36 и получаем каноническое уравнение эллипса
a=3, b=2
Делаем чертёж
c2=a2-b2=32-22=9-4=5
Отсюда находим Фокусы F1(-2,2;0) F2(2,2;0)
Фокальный параметр находим следующим образом
Эксцентриситет эллипса
Пример 3
Постройте кривую . Найдите фокусы и эксцентриситет.
Решение
Уравнение запишем в виде
a=1, b=5
Это уравнение не является каноническим уравнением эллипса, так как b>a, а должно быть b<а. А если переобозначить оси, то есть x=x’ , y=y’, тогда уравнение примет вид:
А если переобозначить оси, то есть x=x’ , y=y’, тогда уравнение примет вид:
И тогда a=5, b=1
Делаем чертёж
c2=a2 − b2=52 −12=25 − 1=24
Следовательно, фокусы в системе координат (x’;y’) имеют координаты (-4,9;0) и (4,9;0), а в системе (x;y) координаты
Эксцентриситет эллипса равен
Каноническое уравнение эллипса с примерами решения
Содержание:
- Эллипс
- Директрисы эллипса
Каноническое уравнение эллипса (координатные оси совпадают с осями эллипса):
Параметрические уравнения:
Эллипс
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек есть величина постоянная большая расстояния между этими заданными точками (рис. ). Это геометрическое определение выражает фокальное свойство эллипса.
). Это геометрическое определение выражает фокальное свойство эллипса.
Точки называются фокусами эллипса, расстояние между ними
фокусным расстоянием, середина отрезка — центром эллипса, число — длиной большой оси эллипса (соответственно, число — большой полуосью эллипса). Отрезки соединяющие произвольную точку эллипса с его фокусами, называются фокальными радиусами точки Отрезок, соединяющий две точки эллипса, называется хордой эллипса.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Отношение называется эксцентриситетом эллипса. Из определения следует, что При т.е. при фокусы а также центр совпадают, и эллипс является окружностью радиуса (рис.3.36,6).
Геометрическое определение эллипса, выражающее его фокальное свойство, эквивалентно его аналитическому определению — линии, задаваемой каноническим уравнением эллипса:
Директрисы эллипса
Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее. При когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
При когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
Эллипс с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство эллипса).
Возможно вам будут полезны данные страницы:
- Здесь -один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е. или
В самом деле, например, для фокуса и директрисы (рис.3.37,б) условие можно записать в координатной форме:
Избавляясь от иррациональности и заменяя приходим к каноническому уравнению эллипса (3.49). Аналогичные рассуждения можно провести для фокуса и директрисы
Уравнение эллипса в полярной системе координат (рис.
3.37, имеет вид
где —фокальный параметр эллипса.
В самом деле, выберем в качестве полюса полярной системы координат левый фокус эллипса, а в качестве полярной оси — луч
(рис.3.37,в). Тогда для произвольной точки согласно геометрическому определению (фокальному свойству) эллипса, имеем Выражаем расстояние между точками (см. п.2 замечаний 2.8):
Следовательно, в координатной форме уравнение эллипса имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замену
что и требовалось доказать. Замечания 3.9.
1. Прямые ограничивают на координатной плоскости основной прямоугольник, внутри которого находится эллипс (см. рис.3.37,а).
2. Эллипс можно определить, как геометрическое место точек, получаемое в результате сжатия окружности к ее диаметру.
Действительно, пусть в прямоугольной системе координат уравнение окружности имеет вид При сжатии к оси абсцисс с коэффициентом (см. разд.2.2.4) координаты произвольной точки принадлежащей окружности, изменяются по закону Подставляя в уравнение окружности получаем уравнение для координат образа точки
разд.2.2.4) координаты произвольной точки принадлежащей окружности, изменяются по закону Подставляя в уравнение окружности получаем уравнение для координат образа точки
поскольку Это каноническое уравнение эллипса.
3. Координатные оси (канонической системы координат) являются осями симметрии эллипса (называются главными осями эллипса), а его центр — центром симметрии.
Действительно, если точка принадлежит эллипсу то и точки симметричные точке относительно координатных осей, также принадлежат тому же эллипсу.
4. Из уравнения эллипса в полярной системе координат (см. рис.3.37,в), выясняется геометрический смысл фокального параметра -это половина длины хорды эллипса, проходящей через его фокус перпендикулярно фокальной оси 5. Эксцентриситет характеризует форму эллипса, а именно отличие эллипса от окружности. Чем больше тем эллипс более вытянут, а чем ближе к нулю, тем ближе эллипс к окружности (рис.3.38,а).
- Действительно, учитывая, что получаем
где — коэффициент сжатия эллипса, Следовательно,
Чем больше сжат эллипс по сравнению с окружностью, тем меньше коэффициент сжатия и больше эксцентриситет. Для окружности
Для окружности
6. Уравнение при определяет эллипс, фокусы которого расположены на оси (рис.3.38,б). Это уравнение сводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет эллипс с центром в точке оси которого параллельны координатным осям
(рис.3.38,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).
При уравнение описывает окружность радиуса с центром в точке
8. Параметрическое уравнение эллипса в канонической системе координат имеет вид
Действительно, подставляя эти выражения в уравнение (3.49), приходим к основному тригонометрическому тождеству
Пример 3.20. Изобразить эллипс
в канонической системе координат Найти полуоси, фокусное
расстояние, эксцентриситет, коэффициент сжатия, фокальный параметр, уравнения директрис.
Сравнивая заданное уравнение с каноническим, определяем полуоси: — большая полуось, — малая полуось эллипса. Строим основной прямоугольник со сторонами с центром в начале координат (рис.3.39). Учитывая симметричность эллипса, вписываем его в основной прямоугольник. При необходимости определяем координаты некоторых точек эллипса. Например, подставляя в уравнение эллипса, получаем
Следовательно, точки с координатами принадлежат эллипсу.
Вычисляем коэффициент сжатия фокусное расстояние эксцентриситет фокальный параметр Составляем уравнения директрис:
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 6.1. Найти полуоси, координаты фокусов и эксцентриситет эллипса
Решение. Разделив данное уравнение эллипса на , приведем его к виду . Отсюда следует, что большая полуось эллипса , а малая полуось . Известно, что , поэтому
.
Следовательно, координаты фокусов и , а его эксцентриситет .
Ответ.
Задача 6.2. Эллипс касается оси ординат в начале координат, а центр симметрии его находится в точке . Составить уравнение эллипса, если его эксцентриситет равен .
Решение. Выполним чертеж (рис. 2.35).
| Каноническое уравнение такого эллипса В нашем случае | Рис. 2.35 |
Известно, что . Следовательно, для нахождения надо знать . Найдем из формулы эксцентриситета: , , откуда . Значит, ,
Итак, уравнение искомого эллипса
Ответ.
Задача 6.3. Определитель траекторию точки , которая при своем движении остается втрое ближе к точке , чем к прямой
После преобразований получаем искомое уравнение:
.
Таким образом, точка движется по эллипсу. При этом большая ось эллипса и его фокусы расположены на оси
Ответ. .
Задача 6.4.Действительная полуось гиперболы , эксцентриситет Составить каноническое уравнение гиперболы и начертить ее.
Решение. Эксцентриситет гиперболы Следовательно,
, ,
откуда фокусы гиперболы , , а мнимая полуось . Искомым уравнением гиперболы будет
.
Ответ. .
Задача 6.5.Дана равносторонняя гипербола . Найти уравнение эллипса, фокусы которого находятся в фокусах гиперболы, если известно, что эллипс проходит через точку .
Решение. Для данной гиперболы . Следовательно, из соотношения получаем , откуда . Значит, фокусы гиперболы и . В этих же точках находятся фокусы эллипса.
Обозначим через и соответственно большую и малую полуоси эллипса. Тогда при условии, что , будем иметь Для определения и используем еще одно условие: что точка лежит на эллипсе, т.е. ее координаты должны удовлетворять уравнению эллипса
(6.8)
Это значит, что Таким образом, для определения и имеем систему уравнений
решив которую, получим , Подставив эти значения в уравнение (6.8), найдем
Ответ.
Задача 6.6. Асимптоты гиперболы имеют уравнения . Фокусы лежат на оси и расстояние между ними равно . Написать каноническое уравнение гиперболы и начертить ее.
Решение. Так как фокусы гиперболы лежат на оси , то ее каноническое уравнение имеет вид
Разрешив уравнение асимптот относительно , получим , откуда . Кроме того, , т.е. Так как для гиперболы , то для нахождения и получим систему уравнений
| Рис. 2.38 | решив которую, будем иметь , . Следовательно, каноническое уравнение гиперболы (рис. 2.38) |
Ответ.
Задача 6.7. Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой и окружности и симметрична относительно оси .
Решение. Найдем точки пересечения заданных линий, решив совместно их уравнения:
В результате получим два решения и . Точки пересечения и . Так как парабола проходит через точку и симметрична относительно оси , то в этой точке будет находиться вершина параболы. Поэтому уравнение параболы имеет вид . Так как парабола проходит через точку , то координаты этой точки удовлетворяют уравнению параболы: , ,
Итак, уравнением параболы будет , уравнение директрисы или , откуда
Ответ. ;
Задача 6.8. Мостовая арка имеет форму параболы. Определить параметр этой параболы, зная, что пролет арки равен , а высота
Решение.выберем прямоугольную систему координат так, чтобы вершина параболы (мостовой арки) находилась в начале координат, а ось симметрии совпадала с отрицательным направлением оси . В таком случае каноническое уравнение параболы имеет вид , а концы хорды арки и . Подставив координаты одного из концов хорды (например, ) в уравнение параболы и решив полученное уравнение относительно , получим
Ответ.
Задача 6.9. Привести уравнение кривой к каноническому виду и построить эту кривую.
Решение. В уравнении , , , , , Вычислим дискриминант старших членов:
.
Так как , данная линия является кривой эллиптического типа.
Найдем центр кривой из системы
Решив ее, получим , .
С помощью параллельного переноса осей координат в центр уравнение кривой в новой системе приводится к виду:
,
подставив в исходное уравнение кривой, получим
(6.9)
Для дальнейшего упрощения уравнения (6.9) применим правило приведения квадратичной формы к каноническому виду. Составим характеристическое уравнение
или .
Отсюда .
Повернув теперь оси координат так, чтобы направления осей и совпадали с главными направлениями квадратичной формы, уравнение (6.5) приведем к каноническому виду
или .
Из уравнения видно, что это эллипс с полуосями , . Чтобы построить этот эллипс найдем главное направление, соответствующее характеристическому числу (его мы приняли за ось в каноническом уравнении). Подставив коэффициенты нашего уравнения в систему
получим
Полагая , находим, что . Единичный вектор оси имеет в системе координаты и . Следовательно, , а .
Решение. В исходном уравнении , , , , , Дискриминант старших членов
Следовательно, уравнение определяет нецентральную линию второго порядка, т.е. линию параболического типа.
Составим характеристическое уравнение квадратичной формы старших членов:
или
Отсюда ,
Найдем главное направление, соответствующее характеристическому числу . Для этого подставим в систему
коэффициенты нашего уравнения. Получим
Полагая , имеем . Следовательно, главное направление, соответствующее характеристическому числу , определяется вектором . Нормируя его, находим единичный вектор: . Это значит, что , а , т.е. поворачиваем систему на угол .
Используя теперь равенства (6.10), имеем:
Следовательно, уравнение (10.17) в системе координат принимает вид
(6.11)
Уравнение (6.11) определяет параболу. Для приведения его к каноническому виду найдем координаты нового начала. Сгруппируем члены с одинаковыми переменными и выделим полный квадрат:
Узнать еще:
Эллипс — Математическая энциклопедия
(реальный)
2010 Классификация предметов по математике: Начальная школа: 51-XX [MSN] [ZBL]
Эллипс плоская кривая, полученная пересечением кругового конуса с плоскостью, не проходящей через вершину конуса и пересекающей все его образующие в точках одного из его листов. Эллипсом также оказывается множество точек $ M $ плоскости (см. Рисунок 1), для каждой из которых сумма расстояний от двух заданных точек $ F_1 $ и $ F_2 $ (фокусы) постоянна и равна в $ 2a> F_1F_2 $.Расстояние между фокусами называется фокусным расстоянием и обычно обозначается $ 2c $. Середина отрезка $ F_1F_2 $ называется центром эллипса.
Рисунок 1. Эллипс (pdf)Линия, на которой расположены фокусы эллипса, называется первой (или фокусной) осью. Линия, проходящая через центр эллипса и перпендикулярная первой оси, называется второй осью. Оси эллипса — его оси симметрии. Точки пересечения эллипса с осями симметрии называются его вершинами.Большая ось эллипса — это отрезок (а также его длина $ 2a $) первой оси между вершинами. Малая ось — это отрезок (а также его длина $ 2b $) второй оси между вершинами. Число $ e = c / a <1 $ называется эксцентриситетом эллипса. Диаметр эллипса - это любая прямая линия, проходящая через центр; диаметр также можно определить как прямую линию, проходящую через середины параллельных хорд. Директрисой эллипса, соответствующего данному фокусу $ F $ (ассоциированная директриса), является прямая $ D $, перпендикулярная первой оси на расстоянии $ d = a / e $ от центра.2 / a $. С помощью фокального параметра можно записать уравнение эллипса в виде $$ \ rho = \ frac {p} {1 + e \ cos \ phi}, $$ где $ \ rho $ и $ \ phi $ - полярные координаты, $ 0 \ leq \ phi <2 \ pi $.
Если $ a = b $, эллипс становится окружностью, $ F_1 \ Equiv F_2 \ Equiv 0 $ — его центром, $ a $ — его радиусом, $ e = 0 $, и директрисы нет.
Эллипс обладает следующим оптическим свойством: световой луч, исходящий из одного фокуса, проходит через другой фокус после зеркального отражения в эллипсе.2} = -1 $$ где $ a $ и $ b $ — действительные числа, называется мнимым эллипсом.
Как следует из названия, у воображаемого эллипса нет реальных точек.
Другие характеристики эллипса следующие.
Эллипс — это аффинное изображение круга; эллипс — это невырожденная коника (т. е. кривая второго порядка), которая не пересекает линию на бесконечности; эллипс — это набор точек, расстояние от которых до данной точки (фокус) и до данной линии (связанная директриса) постоянно пропорционально; а эллипс — плоская компактная неособая алгебраическая кривая второй степени.
Систематическое описание свойств эллипсов см. В [Be], стр. 245–247 и гл. 17 и [Co].
Список литературы
Как процитировать эту запись:
Эллипс. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Ellipse&oldid=25305
тригонометрия — каноническая в параметрическую, уравнение эллипса
К какому типу «хорошо» вы стремитесь здесь — обычно «хорошо» использовать хитрые шаги, чтобы найти ответ, если только вы можете доказать, что он правильный, когда вы знаете, что это такое.
Математика состоит из двух частей: (1) вам нужно выяснить, что доказывать, и (2) вам нужно это доказать. Последняя часть — точная наука; в нем есть четкие и строгие правила относительно того, что разрешено, а что нет, и именно он обычно привлекает внимание прессы. Однако не менее важно первое. Иногда это проще, а иногда сложнее, но правила у него совсем другие, а именно: все идет! Да, действительно. Независимо от того, как у вас возникла идея доказать то-то и то-то, единственное, что имеет значение, — это то, что вы можете выполнить на этапе 2 (и то, что вы доказали, затем окажется полезным в контексте той проблемы, с которой вы столкнулись изначально но это другое дело).
Иногда процесс, с помощью которого вы приходите к тому, что нужно доказать, настолько прост, что вы можете прочитать доказательство прямо с него, практически без усилий. Учителям нравятся эти кейсы (и иногда создается впечатление, что они все есть), потому что они делают вещи красивыми и упорядоченными, и их легко оценивать. Но в реальной математике совсем не стыдно, использовать менее прямые методы, чтобы найти ответ, который окажется правильным позже. Неважно, разделили ли вы на ноль, чтобы найти его, или если ангел явился во сне и сказал вам — если вы можете предоставить доказательство того, что ответ верен в конце дня, то это «правильно», как бы вы это ни нашли.2} = 1 $$ и тогда остается простой вопрос строгого, но скучного переписывания, чтобы доказать, что это действительно тождество. (Этот вид проверки обычно подразумевается под «осмотром»). Теперь мы доказали, что изображение вашей кривой — это подмножество и набора решений.
Затем остается доказать, что множество решений является подмножеством изображения кривой. Для этого мы предполагаем, что некоторые заданные $ x $ и $ y $ удовлетворяют уравнению, а затем стремимся доказать, что должно существовать такое $ \ theta $, что $ x = a \ cos \ theta $ и $ y = b \ sin \ theta $.как нам это сделать? Что ж, в это время ночи лучшее, о чем я могу думать, — это ужасно запутанный анализ различных комбинаций знаков для $ x $ и $ y $, с особыми случаями, если один из них равен 0, а в противном случае — что-то вроде $ Где-то появляется \ arctan (\ frac {ay} {bx}) $ — возможно, это лемма, доказывающая, что $ (tx, ty) $ может быть решением только в том случае, если $ | t | = 1 $ будет необходимо по пути. Если бы со временем получилось, но это было бы некрасиво. Я даже не собираюсь сейчас вдаваться в подробности.
Возможно, вам удастся найти более приятный аргумент. Возможно, нет. Возможно, ваша аудитория будет довольна более сложным аргументом, чем тот, который я себе представляю.
Уравнение эллипса в стандартной форме и его связь с графиком эллипса.
Прежде чем рассматривать приведенное ниже уравнение эллиспа, вы должны знать несколько терминов.
Больше примеровЕще примеры осей, вершин и совпадений
Пример большой горизонтальной оси
Пример графика и уравнения эллипса на
- Большая ось этого эллипса горизонтальна и представляет собой красный сегмент от (-2, 0) до (2, 0).
- Центр этого эллипса — начало координат, поскольку (0, 0) — середина большой оси.
- Значение a = 2 и b = 1.
Пример большой вертикальной оси
Пример графика и уравнения эллипса на:
- Большая ось этого эллипса вертикальна и представляет собой красный сегмент от (2, 0) до (-2, 0).
- Центр этого эллипса — начало координат, поскольку (0, 0) — середина большой оси.
- Значение a = 2 и b = 1.
Проблема 1
Можете ли вы определить значения a и b для уравнения эллипса, изображенного на графике ниже?
Покажи ответПроблема 2
Можете ли вы определить значения a и b для уравнения эллипса, изображенного ниже?
Покажи ответПроблема 3
Каковы значения a и b для уравнения стандартной формы эллипса на графике?
Покажи ответ Больше проблемПодробнее Попрактикуйтесь в написании уравнения из графика
График эллипса из уравнения
Приведенные ниже задачи обеспечивают практическое создание графика эллипса из уравнения эллипса.2 = 36 $
Покажи ответВот изображение графика эллипса.
Приведенные и канонические уравнения коник
Мы узнаем, как найти прямоугольную декартову систему отсчета, в которой уравнение аналитического конуса будет как можно более простым.
Мы собираемся решить эту проблему с помощью последовательных сокращений или изменений координат так, чтобы после каждого из них формулировалось уравнение коники, упрощающее некоторые аспекты уравнения на предыдущем шаге.2+ \ mu $
где $$ \ lambda_1, \ lambda_2 $$ и $$ e $$ — действительные числа, отличные от нуля, а $$ \ mu $$ — произвольное действительное число. Назовем предыдущие выражения сокращенными формами.
По некоторым причинам (которые мы увидим далее) мы будем говорить, что они центрированного, параболического типа и параллельных прямых.
Редукция первая
Первым шагом будет вычисление связанной матрицы $$ A ‘$$ с учетом коники с уравнением $$ q (x, y) = 0 $$.2 + 2dx + 2ey + f = 0 $$$ Обратите внимание, что это уравнение имеет две ситуации, которые следует учитывать: $$ \ lambda_1 \ lambda_2 = 0 $$ и $$ \ lambda_1 \ lambda_2 \ neq 0 $$.
В первом случае существует собственное значение, равное нулю, а другое — нет (вспомним, что мы предполагали, что матрица $$ A $$ не является нулевой матрицей $$ 0 $$). Меняя при необходимости оси местами, мы можем предположить, что $$ \ lambda_1 \ neq 0 $$ и $$ \ lambda_2 = 0 $$.
Мы также можем предположить, что собственное значение положительно. На этом этапе мы можем различить два новых случая, если $$ e $$ равен нулю или отличен от нуля.2 (k> 0) $$$
Первая дает нам две параллельные прямые ($$ x = k $$ и $$ x = -k $$, $$ k $$ — это полупространство между двумя прямыми линиями), а вторая дает две совпадающие прямые. линий. Мы скажем, что третий дает нам две совмещенные параллельные прямые.
Вкратце, эта процедура дает нам эффективный алгоритм перехода от общего уравнения коники к каноническому уравнению. Для его получения используем следующие шаги:
Рассматривая уравнение коники, вычисляем ее основную матрицу $$ A ‘$$ и вычисляем собственные значения для диагонализации $$ A’ $$.2-4y- \ frac {19} {2} = 0 $$$ Поскольку у нас есть только квадратичный член для $$ x $$, это парабола.
Как получить каноническое уравнение эллипса для точки N?
В результате серии операций с окружностью с известными координатами, а именно поворота его оси на углы a, b вокруг осей Z, Y соответственно, и последующего проецирования на плоскость OXZ на углы c, d, были выполнены получился эллипс.
Известно: координаты центра эллипса,
его смещение относительно нулевой точки системы координат
координаты необходимое количество точек для вывода уравнения эллипса (закрашена кружком до начала всех преобразований).Неизвестно:
длина стержня;
угол поворота стержня;Должно:
иметь возможность проверить принадлежность произвольной точке эллипса, что требует вывода уравнения.
для вычисления площади эллипса.Расчетный алгоритм реализован на JAVA, валидация расчетов через рисование IN Kompas.
Изучал интернет на предмет возможных решений, но слишком плохо разбираюсь в деле, почти ничего.
См. Вариант два: эллипс контрольной точки, контрольная точка обратного преобразования и проверка его принадлежности к кругу, но он не позволит вам вычислить площадь эллипса.
Второй вариант: представление эллипса в виде кривой второго порядка и матрицы решений с 5 неизвестными, однако, не очень хорошо в программировании, как в математике, для определения алгоритма. Взял библиотеку JAMA, но так как невозможно задать условия для требуемых значений в матрице решений, просто все слагаемые в уравнении конической кривой делают с нулями, что и есть матрица решений.
Пожалуйста, предложите кратчайший способ решения проблемы или, если применимо, такой общий код.На спроецированном эллипсе синие пересекающиеся прямые — это оси, построенные с помощью функций компаса. В общем задача состоит в том, чтобы понять, как он определяет радиус, зная центр эллипса и все 3 принадлежащие точке
Построение эллипса
Построение эллипса(примечания Р. Бигони)
1.Параметрические уравнения эллипса
Из канонического уравнения эллипса легко вывести выражения декартовы координаты точки P эллипса как функции угла α формируется вектором OP (где O — начало отсчета кадра) и ось абсцисс.
Фактически, если мы позволим а также возвести в квадрат обе стороны обоих уравнений, суммируя квадраты уравнений, мы получаем каноническое уравнение
Итак, у нас
, которые представляют собой параметрических уравнений эллипса .
2. Конструкция линейки и циркуля.
Параметрические уравнения x e y могут быть соответственно интерпретированы как абсцисса и ордината точек A и B , перехваченных лучом, начиная с O и образуя угол α относительно оси x на концентрические окружности с радиусами a и b .
Точка E на рисунке, имеющая ту же абсциссу, что и A , и та же ордината, что и B , представляет собой точку эллипса с полуосями a и b .
3. Площадь эллипса
Ординаты y E e y A точек E и А сот
, так что у нас
, то есть отношение ординат точки E эллипса с полуосями a и b и ордината точки A с той же абсциссой окружность с таким же центром и радиусом , а — это б / а .
Если, учитывая для простоты только точки с положительной ординатой, для каждого point E и A строим прямоугольники на одном основании dx и высоты y E e y A , бывшие прямоугольники имеют площадь b / a по сравнению с последними.
Следовательно, сумма всех первых прямоугольников равна b / a по сумме вторых.Если dx бесконечно малая, первая сумма равна площади половины эллипса, второй — площадь половины круга. В заключение, площадь половины эллипса составляет b / a относительно площади половины круг и, очевидно, площадь эллипса b / a относительно круга.
4.Площадь эллиптического сегмента
Прямая линия, параллельная оси Y, с уравнением ограничивает цифру EE’V (окрашена в синий цвет), которая называется эллиптической правой сегмент . Площадь ε этого рисунка равна b / a относительно площади η кругового сегмента AA’V .
Площадь η, в свою очередь, может быть получена вычитанием из площади σ кругового сектора AOA’V площадь τ треугольника AOA’
Площадь σ соответствует площади окружности, поскольку ее центральный угол AOA ‘ соответствует полному углу, то есть его половина α = AOV соответствует прямому углу.
Площадь τ составляет
, следовательно, площадь η составляет
, а площадь ε составляет
Чтобы выразить эту площадь как функцию h , заметим, что
следовательно
Пример.
Для эллипса γ с полуосями a = 4 и b = 3 площади эллиптические сегменты, полученные путем разрезания γ параллельно малой оси на расстоянии h = 2 от него, имеют размеры
5.Периметр эллипса
Мы можем показать, что периметр эллипса с большой полуосью a и эксцентриситетом e равен
Следующее приложение Javascript позволяет приблизить периметр эллипса.
Параметрическое уравнение эллипса
Параметрическое уравнение эллипса — Math Open Reference Эллипс можно определить как локус всех точек, удовлетворяющих уравнениямx = a cos t
где:
y = b sin t
x, y — координаты любой точки эллипса,
a, b — радиус по осям x и y соответственно ( * см. примечания к радиусам ниже)
t — параметр, который находится в диапазоне от 0 до 2π радиан.Это уравнение очень похоже на уравнение, используемое для определения круга, и большая часть обсуждения здесь опущена, чтобы избежать дублирования. См. «Параметрическое уравнение круга» как введение в эту тему.
Единственная разница между кругом и эллипсом состоит в том, что у круга один радиус, а у эллипса два:
- Один радиус измеряется по оси x и обычно называется a .
- Другой измеряется по оси Y и обычно называется b .
Эллипсы с центром в начале координат
Если центр эллипса находится в начале координат (0,0), уравнения имеют вид
где
a — радиус по оси x ( * См. примечания к радиусам ниже)
b — радиус по оси yОбратите внимание, что уравнения на этой странице верны только для эллипсов, выровненных по координатной плоскости, то есть где основные и второстепенные оси параллельны системе координат.
В приведенном выше апплете перетащите одну из четырех оранжевых точек вокруг эллипса, чтобы изменить его размер, и обратите внимание, как уравнения меняются, чтобы соответствовать.
Эллипсы не отцентрированы в начале координат
Как и в случае с круговые уравнения, мы добавляем смещения к элементам x и y, чтобы перевести (или «переместить») эллипс в правильное место. Итак, полная форма уравнений
где, как и раньше,
a — радиус по оси x ( * См. примечание о радиусах ниже)
b — радиус по оси y(h, k) — координаты x и y центр эллипса.
В приведенном выше апплете перетащите оранжевую точку в центре, чтобы переместить эллипс, и обратите внимание, как уравнения меняются, чтобы соответствовать. Кроме того, отрегулируйте эллипс так, чтобы a и b были одинаковой длины, и убедитесь, что в этом случае это те же уравнения, что и для круга.
Круг — это просто определенный эллипс
В приведенном выше апплете перетащите правую оранжевую точку влево, пока два радиуса не станут одинаковыми. Это круг, и уравнения для него выглядят так же, как параметрические уравнения для окружности.Это демонстрирует, что круг — это просто частный случай эллипса.
Параметр t
Параметр t может немного запутать эллипсы. Для любого значения t будет соответствующая точка на эллипсе. Но t — это , а не угол, образуемый этой точкой в центре. Чтобы понять, почему это так, представьте эллипс как круг, растянутый или сжатый вдоль каждой оси. На рисунке ниже мы начинаем с круга и для простоты даем ему радиус, равный единице. («единичный круг»).
Угол t определяет точку на окружности, имеющую координаты
Радиус равен единице, поэтому он опускается. Синий эллипс определяется уравнениями Таким образом, чтобы получить соответствующую точку на эллипсе, координата x умножается на два, таким образом перемещая ее вправо. Это приводит к тому, что эллипс становится шире круга в два раза, тогда как высота остается той же, что определяется значениями 2 и 1 в уравнениях эллипса.Итак, как вы можете видеть, угол t не совпадает с углом, который точка на эллипсе образует в центре.
Однако, когда вы строите график эллипса с помощью параметрических уравнений, просто позвольте t находиться в диапазоне от 0 до 2π радиан, чтобы найти координаты (x, y) для каждого значения t.
Другие формы уравнения
Используя теорему Пифагора, чтобы найти точки на эллипсе, мы получаем более общую форму уравнения. Подробнее см. Общее уравнение эллипса.
Алгоритм рисования эллипсов
Эта форма определения эллипса очень полезна в компьютерных алгоритмах, которые рисуют круги и эллипсы.Фактически, все круги и эллипсы в апплетах на этом сайте нарисованы с использованием этой формы уравнения. Подробнее об этом см. Алгоритм рисования кругов.
Что попробовать
- В приведенном выше апплете нажмите «Сброс» и «Скрыть детали».
- Перетащите пять оранжевых точек, чтобы создать новый эллипс в новой центральной точке.
- Запишите уравнения эллипса в параметрической форме.
- Нажмите «показать подробности», чтобы проверить свои ответы.
Во многих учебниках два радиуса указаны как полу-большие и полу-малые оси.Напомним, что это самый длинный и самый короткий радиус эллипса соответственно. Проблема в том, что если эллипс высокий и узкий, их нужно перевернуть, поэтому вы получите две формы уравнений: одну для высоких тонких эллипсов, а другую — для коротких широких.
Независимо от того, как вы называете эти радиусы, помните, что уравнение x должно использовать радиус по оси x, а уравнение y должно использовать радиус по оси y:
Связанные темы
(C) Открытый справочник по математике, 2011 г.
.
Все права защищены.



 3.37, имеет вид
3.37, имеет вид