Кривые второго порядка. Эллипс: формулы и задачи
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
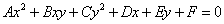 ,
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 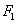 и
и
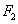 на рисунке ниже.
на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
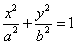 ,
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
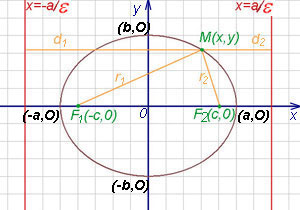
Прямая, проходящая через фокусы эллипса, является его осью симметрии.
Другой осью симметрии эллипса является прямая, проходящая через середину отрезка
 перпендикулярно этому отрезку. Точка
перпендикулярно этому отрезку. Точка
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b,
то уравнение эллипса принимает вид 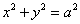 .
Это уравнение окружности радиуса a, а
окружность — частный случай эллипса. Эллипс можно получить из окружности
радиуса a, если сжать её в a/b
раз вдоль оси Oy.
.
Это уравнение окружности радиуса a, а
окружность — частный случай эллипса. Эллипс можно получить из окружности
радиуса a, если сжать её в a/b
раз вдоль оси Oy.
Пример 1.
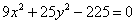 ,
эллипсом.
,
эллипсом.Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
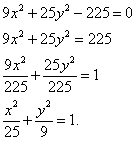
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5, меньшая полуось — это b = 4. Получаем каноническое уравнение эллипса:
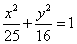 .
.Точки 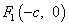 и
и
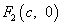 , обозначенные зелёным на большей оси, где
, обозначенные зелёным на большей оси, где
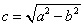 ,
,
называются фокусами.
Число
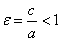
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
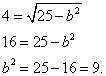
Результат — каноническое уравнение эллипса:
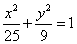 .
.
Пример 4. Составить каноническое уравнение эллипса,
если его бОльшая ось равна 26 и эксцентриситет 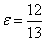 .
.
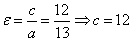 .
.
Вычисляем квадрат длины меньшей полуоси:
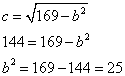
Составляем каноническое уравнение эллипса:
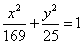
Пример 5. Определить фокусы эллипса, заданного
каноническим уравнением 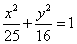 .
.
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
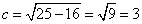
Получаем фокусы эллипса:
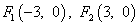
Если 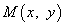 —
произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и
—
произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и
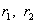 —
расстояния до этой точки от фокусов
—
расстояния до этой точки от фокусов 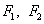 , то
формулы для расстояний — следующие:
, то
формулы для расстояний — следующие:
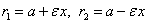 .
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
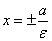 ,
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Пример 7. Дан эллипс 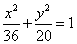 .
Составить уравнение его директрис.
.
Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется
найти эксцентриситет эллипса, т. е. 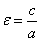 .
Все данные для этого есть. Вычисляем:
.
Все данные для этого есть. Вычисляем:
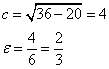 .
.
Получаем уравнение директрис эллипса:
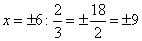
Пример 8. Составить каноническое уравнение
эллипса, если его фокусами являются точки 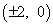 ,
а директрисами являются прямые
,
а директрисами являются прямые 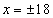 .
.
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
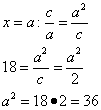 .
.
Теперь можем получить и квадрат длины меньшей полуоси:
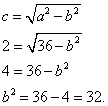
Уравнение эллипса готово:
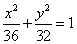
Пример 9. Проверить, находится ли точка 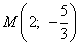 на эллипсе
на эллипсе 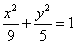 .
Если находится, найти расстояние от этой точки до фокусов эллипса.
.
Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и
y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем: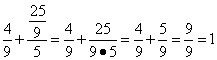 .
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
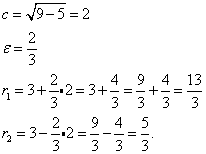
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
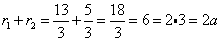 ,
,
так как из исходного уравнения эллипса 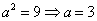
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.

Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
Эллипс. Формулы, признаки и свойства эллипсa
F1 и F2 — фокусы эллипсa
Оси эллипсa.А1А2 = 2a — большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2b — малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a — большая полуось эллипса
b — малая полуось эллипса
O — центр эллипса (точка пересечения большей и малой осей эллипса)
Вершины эллипсa A1, A2, B1, B2 — точки пересечения эллипсa с малой и большой осями эллипсa
Диаметр эллипсa — отрезок, соединяющий две точки эллипса и проходящий через его центр.
Фокальное расстояние c — половина длины отрезка, соединяющего фокусы эллипсa.
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 e e = 0, для параболы e = 1, для гиперболы e > 1.Фокальные радиусы эллипсa r1, r2 — расстояния от точки на эллипсе до фокусов.
Радиус эллипсa R — отрезок, соединяющий центр эллипсa О с точкой на эллипсе.| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 — e2cos2φ |
где e — эксцентриситет эллипсa, φ — угол между радиусом и большой осью A1A2. Фокальный параметр эллипсa p — отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси: Коэффициент сжатия эллипсa (эллиптичность) k — отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k k = 1:
k = √1 — e2
где e — эксцентриситет. Сжатие эллипсa (1 — k ) — величина, которая равная разности между единицей и эллиптичностью:
Директрисы эллипсa — две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии ae от центра эллипса. Расстояние от фокуса до директрисы равно pe.
Эллипс
Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\label{ref1}
$$
при условии \(a \geq b > 0\).
Из уравнения \eqref{ref1} следует, что для всех точек эллипса \(|x| \leq a\) и \(|y| \leq b\). Значит, эллипс лежит в прямоугольнике со сторонами \(2a\) и \(2b\).
Точки пересечения эллипса с осями канонической системы координат, имеющие координаты \((a, 0)\), \((-a, 0)\), \((0, b)\) и \((0, -b)\), называются вершинами эллипса. Числа \(a\) и \(b\) называются соответственно большой и малой полуосями эллипса.
 Рис. 8.1. Эллипс
Рис. 8.1. ЭллипсВ каноническое уравнение входят только квадраты координат. Поэтому, если координаты \((x, y)\) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты \((-x, y)\), \((x, -y)\) и \((-x, -y)\) точек \(M_{1}\), \(M_{2}\) и \(M_{3}\) (рис. 8.1). Следовательно, справедливо следующее утверждение.
Утверждение 1.
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса \(a\) с центром в центре эллипса: \(x^{2}+y^{2}=a^{2}\). При каждом \(x\) таком, что \(|x| < a\), найдутся две точки эллипса с ординатами \(\pm b \sqrt{1-x^{2}/a^{2}}\) и две точки окружности с ординатами \(\pm a \sqrt{1-x^{2}/a^{2}}\). Пусть точке эллипса соответствует точка окружности с ординатой того же знака. Тогда отношение ординат соответствующих точек равно \(b/a\). Итак, эллипс получается из окружности таким сжатием ее к оси абсцисс, при котором ординаты всех точек уменьшаются в одном и том же отношении \(b/a\) (рис. 8.2).
 Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении \(b/a\).
Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении \(b/a\).Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Определение.
Пусть по определению
$$
c^{2}=a^{2}-b^{2}\label{ref2}
$$
и \(c \geq 0\).
Фокусами называются точки \(F_{1}\) и \(F_{2}\) с координатами \((c, 0)\) и \((-c, 0)\) в канонической системе координат (рис. 8.3).
 Рис. 8.3. Фокусы эллипса.
Рис. 8.3. Фокусы эллипса.Для окружности \(c=0\), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Определение.
Отношение
$$
\varepsilon=\frac{c}{a}\label{ref3}
$$
называется эксцентриситетом эллипса.
Отметим, что \(\varepsilon < 1\).
Утверждение 2.
Расстояние от произвольной точки \(M(x, y)\), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы \(x\):
$$
r_{1}=|F_{1}M|=a-\varepsilon x,\ r_{2}=|F_{2}M|=a+\varepsilon x.\label{ref4}
$$
Доказательство.
Очевидно, что \(r_{1}^{2}=(x-c)^{2}+y^{2}\). Подставим сюда выражение для \(y^{2}\), найденное из уравнения эллипса. Мы получим
$$
r_{1}^{2}=x^{2}-2cx+c^{2}+b^{2}-\frac{b^{2}x^{2}}{a^{2}}.\nonumber
$$
Учитывая равенство \eqref{ref2}, это можно преобразовать к виду
$$
r_{1}^{2}=a^{2}-2cx+\frac{c^{2}x^{2}}{a^{2}}=(a-\varepsilon x)^{2}.\nonumber
$$
Так как \(x \leq a\) и \(\varepsilon < 1\), отсюда следует, что справедливо первое из равенств \eqref{ref4}: \(r_{1}=a-\varepsilon x\). Второе равенство доказывается аналогично.
Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса \(2a\).
Доказательство.
Необходимость. Если мы сложим равенства \eqref{ref4} почленно, то увидим, что
$$
r_{1}+r_{2}=2a.\label{ref5}
$$
Достаточность. Пусть для точки \(M(x, y)\) выполнено условие \eqref{ref5}, то есть
$$
\sqrt{(x-c)^{2}+y^{2}}=2a-\sqrt{(x+c)^{2}+y^{2}}.\nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^{2}=a\sqrt{(x+c)^{2}+y^{2}}.\label{ref6}
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение \eqref{ref2}. Мы придем к \(b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}\), равносильному уравнению эллипса \eqref{ref1}.
С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе координат (рис. 8.4)
$$
x=\frac{a}{\varepsilon},\\ x=-\frac{a}{\varepsilon}.\label{ref7}
$$
Директрису и фокус, которые лежат по одну сторону от центра, будем считать соответствующими друг другу.
 Рис. 8.4. Фокусы и директрисы эллипса.
Рис. 8.4. Фокусы и директрисы эллипса.Утверждение 4.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса \(\varepsilon\).
Доказательство.
Докажем это предложение для фокуса \(F_{2}(-c, 0)\). Пусть \(M(x, y)\) — произвольная точка эллипса. Расстояние от \(M\) до директрисы с уравнением \(x=-a/\varepsilon\) по формуле (9) §3 гл. II равно
$$
d_{2}=|x+\frac{a}{\varepsilon}|=\frac{1}{\varepsilon}(\varepsilon x+a).\nonumber
$$
Из формулы \eqref{ref4} мы видим теперь, что \(r_{2}/d_{2}=\varepsilon\).
Обратно, пусть для какой-то точки плоскости \(r_{2}/d_{2}=\varepsilon\), то есть
$$
\sqrt{(x+c)^{2}+y^{2}}=\varepsilon \left(x+\frac{a}{\varepsilon}\right).\nonumber
$$
Так как \(\varepsilon=c/a\), это равенство легко приводится к виду \eqref{ref6}, из которого, как мы знаем, следует уравнение эллипса.
Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть \(M_{0}(x_{0}, y_{0})\) — точка на эллипсе и \(y_{0} \neq 0\). Через \(M_{0}\) проходит график некоторой функции \(y=f(x)\), который целиком лежит на эллипсе. (Для \(y_{0} > 0\) это график \(f_{1}(x)=b\sqrt{1-x^{2}/a^{2}}\), для \(y_{0} < 0\) — график \(f_{2}(x)=-b\sqrt{1-x^{2}/a^{2}}\). Не уточняя знака \(y_{0}\), обозначим подходящую функцию \(f(x)\).) Для нее выполнено тождество
$$
\frac{x^{2}}{a^{2}}+\frac{(f(x))^{2}}{b^{2}}=1.\nonumber
$$
Дифференцируем его по \(x\):
$$
\frac{2x}{a^{2}}+\frac{2ff’}{b^{2}}=0.\nonumber
$$
Подставляя \(x=x_{0}\) и \(f(x_{0}=y_{0})\), находим производную от \(f\) в точке \(x_{0}\), равную угловому коэффициенту касательной:
$$
f'(x_{0})=\frac{b^{2}}{a^{2}} \frac{x_{0}}{y_{0}}.\nonumber
$$
Теперь мы можем написать уравнение касательной:
$$
y-y_{0}=-\frac{b^{2}}{a^{2}} \frac{x_{0}}{y_{0}}(x-x_{0}).\nonumber
$$
Упрощая это уравнение, учтем, что \(b^{2}x_{0}^{2}+a^{2}y_{0}^{2}=a^{2}b^{2}\), так как \(M_{0}\) лежит на эллипсе. Результату можно придать вид
$$
\frac{xx_{0}}{a^{2}}+\frac{yy_{0}}{b^{2}}=1.\label{ref8}
$$
При выводе уравнения \eqref{ref8} мы исключили вершины эллипса \((a, 0)\) и \((-a, 0)\), положив \(y_{0} \neq 0\). Для этих точек оно превращается, соответственно, в уравнения \(x=a\) и \(x=-a\). Эти уравнения определяют касательные в вершинах. Проверить это можно, заметив, что в вершинах ж как функция от у достигает экстремума. Предоставим читателю проделать это подробно и показать тем самым, что уравнение \eqref{ref8} определяет касательную для любой точки \(M_{0}(x_{0}, y_{0})\) на эллипсе.
Утверждение 5.
Касательная к эллипсу в точке \(M_{0}(x_{0}, y_{0})\) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Доказательство.
Нам надо сравнить углы \(\varphi_{1}\) и \(\varphi_{2}\), составленные векторами \(\overrightarrow{F_{1}M_{0}}\) и \(\overrightarrow{F_{2}M_{0}}\) с вектором \(\boldsymbol{n}\), перпендикулярным касательной (рис. 8.5). Из уравнения \eqref{ref8} находим, что \(\boldsymbol{n}(x_{0}/a^{2}, y_{0}/b^{2})\), и потому
$$
(\overrightarrow{F_{1}M_{0}}, \boldsymbol{n})=\frac{x_{0}}{a^{2}}(x_{0}-c)+\frac{y_{0}}{b^{2}}y_{0}=1-\frac{x_{0}c}{a^{2}}=\frac{a-\varepsilon x_{0}}{a}.\nonumber
$$
Используя \eqref{ref4}, мы получаем отсюда, что \(\cos \varphi_{1}=1/(a|\boldsymbol{n}|)\). Аналогично находим \(\cos \varphi_{2}=1/(a|\boldsymbol{n}|)\). Утверждение доказано.
 Рис. 8.5.
Рис. 8.5. Эллипсом называется
множество точек плоскости, сумма
расстояний которых до двух данных точек 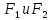 ,
называемых фокусами, есть величина
постоянная
,
называемых фокусами, есть величина
постоянная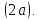 Расстояние
между фокусами эллипса
Расстояние
между фокусами эллипса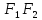 называется
фокусным расстоянием и обозначается
называется
фокусным расстоянием и обозначается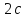
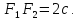
Общее уравнение эллипса
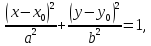
где 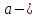 большая полуось,
большая полуось,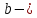 малая
полуось,
малая
полуось,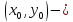 координаты
центра эллипса.
координаты
центра эллипса.
Если
центр эллипса находится в начале
координат и фокусы эллипса находятся
на оси 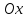 на
равных расстояниях от начала координат,
то уравнение примет вид
на
равных расстояниях от начала координат,
то уравнение примет вид
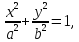
причем, 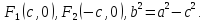
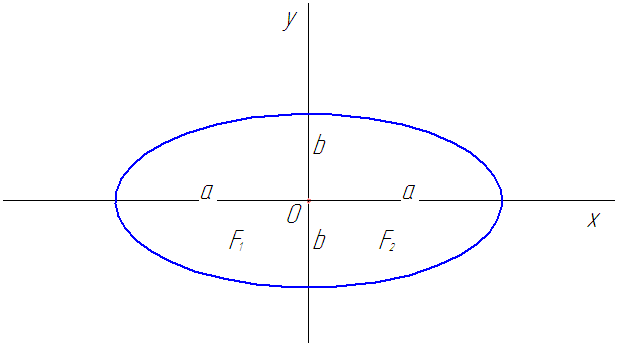
Рис. 13
Эллипс с центром в начале координат
Отношение
фокусного расстояния к большой оси,
т.е. 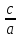 называетсяэксцентриситетом
(мера сжатия)
называетсяэксцентриситетом
(мера сжатия) 
Эксцентриситет 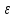 и
коэффициент сжатия эллипса
и
коэффициент сжатия эллипса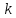 связаны
соотношением
связаны
соотношением
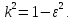
Директрисы эллипса.
Пусть дан эллипс
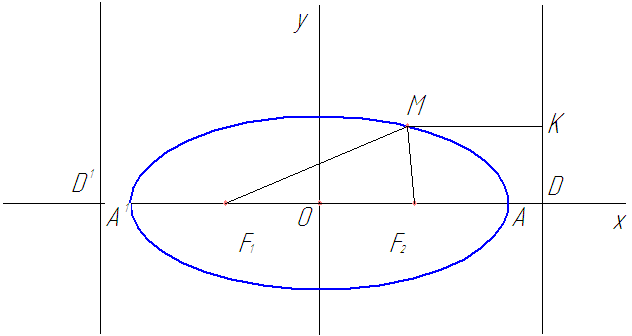
Рис. 14
Дирректрисы эллипса
с
большой осью 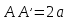 и эксцентриситетом
и эксцентриситетом
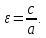
Отложим
от центра 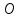 эллипса
на его большой оси отрезки
эллипса
на его большой оси отрезки
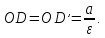
Прямые,
проходящие через точки 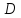 и
и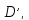 параллельно
малой оси
параллельно
малой оси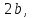 называютсядиректрисами
эллипса.
называютсядиректрисами
эллипса.
Для
любой точки 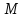 эллипса
отношение ее расстояния до фокуса к
расстоянию до соответствующей директрисы
равно эксцентриситету
эллипса
отношение ее расстояния до фокуса к
расстоянию до соответствующей директрисы
равно эксцентриситету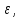 т.е.
т.е.
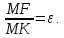
Рассмотрим пример. На эллипсе
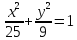
найти точку, разность фокальных радиус-векторов которой равна 6,4.
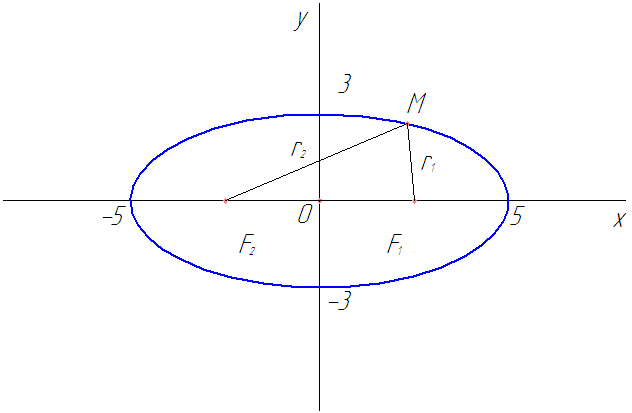
Рис. 15
Согласно
уравнению эллипса 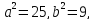 определим расстояние от цента эллипса
до фокусов
определим расстояние от цента эллипса
до фокусов
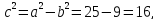
тогда
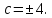
Кроме
того, 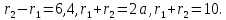
Составим систему и решим ее
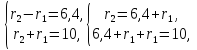
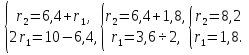
Получим
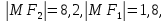
так как
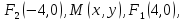
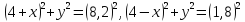
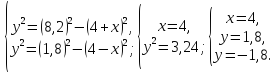
Вывод:
таких точек может быть две 
8.3. Каноническое уравнение гиперболы и ее характеристики
Гиперболой называется
множество всех точек плоскости, абсолютная
величина разности расстояний которых
до двух данных точек, называемых фокусами,
есть величина постоянная 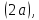 причем
эта постоянная меньше расстояния между
фокусами. Если поместить фокусы гиперболы
в точках
причем
эта постоянная меньше расстояния между
фокусами. Если поместить фокусы гиперболы
в точках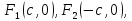 то
получается каноническое уравнение
гиперболы
то
получается каноническое уравнение
гиперболы
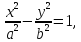
где 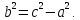 Вершинами гиперболы являются точки
Вершинами гиперболы являются точки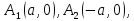 тогда
тогда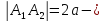 действительная
ось гиперболы,
действительная
ось гиперболы,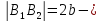 мнимая
ось гиперболы.
мнимая
ось гиперболы.
Рис. 16
Гипербола
Гипербола
имеет две асимптоты 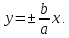
Эксцентриситет
гиперболы 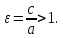
Фокальные радиус-векторы левой ветви гиперболы:
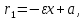
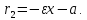
Фокальные радиус-векторы правой ветви гиперболы:
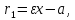
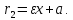
Рассмотрим пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллипса
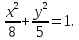
Найдем координаты фокусов, в которых лежат вершины гиперболы
следовательно
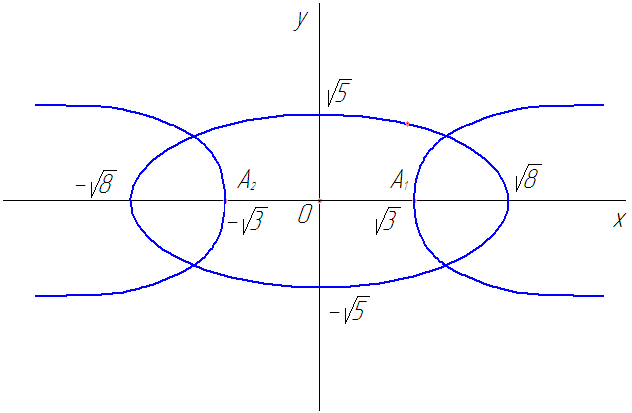
Рис. 17
Вершины гиперболы лежат в фокусах эллипса, следовательно
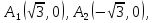
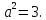
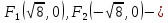 фокусы
гиперболы, т.е.
фокусы
гиперболы, т.е. 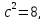
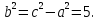
Тогда
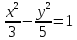
— уравнение гиперболы.
8.4. Каноническое уравнение параболы и ее характеристики
Парабола
– это множество
всех точек плоскости, равноудаленных
от данной точки, называемой фокусом, и
данной прямой, называемой директрисой.
Если директрисой параболы является
прямая 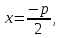 а
фокусом является точка
а
фокусом является точка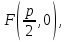 то
уравнение параболы имеет вид
то
уравнение параболы имеет вид
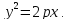
Парабола
симметрична относительно оси абсцисс 
Рис. 18
Парабола
Рассмотрим
пример. Составить
простейшее уравнение параболы, если
известно, что ее фокус находится в точке
пересечения прямой 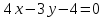 и
осью
и
осью
В
точке пересечения с осью  координата
координата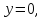 тогда
тогда
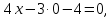
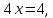
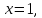
следовательно, 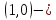 фокус
параболы.
фокус
параболы.
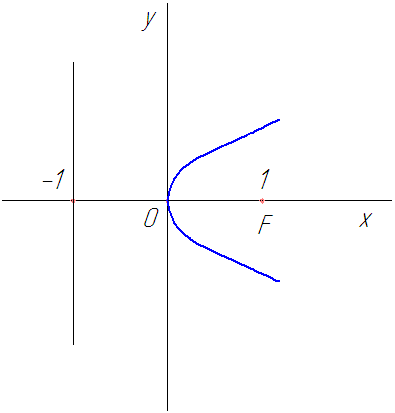
Рис. 19
Парабола
Парабола
симметрична 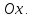 Так
как
Так
как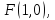
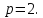
Тогда 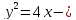 искомое
уравнение параболы.
искомое
уравнение параболы.
Эллипс | matematicus.ru
Эллипс – геометрическое место точек M(x;y), сумма расстояний которых до двух данных точек F1F2 имеет одно и то же значение 2a:
F1M+F2M=2a
точки F1 и F2 – называются фокусами эллипса;
расстояние F1F2 – фокусное расстояние и равно F1F2=2с;
a — большая полуось;
b — малая полуось;
c — фокальный радиус, то есть полу расстояние между фокусами;
p — фокальный параметр;
Rmin – минимальное расстояние от фокуса до точки на эллипсе;
Rmax — максимальное расстояние от фокуса до точки на эллипсе;
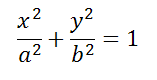
где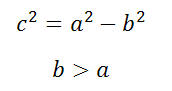
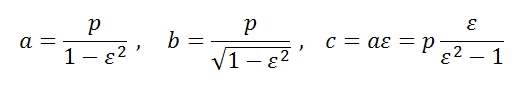
Пример 1
Длина малой оси эллипса 134 м. Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Решение
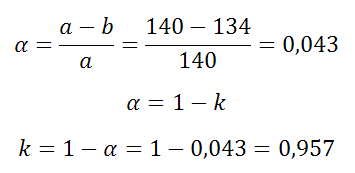
Пример 2
Постройте кривую 4x2+9y2=36. Найдите фокусы, фокальный параметр и эксцентриситет.
Решение
Делим обе части на 36 и получаем каноническое уравнение эллипса
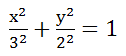
a=3, b=2
Делаем чертёж

c2=a2-b2=32-22=9-4=5
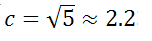
Отсюда находим Фокусы F1(-2,2;0) F2(2,2;0)
Фокальный параметр находим следующим образом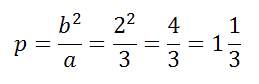
Эксцентриситет эллипса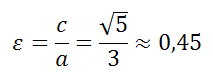
Пример 3
Постройте кривую 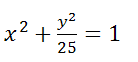 . Найдите фокусы и эксцентриситет.
. Найдите фокусы и эксцентриситет.
Решение
Уравнение запишем в виде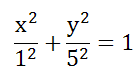
a=1, b=5
Это уравнение не является каноническим уравнением эллипса, так как b>a, а должно быть b<а. А если переобозначить оси, то есть x=x’ , y=y’, тогда уравнение примет вид:
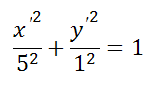
И тогда a=5, b=1
Делаем чертёж

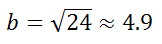
c2=a2 − b2=52 −12=25 − 1=24
Следовательно, фокусы в системе координат (x’;y’) имеют координаты (-4,9;0) и (4,9;0), а в системе (x;y) координаты 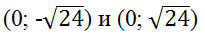
Эксцентриситет эллипса равен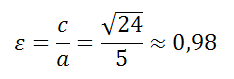
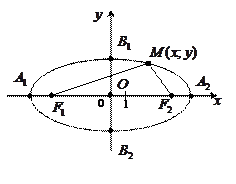
Определение: эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух данных точек 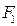 и
и 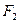 (называемых фокусами) есть величина постоянная, равная
(называемых фокусами) есть величина постоянная, равная 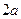 .
.
Чертеж эллипса: выберем прямоугольную систему координат так, чтобы ось Ox проходила через фокусы 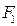 и
и 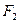 (
( 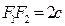 ), а начало координат находилось в середине
), а начало координат находилось в середине 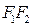 . Фокусы будут иметь координаты
. Фокусы будут иметь координаты 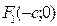 и
и 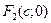 . Пусть
. Пусть 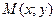 – произвольная точка эллипса. По определению эллипса
– произвольная точка эллипса. По определению эллипса 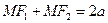 или по формуле расстояний:
или по формуле расстояний: 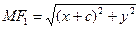 ,
, 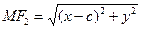 , т.е.
, т.е. 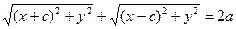 – это и есть уравнение эллипса.
– это и есть уравнение эллипса.
Канонический (простейший) вид уравнения эллипса:
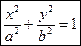 – каноническое уравнение эллипса.
– каноническое уравнение эллипса.
Заметим, что
1) 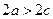 ;
;
2) 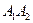 – большая ось эллипса,
– большая ось эллипса, 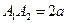 ;
;
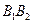 – малая ось эллипса,
– малая ось эллипса, 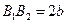 ;
;
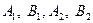 – вершины эллипса;
– вершины эллипса;
3) Эксцентриситет 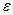 эллипса – отношение расстояния между фокусами к длине его большой оси, т.е.
эллипса – отношение расстояния между фокусами к длине его большой оси, т.е. 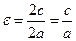 . Он характеризует степень сжатия эллипса: чем больше
. Он характеризует степень сжатия эллипса: чем больше 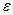 тем больше вытянут эллипс.
тем больше вытянут эллипс.
4) Величины 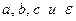 – параметры эллипса.
– параметры эллипса.
Уравнение эллипса, формулы и примеры
Определение и уравнение эллипса
ОПРЕДЕЛЕНИЕ Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух данных точек и есть величина постоянная. Точки и называются фокусами эллипса.Каноническое (или простейшее) уравнение эллипса с центром в начале координат
Здесь — длина большей полуоси эллипса, — длина малой полуоси эллипса. Фокальным расстоянием называется расстояние между фокусами рассматриваемого эллипса.
Примеры решения задач
ПРИМЕР 1| Задание | Эллипс задан своим каноническим уравнением . Найти длины его большой и малой осей. |
| Решение | Из заданного канонического уравнения эллипса можно сделать вывод, что
Тогда . Следовательно, искомые длины большой и малой осей соответственно
|
| Ответ |
Величина
Величины и эллипса связаны соотношением:
Эксцентриситетом эллипса называется величина
Для эллипса
ПРИМЕР 2| Задание | Составить каноническое уравнение эллипса, если его полуоси |
| Решение | Каноническое уравнение эллипса имеет вид:
Подставляя в него заданные значения полуосей, получим:
|
| Ответ |
Ellipse: стандартное уравнение
Эллипс — это коническое сечение, которое описывается как:ОПРЕДЕЛЕНИЕ ЭЛЛИПСА:
Множество всех точек (x, y) на плоскости, сумма расстояний которых от двух неподвижных точек, называемых фокусами, является постоянной.
На рисунке 1 показано изображение эллипса:
Таким образом, для всех (x, y), d 1 + d 2 = константа. Когда речь идет об эллипсе, используются следующие термины:
- Очаги — это две фиксированные точки, равноудаленные от центра эллипса.
- Вершины — это точки эллипса, которые попадают на линию, содержащую фокусы.
- Сегмент линии или хорды, соединяющий вершины — это , , большая ось, , .
- Серединой большой оси является , центр .
- Ось, перпендикулярная большой оси, является вспомогательной осью .
На рисунке 1 показан эллипс с большой горизонтальной осью.Однако эллипс может также иметь большую ось, которая является вертикальной, как показано на рисунке 2.
Стандартное уравнение эллипса:
СТАНДАРТНОЕ УРАВНЕНИЕ ЭЛЛИПСА:
➢ Координаты центра (h, k)
➢ Большая ось 2a
➢ Большая ось 2b
➢ 0
( х-ч ) 2 2 + ( у-к ) 2 б 2 = 1 большая ось горизонтальная
( х-ч ) 2 б 2 + ( у-к ) 2 2 = 1 большая ось вертикальная
Очаги лежат на большой оси, c единиц от центра, с c 2 = a 2 — b 2 .
Давайте использовать эти уравнения в некоторых примерах:
Пример 1: Найти стандартное уравнение эллипса, имеющего фокусы в (2, 1) и (-4, 1) и малую ось 10.
Шаг 1: Определите следующее: ➢ Координаты центра (ч, к). ➢ Расстояние от половины малой оси (б). ➢ Длина половины большой оси (а). ➢ Ориентация большой оси. | Центр: Так как фокусы находятся на равном расстоянии от центра эллипса, центр можно определить, найдя среднюю точку фокусов. ( ч, к знак равно 2+ ( -4 ) 2 , 1 + 1 2 знак равно — 2 2 , 2 2 знак равно -1,1 ) Длина б: Младшая ось задается как 10, что равно 2b. 2b = 10 → B = 5 Длина a: Для нахождения уравнения можно использовать c 2 = a 2 + b 2 , но необходимо определить значение c. Поскольку c — это расстояние от фокусов до центра, возьмите любой из фокусов и определите расстояние до центра. Тогда решите за. Очаги (2, 1): с = | 2- ( -1 ) | = | 3 | = 3 Очаги (-4, 1): с = | -4- ( -1 ) | = | −3 | = 3 с = 3 с 2 знак равно 2 — б 2 → а = с 2 + б 2 а = 3 2 + 5 2 → а = 34 Ориентация большой оси: Поскольку два очага падают на горизонтальную линию y = 1, большая ось является горизонтальной. |
Шаг 2. Подставьте значения h, k, a и b в уравнение для эллипса с большой горизонтальной осью. | Горизонтальное уравнение большой оси: ( х-ч ) 2 2 + ( у-к ) 2 б 2 = 1 Подстановочные значения: [ х- ( -1 )] 2 34 2 + ( Y-1 ) 2 5 2 = 1 Упрощать: ( х + 1 ) 2 34 2 + ( Y-1 ) 2 5 2 = 1 |
Пример 2: Найти ул
.Ellipse — Бесплатная математическая помощь
Аналитическая геометрия: (урок 2 из 3)
Эллипс
Определения:
1. Эллипс — это фигура состоящий из всех тех точек, для которых сумма их расстояний до двух Неподвижные точки (называемые фокусами) являются константой.
2. Эллипс — это фигура состоящий из всех точек на плоскости, чьи декартовы координаты удовлетворяют уравнение
$ \ frac {(x — h) ^ 2} {a ^ 2} + \ frac {(y — k) ^ 2} {b ^ 2} = 1 $
Где $ h $, $ k $, $ a $ и $ b $ — действительные числа, а $ a $ и $ b $ — положительные.2} {4} = 1 $.
Решение:
Видно, что центр эллипса равен $ (h, k) = (2, -1) $. Далее обратите внимание, что $ a = 3, b = 2 $.
Известно, что конечные точки большая ось ровно на 3 единицы слева и справа от центра, что ставит их в точки $ (- 1, -1) $ и $ (5, -1) $.
Также известно, что конечные точки малая ось ровно на 2 единицы выше и ниже центра, что ставит их в точках $ (2, 1) $ и $ (2, -3) $.2}, -1 \ right) = \ left (2 + \ sqrt {5}, -1 \ right) \ {Конец выровнен} $$
,Коники: эллипсы: введение
Коники: Эллипсы: Введение (страница 1 из 4) Разделы: Введение, Поиск Информация из уравнения, Нахождение уравнение из информации, Word Задачи  Эллипс, неформально, представляет собой овал или «сплющенный» круг.В «примитив» геометрические условия, эллипс — это фигура, которую вы можете нарисовать на песке следующий процесс: толкните две палки в песок. Возьми кусочек нанизывайте и формируйте петлю, достаточно большую, чтобы обойти две палочки и все еще немного расслабиться. Возьмите третью палку, зацепите ее за шнур петлю, потяните петлю туго, потянув палку от первых двух палки, и тянуть эту третью палку через песок на самом дальнем расстоянии петля позволит.Полученная форма, нарисованная на песке, представляет собой эллипс. Каждая из двух палочек, которые вы сначала нажали в песок « фокус » эллипса; оба вместе называются «фокусами» (FOH-сий). Если вы проведете линию на песке «через» эти две палки, из один конец эллипса к другому, это будет означать «майор» ось эллипса. Точки, где главная ось касается эллипса « вершин » эллипса.Точка на полпути между двумя палками — « центр » эллипса. Если вы проведете линию через этот центр, перпендикулярно большой оси и от одной стороны эллипса к другой, это отметит «второстепенную» ось. Точки, где второстепенная ось, касающаяся эллипса — это « ко-вершин «. Полуось, от центра к эллипсу, называется «большой полу» или «полу-малая» ось, в зависимости от того, какую ось вы берете половина от. Расстояние от центра до Фокус является фиксированным значением c . Расстояние от центра до вершины является фиксированным значением a . Значения и и с будет варьироваться от одного эллипса к другому, но они фиксированы для любого данного эллипс. Я продолжаю понимать смысл этих двух букв, неправильно произнося фраза «очаги за c » как «FOH-ciy foh SEE», чтобы напомнить мне, что c относится к фокусу.Тогда другое письмо ( ) для другого типа точки (вершины). Длина большой полуоси и длина всей большой оси составляет 2 a ,
и расстояние между очагами составляет 2 c .
Итак, теперь у нас есть отношения для и с ,
что заставляет задуматься: «Что случилось с б ?»
Три буквы связаны уравнением b 2 = a 2 c 2 или, альтернативно (в зависимости от вашей книги или инструктора), по уравнению b 2 + c 2 = а 2 . (для доказательства отношений требуются страницы и страницы алгебраических вычислений, так что просто поверьте мне, что уравнение правда. Также может быть болезненно показано, что б также длина малой оси, поэтому расстояние через эллипс в «более коротком» направлении составляет 2 b . Да, теорема Пифагора участвует в доказательстве этого материала. Да, эти те же буквы, что и в теореме Пифагора.Нет, это , а не так же, как теорема Пифагора. Да, это очень запутанно. принимать это, не забудьте запомнить отношения до следующего теста, и переместить на.)
Уравнение эллипса в форме коники всегда «= 1».Обратите внимание, что в обоих приведенных выше уравнениях ч всегда оставался с x а к всегда остался с у . Единственное, что изменилось между двумя уравнениями, было размещение 2 и b 2 . 2 всегда идет с переменной, ось которой параллельна более широкому направлению эллипса; б 2 всегда идет с переменной, ось которой параллельна более узкому направлению.Если посмотреть на уравнения с другой стороны, больший знаменатель всегда дает вам значение 2 , меньший знаменатель всегда дает значение b 2 , и два знаменателя вместе позволяют найти значение c 2 и ориентация эллипса. Эллипсы по своей природе не «идеально круглый »в техническом смысле, что круги являются круглыми.Мера суммы, на которую эллипс «раздавлен» от идеально круглый называется «эксцентриситетом» эллипса, и значение эксцентриситета эллипса обозначается как e = с / а . С очагов ближе к центру, чем вершины, то c < a , поэтому значение e всегда будет меньше 1. Если фокусы эллипса тянутся к центру, эллипс будет постепенно приближаться к тому, чтобы быть кругом.Продолжая этот процесс, если мы допустим с = 0 (таким образом, очаги на самом деле в центре), это будет соответствовать и = 0, причем эллипс действительно круг. Это говорит нам о том, что значение е для истинного (не кругового) эллипса всегда будет больше 0. Собирая это вместе, мы видим, что 0 < e <1 для любого эллипса. Когда ученые ссылаются на что-то (такое как Плутон), имея «эксцентричную» орбиту, они не означают, что орбита «странная»; они имеют в виду, что это «далеко не круговая».В случае Плутона, его орбита фактически пересекает внутри Нептуна время от времени. Чем больше значение и , тем более «раздавлен» эллипс. Физическое свойство эллипсов состоит в том, что звуковые или световые лучи, исходящие от одного фокуса, отражаются обратно к другой фокус. Это свойство можно использовать, например, в медицине. Пациент страдающих, скажем, желчными камнями можно поставить рядом с машиной, которая испускает ударные волны от пациента и в эллиптическую чашу. пациент тщательно расположен так, чтобы желчные камни были в одном фокусе эллипса, с заполненной водой подушкой между машиной и пациент с учетом эффективной передачи ударных волн. Машина излучает волны из другого фокуса эллипса; эти волны безобидно рассеиваются от излучателя в эллиптическую чашу, отскочить от чаши, и, наконец, сконцентрироваться на другом фокусе (внутри пациента). ударные волны достигают полной силы только в фокусе пациента, где они разбивают камень на достаточно мелкие кусочки, что сможет тело пациента избавиться от них самостоятельно. Пациент может пойти домой в тот же день, имея не требует инвазивной хирургии. Топ | 1 | 2 | 3 | 4 | Возвращение Индексировать Далее >>
|
Общее уравнение эллипса
Общее уравнение эллипса — математическая открытая ссылка Эллипс можно определить как годограф всех точек, которые удовлетворяют уравнению где:х, у — координаты любой точки на эллипсе,
a, b — радиус по осям x и y соответственно (* см. примечание по радиусам ниже)
Это уравнение очень похоже на то, которое используется для определения круга, и большая часть обсуждения здесь опущена, чтобы избежать дублирования.См. Основное уравнение круга и Общее уравнение круга как введение в эту тему.
Единственная разница между кругом и эллипсом состоит в том, что в эллипсе есть две меры радиуса, один по горизонтали вдоль оси x, а другой по вертикали вдоль оси y. Очевидно, что для круга оба они имеют одинаковое значение.

По соглашению радиус y обычно называется b , а радиус x называется a .
Эллипсы с центром в начале координат
Если эллипс центрирован на начале координат (его центр в 0,0), уравнение где
a — радиус вдоль оси x ( * См. примечание по радиусам ниже)
b — радиус вдоль оси y
Обратите внимание, что уравнения на этой странице верны только для эллипсов, которые выровнены с координатной плоскостью, то есть где большие и второстепенные оси параллельны системе координат.
В приведенном выше апплете перетащите одну из четырех оранжевых точек вокруг эллипса, чтобы изменить его размер, и обратите внимание на то, как уравнение изменяется в соответствии.
Эллипсы не центрированы в начале координат
Так же, как с
круговые уравнения,
мы вычитаем смещения из слагаемых x и y, чтобы перевести (или «переместить») эллипс обратно в начало координат.
Таким образом, полная форма уравнения где
a — радиус вдоль оси x
b — радиус вдоль оси y
h, k — координаты x, y центра эллипса.
В приведенном выше апплете перетащите оранжевую точку в центре, чтобы переместить эллипс, и обратите внимание, как уравнения изменяются в соответствии.
Деривация
Начнем с основного уравнения круга: Разделите обе стороны на r 2 : Замените радиус отдельным радиусом для осей x и y:
Круг — это просто особый эллипс
В приведенном выше апплете нажмите «сброс» и перетащите правую оранжевую точку влево, пока оба радиуса не станут одинаковыми.Это круг, и вы получите уравнение, которое выглядит как где r — какой бы радиус вы ни установили. Если умножить на r 2 , вы получите которое является общим уравнением круга. Это показывает, что круг — это особый случай эллипса.
Другие формы уравнения
Используя тригонометрию, чтобы найти точки на эллипсе, мы получаем другую форму уравнения. Подробнее см. Параметрическое уравнение эллипса
Что нужно попробовать
- В вышеприведенном апплете нажмите «сбросить» и «скрыть детали».
- Перетащите пять оранжевых точек, чтобы создать новый эллипс в новой центральной точке.
- Напишите уравнения эллипса в общем виде.
- Нажмите «показать подробности», чтобы проверить свои ответы.
* Примечание по радиусам
Во многих учебниках два радиуса указаны как полу-большие и полу-малые оси. Напомним, что это самые длинные и самые короткие радиусы эллипса соответственно. Проблема в том, что если эллипс высокий и узкий, их нужно повернуть вспять, поэтому вы получите две формы уравнений: одну для высоких тонких эллипсов и другую для коротких широких.
Независимо от того, что вы называете этими радиусами, помните, что термин x должен использовать радиус вдоль оси x, а термин y должен использовать радиус вдоль оси y: 
Похожие темы
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
