Уравнения с частными производными » СтудИзба
Васенин.
Уравнения с частными производными
Некоторые определения и понятия
Для функции u(x,y,…) независимых переменных x,y,… имеем соотношение вида
(1)
называется уравнением с частными производными. В дальнейшем мы всегда будем считать, что функция F непрерывна и имеет частные производные по всем своим аргументам в областях их изменения.
Функция u(x,y,…) называется решением дифференциального уравнения (1) если, будучи подставленной в это уравнение, она обращает его в тождество.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в него, например
— 1-го порядка, — 2-го порядка.
Уравнение (1) называется линейным, если оно линейно относительно функции u и всех ее частных производных. В то же время коэффициенты могут зависеть от независимых переменных x,y,…, например
Уравнение (1) называется квазилинейным если оно линейно относительно старших производных, в то время как его коэффициенты зависят от независимых переменных, искомой функции и производных более низкого порядка, например
В случае двух независимых переменных решение д. у. (1) можно геометрически рассматривать как поверхность в пространстве x,y,u.
Уравнение (1) превращается в обыкновенное дифференциальное уравнение, если независимая переменная одна.
Некоторые сведения о совокупности решений уравнений с частными производными
В отличие от обыкновенных д. у. в случае уравнения с частными производными элементы общего решения являются не константами, а функциями. При этом, выбирая указанные функции с помощью дополнительных условий, мы получим частное решение уравнения в частных производных.
Рассмотрим ряд примеров:
Пример 1. Для функции u=u(x,y) решим д. у. . Очевидно, что функция u не зависит от x, следовательно, u=f(y), где f(y) – произвольная функция y.
Пример 2. Для функции u=u(x,y)
, , ,
Интеграл от произвольной функции также является произвольной функцией. . Таким образом, общее решение уравнения второго порядка содержит две произвольные функции f(y) и φ(x).
Пример 3. Рассмотрим более сложный пример .
Для упрощения сделаем замену ξ=y—x, η=y+x.
подставим производные в новых переменных в д. у.
, следовательно, .
u не зависит от η, следовательно , f – произвольная функция.
Пример 4. Найдем общее решение уравнения колебаний струны
Разделим все уравнение на а2, которую считаем постоянной.
, обозначим at=y, .
Введем новые переменные ξ=x—y, η=x+y, и вычислим в этих переменных производные 1-го и 2-го порядков:
Найденные решения подставим в уравнение, получим .
При решении примера 2 мы получили, что решением такого д. у. является сумма двух произвольных функций . Возвращаясь к старым переменным найдем общее решение уравнения колебаний:
.
Пример 5. (якобиан равен нулю).
Следовательно, функции u и v зависимы и общее решение данного д. у. . Произвольные функции могут входить в общее решение достаточно сложным образом.
Пример 6. Рассмотрим простое д. у. , u=u(x,t). Общим решением будет , где φ – произвольная функция. Проверим, что данная функция есть общее решение:
, откуда .
, откуда .
Подставим все в д. у. , получили тождество.
Пример 7. Рассмотрим уравнение 4-го порядка
(бигармоническое уравнение). . Интегрируя по x получаем . Полученное выражение проинтегрируем по y: . Интегрируя еще раз по y получим .
Учитывая, что интегралы от произвольных функций также являются произвольными функциями, можно записать . Таким образом, общее решение уравнения 4-го порядка содержит 4 произвольные функции.
Пример 8. u=u(x,y,z), , .
Рассматривая приведенные примеры можно сделать предварительные выводы. Общее решение д. у. в частных производных зависит от произвольных функций. Число этих функций совпадает с порядком д. у., а число независимых переменных входящих в эти произвольные функции на единицу меньше, чем число независимых переменных входящих в д. у. Данный вывод подтверждается всеми существующими решениями уравнений в частных производных, однако существует достаточно общая теорема, которая фактически содержит это утверждение.
Теорема существования Коши-Ковалевской (для одного д. у.)
В этой теореме рассматривается д. у. порядка k, записанное в нормальном виде:
(1)
где x – некоторое выделенное направление в пространстве. Рассматривается решение в окрестности точки x=0. Предполагается, что в окрестности начальной точки: x=0, y1=0, …, yn=0.
Заданы дополнительные условия вида
(2)
Если функция f в уравнении (1) и функции φi(y1,y2,..,yn), входящие в начальные условия (2) аналитичны в окрестности начала координат, то задача Коши для уравнения (1) с условиями (2) имеет в этой окрестности единственное решение (без доказательства).
Из этой теоремы следует, что решение уравнения k-го порядка должно содержать k произвольных функций, которые можно определить из k начальных условий (2). Заметим, что решение состоит из произвольных функций, которые содержат число независимых переменных на единицу меньше, чем их число в уравнении.
Задача Коши состоит в том, чтобы построить решение уравнения (1), которое при x=0 принимает начальные значения (2).
studizba.com
Метод Фурье решения уравнений с частными производными
Метод Фурье (или метод разделения переменных), широко используемый при решении ряда задач математической физики, состоит в следующем. Искомая функция (решение), зависящая от нескольких переменных, ищется в виде произведения функций, каждая из которых зависит лишь от одной переменной. После подстановки этого произведения в исходное уравнение получается несколько обыкновенных дифференциальных уравнений, решения которых вместе с краевыми условиями исходной задачи позволяют найти искомое решение.
Сущность этого метода рассмотрим на следующем примере.
Пусть требуется найти решение одномерного волнового уравнения
, (5.31)
удовлетворяющее граничным условиям
, (5.32)
(для струны эти условия означают, что ее концы при и неподвижны (закреплены)), и начальным условиям
, . (5.33)
Ищем решение в виде произведения
,
.
Каждое отношение зависит здесь от своей переменной, а потому равенство возможно только в том случае, когда каждое из этих отношений равно постоянному числу. Полагая , , где постоянная (случай будет рассмотрен позднее), получаем два уравнения:
, (5.34)
. (5.35)
Оба уравнения являются линейными однородными уравнениями 2-го порядка с постоянными коэффициентами, характеристические уравнения которых при имеют комплексные корни. Общие решения этих уравнений будут:
, (5.36)
, (5.37)
где , , , – произвольные постоянные.
Постоянные и определяются из граничных условий (5.32). Так как не равна тождественно нулю (в противном случае ), функция должна удовлетворять условиям (5.32), т. е. должно быть , . Отсюда получаем систему уравнений:
Из первого уравнения находим . Тогда из второго уравнения следует
.
Так как (в противном случае было бы и ), имеем тригонометрическое уравнение , из которого получаем
( =1, 2, …) (5.38)
( =0 не берется, так как и в этом случае было бы и ). Числа называются собственными числами для уравнения (5.34) с граничными условиями (5.32), а соответствующие им решения
(5.39)
– собственными функциями.
Если же взять , то уравнение (5.34) будет иметь отличное от нуля общее решение
,
которое не может удовлетворять граничным условиям (5.32).
Для каждого собственного числа получается решение исходного волнового уравнения (5.31):
, (5.40)
которое удовлетворяет граничным условиям (5.32) (постоянная включена в и ). Так как заданное волновое уравнение линейное и однородное, то сумма решений
(5.41)
также будет его решением, удовлетворяющим граничным условиям (5.32). Это решение должно еще удовлетворять начальным условиям (5.33). Подставив в (5.41), получаем из первого начального условия
. (5.42)
Дифференцируя члены равенства (5.41) по и подставляя затем , получаем из второго начального условия
. (5.43)
Из этих равенств следует, что если числа являются коэффициентами ряда Фурье функции , т. е. если
,
а числа – коэффициентами Фурье функции , т. е. если
,
то ряд (5.41) представляет функцию , которая является искомым решением задачи (5.31) – (5.33).
В случае, когда исходное уравнение в частных производных является неоднородным, т. е. в характеризуемом этим уравнением физическом процессе имеются внешние силы и источники, предварительно находится система собственных функций соответствующего однородного уравнения, и решение ищется в виде ряда по этим собственным функциям с переменными коэффициентами.
infopedia.su
Использование производной для решения уравнений и неравенств
Использование производной для решения
уравнений и неравенств
Бирагова Л.Л.МБОУ лицей г.Владикавказ
При решении уравнения или неравенства часто бывает полезно доказать возрастание (убывание) на некотором промежутке функций, в него входящих. При этом часто пользуются производными.
Пример 1.
Решим уравнение
. (1)
Решение.
Рассмотрим функцию . Область существования этой функции есть промежуток 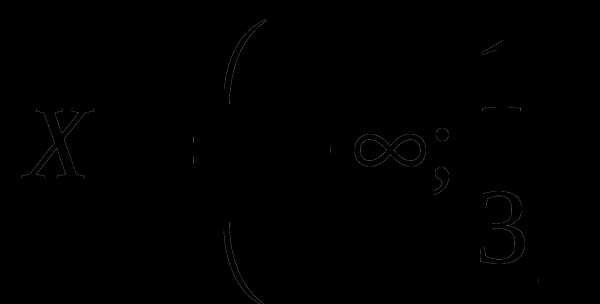 . Функция f
. Функция f
Следовательно, функция f(x) возрастает на промежутке Х, и так как она непрерывна на этом промежутке, то каждое свое значение она принимает ровно в одной точке. А это означает, что уравнение (1) имеет не более одного корня. Легко видеть, что число  удовлетворяет уравнению (1). Следовательно, уравнение (1) имеет единственный корень
удовлетворяет уравнению (1). Следовательно, уравнение (1) имеет единственный корень 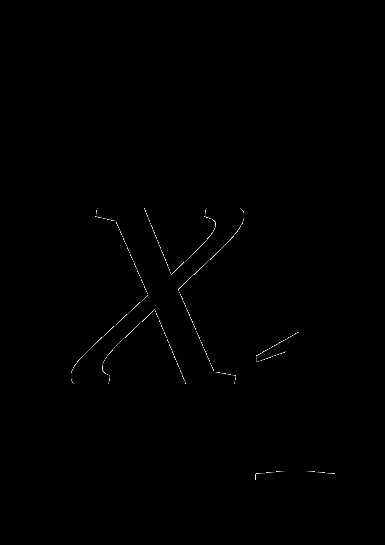 .
.
Ответ: -1.
Пример 2.
Решим неравенство
(2)
Решение.
Рассмотрим функцию f(x)= . Поскольку эта функция на интервале X= имеет производную , которая положительна на этом интервале, то функция f(x) возрастает на интервале Х. Так как функция f непрерывна на интервале Х, то каждое свое значение она принимает ровно в одной точке. Следовательно, уравнение f(x)=0 может иметь не более одного корня. Легко видеть, что число
имеет производную , которая положительна на этом интервале, то функция f(x) возрастает на интервале Х. Так как функция f непрерывна на интервале Х, то каждое свое значение она принимает ровно в одной точке. Следовательно, уравнение f(x)=0 может иметь не более одного корня. Легко видеть, что число  является корнем уравнения f(x)=0. Поскольку функция f(x) непрерывна и возрастает на интервале Х, то f(x)<0 при x<0 и f(x)>0 при x>0. Поэтому решениями неравенства (2) являются все х из промежутка
является корнем уравнения f(x)=0. Поскольку функция f(x) непрерывна и возрастает на интервале Х, то f(x)<0 при x<0 и f(x)>0 при x>0. Поэтому решениями неравенства (2) являются все х из промежутка  .
.
Ответ:  .
.
Пример 3.
Выяснить, сколько действительных корней имеет уравнение:
Решение.
Рассмотрим функцию . Она на интервале  имеет производную .
имеет производную .
Производная обращается в нуль точках: 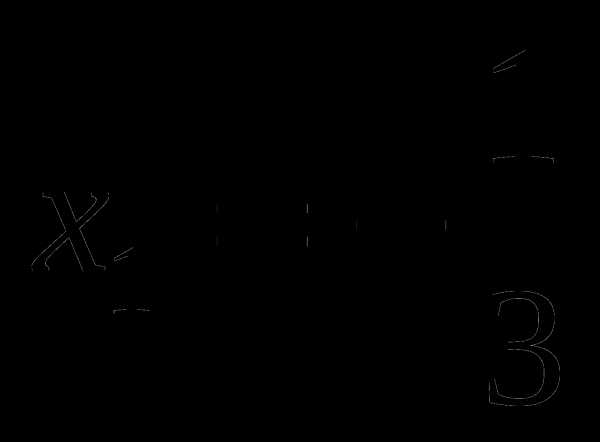 и
и  . Так как
. Так как  для любого х из интервалов
для любого х из интервалов 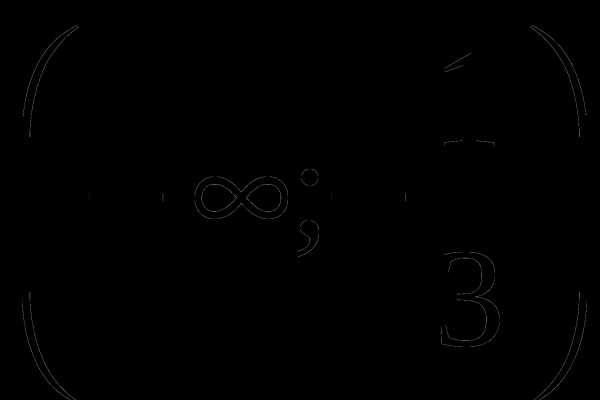 и
и 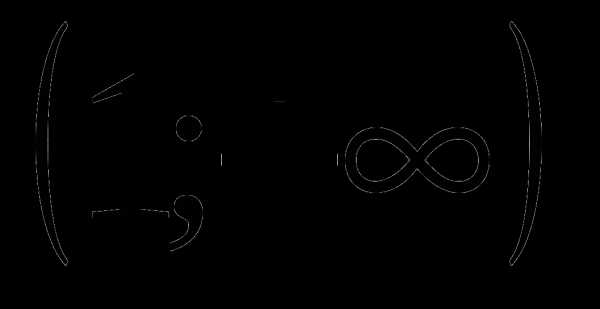 , то на каждом из промежутков
, то на каждом из промежутков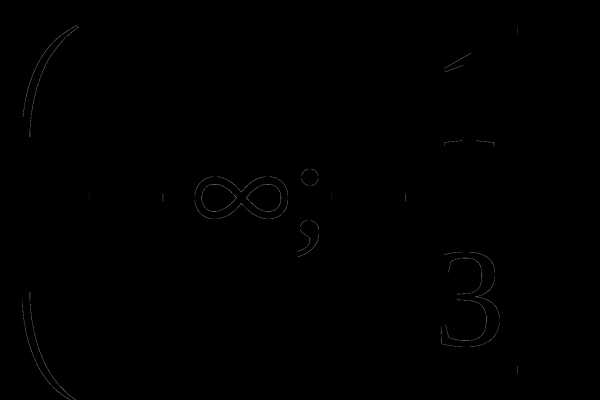 и
и 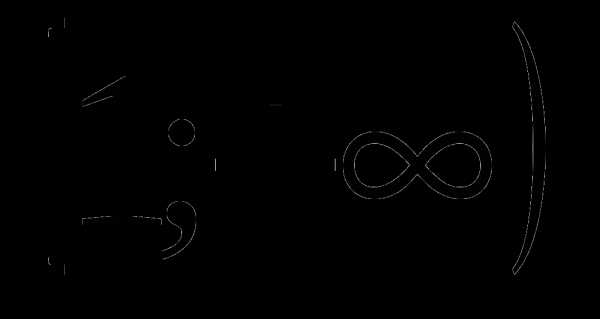 функция
функция  возрастает. Так как
возрастает. Так как 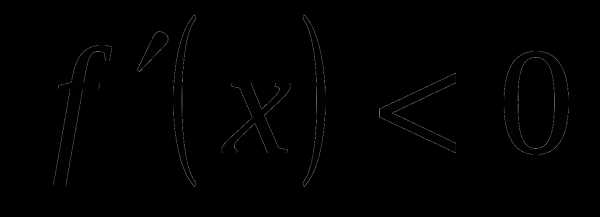
 , то на промежутке
, то на промежутке 
 функция
функция 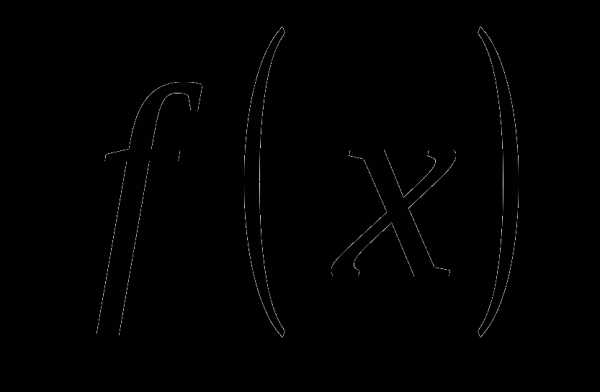 убывает.
убывает. Так как , , 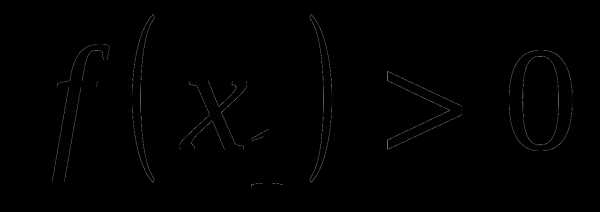 ,
, 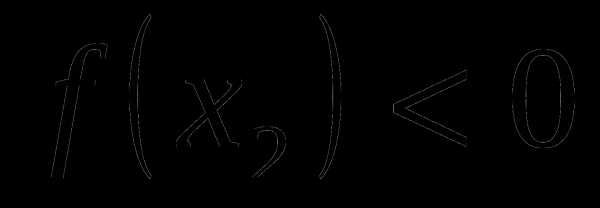 и функция
и функция 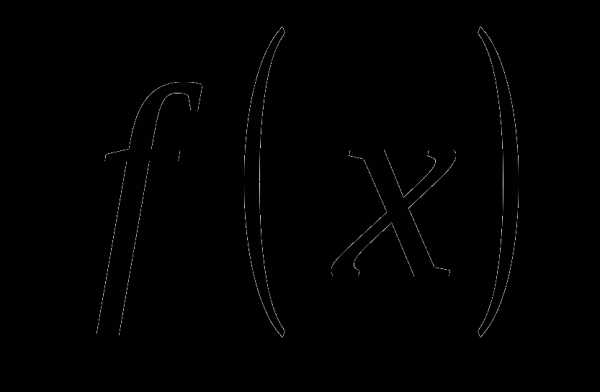 непрерывна на каждом из интервалов
непрерывна на каждом из интервалов  ,
, 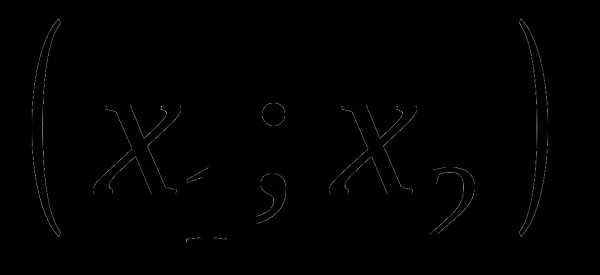 и
и  , то на каждом из них есть единственная точка, в которой эта функция обращается в нуль. Следовательно, функция имеет три нуля, т.е. уравнение (1) имеет три действительных корня.
, то на каждом из них есть единственная точка, в которой эта функция обращается в нуль. Следовательно, функция имеет три нуля, т.е. уравнение (1) имеет три действительных корня.
Ответ: три действительных корня.
Пример 4.
Решить уравнение:
(1)
Решение.
Обе части уравнения (1) определены на отрезке 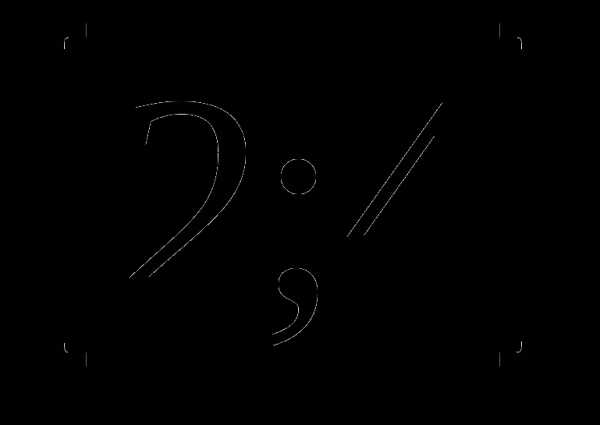 . Рассмотрим функцию
. Рассмотрим функцию
.
Эта функция на интервале 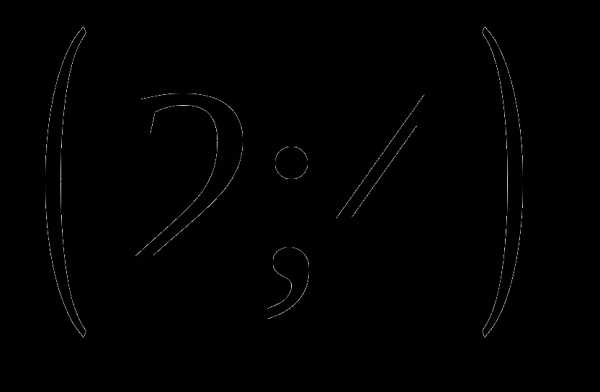 имеет производную
имеет производную
,
которая обращается в ноль в единственной точке 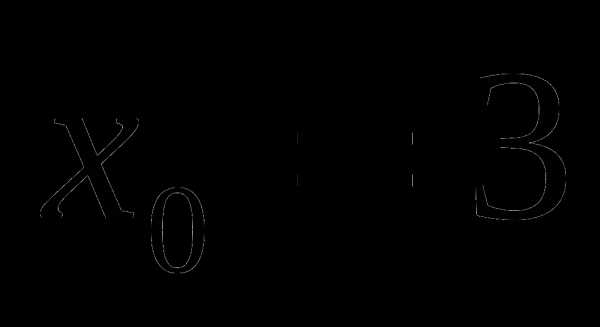 .Так как функция
.Так как функция 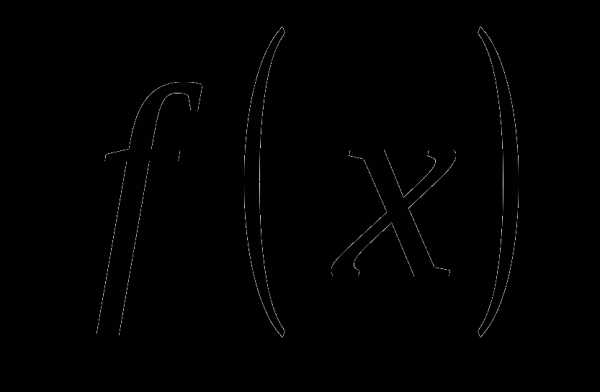 непрерывна на отрезке
непрерывна на отрезке 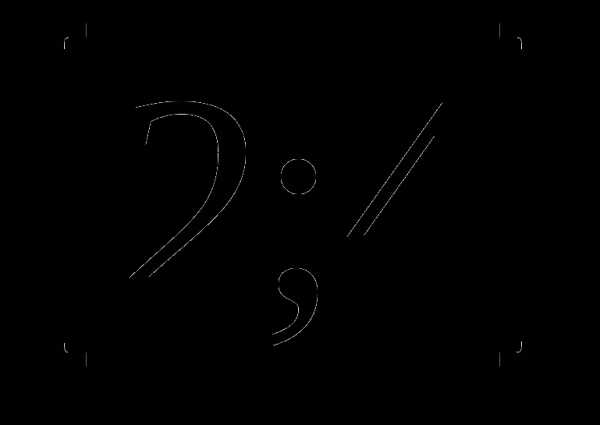
 ,
, 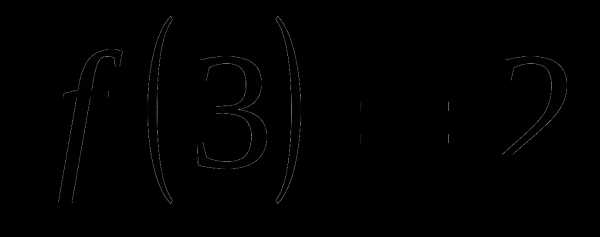 ,
,  .
. Так как , то наибольшее значение 2 на отрезке  функция достигает в единственной точке
функция достигает в единственной точке 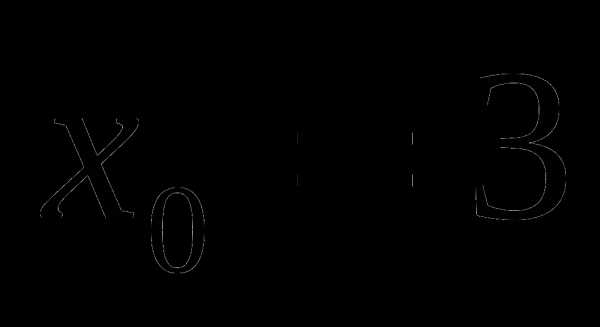 . Следовательно, уравнение (1) имеет единственный корень
. Следовательно, уравнение (1) имеет единственный корень 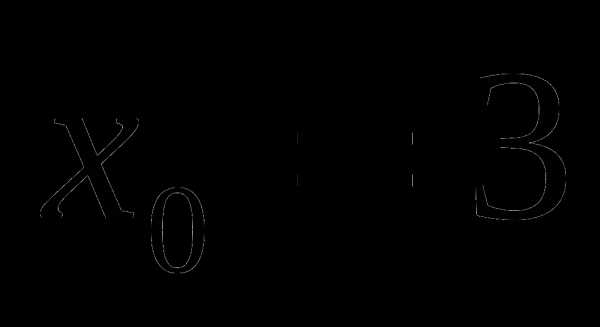 .
.
Ответ: 3.
infourok.ru
Глава 10. Численные методы решения дифференциальных уравнений с частными производными
10.1. Классификация дифференциальных уравнений с частными производными
(1) |
Где xиy– независимые переменные,z– искомая функция,– первые и вторые частные производные по аргументамxиy.
Решением уравнения (1) называется функция , обращающая это уравнение в тождество. График решения представляет собой поверхность в пространствеOxyz.
Уравнение (1) называетсялинейным, если оно первой степени относительно искомой функции и всех ее производных и не содержит их произведений, т.е. если это уравнение может быть записано в виде:
(2) |
Причем коэффициенты могут зависеть лишь отxиy. В частности, если эти коэффициенты не зависят отxиy, то уравнение (2) представляет собойлинейное дифференциальное уравнение с постоянными коэффициентами. Остановимся на этом случае подробнее.
Пусть – дискриминант уравнения. В зависимости от знака функцииDлинейное дифференциальное уравнение (2) относится в данной области к одному из следующих типов:
D<0– эллиптический тип
D=0– параболический тип
D>0– гиперболический тип
Если Dне сохраняет постоянного значка – то уравнение будет смешанного типа.
10.2. Метод сеток
Метод сетокилиметод конечных разностей, является одним из самых распространенных методов численного решения дифференциальных уравнений с частными производными.
Воснове метода лежит идея замены производных конечно-разностными отношениями. Ограничимся случаем двух независимых переменных.
Пусть в плоскости 0xyимеется некоторая областьGс границейГ. Построим на плоскости два семейства параллельных прямыхи
.
Точки пересечения этих прямых назовем узлами.
● Два узла называются соседними, если они удалены друг от друга в направлении оси0xили0yна расстояние, равное шагу сеткиhилиlсоответственно.
Выделим узлы, принадлежащие области G+Г, а также некоторые узлы, не принадлежащие этой области, но расположенные на расстоянии, меньшем, чем шаг от границыГ.
● Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству узлов, называются внутренними(например, узелА). Оставшиеся из выделенных узлов называютсяграничными(например, узлыВиС).
Значения искомой функции в узлах сетки будем обозначать через.
В каждом внутреннем узле заменим частные производные разностными отношениями:
| (3) |
В граничных точках будем пользоваться менее точными формулами:
| (4) |
Аналогично заменяем производные второго порядка:
, | (5) |
Указанные замены производных в каждом узле сетки позволяют свести решение дифференциальных уравнений с частными производными к решению системы разностных уравнений.
10.3. Итерационные методы решения системы конечно-разностных уравнений
В некоторых случаях требуется решить дифференциальное уравнение с частными производными с заданной точностью. Одним из наиболее простых методов является процесс усреднения Либмана.
Согласно этому методу вычисления ведутся следующим образом: вначале вычисляются (находятся) начальные приближения значений искомой функции, а затем последовательнее приближения для внутренних узлов определяются по формуле:
(6) |
Начальные приближения значений функции во внутренних точках можно получить следующими способами:
путем интерполяции, используя известные граничные значения;
составляют систему конечно-разностных уравнений для сетки с более крупным шагом, а затем полученные значения интерполируют на узлы даннойсетки.
Если
границаГобластиGкриволинейна, то значения искомой
функции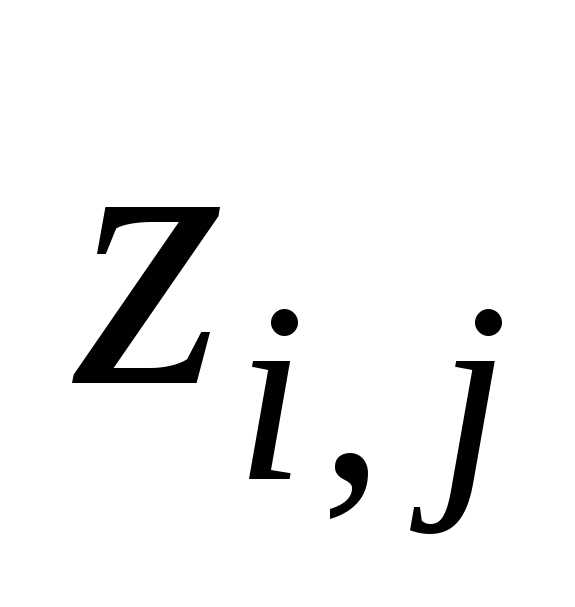 дляграничных узловполучают путем
переноса значений из точек на границеГ. Погрешность, получающуюся в
результате такого переноса можно
значительно уменьшить, если для каждого
граничного узла составить уравнения
следующего вида:
дляграничных узловполучают путем
переноса значений из точек на границеГ. Погрешность, получающуюся в
результате такого переноса можно
значительно уменьшить, если для каждого
граничного узла составить уравнения
следующего вида:
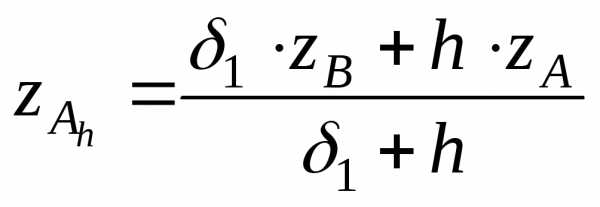 для узлаAh
для узлаAh
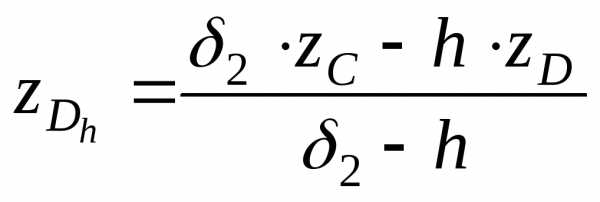 для узлаDh,
для узлаDh,
где AhиDh– узловые граничные точки,АиD– ближайшие кAhиDhточки, лежащие на границе, δ1и δ2– расстояния междуAиAh, иDиDhсоответственно, причем, со знаком «+», если точка внутри области, и знаком «–», если точка вне области.
Пересчет граничных значений методом Либмана проводится по формулам:
(7) |
Итерации продолжают до тех пор, пока в двух последовательных приближениях значений функции, причем, как во внутренних, так и в граничных точках не совпадут требуемое количество десятичных знаков, т.е. .
studfiles.net

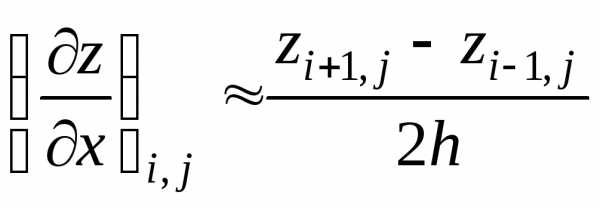 ,
,
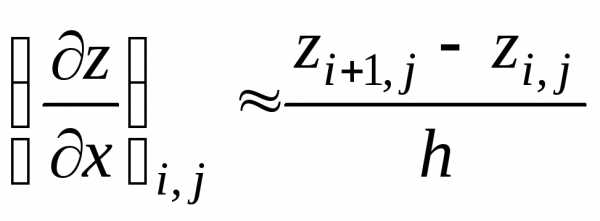 ,
,