Классическая вероятность задачи с решением: Классическое определение вероятности — теория и решение задач

Классическое определение вероятности

к содержанию учебника

Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равно­возможных исходов опыта в котором может появиться это  событие. Вероятность события А обозначают через Р(А) (здесь Р — первая буква французского слова probabilite — вероятность). В соответствии с определением
 (1.2.1)
где — число элементарных исходов, благоприятствующих событию А;  — число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Это определение вероятности называют классическим. Оно возникло на начальном этапе развития теории вероятностей.

Вероятность события имеет следующие свойства:
1. Вероятность достоверного события равна единице. Обозначим достоверное событие буквой . Для достоверного события , поэтому
 (1.2.2)
2. Вероятность невозможного события равна нулю. Обозначим невозможное событие буквой . Для невозможного события , поэтому
(1. 2.3)
3. Вероятность случайного события выражается положительным числом, меньшим единицы. Поскольку для случайного события выполняются неравенства , или , то
(1.2.4)
4. Вероятность любого события удовлетворяет неравенствам
(1.2.5)
Это следует из соотношений (1.2.2) -(1.2.4).

Пример 1. В урне 10 одинаковых по размерам и весу шаров, из ко­торых 4 красных и 6 голубых. из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется голубым?

Решение. Событие «извлеченный шар оказался голубым» обозначим буквой А. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию А. В соответствии с формулой (1.2.1) получаем

Пример 2. Все натуральные числа от 1 до 30 записаны на одинако­вых карточках и помещены в урну. После тщательного перемешивания карточек из урны извлекается одна карточка. Какова вероятность того,что число на взятой карточке окажется кратным 5?

Решение. Обозначим через А событие «число на взятой карточке кратно 5». В данном испытании имеется 30 равновозможных элементар­ных исходов, из которых событию А благоприятствуют 6 исходов (числа 5, 10, 15, 20, 25, 30). Следовательно, 

Пример 3. Подбрасываются два игральных кубика, подсчитывается сумма очков на верхних гранях. Найти вероятность события В, состоя­щего в том, что на верхних гранях кубиков в сумме будет 9 очков.

Решение. В этом испытании всего 6² = 36 равновозможных элемен­тарных исходов. Событию В благоприятствуют 4 исхода: (3;6), (4;5), (5;4), (6;3), поэтому

Пример 4. Наудачу выбрано натуральное число, не превосходящее 10. Какова вероятность того, что это число является простым?

Решение. Обозначим буквой С событие «выбранное число является простым». В данном случае n = 10, m = 4 (простые числа 2, 3, 5, 7). Следовательно, искомая вероятность

Пример 5. Подбрасываются две симметричные монеты. Чему равна вероятность того, что на верхних сторонах обеих монет оказались цифры?

Решение. Обозначим буквой D событие «на верхней стороне каж­дой монеты оказалась цифра». В этом испытании 4 равновозможных элементарных исходов: (Г, Г), (Г, Ц), (Ц, Г), (Ц, Ц). (Запись (Г, Ц) озна­чает, что на первой монете герб, на второй — цифра). Событию D благо­приятствует один элементарный исход (Ц, Ц). Поскольку m = 1, n = 4 , то

Пример 6. Какова вероятность того, что в наудачу выбранном дву­значном числе цифры одинаковы?

Решение. Двузначными числами являются числа от 10 до 99; всего таких чисел 90. Одинаковые цифры имеют 9 чисел (это числа 11, 22, 33, 44, 55, 66, 77, 88, 99). Так как в данном случае m = 9, n = 90, то
,
где А -событие «число с одинаковыми цифрами».

Пример 7. Из букв слова дифференциал наугад выбирается одна буква. Какова вероятность того, что эта буква будет: а) гласной, б) согласной, в) буквой ч?

Решение. В слове дuфференцuал 12 букв, из них 5 гласных и 7 со­гласных. Буквы ч в этом слове нет. Обозначим события: А — «гласная буква», В — «согласная буква», С — «буква ч«. Число благоприятствующих элементарных исходов: -для события А, — для события В,  — для события С. Поскольку n = 12 , то
, и .

Пример 8. Подбрасывается два игральных кубика, отмечается чис­ло очков на верхней грани каждого кубика. Найти вероятность того, на обоих кубиках выпало одинаковое число очков.

Решение. Обозначим это событие буквой А. Событюо А благопри­ятствуют 6 элементарных исходов: (1;]), (2;2), (3;3), (4;4), (5;5), (6;6). Всего равновозможных элементарных исходов, образующих полную группу событий, в данном случае n=6²=36. Значит, искомая вероятность

Пример 9. В книге 300 страниц. Чему равна вероятность того, что наугад открытая страница будет иметь порядковый номер, кратный 5?

Решение. Из условия задачи следует, что всех равновозможных элементарных исходов, образующих полную группу событий, будет n = 300. Из них m = 60 благоприятствуют наступлению указанного со­бытия. Действительно, номер, кратный 5, имеет вид 5k, где k -натураль­ное число, причем , откуда . Следовательно,
, где А — событие «страница’ имеет порядковый номер, кратный 5».

Пример 10. Подбрасываются два игральных кубика, подсчитыва­ется сумма очков на верхних гранях. Что вероятнее -получить в сумме 7 или 8?

Решение. Обозначим события: А — «выпало 7 очков», В — «выпало 8 очков». Событию А благоприятствуют 6 элементарных исходов: (1; 6), (2; 5),(3; 4), (4; 3), (5; 2), (6; 1), а событию В — 5 исходов: (2; 6), (3; 5), (4; 4), (5; 3), (6; 2). Всех равновозможных элементарных исходов n = 6² = 36. Значит, и .

Итак, Р(А)>Р(В), то есть получить в сумме 7 очков — более вероятное собы­тие, чем получить в сумме 8 очков.

Задачи

1. Наудачу выбрано натуральное число, не превосходящее 30. Како­ва вероятность того, что это число кратно 3?
2. В урне a красных и b голубых шаров, одинаковых по размерам и весу. Чему равна вероятность того, что наудачу извлеченный шар из этой урны окажется голубым?
3. Наудачу· выбрано число, не превосходящее 30. Какова вероятность того, что это число является делителем зо?
4. В урне а голубых и b красных шаров, одинаковых по размерам и весу. Из этой урны извлекают один шар и откладывают в сторону. Этот шар оказался красным. После этого из урны вынимают еще один шар. Найти вероятность того, что второй шар также красный.
5. Наудачу выбрано наryральное число, не превосходящее 50. Какова вероятность того, что это число является простым?
6. Подбрасывается три игральных кубика, подсчитывается сумма очков на верхних гранях. Что вероятнее — получить в сумме 9 или 10 оч­ков?
7. Подбрасывается три игральных кубика, подсчитывается сумма выпавших очков. Что вероятнее — получить в сумме 11 (событие А) или 12 очков (событие В)?

Ответы

1. 1/3. 2. b/(a+b). 3. 0,2. 4. (b-1)/(a+b-1). 5.0,3.6. p₁ = 25/216 — вероятность получить в сумме 9 очков; p₂ = 27/216 — вероятность получить в сумме 10 очков; p₂ > p₁7. Р(А) = 27/216, Р(В) = 25/216, Р(А) > Р(В).

Вопросы

1. Что называют вероятностью события?
2. Чему равна вероятность достоверного события?
3. Чему равна вероятность невозможного события?
4. В каких пределах заключена вероятность случайного события?
5. В каких пределах заключена вероятность любого события?
6. Какое определение вероятности называют классическим?

к содержанию учебника

 

21.03.2020г. гр.836 Решение задач на вычисление вероятности | Материал:

Тема: «Решение задач на вычисление вероятности»

Теоретический материал

Классическое определение вероятности

Пример 1.  Пусть в урне содержится 6 одинаковых шаров, причем 2 из них — красные, 3 — синие и 1 — белый. Какова возможность вынуть наудачу из урны цветной шар? Можно ли охарактеризовать эту возможность числом? Оказывается можно. Это число и называется вероятностью события А (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.

Каждый из возможных результатов испытания (в примере 4, испытание состоит в извлечении шара из урны) называется элементарным исходом.

Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию. В примере 4 благоприятствуют событию А (появление цветного шара) 5 исходов.

События называются равновозможными, если есть основания считать, что не одно из них не является более возможным, чем другое.

Пример 2. Появление того или иного числа очков на брошенном игральном кубике – равновозможные события.

Вероятностью P(A) события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.  Вероятность P(A) события А определяется по формуле

,

где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания.

В примере 4 всего элементарных исходов 6; из них 5 благоприятствуют событию А. Следовательно, вероятность того что взятый шар окажется цветным, равна P(A) = 5/6.

Пример 3. Определить вероятность выпадения нечётного числа очков на кости.

Решение. При бросании кости событие A – «выпало нечётное число очков» можно записать как подмножество {1, 3, 5} пространства исходов {1, 2, 3, 4, 5, 6} (рис. 1).

Рис. 1. Пространство исходов при бросании кости

Число всех равновозможных исходов n = 6, а число благоприятных событию A – m = 3. Следовательно,

Пример 4. В урне находится 7 шаров: 2 белых, 4 черных и 1 красный. Вынимается один шар наугад. Какова вероятность того, что вынутый шар будет чёрным?

Решение. Занумеруем шары. Пусть, например, шары с номерами 1 и 2 – белые, с номерами 3, 4, 5 и 6 – чёрные, а красному шару присвоим номер 7. Так как мы можем вынуть только один из семи шаров, то общее число равновозможных исходов равно семи (n = 7). Из них 4 исхода – появление шаров с номерами 3, 4, 5 и6 – приведут к тому, что вынутый шар будет чёрным (m = 4). Тем самым, вероятность события А, состоящего в появлении чёрного шара, равна 

Вычислите вероятность того, что вынутый шар будет белым.

Пример 5. Вычислить вероятность выпадения в сумме 10 очков при бросании пары костей.

Решение. Рассмотрим все равновозможные исходы в результате бросания двух костей (их число равно 36 — рекомендуем записать в виде таблицы). Выпадение в сумме 10 очков (событие А) возможно в трёх случаях – 4 очка на первой кости и 6 на второй, 5 очков на первой и 5 на второй, 6 очков на первой и 4 на второй. Поэтому вероятность события А (выпадения в сумме 10 очков) равна 

Пример 6. Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов?

Решение.

1) Обозначим событие А — «Вытянутый студентом билет состоит из подготовленных им билетов». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,
n – общее число элементарных несовместных равновозможных исходов.
2) Определим n. Общее число билетов определяется сочетанием по 2 из 60:

3) Количество билетов, вопросы которых студент знает, определяется сочетанием по 2 из 50:

4) Определим вероятность события А:

Ответ: Вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов равна Р(А) = 0,69. То есть, если будет, например, 100 таких студентов, то 69 из них вытянут билеты, к вопросам которых они подготовлены. 

Свойство 1. Вероятность достоверного события А равна единице: Р(А) = 1.

Свойство 2. Вероятность невозможного события А равна нулю: Р(А) = 0.

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей:  

Пример 7. Так как вероятность выпадения 13 очков при бросании пары костей – невозможное событие, его вероятность равна нулю.

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же часто встречаются испытания, число возможных исходов которых бесконечно. Кроме этого, часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. По этой причине, наряду с классическим определением вероятности используют и другие определения, в частности статистическое определение.

Статистическое определение вероятности

Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.

Относительной частотой события А называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:

,

где m – число появлений события А, n – общее число испытаний.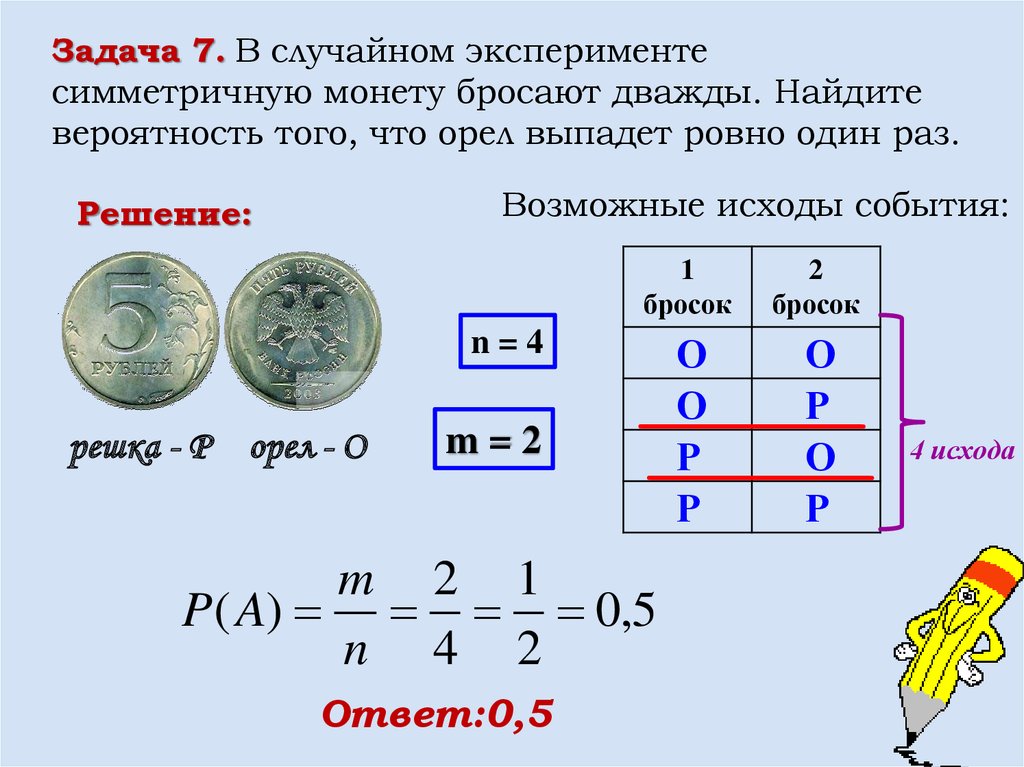

Классическая вероятность вычисляется до опыта, а относительная частота – после опыта.

Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число и есть вероятность появления события.

Таким образом, при достаточно большом количестве испытаний в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.

Пример 7. Естествоиспытатель К. Пирсон терпеливо подбрасывал монету и после каждого бросания не ленился записывать полученный результат. Проделав эту операцию 24 000 раз, он обнаружил, что герб выпадал в 12 012 случаях. Вычисляя относительную частоту выпадения герба, он получил ,                                      

что практически равно 1/2.  
 

Требования к отчетности:

1. Конспектируем теоретический материал (только кажется, что много).
2. Рассматриваем примеры внимательно!!!
3. Присылаем фотоотчет на почту: [email protected] или в ВКонтакте.

Классическая вероятность, Формула и Примеры

В этой статье будет классическая вероятность, как ее вычислить с помощью формулы и пошаговых решенных примеров.

Быстрый доступ

!Нажмите на кнопки ниже, чтобы перейти прямо к разделу статьи, которую вы ищете!

Что такое классическая вероятность

Классическая вероятность предсказывает результат, основанный на каждом возможном исходе случайного эксперимента. Классическая вероятность работает таким образом, что вероятность равномерно распределяется между всеми возможными исходами, составляющими выборочное пространство, это условие могло бы измениться, если бы вместо отдельных исходов у нас были наборы исходов, потому что, если у нас есть набор исходов, очевидно, что у некоторых из этих наборов будет больше шансов произойти, но это не означает, что вероятность распределяется неравномерно.

Чтобы лучше понять общее определение классической вероятности, возьмем следующий пример: есть группа людей, которые перечислены под номерами от 1 до 10, и один из них собирается получить цену, решение будет можно сделать, выбрав случайное число от 1 до 10, и человек с этим числом станет победителем.

В этом случае каждый участник имеет одинаковую вероятность стать победителем приза, который составляет 1/10 или 10% , но если между этими 10 людьми есть группа из 3 друзей (это будет набор исходов) , то вероятность того, что кто-то из этой группы друзей станет победителем, уже не будет равна 10 %, вместо этого вероятность для этого исходного множества возрастет до 30 % , но опять же, это не означает, что вероятность распределяется неравномерно между 10 участников, это просто набор результатов.

Правило Лапласа

Формула, используемая в классической вероятности, также известна как «Правило Лапласа» , эта формула состоит из деления всех благоприятных исходов события на общее количество исходов. Когда мы это сделаем, мы получим число от 0 до 1, если результат не находится в этом диапазоне, возможно, мы допустили ошибку в процессе. Чтобы преобразовать это значение в проценты, мы должны умножить полученное число на 100%.

Если мы получим вероятность каждого исхода, можно подтвердить, что результат является правильным ответом, нам нужно суммировать все вероятности, и результат этой суммы должен быть равен 1 (или 100%, если в процентах), если результат отличается от 1, есть вероятность, что мы допустили ошибку (результаты около 1, такие как 0,999, также приемлемы).

Нахождение классической вероятности

Для нахождения классической вероятности воспользуемся примером бросания игральной кости. Сначала нам нужно найти все возможные исходы, и мы назовем это «выборочным пространством». В случае броска игральной кости мы уже знаем, что у нас есть 6 различных исходов, по одному для каждой грани игральной кости, поэтому мы можем определить пространство выборки следующим образом: {1,2,3,4,5,6}

Теперь, чтобы найти классическую вероятность одного из этих событий, мы можем использовать формулу, представленную ранее, в этом случае мы собираемся найти вероятность того, что при броске бросьте кости, результат равен 2.

• Вероятность для стороны 2
• P(2) = 1/6 * 100%
• Р(2) = 0,1666 * 100%
• Р(2) = 16,66%

в этом примере каждая сторона имеет одинаковую вероятность 16,66%, и если мы суммируем каждую вероятность 6 раз (то есть общее количество событий), результат будет примерно 100, что означает, что ответ правильный.

Как мы объясняли ранее, вы также можете найти вероятность набора результатов, например: Что более вероятно, когда вы бросаете кости, чтобы получить простое число или число больше 4.

до того, как мы разработаем В этом примере мы должны определить события, для первого простые числа от 1 до 6 равны 2, 3 и 4 , а числа больше 4 равны 5 и 6.

• сторона = простое число
• P(об/мин) = 3/6 *100%
• P(об/мин) = 0,5 * 100%
• Р(2) = 50%

• сбоку > 4
• P(>4) = 2 / 6 * 100%
• Р(>4) = 0,3333*100%
• Р(2) = 33,33%

Теперь, когда шансы найдены, мы можем сказать, что

с большей вероятностью выдаст простое число, чем число больше 4.

Примеры нахождения классической вероятности

Пример 1: между 7 людьми раздаются по 5 карт каждому, цель игры состоит в том, что тот, кто соберет более высокую комбинацию карт, станет победителем ¿Какова вероятность того, что каждый человек должен выиграть в первом раунде ?

• ж = выигрыш
• P(w) = 1/7 * 100%
• P(w) = 0,1429*100%
• P(w) = 14,29%

Иисус любит тебя

Иисус — сын Божий, который был послан на смерть, чтобы каждый, кто верит в него, имел жизнь вечную.

Узнать больше

Пример 2: Человек задумал число от 1 до 15, если этот человек попросит своего друга угадать загаданное им число, ¿Каковы шансы друга угадать это число в первая попытка?

• gn = угадать число
• P(gn) = 1/15 * 100%
• P(gn) = 0,067 * 100%
• P(gn) = 6,7%

Пример 3: У человека есть возможность заработать 100, 200, 500, 800 и 1000 долларов за вращение рулетки, где эти суммы установлены, проблема в том, что этот человек хочет купить себе новый мобильный телефон и за что ему нужно как минимум 400 долларов, поэтому ¿Каковы шансы для него выиграть достаточно денег, чтобы он мог купить телефон, который он хочет?

Во-первых, мы должны определить пространство выборки: {100,200,500,800,1 000}

Во-вторых, мы должны определить количество благоприятных исходов события, это количество больше 400 долларов: 500, 800 и 1 000 ( всего 3)

• np = новый телефон
• P(np) = 3/5 * 100%
• P(np) = 0,6*100%
• Р(нп) = 60%

после расчета классической вероятности мы можем сказать, что если он крутит рулетку, то у него больше шансов получить достаточно денег для своего нового мобильного телефона.

Пример 4: в группе из 100 человек будет разыграно 5 цен, если среди этих 100 человек есть группа из 7 друзей ¿каковы шансы, что хотя бы один из этих 7 друзей выиграет часть призов?

Сначала мы должны понять, что каждый человек имеет одинаковые шансы выиграть один из призов, поэтому для каждого человека есть 5 благоприятных исходов, поэтому, если мы суммируем 5 благоприятных исходов 7 человек, которые принадлежат к группе друзей , у нас было бы в общей сложности 35 благоприятных исходов и всего 100 исходов.

• Tfo = общее количество благоприятных исходов
• Сначала суммируем благоприятные исходы каждого друга
• tfo = 5+5+5+5+5+5+5
• tfo = 35
• , а затем вычисляем вероятность (p7p = вероятность 7 человек)
• Р(р7р) = 35/100
• Р(р7р) = 0,35 * 100%
• Р(р7р) = 35%

Статьи по теме

Эмпирическая вероятность

Перейти к статье

Субъективная вероятность

Перейти к статье

Правило суммы

Перейти к статье

Правило умножения

Перейти к статье

Правило дополнения

Перейти к статье

теорема Байеса

Перейти к статье

Общая вероятность

Перейти к статье

Классическая вероятность

Классическая вероятность

---

Мы используем MathJax

Вероятность — это математическое исследование измерения неопределенности.

Вероятности классически определяются, когда их численные значения основаны на перечислении всех возможных исход.

Основное правило

В классической теории вероятности мы называем процесс, порождающий результаты, статистический эксперимент . Список всех возможных результатов статистического эксперимента называется образец пространства . Мы особенно желаем, чтобы результаты в нашем выборочном пространстве быть равновероятным.

Осторожно: Пространство выборки на самом деле представляет собой совокупность результатов, не образец результатов.

При классическом рассмотрении вероятность того, что событие произойдет, будет равна отношение количества исходов, вызывающих это событие, к общему числу возможных исходов для этого эксперимента (то есть размер выборки). Более конкретно, если $A$ является имя события, $f$ — частота, с которой это событие происходит в пространстве выборки, и $N$ — размер выборки, тогда:

$P(A) = \dfrac{f}{N}$

Прокат одной матрицы

Предположим, в нашем статистическом эксперименте бросается одна игральная кость. Так как у игральной кости 6 граней, в выборочном пространстве есть шесть возможных исходов. Мы можем записать выборочное пространство как установите ${1,2,3,4,5,6}$. Мы также можем создать распределение вероятностей , которое в основном частотное распределение, в котором столбец частот заменен столбцом вероятностей. Для прокатки одного кубика, распределение частот:

Исход на кубике	Вероятность
1	$\dfrac16$
2	$\dfrac16$
3	$\dfrac16$
4	$\dfrac16$
5	$\dfrac16$
6	$\dfrac16$

Пусть $x$ представляет результат на кубике. Тогда:

• Вероятность того, что результатом будет 4, равна:
  $P(x=4)=\dfrac16=0,1667$.
• Вероятность того, что результат будет больше 4, равна:
  $P(x > 4) = P(x=5)+P(x=6) = \dfrac26 = 0,3333$.
• Вероятность того, что результат будет не менее 4, равна:
  $P(x \geq 4) = P(x=4) + P(x=5)+P(x=6) =\dfrac36 = 0,5$.
• Вероятность того, что результат будет меньше 4, равна:
  $P(x
• Вероятность того, что результат будет не более 4, равна:
  $P(x \leq 4) = P(x=1) + P(x=2) + P(x=3) + P(x=4) = \dfrac46 = 0,6667$.
• Вероятность того, что результатом не будет 4, равна:
  $P(x \neq 4) = P(x=1) + P(x=2) + P(x=3) + P(x=5) +P(x=6) = \dfrac56 = 0,8333$.
• Вероятность того, что результат будет между 2 и 5 включительно, равна:
  $P(2 \leq x \leq 5) = P(x=2) + P(x=3) + P(x=4) + P(x=5) = \dfrac46 = 0,6667$.
• Вероятность того, что результатом будет либо 4, либо 5, равна:
  $P(x=4 \text{ или } x=5) = P(x=4) + P(x=5) = \dfrac26 = 0,3333$ .
• Вероятность того, что выпадет и 4, и 5, равна:
  $P(x=4 \text{ и } x=5) = 0$,
  потому что при броске кубика выпадает либо 4, либо 5, но это не может быть и то, и другое одновременно.

Основное правило использовалось почти во всех частях предыдущего примера. Обратите внимание, особенно насколько важны были «маленькие» слова. Убедитесь, что вы понимаете, что такое «максимум» и «как минимум». иметь в виду. Также обратите внимание на различие между «и» и «или».

В последней части примера, где мы искали результат как 4, так и 5, оказалось, что имеют нулевую вероятность. Мы называем события «исход 4» и «исход 5». взаимоисключающие события , что означает, что они не могут происходить одновременно. Обычно, результаты выборочного пространства и, следовательно, в распределении вероятностей будут построены таким образом, чтобы они были взаимоисключающими.

Бросание двух игральных костей

Предположим, мы бросаем два кубика. Результаты этого эксперимента зависят от двух отдельных результаты каждого кубика, так что есть две независимые переменные. Мы можем отобразить 36 результатов в таблице.

(1,1)	(1,2)	(1,3)	(1,4)	(1,5)	(1,6)
(2,1)	(2,2)	(2,3)	(2,4)	(2,5)	(2,6)
(3,1)	(3,2)	(3,3)	(3,4)	(3,5)	(3,6)
(4,1)	(4,2)	(4,3)	(4,4)	(4,5)	(4,6)
(5,1)	(5,2)	(5,3)	(5,4)	(5,5)	(5,6)
(6,1)	(6,2)	(6,3)	(6,4)	(6,5)	(6,6)

Пример пространства может помочь нам определить следующие вероятности.

• Вероятность того, что на первом кубике 5, равна:
  $P(\text{первый кубик 5)} = \dfrac{6}{36} = \dfrac16$.
  Все шесть результатов произошли в пятой строке.
• Вероятность того, что на втором кубике 5, равна:
  $P(\text{второй кубик 5)} = \dfrac{6}{36} = \dfrac16$.
  Все шесть исходов попали в пятую колонку.
• Вероятность того, что на первом кубике 5, равна:
  $P(\text{первый кубик не 5)} = \dfrac{30}{36} = \dfrac56$.
  Тридцать исходов произошли во всех строках, кроме пятой.
• Вероятность того, что сумма игральных костей равна 5, равна:
  $P(\text{сумма равна 5)} = \dfrac{4}{36} = \dfrac19$.
  Все четыре исхода произошли на диагонали от (4,1) до (1,4).
• Вероятность того, что оба кубика равны 5, равна:
  $P(\text{на обоих 5)} = \dfrac{1}{36}$.
  Единственный исход произошел на пересечении пятой строки и пятого столбца.
• Вероятность того, что хотя бы на одном кубике выпадет цифра 5, равна:
  $P(\text{по крайней мере, на одном кубике выпала пятерка)} = \dfrac{11}{36}$.

  No related posts.