Клумба имеет форму квадрата со стороной а м записать формулу: Клумба имеет форму квадрата со стороной a м. Записать формулу площади (s) этой клумбы

Содержание

Круг. Площадь круга — МАТЕМАТИКА — Уроки для 6 классов — конспекты уроков — План урока — Конспект урока — Планы уроков

Урок № 57

Тема. Круг. Площадь круга

Цель: сформировать представление учащихся о геометрической фигуре круг и понятие площади круга; научить пользоваться формулой S = nR2 для решения задач.

Тип урока: усвоение знаний, умений и навыков.

Ход урока

I. Проверка домашнего задания

Математический диктант

Вариант 1 [2]

1. Запишите формулу, по которой вычисляется длина окружности, если известен его радиус [диаметр].

2. Вычислите длину окружности, если длина диаметра [радиус] 10 м [5 дм], число π округлите до сотых.

3. Длина круга 9,42 дм. Округлив число π до сотых, найдите диаметр [радиус] этого круга.

4. Диаметр круга больше радиуса окружности на 7 см. [Радиус круга меньше его диаметра на 14 дм]. Какова длина круга? Число π выразите обычай им неправильным дробью.

II. Актуализация опорных знаний

1. Во время проверки результатов выполнения диктанта повторяем основное содержание материала предыдущего урока (представление о круг, радиус, диаметр окружности; длина окружности и число в виде десятичной и обыкновенной дроби).

2. Кроме этого, следует еще повторить некоторые понятия. Для этого выполняем устные упражнения:

1) Назовите геометрические фигуры, которые вы видите на рисунке:

Какая из них лишняя?

2) Какой величиной характеризуется любой отрезок? Какие единицы измерения длины вы знаете?

3) Какой величиной характеризуется часть плоскости, ограниченная сторонами квадрата? прямоугольника? Которые наедине измерения площади вы знаете?

4) Вычислите площадь и периметр:

а) квадрата со стороной 7 см;

б) прямоугольника со сторонами 7,5 см и 6см.

III. Усвоение знаний

@ Как и на предыдущем уроке, начать надо с того, что повторить содержание понятия «круг» и показать разницу между этим понятием и понятием «круга», только после этого знакомим учащихся с формулой площади круга и показываем ее применение для решения задач.

1. Круг. Элементы круга

Начертим окружность с центром в т. О и радиусом ОА = R = 3 см. Это круг разделит плоскость (лист) 2 части, одна из которых лежит снаружи, а другая — внутри круга.

Тогда часть плоскости, которая находится внутри круга вместе с кругом — круг, О — центр и R = OA — радиус.

2. Площадь круга.

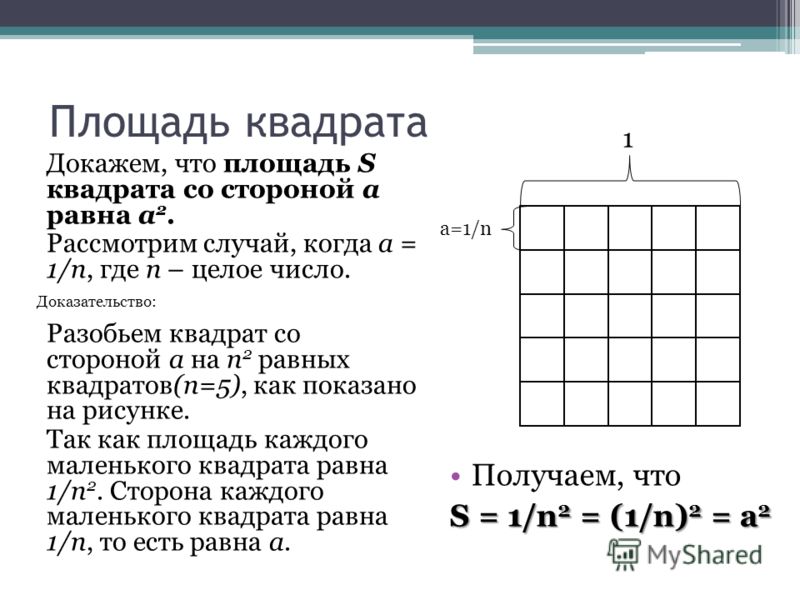
@ Опыт автора показывает, что вывод формулы площади круга через площадь вписанного и описанного квадратов шестиклассникам не очень понятно. Поэтому, на усмотрение учителя, или «выводим» формулу, как это делается традиционно в учебниках по математике для 6 класса, или объясняем, что эта формула будет выведена нами в 9 классе, когда мы научимся это делать, опираясь на соответствующие геометрические сведения, и записываем формулу S = nR2. В конце объяснений, должны записать в тетрадях учащихся (конспект 27).

Конспект 27

Круг. Площадь круга

Круг с центром О,

радиус ОА = R;

S = nR2 — площадь круга

Примеры

1) Если R = 2 см,

то S = nR2 = n·22 = 4n (см2).

2) Если D = 2 см,

то R = D : 2 = 2 : 2 = 1см.

S = nR2 = n (см2)

IV. Усвоение умений

Устные упражнения

1. Вычислите: 12; 32; 0,12; ; 1,12.

2. Найдите площадь круга радиуса 1 м; 10 дм.

3. От геометрической фигуры площадью 10 дм2 отрезали часть площадью 2 дм2; 15 см2. Какова площадь той части, что осталась?

Письменные упражнения

1. Найдите площадь круга: а) радиуса 5 см; 11 см; 0,2 м; б) диаметра 0,5 м; 8 м.

2. Длина окружности арены цирка равен 47,1 м. Найдите площадь арены (результат округлите до м2).

3. Сделайте необходимые измерения и найдите площади заштрихованных фигур, изображенных на рисунке.

Перед выполнением задачи 3 желательно рассмотреть дополнительные задачи.

Дополнительные задачи

Задача 1. Найдите площадь заштрихованных фигур 1-3, если площадь данной фигуры S (ед. кв.)

Задача 2. Как Найдите площадь заштрихованных фигур 4-6 :

Итоги урока

VI. Домашнее задание

Задача 1. Найдите площадь круга:

а) радиуса 8 см; 14 дм; 3,5 м; б) диаметра 1,6 м; 5 дм.

Задача 2. Найдите площадь круга, если длина его окружности равна 25,12 см.

Задача 3. Надо покрасить круг радиуса 3 м. Сколько нужно для этого краски, если на каждый квадратный метр расходуется 120 г краски (результат округлите до десятков граммов)?

Задача 4. Клумба имеет форму круга. Длина окружности, ограничивающей клумбу, равна 31,4 м. На клумбе высаживают кусты роз, отводя под каждый куст 0,8 м2 земли. Какое наибольшее количество кустов роз можно высадить на клумбе?

Содержание

Вперед

Использование технологии проблемного диалога, формирующего навыки исследовательской деятельности на уроках математики

1.

Использование технологии проблемного диалога, формирующего навыки исследовательской деятельности на уроках математики1 этап : Мотивация
Предъявляется ученикам (м.б., через задание) одновременно
два противоречивых факта, мнения. Какое вы заметили
противоречие?
Задается вопрос (задание), которое выявляет разные мнения
учеников класса, сталкивая их. Какие же мнения верные?
Задается вопрос (задание), которое обнажает житейское, но
ошибочное представление учеников, а потом предъявляет
противоречащий ему научный факт (сообщением,
экспериментом, наглядно). Что удивило? Как думали
сначала, а как на самом деле?
Дается задание, выполнение которого вызывает затруднения
при имеющемся уровне знаний и умений. Почему не смогли
выполнить задание?
Прием «яркое пятно» — заключается в сообщении классу
интригующего материала, но при этом связанного с темой
урока. Это может быть использование сказки, легенды,
фрагмента из художественной литературы, случая из истории
науки, культуры, повседневной жизни и т.

д.
Прием «актуальность» — состоит в обнаружении смысла,
значимости предлагаемой темы для самих обучающихся,
лично для каждого.

3. Урок-путешествие

Борисова Светлана
Александровна, МОУ СОШ №3
г. Волгоград, 2012

4. Разрежьте квадрат по схеме и составьте из получившихся фигур прямоугольник. Равны ли их площади?

8
А
13
В
5
8
Е
К
Ошибка в чертеже. Точки А,В,Е и К
не лежат на одной прямой

5. Тема: задачи на части( 5 класс)

Придумайте и решите задачу с помощью схемы.
1 полка
2 полка
150 книг
Объясните, как вы рассуждали.
Пользовались ли вы при решении этой задачи
понятием ЧАСТЬ?
Каким образом можно использовать это понятие
при решении данной задачи?

6. тема: Сумма углов треугольника (7 класс)

1 группа: Измерьте углы остроугольного треугольника и
найдите их сумму.
2 группа: Измерьте углы прямоугольного треугольника и
найдите их сумму.
3 группа: Измерьте углы тупоугольного треугольника и
найдите их сумму.

Чему равна сумма углов треугольника?
Как вы думаете, в любом ли треугольнике такая сумма
углов?
Давайте найдем ответ на этот вопрос на сегодняшнем уроке.

7. Тема: признаки делимости ( 5 класс)

123456789*
Поставьте вместо * цифру так, чтобы число
делилось на 2 ; на 3; на 9; на 5; на 10.
Объясните, как вы рассуждали?
Можно ли это сделать не выполняя деления?

8. Тема: Параллельность прямых ( 7 класс) Параллельны ли горизонтальные прямые?

9. На каких рисунках изображены параллельные прямые?

А
В
Б
Г

10. Прием «Яркое пятно» Тема: Умножение и деление десятичных дробей на натуральное число ( 5 класс)

Держим путь к берегам
западной Африки, где живет
самая большая лягушка в мире.

11. Узнайте, как ее зовут, вставив пропущенные числа:

1) 18,75
: 15= 1,25;
2)184,5:15 = 12,3
3)166,26
: 51=3,26;
4)72,38: (3,7+6,3)= 7,238 ;
5)( 6,8-2,6):21= 0,2
;
6) ( 1 + 2,4
) * 12= 40,8
н
о
и
м
1,85 12,3 7,238 0,24
г
л
ф
18,75 166,26 2,4
а
0,2
Была поймана лягушка, которая весила
3кг 306г.

Длина ее тела составляла 34 см, а с
учетом вытянутых ног – 81 см. Лягушку голиаф недаром назвали именем
ветхозаветного великана – она и вправду
великан среди рептилий.
2 этап: Формулирование проблемной ситуации
Какой у вас возникает вопрос
(проблема)?
Что предстоит выяснить?
Прием «Побуждающий диалог»
– вопросы, на которые возможны
разные правильные варианты
ответа (развитие творчества).

14. Тема: Свойства площадей ( 5 класс)

2м
4м
1м
3м
Незнайка решил застелить в своем домике пол
линолеумом, но в углу стоит тяжелый угловой
шкаф. Давайте попробуем ему помочь посчитать,
сколько линолеума ему надо купить, чтобы не
убирать шкаф.

15. Тема: Площадь прямоугольника (5 класс)

Нашему классу в рамках школьного проекта
«Школьная клумба» необходимо посадить цветы на
нашем участке. Давайте рассчитаем сколько
пакетиков семян нам понадобиться, если клумба
нашего класса имеет вот такую форму: в одной
пачке семян 15 гр.

, необходимо 10 г на 1 м²
5м
1м
3м
1м
1м

16. 3 этап: Актуализация знаний Прием «Подводящий диалог» Логическая цепочка заданий, подводящих к формулировке темы

Что мы уже знаем по этой
проблеме?
Что нужно узнать для решения
проблемы?

17. Тема: Чтение и составление таблиц ( 5 класс) репродуктивные задания

Что вы знаете о таблицах?
Какие таблицы вы встречали в учебниках?
Какие таблицы вам встречались в газетах,
журналах? При работе на компьютере? На
вокзалах? Запись в виде таблицы удобнее , чем в
виде текста?
Как устроены таблицы?
Как заполняются таблицы?
Как вы думаете, чем мы будем заниматься на
сегодняшнем уроке?
Собери чемодан
в дорогу
15 6 10 21 15 5 6 7
4 3 10 11 7 9 8 21
Найдите площадь фигуры, изображённой на рисунке, если
условиться, что длина стороны каждой клетки равна 1 см.
15

20. Мыслительные ( упражнения на анализ, сравнение, обобщение) Биссектриса угла( 7 класс)

2.
3.
Один из вертикальных углов равен 80 ̊. Чему
равна градусная мера угла, образованного
биссектрисами?
Сами задайте градусную меру одного из
вертикальных углов. Вычислите градусную
меру угла между их биссектрисами.
Запишите общее предположение о величине
угла между биссектрисами вертикальных углов.

21. Тема: Линейная функция и ее график ( 7 класс)

Разделите данные функции на 2 группы:
(по какому принципу вы их объединили)
Прямая
у= 5х+3
у=2х
пропорциональность
у=кх
у= х-7
у= 7х+13
у= 4х
функция
у= 6х

22. Задачи на движение ( 5 класс)

1.
2.
Собственная скорость первой лодки- 6 км/ч.
Какое расстояние она проплывет за 2 часа,
двигаясь в стоячей воде?
Собственная скорость второй лодки – 6 км/ч.
Двигаясь по течению реки, она за 2 часа
проплыла 16 км.
Почему имея одинаковую собственную
скорость и одинаковое время движения лодки
проплыли разное расстояние? Чем решение
задачи на движение по реке отличается от уже
известных нам задач?

23.

4 этап:Поиск решения
Выполнение продуктивных заданий.
Осмыслить задание.
Добыть информацию (из текста, схемы и т.д.).
Преобразовать информацию в соответствии с заданием
(найти закономерность, вывести правило, понятие).
Мысленно сформулировать ответ.
Дать развернутый устный ответ: «Я считаю, что…»;
«потому что…»; «во-первых… , во вторых…».
Чередование формы работы: индивидуальную, парную,
групповую с общей беседой;
Приемы: Рабочий лист; Сигнальные карточки;
Составление кластера; Презентации; Комментированное
чтение; Эксперименты; Опыты; Мини-проекты; Миниисследования; Диктант; Текст с ошибками; Синквейн;
Составление определения; Работа с диаграммами,
графиками, статданными; Заполнение таблицы, схем;
Метод «Найди связь с жизнью»; Работа с иллюстрацией
и др.

25. Треугольники и их виды ( 5 класс)

Продолжите предложения.
— Если у треугольника есть один прямой угол, то треугольник
называется…..
— Треугольник называется тупоугольным, если….

-Количество тупых углов тупоугольного треугольника равно ….
— Количество острых углов остроугольного треугольника равно ….
2.
Дополните предложения.
-Сумма всех углов треугольника равна ….
-Если у треугольника есть тупой угол, то два других его угла….
— Если у треугольника есть прямой угол, то два других его угла….
— Количество острых углов тупоугольного треугольника равно…
— Сумма любых двух сторон треугольника ….его третьей стороны.
3. Может ли у треугольника быть три прямых угла? Два прямых
угла?
4. Какое наибольшее количество тупых углов может иметь
треугольник?
1.

26. Тема: Теорема Виета и теорема,обратная к ней . ( 8 класс)

Решите квадратные уравнения и найдите сумму и
произведение получившихся корней
(проанализируйте результаты)
№ уравнения
п/
п
1
х2 х 6 0
2
х2 х 6 0
3
х2 х 6 0
4
х 2 5х 6 0
Исследование
существования
корней
х1 х2
С
х1 х2
b

27.

Проанализируйте данные и узнайте числа m и n: Проанализируйте данные и заполните пропуски:m n 14,
m n 9.
m n 15,
m n 8.
m n 35,
m n 2.
х ___ х ____ 0;
2
х1 2, х2 8

28. Площадь прямоугольника ( 5 класс)

Есть кусок старинной
драгоценной ткани,
имеющей форму квадрата со стороной 3 м 60 см,
из которого нужно вырезать одинаковые детали
прямоугольной формы размером 2м х 40 см.
Главное условие- они должны быть цельными,
то есть не могут быть составлены из меньших
частей. Необходимо вырезать наибольшее
возможное число требуемых деталей.

29. Чтение и составление таблиц ( 5 класс)

Рассмотрите таблицу и расскажите, какая
информация в ней собрана и как это
сделано.Обратите внимание на условное
обозначение: — 1 человек,
— 6 человек.
№
п/п
Время за
компьютером
Проведение подсчетов
количество
1
Не провожу вообще
14
2
Менее 1 часа
7
3
От 1 часа до 2 часов
3
4
От 2 часов до 3 часов
2
5
Более 3 часов
1
Основное свойство дроби ( 6 класс)
Какими еще дробями можно выразить закрашенную
часть фигуры?
3
8
3 2 6
8 2 16
3 3 9
8 3 24
3 4 12
8 4 32

31.

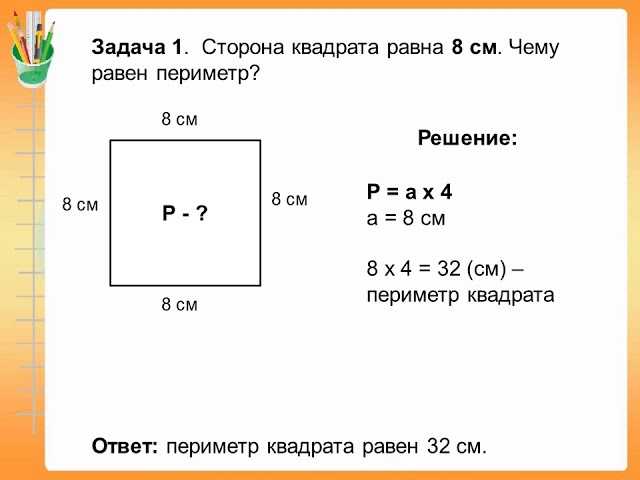Признак параллельности прямых ( 7 класс)Измерьте градусные меры углов на рисунках 1 и 2.
1
1
3
2
3
2
Рис.1
Рис.2
Сравните внутренние накрест лежащие углы и сумму
внутренних односторонних углов на рисунках.
Запишите условия, которые должны выполняться,
чтобы прямые были параллельны.

32. Возьмите 2 прямоугольника красного цвета. Совместите эти прямоугольники и заполните пропуски в тексте:

Эти прямоугольники совпадают при наложении,
равны
значит они ______.
Площадь первого прямоугольника
10
равна_____кв.единиц,
площадь второго
10 кв.единиц. У
прямоугольника равна ____
равных фигур ________
площади. У равных
равные
фигур _________
периметры.
равные

33. возьмите сиреневые фигурки из вашего конверта и найдите их площадь. Проверьте, равны ли фигуры 1 и 2 варианта? Обменяйтесь и

4
Фигура разбита на _____
части. Площадь
первой части равна ______,
площадь
8
второй части равна _____,
площадь третьей
4
части равна ___,площадь
четвертой части
6
3
равна _____.

Сумма площадей этих частей
равна_____
21 квадратных единиц , площадь
21
всей фигуры равна _______
квадратных
единиц. Значит, площадь всей фигуры
равна _______
сумме площадей всех её ______.
частей

34. Возьмите 2 треугольника зелёного цвета. Как называются эти треугольники? Проверьте, равны ли треугольники. Можно ли составить

Так как треугольники _____________,
то
равны
их площади _________.
Площадь
равны
прямоугольника вычисляется по
a·b
формуле S=__________,
значит, площадь
каждого из полученных прямоугольных
треугольников может быть подсчитана
так: S=a ·_b :_ 2
5 этап: Применение нового знания
Какой ответ на основной вопрос урока мы можем дать?
Чьи версии подтвердились?
Как оцените свою работу?
Используя свои новые знания … (дается задание на
продуктивное применение – рассказ, рисунок и т.п.)
Приемы: «Найди ошибку»; Диктант; Словарная работа;
Кроссворды; Коллаж; Работа по опорному конспекту;
Работа по ТПО; Рассказ-эстафета; Логические цепочки,
схемы; Составление конспекта, тезиса; Классификация;
Аукцион знаний; Викторина; Тестирование; Тест;
Составление таблицы, схемы;
Задание на соответствие; Группировка материала;
Взаимопроверка; Составление кластера; Практическая
или лабораторная работа и др.

36. Треугольники и их виды ( 5 класс)

Внимательно изучите рисунок. Выпишите все
треугольнике по видам:
а) остроугольные; б) прямоугольные; в) тупоугольные;
г)равнобедренные; д) равносторонние; е) разносторонние;
ж) Равнобедренные остроугольные; з) Равнобедренные
тупоугольные; и) равнобедренные прямоугольные.

37. Заполните таблицу, сделав чертежи

остроугольный
разносторонний
равнобедренный
равносторонний
прямоугольный
тупоугольный

38. Площади фигур ( 5 класс)

Определите площади фигур, выполнив
необходимые построения и измерения:

39. Тема: Квадратные уравнения ( 8 класс)

Выясните , при каких значениях параметра с
уравнение:
2
а) х 4 х с 0 имеет два различных корня;
2
б) 2 х х с 0 имеет хотя бы один корень;
в) 0,1х 2 0,6 х с 0 не имеет корней.
Решения:
2
а) х 4 х с 0
D b 2 4ac _______
Уравнение будет иметь два различных корня, если
D
0. Поэтому составим и решим ___________

41.

1 признак равенства треугольников (7 класс)Какое условие необходимо добавить для того,
чтобы можно было воспользоваться признаком
равенства треугольников? 5 см
12 см
60̊
90̊
8 см
6 см
4 см
60̊
6 см
12 см
30̊
8 см
90̊
8 см
8 см
1
1 вариант
2 вариант
Используя формулу S = ab, найдите неизвестную величину :
a (м)
5
280
a (м)
5
23
240
3
4
24
b (м)
74
b (м)
94
4
3
S (м2)
370
840
96
S (м2)
470
92
720
2
Найти площадь фигуры
M
A
2 см
B
5 см
15 см²
4 см²
4 см
C
N
6 см
K
1 вариант
2 вариант
3
B
N
6 см
18
см²
A
4 см
2 см
168см²
см
C
M
1 см
3 см
K
Положительные и отрицательные числа
( 6 класс)
6 этап: Домашнее задание
Задание на выбор; Составь задачу; Сочини
шпаргалку; Составь тест, задание; Задание
с использованием Интернета; Творческое
задание; Публичная лекция; Рекламный
плакат; Работа с сайтом по предмету;
«Напиши письмо…»; Составь
презентацию; Составь буклет по теме;
Составь вопросы к документу, по карте;
Подбери подобное и реши; Найди в
словаре; «Займи позицию» и др.

Найдите площадь фигуры и составьте
подобные задания (2-3 варианта).

50. 51. Исследователь старинных рукописей

Найдена старинная рукопись , в которой известны
расшифровки записи некоторых чисел,
записанных способом, принятым на Руси до
правления Петра :
Расшифруйте записи:
Запишите допетровским способом следующие
числа:
7; 11; 56; 712; 444; 2008.
Таблицы и диаграммы (5 класс)
Проведи опрос среди учащихся класса, какие виды
спорта они предпочитают. По результатам опроса
постройте круговую диаграмму.
В старосты выдвинуты 5 кандидатов вашего класса.
Голосуют все учащиеся. Голосование проходит так:
голосующий школьник получает бюллетень с
фамилиями кандидатов и вычеркивает все фамилии,
кроме одной. Если вычеркнуты все фамилии или
оставлено больше одной, то бюллетень
недействителен. Старостой выбирается кандидат,
набравший наибольшее количество голосов.
Задание: придумайте:
а)таблицу обработки бюллетеней;
б) как быть если несколько кандидатов наберут
одинаковое количество голосов.

Рецепты ( задачи на части)
1)Для того, чтобы приготовить фруктово-ореховую
смесь, необходимо 5 частей сушеных бананов,
4 части изюма и 3 части миндальных орехов.
Сколько нужно взять бананов, изюма и орехов,
чтобы приготовить 600 г. смеси?
Придумайте рисунок на координатной плоскости и
зашифруйте его.

56. 7 этап: Рефлексия Закончи предложения:

Я узнал….
Теперь я могу…….
Было интересно… я научился……
Было трудно….
У меня получилось….
Я попробую…..
меня удивило….
Мне захотелось….

57. анкета

На уроке я работал
активно / пассивно
Своей работой на уроке я
доволен / не доволен
Урок для меня показался
коротким / длинным
За урок я
не устал / устал
Мое настроение
Материал урока мне был
стало лучше / стало хуже
понятен / не понятен
полезен / бесполезен
интересен / скучен
Домашнее задание
легким / трудным
интересно / не интересно

58. «Полянка»

59.

смайлики

60. Лесенка успеха

Знаю, умею и
применяю
знаю и умею
знаю

61. Дерево успеха

Нет ошибок
1-2 ошибки
Более 2 ошибок
Собираемся
в путь
Поиск
решения
задачи
Проверь
свои знания

63. Рефлексивная мишень

Активно
участвовал
Было
интересно
3
4
5
3
4
5
5
4
3
5
4
Было
понятно
3
Узнал новое

64. Графическая рефлексия

Наш урок подходит к концу. В течение урока вы работали в картах.
Оцените свою работу на уроке, закрасив соответствующий
значок.
— понравилось выполнять
— было трудно
— не очень понравилось
— не очень было трудно
— не понравилось вообще
— не трудно
Все задания я выполнил самостоятельно
Некоторые задания я выполнял с помощью учителя или
ребят в группе
Мне еще необходимо потренироваться в решении задач по
этой теме

Математическая задача: Клумба 2 — вопрос №1115, алгебра, выражение переменной из формулы

Вокруг квадратной клумбы в парке проходит тротуар шириной около 2 м. Площадь этого тротуара составляет 243 м ² . Какова площадь клумбы?

Правильный ответ:

S = 805,1 м ²

Пошаговое объяснение:

S+243=S2 a2+243=(a+2⋅2)2 a2+243=a2+2a ⋅4+42 243−16=8a a=(243−16)/8=28,38 м S=a2=28,382=805,1 м2

Вы нашли ошибку или неточность? Не стесняйтесь

напишите нам

. Благодарю вас!

Вам необходимо знать следующие знания для решения этой задачи по математике:

Алгебра
Экспрессия переменной из Формулы
Arithmetic
квадрат (вторая энергия, квадратично)
9009
.
контуры
площадь формы
квадрат

Оценка слов Проблема:

Практика для 110029
Практика для 12 -летних
для 13 -летнего возраста
Практика для 14 -летнего возраста

Мы поощряем вас. видео по этой математической задаче: видео1

Тротуар
Городской парк представляет собой круглую клумбу из цветов диаметром 8 метров. Вокруг него на всю длину тротуар шириной 1 метр. Какая площадь тротуара?
Около
Вокруг круглой клумбы радиусом 2 м проходит тротуар шириной 80 см. Сколько квадратных метров имеет тротуар?
Тротуар 63134
Тротуар шириной 2 м построен вокруг круглого фонтана. Радиусы окружностей, ограничивающих путь с обеих сторон, равны 4:3. Какую площадь в квадратных метрах занимает этот тротуар?
Коза
Огражденная клумба имеет форму правильного шестиугольника. Вершины образованы заборными столбами. Забор вокруг клумбы составляет 60 м. Козу привязывают к одному из столбов снаружи и пасут на окрестном лугу (коза не должна заходить
Круглая клумба
Вокруг круглой клумбы диаметром 6 метров сделаю тротуар шириной до 0,5 метра. Сколько нужно щебня, если высота слоя 5 см?
Клумба
В парке есть прямоугольная клумба размерами 3,2м и 1,5м. Сколько кустов роз мы посадим на клумбе, если на один куст нужно 20 дм²?
Равносторонний 26601
Садовник засыпал клумбу в форме равностороннего треугольника со стороной 8 м щебнем. Сколько крошки ушло на всю клумбу, если ее расходуется 25 кг на 1 м² площади?
Клумба 22573
Вокруг круглой клумбы диаметром 6м сделать тротуар шириной 0,5м. Сколько квадратных метров материала нам нужно?
Тротуар 6347
Тротуар шириной 70 см вокруг кольцевого закона радиусом 2,3 м. Сколько квадратных метров имеет тротуар?
Клумба
У семьи тюльпаны на квадратной клумбе 6 метров. Позже они пристроили к своему дому квадратную террасу со стороной 7 метров. Одна вершина террасы лежала ровно посередине тюльпановой клумбы, а одна сторона террасы разделяла сторону тула
Прямоугольный 7072
Прямоугольный бассейн имеет размеры 25 м и 12,5 м. Вокруг него асфальтированная площадка шириной 3 метра. Чему равна площадь тротуара?
Круглый газон
Вокруг круглого газона проходит тротуар шириной 2 м. Внешний край тротуара представляет собой бордюр шириной 2 м. Тумба и внутренняя сторона тротуара вместе образуют концентрические окружности. Вычислите площадь круглого газона, и результат rou
Прямоугольная клумба
Вокруг прямоугольной клумбы размерами 5,25 м и 3,50 м розы должны быть высажены на одинаковом расстоянии друг от друга так, чтобы розы располагались в каждом углу клумбы и потребляются как можно меньше. Как далеко мы сажаем
Прямоугольный 18333
Прямоугольный бассейн имеет размеры 10,5м и 8м. Вокруг проложена дорожка шириной 1 метр. Сколько м² плитки нужно для мощения тротуара?
Тротуар
Рабочие будут вымостить тротуар шириной 1 метр в саду плиткой вокруг блочного бассейна. На картинке тротуар показан серым цветом. Размеры дна бассейна 8,5 метров и 6 метров. Высота стен бассейна 2 метра.
В
Рабочие вымостят тротуар шириной 1 метр в саду плиткой вокруг блочного бассейна. Размеры дна бассейна 8,5 метров и 6 метров. Высота стен бассейна 2 метра. Сколько м² тротуара будет уложено плиткой
Клумба 2801
Вокруг круглой клумбы диаметром 3,6 м проложена пешеходная дорожка шириной 50 см. Рассчитать площадь пешеходной дорожки

Калькулятор площади сада | Измерения садовой грядки

1Определите, сколько квадратных футов у вас есть:

Чтобы определить, сколько квадратных футов у вас есть, вы будете использовать приведенные ниже формулы, чтобы найти площадь (A) — эта математическая формула будет отличаться в зависимости от формы вашего сад. Во-первых, вам нужно будет выйти на улицу и измерить грядку. Вам нужно будет иметь под рукой правильные измерения, такие как ширина (W), длина (L), радиус (R), основание (B) или высота (H).

Прямоугольный/Квадратный Сад

Прямоугольник и квадрат имеют четыре прямых угла. Площадь прямоугольника или квадрата находится путем умножения длины (L) на ширину (W).

Круглый сад

Окружность — это замкнутая кривая, каждая точка на краю которой находится на одинаковом расстоянии от центральной точки. Площадь круга равна квадрату радиуса (R)x(R), умноженному на число пи (~3,14). Радиус равен половине диаметра окружности.

Овальный сад

Овал имеет эллиптическую или яйцевидную форму. Площадь овала равна длине (L), умноженной на ширину (W), умноженной на 0,8.

Треугольный сад

Треугольник — это многоугольник с тремя сторонами. Площадь треугольника равна половине основания (В), умноженной на высоту (Н).

Сад неправильной формы

Чтобы найти площадь большой неправильной формы, разделите ее на ряд меньших частей, равномерно расположенных вдоль измеренной линии. Этот метод рассчитает площадь с точностью до 5%.

Определите длину линии. Это самая длинная ось фигуры, как показано на изображении, от точки A до точки B.
Разметьте линии ширины вдоль линии A-B на несколько сегментов одинаковой ширины. Чтобы обеспечить точность, используйте как можно больше линий ширины. Чем более неправильная форма, тем более широкие линии вам понадобятся.
No related posts.