Когда меняем синус на косинус: Формулы приведения

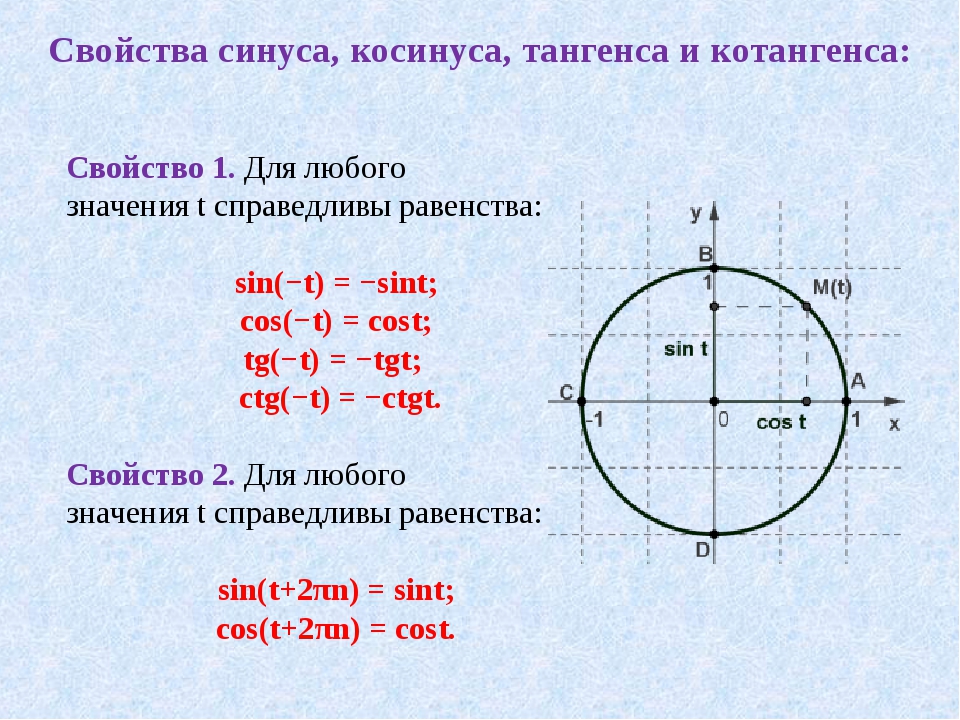
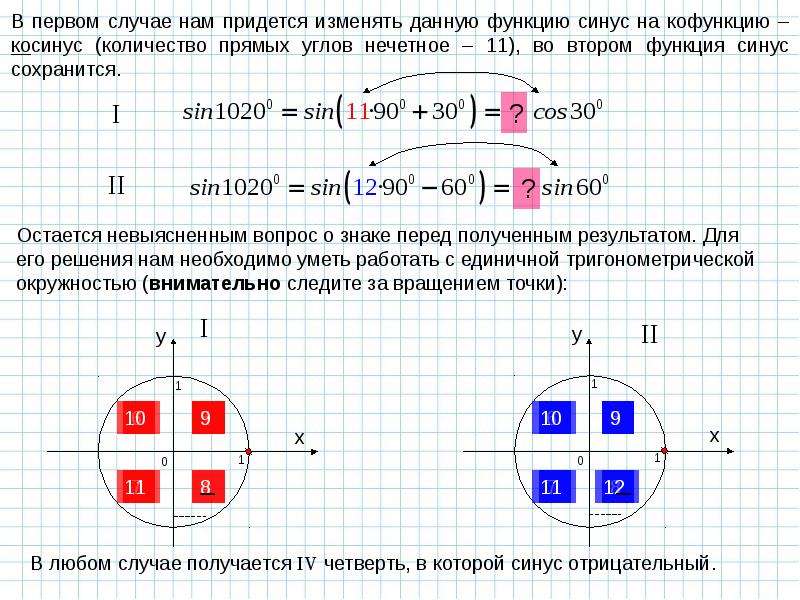
Как пользоваться формулами приведения. Изменение синуса, косинуса и тангенса при возрастании угла

Здоровье детей

Тригонометрия.Формулы приведения.

Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!

Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.

Разберем в каждой четверти функции sin(a) и cos(a).

Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.

В первой четверти видно, что функция sin(a)>0
И функция cos(a)>0
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).

Во второй четверти видно, что функция sin(a)>0 , потому что ось Y положительна в этой четверти.
А функция cos(a) , потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).

В третьей четверти видно, что функции sin(a) Третья четверть можно описать через градусную меру, как (180+α) или (270-α).

В четвертой четверти видно, что функция sin(a) , потому что ось Y отрицательна в этой четверти.
А функция cos(a)>0 , потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).

Теперь рассмотрим сами формулы приведения.

Запомним простой алгоритм :
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется .

И так начнем разбирать по четвертям данный алгоритм.

Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.

Будет cos(90-α) = sin(α)

Выясни чему будет равно выражение sin(90-α)

Рассуждаем по алгоритму:
1. Четверть первая.

Будет sin(90-α) = cos(α)

Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.

Будет cos(360+α) = cos(α)

Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)

Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.

3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)

Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:

1. Четверть вторая.

3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)

Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)

Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)

Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Урок и презентация на тему: «Применение формул приведения при решении задач»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
1С: Школа. Интерактивные задания на построение для 7-10 классов
1С: Школа. Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов

Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.

Повторение тригонометрических функций

Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли. Как думаете: где?

Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.

Правило для формул приведения

Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.

Вспомним некоторые формулы:

• sin(t + 2π*k) = sin(t)
• cos(t + 2π*k) = cos(t)
• sin(t + π) = -sin(t)
• cos(t + π) = -cos(t)
• sin(t + π/2) = cos(t)
• cos(t + π/2) = -sin(t)
• tg(t + π*k) = tg(x)
• ctg(t + π*k) = ctg(x)

формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения :

• Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.
• Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
  3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом.
• Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0

Эти правила применимы и когда аргумент функции задан в градусах!

Так же мы можем составить таблицу преобразований тригонометрических функций:

Примеры применения формул приведения

1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2

2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)

3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0

4. Преобразуем ctg(270 0 + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что 0

Задачи с формулами приведения для самостоятельного решения

Ребята, преобразуйте самостоятельно, используя наши правила:

1) tg(π + t),
2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).

Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!

Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.

Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.

Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:

– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.

– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.

– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.

– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.

И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.

Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?

Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:

угол альфа лежит пределах от 0 до 90 градусов

* * *

Итак, необходимо уяснить «закон», который здесь работает:

1. Определите знак функции в соответствующей четверти.

Напомню их:

2. Запомните следующее:

функция изменяется на кофункцию

функция на кофункцию не изменяется

Что означает понятие — функция изменяется на кофункцию?

Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.

Вот и всё!

Теперь по представленному закону запишем несколько формул приведения самостоятельно:

Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:

Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:

Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:

Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:

Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.

***

В статье на решение был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.

И еще одна задача B11 на ту же тему — из реального ЕГЭ по математике.

Задача. Найдите значение выражения:

В этом коротком видеоуроке мы узнаем, как применять формулы приведения для решения реальных задач B11 из ЕГЭ по математике. Как вы видите, перед нами — два тригонометрических выражения, каждое из которых содержит синусы и косинусы, а также довольно зверские числовые аргументы.

Прежде чем решать эти задачи, давайте вспомним, что такое формулы приведения. Итак, если у нас есть выражения вида:

То мы можем избавиться от первого слагаемого (вида k · π/2) по специальным правилам. Начертим тригонометрическую окружность, отметим на ней основные точки: 0, π/2; π; 3π/2 и 2π. Затем смотрим на первое слагаемое под знаком тригонометрической функции. Имеем:

1. Если интересующее нас слагаемое лежит на вертикальной оси тригонометрического круга (например: 3π/2; π/2 и т.д.), то исходная функция заменяется на ко-функцию: синус заменяется косинусом, а косинус — наоборот, синусом.
2. Если же наше слагаемое лежит на горизонтальной оси, то исходная функция не меняется. Просто убираем первое слагаемое в выражении — и все.

Таким образом, мы получим тригонометрическую функцию, не содержащую слагаемых вида k · π/2. Однако на этом работа с формулами приведения не заканчивается. Дело в том, что перед нашей новой функцией, полученной после «отбрасывания» первого слагаемого, может стоять знак плюс или минус. Как определить этот знак? Вот сейчас и узнаем.

Представим, что угол α, оставшийся внутри тригонометрической функции после преобразований, имеет очень малую градусную меру. Но что значит «малая мера»? Допустим, α ∈ (0; 30°) — этого вполне достаточно. Рассмотрим для примера функцию:

Тогда, следуя нашим предположениям, что α ∈ (0; 30°), заключаем, что угол 3π/2 − α лежит в третьей координатной четверти, т.е. 3π/2 − α ∈ (π; 3π/2). Вспоминаем знак исходной функции, т.е. y = sin x на этом интервале. Очевидно, что синус в третьей координатной четверти отрицателен, поскольку по определению синус — это ордината конца подвижного радиуса (короче синус — это координата y ). Ну, а координата y в нижней полуплоскости всегда принимает отрицательные значения. Значит, и в третьей четверти y тоже отрицателен.

На основании этих размышлений мы можем записать окончательное выражение:

Задача B11 — 1 вариант

Вот эти же самые приемы вполне подходят для решения задачи B11 из ЕГЭ по математике. Разница лишь в том, что во многих реальных задачах B11 вместо радианной меры (т.е. чисел π, π/2, 2π и т.д.) используется градусная мера (т.е. 90°, 180°, 270° и т.д.). Давайте посмотрим на первую задачу:

Сначала разберемся с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем сделать с ним. Пока так и оставим.

Теперь смотрим на знаменатель:

sin 131° = sin (90° + 41°) = cos 41°

Очевидно, что перед нами формула приведения, поэтому синус заменился на косинус. Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y = sin x там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).

Осталось разобраться с последним элементом:

cos 240° = cos (180° + 60°) = −cos 60° = −0,5

Здесь мы видим, что 180° — это горизонтальная ось. Следовательно, сама функция не поменяется: был косинус — и останется тоже косинус. Но вновь возникает вопрос: плюс или минус будет стоять перед полученным выражением cos 60°? Заметим, что 180° — это третья координатная четверть. Косинус там отрицательный, следовательно, перед косинусом в итоге будет стоять знак «минус». Итого, получаем конструкцию −cos 60° = −0,5 — это табличное значение, поэтому все легко считается.

Теперь подставляем полученные числа в исходную формулу и получаем:

Как видим, число cos 41° в числителе и знаменателе дроби легко сокращается, и остается обычное выражение, которое равно −10. При этом минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений. Ответ в любом случае получится −10. Все, задача B11 решена!

Задача B14 — 2 вариант

Переходим ко второй задаче. Перед нами снова дробь:

Ну, 27° у нас лежит в первой координатной четверти, поэтому здесь ничего менять не будем. А вот sin 117° надо расписать (пока без всякого квадрата):

sin 117° = sin (90° + 27°) = cos 27°

Очевидно, перед нами снова формула приведения : 90° — это вертикальная ось, следовательно, синус поменяется на косинус. Кроме того, угол α = 117° = 90° + 27° лежит во второй координатной четверти. Исходная функция y = sin x там положительна, следовательно, перед косинусом после всех преобразований все равно остается знак «плюс». Другими словами, там ничего не добавляется — так и оставляем: cos 27°.

Возвращаемся к исходному выражению, которое требуется вычислить:

Как видим, в знаменателе после преобразований возникло основное тригонометрическое тождество: sin 2 27° + cos 2 27° = 1. Итого −4: 1 = −4 — вот мы и нашли ответ ко второй задаче B11.

Как видите, с помощью формул приведения такие задачи из ЕГЭ по математике решаются буквально в пару строчек. Никаких синусов суммы и косинусов разности. Все, что нам нужно помнить — это только тригонометрический круг.

Для использования формул приведения существует два правила.

1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.

Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет.

2. Правило «каким ты был, таким ты и остался».

Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».

На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.

Вычислить Sin(150˚)

Воспользуемся формулами приведения:

Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен +. Значит у приведенной функции тоже будет знак «плюс». Это мы применили второе правило.

Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.

При желании все формулы приведения можно свести в одну таблицу. Но все же легче запомнить эти два правила и пользоваться ими.

Нужна помощь в учебе?

Предыдущая тема:

Произведение синусов и косинусов: формулы, примеры

Формула произведения косинуса, синуса используется в школьной алгебре для обучения школьников, а также в математическом анализе в расчетах. 

В этой статье разберем важные формулы для понятия тригонометрии: умножение косинусов и синусов, другие формулы, связанные с произведением двух алгебраических функций.

Важно

Теоремы умножения синусов и косинусов для α и β помогают превратиться из произведения в разность, сумму других углов.

Появилась необходимость, чтобы найти произведение косинусов, синусов углов α и , поэтому стоит изучить данную статью.

Данные формулы помогают преобразовать выражение от произведения к разности, сумме синусов и косинусов α−β и α+β.

Рассмотрим и выведем формулы синуса на синус, произведение синусов и косинусов. Также ниже разберем примерные задания с использованием формул.

Тригонометрические формулы произведения

Рассмотрим формулировки, формулы произведений. В независимости какими значениями обладают углы α и β или какие греческие буквы используются вместо обозначений α и β, применяются данные формулы и вычисляют с помощью них.

Произведение синусов формула

Произведение sin угла α и sin угла β будет равно половине разности косинуса угла (α−β) и (α+β).

\[\sin \alpha \cdot \sin \beta=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))\]

Произведение косинусов формула

Произведение cos угла α и cos угла β равно половине сумме косинуса угла (α-β) и (α+β).

\[\cos \alpha \cdot \cos \beta=\frac{1}{2}(\cos (\alpha-\beta)+\cos (\alpha+\beta))\]

Произведение синусов и косинусов формулы

Произведение синуса угла α на косинус угла β равно половине сумме синуса угла (α-β) и синуса угла (α+β).

\[\sin \alpha \cdot \cos \beta=\frac{1}{2}(\sin (\alpha-\beta)+\sin (\alpha+\beta))\]

Выведение тригонометрических формул

Для выведения формул, которые расположены выше, используется формулы сложения функций cos и sin, а также свойства равенства. В свойстве подразумевается, что если просуммировать правую и левую часть правильного равенства с другим таким же верным равенством, образуется новое правильное равенство.

Произведение косинусов

Приведем подробный вывод изучаемых формул

Для этого возьмем формулы косинуса разности и суммы:

\[\cos (\alpha+\beta)=\cos \alpha \cdot \cos \beta-\sin \alpha \cdot \sin \beta\]

\[\cos (\alpha-\beta)=\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta\]

Далее, с каждой стороны проведем сложение двух формул. Получается следующее:

\[\cos (\alpha+\beta)+\cos (\alpha-\beta)=\cos \alpha \cdot \cos \beta-\sin \alpha \cdot \sin \beta+\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta\]

Одинаковые слагаемые складываем: \[\cos \alpha \cdot \cos \beta+\cos \alpha \cdot \cos \beta=2 \cdot \cos \alpha \cdot \cos \beta\]

Разноименные слагаемые отнимаем: \[-\sin \alpha \cdot \sin \beta+\sin \alpha \cdot \sin \beta=0\]

Следовательно, \[\cos (\alpha+\beta)+\cos (\alpha-\beta)=2 \cdot \cos \alpha \cdot \cos \beta\]

В данном равенстве делим правую, левую часть на 2 , меняем местами слагаемые.

Получается следующее выражение \[\cos \alpha \cdot \cos \beta=\frac{1}{2}(\cos (\alpha+\beta)+\cos (\alpha-\beta))\]

Мы доказали формулу умножения cos одного угла на cos другого угла.

Произведение синусов

Теперь докажем следующую. Распишем формулу суммы косинусов так:

\[-\cos (\alpha+\beta)=-\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta\]

Прибавим к данному равенству \[\cos (\alpha-\beta)=\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta\]

Слагаемые одноименными знаками и функциями сложим, разноименные — вычтем, преобразуем выражение:

\[-\cos (\alpha+\beta)+\cos (\alpha-\beta)=-\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta+\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta-\cos (\alpha+\beta)+\cos (\alpha-\beta)=2 \cdot \sin \alpha \cdot \sin \beta\]

В данном равенстве делим правую, левую часть на 2, меняем местами слагаемые.

\[\sin \alpha \cdot \sin \beta=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))\]

Мы вывели формулу умножения синуса одного аргумента на синус другого аргумента.

Произведение синуса на косинус

Сделаем вывод формулы произведения синуса и косинуса разных аргументов. Теперь воспользуемся формулой суммы и разности функций sin. Складываем и правую, и левую часть выражений:

\[\sin (\alpha+\beta)=\sin \alpha \cdot \cos \beta+\cos \alpha \cdot \sin \beta\]

\[\sin (\alpha-\beta)=\sin \alpha \cdot \cos \beta-\cos \alpha \cdot \sin \beta\]

\[\sin (\alpha+\beta)+\sin (\alpha-\beta)=\sin \alpha \cdot \cos \beta+\cos \alpha \cdot \sin \beta+\sin \alpha \cdot \cos \beta-\cos \alpha \cdot \sin \beta\]

Слагаемые одноименными знаками и функциями сложим, разноименные — вычтем, преобразуем выражение:

\[\sin (\alpha+\beta)+\sin (\alpha-\beta)=2 \cdot \sin \alpha \cdot \cos \beta\]

В данном равенстве делим правую, левую часть на 2 , меняем местами слагаемые. {\circ}=\frac{1}{2}\left(\frac{\sqrt{3}}{2}+1\right)=\frac{\sqrt{3}}{4}+\frac{1}{2}\]

Ответ: \[\frac{\sqrt{3}}{4}+\frac{1}{2}\]

---

Пример 3

Пусть углы обладают значениями: \[\alpha=\frac{\Pi}{2}, \beta=\frac{\Pi}{6}\]. Найти значение произведение sin этих углов.

Решение:

Воспользуемся произведение синусов формулой:

\[\sin \alpha \cdot \sin \beta=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))\]

Подставим данные и получим:

\[\sin \frac{\pi}{2} \cdot \sin \frac{\pi}{6}=\frac{1}{2}\left(\cos \left(\frac{\pi}{2}-\frac{\pi}{6}\right)-\cos \left(\frac{\pi}{2}+\frac{\pi}{6}\right)\right)\]

Найдем знаменатель для двух дробей:

\[\sin \frac{\pi}{2} \cdot \sin \frac{\pi}{6}=\frac{1}{2}\left(\cos \left(\frac{\pi}{3}\right)-\cos \left(\frac{2 \pi}{3}\right)\right)\]

Для этого нам понадобится таблица со значениями функций косинуса и синуса, трансформируем  произведение синусов в сумму чисел:

\[\sin \frac{\pi}{2} \cdot \sin \frac{\pi}{6}=\frac{1}{2} \cdot\left(\frac{1}{2}-\left(-\frac{1}{2}\right)\right)\]

Вычислим и запишем ответ:

\[\sin \frac{\pi}{2} \cdot \sin \frac{\pi}{6}=\frac{1}{2}\]

Ответ: \[\frac{1}{2}\]

---

Пример 4

Дано следующее значение: \[\cos \cos \alpha=0,3\]. {2}-1=0,18-1=-0,82\]

Воспользуемся значениями в наше выражение, получим и запишем ответ:

\[\frac{1}{2} \cdot\left(\frac{1}{2}+\sin \sin \left(2 \alpha-\frac{\pi}{12}\right)\right) \cdot \frac{1}{2} \cdot\left(\frac{1}{2}-1\right)=-\frac{1}{4}\]

Ответ: \[-\frac{1}{4}\]

Замечание. Данные формулы произведения применяются, чтобы преобразовать сложные тригонометрические выражения в наиболее простые.

Почему синус (и косинус) образуют волны

Представьте себе прямоугольный треугольник. Тогда вы, вероятно, помните из школы, что вы можете использовать функции синуса и косинуса, чтобы узнать больше о треугольнике. Если один из углов не является прямым, то у вас есть

и

Для угла α синус дает отношение длины противоположной стороны к длине гипотенузы. Косинус дает отношение длины прилежащего катета к длине гипотенузы. (Изображение Dnu72 — CC BY-SA 3.0.)

Функции синуса и косинуса могут сделать гораздо больше, чем просто помочь вам решить геометрические задачи. Их можно использовать для создания волн любой формы — музыки, которую вы слушаете, цифрового сигнала, который вы отправляете через Wi-Fi, даже волны на море — независимо от того, насколько сложными могут быть эти естественные или созданные человеком колебания.

Идем по кругу

Первый шаг к построению волны состоит в том, чтобы представить круг радиусом 1, начерченный в декартовых координатах, с центром круга, лежащим в точке. Представьте себе движение по кругу против часовой стрелки, начиная с самая правая точка, . После того, как вы повернетесь на угол, который меньше 90 градусов (соответствует меньше, чем в радианах), точка, в которой вы находитесь, определяет прямоугольный треугольник с углами и Гипотенуза этого треугольника имеет длину 1, потому что точка лежит на наш круг радиуса равен 1. Для этого треугольника у нас есть и

Прямоугольный треугольник, образованный точкой единичной окружности.

Вы можете продолжать двигаться по кругу против часовой стрелки, чтобы сделать угол больше, чем Когда вы сделаете это, треугольник с углами и больше не будет иметь один из углов.

Когда α больше π/2, то прямоугольный треугольник, образованный из точки на единичной окружности, больше не содержит угол α.

Однако ничто не мешает вам расширить определения синуса и косинуса по аналогии с тем, что мы имели раньше:

где координаты точки, в которой вы находитесь.

Что происходит с синусом и косинусом при движении по кругу? За один оборот круга вы повернетесь на угол . Когда вы двигались по кругу, ваша вертикальная координата (синус) начиналась с и постоянно увеличивалась, пока не достигла максимума, когда вы были на вершине круга. По мере того, как вы продолжали двигаться, оно снова опускалось до симметричным образом, прежде чем достигло минимума, и, наконец, снова возвращалось к 0,9.0003

Если вы начертите, как вертикальная координата (выделена красным на рисунке ниже) изменяется в зависимости от угла поворота (от 0 до ), вы получите правильную форму волны. Он начинается с 0, поднимается до максимума 1, затем снова снижается до 0, прежде чем упасть до минимума -1, и снова вверх до 0.

Красная волна представляет собой синус угла, построенный по отношению к углу ( исходя из вертикальной координаты), а синяя волна представляет собой косинус угла, построенный по отношению к углу (исходя из горизонтальной координаты).

Эта волновая картина повторяется, когда вы продолжаете движение по кругу во второй раз, увеличивая угол, на который вы повернули от до, и в третий раз, путешествуя от до , и так далее. В итоге вы получите бесконечно длинную, совершенно правильную волну. Горизонтальные координаты (косинус) дают точно такую ​​же идеальную волну (показана синим цветом выше), смещенную относительно первой на расстояние вдоль горизонтальной оси. Это расширяет наше определение синуса и косинуса до углов, превышающих . (Вы также можете определить синус и косинус для отрицательных чисел, двигаясь по окружности по часовой стрелке.)

Красная волна представляет собой синус угла, построенный по отношению к углу (исходя из вертикальной координаты), а синяя волна представляет собой косинус угла, построенный по отношению к углу (исходя из горизонтальной координаты).

Сжатие и растяжение

Теперь мы увидели, как перемещение по единичному кругу может дать нам две функции, функцию синуса и функцию косинуса, каждая из которых имеет график, описывающий правильную волну. Когда вы сталкиваетесь с этими функциями в учебниках, обычно вызывается переменная, а не , поэтому вы увидите что-то вроде

Сейчас мы перейдем к этому обозначению. Это означает, что теперь он представляет то, что раньше было нашим углом, и что он больше не представляет координату точки на единичной окружности. Это потенциально немного сбивает с толку, но держитесь там, и вы привыкнете к этому.

Длина волны — это расстояние между двумя пиками волны, и в нашем примере пока это . Это потому, что для того, чтобы пройти один полный цикл нашей волны, мы должны были повернуться на угол .

Также можно создавать волны с разной длиной волны. Чтобы создать волну с длиной волны, вы умножаете переменную на, чтобы получить функции

Уменьшая длину волны, вы существенно сжимаете волну, а увеличивая ее, вы растягиваете ее.

В расположенном ниже приложении Geogebra используйте ползунок, чтобы изменить длину волны синуса (красный) и косинус (синий).

Движение выше и снижение

Пики волн, которые мы создали до сих пор, имеют значение 1, а впадины имеют значение -1. Чтобы создать волну с более высокими пиками и более низкими впадинами, вы просто умножаете всю функцию на константу, чтобы получить

Эта константа называется амплитудой волны.

В приведенном ниже приложении Geogebra используйте ползунки для изменения амплитуды и длины волны синусоиды (красный) и волны косинуса (синий).

Ускорение и замедление

Пока что волны, которые мы создали, являются стационарными: они не меняются со временем. Однако также возможно создавать волны, которые движутся вдоль. Наша волновая функция теперь будет функцией двух переменных и, как и раньше, представляет положение на горизонтальной оси, а обозначает время. Предположим, вы хотите, чтобы ваша волна двигалась со скоростью Функции

производят такие движущиеся волны. Если вы сохраняете временную переменную фиксированной, то вы, по сути, видите моментальный снимок во времени, давая вам стационарную волну, такую ​​же, как те, которые мы видели выше. Если вы сохраняете свое местоположение на -оси фиксированным, то вы видите соответствующую -переменную, когда она перемещается вверх и вниз с течением времени. Это немного похоже на наблюдение за тем, как определенная точка на поверхности озера двигается вверх и вниз, когда волны перекатываются через нее.

В апплете Geogebra ниже используйте ползунок для изменения скорости. Установка скорости на 0 (или нажатие кнопки паузы) соответствует времени остановки, поэтому вы сохраняете переменную времени фиксированной. В этом случае вы видите снимок во времени, который выглядит как обычная синусоида (или косинусоидальная) волна, только возможно сдвинутая по горизонтальной оси на некоторое расстояние. Фокусировка на синей точке соответствует фиксации переменной. (Здесь мы не даем вам возможность изменить длину волны и амплитуду, так как слишком большой выбор может сбить с толку!)

Причина, по которой аргумент наших функций теперь заключается в том, что за период времени длина волны, движущейся со скоростью, пройдет расстояние. Следовательно, высота волны в точке вдоль оси во времени будет такой же, как и высота была в то время 0 в точке, потому что это то, как далеко волна прошла во времени.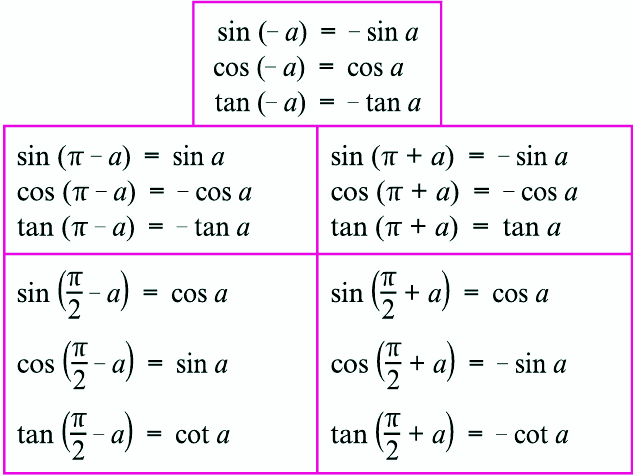

Расшифровка сообщений

На первый взгляд созданные нами синусоидальные и косинусоидальные волны кажутся слишком совершенными, чтобы рассказать вам о волнах, с которыми мы сталкиваемся в реальной жизни. Но вы можете услышать его в действии, если ударите по камертону. Звук, который вы слышите, является результатом вибрации барабанной перепонки, вызванной звуковой волной от камертона, распространяющегося по воздуху. Для камертона, если вы отобразите интенсивность или давление этой вибрации во времени, вы увидите идеальную синусоиду в действии.

Звуковая волна камертона (вверху) по сравнению с человеческой речью (внизу).

Как видите, звуковая волна чего-то вроде речи сложнее. Но любую звуковую волну, да и любую повторяющуюся функцию, можно разбить на ряд синусоид различных частот и амплитуд (интенсивностей). Это результат работы, начатой ​​французским математиком Жозефом Фурье, пережившим французскую революцию в восемнадцатом веке. Выражение звуковой волны или любого сигнала, изменяющегося во времени, как суммы составляющих его синусоидальных волн, известно как Преобразование Фурье этого сигнала. (Вы можете прочитать более подробное объяснение математики здесь — математика довольно сложна, но используемые математические идеи прекрасны!)

Функция f меняется во времени – представляющий звуковую волну. Процесс преобразования Фурье берет f и разлагает его в составляющие его синусоидальные волны с определенными частотами и амплитуды. Преобразование Фурье представлено в виде всплесков в частотной области, причем высота всплеска показывает амплитуду волны этой частоты.

---

Об этой статье

Эта статья была подготовлена ​​в рамках нашего освещения программы Дисперсионная гидродинамика: математика, моделирование и эксперименты с приложениями к нелинейным волнам , организованной Институтом математических наук Исаака Ньютона. Вы можете найти больше материалов о программе здесь.

Рэйчел Томас и Марианна Фрейбергер — редакторы Plus .

Эта статья основана на книге Нумерикон: путешествие по скрытым жизням чисел Марианны Фрейбергер и Рэйчел Томас и наша статья Преобразование Фурье изображений .

---

Эта статья была подготовлена ​​в рамках нашего сотрудничества с Институтом математических наук имени Исаака Ньютона (INI). Вы можете найти все материалы сотрудничества здесь.

INI — международный исследовательский центр и наш сосед по математическому кампусу Кембриджского университета. Он привлекает ведущих ученых-математиков со всего мира и открыт для всех. Посетите сайт www.newton.ac.uk, чтобы узнать больше.

Интуитивное понимание синусоидальных волн – BetterExplained

Синусоидальные волны меня смутили. Да, я могу бормотать «SOH CAH TOA» и рисовать линии внутри треугольников. Но что значит ?

Я застрял на мысли, что синус нужно извлекать из других форм. Быстрая аналогия:

Вы: Геометрия — это фигуры, линии и так далее.

Чужой: О? Можете ли вы показать мне линию?

Вы (оглядываясь): Э… видишь вон тот кирпич? Линия — это один край этого кирпича.

Инопланетянин: Значит, линии — это часть фигуры?

Вы: Вроде того. Да, в большинстве фигур есть линии. Но линия сама по себе является базовым понятием: луч света, маршрут на карте или даже…

Чужой: У кирпичей есть линии. Линии идут из кирпичей. Кирпичи кирпичи кирпичи.

Большинство уроков математики проходят именно так. «У кругов есть синус. Синус получается из кругов. Круги круги круги».

Арх! Нет — круги один пример синуса. В предложении: Синус — это естественное влияние, воплощение плавности: он делает круги «круглыми» точно так же, как линии делают квадраты «квадратными».

Давайте построим нашу интуицию, рассматривая синус как его собственную форму, а , а затем поймем, как он вписывается в круги и тому подобное. Вперед!

Синус против линий

Не забудьте отделить идею от примера : квадраты — это примеры линий. Синус щелкнул, когда он стал собственной идеей, а не «частью круга».

Давайте посмотрим на синус в симуляторе:

Хьюберт проведёт экскурсию:

• Нажми старт . Иди, Хьюберт, иди! Заметили это плавное движение вперед и назад? Это Хьюберт, но что более важно (извините, Хьюберт), это синус! Это естественно, как пружины подпрыгивают, маятники качаются, струны вибрируют… и многие вещи движутся.
• Изменить «вертикальный» на «линейный» . Большая разница — видите, как движение становится постоянным и роботизированным, как игра в понг?

Давайте рассмотрим различия с видео:

• Линейное движение постоянно: мы движемся с заданной скоростью и мгновенно разворачиваемся. Это неестественное движение в танце робота (обратите внимание на линейный отскок без замедления по сравнению со стробирующим эффектом).

• Синус меняет скорость: начинает быстро, замедляется, останавливается и снова ускоряется. Это чарующая плавность плавного танца (человеческая синусоида и естественный отскок).

К сожалению, в учебниках синус с анимацией или танцами не показан. Нет, они предпочитают вводить синус с временной шкалой (попробуйте установить «горизонтальную» на «временную шкалу»):

(источник)

Эгадс. Это схематическая диаграмма, которую нам всегда показывали. Это дает вам ощущение синуса? Не больше, чем скелет изображает ловкость кошки. Давайте посмотрим на синусоидальное движение и , а затем на графике его курса.

Неизбежный круг

Круги имеют синус. Да. Но увидеть синус внутри круга — это все равно, что достать яйца из омлета. Это все смешано!

Давайте помедленнее. В симуляции установите для Хьюберта значение vertical:none и horizontal: sine*. Видишь, как он извивается вбок? Это движение синуса. Есть небольшая поправка: обычно синусоидальный цикл начинается с нейтральной средней точки и достигает максимума. На этот раз мы начинаем с максимума и опускаемся к середине. Синус, который «начинается с максимума», называется косинусом, и это просто версия синуса (например, горизонтальная линия — это версия вертикальной линии).

Хорошо. Время для обеих синусоид: укажите вертикальную как «синус» и горизонтальную как «синус*». И… у нас есть круг!

Горизонтальная и вертикальная «пружины» вместе создают круговое движение. Большинство учебников рисуют круг и пытаются извлечь синус, но я предпочитаю наращивать: начинать с чистого горизонтального или вертикального движения и добавлять другое.

Быстрые вопросы и ответы

Несколько идей, которые я упустил при первом изучении синуса:

Синус действительно является одномерным

Синус колеблется в одном измерении. Действительно. Мы часто строим график синуса с течением времени (чтобы не писать поверх себя), и иногда «вещь», производящая синус, тоже движется, но это необязательно! Пружина в одном измерении — это совершенно счастливая синусоида.

(Источник: Википедия, постарайтесь не поддаваться гипнозу. )

Круги пример двух синусоид компоненты (синусы и прямые). Круг состоит из двух связанных одномерных волн, каждая из которых движется в горизонтальном и вертикальном направлениях.

(Источник http://1ucasvb.tumblr.com/)

Но помните, круги не являются началом синусов, так же как квадраты не являются началом линий. Это примеры двух синусоидальных волн, работающих вместе, а не их источника.

Что означают значения синуса?

Синусоидальный цикл между -1 и 1. Он начинается с 0, увеличивается до 1,0 (макс.), опускается до -1,0 (мин.) и возвращается в нейтральное положение. Я также вижу синус как процент от 100% (полный ход вперед) до -100% (полный отход).

Что такое ввод ‘x’ в sin(x)?

Каверзный вопрос. Синус — это цикл, а x, вход, равен , как далеко мы продвинулись в цикле .

Посмотрим на строки:

• Вы едете по квадрату. Каждая сторона занимает 10 секунд.
• Через 1 секунду вы завершили 10% на этой стороне
• Через 5 секунд вы готовы на 50%
• Через 10 секунд вы закончили сторону

В линейном движении мало сюрпризов. Теперь для синуса (сосредоточившись на цикле «от 0 до максимума»):

• Мы путешествуем по синусоиде от 0 (нейтраль) до 1,0 (максимум). Эта часть занимает 10 секунд.
• Через 5 секунд мы… на 70% готовы! Синус вылетает из ворот и замедляется. Большая часть выигрыша приходится на первые 5 секунд
• Требуется еще 5 секунд, чтобы перейти от 70% к 100%. А переход с 98% на 100% занимает почти целую секунду!

Несмотря на нашу начальную скорость, синус замедляется, поэтому мы осторожно целуем максимальное значение, прежде чем развернуться. Эта плавность делает синус синусом.

Для гиков: Нажмите «показать статистику» в симуляции. Вы увидите процент завершения всего цикла, мини-цикла (от 0 до 1,0) и достигнутое значение. Остановитесь, пройдите и переключитесь между линейным и синусоидальным движением, чтобы увидеть значения.

Быстрый тест: что дальше, 10% линейного цикла или 10% синусоидального цикла? Синус. Помните, он вылетает из ворот на максимальной скорости. К тому времени, когда синус достигает 50% цикла, он движется со средней скоростью линейного цикла, а за пределами этого он движется медленнее (пока не достигнет максимума и не развернется).

Итак, x — это «количество вашего цикла». Какой цикл?

Это зависит от контекста.

• Базовый триггер: «x» — градусы, а полный цикл — 360 градусов
• Расширенный триггер: «x» — это радианы (они более естественны!), а полный цикл проходит по единичному кругу (2*пи радиан)

Поиграйте со значениями x здесь:

Но опять же, циклы зависят от кругов! Можем ли мы избежать их тирании?

Пи без картинок

Представьте себе слепого инопланетянина, который замечает только оттенки света и тени. Не могли бы вы описать число пи? Трудно представить себе длину окружности, верно?

Вернемся немного назад. Синус — это повторяющийся узор, а это значит, что он должен… повторяться! Он идет от 0 до 1, до 0, до -1, до 0 и так далее.

Определим число пи как время, которое требуется синусу от 0 до 1 и обратно до 0. Ого! Теперь мы используем пи и без круга! Пи — это концепция, в которой просто случайно появляется в кругах:

• Синус — это мягкое раскачивание вперед-назад
• Pi — время от нейтрального до максимального и обратно
• n * Пи (0 * Пи, 1 * Пи, 2 * Пи и т. д.) — это время, когда вы находитесь в нейтральном положении
• 2 * пи, 4 * пи, 6 * пи и т. д. являются полными циклами

Ага! Вот почему число Пи появляется во многих формулах! Пи не «принадлежит» к окружностям больше, чем 0 и 1 — пи примерно по синусу возвращается в центр ! Окружность — это пример формы, которая повторяется и возвращается в центр каждые 2*пи. Но пружины, вибрации и т.д. возвращаются в центр после пи тоже!

Вопрос: Если пи — это половина естественного цикла, то почему это не простое число?

Ответим вопросом на вопрос.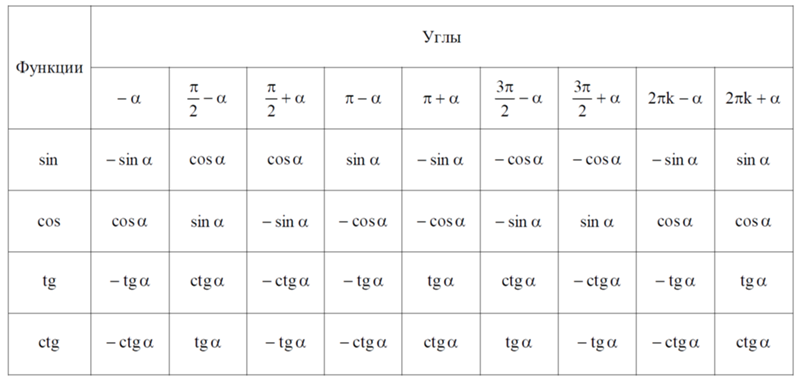 Почему квадрат 1×1 имеет длину диагонали $\sqrt{2} = 1,414…$ (иррациональное число)?

Философски неудобно, когда природа не совпадает с нашей системой счисления. У меня нет хорошей интуиции. Я подозреваю, что простые правила (квадрат 1×1 + теорема Пифагора) могут привести к сложным результатам.

Какова скорость синуса?

Я был хитрым. Раньше я говорил: «Представьте, что требуется синус 10 секунд от 0 до максимума». И теперь это пи секунд от 0 до максимума обратно к 0? Что дает?

• sin(x) — это по умолчанию , стандартная синусоидальная волна, которая действительно требует пи единиц времени от 0 до максимума до 0 (или 2*пи для полного цикла)
• sin(2x) — волна, которая движется в два раза быстрее
• sin(0.5x) — волна, которая движется в два раза медленнее

Итак, мы используем sin(n*x) для получения синусоиды, циклически повторяющейся так быстро, как нам нужно. Часто фраза «синусоида» относится к общей форме, а не к конкретной скорости.

Часть 2: Понимание определений синуса

Это познавательно — сделайте перерыв, если вам это нужно. Будем надеяться, что синус становится самостоятельным паттерном. Теперь давайте разовьем нашу интуицию, увидев, как связаны общие определения синуса.

Определение 1: Высота треугольника / круга!

Синус был впервые обнаружен в треугольниках. Возможно, вы помните «SOH CAH TOA» как мнемонику

• SOH: синус противоположен / гипотенуза
• CAH: косинус смежный / гипотенуза
• TOA: касательная противоположна/прилегает

Для прямоугольного треугольника с углом x sin(x) — это длина противоположной стороны, деленная на гипотенузу. Если мы сделаем гипотенузу 1, мы можем упростить до:

• Синус = Противоположный
• Косинус = Смежный

А если поумнеть, то мы можем начертить наши треугольники с гипотенузой 1 в круге с радиусом 1:

Вуаля! Круг, содержащий все возможные прямоугольные треугольники (поскольку их можно увеличить, используя сходство). Например:

• sin(45) = 0,707
• Положите 10-футовый шест и поднимите его на 45 градусов. 10 * sin(45) = 7,07 фута от земли
• 8-футовый шест будет равен 8 * sin(45) = 5,65 фута

Эти прямые манипуляции отлично подходят для построения (пирамиды сами себя не вычислят). К сожалению, спустя тысячи лет мы начинаем думать, что означает, что синуса — это высота треугольника. Нет-нет, это фигура, в которой показывает в кругах (и треугольниках).

На самом деле, для решения многих задач мы переходим в «режим геометрии» и начинаем думать «синус = высота», чтобы ускорить решение задач. Это нормально — просто не застрять там.

Определение 2: Бесконечный ряд

Я избежал слона в комнате: как, черт возьми, мы вычисляем синус!? Мой калькулятор рисует круг и измеряет его?

Рад вас разозлить. Вот секрет синуса без круга:

Синус — это ускорение, противоположное вашему текущему положению

Используя нашу метафору банковского счета: представьте себе извращенного босса, который дает вам повышение на против вашего текущего банковского счета! Если у вас есть 50 долларов в банке, то ваша надбавка на следующей неделе составит 50 долларов. Конечно, ваш доход может составлять $75 в неделю, так что вы все равно будете зарабатывать $75-$50 за эту неделю), но в конечном итоге ваш баланс уменьшится, так как «повышения» превысят ваш доход.

Но не бойся! Как только ваш счет станет отрицательным (скажем, вы на 50 долларов), тогда ваш босс даст законную прибавку в 50 долларов в неделю. Опять же, ваш доход может быть отрицательным, но в конечном итоге повышение превысит его.

Это постоянное притяжение к центру поддерживает цикл: когда вы поднимаетесь вверх, «притяжение» снова втягивает вас внутрь. Это также объясняет, почему нейтральная максимальная скорость для синуса: если вы находитесь на максимальной скорости, вы начинаете падать и накапливать все больше и больше «отрицательных подъемов» по ​​мере падения. Когда вы проходите через нейтральную точку, вы чувствуете все возможные отрицательные подъемы (как только вы пересекаете их, вы начинаете получать положительные подъемы и замедляетесь).

Кстати: поскольку синус — это ускорение, противоположное вашему текущему положению, а окружность состоит из горизонтального и вертикального синуса.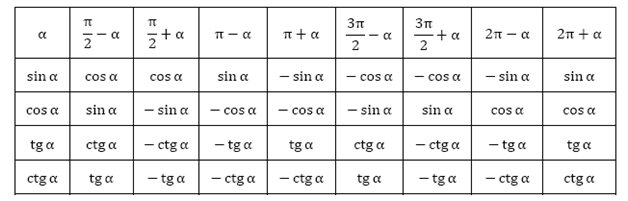 .. вы поняли! Круговое движение можно описать как «постоянное притяжение, противоположное вашему текущему положению, к вашему горизонтальному и вертикальному центру».

Знакомство с исчислением

Давайте опишем синус с помощью исчисления. Как и e, мы можем разбить синус на более мелкие эффекты:

• Начать с 0 и увеличивать с единичной скоростью
• В каждое мгновение отталкиваться отрицательным ускорением

Как мы должны думать об этом? Посмотрите, как каждый эффект изменяет наше расстояние от центра:

• Наш начальный удар увеличивает расстояние линейно: y (расстояние от центра) = x (затраченное время)
• В любой момент мы чувствуем возвращающую силу $-x$. Мы дважды интегрируем, чтобы превратить отрицательное ускорение в расстояние:

Наблюдать за тем, как ускорение влияет на расстояние, все равно, что наблюдать, как повышение зарплаты бьет по вашему банковскому счету. «Повышение» должно изменить ваш доход, а ваш доход меняет ваш банковский счет (два интеграла «вверх по цепочке»). 97}{7!}$, создающий восстанавливающую силу удара…

Как и е, синус можно описать бесконечным рядом:

Я много раз видел эту формулу, но она сработала только тогда, когда я увидел синус как комбинацию начального импульса и восстанавливающих сил . Первоначальный толчок (y = x, становится положительным) в конечном итоге преодолевается восстанавливающей силой (которая притягивает нас к отрицательному значению), которая подавляется собственной восстанавливающей силой (которая притягивает нас к положительному) и так далее.

Несколько забавных заметок:

• Рассмотрим «возвращающую силу», например «положительный или отрицательный процент». Это облегчает понимание связи синус/е в формуле Эйлера. Синус похож на e, за исключением того, что иногда он приносит отрицательный процент. Здесь есть чему поучиться :).
• Для очень малых углов «y = x» является хорошим приближением для синуса. Мы просто принимаем первоначальный импульс и игнорируем любые восстанавливающие силы.

Вычисление косинуса

Косинус — это просто сдвинутый синус, и это весело (да!) теперь, когда мы понимаем синус: 92}{2!}$. Но это запускает другую восстанавливающую силу, которая запускает другую, и прежде чем вы это узнаете:

Определение 3: Дифференциальное уравнение

Мы описали поведение синуса с помощью конкретных уравнений. Более краткий способ (уравнение):

Эта красота говорит:

• Наша текущая позиция y
• Наше ускорение (вторая производная или y») противоположно нашему текущему положению (-y)

И синус, и косинус подтверждают это. Сначала я ненавидел это определение; это так далеко от визуализации. Я не знал, что это описывает сущность синуса, «ускорение против вашего положения». 9x$ можно описать (уравнением):

То же уравнение с положительным знаком («ускорение равно вашему положению»)! Когда синус — это «высота круга», очень сложно установить связь с e.

Одно из моих величайших математических сожалений — это то, что я не выучил дифференциальные уравнения. Но я хочу, и я подозреваю, что наличие интуиции для синуса и е будет иметь решающее значение.

Подведение итогов

Цель состоит в том, чтобы перевести синус из некоторой математической мелочи («части круга») в его собственную форму:

• Синус — это плавное колебательное движение между минимумом (-1) и максимумом (1). Математически вы ускоряетесь против своей позиции. Этот «отрицательный процент» держит синусоиды вечно.
• Синус появляется в кругах и треугольниках (и пружины, маятники, вибрации, звук…).
• Pi — это время от нейтрального до нейтрального в sin(x). Точно так же число «пи» не «принадлежит» кругам, оно просто появляется там.

Позвольте синусу войти в ваш набор умственных инструментов ( Хм, мне нужна формула для плавных изменений… ). В конце концов, мы интуитивно поймем основы (е, пи, радианы, мнимые числа, синус…), и их можно смешать в восхитительный математический салат. Наслаждаться!

Приложение

Используя этот подход, Алистер Макдональд создал отличный учебник с кодом для создания собственных функций синуса и косинуса.