| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.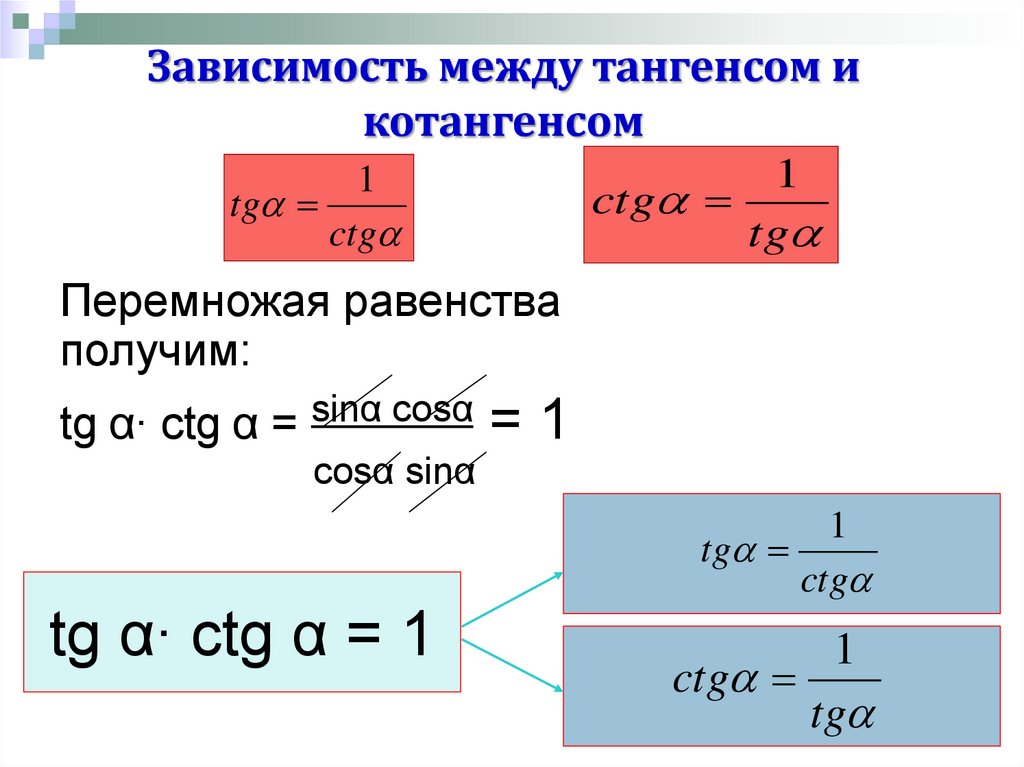 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.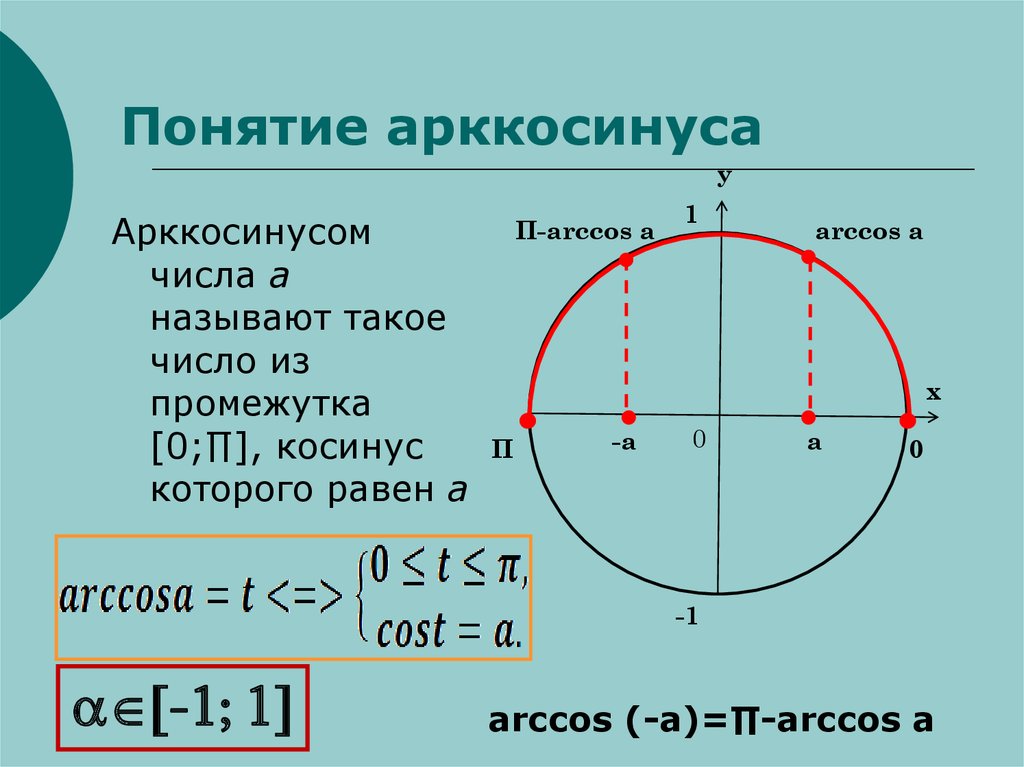 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
|
Пожалуйста активируйте JavaScript в настройках браузера.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Как угол может быть отрицательным?
спросил
Изменено 6 лет, 11 месяцев назад
Просмотрено 12 тысяч раз
$\begingroup$
Как угол может быть отрицательным, как синус (-60), косинус (-50) ?
В какой квадрант они попадают, если у нас отрицательные углы? Я не вижу никаких отрицательных углов в полном круге 360
- исчисление
- геометрия
- тригонометрия
- треугольники
$\endgroup$
5
$\begingroup$
Углы увеличиваются положительно при увеличении против часовой стрелки. Таким образом, отрицательный угол — это угол, который начинается в направлении по часовой стрелке . 60 — это угол 60 градусов над осью x, поэтому -60 — это угол 60 градусов ниже по оси x.
Таким образом, отрицательный угол — это угол, который начинается в направлении по часовой стрелке . 60 — это угол 60 градусов над осью x, поэтому -60 — это угол 60 градусов ниже по оси x.
Угловые меры считаются циклическими и любой угол $x$ равен $x \pm 360$. Так что $-60$ это то же самое, что и $300$.
В частности 180 = -180. Также удобны -90=270. Ну и конечно 0=360.
====
Верьте или нет вы столкнетесь с ситуациями, когда нужно считать углы в 720 градусов. Это просто 0.
Иногда вам придется сделать что-то вроде sin(x + y) или cos(x — y) и получить такие вещи, как x = 135 и y = 243. Полезно знать, что 125 + 243 = 368 = 8 и 135 — 243 = -108 имеют смысл. (На самом деле -108 = 108 по часовой стрелке гораздо удобнее, чем 252 градуса.) 9\circ$.
$\endgroup$
$\begingroup$
Отрицательные углы связаны с ориентацией по окружности, так же как отрицательные абсциссы связаны с направлением движения по прямой линии: как только вы решили, что является положительным направлением движения (слева направо , или справа налево), прямая линия становится ( ориентированной ) осью , и точки на этой оси могут иметь положительную или отрицательную абсциссу.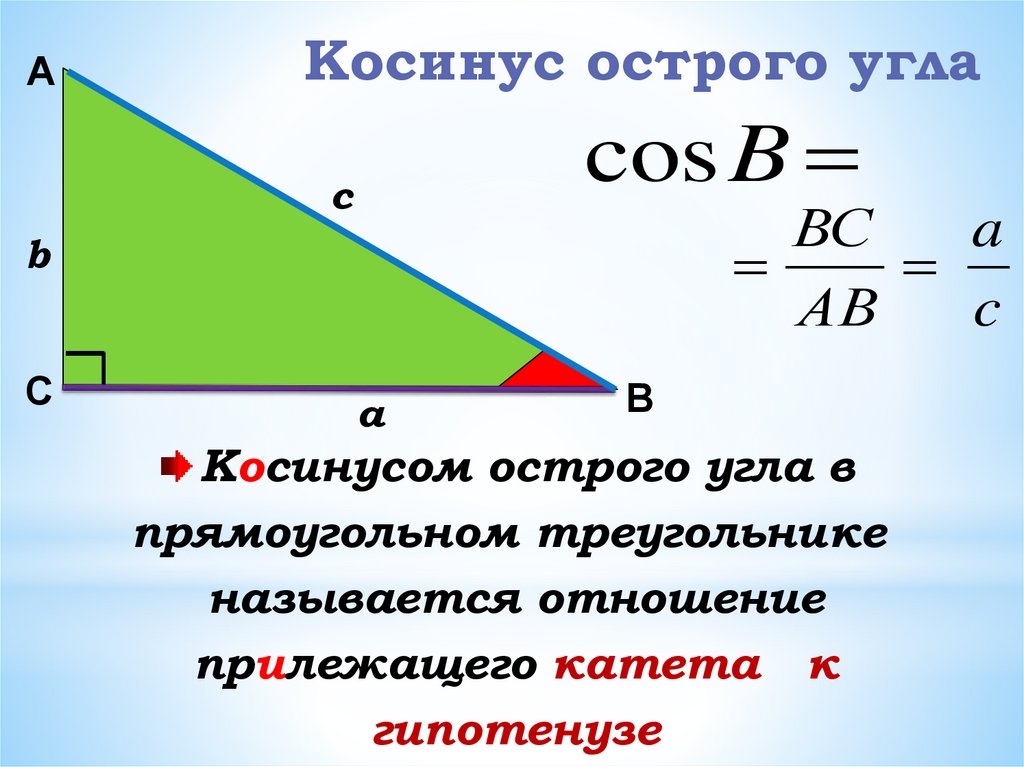
Точно так же, как только вы решили, что такое положительное вращение на окружности (по часовой стрелке или против часовой стрелки), она становится ориентированной (или тригонометрической ) окружностью. Помните, что угол в каком-то смысле является всего лишь криволинейной абсциссой на окружности с радиусом $1$.
$\endgroup$
Что такое инверсия косинуса?
TranscriptPractice
Привет и добро пожаловать в это видео на Обратные триггерные функции ! Чтобы понять, что такое обратные тригонометрические функции, давайте сначала рассмотрим, что такое нормальные тригонометрические функции. Помните, общие три функции триггера синус , косинус и тангенс . Эти триггерные функции используются для связывания мер стороны и угла треугольника друг с другом. Например, мы бы использовали тангенс в задаче, где нам нужно найти недостающую длину стороны треугольника.
Эти триггерные функции используются для связывания мер стороны и угла треугольника друг с другом. Например, мы бы использовали тангенс в задаче, где нам нужно найти недостающую длину стороны треугольника.
Если мы вспомним SOH-CAH-TOA, мы увидим, что в этом треугольнике используется TOA, что означает:
\(\tan{\Theta} =\frac{противоположный}{прилегающий} \)
.
Если мы подставим значения для нашего треугольника, мы получим:
\(\tan {30} =\frac{3}{x}\)
.
Перестановка для получения x сама по себе дает нам:
\(x=\frac{3}{tan 30}\)
.
Что затем упрощается до:
\(x\примерно 5,20\)
.
Но что, если нам дан треугольник, стороны которого известны, но мы хотим знать угол, например:
=\фракция{7}{18}\) 9{-1}{x}\) (или tan inverse x ). {\circ}\) 9{\circ}\).
{\circ}\) 9{\circ}\).
Я хочу, чтобы вы попробовали еще раз, но на этот раз сделайте это самостоятельно. После того, как я покажу вам проблему, остановите видео и проработайте ее. Затем, когда вы закончите, посмотрите, совпадает ли ваш ответ с моим.
Найти x .
В этой задаче нам даны прилежащие стороны и гипотенуза, и мы ищем угол между ними. Это означает, что мы собираемся использовать CAH. Если мы составим наше уравнение, оно будет выглядеть так:
\(\cos {x} =\frac{9{\circ}\)
.
Помните, что обратные триггерные функции прямо противоположны триггерным функциям. Триггерные функции используются для нахождения отношения сторон треугольника к углу, а обратные триггерные функции помогают определить, какова мера угла при заданном отношении сторон.
Надеюсь, этот обзор обратных триггерных функций был полезен. Спасибо за просмотр и удачной учебы!
Вопрос № 1:
В каком из пунктов показан неправильный способ выражения обратной функции триггера тангенса? 9{-1}х\). Обратные триггерные функции используются для вычисления мер углов прямоугольного треугольника, когда известны меры сторон.
Обратные триггерные функции используются для вычисления мер углов прямоугольного треугольника, когда известны меры сторон.
Скрыть ответ
Вопрос №2:
Какова мера угла \(x\)?
\(53,7°\)
\(46,7°\)
\(36,7°\)
\(40,7°\)
Показать ответ
сторона равна \(8\), а гипотенуза равна \(11\). Это означает, что будет использоваться SOH или 9{-1}\frac{8}{11}\), что упрощается примерно до \(46,7°\).
Скрыть ответ
Вопрос №3:
Какой угол будет найден с помощью синуса, косинуса или тангенса?
Синус
Косинус
Тангенс
Инверсия
Показать Ответ
Ответ:
Неизвестный угол будет определен с помощью функции косинуса. Длина смежной стороны и гипотенуза 9{-1}\frac{9}{12}\), что упрощается до \(41,4°\).
Длина смежной стороны и гипотенуза 9{-1}\frac{9}{12}\), что упрощается до \(41,4°\).
Скрыть ответ
Вопрос № 4:
Дерево высотой \(51\) футов отбрасывает тень длиной \(62\) футов. Какой угол возвышения образуется между землей и синей линией?
\ (29,4 ° \)
\ (51,4 ° \)
\ (39,4 ° \)
\ (44,4 ° \)
Покажите Ответ
Ответ:
противоположность
. рядом 9{-1}\frac{51}{62}\), что упрощается до \(x=39,4°\).
Скрыть Ответ
Вопрос № 5:
Какой угол образует лестница с землей, чтобы лестница достигла вершины десятифутовой стены, которая находится в трех футах от основания лестница?
\(73,3°\)
\(63,3°\)
\(81,3°\)
\(79,3°\)
Показать ответ
90 \ ) можно рассчитать с помощью обратной триггерной функции.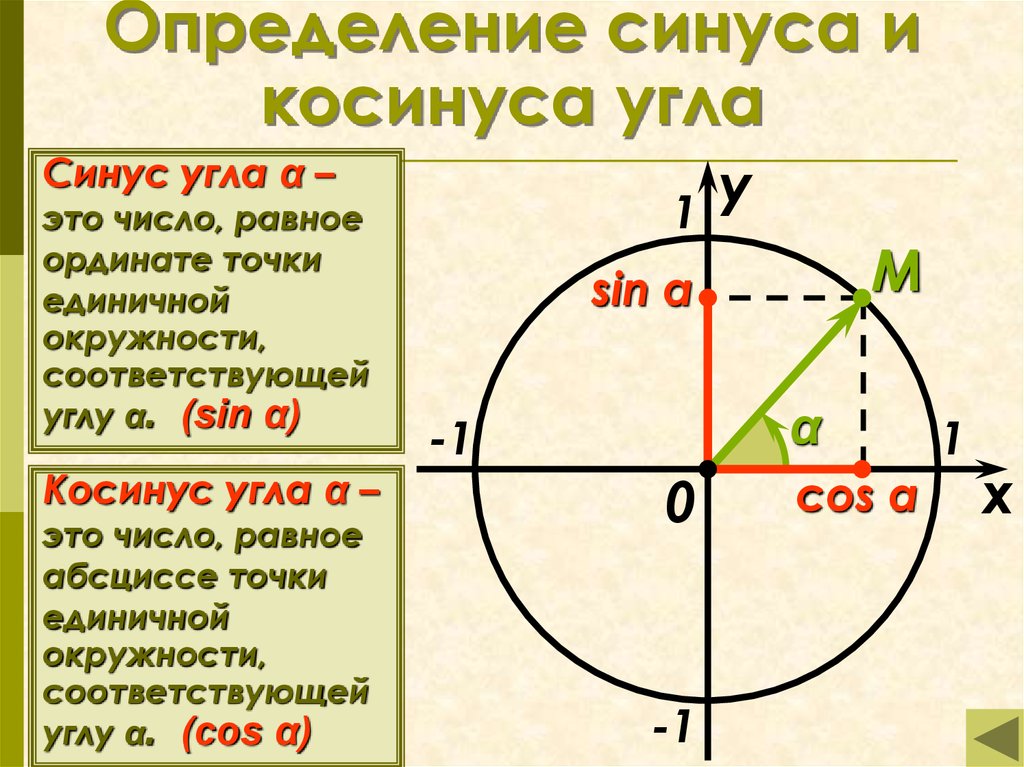

 Обмену опытом эксплуатации РЗА. Общению релейщиков ЕЭС России.
Обмену опытом эксплуатации РЗА. Общению релейщиков ЕЭС России. 08.2008
08.2008 ..
.. 04.2007
04.2007 11.2010 13:21
11.2010 13:21 03.2008
03.2008 11.2010 13:40
11.2010 13:40 11.2009
11.2009
 замеряют до сотен всяких параметров, определяют «качество» электроэнергии.
замеряют до сотен всяких параметров, определяют «качество» электроэнергии. 04.2007
04.2007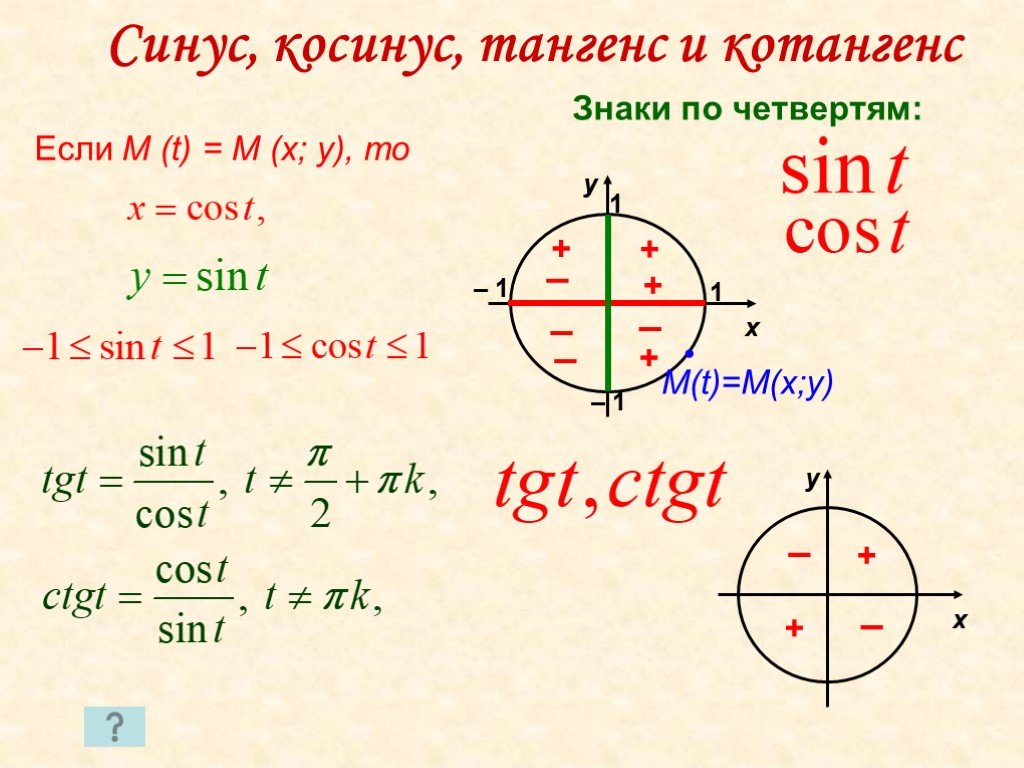 11.2010 15:01
11.2010 15:01 03.2008
03.2008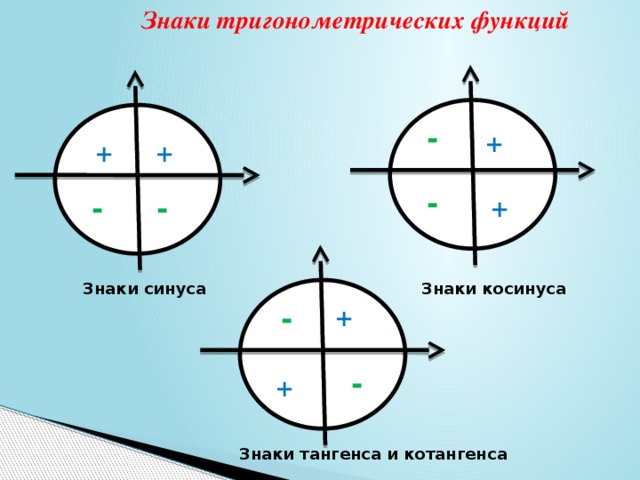 Посколько косинус функция четная, то при углах от меньше 90 по модулю он положителен.
Посколько косинус функция четная, то при углах от меньше 90 по модулю он положителен.