2. Правила двоичной арифметики
В любой позиционной системе счисления операции сложения и вычитания двух чисел A B=С осуществляются поразрядно, начиная с младших разрядов.
При сложении переполнение из младшего разряда переносится в старший разряд, т. е. код суммы каждого i-ого разряда сi получается в результате сложения ai + bi + 1, где 1 соответствует переносу из младшего (i -1)-разряда в i-ый, если в младшем разряде код суммы получился больше или равным основанию системы счисления.
При вычитании требуемый заем производится из старшего разряда, т. е. код разности каждого i-ого разряда сi получается в результате вычитания ai —

2.1. Правила сложения двоичных чисел.
В каждом разряде выполняется сложение двух цифр слагаемых и единицы переноса из соседнего младшего разряда, если она есть.
Поразрядная сумма формируется по следующим правилам:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 – осуществляется перенос 1 в старший разряд
Например, сложение 510 + 310 = 810
1012 = 510
+ 0112 = 310
10002 = 810
Суммирование двоичных чисел в компьютерах осуществляется при помощи устройств, называемых двоичными сумматорами.
2.2. Правила вычитания двоичных чисел.
В
каждом разряде выполняется вычитание
из цифры числа цифры вычитаемого, при
вычитании из нуля единицы происходит
заем единицы из соседнего старшего
разряда, которая равна 2 единицам данного
разряда.
Поразрядная разность формируется по следующим правилам:
0 — 0 = 0
1 — 0 = 1
1 — 1 = 0
0 — 1 = 1 – после заема 1 из старшего разряда
Например, вычитание 610 – 310 = 310
01102 = 610
–00112 = 310
00112 = 310
Как правило, вычитание двоичных чисел в компьютерах осуществляется при помощи двоичных сумматоров: при представлении вычитаемого в дополнительном или обратном коде операцию вычитания можно заменить операцией сложения.
2.3. Правила умножения двоичных чисел.
Умножение двоичных чисел производится путем образования промежуточных произведений и последующего их суммирования.
Поразрядные произведения формируются по следующим правилам:
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
Например, умножение 510 x 310 = 1510
101
11
101+101
1111
2.
 4. Правила деления двоичных чисел.
4. Правила деления двоичных чисел.Деление двоичных чисел производится по правилам умножения и вычитания.
Например, деление 610 : 310 = 210
110 : 11 = 10
110 11
–11 10
00
3. Операция сдвига по разрядной сетке
В компьютерах, кроме операции алгебраического суммирования двоичных чисел, к которой относятся операции сложения и вычитания, выполняется операция сдвига числа по разрядной сетке влево и вправо, осуществляющая, фактически, умножение и деление двоичных чисел.
В случае сдвига влево осуществляется умножение двоичного числа на 2j, а при сдвиге вправо – деление на 2j, где j – количество разрядов, на которое сдвигается двоичное число.
Например, осуществить сдвиг на 2 разряда
1) 0000112 = 310 влево
0011002 = 1210
т. е. 3 х 4(22)
= 1210
е. 3 х 4(22)
= 1210
2) 0010002 = 810 вправо
0000102 = 210
т. е. 8 : 4(22) = 210
В компьютерах часто используется циклический сдвиг, при выполнении которого разрядная сетка, отведенная для операнда (числа, над которым производится действие), представляется замкнутой в кольцо. Тогда при сдвиге влево содержимое старшего разряда попадает в младший разряд операнда, а при сдвиге вправо
содержимое младшего разряда попадает в старший разряд операнда.3. Умножение в двоичной системе счисления.
Умножение двух
двоичных много разрядных цифр выполняется
аналогично умножению десятичных чисел.
Сначала вычисляются частичные произведения
множимого на каждый разряд множителя.
Если умножение начинается со старшего
разряда множителя, то каждое следующее
частное произведение сдвигается на
один разряд вправо по отношению к
произведению, полученному ранее. Затем
полученные частные произведения
складываются по правилам двоичного
сложения, причем суммирование частных
произведений выполняется последовательно.
Затем
полученные частные произведения
складываются по правилам двоичного
сложения, причем суммирование частных
произведений выполняется последовательно.
Положение запятой определяется также, как при умножении десятичных чисел.
Для выполнения операции умножения в двоичной системе счисления необходимо помнить следующее правило:
0*0=0
0*1=0
1*0=0
Пример 4.
Умножить двоичное число А на число В.
А 1101 — множимое
В 1010 — множитель
1101
+ 0000 — частное
1101 произведение
0000
10000010
1111000 — перенос
Пример 5. Выполнить умножение:
Выполнить умножение:
а) 100111(2) х 1000111(2) = 101011010001(2);
б) 1170,64(8) х 46,3(8) = 57334,134(8);
в) 61,А(1б) х 40,D(16) = 18В7,52(1б).
4. Деление в двоичной системе счисления.
Деление в двоичной системе счисления выполняется, так же как и в десятичной системе, путем подбора очередной цифры частного, которая затем умножается на делитель. Полученное произведение вычитается из делимого для проверки правильности подобранной цифры. Затем процесс повторяется до тех пор, пока остаток не окажется меньше делителя.
В целом процесс деления числе в двоичной системе счисления сводится к операциям умножения и вычитания.
Пример 6.
1 10000 110
110 10000
000
5. Машинные коды чисел.
Для выполнения
операций в ЭВМ числа кодируются
специальными машинными кодами. Эти коды
позволяют свести операцию вычитания к
сложению и сдвигу вправо или влево. При
использовании машинных кодов автоматически
учитываются знаки чисел, определяется
знак результата и переполнение разрядной
сетки. Обычно применяются прямой,
обратный и дополнительный коды чисел.
Эти коды
позволяют свести операцию вычитания к
сложению и сдвигу вправо или влево. При
использовании машинных кодов автоматически
учитываются знаки чисел, определяется
знак результата и переполнение разрядной
сетки. Обычно применяются прямой,
обратный и дополнительный коды чисел.
Прямой, обратный и дополнительный коды положительного двоичного числа совпадают с самим числом, причем значение знакового разряда применяется равным нулю. Например, число +0,1001101 в прямом, обратном и дополнительном кодах записывается в виде 0,1001101.
Прямой код отрицательного числа — это само двоичное число, причем в разряде фиксируется единица. Например, для числа –0,1001101 прямой код соответствует 1,1001101.
Прямой код используется для хранения числе в ЗУ, в устройствах ввода и вывода, а также при выполнении операций умножения.
Обратный
код отрицательного числа образуется
заменой единиц мантиссы числа нулями,
а нулей – единицами, код знака при этом
сохраняется, то есть остается единичным. Например, для числа — 0,1001101 обратный код
будет 1,0110010.
Например, для числа — 0,1001101 обратный код
будет 1,0110010.
Дополнительный код отрицательного числа образуется как результат суммирования обратного кода числа с единицей младшего разряда, а в знаковом разряде содержится единица. Например, для числа — 0,1001100 дополнительным кодом является 1,0110011.
Чтобы преобразовать дополнительный код отрицательного числа в прямой код, необходимо в числовых разрядах этого числа заменить нули на единицы, а единицы на нули и прибавить к полученному результату единицу младшего разряда.
В современных ЭВМ в арифметических операциях, как правило, используется дополнительный код, причем отрицательные числа хранятся в памяти в дополнительном коде.
| | |||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||
Умножение — TRCCompSci — AQA Computer Science
Видео с 5:46
https://www.youtube.com/watch?v=t15dhDG_WUA&list=PLCiOXwirraUDGCeSoEPSN-e2o9exXdOka&index=2 (5:46 – конец)
Двоичное умножение использует комбинацию умножения на единицу, сдвига и сложения. При умножении двоичного числа на 10 оно просто сдвигается влево в следующий столбец, при этом исходное число умножается на 2. Умножение на 100 вызывает сдвиг на два разряда влево, в результате чего исходное число умножается на четыре.
Умножение на 100 вызывает сдвиг на два разряда влево, в результате чего исходное число умножается на четыре.
Правила умножения двоичного числа на другое двоичное число:
Для каждой единицы в множителе повторите умножаемое число с таким количеством нулей справа от него, сколько цифр перед единицей в множителе. На каждый 0 в множителе ничего не пишется.
Например, умножьте 22 на 5, что в двоичном формате равно 10110 на 101:
10110 х 101 (множитель)
, начиная справа налево, в множителе стоит 1, поэтому мы записываем умножаемое число как обычно 10110.
10110 х 101 (множитель) ----- 10110
Второе число в множителе равно 0, поэтому ничего не пишем.
Последнее число в множителе — 1, а перед ним две цифры 0 и 1, 2 цифры, поэтому мы записываем умножаемое число с 2 нулями справа от него, 10110 00
10110 х 101 (множитель) ------- 10110 1011000 -------
После того, как число умножено на все цифры множителя, мы просто складываем их, используя двоичное сложение, будьте внимательны при записи чисел, чтобы они правильно выстроились для сложения.
10110 + 1011000 ------- 1101110 -------
Преобразование 1101110 в денарии дает нам 110, то есть 22×5.
| 100111 | |||||||||||||
| → | Правильно. | ||||||||||||
| 10000 | |||||||||||||
| → | Вы сложили их вместе. | ||||||||||||
| 10101 | |||||||||||||
| Умножьте 10101 на 11. Ответ оставьте в виде 8-битного двоичного числа. |
| → Первая единица равна 1, поэтому мы добавляем первое число один раз. |
| → 10101 |
| → Вторая единица также равна 1, поэтому мы добавляем первое число, но сдвигаем его влево на одну единицу. |
| → 101010 |
| → Затем мы складываем эти два числа вместе. |
| → 111111 |
| → Наконец, добавьте дополнительные биты, чтобы сделать его 8-битным |
| → 00111111 |
Умножьте 10111 на 101. Ответ оставьте в виде 8-битного двоичного числа. Ответ оставьте в виде 8-битного двоичного числа. |
| Умножьте 11111 на 101. Оставьте свой ответ в виде 8-битного двоичного числа. |
| → Первая единица равна 1, поэтому мы добавляем первое число один раз. |
| → 11111 |
| → Вторая единица равна 0, поэтому ничего не делаем. |
| → Третья единица равна 1, поэтому мы добавляем первое число один раз, но сдвигаем его влево на две единицы. |
| → 1111100 |
| → Затем мы складываем два двоичных числа вместе. |
| → 00011111 |
| → + |
| → 01111100 |
| → 10011011 |
| 100100 | |||||||||||||
| → | You added them together | ||||||||||||
| 100010011 | |||||||||||||
| → | Correct | ||||||||||||
| 1100100 | |||||||||||||
Multiply 110111 by 011. Leave your answer as an 8-bit binary number . Leave your answer as an 8-bit binary number . |
| → Первая единица равна 1, поэтому мы добавляем первое число один раз. |
| → 110111 |
| → Вторая единица равна 1, поэтому мы добавляем первое число один раз, но один раз перемещаем его влево. |
| → 1101110 |
| → Третья единица равна 0, поэтому ничего не делаем. |
| → Сложите два числа вместе. |
| → 110111 + 1101110 |
| → 10100101 |
| Умножение 1011001 на 1101. Оставьте свой ответ в качестве 8-битного бинарного номера. |
| 101010100 | |||||||||||||
| → | Правильно. | ||||||||||||
| 100001010 | |||||||||||||
| → | Вы сложили их вместе. | ||||||||||||
| 101010010 | |||||||||||||
Умножьте 1010011 на 101. Оставьте свой ответ в виде 8-битного двоичного числа. Оставьте свой ответ в виде 8-битного двоичного числа. |
| Умножьте 11011 на 110. Ответ оставьте в виде 8-битного двоичного числа. |
| Умножьте 01101 на 11. Оставьте свой ответ в виде 8-битного двоичного числа. |
| Умножьте 101010 на 111. Ответ оставьте в виде двоичного числа. |
| Умножьте 11111 на 11. Ответ оставьте в виде 8-битного двоичного числа. |
| Умножьте 110011 на 101. Оставьте свой ответ в виде 8-битного двоичного числа. |
| Умножьте 00110101 на 1111. Ответ оставьте в виде 8-битного двоичного числа. |
Умножьте 1111 на 1111. |

 Этот калькулятор предназначен для умножения и деления значений любых двоичных чисел . Сначала введите основное число (в двоичном формате; убедитесь, что оно допустимо), затем введите дополнительное число (также в двоичном формате) для расчета и нажмите «Рассчитать». Второе число умножается на первое и делится на первое; значения рассчитываются до 18 цифр как в десятичном, так и в двоичном формате. Вы можете нажать «Очистить значения», чтобы сделать другое.
Этот калькулятор предназначен для умножения и деления значений любых двоичных чисел . Сначала введите основное число (в двоичном формате; убедитесь, что оно допустимо), затем введите дополнительное число (также в двоичном формате) для расчета и нажмите «Рассчитать». Второе число умножается на первое и делится на первое; значения рассчитываются до 18 цифр как в десятичном, так и в двоичном формате. Вы можете нажать «Очистить значения», чтобы сделать другое.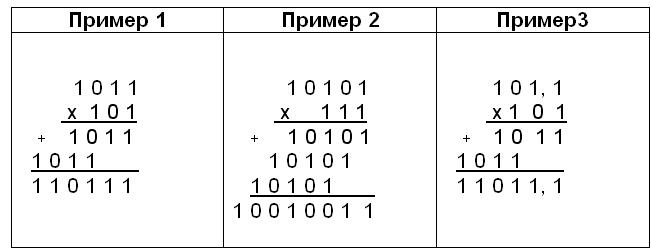 0.9
0.9