Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
04.18Другие ответы
| ||||||||||||
2 = 9 <=> m = ± 3
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
В гнезде стрижей четверо птенцов.
Масса каждого вылупившегося птенца -10 г. При переходе к самостоятельному питанию она увеличилась до 50 г. Какую массу и количество насекомых ( масса одного 0,01 г)
Для функции f(x)=-2 cos x найдите первообразную, график которой проходит через точку A(π/6;√3)
В бильярд играют два человека. Через некоторое время на сто-ле осталось 8 шаров. Найти вероятность того, что на этот момент вре-мени счет игры
Найдите определения область функции.
Найдите площадь данных фигур с помощью интеграла:
Несколько решений одной задачи | Образовательная социальная сеть
Автор:
Воронов Пётр
В презентации рассмотрено 5 способов решения иррационального уравнения с параметром, а также 4 способа решения системы двух уравнений с тремя неизвестными. Одно уравнение первой степени, другое второй степени
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.
google.com
Подписи к слайдам:
Слайд 1
НЕСКОЛЬКО РЕШЕНИЙ ОДНОЙ ЗАДАЧИ Работу выполнил Ученик 11б класса Гимназии №2 Воронов Пётр. Руководитель: Лысенко Н.А. 2010 г.
Слайд 2
Задача №1: Найти все значения параметра а, при которых не имеет корней уравнение. (1) Решение : Данное уравнение равносильно системе: (2) Уравнение (1) не имеет корней тогда и только тогда, когда не имеет решений полученная система. Это возможно в двух случаях: а) квадратное уравнение (2) не имеет корней; б) корни уравнения (2) не удовлетворяют условию Найдём все значения параметра, при котором выполняется хотя бы один случай: а) уравнение не имеет корней, если D
Слайд 3
1 способ . Корни уравнения меньше 1, если больший корень уравнения меньше 1 (достаточное условие): Ответ:
Слайд 4
2 способ. Рассмотрим квадратичную функцию Её корни меньше 1 тогда и только тогда, когда одновременно выполняются условия: Отсюда: Ответ:
Слайд 5
3 способ.
Пусть t = x -1. Тогда x
Слайд 6
Другие способы . 4 способ. Решим противоположную задачу: найдём множество всех значений параметра а, при которых уравнение имеет хотя бы одно решение (множество Х). А это возможно только, если больший корень уравнения больше или равен 1, следовательно получаем: Значит искомые решения параметра не принадлежат только полуинтервалу Ответ: 1 .
Слайд 7
5 способ. Возведём в квадрат обе части уравнения , получаем: Последняя система позволяет графически найти все значения а, при котором она не имеет решения. Мы ищем все такие значения параметра а, при которых прямые пучка y =- a ( x +2) не имеет общих точек с параболой на промежутке [1; +). При общих точек нет. Значение найдём из того условия, что прямая y = — a ( x +2) проходит через точку М(1;12):
Слайд 9
Задача №2: Решить систему уравнений Решение: 1 способ . Следовательно: Получаем систему уравнений в которой очевидны корни . Ответ: x=1, y=1, z=1.
Слайд 10
2 способ .
Выразив из первого уравнения z через x и y и подставив найденное выражение во второе уравнение, после несложных преобразований получаем уравнение: Очевидно, что дискриминант не положителен при всех значениях у. Следовательно, уравнение может иметь решения только при D =0 , т.е. у=1. Тогда Ответ: x=1, y=1, z=1.
Слайд 11
3 способ. 3 способ: Рассмотрим геометрическую интерпретацию задачи. Уравнение описывает плоскость, пересекающую координатные оси в точках А(3; 0; 0), В(0; 3; 0) и С(0; 0; 3), а уравнение (2)- сферу с центром в начале координат О и радиусом, равным . Для выяснения того, что представляет собой пересечение сферы с плоскостью, нужно сравнить радиус сферы с расстоянием от её центра до плоскости. Расстояние от точки О до плоскости АВС можно найти, вычислив высоту OD тетраэдра ОАВС. Отсюда находим что OD = , радиус сферы в точности равен расстоянию от её центра до плоскости. Это означает, что плоскость касается сферы и исходная система имеет единственное решение, которое легко угадывается.
Ответ: x=1, y=1, z=1.
Слайд 12
4 Способ. Решение x =у= z =1 легко угадывается. Докажем, что система не имеет других решений. Сделаем замену переменных: а=х+1, b = y +1, c = z +1. Тогда в новых переменных уравнение x+y+z=3 примет вид a+b+c=0 . Преобразуем второе уравнение системы: Осталось решить полученную систему уравнений, ответ в которой очевиден: Ответ: x=1, y=1, z=1.
Слайд 13
Список используемой литературы: Научно-методический журнал «Математика в школе» Научно-популярный журнал «Квант» Першин А.И. Воронина О.А. «Задачи с параметрами» С. Н. Олехник , М. К. Потапов Б. И. Пасиченко «Алгебра и начало анализа» «Уравнение и не равенства: учебно-методическое пособие для учащихся 10-11 классов» В. П. Моденов «Задачи с параметрами. Координатно-параметрический метод: учебное пособие»
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.
com
Подписи к слайдам:
Слайд 1
НЕСКОЛЬКО РЕШЕНИЙ ОДНОЙ ЗАДАЧИ Работу выполнил Ученик 11б класса Гимназии №2 Воронов Пётр. Руководитель: Лысенко Н.А. 2010 г.
Слайд 2
Задача №1: Найти все значения параметра а, при которых не имеет корней уравнение. (1) Решение : Данное уравнение равносильно системе: (2) Уравнение (1) не имеет корней тогда и только тогда, когда не имеет решений полученная система. Это возможно в двух случаях: а) квадратное уравнение (2) не имеет корней; б) корни уравнения (2) не удовлетворяют условию Найдём все значения параметра, при котором выполняется хотя бы один случай: а) уравнение не имеет корней, если D
Слайд 3
1 способ . Корни уравнения меньше 1, если больший корень уравнения меньше 1 (достаточное условие): Ответ:
Слайд 4
2 способ. Рассмотрим квадратичную функцию Её корни меньше 1 тогда и только тогда, когда одновременно выполняются условия: Отсюда: Ответ:
Слайд 5
3 способ.
Пусть t = x -1. Тогда x
Слайд 6
Другие способы . 4 способ. Решим противоположную задачу: найдём множество всех значений параметра а, при которых уравнение имеет хотя бы одно решение (множество Х). А это возможно только, если больший корень уравнения больше или равен 1, следовательно получаем: Значит искомые решения параметра не принадлежат только полуинтервалу Ответ: 1 .
Слайд 7
5 способ. Возведём в квадрат обе части уравнения , получаем: Последняя система позволяет графически найти все значения а, при котором она не имеет решения. Мы ищем все такие значения параметра а, при которых прямые пучка y =- a ( x +2) не имеет общих точек с параболой на промежутке [1; +). При общих точек нет. Значение найдём из того условия, что прямая y = — a ( x +2) проходит через точку М(1;12):
Слайд 9
Задача №2: Решить систему уравнений Решение: 1 способ . Следовательно: Получаем систему уравнений в которой очевидны корни . Ответ: x=1, y=1, z=1.
Слайд 10
2 способ .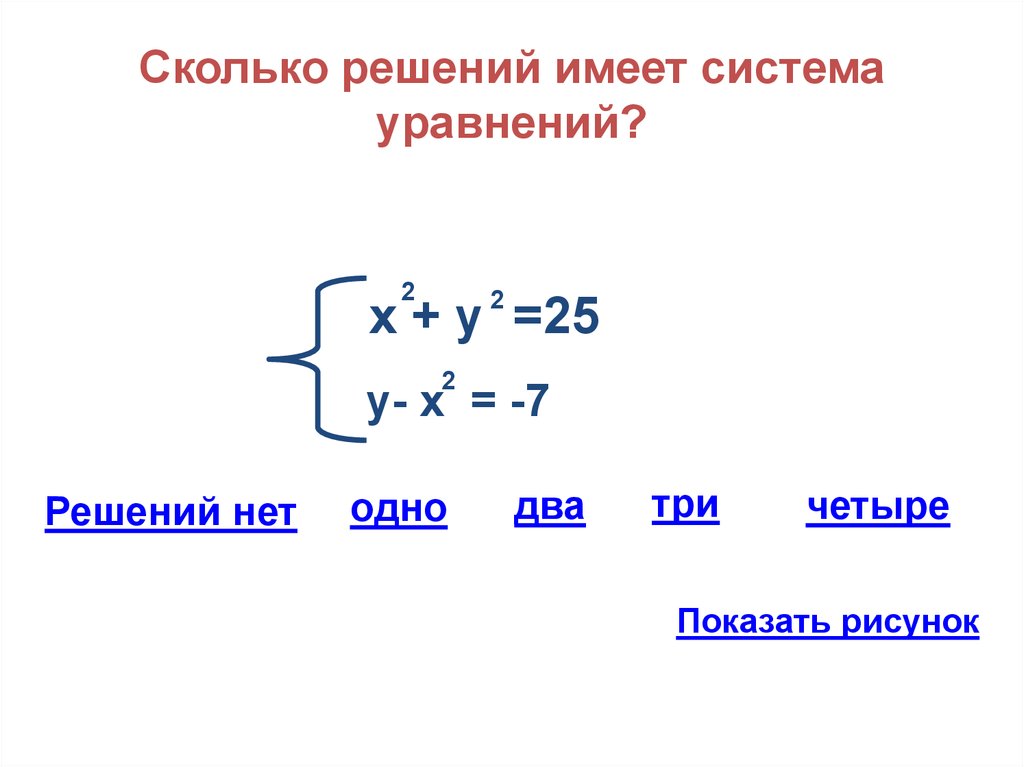
Выразив из первого уравнения z через x и y и подставив найденное выражение во второе уравнение, после несложных преобразований получаем уравнение: Очевидно, что дискриминант не положителен при всех значениях у. Следовательно, уравнение может иметь решения только при D =0 , т.е. у=1. Тогда Ответ: x=1, y=1, z=1.
Слайд 11
3 способ. 3 способ: Рассмотрим геометрическую интерпретацию задачи. Уравнение описывает плоскость, пересекающую координатные оси в точках А(3; 0; 0), В(0; 3; 0) и С(0; 0; 3), а уравнение (2)- сферу с центром в начале координат О и радиусом, равным . Для выяснения того, что представляет собой пересечение сферы с плоскостью, нужно сравнить радиус сферы с расстоянием от её центра до плоскости. Расстояние от точки О до плоскости АВС можно найти, вычислив высоту OD тетраэдра ОАВС. Отсюда находим что OD = , радиус сферы в точности равен расстоянию от её центра до плоскости. Это означает, что плоскость касается сферы и исходная система имеет единственное решение, которое легко угадывается.
Ответ: x=1, y=1, z=1.
Слайд 12
4 Способ. Решение x =у= z =1 легко угадывается. Докажем, что система не имеет других решений. Сделаем замену переменных: а=х+1, b = y +1, c = z +1. Тогда в новых переменных уравнение x+y+z=3 примет вид a+b+c=0 . Преобразуем второе уравнение системы: Осталось решить полученную систему уравнений, ответ в которой очевиден: Ответ: x=1, y=1, z=1.
Слайд 13
Список используемой литературы: Научно-методический журнал «Математика в школе» Научно-популярный журнал «Квант» Першин А.И. Воронина О.А. «Задачи с параметрами» С. Н. Олехник , М. К. Потапов Б. И. Пасиченко «Алгебра и начало анализа» «Уравнение и не равенства: учебно-методическое пособие для учащихся 10-11 классов» В. П. Моденов «Задачи с параметрами. Координатно-параметрический метод: учебное пособие»
линейная алгебра — Система уравнений не имеет решения
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 2к раз
$\begingroup$
Если система линейных уравнений, \begin{случаи} х &+ ау &+ z &= 3\\ х &+ 2у &+ 2г &= 6\\ х &+ 5y &+ 3z &= b\\ \end{случаи} не имеет решения, то:
- $a=-1,b=9$
- $a=-1,b\ne 9$
- $a\ne-1,b = 9$
- $a=1,b \ne 9$
Я действительно не понимаю, почему ответ не может быть вариантом (1).
Вот мой метод:
При $a = -1$ определитель определителя коэффициентов равен 0. А если мы создадим $\Delta_z$, определитель, в котором коэффициенты при $z$ заменяются на $3,6,b$ , (b = 9), этот определитель отличен от нуля.
В моей книге говорится, что если определитель коэффициента равен $0$ и хотя бы один из $\Delta_y, \Delta_z, \Delta_x$ отличен от $0$, то система не имеет решения.
Но получен ответ: $(2)$. Что не так с моим методом? Как лучше всего решать такие проблемы?
- линейная алгебра
- матрицы
- системы уравнений
- определитель
$\endgroup$
1
Вы неверно рассчитали $\Delta_z$. Решение книги правильное.
Чтобы не было решения, необходимо, чтобы определитель матрицы коэффициентов был равен нулю: это действительно дает $a=-1$.
Ранг матрицы в этом случае равен $2$, и с точностью до постоянного кратного единственной нетривиальной «зависимостью» уравнений может быть $1\cdot (1)-2\cdot (2) +1\cdot (3) = 0$.
Таким образом, в предположении $a=-1$ существует бесконечно много решений, если и только если это обобщается на правые части, то есть тогда и только тогда, когда $3-2\cdot 6 + b =0$, т. е. $b=9$.
Следовательно, ответ $a=-1, b\neq 9$.
$\endgroup$
$\begingroup$
Я полагаю, что лучший способ решить эту проблему — сократить матрицу по строкам и посмотреть, что получится. Вы должны исключить третий и первый столбцы:
$$
\begin{pматрица}
1 и а и 1 и 3\\
1 и 2 и 2 и 6 \\
1 и 5 и 3 и б
\end{pматрица}
\к
\begin{pmatrix}
1 и а и 1 и 3\\
0 и 2-а и 1 и 3 \\
0 и 5-а и 2 и б-3
\end{pматрица}
\к
\begin{pmatrix}
1 и 2а-2 и 0 и 0\\
0 и 2-а и 1 и 3 \\
0 и 1+а и 0 и б-9\end{pматрица}
$$
поэтому, если $a=-1$, последнее уравнение читается как $0=b-9$, таким образом, имея $b=9$, вы получаете $0=0$, что устраняет уравнение, и теперь у вас есть 2 уравнения с 3 неизвестными, следовательно, бесконечное количество решений.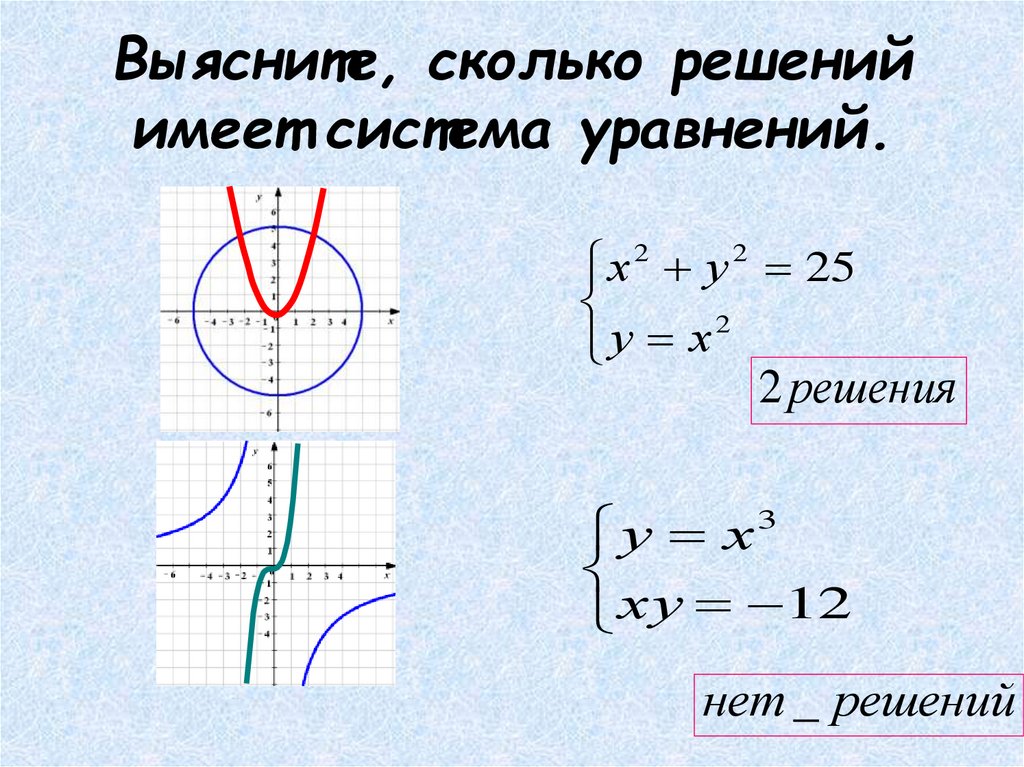
Условие отсутствия решений требует, чтобы $a=-1$ (заставляя последнее уравнение читать $0=b-9$) и $b \ne 9$ (заставляя его быть ложным).
ОБНОВЛЕНИЕ
Оглядываясь назад, как вы говорите, если $a=-1$, то $\Delta = 0$, поэтому уникального решения не будет. Однако, если $b = 9$, последний столбец $\Delta_z$ равен $(3,6,9) = 3 \times (1,2,3)$, поэтому ровно $3$ умножается на последний столбец $\Delta$, следовательно, $\ Delta_z = 3\Delta = 0$, и идея в вашей книге правильная.
$\endgroup$
8
$\begingroup$
Я бы сделал так, используя сокращение строк. Критерий того, что неоднородная линейная система имеет решения, состоит в том, что матрица линейной системы (л.с.с.) и расширенная матрица имеют одинаковый ранг.
Из этого критерия легко сделать вывод, что если эта система не имеет решения, то матрица л.
ч.с. не может иметь ранг $3$, поэтому его определитель, равный $-(a+1)$, равен нулю, откуда $a=-1$. Вычисление определителя методом редукции строк показывает, что эта матрица имеет ранг $2$.
Теперь, если $a=-1$, расширенная матрица уменьшается следующим образом: $$\begin{bmatrix}1&-1&1&3\\1&2&2&6\\1&5&3&b\end{bmatrix}\rightsquigarrow \begin{bmatrix}1&-1&1&3\\0&3&1&3\\0&3&1&b-6\end{bmatrix}\rightsquigarrow \begin{bmatrix}1&-1&1&3\\0&3&1&3\\0&0&0&b-9т$ и $$A = \begin{bmatrix} 1 и а и 1 \\ 1 и 2 и 2 \\ 1 и 5 и 3 \end{bmatrix}$$
Сначала необходимо иметь $det(A)=0$, что после вычислений дает $a=-1$. Таким образом, система становится такой:
$$A = \begin{bmatrix} 1 и -1 и 1 \\ 1 и 2 и 2 \\ 1 и 5 и 3 \end{bmatrix}$$
Теперь строка 3 становится нулевой, когда $r_3\rightarrow r_3-2r_2+r_1$. Применение этого к расширенной матрице $[A|B]$ дает запись $(3,4)$: $$ б-9$$
Требуется, чтобы эта запись была отличной от нуля, чтобы иметь несогласованную матрицу.
Таким образом, $a=-1, b\neq 9$.
$\endgroup$
Решения Classify для систем | Магазин развивающей математики
Результаты обучения
- Классификация решений для систем
Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
Используйте график для классификации решений систем
Вспомните, что график линейного уравнения представляет собой линию, которая указывает на то, что все точки на линии являются решениями этого линейного уравнения. Существует бесконечное количество решений. Как мы видели в предыдущем разделе, если у вас есть система линейных уравнений, которые пересекаются в одной точке, эта точка является решением системы. Что произойдет, если прямые никогда не пересекутся, как в случае с параллельными прямыми? Как бы вы описали решения для такой системы? В этом разделе мы рассмотрим три возможных результата решения системы линейных уравнений.
Три возможных результата для решений систем уравнений
Напомним, что решением системы уравнений является значение или значения, которые верны для всех уравнений в системе. Есть три возможных результата для решений систем линейных уравнений. Графики уравнений в системе могут сказать вам, сколько решений существует для этой системы. Посмотрите на изображения ниже. На каждом изображены две линии, составляющие систему уравнений.
| Одно решение | Нет решений | Бесконечные решения |
|---|---|---|
| Если графики уравнений пересекаются, то существует одно решение, верное для обоих уравнений. | Если графики уравнений не пересекаются (например, если они параллельны), то нет решений, верных для обоих уравнений. | Если графики уравнений одинаковы, то существует бесконечное число решений, верных для обоих уравнений. |
- Одно решение: Когда система уравнений пересекается по упорядоченной паре, система имеет одно решение.
- Бесконечное количество решений: Иногда два уравнения представляют собой одну линию, и в этом случае у нас есть бесконечное количество решений.
- Нет решения: Когда линии, составляющие систему, параллельны, решений нет, потому что две линии не имеют общих точек.
Поскольку количество решений, которые имеет система уравнений, очень важно, у нас фактически есть специальные категории систем линейных уравнений, основанные на количестве решений, которые имеет система. непротиворечивая система уравнений имеет по крайней мере одно решение. Непротиворечивая система считается независимой системой , если она имеет единственное решение, подобное первому рассмотренному нами примеру. Две линии имеют разные наклоны и пересекаются в одной точке плоскости. Непротиворечивая система считается зависимая система если существует бесконечное количество решений, как в третьем рассмотренном нами примере.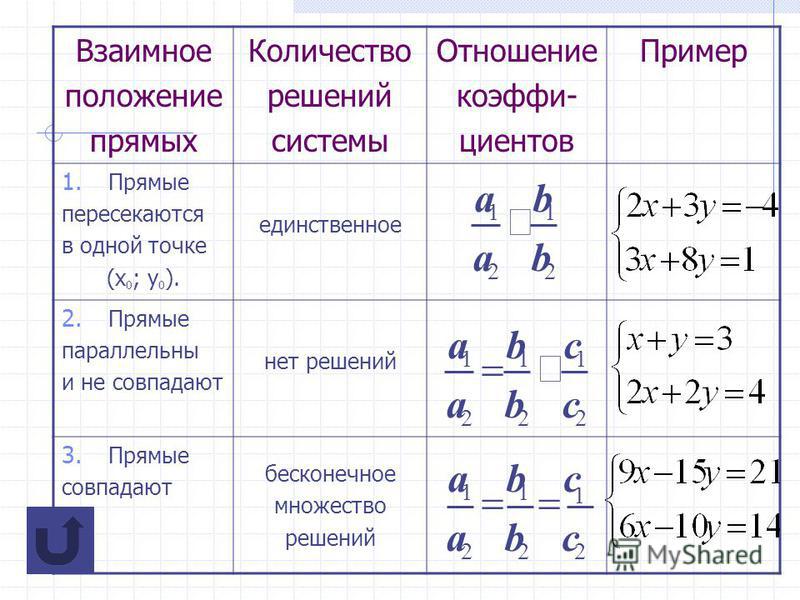
Система уравнений является зависимой, если уравнения имеют одинаковый наклон и одинаковые и -перехваты. Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую, и каждая точка на прямой представляет пару координат, удовлетворяющую системе.
Другим типом системы линейных уравнений является несовместная система, когда нет общих точек для обеих прямых и, следовательно, нет решения системы, как во втором примере, который мы исследовали. В несовместной системе уравнения представляют собой две параллельные линии с одинаковым наклоном и разными углами наклона.0171 г- перехвата.
A Общее примечание: Типы линейных систем
Существует три типа систем линейных уравнений с двумя переменными и три типа решений.
- Независимая система имеет ровно одну пару решений [латекс]\влево(х,у\вправо)[/латекс]. Точка пересечения двух прямых является единственным решением.
