Количество комбинаций из 3 букв: Сколько различных комбинаций из трех букв можно построить используя буквы из слова PINEAPPLE? — Комбинаторика — Спроси!

8=72057594037927936 комбинаций.

1. Как рассчитать количество комбинаций?
2. Как рассчитать количество комбинаций символов?
3. Какое количество комбинаций из 12 символов?
4. Сколько комбинаций из 10 букв?
5. Сколько комбинаций цифр от 0 до 9?
6. Сколько решений в неотрицательных числах имеет уравнение X Y Z Q 8?
7. Сколько комбинаций у 9 цифр?
8. Сколько комбинаций получится из 6 цифр?
9. Сколько может быть комбинаций из 6 букв?
10. Сколько комбинаций из 10 цифр по 3?
11. Сколько комбинаций из цифр 1 2 3 4?
12. Сколько вариантов подбора пароля из 4 цифр?
13. Как посчитать количество комбинаций из 8 цифр?
14. Сколько комбинаций из 3цифр?
15. Сколько комбинаций можно составить из 33 букв?
16. Как посчитать количество вариантов комбинаций без повторений?
17. Сколько комбинаций из цифр 1 2 3 без повторений?
18. Сколько вариантов игры в шахматы?
19. Сколько бывает трехзначных комбинаций?
20. Сколько вариантов комбинаций из 24 цифр?
21. Сколько может быть вариантов номеров?
22. Сколько комбинаций из 3 букв русского алфавита?
23. Сколько возможных комбинаций нот?
24. Что такое сочетание с повторениями?
25. Как найти число размещений из n по m?
26. Сколько всего автомобильных номеров можно составить?
27. Как посчитать количество возможных комбинаций пароля?
28. Сколько комбинаций из 6 вариантов?

Как рассчитать количество комбинаций?

Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n! (n−k)! ⋅k!.

Как рассчитать количество комбинаций символов?

Формула для определения количества возможных комбинаций выглядит следующим образом: nCr = n! / р! (н-р)!

Какое количество комбинаций из 12 символов?

Итого, получили 12 букв. Комбинаций цифр 999. 12*999)12*12 = 1 726 272 вариантов номеров.

Сколько комбинаций из 10 букв?

Если символы могут повторяться, то любой из 10-ти символов может принимать одно 36 значений (26 латинских букв плюс 10 цифр). Можно сказать, что это 10-тизначное число в 36-ричной системе счисления. Количество комбинаций будет равно 3610 или 3,6561584×1015.

Сколько комбинаций цифр от 0 до 9?

Можно сказать что это числа от 0 до 9999. Значит всего возможных комбинаций 10 000. Ответ: 10 000 комбинаций.

Сколько решений в неотрицательных числах имеет уравнение X Y Z Q 8?

Сколько решений в неотрицательных числах имеет уравнение x+y+z+q=8? Решение.

Сколько комбинаций у 9 цифр?

Это ж порядка 400-410 тясяч комбинаций, если не ошибаюсь. Количество размещений 9 цифр в 9-значном числе 363000 + 8,7,6, значные числа.

Сколько комбинаций получится из 6 цифр?

Допустим, есть шесть цифр. То есть N=6, и число возможных комбинации N!, 6!= 720 вариантов.

Сколько может быть комбинаций из 6 букв?

Д. N = 6*5*4*3*2*1 = 720 Ответ: 720.

Сколько комбинаций из 10 цифр по 3?

Точно также в качестве второй и третьей цифр данного кодового замка можно выбрать любую цифру из этих десяти цифр. Следовательно, всего в этом кодовом замке существует 10 * 10 * 10 = 100 * 100 = 1000 трехкнопочных комбинаций. Ответ: для данного кодового замка существует 1000 трехкнопочных комбинаций.

Сколько комбинаций из цифр 1 2 3 4?

Следовательно комбинаций будет: 4 * 3 * 2 * 1 = 4! = 24.

Сколько вариантов подбора пароля из 4 цифр?

Из них 11% составила комбинация 1234, 1111 — 6%, 0000 — 2%, хотя набор возможных комбинаций для PIN-кодов с четырьмя цифрами — от 0 до 9 насчитывает 10 тыс вариантов.

Как посчитать количество комбинаций из 8 цифр?

N = m ^ k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, k — длина пароля. 15.

Сколько комбинаций из 3цифр?

3 = 60 способов расстановки цифр, т. е. искомое количество трехзначных чисел есть 60. (Вот некоторые из этих чисел: 243, 541, 514, 132, )

Сколько комбинаций можно составить из 33 букв?

Ответы1. В русском алфавите содержится 33 буквы, а это значит, что возможных комбинаций из двух русских букв может быть 33 * 33, что равно 1089.

Как посчитать количество вариантов комбинаций без повторений?

В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ(), английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4), разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4).

Сколько комбинаций из цифр 1 2 3 без повторений?

Комбинации из трёх элементов без повторений

Рассмотрим комбинации из трёх цифр 1,2,3 без повторений. Таких комбинаций 6.

Сколько вариантов игры в шахматы?

Динамику роста этого числа можно проследить на примере обычной шахматной партии: для первого хода у обеих сторон есть 400 различных вариантов, для второго — ещё 676, для третьего — еще 576. 3 = 27 000. 2.

Сколько возможных комбинаций нот?

625 вариантов. Теперь вообразите не особенно длинную мелодию, например в восемь нот.

Что такое сочетание с повторениями?

Определение: Сочетания с повторениями (англ. combinations with repetitions) — те же сочетания, только теперь даны типов элементов, из которых нужно выбрать элементов, причем элементов каждого типа неограниченное количество, и элементы одного типа должны стоять подряд друг за другом.

Как найти число размещений из n по m?

Формула для числа размещений. Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения. Anm = n·(n − 1)·(n − 2)· ·(n − m + 1) = n!/(n − m)!

Сколько всего автомобильных номеров можно составить?

Каждую из цифр можно выбрать десятью способами. Каждую из букв можно выбрать двадцатью четырьмя способами. k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, k — длина пароля.

Сколько комбинаций из 6 вариантов?

Закрыт 6 лет назад. Допустим, есть шесть цифр. То есть N=6, и число возможных комбинации N!, 6!= 720 вариантов.

Число возможных комбинаций, сочетаний букв, слов : VIKENT.RU

«Одна из особенностей борхесовской Библиотеки заключается в том, что там стоят тома, содержащие все возможные комбинации из 25 букв, так что никакое сочетание букв, не содержащееся в Библиотеке, найти невозможно.

Об этом с древности мечтали каббалисты, потому что, только бесконечно комбинируя конечное число букв, можно надеяться когда-нибудь воссоздать тайное имя Бога.

В 1622 году Пауль Гульдин в работе Problema arithmeticum de rerum combinationibus (Арифметическая задача сочетаний вещей) посчитал, сколько слов можно составить из 23 букв бывшего тогда в ходу алфавита, сочетая их попарно, потом по три и так до составления слов из 23 букв, без учёта повторений и невзирая на то, есть ли у получившихся слов какой-то смысл и можно ли их произнести.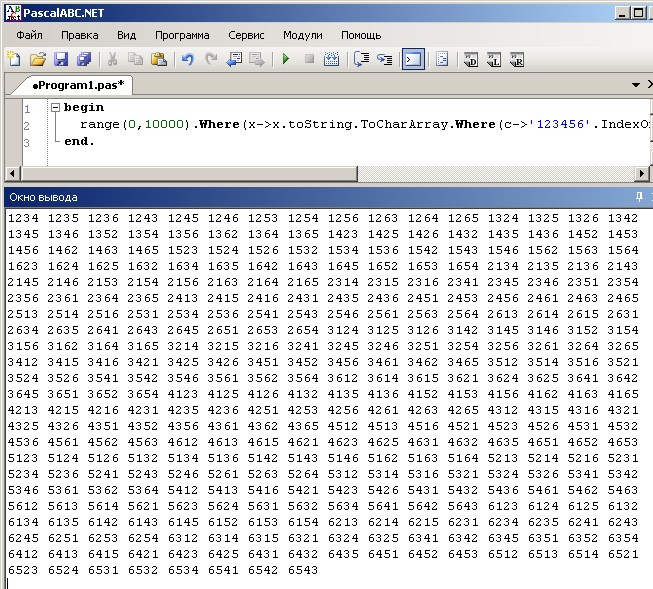 Получилось более 70 тысяч миллиардов миллиардов слов, для написания которых понадобятся более миллиона миллиардов миллиардов букв. Если записать все эти слова в тетрадях в тысячу страниц по 100 строк на странице и 60 знаков в строке, потребуется 257 миллионов миллиардов подобных тетрадей; а если разместить их в библиотеке, располагая кубическими помещениями со стороной 432 фута, каждое из которых вмещает 32 миллиона томов, понадобится 8 052 122 350 таких библиотек. И в каком же тридевятом царстве поместятся столько зданий? Если принять в расчёт всю земную поверхность, на нашей планете есть место только для 7 575 213 799 библиотек!

То же увлечение комбинаторикой побудило Марена Мерсенна (Harmonie universelle — Универсальная гармония, 1636) рассмотреть не только пригодные к произнесению слова французского, греческого, древнееврейского, арабского, китайского и любого другого возможного языка, но и все мыслимые музыкальные секвенции на этих языках. Как утверждает Мерсенн, чтобы записать все возможные песнопения, потребовались бы кипы бумаги выше, чем расстояние от земли до неба; и если бы каждый лист содержал 720 песнопений, из 22 нот каждое, а каждая кипа была бы ужата так тонко, чтобы не превышать толщиной дюйма, и учитывая, что из 22 нот можно составить более 12 тысяч миллиардов миллиардов песнопений, и поделив это число на 362 880 песнопений, которые могут быть ужаты в стопку, получим шестнадцатизначное число, между тем как число дюймов, отделяющих центр земли от звёзд, исчисляется числом всего лишь четырнадцатизначным. А если попытаться записывать все эти песнопения по тысяче штук в день, потребуются почти 23 тысячи миллионов лет.

Вопросом о том, каково максимальное число истинных, ложных и даже вовсе не имеющих смысла фраз, которые можно сформулировать, используя конечный алфавит из 24 букв, задавался и Лейбниц в своём небольшом сочинении под названием Horizon de la doctrine humaine (Горизонт человеческой доктрины). Учитывая, что бывают слова из 31 буквы (примеры Лейбниц находит в греческом и латыни), алфавит позволяет произвести 24³² таких слов. А какова может быть длина фразы? Поскольку представимы фразы длиной в целую книгу, число фраз, истинных или ложных, которые человек может прочесть за жизнь, если читать по 100 страниц в день, в каждой странице по тысяче букв, составит 3 650 000 000. И даже если этот человек проживет тысячу лет, «самая длинная фраза, или же самая большая книга, которую может прочесть человек, все равно составит 3 650 000 000 [букв], а все истинные и ложные фразы, все излагаемые, вернее, читаемые периоды, произносимые или непроизносимые, наделенные смыслом или нет, в сумме дадут  24 ^{365 000 000 000} — 24/23 [буквы]».

Всё это фантазии, где математика соседствует с метафизикой. Однако современная литература попыталась извлечь из этих комбинаторных возможностей реальные перечни или же предложить сделать это читателю. Примером могут служить Сто тысяч миллиардов стихотворений Ремона Кено (Париж, Gallimard, 1961) — книга, страницы которой разделены на горизонтальные полосы, и, листая их, можно по-разному сопоставлять 14 строк сонета, так что в результате можно получить 100 тысяч миллиардов стихотворений… Автор уточняет, что всего текстов может быть 10¹⁴ (то есть конечное число), однако, если читать по 24 часа в сутки, на то чтобы осилить всю книгу, понадобится 200 миллионов лет».

Умберто Эко, Vertigo: круговорот образов, понятий, предметов, М., «Слово», 2009 г., с. 366 и 369.

комбинаторика — Способы составления 10 буквенных комбинаций из 3 заданных букв

Задавать вопрос

спросил 2 года 3 месяца назад

Изменено 2 года, 3 месяца назад

Просмотрено 456 раз

$\begingroup$

Найдите количество комбинаций из 10 букв из ${a, b, c}$, содержащих:

1. Хотя бы одну из каждой буквы
2. Не менее двух каждой буквы
3. Минимум один A, два B, три C
4. Любое количество каждой буквы

(Также разрешено повторение)

Для номера 1 я думаю, что ответ $\binom{9}{2}$, так как есть n-1 мест, где я могу разместить полосу из звездочек и полосок. Для номера 2, хотя я не уверен, как я могу применить это, чтобы разместить столбцы так, чтобы я получил как минимум 2 каждого элемента $a,b,c$.

Редактировать 2: Я немного подумал над вопросом 2 и думаю, что у меня может быть правильный ответ. Поскольку мне нужно как минимум 2 каждой буквы, я решил сгруппировать 1 из $AA, BB, CC$, чтобы $AA$ был одним объектом, а это означает, что теперь у меня всего 7 объектов. Это означает, что у меня будет $\binom{6}{2}$ мест, чтобы разделить эту группу. Пожалуйста, дайте мне знать, если этот подход правильный. Или если я ошибся. Спасибо.

• комбинаторика
• комбинации

$\endgroup$

4

$\begingroup$

Пусть частота $a,b,c$ равна $x,y,z$ соответственно. Вы ищете интегральные решения для следующих случаев:

1. $x \ge 1, y \ge 1, z \ge 1$ и $x+y+z=10$
2. $x \ge 2, y \ge 2, z \ge 2$ и $x+y+z=10$

То же, что и $u \ge 1, v \ge 1, w \ge 1$ и $u+v+w=7$

3. $x \ge 1, y \ge 2, z \ge 3 $ и $x+y+z=10$

То же, что и $x \ge 1, p \ge 1, q \ge 1$ и $x+p+q=7$

4. $x \ge 0, y \ge 0, z \ge 0 $ и $x+y+z=10$

Следовательно, ответы будут $\binom{9}{2}, \binom{6}{2},\binom{6}{2}, \binom{12}{2}$ соответственно.

7). 910 таких комбинаций.

$\endgroup$

4

Сколько различных комбинаций из трех букв можно составить из алфавита?

Как следует из названия, система счисления — это математическая система, которая используется для представления чисел с использованием различных символов и переменных. В системе счисления числа, которые могут быть нанесены на числовую прямую, обычно называемые действительными числами, представлены набором значений или величин. В зависимости от их различных характеристик различные виды чисел классифицируются в разные наборы или группы. Например, рациональные числа — это любые целые числа, которые могут быть представлены в виде p/q, где q — ненулевое целое число. Десятичная, двоичная, восьмеричная и шестнадцатеричная системы являются примерами различных типов систем.

Комбинации

Определяется как процесс выбора одного, двух или нескольких элементов из заданной последовательности, независимо от порядка их появления. Если вы выберете два компонента из серии, в которой изначально всего два элемента, порядок этих элементов не будет иметь значения.

Формула комбинации

При выборе r элементов из n элементов в последовательности число комбинаций равно

ⁿ C _р = н! / р! (н-р)!

Например, пусть n = 7 и r = 3, тогда количество способов выбрать 3 элемента из 7 = ⁷ C ₃ = 7!/3!(7 – 3)! = 35.

Сколько различных комбинаций из 3 букв можно составить из алфавита?

Решение:

Если разрешено повторение букв, то каждый алфавит можно выбрать из заданных 26 алфавитов.

Отсюда общее количество комбинаций = ²⁶ C ₁ × ²⁶ C ₁ × ²⁶ C ₁

= 26 × 26 × 26

= 17576

Однако, если повторение не разрешено, то номера сочетки = ^{. 26} C ₁ × ²⁵ C ₁ × ²⁴ C ₁

= 26 × 25 × 24

= 156009

Проблемы

95999999999999999999999999999939003

. Банк, содержащий 20 монет, определите количество перестановок пятаков, десятицентовиков и четвертаков, которые он содержит.

Решение:

В данном случае порядок монет явно не имеет значения. Также нет упоминания о том, разрешено ли повторение.

Следуя формуле, имеем: ^n+r−1 C _r = ^n+r−1 C _n−1 , в случае r числа комбинаций из последовательности с n числом элементы, в которых элементы могут повторяться:

Количество возможных пар = ^20+3-1 C ₂₀ = ²² С

20

= 22! / (22 – 20)! 20!

= 11(21)

= 231

Задача 2. Скажите, сколько существует различных способов распределения 7 студентов на поездку в колледж, если у нас есть только одна трехместная комната и две двухместные комнаты.

Решение:

Эту задачу можно понять как необходимость разделить семерых учеников на три группы по три, два и два ученика.

Количество способов выбрать 3 студентов в тройке = ⁷ С ₃ = 7! / 3!4! = 35  

Количество способов выбрать 2 из оставшихся 4 учеников = ⁴ C ₂ = 4!/ 2!2! = 6

Количество возможных способов выбрать двух учеников из оставшихся двух равно одному.

Общее количество расстановок = 35 × 6 × 1 = 210.

Во время конференции 7 студентов могут быть распределены в 1 трехместный и 2 двухместных гостиничных номера 210 различными способами.

Задача 3. Определить, сколькими способами можно создать комитет из пяти человек из группы из семи мужчин и шести женщин, при этом в комитете должно быть не менее трех мужчин.

Решение:

По крайней мере три человека в комитете означает, что в комитете может быть ровно три, четыре или все пять человек.

Количество договоренностей, когда в комитете 3 мужчины и 2 женщины = (7C3 x 6C2) = 525

Количество договоренностей, когда в комитете 4 мужчины и 1 женщина =  (7C4 x 6C1) = 210

Количество договоренностей, когда в комитет входят все 5 человек = (7C5) = 21

Всего договоренностей = 525 + 210 + 21

= 756

Задача 4. Найдите количество способов расставить буквы в слове «НАЧАЛО» так, чтобы гласные всегда стояли вместе.

Решение:

Если гласные появляются вместе, они образуют в слове отдельную букву. Следовательно, у нас осталось 4 + 1 = 5 букв, которые можно расположить в 5! = 120 способов.

Более того, их 3! = 6 способов расположить гласные вместе.

Общее количество способов расположения букв = 120 x 6 = 720.

Задача 5. Найдите количество слов с четырьмя согласными и тремя гласными, которые можно составить из восьми согласных и пяти гласных.