Количество сочетаний без повторений: Математическое Бюро. Страница 404

4.2.3. Сочетания

Глава 4. Комбинаторика

4.2.

4.2.3.

Допустим теперь, что нас не интересует порядок, в котором идут выбранные элементы. Например, нужно из десяти человек выбрать троих дежурных. Такая операция называется неупорядоченной выборкой, или сочетанием, в отличие от упорядоченной выборки – размещений.

Символ читается «це из эн по ка».

Формулу для можно получить из следующих соображений.

Из любого набора, содержащего k элементов, можно получить k! перестановок. Поэтому упорядоченных выборок объёма k существует

штук. Значит,

Модель 4.4. Сочетания

Пример 1

Для проведения письменного экзамена нужно составить 3 варианта по 5 задач в каждом. Сколькими способами можно разбить 15 задач на 3 варианта?

Пример 2

Сколькими способами можно разместить 10 различных шаров по 4 ящикам так, чтобы в первом ящике оказалось 2 шара, во втором – 3, в третьем – 3 и в четвёртом снова два?

Для числа сочетаний справедливы некоторые тождества, в частности:

Пример 3

Докажите тождество

С помощью формулы для  получаем:

Запишем в «нулевой» строке число В первой строке напишем значения чисел и каждое из которых тоже равно 1, так, чтобы значение оказалось над промежутком между этими двумя числами. Во второй строке запишем числа и тоже равные 1, а между ними – число Обратим внимание, что число равно сумме двух чисел, стоящих над ним: Продолжим построение, записывая в n-й строке числа от до включительно.

1

Рисунок 4.2.3.1. Треугольник Паскаля

Полученный числовой треугольник называется треугольником Паскаля. Согласно свойству любое число в этом треугольнике равно сумме двух чисел, расположенных над ним в предыдущей строке.

При помощи треугольника Паскаля удобно доказывать различные комбинаторные тождества.

На языке множеств утверждение, доказанное в задаче, выглядит по-другому.

Число подмножеств множества из n элементов равно 2n.

Еще один интересный факт, связанный с треугольником Паскаля, мы приведём здесь без доказательства:

Бином Ньютона

Приведённое тождество называется биномом Ньютона.

 

Как и в случае с размещениями, существует понятие числа сочетаний с повторениями. Рассмотрим его на следующем примере.

Пример 5

В палитре художника 8 различных красок. Художник берет кистью наугад любую из красок и ставит цветное пятно на ватмане. Затем берет следующую кисть, окунает её в любую из красок и делает второе пятно по соседству. Сколько различных комбинаций существует для шести пятен? Порядок пятен на ватмане не важен.

2

Решим задачу следующим образом. Пусть количество пятен первого цвета равно k1, второго цвета – k2, третьего – k3 и так далее. Запишем каждое из этих чисел последовательностью из соответствующего количества единиц, а на границах между числами поставим нули. Так, если у нас первого цвета 1 пятно, второго – 3 пятна, третьего и четвёртого – ни одного, пятого и шестого – по одному пятну, а седьмого и восьмого – снова не одного, то запись будет выглядеть следующим образом: 1011100010100. В этой цепочке содержится m1 = 6 единиц, m0 – 1 = 8 – 1 = 7 нулей – всего n = m0 + m1 – 1 = 13 цифр. Количество перестановок с повторениями этих цифр равно Именно столько существует различных вариантов раскраски ватмана (без учёта порядка цветных пятен).

Вообще, можно сформулировать следующее правило.



Формула количества сочетаний без повторений

Число всех сочетаний без повторений по m из n элементов обозначается .

Буква C от французского «combinaison» («сочетание»).

Теорема. .

Доказательство. Каждое размещение без повторений (x₁,…,x_m) по m из n можно построить в 2 шага: вначале строится сочетание без повторений <x₁,…,x_m> по m из n, а затем – перестановка (x₁,…,x_m) из m элементов множества <x₁,…,x_m>. По правилу произведения

Из теоремы и формул для числа размещений без повторений следуют еще 2 формулы для числа сочетаний без повторений:

.

.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8921 — | 7230 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Определение числа сочетаний

Пусть имеется $n$ различных объектов. Чтобы найти число сочетаний из $n$ объектов по $k$, будем выбирать комбинации из $m$ объектов все возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок (он тут не важен, в отличие от размещений).

Например, есть три объекта <1,2,3>, составляем сочетания по 2 объекта в каждом. Тогда выборки <1,2>и <2,1>- это одно и то же сочетание (так как комбинации отличаются лишь порядком). k$ онлайн, используйте калькулятор ниже.

Видеоролик о сочетаниях

Не все понятно? Посмотрите наш видеообзор для формулы сочетаний: как использовать Excel для нахождения числа сочетаний, как решать типовые задачи и использовать онлайн-калькулятор.

Расчетный файл из видео можно бесплатно скачать

Полезные ссылки

Решебник по ТВ

Решебник с задачами по комбинаторике и теории вероятностей:

Основные формулы комбинаторики

Задачи, в которых речь идет о тех или иных комбинациях объектов, их называют комбинаторными задачами. Область математики, в которой рассматриваются комбинаторные задачи, называют комбинаторикой.

Комбинаторика – область математики, в которой рассматриваются задачи о тех или иных комбинациях объектов.

Правило суммы

Пусть имеется n попарно непересекающихся множеств A₁, A₂,…A_n, содержащих m₁, m₂,…, m_n элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно

Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в третьей – 20. Сколькими способами из них можно выбрать одного студента?

Решение. Из первой группы одного человека можно выбрать 25 способами, из второй – 30, из третьей – 20. Чтобы найти ответ, нужно сложить все эти способы:

Ответ: выбрать одного студента из трех групп можно 75 способами.

Правило произведения

Пусть имеется . n множеств A₁, A₂,…A_n,содержащих m₁, m_2,,…, m_n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества

Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в третьей – 20. Сколькими способами из каждой из них можно выбрать по одному студенту?

Решение. Из первой группы одного человека можно выбрать 25 способами, из второй – 30, из третьей – 20. Если выбираем один элемент из нескольких множеств, то применяем правило суммы.

Если выбираем по одному элементу из нескольких множеств, то применяем правило произведения.

Факториаломчислаn называется последовательное произведение натуральных чисел от единицы до самого числа n:

Перестановки без повторений

Перестановками из n различных элементов называются размещения из этих n элементов по n. Перестановки — частный случай размещений.

Пример. Сколькими способами можно расставить в шеренгу студентов группы из 25 человек?

Решение. Число способов есть число перестановок из 25 элементов, то есть:

Ответ: расставить в шеренгу студентов группы из 25 человек можно 1,55ּ10 25 способами.

Размещения без повторений

Различные упорядоченные подмножества по m элементов данного множества, содержащего n элементов, называются размещениями из n по m. Их число равно:

В частности: .

Пример. Из группы, состоящей из 25 человек, надо выбрать шахматную команду из четырех человек на I, II, III и IV доски. Сколькими способами это можно сделать?

Решение. Так как из 25 человек выбираются 4 и порядок важен, то число способов есть число размещений из 25 по 4, то есть:

.

Ответ: выбрать из 25 человек шахматную команду из четырех человек на I, II, III и IV доски можно 303600 способами.

Сочетания без повторений.

Различные неупорядоченные подмножества по m элементов из данного множества, содержащего n элементов, называются сочетаниями из n по m. Их число равно:

В частности, .

Пример. Сколькими способами из группы в 25 человек можно выбрать баскетбольную команду из пяти человек?

Решение. Так как из 25 человек выбираются 5 и порядок не важен, то число способов есть число сочетаний из 25 по 5, то есть:

Ответ: из группы в 25 человек можно выбрать баскетбольную команду 53130 способами.

Сочетания с повторениями без ограничения на число повторений

---

Теорема: пусть множество М={х₁,…,х_n}

Функции f (t, х₁,…,х_n)= ∏ (1+x_kt + [x_kt]² + …) и g (t)= f (t, 1,…1) = ∏ (1+t+t² + …)
являются порождающими функциями для сочетаний и для числа сочетаний из n элементов с повторами без ограничений на число повторов.

Доказательство: функция f(t,х₁,…,х_n)= ((x₁t )⁰+(x₁t)¹+(x₁t)²+…)(x₂t)⁰+(x₂t)¹+(x₂t)²+…)*…..*((x_nt)⁰+(x_nt)¹+(x_nt)²+ …)=
= \\ группируем относительно t^r \\=
= ∑{∑[x₁^a1x₂^a2…x_n^an]}t^r; \\ в [ ] –одно сочетание из n по r с повторами элементов.
\\ в { }- все сочетания с повторами из n по r является порождающей функцией для сочетаний с повторами из n элементов множества М.

В функции f (t, х₁,…,х_n ) положим х₁=…=х_n=1 ,
тогда g (t)= f (t, 1,…1)= ∏(1 + t + t² + …) = ∑{∑[x₁^a1x₂^a2…x_n^an]}t^r\\ в [ ] –одно сочетание с повтором
\\ в { }- число всех сочетаний из n по r с повторами элементов без ограничения на число повторов.

Является порождающей функцией для числа сочетаний с повторами из n элементов без ограничений на число элементов.

Замечание: g (t)= f (t, 1,…1)= ∏(1 + t + t² + …) =(1 + t + t² + …)ⁿ = \\ в скобках сумма членов геом. прогрессии\\ =(1/1-t)ⁿ=(1-t)^-n = ∑(-n)(-n-1)(-n-2)…(-n-r+1)/r! (-t)^r = ∑(n)(n+1)(n+2)…(n+r-1)/r! (t)^r = ∑A^r_n+r-1/r!)t^r = ∑(n+r-1)!/((n+r-1-r)!r!)t^r = C^r_n+r-1 t^r) .

Комбинаторика

Замечание 1

При решении многих практических задач часто приходится выбирать из некоторой совокупности объектов элементы, которым свойственны те или иные особенности, размещать элементы в некотором порядке, подсчитывать их количества и т.п. Поскольку в таких задачах речь идёт о комбинациях объектов, их называют комбинаторными.

Основные элементы комбинаторики, используемые при решении комбинаторных задач, таковы:

1. Правила суммы и произведения;
2. Перестановки без повторений;
3. Размещения без повторений;
4. Сочетания без повторений;
5. Перестановки с повторениями;
6. Размещения с повторениями;
7. Сочетания с повторениями.

Правило произведения

Если элемент a множества $A$ можно выбрать $m$ способами и при каждом из этих выборов элемент $b$ множества $B$ можно выбрать $n$ способами, то упорядоченную пару ($a$;$b$) можно выбрать $m$•$n$ способами.

Правило суммы

Если элемент $a$ из множества $A$ можно выбрать $m$ способами, а элемент $b$ из множества $B$ можно выбрать $n$ способами, то число способов, которыми можно осуществить выбор хотя бы одного элемента $a$ или $b$, равно сумме $m$+$n$.

Предполагается, что выборы $a$ и $b$ взаимно исключительны, то есть ни один из способов выбора элемента a не совпадает со способом выбора элемента $b$. При наличии таких совпадений результат выбора будет равен $m$+$n$-$p$,где $p$-количество совпадений.

Замечание 2

Правила суммы и произведения справедливы не только для двух, но и для любого числа объектов.

При выборе элементов по правилу суммы используется соединитель «или»‘ (выбираем элемент из первого конечного множества, или из второго, или из третьего и т.д.).

При образовании пары (тройки, четверки и т.д.) элементов по правилу произведения используется соединитель «и»‘ (из первого множества выбираем первый элемент и к нему присоединяем второй элемент из второго множества — образуется пара, и к паре присоединяем третий элемент из третьего множества — образуется тройка и т.д.).

Количество перестановок без повторений

Рассмотрим свойства сочетаний без повторений в комбинаторике. Разные последовательности, которые можно построить из элементов данного множества, взятых ровно по одному разу, называются перестановками. Эти последовательности отличаются друг от друга только порядком расположения элементов.

Например, из двухэлементного множества $M2$={$a$,$b$} можно образовать два упорядоченных двухэлементных множества: {$a$,$b$} или {$b$,$a$}.

Формула числа перестановок в комбинаторике: $Pn$ = $n$!

Комбинаторика: правило размещения без повторений

Подмножество, выбираемое из данного множества предметов, называют выборкой. Выборки бывают упорядоченные и неупорядоченные. Для упорядоченной выборки существенен порядок элементов. Иначе говоря, меняя порядок элементов, мы получаем другие выборки. Составим, например, из цифр 1, 2, 3, 4, 5 трехзначные числа: 123, 431, 524 и т.д. Это упорядоченные трехэлементные выборки, отличающиеся составом или порядком элементов.

Размещениями из $n$ элементов по $m$ элементов ($m$≤$n$) называют упорядоченные $m$-элементные выборки из данных $n$ элементов.

Формула размещения без повторений в комбинаторике $n$ по $m$ элементов имеет вид: $A_{n}^{m} =\frac{n!}{\left(n-m\right)!} $. {m} =\frac{\left(n+m-1\right)!}{m!\cdot \left(n-1\right)!} $.

Рассмотрим теперь как решать задачи на комбинаторику — ниже приведены различные примеры и задачи с сочетаниями, размещениями и перестановками.

Пример 1

Задание: химик использует семь ингредиентов для приготовления нужного состава. Сколькими способами можно осуществить порядок приготовления?

Решение. Давайте применим элементы комбинаторики и осуществим решение. Как известно, перестановками из $n$ элементов называются комбинации, состоящие из $n$ элементов и отличающиеся порядком расположения элементов.

Количество перестановок вычисляется по формуле $P_{n} =n!$.

Количество различных порядков вливания семи ингредиентов в сосуд — это число перестановок из семи элементов: $P_{7} =7!=1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7=5040$.

Разберём еще один пример задачи на размещение в комбинаторике с решением.

Пример 2

Задание: На собрании присутствуют 20 человек. {3} =\frac{10!}{\left(10-3\right)!} =\frac{10!}{7!} =8\cdot 9\cdot 10=720$.

Рекуррентная формула для числа сочетаний без повторений — Студопедия

Используя формулу для числа сочетаний без повторений, можно доказать следующую теорему.

Теорема. , , .

Доказательство. . .

.

Пример. Найти все биномиальные коэффициенты для .

Решение запишем в виде треугольника Паскаля – бесконечной таблицы, имеющей треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы, так как . Каждое внутреннее число равно сумме двух расположенных над ним чисел: . Строки треугольника симметричны относительно вертикальной оси: .

Биномиальный коэффициент лежит на пересечении строки n и столбца m.

m n

Комбинаторика в Excel

Комбинаторика в Excel

Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:

1. Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
2. Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
3. Важен ли порядок элементов в выборке?
4. После выбора элемента мы его возвращаем назад?

Рис. 1. Дерево решений, какую формулу комбинаторики использовать

Скачать заметку в формате Word или pdf, примеры в формате Excel

Перестановки без повторений

Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.

Рис. 2. Перестановки (картинка взята здесь)

Если все n элементы разные, то число перестановок обозначается P_n от perturbation.

С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!

Например

По определению: 1! = 1; 0! = 1.

Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).

Рис. 3. Расчет числа перестановок без повторений с помощью факториала

Перестановки с повторениями

Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).

Рис. 4. Перестановки с повторениями (картинка найдена здесь)

В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n₁ раз, второй – n₂ раз, третий – n₃ раз, …, k-й – n_k раз (где n₁ + n₂ + … + n_k = n) называется перестановкой с повторениями из n элементов.

Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?

Решение. Буквы а и н повторяются 2 раза, а буква м один раз.

Размещение без повторений

Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается  от arrangement.

Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):

Рис. 5. Размещение без повторений (картинка из презентации)

Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).

Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)

Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу

Размещение с повторениями

Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.

Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).

Рис. 7. Размещение с повторениями

В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:

В Excel используется функция ПЕРЕСТА(n;k).

Задача. Сколько различных номеров можно составить в одном коде региона?

Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).

Рис. 8. Номер автомобиля

Решение. Можно воспользоваться формулой для размещения с повторениями:

Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.

Сочетания без повторений

Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).

Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):

Рис. 9. Сочетания без повторений из 4 по 2

Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями

где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:

Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

В Excel используется функция =ЧИСЛКОМБ(n;m).

Сочетания с повторениями

Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.

Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).

Рис. 11. Сочетания с повторениями

В общем случае, число сочетаний с повторениями:

Для нашего примера с фруктами

В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.

Комбинаторика в Python

Стандартная библиотека python, начиная с версии 2.2, предоставляет множество средств для генерирования комбинаторных объектов, но в интернете мне не удалось найти ни одной статьи, которая подробно рассказывала бы о работе с ними. Поэтому я решил исправить это упущение.

Начну с того, что расскажу о комбинаторике и ее основных формулах. Если же вы уже знакомы с этим разделом математики — можете пропустить эти абзацы.

Допустим, у нас есть строка, состоящая из n разных букв и мы хотим вычислить все способы переставить эти буквы местами так, чтобы получить новую строку. k количество размещений из n по k с повторениями.

До этого мы перебирали последовательности с учетом порядка элементов, а что если порядок для нас не имеет значения. Например, у нас есть есть n разных конфет и мы хотим выбрать k из них, чтобы подарить другу, при чем k < n. Сколько существует способов выбрать k конфет из n без учета порядка? Ответ прост, в начале найдем размещение из n по k без повторений, но тогда одинаковые наборы конфет, имеющие разный порядок их следования будут повторяться. Сколько существует способов переставить k конфет? Правильно, перестановка из k элементов без повторений. Итоговый ответ: размещения из n по k делим на перестановки из k без повторений. Формула:количество сочетаний из n по k.

Рассмотрим случай посложнее, у нас есть n коробок каждая из которых содержит множество конфет одного вкуса, но в разных коробках вкусы разные. Сколько существует способов составить подарок другу из k конфет, при чем один и тот же вкус может встречаться любое количество раз? Так как порядок для нас значения не имеет, давайте разложим подарочные сладости следующим образом: в начале будут лежать последовательно конфеты первого вкуса, затем второго и так далее, а между конфетами разных вкусов положим спички, если конфеты какого-то вкуса отсутствуют в нашем подарке — спички, которые должны были окаймлять этот вкус слева и справа будут стоять рядом. Того у нас получится последовательность, состоящая из k конфет и n-1 спички, ибо вкусов всего n, а спички разделяют их. Теперь заметим, что по расположению спичек, мы можем восстановить исходное множество. Тогда ответом будет количество способов разместить n-1 спичку в n+k-1 ячейку без учета порядка, что равно количеству сочетаний из n+k-1 по n-1, формула:количество сочетаний из n по k с повторениями.

Теперь рассмотрим несколько задач на комбинаторику, чтобы закрепить материал.

Задача 1

Есть 20 человек, сколько существует способов разбить их на пары
Решение: возьмем первого человека, сколько существует способов выбрать ему пару:, возьмем второго человека, сколько существует способов выбрать ему пару:. Ответ: 19!!! = 654729075

Задача 2

Есть 10 мужчин и 10 девушек, сколько существует способов разбить их на компании, состоящие из одинакового количества и мужчин и девушек, пустая компания не считается
Решение:
Cпособ 1: количество способов собрать компанию из одного мужчины и одной девушки равно произведению количества способов выбрать одну девушку и количества способов выбрать одного мужчину. Количество способов выбрать одну девушку из 10 равно сочетанию из 10 по 1 без повторений, с мужчинами аналогично, поэтому возведем в квадрат. Далее аналогично вычислим сочетания из 10 по 2, из 10 по 3 и так далее до сочетания из 10 по 10. Итоговая формула:.
Способ 2: рассмотрим множество мужчин, входящих в компанию и множество девушек, не входящих в нее. По этому множеству можно однозначно восстановить компанию, а количество людей в нем всегда равно 10, так как, k — количество мужчин в компании,— количество девушек, не вошедших в нее. Количество таких множеств равно количеству сочетаний из 20 по 10, в конечном ответе мы также вычтем единицу, чтобы не учитывать пустую компанию, когда в нашем множестве 10 девушек. Итоговая формула:.

Итак, мы разобрались с теорией, теперь научимся генерировать комбинаторные объекты с помощью стандартной библиотеки python.
Работать мы будем с библиотекой itertools

from itertools import *

С помощью функции permutations можно сгенерировать все перестановки для итерируемого объекта.

Пример 1

for i in permutations('abc'):
    print(i, end=' ') # abc acb bac bca cab cba
print()
for i in permutations('abb'):
    print(i, end=' ') # abb abb bab bba bab bba 

Исходя из второго вызова заметим, что одинаковые элементы, стоящие на разных позициях, считаются разными.

Пример 2

for i in permutations('abc', 2):
    print(i, end=' ') # ab ac ba bc ca cb 

Размещение отличается от перестановки ограничением на количество доступных ячеек

Пример 3

for i in product('abc', repeat=2):
    print(i, end=' ') # aa ab ac ba bb bc ca cb cc

C помощью размещений с повторениями можно легко перебрать все строки фиксированной длины, состоящие из заданных символов

Пример 4

for i in combinations('abcd', 2):
    print(i, end=' ') # ab ac ad bc bd cd 

С помощью сочетаний без повторений можно перебрать все наборы не повторяющихся букв из заданной строки, массива или другого итерируемого объекта без учета порядка

Пример 5

for i in combinations_with_replacement('abcd', 2):
    print(i, end=' ') # aa ab ac ad bb bc bd cc cd dd  

Результат аналогичен вызову combinations, но в результат также добавлены множества с одинаковыми элементами.

Материалы:
Н.В. Горбачев «Сборник олимпиадных задач по математике»
Документация по python на русском

Лотереи

Лотерея — это разновидность азартных игр, при которой люди покупают билеты, а затем выигрывают, если выберут их числа.

«Лот» — это то, что происходит случайно. Возможно, вы слышали, как люди говорят: «Давайте решим жеребьевкой» или «Так что это мой удел».

Правила

У разных лотерей разные правила.

Здесь мы будем использовать типичную лотерею, в которой игрок выбирает 6 различных чисел из 49 .

Пример:

Вы участвуете в лотерее, покупая билет и выбирая свои шесть чисел.

Вы выбираете: 1, 2, 12, 14, 20 и 21

В субботу проводится розыгрыш лотереи, и выпадают выигрышных номеров :

3, 12, 18, 20, 32 и 43

Вы сопоставили два чисел (12 и 20):

• Этого достаточно, чтобы выиграть что-нибудь? №
• Обычно вы должны угадать не менее трех чисел , чтобы получить небольшой приз.
• Соответствие четырем номерам дает больший приз,
• Соответствие пяти еще больше.
• Но если вы угадаете ВСЕ ШЕСТЬ чисел, вы сможете выиграть миллионов .

Шансы на выигрыш всех 6 номеров равны 1 из 13 983 816 (рассчитано ниже).

Выбор чисел

Эти могут выиграть.

Цифры не знают, какие они!

Лотерея — это с такой же вероятностью, что выпадет «1,2,3,4,5,6», как «9,11,16,23,27,36»

Серьезно!

Вместо чисел это могут быть символы или цвета, лотерея все равно будет работать.

На самом деле результат, приведенный ниже, действительно имел место (Florida Fantasy 5 от 21 марта 2011 г.):

Так что неважно, какие числа вы выберете, шансы одинаковы.

Более вероятные номера?

Значит, вы читали, что одни числа встречаются чаще, чем другие? Ну, конечно, есть, это случайный случай.

У организаторов лотерей есть строгие правила, запрещающие «фальсификацию» результатов. Но случайный случай может иногда приводить к странным результатам.

Например, с помощью The Spinner я сделал 1000 вращений на 10 чисел и получил следующее:

Вау! 7 выпало 115 раз, ,
и 8 только 81 раз.

Означает ли это, что 7 теперь будет появляться чаще или реже ? На самом деле это ничего не значит, 7 с такой же вероятностью, как и любое число, будет выбрано.

Попробуйте сами и посмотрите, какие результаты вы получите.

Популярные номера

Но есть хитрость! У людей есть любимые числа, поэтому, когда выпадают популярные числа, вы делитесь выигрышем с множеством людей.

Дни рождения — популярный выбор, поэтому люди выбирают 1–12 и 1–31 чаще.Также счастливые числа.

Так что, возможно, вам стоит выбрать непопулярных номеров , чтобы, когда вы ДЕЙСТВИТЕЛЬНО выиграете, вы получите больше денег.

(Предполагается, что в вашей лотерее призы распределяются между победителями. )

Сожаление

Не выбирайте одни и те же номера каждую неделю . Это ловушка! Если вы забыли неделю, вы беспокоитесь, что выпадут ваши числа , и это заставит вас покупать билет каждую неделю (даже если у вас есть другие более важные дела).

Мой совет:

Составьте список из множества непопулярных номеров.
Каждый раз выбирать случайным образом из этого списка.

Синдикаты

«Синдикат» — это группа людей, которые все вкладывают небольшие деньги, чтобы группа могла купить много билетов. Шансы на выигрыш повышаются, но ваша выплата каждый раз меньше (потому что вы делитесь).

Syndicates могут быть забавными, потому что они общительны … способ завести и сохранить дружеские отношения. К тому же некоторые синдикаты любят тратить небольшие выигрыши на всех, кто собирается вместе пообедать.

Еще одна веская причина для присоединения к синдикату заключается в том, что ваши шансы на выигрыш повышаются (а то, что вы выигрываете, снижается).

Подумайте об этом … выигрыш Десяти миллионов действительно изменит вашу жизнь, но Один миллион также значительно улучшит вашу жизнь. Вы можете предпочесть десятикратный шанс выиграть миллион.

Вероятность выиграть большой приз

ОК. Каковы шансы на то, что вы выиграете большой приз?

Шансы на выигрыш всех 6 номеров равны 1 из 13 983816

Вы можете использовать Калькулятор комбинаций и перестановок, чтобы вычислить это (используйте n = 49 , r = 6 , «Нет» для параметра «Важен ли порядок?» И «Нет» для параметра «Разрешено ли повторение?»)

Фактический расчет таков:

⁴⁹ С ₆ = 49! / (43! X 6!) = 13983816

Итак, сколько раз вам нужно сыграть, чтобы выиграть?

1 неделя

Предположим, вы играете каждую неделю

Вероятность выигрыша через 1 неделю:

1 13983816 = 0.0000000715 …

Таким образом, вероятность того, что не выиграют через 1 неделю, составляет:

1 — 1 13983816 = 0,9999999285 . ..

50 лет

Допустим, вы играете 50 лет, это 2600 недель.

Вероятность того, что не выиграют за 2600 недель:

(1 — 1 13983816 ) ²⁶⁰⁰ = 0,999814 …

Это означает, что вероятность выигрыша (через 50 лет) равна: 1 — 0.999814 … = 0,000186 …

Еще только около 0,02%

И вы бы потратили тысячи на этот маленький шанс.

Вы могли хорошо провести отпуск за эти деньги.

НО это весело думать: «Я могу выиграть на этой неделе!»

Просто оставь это как развлечение , хорошо?

Твоя очередь

Теперь ваша очередь:

• Узнайте правила выигрыша в лотерею в вашем регионе.
• Сколько номеров вам нужно выбрать и из скольких номеров вы выбираете?
• Рассчитайте вероятность выигрыша в любую неделю.
• Подсчитайте вероятность выигрыша, если вы будете играть каждую неделю в течение 50 лет.
• Сколько денег вы сэкономите, не играя? Что можно купить за эти деньги?

Треугольник Паскаля

Одним из самых интересных образов чисел является треугольник Паскаля (названный в честь Блеза Паскаля , известного французского математика и философа).

Чтобы построить треугольник, начните с «1» вверху, а затем продолжайте размещать числа под ним в виде треугольника.

Каждое число — это числа непосредственно над ним, сложенные вместе.

(здесь я выделил, что 1 + 3 = 4)

Паттерны внутри треугольника

Диагонали

Первая диагональ, конечно же, всего «1» с

На следующей диагонали расположены счетные числа (1,2,3 и т. Д.).

На третьей диагонали расположены треугольные числа

(Четвертая диагональ, не выделенная, имеет тетраэдрические числа.)

Симметричный

Треугольник тоже симметричный. Цифры на левой стороне имеют одинаковые совпадающие числа на правой стороне, как в зеркальном отображении.

Горизонтальные суммы

Что вы заметили в горизонтальных суммах?

Есть узор?

Они удваивают каждый раз (степени двойки).

Экспоненты из 11

Каждая строка также представляет собой степень (степень) 11:

• 11 ⁰ = 1 (первая строка — просто «1»)
• 11 ¹ = 11 (вторая строка — «1» и «1»)
• 11 ² = 121 (третья строка — «1», «2», «1»)
• и т. Д.!

Но что происходит с 11 ^{5 ? Простой! Цифры просто перекрываются, вот так:}

То же самое происходит с 11 ^{6 и т. Д.}

Квадраты

Для второй диагонали квадрат числа равен сумме чисел рядом с ним и под ними обоими.

Примеры:

• 3 ² = 3 + 6 = 9,
• 4 ² = 6 + 10 = 16,
• 5 ² = 10 + 15 = 25,
• . ..

Есть и веская причина … ты можешь придумать это? (Подсказка: 4 ² = 6 + 10, 6 = 3 + 2 + 1 и 10 = 4 + 3 + 2 + 1)

Последовательность Фибоначчи

Попробуйте следующее: сделайте узор, двигаясь вверх, а затем вдоль, затем сложите значения (как показано на рисунке)… вы получите последовательность Фибоначчи.

(Последовательность Фибоначчи начинается с «0, 1», а затем продолжается добавлением двух предыдущих чисел, например 3 + 5 = 8, затем 5 + 8 = 13 и т. Д.)

Шансы и эвены

Если вы раскрасите четные и нечетные числа, вы получите узор, такой же, как треугольник Серпинского

Использование треугольника Паскаля

Голова и решка

Треугольник Паскаля может показать вам, сколько способов совмещения орла и решки.Это может показать вам вероятность любой комбинации.

Например, если вы подбрасываете монету три раза, есть только одна комбинация, которая даст вам три решки (HHH), но есть три, которые дадут две решки и одну решку (HHT, HTH, THH), а также три, которые дают одну голову и два решки (HTT, THT, TTH) и по одному для всех решек (TTT). Это образец «1,3,3,1» в Треугольнике Паскаля.

Бросок	Возможные результаты (сгруппированные)	Треугольник Паскаля
1	H T	1, 1
2	HH HT TH TT	1, 2, 1
3	HHH HHT, HTH, THH HTT, THT, TTH TTT	1, 3, 3, 1
4	HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT	1, 4, 6, 4, 1
	… и т.д …

Пример: Какова вероятность выпадения ровно двух орлов при подбрасывании 4 монет?

Есть 1 + 4 + 6 + 4 + 1 = 16 (или 2 ⁴ = 16) возможных результатов, и 6 из них дают ровно две решки. Таким образом, вероятность составляет 6/16, или 37,5%

Комбинации

Треугольник также показывает, сколько комбинаций объектов возможно.

Пример: у вас есть 16 бильярдных шаров.Сколько разных способов вы можете выбрать только 3 из них (игнорируя порядок, в котором вы их выбираете)?

Ответ: спуститесь в начало строки 16 (верхняя строка — 0), а затем по трем разрядам (первое место — 0) и там значение будет вашим ответом, 560 .

Вот отрывок из строки 16:

 1 14  ...
1 15 105 455 1365 ...
1 16120  560  1820 4368 ... 

Формула для любого входа в треугольник

На самом деле существует формула из Комбинации для вычисления значения в любом месте треугольника Паскаля:

Обычно это называется «n выберите k» и записывается так:

Обозначение: «n выберите k» также можно записать C (n, k) , ⁿ C _k или даже _n C _k .

Знак «!» является «факториалом» и означает умножение ряда убывающих натуральных чисел. Примеры: 4! = 4 × 3 × 2 × 1 = 24 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040 1! = 1

Таким образом, треугольник Паскаля также может быть
, треугольником «n выбрать k» и , подобным этому.

(обратите внимание, что верхняя строка равна нулю строки
, а также крайний левый столбец равен нулю)

Пример: строка 4, член 2 в треугольнике Паскаля равен «6» …

… посмотрим, работает ли формула:

Да, работает! Попробуйте другое значение для себя.

Это может быть очень полезно … теперь вы можете вычислить любое значение в треугольнике Паскаля непосредственно (без вычисления всего треугольника над ним).

Полиномы

Треугольник Паскаля также может показать вам коэффициенты в биномиальном разложении:

Мощность	Биномиальное расширение	Треугольник Паскаля
2	(x + 1) 2 = 1 x 2 + 2 x + 1	1, 2, 1
3	(x + 1) 3 = 1 x 3 + 3 x 2 + 3 x + 1	1, 3, 3, 1
4	(x + 1) 4 = 1 x 4 + 4 x 3 + 6 x 2 + 4 x + 1	1, 4, 6, 4, 1
	. .. и т.д …

Первые 15 строк

Для справки, я включил строки с 0 по 14 треугольника Паскаля

.

1

10

45

120

210

252

210

120

45

10

1

1

11

55

165

330

462

462

330

165

55

11

1

1

12

66

220

495

792

924

792

495

220

66

12

1

1

13

78

286

715

1287

1716

1716

1287

715

286

78

130002 130002

1

14

91

364

1001

2002

3003

3432

3003

2002

1001

364

91

364

91

Китайцы знали об этом

Этот рисунок называется «Схема семи квадратов умножения по старинному методу». Просмотр полного изображения

Это с лицевой стороны книги Чу Ши-Цзе « Ssu Yuan Yü Chien» (Драгоценное зеркало четырех элементов) , написанной в году нашей эры 1303 (более 700 лет назад и более чем на 300 лет до Паскаля!) В книге говорится, что треугольник был известен более чем за два столетия до этого.

Квинканкс

Удивительная маленькая машина, созданная сэром Фрэнсисом Гальтоном, представляет собой треугольник Паскаля, сделанный из колышков. Он называется Quincunx.

Шарики падают на первый колышек, а затем отскакивают к нижней части треугольника, где они собираются в маленькие ящики.

Сначала это выглядит совершенно случайным (и это так), но затем вы обнаруживаете, что шары складываются в красивый узор: нормальное распределение.

Действие: Подмножества

Прочтите введение установить в первую очередь!

Это упражнение исследует , сколько подмножеств имеет набор.

Что такое подмножество?

Подмножество — это набор , содержащийся в другом наборе

Это как если бы вы могли выбрать мороженое со следующими вкусами:

{банан, шоколад, ваниль}

Вы можете выбрать любой аромат {банан} , {шоколад} или {ваниль} ,

Или любые два вкуса: {банан, шоколад} , {банан, ваниль} или {шоколад, ваниль} ,

Или все три вкуса (нет, не жадные),

Или , вы можете сказать «совсем нет, спасибо», что означает «пустой набор»: {}

Пример: набор {alex, billy, casey, dale}

Имеет подмножества:

Также есть подмножества:

• {Алекс, Билли}
• {Алекс, Кейси}
• {билли, дол}
• и др…

Также:

• {Алекс, Билли, Кейси}
• {alex, billy, dale}
• и т.д …

А также:

• весь набор: {alex, billy, casey, dale}
• пустой набор: {}

Теперь давайте начнем с Пустого набора и продолжим . ..

Пустой набор

Сколько подмножеств в пустом наборе?

Вы могли выбрать:

• весь комплект: {}
• пустой комплект: {}

Но погодите минутку, в данном случае это одно и то же!

Итак пустой набор действительно имеет только 1 подмножество (которое есть само, пустое множество).

Это все равно что спросить: «Нет ничего доступного, что вы выберете?» Ответьте «ничего». Это твой единственный выбор. Сделанный.

А Набор с одним элементом

Набор может быть любым, но скажем так:

{яблоко}

Сколько поднаборов есть в наборе {яблоко}?

• весь комплект: {яблоко}
• пустой набор: {}

И все. Вы можете выбрать один элемент или ничего.

Таким образом, любой набор с одним элементом будет иметь 2 подмножеств.

А Набор из двух элементов

Давайте добавим еще один элемент в наш набор примеров:

{яблоко, банан}

Сколько подмножеств в наборе {яблоко, банан}?

Это может быть {яблоко} или {банан} , и не забудьте:

• весь набор: {яблоко, банан}
• пустой комплект: {}

Итак, набор с двумя элементами имеет 4 подмножеств.

А Набор из трех элементов

Как насчет:

{яблоко, банан, вишня}

Хорошо, давайте теперь будем более систематичными и перечислим подмножества по количеству элементов в них:

Подмножества с одним элементом: {яблоко} , {банан} , {вишня}

Подмножества с двумя элементами: {яблоко, банан} , {яблоко, вишня} , {банан, вишня}

А:

• весь набор: {яблоко, банан, вишня}
• пустой комплект: {}

Фактически мы могли бы поместить это в таблицу:

	Список	Количество частей
нулевые элементы	{}	1
один элемент	{яблоко}, {банан}, {вишня}	3
два элемента	{яблоко, банан}, {яблоко, вишня}, {банан, вишня}	3
трехэлементный	{яблоко, банан, вишня}	1
Всего:		8

(Примечание: вы заметили закономерность в цифрах?)

Наборы с четырьмя стихиями (ваша очередь!)

Теперь попробуйте проделать то же самое для этого набора:

{яблоко, банан, вишня, финик}

Вот вам стол:

	Список	Количество подмножеств
нулевые элементы	{}
один элемент
два элемента
трехэлементный
четыре элемента
Всего:

(Примечание: если вы все сделали правильно, в числах будет узор. )

Наборы с пятью элементами

А сейчас:

{яблоко, банан, вишня, финик, яйцо}

Вот вам стол:

	Список	Количество подмножеств
нулевые элементы	{}
один элемент
два элемента
трехэлементный
четыре элемента
пять элементов
Всего:

(Был ли узор на числах?)

Наборы с шестью элементами

А как насчет:

{яблоко, банан, вишня, финик, яйцо, помадка}

ОК. .. нам не нужно заполнять таблицу, потому что …

… вы должны уметь увидеть образец сейчас!

Удвоение

Первое, что следует заметить, это то, что общее количество подмножеств каждый раз удваивается:

Набор с элементами n имеет 2 ⁿ подмножеств

Итак, вы сможете ответить:

• Сколько существует подмножеств в наборе из 6 элементов? _____
• Сколько существует подмножеств в наборе из 7 элементов? _____

Другой Выкройка

А теперь подумаем о подмножеств и размеров:

• пустой набор имеет просто 1 подмножество : 1
• Набор с одним элементом имеет 1 подмножество без элементов и 1 подмножество с одним элементом: 1 1
• Набор с двумя elements имеет 1 подмножество без элементов, 2 подмножества с одним элементом и 1 подмножество с двумя элементами: 1 2 1
• Набор из трех элементов имеет 1 подмножество без элементов, 3 подмножества с одним элемент, 3 подмножества с двумя элементами и 1 подмножество с тремя элементы: 1 3 3 1
• и так далее!

Знаете ли вы это узор чисел?

Это числа Паскаля. Треугольник!

Это очень полезный , потому что теперь вы можете проверить, есть ли у вас нужное количество подмножеств.

Примечание: строки начинаются с 0, как и столбцы.

Пример: для набора {яблоко, банан, вишня, финик, яйцо} вы перечисляете подмножества длины три:

• {яблоко, банан, вишня}
• {яблоко, банан, финик}
• {яблоко, банан, яйцо}
• {яблоко, вишня, яйцо}

Но это всего лишь 4 подмножеств, сколько их должно быть?

Итак, вы выбираете 3 из 5, поэтому перейдите к строке 5, позиции 3 Треугольника Паскаля (не забудьте начать отсчет с 0), чтобы найти, что вам нужно 10 подмножеств , так что вы должны подумать больше!

Фактически это результаты: {яблоко, банан, вишня} {яблоко, банан, финик} {яблоко, банан, яйцо} {яблоко, вишня, финик} {яблоко, вишня, яйцо} {яблоко, финик, яйцо} {банан, вишня, финик} {банан, вишня, яйцо} {банан, финик, яйцо} {вишня, финик, яйцо}

Расчет чисел

Есть ли способ вычислить числа, такие как 1, 4, 6, 4 и 1 (вместо того, чтобы искать их в Треугольнике Паскаля)?

Да, мы можем найти количество способов выбора каждого количества элементы с использованием комбинаций.

В наборе четыре элемента, и:

• Количество способов выбора 0 элементов из 4 = ⁴ C ₀ = 1
• Количество способов выбор 1 элемента из 4 = ⁴ C ₁ = 4
• Количество способов выбора 2 элементов из 4 = ⁴ C ₂ = 6
• Количество способов выбора 3 элементов из 4 = ⁴ C ₃ = 4
• Количество способов выбора 4 элементов из 4 = ⁴ C ₄ = 1
• Общее количество подмножества = 16

Можете ли вы сделать то же самое для набора из пяти элементов?

Выполните следующее:

• Количество путей выбора 0 элементов из 5 = ⁵ C ₀ = 1
• Количество способов выбор 1 элемента из 5 = ___________
• Количество способов выбора 2 элементов из 5 = ___________
• Количество способов выбора 3 элементов из 5 = ___________
• Количество способов выбора 4 элементов из 5 = ___________
• г. количество способов выбора 5 элементов из 5 = ___________
• Общее количество подмножеств = ___________

Заключение

В этом упражнении у вас:

• Обнаружено правило для определение общего количества подмножеств для данного набора: набор с n elements имеет 2 ⁿ подмножеств.
• Обнаружена связь между количество подмножеств каждого размера с числами в языке Паскаля треугольник.
• Обнаружен быстрый способ вычислите эти числа, используя Комбинации.

Подробнее что важно, вы узнали, как различные разделы математики могут быть объединенными вместе.

Комбинаторный калькулятор, калькулятор комбинаций, вариаций, перестановок

Узнайте, сколькими различными способами вы можете выбрать k предметов из n предметов набора.С / без повторения, с / без заказа.

Расчет:

Ck (n) = (nk) = n! K! (N − k)! n = 10 k = 4 C4 (10) = (104) = 10! 4! (10−4)! = 10⋅9⋅8⋅74⋅3⋅2⋅1 = 210Ck (n) = (kn) = k! (n − k)! n! n = 10 k = 4 C4 (10) = (410) = 4! (10−4)! 10! = 4⋅3⋅2⋅110⋅9 ⋅8⋅7 = 210

Количество комбинаций: 210

Варианты

Вариантом k-го класса из n элементов является упорядоченная группа из k элементов, сформированная из набора из n элементов. Элементы не повторяются и зависят от порядка элементов группы (следовательно, упорядочены).

Количество вариантов легко вычислить, используя комбинаторное правило произведения. Например, если у нас есть набор n = 5 чисел 1,2,3,4,5 и мы должны сделать вариации третьего класса, их V ₃ (5) = 5 * 4 * 3 = 60.

Vk (n) = n (n − 1) (n − 2) … (n − k + 1) = n! (N − k)! Vk (n) = n (n − 1) ( п-2) … (п-к + 1) = (п-к)! п!

п! мы называем факториалом числа n, которое является произведением первых n натуральных чисел. Обозначения с факториалом только нагляднее, эквивалентны.Для расчетов вполне достаточно использовать процедуру, вытекающую из комбинаторного правила произведения.

Перестановки

Перестановка является синонимом варианта n-го класса n-элементов. Таким образом, это любая упорядоченная группа из n элементов, состоящая из n элементов. Элементы не повторяются и зависят от порядка элементов в группе.

P (N) = N (N — 1) (N — 2) . .. 1 = N! P (N) = N (N — 1) (N — 2) … 1 = N!

Типичный пример: у нас есть 4 книги, и сколькими способами мы можем расположить их рядом на полке?

Вариации с повторением

Разновидностью k-го класса из n элементов является упорядоченная группа из k элементов, образованная набором из n элементов, причем элементы могут повторяться и зависит от их порядка.Типичный пример — формирование чисел из чисел 2, 3, 4, 5, и нахождение их количества. Подсчитываем их количество по комбинаторному правилу произведения:

Vk ′ (n) = n⋅n⋅n⋅n … n = nkVk ′ (n) = n⋅n⋅n⋅n … n = nk

Перестановки с повторением

Повторяющаяся перестановка — это упорядоченная k-элементная группа из n-элементов, при этом некоторые элементы повторяются в группе. Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок.

Pk1k2k3 … км ′ (п) = п! K1! K2! K3! … км! Pk1 k2 k3 . .. км ′ (п) = k1! K2! K3! … км! п!

Типичный пример — узнать, сколько семизначных чисел образовано из чисел 2,2,2, 6,6,6,6.

Комбинации

Комбинация k-го класса из n элементов представляет собой неупорядоченную группу из k элементов, сформированную из набора из n элементов. Элементы не повторяются, и порядок элементов в группе не имеет значения. В математике неупорядоченные группы называются множествами и подмножествами.Их количество является комбинационным числом и рассчитывается следующим образом:

Ck (n) = (nk) = n! K! (N − k)! Ck (n) = (kn) = k! (N − k)! N!

. Типичный пример комбинаций: у нас 15 учеников, и нам нужно выбрать троих. Сколько их будет?

Комбинации с раппортом

Здесь мы выбираем k групп элементов из n элементов, независимо от порядка, и элементы могут повторяться. k логически больше n (иначе мы получили бы обычные комбинации). Их количество:

Ck ′ (n) = (n + k − 1k) = (n + k − 1)! K! (N − 1)! Ck ′ (n) = (kn + k − 1) = k! ( п — 1)! (п + к — 1)!

Пояснение к формуле — количество комбинаций с повторением равно количеству расположений n — 1 разделителей на n-1 + k местах. Типичный пример: мы идем в магазин, чтобы купить 6 конфет. Предлагают всего 3 вида. Сколько у нас вариантов? к = 6, п = 3.

Основы комбинаторики в словесных задачах

следующие математические задачи »

комбинаторика — Каково общее количество комбинаций из 5 элементов вместе, если нет дубликатов?

комбинаторика — Каково общее количество комбинаций из 5 элементов вместе, если нет дубликатов? — Обмен стеками математики

Сеть обмена стеков

Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0
3. +0
6. Авторизоваться Зарегистрироваться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 8 лет, 11 месяцев назад

Просмотрено 67к раз

$ \ begingroup $

У меня 5 категорий — A, B, C, D и E.

Я хочу в основном создавать группы, которые отражают каждую комбинацию этих категорий без дублирования.

Итак, группы будут выглядеть так:

• А
• B
• C
• D
• E
• А, В
• А, С
• А, Д
• A, E
• B, C
• B, D
• B, E
• C, D . . . пр.

Похоже на то, что я бы использовал биномиальный коэффициент $ n \ choose r $ для, но я довольно нечеткий в расчетах и ​​не могу точно вспомнить, как это сделать.

Любая помощь будет оценена.

Спасибо.

АакашМ

54711 золотой знак77 серебряных знаков1818 бронзовых знаков

Создан 22 июн.

маркамиллион

215 11 золотой знак22 серебряных знака88 бронзовых знаков

$ \ endgroup $ $ \ begingroup $

Существуют комбинации $ \ binom {5} {1} $ с 1 элементом, комбинации $ \ binom {5} {2} $ с элементами $ 2 $ ,. n $$

Создан 22 июня ’12 в 11: 312012-06-22 11:31

JBCJBC

2,1661818 серебряных знаков2121 бронзовый знак

$ \ endgroup $ 5 $ \ begingroup $

Пусть $$ nCr = \ binom {n} {r} = \ frac {n!} {K! (N-k)!} $$ Помните, что $ \ frac {n!} {(N-k)!} $ Дает все перестановки, а $ k! $ В знаменателе — это то, что игнорирует дубликаты.п-1 $$ Таким образом, когда $ n = 5 $, мы получаем вышеуказанный ответ.

Приложение : Чтобы решить вашу озабоченность по поводу того, что, похоже, существует более 31 $ комбинаций, вот список всех возможных вариантов: $$ \ begin {array} {| c | c | c | c | c | c | c |} & 1 \ текст {категория} & 2 \ текст {категории} & 3 \ текст {категории} & 4 \ текст {категории} & 5 \ текст {категории} & \ текст {Сумма} \\ \ hline & A & AB & ABC & ABCD & ABCDE \\ \ hline & B & AC & ABD & ABCE \\ \ hline & C & AD & ABE & ABDE \\ \ hline & D & AE & ACD & ACDE \\ \ hline & E & BC & ACE & BCDE \\ \ hline & & BD & ADE \\ \ hline & & BE & BCD \\ \ hline & & CD & BCE \\ \ hline & & CE & BDE \\ \ hline & & DE & CDE \\ \ hline \ text {Всего} & 5, 10, 10, 5, 1, 31 \\ \ hline \ end {array} $$

Создан 22 июн.

Э.О.Е.О.

6,46666 золотых знаков3131 серебряный знак5353 бронзовых знака

$ \ endgroup $ 3 $ \ begingroup $

Подумайте об этом с другой стороны. Вам нужно какое-то количество из этих пяти категорий без повторения.

Ну, каждая категория либо выбрана вами, либо не вами. Каждый такой выбор не имеет отношения к другим вариантам.5 = 32 $ возможности. Однако вы не учитываете выбор ни в одной из пяти категорий, поэтому мы вычитаем 1 доллар, чтобы получить 31 вариант.

Создан 22 июн.

раздражительный

10.2k11 золотых знаков2020 серебряных знаков3535 бронзовых знаков

$ \ endgroup $ 1 $ \ begingroup $

Используйте двоичный код! 1, 2, 4, 8, 16 в сумме дает 31
Количество комбинаций из 6 чисел составит 63
Семь цифр будут 127 и т. Д.

Создан 05 авг.

Джимпи

1111 бронзовый знак

$ \ endgroup $ $ \ begingroup $

Я ценю математику, которая привела вас к ответу, но если вы посмотрите на проблему как на двоичные числа, 0 — не используется, 1 — используется и каждую битовую позицию как элемент, вы придете к такому же выводу…для N бит, сколько значений вы можете закодировать? Не считая значения 0. A__ = 100 (старшая позиция — 1) В = 010 AB_ = 110 __C = 001 A_C = 101 _BC = 011 ABC = 111

Создан 11 июл.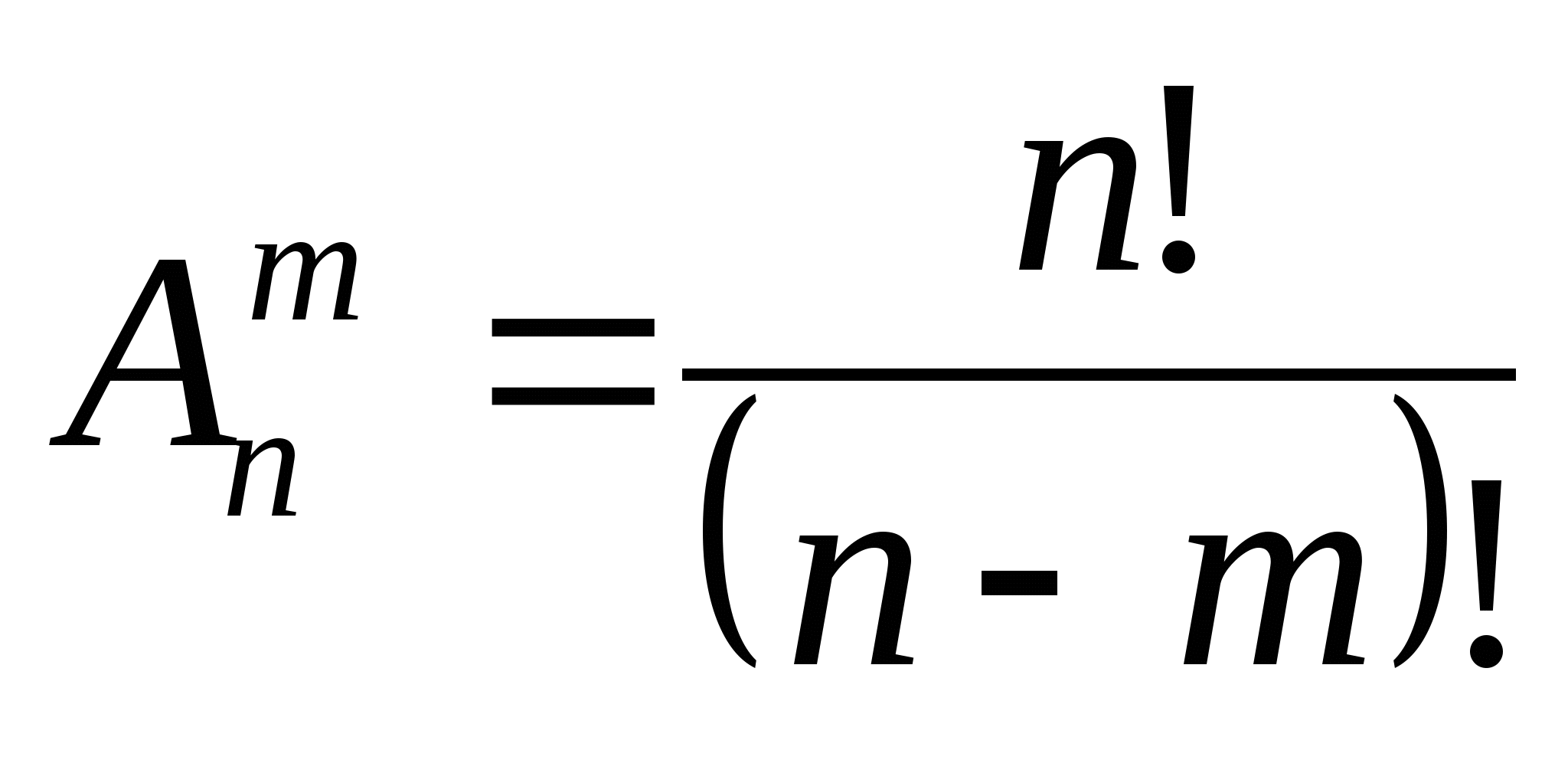

$ \ endgroup $ 1 Очень активный вопрос .Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов.

Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками комбинаторика или задайте свой вопрос.

Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

Упражнения по математике

]]> Матрицы Алгебра Геометрия Funciones Тригонометрия Координатная геометрия Комбинаторика Сумма и ресторан Продукт на эскаларе Изделие Inversa Мономы Полиномы Особые продукты Уравнения Квадратные уравнения Радикальные выражения Системы уравнений Последовательности и серии Внутренний продукт Экспоненциальные уравнения Матрицы Детерминанты Инверсия матрицы Логарифмические уравнения Системы трех переменных уравнений Двумерные фигуры Площади Теорема Пифагора Расстояния Графики Определение уклона Положительный или отрицательный наклон Определить наклон прямой Ecuación de una recta Уравнение прямой (с графика) Квадратичная функция Posición relativa de dos rectas Асимптоты Пределы Distancias Непрерывность и разрывы Теорема Пифагора Синус Косинус Касательная Косеканс Секант Котангенс Тригонометрические идентификаторы Тригонометрические функции острого угла Тригонометрические функции связанных углов Решение прямоугольных треугольников Закон косинусов Закон синусов Ecuación de una recta Posición relativa de dos rectas Distancias Углы в пространстве Внутренний продукт Факториал Варианты без повторов Вариации с повторением Перестановки с повторением Перестановки без повторов Упражнения Круговые перестановки Биномиальный коэффициент Комбинации с повторением Комбинации без повторов Среднее арифметическое

с повторением и без повторения с примерами

В этой статье будет примерно Комбинация и когда она используется, типы комбинаций, с формулами и примерами обоих типов комбинаций.

Быстрый доступ

! Нажмите на кнопки ниже, чтобы перейти прямо к нужному разделу статьи!

Перейти к примерам

Определение комбинации

Комбинация — это используемый метод статистики, который состоит в поиске способов, которыми мы можем выбрать некоторые элементы из набора данных. Общая концепция комбинации и перестановки довольно схожа, и из-за этого сначала мы не можем увидеть разницу между ними, но разница между комбинацией и перестановкой заключается в том, что в комбинации порядок элементов не имеет значения, это означает, что пока комбинация выбранных элементов одинакова, это будет считаться только одной комбинацией.

Чтобы лучше понять значение и использование комбинации, мы собираемся показать следующий пример: если из 5 человек мы хотим случайным образом выбрать двух из них для участия в действии, в перестановке порядок, в котором мы выбираем людей будет иметь значение, например, если мы сначала выберем человека A, а затем человека B, это будет одна перестановка, и если мы выберем человека B, а затем человека A, это будет другая перестановка, , но в сочетании, это два сценария будут учитываться только как одна комбинация, независимо от того, будет ли порядок выбора «A и B» или «B и A»

Комбинация записывается буквами nCr, где «n» — это количество элементов в наборе, а «r» — это количество элементов, которые мы собираемся выбрать, где «r» не может быть большим, чем «n», потому что это приведет к ошибке.

Еще одно свойство комбинации состоит в том, что существует два типа комбинаций: одна с повторением, а другая без повторения.

Комбинация с повторением

Это когда элементы набора могут повторяться, чтобы прояснить этот тип, вот пример: человек идет в кондитерскую, где есть 10 разных вкусов конфет, но этот человек собирается взять только 4, по одному для каждого из его детей, это пример комбинации с повторением, потому что, хотя существует 10 разных вкусов, что-либо не позволяет этому человеку выбрать один и тот же аромат дважды, трижды или даже четыре раза.

Формула с повторением

Комбинация без повтора

Это когда элементы набора не могут быть повторены, например: в компании, где работают 20 человек, они принимают решение о формировании директивы, составленной из 3 человек, в этом случае у нас будет комбинация без повторения, потому что человека нельзя выбрать дважды.

Формула без повторов

Примеры комбинации

Пример 1: Человек идет в кондитерскую, где есть 8 типов вкусов, если этот человек собирается купить только 3, определите все возможные комбинации

С повторением n = 8 r = 3 nCr =?

Иисус — сын Божий, посланный на смерть, чтобы каждый, кто верит в него, имел жизнь вечную.

Узнать больше

Пример 2: 2 девушки пойдут на вечеринку, если у них есть 4 пары модной обуви, определите комбинацию обуви, которую могут носить эти две девушки

Без повторения n = 4 r = 2 nCr =?

Пример 3: Мужчина отправится в путешествие на 3 дня, поэтому он возьмет с собой 3 рубашки, если у него 7 рубашек, сколько комбинаций рубашек он может взять.

Без повторения n = 7 r = 3 nCr =?

Пример 4: В ведре 10 шаров, каждый шар пронумерован от 1 до 10, если кто-то случайно вытащит 3 из этих шаров, сколько комбинаций он сможет взять.

Без повторения n = 10 r = 3 nCr =?

Пример 5: Спортсмен идет в магазин, чтобы купить 4 пары обуви, если в магазине много обуви 5 доступных цветов, сколько комбинаций цветов может купить этот мужчина.

С повторением n = 5 r = 4 nCr =?

.

No related posts.