Сочетание без повторений | matematicus.ru
Сочетанием без повторений называют комбинации, составленные из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом.
Обозначение: $С_n^m$
Допустим, имеется три буквы А, В и С.
Составим всевозможные комбинации только из двух букв, которые отличаются друг от друга хотя бы одним элементом: АВ, АС, ВС.
При подсчете числа сочетаний элементов — порядок не важен.
Запишем формулу сочетания

Пример 1
В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства? Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем
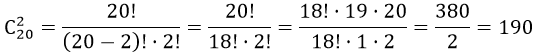
Пример 2
Пусть имеется множество, содержащие 4 буквы: {А,В,С,D}.
Записать все возможные сочетания из указанных букв по три.
Решение
По формуле сочетания имеем,
$C_4^3 =\frac{{4!}}{{\left( {4 — 3} \right)!\cdot3!}} = \frac{{4!}}{{3!}} = \frac{{1\cdot2\cdot3\cdot4}}{{1\cdot2\cdot3}} = 4$
Пример 3
В ящике 15 деталей, среди которых 6 бракованных. Наугад выбирается комплект из 5 деталей. Сколькими способами можно составить такой комплект, в котором 2 детали бракованные?
Решение
$C_{6}^2$ — количество способов выбора двух бракованных деталей из шести
$C_{3}^9$ — количество способов выбора трех исправных деталей из девяти
Тогда количество комбинаций по правилу умножения будет
$C_{6}^2·C_{3}^9=\frac{{6!}}{{(6-2)!2!}}·\frac{{9!}}{{(9-3)!3!}}=15·84=1260$
Пример 4
Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?
Решение
Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения равно
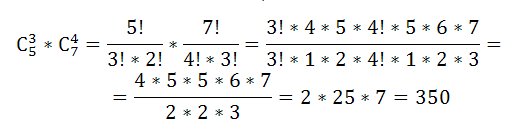
Пример 5
В научном конкурсе участвует 12 человек, из них 5 женщин и 7 мужчин. Сколькими способами можно сформировать группу из 7 человек, чтобы в ней было 3 женщины?
Решение
Из пяти женщин необходимо выбрать по три. Следователь, число таких способов отбора равно $С_5^3$
Число способов отбора мужчин, четырех из семи равно $С_7^4$
По формуле комбинаторики – сочетания, группу можно сформировать способами:
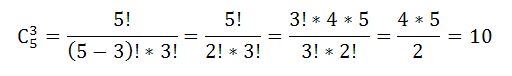
Пример 6
Сколькими способами можно составить суточный наряд по университету из одного офицера, двух сержантов и семи курсантов, если имеется 3 офицера, 6 сержантов и 30 курсантов?
Решение
Число способов выбора офицера: $С_3^1$
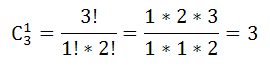
сержантов $С_6^2$
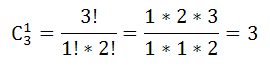
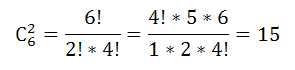
по аналогии, число комбинаций выбора курсантов, получаем $С_30^7$
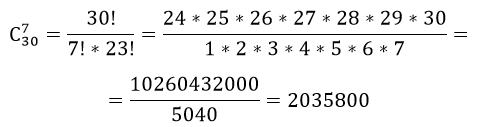
Итак, получаем число способов составления суточного наряда
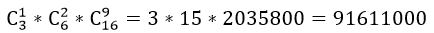
Комбинаторика в Python / Хабр
Стандартная библиотека python, начиная с версии 2.2, предоставляет множество средств для генерирования комбинаторных объектов, но в интернете мне не удалось найти ни одной статьи, которая подробно рассказывала бы о работе с ними. Поэтому я решил исправить это упущение.
Начну с того, что расскажу о комбинаторике и ее основных формулах. Если же вы уже знакомы с этим разделом математики — можете пропустить эти абзацы.
Допустим, у нас есть строка, состоящая из n разных букв и мы хотим вычислить все способы переставить эти буквы местами так, чтобы получить новую строку. На первую позицию в строке мы можем выбрать одну из n букв, имеющихся у нас, на вторую позицию одну из n-1-ой буквы и так далее. В итоге получаем произведение n (n-1)… *1 = n! количество перестановок из n элементов без повторений.
Теперь представим, что количество букв в строке ограничено. У нас есть n доступных букв и мы хотим вычислить количество способов составить из них строку длины k, где k < n, каждую букву мы можем использовать лишь единожды. Тогда на первую позицию в строке мы можем поставить одну из n букв, на вторую позицию одну из n-1 буквы и на k-ую позицию одну из n-k+1 буквы. Общее количество строк будет равно n (n — 1) (n — 2) … (n — k + 2) (n — k + 1) = n!/(n-k)! количество размещений из n по k. Если же уникальность букв не требуется, то мы получим формулу n…nn = n^k количество размещений из n по k с повторениями.
До этого мы перебирали последовательности с учетом порядка элементов, а что если порядок для нас не имеет значения. Например, у нас есть есть n разных конфет и мы хотим выбрать k из них, чтобы подарить другу, при чем k < n. Сколько существует способов выбрать k конфет из n без учета порядка? Ответ прост, в начале найдем размещение из n по k без повторений, но тогда одинаковые наборы конфет, имеющие разный порядок их следования будут повторяться. Сколько существует способов переставить k конфет? Правильно, перестановка из k элементов без повторений. Итоговый ответ: размещения из n по k делим на перестановки из k без повторений. Формула: количество сочетаний из n по k.
Рассмотрим случай посложнее, у нас есть n коробок каждая из которых содержит множество конфет одного вкуса, но в разных коробках вкусы разные. Сколько существует способов составить подарок другу из k конфет, при чем один и тот же вкус может встречаться любое количество раз? Так как порядок для нас значения не имеет, давайте разложим подарочные сладости следующим образом: в начале будут лежать последовательно конфеты первого вкуса, затем второго и так далее, а между конфетами разных вкусов положим спички, если конфеты какого-то вкуса отсутствуют в нашем подарке — спички, которые должны были окаймлять этот вкус слева и справа будут стоять рядом. Того у нас получится последовательность, состоящая из k конфет и n-1 спички, ибо вкусов всего n, а спички разделяют их. Теперь заметим, что по расположению спичек, мы можем восстановить исходное множество. Тогда ответом будет количество способов разместить n-1 спичку в n+k-1 ячейку без учета порядка, что равно количеству сочетаний из n+k-1 по n-1, формула: количество сочетаний из n по k с повторениями.
Теперь рассмотрим несколько задач на комбинаторику, чтобы закрепить материал.
Задача 1
Есть 20 человек, сколько существует способов разбить их на пары
Решение: возьмем первого человека, сколько существует способов выбрать ему пару: , возьмем второго человека, сколько существует способов выбрать ему пару: . Ответ: 19!!! = 654729075
Задача 2
Есть 10 мужчин и 10 девушек, сколько существует способов разбить их на компании, состоящие из одинакового количества и мужчин и девушек, пустая компания не считается
Решение:
Cпособ 1: количество способов собрать компанию из одного мужчины и одной девушки равно произведению количества способов выбрать одну девушку и количества способов выбрать одного мужчину. Количество способов выбрать одну девушку из 10 равно сочетанию из 10 по 1 без повторений, с мужчинами аналогично, поэтому возведем в квадрат. Далее аналогично вычислим сочетания из 10 по 2, из 10 по 3 и так далее до сочетания из 10 по 10. Итоговая формула: .
Способ 2: рассмотрим множество мужчин, входящих в компанию и множество девушек, не входящих в нее. По этому множеству можно однозначно восстановить компанию, а количество людей в нем всегда равно 10, так как , k — количество мужчин в компании, — количество девушек, не вошедших в нее. Количество таких множеств равно количеству сочетаний из 20 по 10, в конечном ответе мы также вычтем единицу, чтобы не учитывать пустую компанию, когда в нашем множестве 10 девушек. Итоговая формула: .
Итак, мы разобрались с теорией, теперь научимся генерировать комбинаторные объекты с помощью стандартной библиотеки python.
Работать мы будем с библиотекой itertools
from itertools import *С помощью функции permutations можно сгенерировать все перестановки для итерируемого объекта.
Пример 1
for i in permutations('abc'):
print(i, end=' ') # abc acb bac bca cab cba
print()
for i in permutations('abb'):
print(i, end=' ') # abb abb bab bba bab bba Исходя из второго вызова заметим, что одинаковые элементы, стоящие на разных позициях, считаются разными.
Пример 2
for i in permutations('abc', 2):
print(i, end=' ') # ab ac ba bc ca cb Размещение отличается от перестановки ограничением на количество доступных ячеек
Пример 3
for i in product('abc', repeat=2):
print(i, end=' ') # aa ab ac ba bb bc ca cb ccC помощью размещений с повторениями можно легко перебрать все строки фиксированной длины, состоящие из заданных символов
Пример 4
for i in combinations('abcd', 2):
print(i, end=' ') # ab ac ad bc bd cd С помощью сочетаний без повторений можно перебрать все наборы не повторяющихся букв из заданной строки, массива или другого итерируемого объекта без учета порядка
Пример 5
for i in combinations_with_replacement('abcd', 2):
print(i, end=' ') # aa ab ac ad bb bc bd cc cd dd Результат аналогичен вызову combinations
Материалы:
Н.В. Горбачев «Сборник олимпиадных задач по математике»
Документация по python на русском
Формулы комбинаторики
Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N, состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.
Сформулируем следующие определения:
Размещения без повторения
Размещением без повторения из n элементов по m называется всякое упорядоченное подмножество множества N, содержащее m различных элементов
.Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.
Теорема 3. Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n. Записывают:
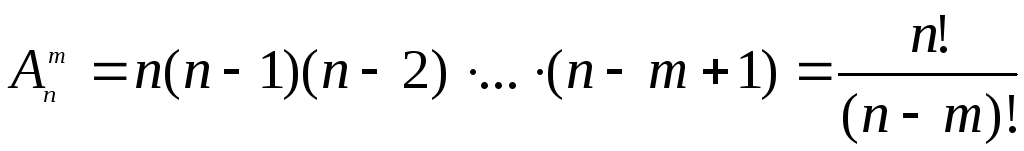
Перестановки без повторений
Перестановками из n элементов называются различные упорядочения множества N.
Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.
Теорема 4. Число различных перестановок без повторений вычисляется по формуле

Сочетания без повторений
Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N, содержащее m различных элементов.
Из определения следует, что два сочетания различаются только элементами, порядок не важен.
Теорема 5. Число сочетаний без повторений вычисляют по одной из следующих формул:

Пример 1. В комнате 5 стульев. Сколькими способами можно разместить на них
а) 7 человек; б) 5 человек; в) 3 человека?
Решение: а) Прежде всего надо выбрать 5 человек
из 7 для посадки на стулья. Это можно
сделать 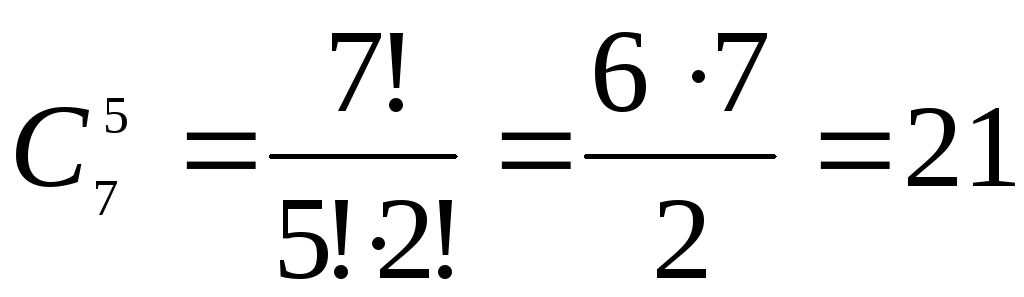
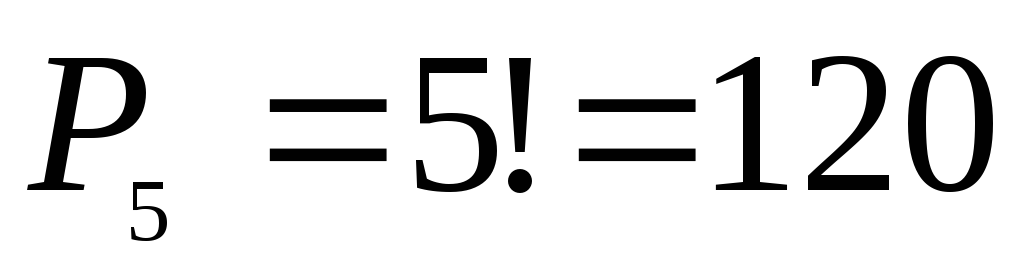 перестановок местами. Согласно теореме
умножения искомое число способов посадки
равно
перестановок местами. Согласно теореме
умножения искомое число способов посадки
равно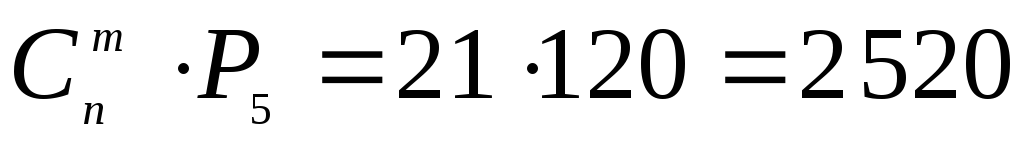 .
. Замечание: Задачу можно решать, используя только
теорему произведения, рассуждая следующим
образом: для посадки на 1-й стул имеется
7 вариантов, на 2-й стул-6 вариантов, на
3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов
посадки 7 человек на 5 стульев равно 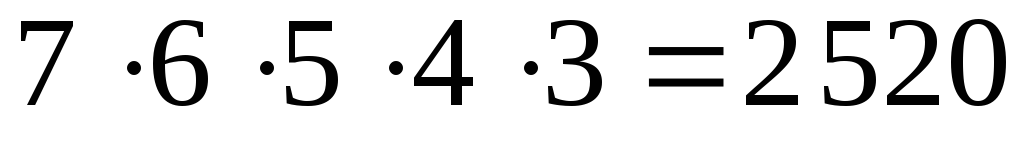 .
Решения обоими способами согласуются,
так как
.
Решения обоими способами согласуются,
так как
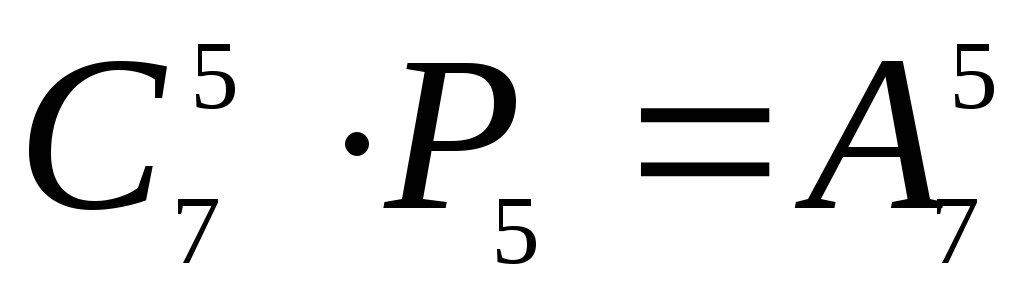
б) Решение очевидно
— 
в)  — число выборов занимаемых стульев.
— число выборов занимаемых стульев.
 — число размещений
трех человек на трех выбранных стульях.
— число размещений
трех человек на трех выбранных стульях.
Общее число выборов
равно 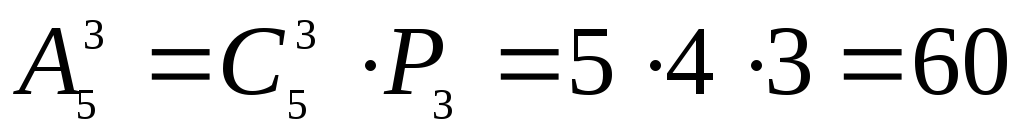 .
.
Не трудно проверить
формулы 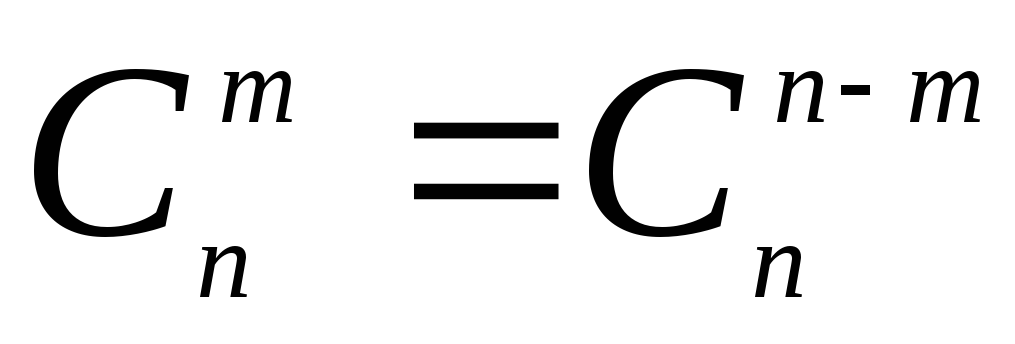 ;
;
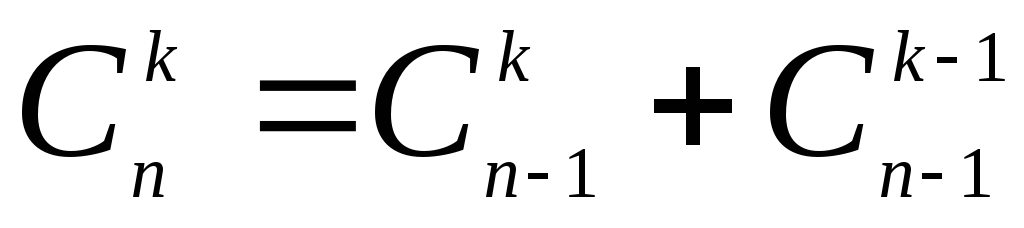 ;
;
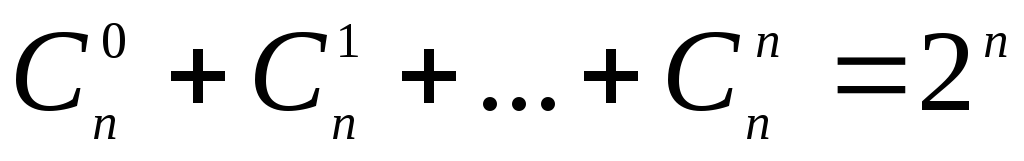 —
число всех подмножеств множества,
состоящего из n элементов.
—
число всех подмножеств множества,
состоящего из n элементов.
Размещения с повторением
Размещением с повторением из
n элементов по m называется всякое упорядоченное подмножество множества N, состоящее из m элементов так, что любой элемент ожжет входить в это подмножество от 1 до m раз, либо вообще в нем отсутствовать. Число
размещений с повторением обозначают  и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
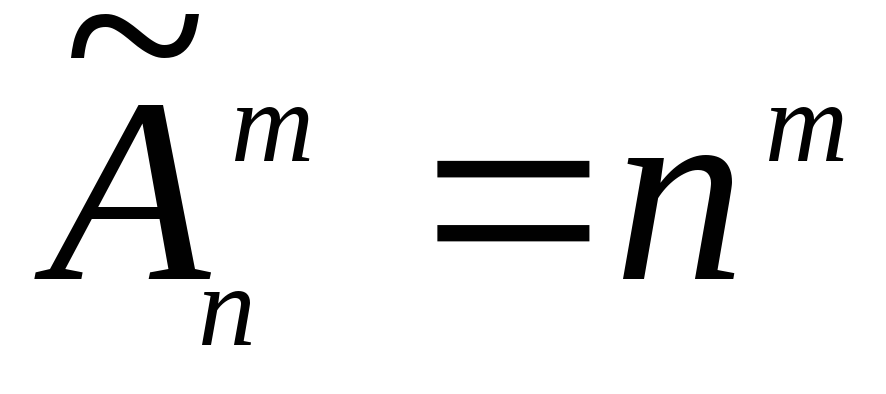
Пример 2.
Пусть дано множество из трех букв N
= {a,
b,
c}.
Назовем словом любой набор из букв,
входящих в это множество. Найдем
количество слов длиной 2, которые можно
составить из этих букв: 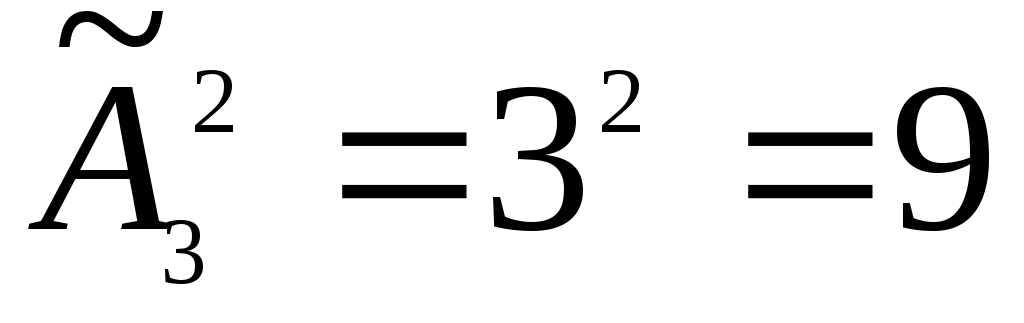 .
.
Замечание: Очевидно, размещения с повторением
можно рассматривать и при 
Пример 3. Требуется из букв {a, b}, составить всевозможные слова длиной 3. Сколькими способами это можно сделать?
Ответ: 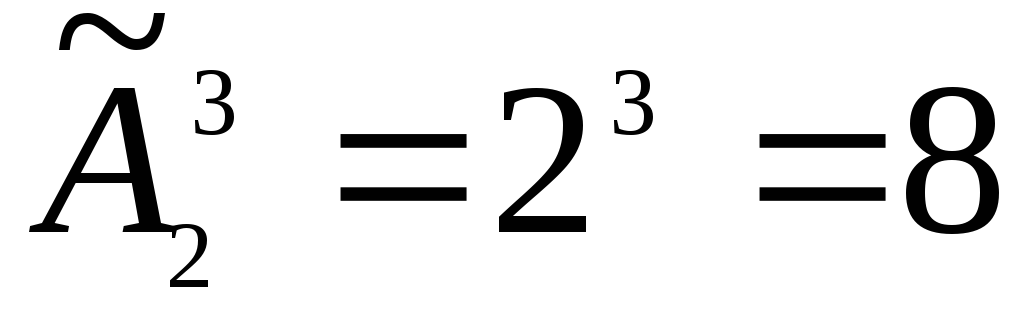
Сочетания без повторений.
Основные формулы комбинаторики
Задачи, в которых речь идет о тех или иных комбинациях объектов, их называют комбинаторными задачами. Область математики, в которой рассматриваются комбинаторные задачи, называют комбинаторикой.
Комбинаторика – область математики, в которой рассматриваются задачи о тех или иных комбинациях объектов.
Правило суммы
Пусть имеется n попарно непересекающихся множеств A1, A2,…An, содержащих m1, m2,…, mn элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно
m1 m2 … mn.
Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в третьей – 20. Сколькими способами из них можно выбрать одного студента?
Решение. Из первой группы одного человека можно выбрать 25 способами, из второй – 30, из третьей – 20. Чтобы найти ответ, нужно сложить все эти способы:
25 30 20=75.
Ответ: выбрать одного студента из трех групп можно 75 способами.
Правило произведения
Пусть имеется .n множеств A1, A2,…An,содержащих m1, m2,,…, mn элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества
m1ּm2 ּ…ּmn.
Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в третьей – 20. Сколькими способами из каждой из них можно выбрать по одному студенту?
Решение. Из первой группы одного человека можно выбрать 25 способами, из второй – 30, из третьей – 20. Чтобы найти ответ, нужно перемножить эти числа:
25ּ30ּ20=15000.
Ответ: для того, чтобы из каждой группы выбрать по одному студенту, существует 15000 способов.
^ Если выбираем один элемент из нескольких множеств, то применяем правило суммы.
Если выбираем по одному элементу из нескольких множеств, то применяем правило произведения.
Факториаломчислаn называется последовательное произведение натуральных чисел от единицы до самого числа n:
Примечание: 0!=1.
Перестановки без повторений
Перестановками из n различных элементов называются размещения из этих n элементов по n. Перестановки — частный случай размещений.
Пример. Сколькими способами можно расставить в шеренгу студентов группы из 25 человек?
Решение. Число способов есть число перестановок из 25 элементов, то есть:
P25 = 25ּ24ּ23ּ…ּ1=25!=1,55ּ1025.
Ответ: расставить в шеренгу студентов группы из 25 человек можно 1,55ּ1025 способами.
Размещения без повторений
Различные упорядоченные подмножества по m элементов данного множества, содержащего n элементов, называются размещениями из n по m. Их число равно:
В частности: .
Пример. Из группы, состоящей из 25 человек, надо выбрать шахматную команду из четырех человек на I, II, III и IV доски. Сколькими способами это можно сделать?
Решение. Так как из 25 человек выбираются 4 и порядок важен, то число способов есть число размещений из 25 по 4, то есть:
.
Ответ: выбрать из 25 человек шахматную команду из четырех человек на I, II, III и IV доски можно 303600 способами.
Сочетания без повторений.
Различные неупорядоченные подмножества по m элементов из данного множества, содержащего n элементов, называются сочетаниями из n по m. Их число равно:
В частности, .
Пример. Сколькими способами из группы в 25 человек можно выбрать баскетбольную команду из пяти человек?
Решение. Так как из 25 человек выбираются 5 и порядок не важен, то число способов есть число сочетаний из 25 по 5, то есть:
Ответ: из группы в 25 человек можно выбрать баскетбольную команду 53130 способами.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Алгебра и начала математического анализа, 11 класс
Урок №32. Сочетания с повторениями.
Перечень вопросов, рассматриваемых в теме:
- Элементы комбинаторики
- Сочетания с повторениями
Глоссарий по теме
Перестановки
В комбинаторике конечное упорядоченное множество называется перестановкой без повторения, а их число обозначают Рn .
Перестановки элементов одного и того же множества отличаются только порядком расположения элементов друг относительно друга.
Pn=1∙2∙3∙4∙…∙(n-1)∙n
Если элементы множества расставлены по кругу, то это так называемые перестановки n элементов по кругу. Их количество равно (n — 1)!
Если множество содержит одинаковые элементы, то подсчет количества перестановок с повторениями производится следующим образом: элементы первого типа можно переставить между собой  (n1 – количество таких элементов) способами, второго типа –
(n1 – количество таких элементов) способами, второго типа –  способами, k -го типа —
способами, k -го типа —  способами. Значит, число перестановок с повторениями меньше n! в
способами. Значит, число перестановок с повторениями меньше n! в  раз, чем число перестановок без повторения, то есть это число равно
раз, чем число перестановок без повторения, то есть это число равно

Размещения
В комбинаторике упорядоченные подмножества данного множества называются «размещениями из n элементов на k мест» или, проще: «размещениями из n по k».

Выбор m элементов из множества, содержащего n элементов с повторением и с упорядочиванием выбранных элементов в последовательную цепочку называют размещениями с повторениями из n элементов по m , а общее число обозначают 
В комбинаторике подмножества данного множества называются «сочетаниями из n по k элементов» или, проще: «сочетания из n по k».

Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Представим себе, что из элементов множества  мы составляем всевозможные трехэлементные комбинации, в которых порядок не важен (как в сочетаниях), но выбрав каждый элемент мы возвращаем его обратно в множество и можем выбирать его снова. Сколько же в таком случае мы получим комбинаций
мы составляем всевозможные трехэлементные комбинации, в которых порядок не важен (как в сочетаниях), но выбрав каждый элемент мы возвращаем его обратно в множество и можем выбирать его снова. Сколько же в таком случае мы получим комбинаций
Считаем, что aab, aba или baa одинаковые наборы
aba и abc –разные наборы
Изучение этого случая начнем с простого примера:
В кондитерской имеются пирожные трех видов. Сколькими способами можно заказать набор, состоящий из пяти пирожных?
Поскольку порядок расположения пирожных в коробке не важен, речь идет о сочетаниях. Кроме того, в наборах обязательно будут повторения.
Зашифруем каждый заказ нулями и единицами. Сначала напишем столько единиц, сколько заказали пирожных первого вида. Потом напишем ноль. Дальше напишем столько единиц, сколько заказали пирожных второго вида. Затем опять ноль. Опять напишем столько единиц, сколько заказали пирожных третьего вида.
пирожные | Шифр заказа | ||
Первый вид | Второй вид | Третий вид | |
2 | 2 | 1 | 1101101 |
5 | 1111100 | ||
Каждый «зашифрованный» заказ представляет собой комбинацию из пяти 1 и двух 0. Число выбора заказа равно числу перестановок с повторениями элементов множества {1,1,1,1,1,0,0}. В этом множестве 1 повторяется пять раз и 0 – два раза
Применим формулу для числа перестановок с повторениями
Значит, способов заказать набор пирожных 21.
Выбор m элементов из множества, содержащего n элементов с повторением и без упорядочивания выбранных элементов в последовательную цепочку называют сочетаниями с повторениями из n элементов по m 
Пусть множество содержит n элементов, а выборка будет содержать m элементов. Аналогично тому, как мы делали в примере, зашифруем каждую выборку единицами и нулями.
Число единиц равно числу выбираемых элементов, то есть m. Поскольку всего различных элементов в множестве n, то мы должны поставить между единицами (n-1) «перегородку», то есть (n-1) нулей. Число размещений с повторениями  равно числу перестановок с повторениями элементов полученного множества из m единиц и (n-1) нулей
равно числу перестановок с повторениями элементов полученного множества из m единиц и (n-1) нулей

Сочетания с повторениями используем тогда, когда порядок расположения элементов в выборке не имеет значения и элементы могут повторяться

Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Сколько существует треугольников, длины сторон которых принимают одно из следующих значений: 5, 6, 7, 8, 9?
Решение:
Данные стороны таковы, что любые три из них соответствуют правилу треугольника, т.е. каждая сторона меньше суммы двух других. Значит, любая комбинация из трех сторон образует треугольник. Здесь речь идет о числе сочетаний из 5 элементов по 3 с повторениями:

Ответ: 35
Пример 2.
Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае.
Поскольку  ,
,  ,
,  ,
,  ,
,  , то существует 5+15+35+70+126=251 чисел, удовлетворяющих условию задачи.
, то существует 5+15+35+70+126=251 чисел, удовлетворяющих условию задачи.
Ответ: 126
Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики: сочетания, размещения, перестановки (смотрите подробнее ниже) и научиться их применять для решения задач.
Как выбрать формулу комбинаторики?
Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:
- алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
- рекомендации по изучению комбинаторики,
- 6 задач с решениями и комментариями на каждую формулу.
Перестановки

Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно
 $$P_n=n!=1\cdot 2\cdot 3 \cdot … \cdot (n-1) \cdot n$$
$$P_n=n!=1\cdot 2\cdot 3 \cdot … \cdot (n-1) \cdot n$$Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
Пример всех перестановок из $n=3$ объектов (различных фигур) — на картинке справа. Согласно формуле, их должно быть ровно $P_3=3!=1\cdot 2\cdot 3 =6$, так и получается.
С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов — уже 3628800 (больше 3 миллионов!).
Еще: онлайн калькулятор перестановок.
Размещения

Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $m$, а их число равно
Пример всех размещений из $n=3$ объектов (различных фигур) по $m=2$ — на картинке справа. Согласно формуле, их должно быть ровно $A_3^2=3\cdot (3-2+1)=3\cdot 2 =6$.
Вычисляем на лету: онлайн калькулятор размещений.
Сочетания
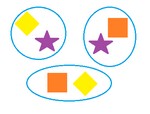
Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $m$, а их число равно
Пример всех сочетаний из $n=3$ объектов (различных фигур) по $m=2$ — на картинке справа. Согласно формуле, их должно быть ровно $C_3^2=\frac{3!}{(3-2)!\cdot 2!} =3$. Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний — нет), причем именно в $m!$ раз, то есть верна формула связи:
$$ A_n^m = C_n^m \cdot P_m.$$Удобный и бесплатный онлайн калькулятор сочетаний.
Решебник задач по комбинаторике
Изучаем комбинаторику: полезные ссылки
Выборки элементов без повторений
Рассмотрим сначала некоторые общие термины.
- Пусть некоторая совокупность содержит n элементов, из которых выбирают k элементов. Каждый такой набор будем называть выборкой объема k из n элементов.
- Будем различать выборки с возвращением и без возвращения. Пусть имеется совокупность n пронумерованных элементов:
- если отобранный элемент после выбора не возвращается в исходную совокупность и не может повторяться в данной выборке больше одного раза, то такая выборка называется выборкой без возвращения или без повторения;
- если отобранный элемент после фиксации номера снова возвращается в исходную совокупность и, таким образом, может вновь оказаться в данной выборке, то говорят о выборке с возвращением или с повторением.
- Выборка называется упорядоченной, если порядок следования элементов в ней задан. Если две упорядоченные выборки отличаются только порядком следования элементов, то они считаются разными (например: 12 и 21).
- Выборка называется неупорядоченной, если порядок элементов в ней не имеет значения (т. е. 12 и 21 неразличимы).
Размещения без повторений.
Размещениями без повторений называются упорядоченные выборки, содержащие k различных элементов из данных n элементов.
Обратим внимание на следующие важные положения:
- Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.
- Порядок элементов в выборке важен.
Формула для определения числа размещений без повторений:
Задача. Дана последовательность символов А, Б, С. Сколько вариантов кода, состоящего из двух разных символов, можно составить из заданной последовательности?
Решение.По условию код состоит «из двух разных символов», при этом коды АБ и БА – не одинаковые, поэтому, выборки – размещения без повторений.
Выборка осуществляется из 3 элементов по 2. Значит, n = 3, k = 2.
Действительно, комбинаций, удовлетворяющих условию, всего шесть: {АБ, АС, БА, БС, СА, СБ}
Перестановки без повторений.
Нетрудно заметить, что размещения, в которые входят все n разных элементов заданного множества (т. е. k = n), будут отличаться только порядком следования входящих элементов. Такие размещения называют перестановками.
Перестановками без повторений называются всевозможные упорядоченные выборки, составленные из всех данных n элементов.
Формула для определения числа перестановок без повторений
Pn = n! = n * (n − 1) * (n − 2) *…* 2 * 1
Задача. Сколько вариантов кода длиной 3 символа можно составить из трех букв А, Б, С, если каждая буква входит в последовательность не более одного раза?
Решение. Так как «каждая буква входит в последовательность не более одного раза», то выборки – перестановки без повторений.
Pn = 3! = 3 * 2 * 1 = 6 {АБC, АCБ, БАС, БСА, САБ, СБА}
Сочетания без повторений.
Сочетаниями без повторений называются неупорядоченные выборки, содержащие k различных элементов из данных n элементов.
Отметим, что
- …«выборки неупорядоченные», т.е. выборки AB и ВА – это одно и тоже сочетание.
- Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.
Формула для определения числа сочетаний без повторений:
Задача. Из 4-х кандидатов происходят выборы участников конференции. Сколько существует вариантов выбора делегации?
Решение. Очевидно, один и тот же кандидат в данную выборку может быть избран только один раз. При этом набор А, Б и Б, А – это одни те же участники. Поэтому выборки есть сочетания без повторений.
Воспользуемся формулой для расчета числа различных сочетаний без повторений:
90000 Combinations without repetition 90001 90002 The combinations without repetition of $$ n $$ elements taken $$ k $$ in $$ k $$ are the different groups of $$ k $$ elements that can be formed by these $$ n $$ elements, so that two groups differ only if they have different elements (that is to say, the order does not matter). They are represented as $$ C_ {n, k} $$. 90003 90002 For example, 90003 90002 Let’s consider the set $$ A = \ {a, b, c, d, e \} $$ of $$ 5 $$ elements. Let’s observe first of all that, for example, the groups $$ abc $$ and $$ cba $$ are considered to be equal, since as has been said the order does not matter while the elements are the same.90003 90002 We are going to see what the different combinations without repetition of these $$ 5 $$ elements are: 90003 90010 90011 Combinations without repetition of $$ 5 $$ elements taken $$ 1 $$ at a time: $$ a $$, $$ b $$, $$ c $$, $$ d $$ and $$ e $$. 90012 90011 Combinations without repetition of $$ 5 $$ elements taken $$ 2 $$ at a time: $$ ab $$, $$ ac $$, $$ ad $$, $$ ae $$, $$ bc $$, $ $ bd $$, $$ be $$, $$ cd $$, $$ ce $$ and $$ de $$. 90012 90011 Combinations without repetition of $$ 5 $$ elements taken $$ 3 $$ at a time: $$ abc $$, $$ abd $$, $$ abe $$, $$ acd $$, $$ ace $$, $ $ ade $$, $$ bcd $$, $$ bce $$, $$ bde $$ and $$ cde $$.90012 90011 Combinations without repetition of $$ 5 $$ elements taken $$ 4 $$ at a time: $$ abcd $$, $$ abce $$, $$ abde $$, $$ acde $$ and $$ bcde $$. 90012 90011 Combinations without repetition of $$ 5 $$ elements taken $$ 5 $$ at a time: The only group of $$ 5 $$ elements that it is possible to form from the elements of $$ A $$ is $$ abcde $$. 90012 90021 90002 In this example all of the combinations could have been written. However, if $$ A $$ had had many more elements, this would have been much more complicated.90003 90002 The following formula allows us to know how many combinations without repetition of $$ n $$ elements taken $$ k $$ in $$ k $$ there are: $$$ \ displaystyle C_ {n, k} = \ binom {n} {k} = \ frac {n!} {K! (N-k)!} $$$ 90003 90002 In the previous example, $$ n = 5 $$. Now, if we want to know how many combinations of $$ 5 $$ elements, taken $$ 3 $$ at a time there are, we use the formula and we obtain: $$$ \ displaystyle C_ {5,3} = \ binom {5} {3} = \ frac {5!} {3! (5-3)!} = 10 $$$ We can check in the previous list that there are $$ 10 $$ sets of $$ 3 $$ elements, indeed.90003 .90000 Python combinations without repetitions — Stack Overflow 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .90000 c # — Words combinations without repetition 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .90000 Combinations and permutations in R 90001 90002 Time to get another concept under my belt, combinations and permutations. While I’m at it, I will examine combinations and permutations in R. As you may recall from school, a 90003 combination 90004 does not take into account the order, whereas a 90003 permutation 90004 does. Using the example from my favourite website as of late, mathsisfun.com: 90007 90008 90009 A fruit salad is a 90003 combination 90004 of apples, bananas and grapes, since it’s the same fruit salad regardless of the order of fruits 90012 90009 To open a safe you need the right order of numbers, thus the code is a 90003 permutation 90004 90012 90017 90002 As a matter of fact, a permutation is an ordered combination.There are basically two types of permutations, with repetition (or replacement) and without repetition (without replacement). 90007 90020 Permutations with repetition 90021 90002 The number of permutations with repetition (or with replacement) is simply calculated by: 90007 90024 90007 90002 where n is the number of things to choose from, r number of times. 90007 90002 For example, you have a urn with a red, blue and black ball. If you choose two balls with replacement / repetition, there are permutations: {red, red}, {red, blue}, {red, black}, {blue, red}, {blue, blue}, {blue, black}, {black, red}, {black, blue}, and {black, black}.In R: 90007 90002 A biological example of this are all the possible codon permutations. We have 4 choices (A, C, G, and T) and we are choosing 3 nucleotides: (though some permutations code for the same amino acid). How about the number of 11-mers that are possible:. For miRNAs of size 21, there are possible miRNAs, but since the majority of these 21-mers are probably not biologically relevant or even possible, they most likely do not exist. 90007 90020 Permutations without repetition 90021 90002 Calculating permutations without repetition / replacement, just means that for cases where r> 1, n gets smaller after each pick.For example, if we choose two balls from the urn with the red, blue, and black ball but without repetition / replacement, the first pick has 3 choices and the second pick has 2 choices: {red, blue}, {red, black }, {blue, red}, {blue, black}, {black, red} and {black, blue}. In R: 90007 90002 Let’s use an example with more choices, say choosing pool balls. If we chose 3 balls without replacement (out of a total of 16), the number of permutations would be: 90007 90024 90007 90002 How do we reach a formula for this? If we chose all 16 balls, there are this many permutations: 90007 90024 90007 90002 Since we want 90007.