Модуль числа это – ( ), , , .

Модуль числа

Модуль числа a — это расстояние от начала координат до точки А(a).

Чтобы понять это определение, подставим вместо переменной a любое число, например 3 и попробуем снова прочитать его:

Модуль числа 3 — это расстояние от начала координат до точки А(3).

Становится ясно, что модуль это ни что иное, как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3)

Расстояние от начала координат до точки А(3) равно 3 (трём единицам или трём шагам).

Модуль числа обозначает двумя вертикальными линиями, например:

Модуль числа 3 обозначается так: |3|

Модуль числа 4 обозначается так: |4|

Модуль числа 5 обозначается так: |5|

Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:

|3| = 3

Читается как: «Модуль числа три равен три»

---

Теперь попробуем найти модуль числа -3. Опять же возвращаемся к определению и подставляем в него число -3. Только вместо точки A используем новую точку B. Точку A мы уже использовали в первом примере.

Модулем числа —3 называют расстояние от начала координат до точки B(—3).

Расстояние от одного пункта до другого не может быть отрицательным. Поэтому и модуль любого отрицательного числа, будучи являясь расстоянием тоже не будет отрицательным. Модуль числа -3 будет число 3. Расстояние от начала координат до точки B(-3) равно также трём единицам:

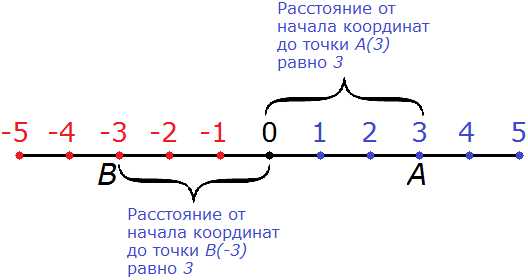
|-3| = 3

Читается как: «Модуль числа минус три равен три»

---

Модуль числа 0 равен 0, та как точка с координатой 0 совпадает  с началом координат, т.е. расстояние от начала координат до точки O(0) равно нулю:

|0| = 0

«Модуль нуля равен нулю»

---

Делаем выводы:

• Модуль числа не может быть отрицательным;
• Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу;
• Противоположные числа имеют равные модули.

Примеры:

| 1 | = 1

| -1| = 1

| 2 | = 2

| -2| = 2

| 0 | = 0

---

Противоположные числа

Числа, отличающиеся только знаками называют противоположными. Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числа −2 знак минуса, а у 2 знак плюса, но мы его не видим, потому что плюс, как мы говорили ранее, по традиции не пишут.

Еще примеры противоположных чисел:

−1 и 1

−3 и 3

−5 и 5

−9 и 9

Противоположные числа имеют равные модули. Например, найдём модули для −2 и 2

|−2| и |2|

2 = 2

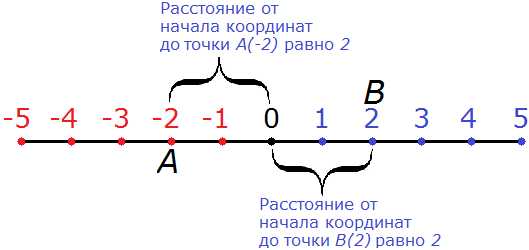
На рисунке видно, что расстояние от начала координат до точек

A(−2) и B(2) одинаково равно двум шагам.

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Навигация по записям

spacemath.xyz

Модуль числа — Физика — легко!

Противоположные числа – это числа, которые отличаются друг от друга только знаком. Выражение –а обозначает, что это число противоположное числу а.

Например, 7  и – 7;
                       41  и – 41  и т.д.

Число 0 противоположно самому себе!

То есть, для того, чтобы показать противоположность чисел в математике используют знак « – ».

Приписав знак « – » перед положительным числом 5, мы получим отрицательное число

– 5.

Приписав знак « – » перед отрицательным числом – 5, мы получим противоположное ему положительное число 5, то есть – (–5) = 5.

– (–а) = а

На координатной прямой точки, у которых противоположные координаты, расположены на одинаковом расстоянии от начала отсчёта.

AO = OC
BO = OD

Модуль числа

Модуль числа – это расстояние (в единичных отрезках) от начала отсчёта до точки, которая изображает это число на координатной прямой.

Точки А(– 4) и В (4) отдалены от начала отсчёта на 4 единичных отрезков, а числа – 4 и 4 имеют одинаковые модули, равные 4.

Модуль числа а обозначают | а |

Так как модуль – это расстояние, а расстояние не может быть отрицательным, то модуль числа не может быть отрицательным числом!!!

Модулем положительного числа и нуля является тоже самое число, а модулем отрицательного числа – противоположное ему число:

| а | = а, если а  ≥ 0  (если а – неотрицательное число)

| а | = – а, если а  <  0  (если а – отрицательное число)

Выводы

Свойства модуля числа:

1. Модуль числа не может быть отрицательным. Модуль числа всегда или положительное число или равен 0.

| 4| = 4

| 0 | = 0

|– 4| = 4

2. Противоположные числа имеют равные модули.

| – а | = | а | = а

Пример, | – 12 | = | 12 | = 12

Решение уравнений (примеры)

1.  – x = 7
вместо – x   и   7  напишем противоположные им числа, используя знак «–»
–(– x) = – 7
воспользуемся правилом, что – (–а) = а получим
x = – 7

2. – x = – 10
–(– x) = –(– 10)
x = 10

3. x = –(– 32)
x = 32

4. | x | = 4
x = 4 или x = – 4
Ответ: 4; – 4

5. | x | = 0
x = 0
Ответ: 0

6. | y | = – 8
модуль не может быть отрицательным числом, а значит данное уравнение не имеет решения
Ответ: нет корней

7. | – x | = 12
вспомним второе свойство модуля, что | – а | = | а | = а, тогда
| x | = 12
x = 12 или x = – 12
Ответ: 12; – 12

8. | y | – 2 = 12
подобные уравнения решаются как простые уравнения, только с учётом модуля
| y | = 12 + 2
| y | = 14
y = 14 или y = – 14
Ответ: 14; – 14

9.  10 – 2| x | = 4
2| x | = 10 – 4
2| x | = 6
| x | = 6 : 2
| x | = 3
x = 3 или x = – 3
Ответ: 3; – 3

То есть при решении уравнений, содержащих модуль мы получим три вида ответа:
два корня (если под знаком модуля положительное число), один корень (если под знаком модуля 0)
нет корней (если под знаком модуля отрицательное число).

Решение простейших неравенств, содержащих модуль

В 5 классе мы решали примеры с простейшими неравенствами. Линейные неравенства бывают строгие и нестрогие.
Строгие неравенства – это неравенства со знаками больше (>) или меньше (<).
x > a; x < a;
Нестрогие неравенства – это неравенства со знаками больше либо равно (≥) или меньше либо равно (≤).
x ≥ a; x ≤ a.

Примеры

1. Найдите все натуральные значения x, при которых является правильным неравенство x < 9

Решение.
Данное неравенство будет правильным при таких значениях x: 1; 2; 3; 4; 5; 6; 7; 8.

Ответ: х = {1; 2; 3; 4; 5; 6; 7; 8} – натуральные решения данного неравенства.

Примечание:
Число 0 не является решением этого неравества, так как 0 не является натуральным числом;
Число 9 не является решением этого неравества, так как данное неравенство строгое, то есть х строго меньше 9 и не может быть равным 9.

2. Какое наименьшее натуральное значение а удовлетворяет неравенство а > 12?

Решение.
Поскольку неравенство строгое, то число 13 является наименьшим натуральным значением а, которое удовлетворяет данному неравенству.
Ответ: 13

3. Какое наименьшее натуральное значение а удовлетворяет неравенство а ≥ 12?

Решение.
Поскольку неравенство нестрогое, то число 12 является наименьшим натуральным значением а, которое удовлетворяет данному неравенству.

Ответ: 12.

4. Найдите все натуральные значения x, при которых является правильным неравенство 2 < x < 9

Решение.
Неравенство двойное (читают как «х больше от 2, но меньше от 9»), строгое, поэтому 3; 4; 5; 6; 7; 8 – натуральные решения данного двойного неравенства.
Ответ: х = {3; 4; 5; 6; 7; 8}

5. Найдите все натуральные значения x, при которых является правильным неравенство 2 < x ≤ 9.

Решение.
3; 4; 5; 6; 7; 8; 9 – натуральные решения данного двойного неравенства.
Ответ: х = {3; 4; 5; 6; 7; 8; 9}

6. Найти все целые числа, которые удовлетворяют неравенству| x | < 5.

Решение.
| x | < 5 (читаем как «расстояние от начала отсчёта до точки изображающей х меньше 5»).
Неравенство | x | < 5 эквивалентно (может быть также записано

) –5 < x < 5. Неравенство двойное, строгое, поэтому данное неравенство будет правильным при таких значениях x: –4; –3; –2; –1; 0; 1; 2; 3; 4.
Ответ: х = {–4; –3; –2; –1; 0; 1; 2; 3; 4}

7. Найти все целые числа, которые удовлетворяют неравенству| x | ≤ 5.

Решение.
Неравенство | x | ≤  5 эквивалентно –5 ≤  x ≤  5. Неравенство двойное, нестрогое, поэтому числа –5 и 5 войдут в множество чисел, при которых данное неравенство будет правильным. Таким образом, данное неравенство будет правильным при таких значениях x: –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5.
Ответ: х = {–5; –4; –3; –2; –1;  0;  1;  2;  3;  4;  5}

8. Найти все целые числа, которые удовлетворяют неравенству | x | > 2 и обозначте их на координатной прямой.

Решение.
Неравенство | x | > 2 эквивалентно x < – 2 или x > 2. Обозначим на координатной прямой точки, координаты которых удовлетворяют данному неравенству

Поскольку неравенство строгое, то числа – 2 и 2 не входят в множество целых чисел, при которых данное неравенство будет правильным. А на координатной прямой эти точки обозначаем в виде незакрашенной точки.

Ответ: х = {…–5; –4; –3;  3;  4;  5…}

9. Найти все целые числа, которые удовлетворяют неравенству | x | ≥ 2 и обозначте их на координатной прямой.

Решение.
Неравенство | x | ≥ 2 эквивалентно x ≤ – 2 или x ≥ 2. Обозначим на координатной прямой точки, координаты которых удовлетворяют данному неравенству

Поскольку неравенство нестрогое, то числа – 2 и 2 входят в множество целых чисел, при которых данное неравенство будет правильным. А на координатной прямой эти точки обозначаем в виде закрашенной точки.

Ответ: х = {…–5; –4; –3; –2;  2;  3;  4;  5…}

10. Найти все целые числа, которые удовлетворяют неравенству 1 < | x | ≤ 3 и обозначте их на координатной прямой.

Решение.
Рассмотрим сначала левую часть неравенства. Она означает, что расстояние от начала отсчёта до точек меньше 1. Рассмотрим правую часть неравенства: расстояние от начала отсчёта до этих же точек меньше или равно 3.
Построим эти точки на координатной прямой:

1 и – 1 не входят в множество целых чисел, которые удовлетворяют неравенству, потому что неравенство строгое.
3 и – 3 входят в множество целых чисел, которые удовлетворяют неравенству, потому что неравенство нестрогое.

Ответ: х = {–3; –2;  2;  3}

 

www.easyphysics.in.ua

Определение модуля | Математика

1. Определение модуля:

Модулем числа а называется расстояние (в единичных отрезках) от начала координат до точки А с координатой а.

Пример.

Модуль числа 7 равен 7, так как точка D с координатой 7 удалена от начала отсчета на 7 единичных отрезков.

Модуль числа -6 равен 6, так как точка С с координатой 6 удалена от начала отсчета на 6 единичных отрезков. Пишут:

   

2. По определению модуля, модуль — это расстояние.

А так как расстояние не может быть отрицательным числом, то и модуль не может быть отрицательным числом.

3. Модуль положительного числа равен самому числу.

Например,

   

4. Модуль отрицательного числа равен противоположному числу.

Например,

   

5. Модуль нуля равен нулю:

   

6. Противоположные числа имеют равные модули:

   

Например,

   

Из определения модуля:

www.for6cl.uznateshe.ru

Модуль числа. Свойства абсолютной величины

Модуль числа – это расстояние от начальной точки до соответствующей точки на координатной прямой. Модуль числа так же называется абсолютной величиной числа.

Для обозначения модуля используются две вертикальные черты, в которые заключается число, абсолютная величина которого берётся.

Рассмотрим координатную прямую с точками A и B:

Точка A соответствует числу -5, которое находится в пяти единичных отрезках от начальной точки, то есть длина отрезка AO равна 5. Так как модуль равен расстоянию от начала координат до точки, то модуль числа -5 равен 5, это можно записать так:

|-5| = 5

Точка B соответствует числу 4,5, значит длина отрезка OB равна 4,5. Следовательно модуль числа 4,5 равен 4,5:

|4,5| = 4,5

Точка O соответствует числу 0 и является начальной точкой, следовательно модулем нуля будет нуль:

|0| = 0

Из данных примеров можно сделать вывод, что модуль числа – это положительное число или нуль.

Следует иметь ввиду, что чем дальше от нуля точка, изображающая данное число, тем больше модуль этого числа.

Свойства абсолютной величины числа

Модулем (или абсолютной величиной) положительного числа называют само это число.

Например, модулем числа +6 является число +6 (или просто 6), пишут:

|+6| = +6.

Модулем (или абсолютной величиной) отрицательного числа называют противоположное ему (положительное) число.

Например, модулем числа -6 является число +6, пишут:

|-6| = +6.

Модулем числа 0 является число 0.

|0| = 0.

Модули противоположных чисел равны: |a| = |-a|:

|+4| = |-4| = 4.

naobumium.info

Модуль числа

Модуль числа — это расстояние от этого числа до нуля на координатной прямой.

Модуль обозначается с помощью символа: | |.

• Запись |6| читается как «модуль числа 6», или «модуль шести».
• Запись |8| читается как «модуль 8-ми».

Модуль положительного числа равен самому числу. Например, |2| = 2.
Модуль отрицательного числа равен противоположному числу <=> |-3| = 3.
Модуль нуля равен нулю, то есть |0| = 0.
Модули противоположных чисел равны, то есть |-a| = |a|.

---

Для лучшего понимания темы: «модуль числа» предлагаем воспользоваться методом ассоциаций.

Представим, что модуль числа — это баня , а знак «минус» — грязь .

Оказываясь под знаком модуля (то есть в «бане») отрицательное число «моется» , и выходит без знака «минус» — чистым .

Модуль

В бане могут «мыться» (то есть стоять под знаком модуля) и отрицательные , и положительные числа , и число ноль . Однако будучи «чистым» положительные числа , и ноль свой знак при выходе из «бани» (то есть из под знака модуля) не меняют !

Модуль числа

 

---

История модуля числа или 6 интересных фактов о модуле числа

1. Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
2. Ввел в обращение этот термин ученик Исаака Ньютона — английский математик и философ Роджер Котс (1682 – 1716).
3. Великий немецкий физик, изобретатель, математик и философ Готфрид Лейбниц в своих работах и трудах использовал функцию модуля, которую он обозначил mod x.
4. Обозначение модуля было введено в 1841 году немецким математиком
Карлом Вейерштрассом (1815 — 1897).
5. При написании модуль обозначается с помощью символа: | |.
6. Еще одной версии термин «модуль» был введен в 1806 году французским
математиком по имени Жан Робер Аргáн (1768 — 1822). Но это не совсем так.
В начале девятнадцатого века математики Жан Робер Аргáн (1768 — 1822)
и Огюстен Луи Коши (1789 — 1857) ввели понятие «модуль комплексного числа»,
который изучается в курсе высшей математики.

---

Решение задач на тему «Модуль числа»

Задача №1. Расположи выражения: -|12|, 0, 54, |-(-2)|, -17 в порядке возрастания.

Решение:

Для начала раскроем скобки и модули:

— | 12 | = — 12
| — ( — 2) | = 2

Далее осталось расположить числа: -12, 0, 54, 2, -17 в порядке возрастания. Получим следующее неравенство:

-17 < -12 < 0 < 2 < 54, что будет равносильно:
-17 < -|12| < 0 < | — ( — 2) | < 54.

Ответ: -17 < -|12| < 0 < | — ( — 2) | < 54.

Задача№2. Нужно расположить выражения: -|-14|, -|30|, |-16|, -21, | -(-9) |
в порядке убывания.

Решение:

Для начала раскроем скобки и модули:

— | — 14| = — 14
— |30| = -30
|-16| = 16
| -(-9) | = 9

Далее осталось расположить числа: -14, -30, 16, -21, 9 в порядке убывания. Получим следующее неравенство:

16 > 9 > -14 > — 21 > — 30 что будет равносильно:
|-16| > | -(-9) | > — | — 14| > — 21 > — |30|.

Ответ: |-16| > | -(-9) | > — | — 14| > — 21 > — |30|

shkolnaiapora.ru

Модуль действительного числа | Формулы с примерами

Модуль действительного числа 8 класс

Определение
Модуль действительного числа — это же число в абсолютной величине, т.е. без знака «минус».

Свойства модуля действительного числа

Свойство 1 1. Модуль действительного числа является положительным числом.

| a | = ? 0.

Пример | 3 | > 0;     | -10 | > 0;     | 129 | > 0.

Свойство 2 2. Модули у которых разные знаки — равны.

| a | = | — a |.

Пример |4| = |- 4| = 4;

|- 3,2| = |3,2| = 3,2;

|4,5| = |- 4,5| = 4,5.

Свойство 3 3. Модуль положительного числа, больше или равен этому
положительному числу. Модуль положительного числа, больше или
равен этому числу со знаком «минус».

|a| ? a; |a| ? — a.

Пример | ? 5 | ? ? 5 и | ? 5 | ? — ? 5, так как | ? 5 | = ? 5;

| ? 12 | ? ? 12 и | ? 12 | ? — ? 12, так как | ? 12 | = ? 12;

| ? 32 | ? ? 32 и | ? 32 | ? — ? 32, так как | ? 32 | = ? 32.

Свойство 4 4. Модуль суммы двух и более чисел меньше или равен сумме
их модулей.

|a + b| ? |a| + |b|.

Пример |3 + 2| ? |3| + |2| = 5;

|1,3 + 4,2| ? |1,3| + |4,2| = 5,5;

|-12,6 + 4,1| ? |-12,2| + |4,1| = 16,3.

Свойство 5 5. Модуль разности двух и более чисел больше или равен разности
их модулей.

|a — b| ? |a| — |b|.

Пример |12 — 11| ? |12| — |11| = 1;

|15 — ( -2 )| ? |15| — |- 2|;

|21 — ( -1,3 )| ? |21| — |-1,3|.

Свойство 6 6. Модуль произведения двух и более чисел равен произведению
их модулей.

|a • b| = |a| • |b|.

Пример |1.2 • 1,3| = |1,2| • |1,3| = 1,56;

|2 • ( -2,2 )| = |2| • |-2,2| = 4,4;

|3,1 • ( -6,4 )| = |3,1| • |- 6,4| = 19,84.

Свойство 7 7. Квадрат модуля числа равен квадрату этого числа.

|a²| = a².

Пример |- 4|² = (- 4)² = 16;

|- 6|² = (- 6)² = 36;

|- 1,2|² = (- 1,2)² = 1,44.

formula-xyz.ru

Модуль числа – что это такое: что значит абсолютная величина

В школе на уроке математики каждый год ученики разбирают новые темы. 6 класс обычно изучает модуль числа – это важное понятие в математике, работа с которым встречается далее в алгебре и высшей математики. Очень важно изначально правильно понять объяснение термина и разобраться в этой теме, чтобы успешно проходить прочие темы.

Величины в математике

Для начала следует понимать, что абсолютная величина – это параметр в статистике (измеряется количественно), который характеризует изучаемое явление по его объему. При этом явление должно осуществляться в определенных временных рамках и с определенным месторасположением. Различают значения:

• суммарные – подходят для группы единиц или полностью всей совокупности;
• индивидуальные – подходят только для работы с единицей некой совокупности.

Это интересно! Основы геометрии: что это такое биссектриса треугольника

Понятия широко используются в статистических измерениях, результатом которых являются показатели, характеризующие абсолютные размеры у каждой единицы некоего явления. Измеряются они в двух показателях: натуральном, т.е. физические единицы (шт., люди) и условно-натуральном. Модуль в математике является отображением данных показателей.

Модуль числа

Что такое модуль числа?

Важно! Данное определение «module» с латыни переводиться как «мера» и означает абсолютную величину любого натурального числа.

Но у данного понятия есть и геометрическое объяснение, поскольку модулю в геометрии равняется расстояние от начала системы координат до точки X, которое измеряется в привычных единицах измерения.

Для того, чтобы определить данный показатель у числа, следует не учитывать его знак (минус, плюс), но при этом следует помнить то, что он никогда не может быть отрицательным. Данное значение на бумаге выделяется графически в виде квадратных скобок — |a|. При этом, математическое определение такое:

|х| = х, если х больше или равен нулю и -х, если меньше нуля.

Английский ученый Р. Котес был тем человеком, кто впервые применил данное понятие в математических расчетах. А вот К. Вейерштрасс, математик из Германии, придумал и ввел в использование графический символ.

Это интересно! Как разложить на множители квадратный трехчлен: формула

В геометрии module можно рассмотреть на примере координатной прямой, на которое нанесены 2 произвольные точки. Предположим, одна — А имеет значение 5, а вторая В — 6. При подробном изучении чертежа станет ясно, что расстояние от А до В – 5 единиц от нуля, т.е. начала координат, а точка В размещена от начала координат на 6 единиц. Можно сделать вывод, что module точки, А = 5, а точки В = 6. Графически это можно обозначить так: | 5 | = 5. Т. е. расстояние от точки до начала координат является модулем данной точки.

Полезное видео: что такое модуль действительного числа?

Свойства

Как у любого математического понятия, у module есть свои математические свойства:

1. Он всегда положительный, поэтому модулем положительного значения будет оно само, например, модуль числа 6 и -6 равен 6. Математически это свойство можно записать как |a| = a, при a> 0;
2. Показатели противоположных чисел равны между собой. Это свойство понятнее в геометрическом изложении, поскольку на прямой данные числа располагаются в разных местах, но при этом от начала отсчета их отделяет равное количество единиц. Математически это записывается так: |а| = |-а|;
3. Модуль нуля равен нулю, при условии, что действительное число – это ноль. Это свойство подтверждается тем фактом, что ноль является началом координат. Графически это записывают так: |0| = 0;
4. Если требуется найти модуль двух умножающихся цифр, стоит понимать, что он будет равен полученному произведению. Другими словами, произведение величин А и В = АВ, при условии, что они положительные или же отрицательные, и тогда произведение равняется -АВ. Графически это можно записать как |А*В| = |А| * |В|.

Это интересно! Считаем правильно: как находить процент от суммы и числа

Успешное решение уравнений с модулем зависит от знания данных свойств, которое поможет любому правильно вычислять и работать с данным показателем.

Свойства модуля

Важно! Показатель не может быть отрицательным, поскольку он определяет расстояние, которое всегда положительное.

В уравнениях

В случае работы и решения математических неравенств, в которых присутствует module, всегда необходимо помнить, что для получения итогового правильного результата следует раскрыть скобки, т.е. открыть знак module. Зачастую, в этом и есть смысл уравнения.

При этом стоит помнить, что:

• если в квадратных скобках записано выражение, его необходимо решить: |А + 5| = А + 5, при А больше или равным нулю и 5-А, в случае А меньше нуля;
• квадратные скобки чаще всего должны раскрываться независимо от значений переменной, например, если в скобках заключено выражение в квадрате, поскольку при раскрытии в любом случае будет положительное число.

Это интересно! Уроки математики: умножение на ноль — главное правило

Очень легко решаются уравнения с module путем занесения значений в систему координат, поскольку тогда легко увидеть визуально значения и их показатели.

Полезное видео: модуль действительного числа и его свойства

Вывод

Принцип понимания такого математического понятия, как module, крайне важен, поскольку оно используется в высшей математике и прочих науках, поэтому необходимо уметь работать с ним.

Вконтакте

Одноклассники

Facebook

Мой мир

Twitter

znaniya.guru