«Занимательная комбинаторика для младших школьников » — Яндекс Кью
В силу профессии постоянно пополняю свою библиотеку интересными книжками по математике. Недавно стала богаче еще на одну книжку И.Б. Румянцевой и И.И.Целищевой «Занимательная комбинаторика для младших школьников». На данный момент я приобрела первый выпуск из серии четырех книг издательства ИЛЕКСА, посвященный сложному и важному разделу математики — комбинаторике. Книга была издана в 2020 году, содержит семьдесят две страницы.
Сама идея написать и выпустить серию книг, посвященную комбинаторике — замечательная. Сейчас активно популяризируется математика среди школьников и взрослых, тема достаточно актуальная и полезная.
Структура книги мне понравилась. Задания объединены в занятия. Всего в первом выпуске предлагается двадцать семь занятий. От занятию к занятию сложность заданий постепенно увеличивается. Так, из опыта практики, я могу сказать, что только в первом выпуске серии можно найти задания и для дошкольников и для школьников третьего-четвертого класса.
Занятия построены так, что ученик постепенно учится логически мыслить и рассуждать, активно участвует в процессе посредством рисования, раскрашивания, ответов на вопросы преподавателя или решения спичечных головоломок. В книге много красивых иллюстраций и она не перегружена текстом. Это является безусловным достоинством.
Книга начинается с элементарных задач, позволяющих научиться сериации, а заканчивается задачами, вводящими в понятия сочетаний и размещений. При этом авторами учитывается, что ребенок младшего возраста может не дать полного ответа на поставленный вопрос, но точно «пощупает» его примерную величину. Так в задании 3.а) занятия 26 первого выпуска предлагается рассадить шесть птичек на два дерева, рассмотрев все возможные варианты рассадки. Но в задании 3.б) автор просит указать лишь несколько возможных вариантов рассадки шести птичек на три дерева, учитывая, что целевая аудитория маленьких слушателей пока не готова увидеть полное решение.
Мне особенно понравились задания на спичках, когда из имеющейся конструкции спичечных квадратов требуется убрать определенное количество спичек, чтобы, не трогая другие, получить меньшее определенное количество спичечных квадратов.
Такие задачи, особенно на очном уроке, очень нравятся школьникам, так как напонимают игру.
В конце книги приводятся ответы на большинство заданий, что, безусловно, облегчает работу педагога и помогает спроектировать занятие со школьником более эффективно. Я рекомендую прочитать все ответы перед началом совместной работы со школьником. Это позволит лучше понять авторов и суть задания, а также верно направить ребенка на решение конкретной задачи. В любом случае, конечным фактором успеха является мастерство и профессионализм педагога.
Я бы рекомендовала авторам пересмотреть ответ на вопрос задания 4 занятия 13. В данном задании предлагается сосчитать количество 1) квадратов 2) прямоугольников на одном приведенном рисунке. Учитывая, что авторы в контекстве других задач верно считают, что любой квадрат является и прямоугольником также, я бы посоветовала придерживаться этой канвы решения и исправить ответ для количества прямоугольников, которые можно найти на рисунке.
Среди незначительных моментов я бы выделила следующие.
Немного точнее формулировала бы некоторые задания. Так, в задании 1 занятия 2 необходимо «определить предметы по форме» и на рисунке предлагается несколько предметов. Мне была бы комфортней такая формулировка как «определи форму приведенных предметов», если я верно истолковала суть задания (на данное задание ответов и пояснений не приводится). Педагогу было бы полезно увидеть более подробный ответ на задание 3 занятия 10. Нумерация подпунктов ответов на задания 2, 4 занятия 14 должна соответствовать нумерации подпунктов самих заданий. В задании 1 занятия 18 мне было бы комфортней увидеть, что рыбки одного размера имеют разную раскраску. Так, на мой взгляд, ребенку на первом этапе легче пояснить понятие сочетаний (различаем элементы исходной совокупности или нумеруем их, но не различаем порядка внутри выборки). В формулировку задания 2 занятия 21 добавила бы столько пустых таблиц для ответа, сколько существует вариантов, чтобы направить школьника.
Ну, и, конечно, очень бы хотелось иметь такую книжку в цветном варианте.
Я считаю, что для детей младшего возраста важно видеть красивые изображения в цвете.
Я прочитала все задания и абсолютно уверена, что буду применять эту книгу на своих занятиях. Я считаю, что книга будет полезна репетиторам по математике, педагогам, руководителям математических кружков начальной школы, родителям для погружения маленьких детей в процесс комбинаторных размышлений.
В заключение отмечу, что обязательно приобрету остальные книги серии «Занимательная комбинаторика для младших школьников» в свою копилку. После приобретения книг материалами разрешается пользоваться на занятиях и кружках.
Благодарю авторов за этот полезный и актуальный труд!
Основы комбинаторики | Физико-математический лицей №30
Курс посвящен основам комбинаторики для школьников и включает в себя все базовые темы этого раздела математики.
Преподаватели: Михаил Владимирович Штильман
Записаться
Этот курс включает:
- Продолжительность курса: 10 ч
- Доступ на разных устройствах
- Неограниченный доступ к материалам
О курсе
Курс посвящен основам комбинаторики для школьников и включает в себя все базовые темы этого раздела математики.
Пройдя курс, вы будете готовы решать все основные типы задач по комбинаторике!
Этот курс подойдет как школьникам, для которых это лишь первое знакомство с темой, так и тем, кто хочет освежить свои знания и существенно углубить их.
В этом курсе вы можете получить электронный сертификат, правильно решив 80 % тестовых заданий. После выполнения всех задач, перейдите во вкладку «Прогресс». Здесь вы увидите количество верно решенных заданий по каждому уроку и общий результат. Нажмите кнопку «Получить сертификат», а затем «Просмотреть сертификат», чтобы сохранить или распечатать сертификат.
Для кого курс
Курс рассчитан на школьников 7-9 классов. Вместе с тем, несомненно, многим старшеклассникам он также может быть полезен. А поскольку для освоения курса требуется лишь только твердое владение арифметикой, то курс подойдет и самым любознательным школьникам из 5-6 классов!
Как проходит обучение
-
Регистрируйтесь
Регистрируйтесь и выбирайте курс — он сразу появится в вашем личном кабинете
-
Смотрите видеолекции
Проходите уроки курса, смотрите видео и дополнительные материалы
-
Выполняйте задания
В курсе нет дедлайнов: можно начать учиться в любое время и выбрать удобный темп
Программа курса
Блок 1.
Правило суммы и произведенияБлок, без которого невозможен дальнейший путь! Данный блок – это знакомство с темой «комбинаторика». Тут будут рассмотрены два базовых правила – «правило суммы» и «правило произведения». Несмотря на то, что разобранные задачи действительно совсем легкие, они позволяют хорошо «почувствовать» два главных правила. А без этого двигаться дальше не получится!
Блок 2. Перестановки без повторений
В этом блоке вы узнаете, сколькими способами можно расставить несколько предметов в ряд (и не только в ряд).
Блок 3. Перестановки с повторениями
После изучения этого блока вы точно будете знать, сколькими способами можно переставить буквы вашего имени.
Блок 4. Размещения с повторениями
В этом блоке вы научитесь составлять «упорядоченные наборы» из элементов (возможно, повторяющихся).
Блок 5. Размещения без повторений
В этом блоке вы научитесь составлять «упорядоченные наборы» из элементов, не используя их дважды
Блок 6.
Сочетания без повторенийЭтот блок, возможно, самый важный во всем курсе. Ведь «число сочетаний без повторений» – очень активно используемое в математике понятие.
Блок 7. Важные задачи
В этом блоке вам будет предложено несколько задач. Попробуйте сначала решить их сами!
Блок 8. Сочетания с повторениями
В этом блоке вы познакомитесь с одним довольно хитрым приемом
Блок 9. Свойства чисел сочетаний без повторений, треугольник Паскаля, бином Ньютона
В этом блоке вы узнаете про биномиальные коэффициенты, и заодно про то, что бином Ньютона – это совсем не сложно, а треугольник Паскаля – это красиво!
Введение в курс
Преподаватели
Штильман Михаил Владимирович
Преподаватель математики ГФМЛ №30
ссылок — план для класса комбинаторики в старшей школе?
Задавать вопрос
спросил
Изменено 7 лет, 3 месяца назад
Просмотрено 2к раз
$\begingroup$
Я учусь в старшей школе и прошел все математические курсы в моей школе (через исчисление AB). Я искал возможное независимое исследование на следующий год и остановился на комбинаторике и, возможно, на теории графов. Я планирую использовать видеоролики MIT Open «Комбинаторика: изящное искусство счета» и дополнить их учебником.
Есть ли у кого-нибудь какие-либо предложения по учебнику, в котором единственным предварительным условием был бы AP Исчисление AB, и который был бы легко понят старшеклассником? В идеале книга также должна углубляться в теорию графов (я понимаю, что эти два предмета идут рука об руку).
Я также хотел бы, чтобы книга давала решения (или, по крайней мере, некоторые решения) проблем, чтобы убедиться, что я на правильном пути. Кроме того, есть ли у кого-нибудь мнение о следующих книгах?:
[Прогулка по комбинаторике: введение в перечисление и теорию графов][2]
[Комбинаторика и теория графов (тексты для студентов по математике)][3]
[Принципы и методы комбинаторики][4]
[Как считать: Введение в комбинаторику][5]
[Комбинаторика: Экскурсия с гидом (учебники MAA)][6]
*[Введение в счет и теорию вероятности Дэвида Патрика][7]
*[Средний уровень Подсчет и вероятность Дэвида Патрика [8]
*Книги из серии «Искусство решения проблем» (для учащихся средних и старших классов).. Я боюсь, что они могут быть слишком элементарными.
Будем очень признательны за любую помощь, так как я действительно не знаю, с чего начать.
- комбинаторика
- справочно-запросная
- теория графов
- самообучение
$\endgroup$
3
$\begingroup$
Я бы рассмотрел «Математика выбора» Нивена и «Графики и их использование» Оре.
$\endgroup$
1
$\begingroup$
Ваш вопрос довольно общий, но я согласен с Modded Bear, что вычисление AP вряд ли сильно поможет. 9Книга 0053 Concrete Mathematics была бы превосходной, но я мог бы добавить книгу Discrete Mathematics and its Applications Кеннета Розена. Эта книга представляет собой абсолютный фолиант с тысячами упражнений (буквально), которые варьируются от очень простых до чрезвычайно сложных. Новейшее издание книги возмутительно дорогое. К счастью, почти все ресурсы для 5-го издания книги можно найти в Интернете в виде файлов .pdf (хотя я бы порекомендовал купить дешевое подержанное издание для настоящего учебника):
- Учебник
- Справочник по решениям для учащихся
- Руководство по решениям для инструктора
Наличие всех доступных решений сделало бы этот текст отличным для использования.
Удачи.
$\endgroup$
2
$\begingroup$
Для комбинаторики очень рекомендую книгу Яо Чжана. Это огромное количество информации и общие стратегии подсчета, которые решают практически все проблемы. В нем есть как текст, который учит вас, примеры задач, так и «вызовы». Вы можете легко найти его в Интернете.
$\endgroup$
$\begingroup$
знание исчисления AP, вероятно, не очень поможет, если вы не хотите изучать производящие функции. По моему опыту, в некоторых книгах (хотя и не во всех) вы можете не знать предварительных требований по линейной алгебре или теории групп.
Вот некоторые книги, которые я рекомендую по этой теме:
Конкретная математика
Методы решения задач в комбинаторике
Бонди и Мурти GTWA
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Комбинаторика – круг Эйлера
Комбинаторика (Летняя сессия 1, 2021 г.) — это математика конечных или дискретных объектов. Часто, и в большинстве случаев, нас интересует подсчет количества способов решения определенной проблемы. Например, количество способов замостить прямоугольник прямоугольниками и прямоугольниками без промежутков и перекрытий — это число Фибоначчи, очень знакомая последовательность чисел. Многие другие простые задачи на подсчет имеют ответы, включающие биномиальные коэффициенты.
В этом классе предполагается, что учащиеся уже знакомы с этими основными комбинаторными задачами и их решениями, чтобы мы могли изучать комбинаторику на более высоком уровне. После краткого рассмотрения комбинаторики на уровне типичных задач конкуренции мы рассмотрим другие, менее знакомые типы специальных чисел, такие как числа Стирлинга, числа Белла и числа Эйлера. Эти числа удовлетворяют соотношениям, подобным отношениям биномиальных коэффициентов, но они также имеют свои отличительные черты.
Они проявляются в нескольких различных контекстах в математике, от задач подсчета до полиномиальных тождеств, что предполагает, что они являются фундаментальными объектами в математике.
Мы также изучим методы решета, которые позволяют нам считать объекты только с желаемыми свойствами. Очень известная задача метода решета — это задача о психическом расстройстве, в которой нужно указать количество способов, которыми люди могут переставить свои шляпы так, чтобы у всех была неправильная шляпа. Менее известная, но все же важная проблема метода решета спрашивает для данного подмножества доски, сколько существует способов разместить на ней ладьи, чтобы никакие две не атаковали. На самом деле, проблема беспорядка является частным случаем этой проблемы расстановки ладей!
Мы также будем исследовать частично упорядоченные множества. Порядок (или полный порядок) на множестве — это способ взять любые два элемента и сказать, что либо или . Частичный порядок — это обобщение, которое позволяет нам сравнивать некоторые пары элементов, говоря, что другие элементы несравнимы.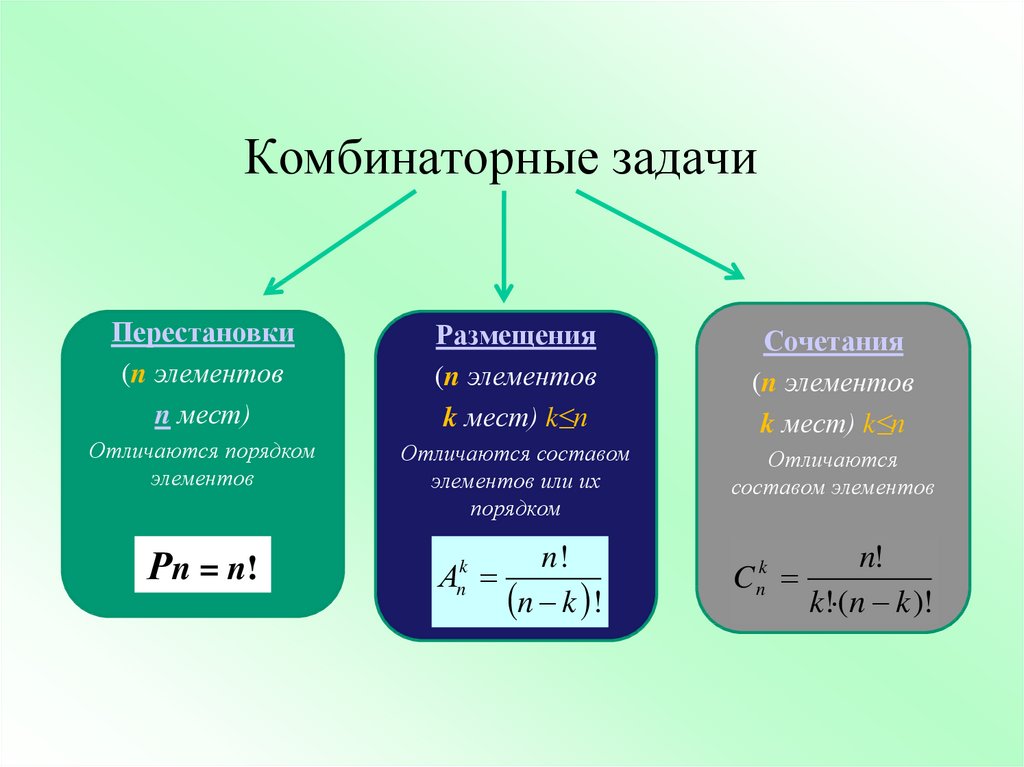
Например, положительные целые числа с делимостью представляют собой частично упорядоченный набор: при наличии двух положительных целых чисел и может быть так, что или , но может быть и так, что ни одно из них не делит другое. С любым частично упорядоченным набором связан набор функций, называемый алгеброй инцидентности, каждая из которых может быть представлена в виде матрицы. Алгебра инцидентности собирает всю комбинаторную информацию о частичном множестве в удобной для использования форме и содержит элементы, которые ведут себя так же, как дзета-функция и функция Мёбиуса для целых чисел.
Наконец, мы изучим производящие функции. Теория производящих функций — очень мощный способ решения комбинаторных задач и исследования их асимптотики. Производящие функции обычно хорошо работают с повторениями: они делают решение линейных повторений таким же простым, как нахождение корней многочленов, и мы также можем использовать их для получения повторений, что приводит к некоторым впечатляющим последствиям.