Мерзляк 5 класс — § 24. Комбинаторные задачи
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какие задачи называют комбинаторными?
Комбинаторные задачи — это задачи, решение которых требует рассмотрения и подсчёта все возможных случаев (всех возможных комбинаций).
2. Как называют схему, с помощью которой удобно и наглядно решать комбинаторные задачи?
Дерево возможных вариантов.
Решаем устно
1. Одним слоем бумаги оклеили куб, длина ребра которого равна 3 дм. Сколько квадратных дециметров бумаги потребовалось на оклеивание куба?
Найдём площадь поверхности куба:
S = 6a² = 6 • 3² = 6 • 9 = 54 (дм²) — бумаги потребовалось для оклеивания куба.
Ответ: 54 дм².
2. Объём прямоугольного параллелепипеда равен 240 см³. Какая из следующих троек чисел может задавать измерения этого параллелепипеда:
1) 4 см, 6 см, 12 см
4 • 6 • 12 = 24 • 12 = 288 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
2) 5 см, 6 см, 8 см
5 • 6 • 8 = 30 • 8 = 240 (см³) — да, эти числа могут быть измерениями данного прямоугольного параллелепипеда.
3) 3 см, 5 см, 10 см
3 • 5 • 10 = 15 • 10 = 150 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
4) 10 см, 10 см, 24 см
10 • 10 • 24 = 100 • 24 = 2 400 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
Ответ: числа 5 см, 6 см и 8 см.
3. Сколько центнеров пшеницы можно засыпать в бункер, имеющий форму прямоугольного параллелепипеда, если его длина равна 8 м, ширина — 2 м, высота — 1 м, а масса 1 м³ зерна составляет 8 ц?
1) 8 • 2 • 1 = 16 (м²) — объём бункера.
2) 16 • 8 = 128 (ц) — пшеницы можно засыпать в бункер.
Ответ: 128 центнеров.
4. Что больше и на сколько:
1) квадрат суммы чисел 4 и 3 или сумма их квадратов
(4 + 3)² > 4² + 3²
7² > 16 + 9
49 > 25
2) разность квадратов чисел 10 и 8 или квадрат их разности
10² — 8² > (10 — 8)²
100² — 64² > 2²
36 > 4
3) разность кубов чисел 5 и 3 или куб их разности
5³ — 3³ > (5 — 3)³
125 — 27 > 2³
98 > 8
Упражнения
645.
Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).
Таких двузначных чисел всего 9:
- 11, 12, 13
- 22, 21, 23
- 33, 31, 32
646. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 0 (цифры могут повторяться).
Таких двузначных чисел всего 6:
- 11, 12, 10
- 22, 21, 20
647. У ослика Иа-Иа есть три надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько у ослика Иа-Иа есть вариантов сделать подарки своим друзьям?
Решим задачу при помощи схемы «Дерево возможных вариантов».
Итак, у нас получилось шесть возможных вариантов:
Винни-Пуха | Пятачок | Кролик | |
Вариант 1 | Зелёный | Красный | Жёлтый |
Вариант 2 | Зелёный | Жёлтый | Красный |
Вариант 3 | Красный | Зелёный | Жёлтый |
| Вариант 4 | Красный | Жёлтый | Зелёный |
| Вариант 5 | Жёлтый | Зелёный | Красный |
| Вариант 6 | Жёлтый | Красный | Зелёный |
Ответ: 6 вариантов.
648. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0, 1 и 2?
Таких двузначных чисел всего 4:
- 12, 10
- 21, 20
649. В футбольном турнире участвуют команды 5 «А» класса, 5 «Б» класса и 5 «В» класса. Сколько существует способов распределения первого и второго мест среди этих команд? Решение какой задачи из номеров 645—648 аналогично решению этой задачи?
Решим задачу при помощи схемы «Дерево возможных вариантов».
Итак, у нас получилось шесть возможных вариантов (последовательно места, занятые 5″А», 5″Б» и 5″В»):
Итак, у нас получилось шесть возможных вариантов (последовательно цвет шарика для Винни-Пуха, Пятачка и Кролика):
5″А» | 5″Б» | 5″В» | |
Вариант 1 | 1 | 2 | — |
Вариант 2 | 1 | — | 2 |
Вариант 3 | 2 | 1 | — |
| Вариант 4 | 2 | — | 1 |
| Вариант 5 | — | 1 | 2 |
| Вариант 6 | — | 2 | 1 |
Задача аналогична задаче № 647.
Ответ: 6 вариантов.
650. Запишите все трёхзначные числа, для записи которых используются только цифры (Цифры не могут повторяться.):
1) 3, 4 и 6
- 346, 364
- 436, 463
- 634, 643
2) 4, 7 и 0
- 470, 407
- 740, 704
651. Сколько различных трёхзначных чисел можно составить из цифр (Цифры могут повторяться.):
1) 1 и 2
- 111, 112, 121, 122
- 222, 221, 212, 211
Ответ: 8 чисел.
2) 0 и 1
- 111, 110, 101, 100
Ответ: 4 числа.
652. Запишите все двузначные числа, в записи которых используются только цифры 2, 4, 9 и 0. (Цифры могут повторяться.)
- 22, 24, 29, 20
- 42, 44, 49, 40
- 92, 94, 99, 90
653. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке возрастания?
- 67, 68, 69
- 78, 79
- 89
Ответ: 6 чисел.
- 98, 97, 96
- 87, 86
- 76
Ответ: 6 чисел.
655. Сколько существует двузначных чисел, сумма цифр которых равна 5?
Всего 5 чисел: 14, 23, 32, 41, 50.
Ответ: 5 чисел.
656. Сколько двузначных чисел, сумма цифр которых равна чётному числу, можно составить из цифр 1, 2, 3, 4 (цифры могут повторяться)?
Всего 8 чисел: 11, 13, 22, 24, 31, 33, 42, 44.
Ответ: 8 чисел.
657. Сколько двузначных чисел, сумма цифр которых равна нечётному числу, можно составить из цифр 0, 1,2, 3?
Всего 6 чисел: 10, 12, 21, 23, 30, 32.
Ответ: 6 чисел.
658. Кот Базилио и лиса Алиса решили украсть золотой ключик, который хранится в каморке папы Карло. Чтобы туда проникнуть, нужно подобрать двузначный код. Им известно, что дверь в каморку закрывает Буратино, который знает пока что только четыре цифры: 0, 1, 2 и 3.
Какое наибольшее количество вариантов придётся перебрать коту и лисе, чтобы открыть дверь?
Составим таблицу:
- в первом столбце запишем возможные варианты первой цифры кода
- в верхней строке — возможные варианты второй цифры кода
- на пересечении строк и столбцов — возможные варианты кодов.
| 0 | 1 | 2 | 3 |
0 | 00 | 01 | 02 | 03 |
1 | 10 | 11 | 12 | 13 |
| 2 | 20 | 21 | 22 | 23 |
| 30 | 31 | 32 | 33 |
Итак, возможное количество вариантов кода — 16.
Ответ: 16 вариантов.
659.
Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?
P = (a + b) • 2
Если P = 24 см, то сумма длин сторон равна 24 : 2 = 12 см.
Существует 6 возможных вариантов таких прямоугольников. Длины сторон у них должны быть:
- 1 см и 11 см
- 2 см и 10 см
- 3 см и 9 см
- 4 см и 8 см
- 5 см и 7 см
- 6 см и 6 см (квадрат, который также соответствует определению прямоугольника).
Ответ: 6 прямоугольников.
660. У Ани есть 30 одинаковых кубиков. Сколько различных прямоугольных параллелепипедов она может из них составить, если для построения одного параллелепипеда надо использовать все имеющиеся 30 кубиков?
V = abc
Если V = 30, то можно подобрать 5 вариантов постройки прямоугольного параллелепипеда из одинаковых кубиков:
- 30 • 1 • 1 = 30
- 15 • 2 • 1 = 30
- 10 • 3 • 1 = 30
- 6 • 5 • 1 = 30
- 5 • 3 • 2 = 30
Ответ: 5 вариантов.
661. На прямой отметили четыре точки А, В, С и D. Сколько отрезков с концами в отмеченных точках можно провести? Какой из рисунков § 24 помогает решить эту задачу?
Для решения этой задачи можно ориентироваться на рисунок 184 § 24:
Но лучше сделать свой рисунок для этой конкретно задачи:
- AB, AC, AD
- BC, BD
- CD
Ответ: 6 отрезков.
662. Подножие горы и её вершину связывают три тропы. Сколько существует маршрутов, ведущих от подножия к вершине и затем вниз к подножию?
Нарисуем эти три маршрута схематично, изобразив их в виде лучей, выходящих из единой точки, где:
- O — вершина горы
- A — первая точка у подножия горы
- B — вторая точка у подножия горы
- C — третья точка у подножия горы.
Тогда возможные следующие варианты маршрутов (начало маршрута — вершина — конец маршрута):
- AOA, AOB, AOC
- BOA, BOB, BOC
- COA, COB, COC
Итого — 9 вариантов маршрутов.
Ответ: 9 вариантов.
663. Спортивной команде предлагают футболки трёх цветов — красного, зелёного и синего, а шорты двух цветов — белого и жёлтого. Сколько вариантов выбора формы есть у команды?
Составим таблицу:
- в первом столбце запишем возможные варианты шорт
- в верхней строке — возможные варианты футболок
- на пересечении строк и столбцов — возможные варианты формы
Форма | Футболки | |||
| Красные | Зелёные | Синие | ||
Шорты | Белые | Красная футболка белые шорты | Зелёная футболка белые шорты | Синяя футболка белые шорты |
| Жёлтые | Красная футболка жёлтые шорты | Зелёная футболка жёлтые шорты | Синяя футболка жёлтые шорты | |
Итак, возможное количество вариантов формы — 6.
Ответ: 6 вариантов.
664. У Тани есть четыре платья и две пары туфель. Сколько у Тани есть вариантов выбора наряда?
Составим таблицу:
- в первом столбце запишем возможные варианты туфель
- в верхней строке — возможные варианты платьев
- на пересечении строк и столбцов — возможные варианты наряда
Наряд
| Платья | ||||
| 1 | 2 | 3 | 4 | ||
Туфли | 1 | Платье № 1 Туфли № 1 | Платье № 2 Туфли № 1 | Платье № 3 Туфли № 1 | Платье № 4 Туфли № 1 |
| 2 | Платье № 1 Туфли № 2 | Платье № 2 Туфли № 2 | Платье № 3 Туфли № 2 | Платье № 4 Туфли № 2 | |
Итак, возможное количество вариантов нарядов — 8.
Ответ: 8 вариантов.
665. В отряде космонавтов есть три пилота и два инженера. Сколько существует способов составить экипаж, состоящий из одного пилота и одного инженера?
Составим таблицу:
- в первом столбце запишем возможные варианты инженеров
- в верхней строке — возможные варианты пилотов
- на пересечении строк и столбцов — возможные варианты экипажа
Экипаж | Пилоты | |||
| 1 | 2 | 3 | ||
Инженеры | 1 | Пилот 1 Инженер 1 | Пилот 2 Инженер 1 | Пилот 3 Инженер 1 |
| 2 | Пилот 1 Инженер 2 | Пилот 2 Инженер 2 | Пилот 3 Инженер 2 | |
Итак, возможное количество вариантов нарядов — 6.
Ответ: 6 вариантов.
666. На рисунке 185 изображён план одного района города. Отрезками изображены улицы. Сколько существует маршрутов из точки А в точку В, если передвигаться разрешено по улицам, идущими вверх или вправо?
Существуют следующие варианты маршрутов:
- Вверх — вверх — вправо — вправо
- Вверх — вправо — вверх — вправо
- Вверх — вправо — вправо — вверх
- Вправо — вверх — вверх — вправо
- Вправо — вверх — вправо — вверх
- Вправо — вправо — вверх — вверх
Итак, возможное количество вариантов маршрутов — 6.
Ответ: 6 вариантов.
667. В записи 1 * 2 * 3 * 4 вместо каждой звёздочки можно поставить один из знаков «+» или «•». Чему равно наибольшее значение выражения, которое можно получить?
Наибольшее значение выражения можно получить, если расставить знаки в таком порядке:
1 + 2 • 3 • 4 = 1 + 6 • 4 = 1 + 24 = 25.
Упражнения для повторения
668.
Расстояние между двумя сёлами равно 28 км. Из этих сёл одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?
1) 56 — 42 = 14 (км/ч) — скорость, с которой мотоциклист догоняет автобус — скорость сближения.
2) 28 : 14 = 2 (часа) — время, за которое мотоциклист догонит автобус.
Ответ: 2 часа.
669. Решите уравнение:
670. 1) Одно из слагаемых в 14 раз больше другого. Во сколько раз их сумма больше меньшего слагаемого?
Пусть х — первое слагаемое. Тогда второе слагаемое равно 14х.
(14х + х) : х = 15х : х = 15
Ответ: в 15 раз.
2) Вычитаемое в 12 раз больше разности. Во сколько раз уменьшаемое больше разности?
Пусть х — разность, тогда вычитаемое равно 12х, а уменьшаемое равно (12х + х).
(12х + х) : х = 13х : х = 13
Ответ: в 13 раз.
671. На ферме есть 156 коров, каждая из которых даёт в день 12 л молока. Молоко с фермы вывозят в бидонах ёмкостью 40 л. В некоторый день на ферме было в наличии 42 пустых бидона. Хватит ли бидонов, чтобы вывезти с фермы надоенное за день молоко?
1) 156 • 12 = 1 872 (литра) — молока надаивают на ферме за 1 день.
2) 42 • 40 = 1 680 (литров) — молока помещается в 42 пустых бидона.
3) 1 680 литров < 1 872 литра, значит 42 бидона не хватит для вывоза всего надоенного за день молока.
Ответ: Нет, не хватит.
672. Решите кроссворд.
По горизонтали:
2. Результат арифметического действия (Частное)
3. Единица измерения времени (Секунда)
4. Единица измерения углов (Градус)
5. Компонент умножения (Множитель)
6. Компонент сложения (Слагаемое)
По вертикали:
1. «Царица наук» (Математика)
Задача от мудрой совы
673. В классе 30 учащихся.
Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?
1) Если половина всех девочек сидят с мальчиками, значит вторая половина девочек сидит друг с другом по двое за партой. Значит половина девочек — это чётное количество человек.
2) Если половина девочек — это чётное количество человек, то общее количество девочек (две половины) также будет чётным числом.
3) Предположим, что условие задачи выполнимо и половину мальчиков можно посадить с девочками. Это значит, что другая половина мальчиков будет сидеть по двое за партой. То есть половина мальчиков также должно быть чётным числом.
4) Половина мальчиков и половина девочек — это ровно половина класса. По нашему предположению это чётное количество человек, так как и половина мальчиков, и половина девочек чётные числа.
5) Но мы знаем, что в классе 30 учащихся, а половина от 30 человек — это 15 человек — нечётное число. Значит наше предположение о мальчиках было неверно и их нельзя посадить так, чтобы половина мальчиков сидела с девочками.
Ответ: Нет, нельзя.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Презентация «Комбинаторные задачи»
КОМБИНАТОРНЫЕ ЗАДАЧИ
УМК: А.Г. Мерзляк и др.
5 класс
Определение
Комбинаторикой называют
раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям можно составить.
Комбинаторными задачами называются задачи, решение которых требует рассмотрения и подсчета всех возможных случаев (комбинаций).
Способы решения задач
- Перебор вариантов (проводят таблицей или схемой)
- Дерево возможных вариантов (схема, графически отражающая условие задачи и ход рассуждений).
ЗАДАЧА
На завтрак Вова может
выбрать плюшку, бутерброд,
пряник или кекс , а запить их он может кофе, соком или кефиром.
Из скольких вариантов Вова может выбирать себе завтрак?
Решение
Ответ: 12 вар.
Задача
Из цифр 2 , 4 и 7 надо составить трёхзначное число , в котором ни одна цифра не может повторятся более двух раз и каждое число начинается с цифры 2 .
Составим дерево решений:
Решение
2
4 7 2 4 7 2 4 7
4
7
2
227
224
242
272
244
277
274
247
Ответ: всего 8 чисел
Задача
Одноклассницы Оля, Валя и Катя дежурят по школе.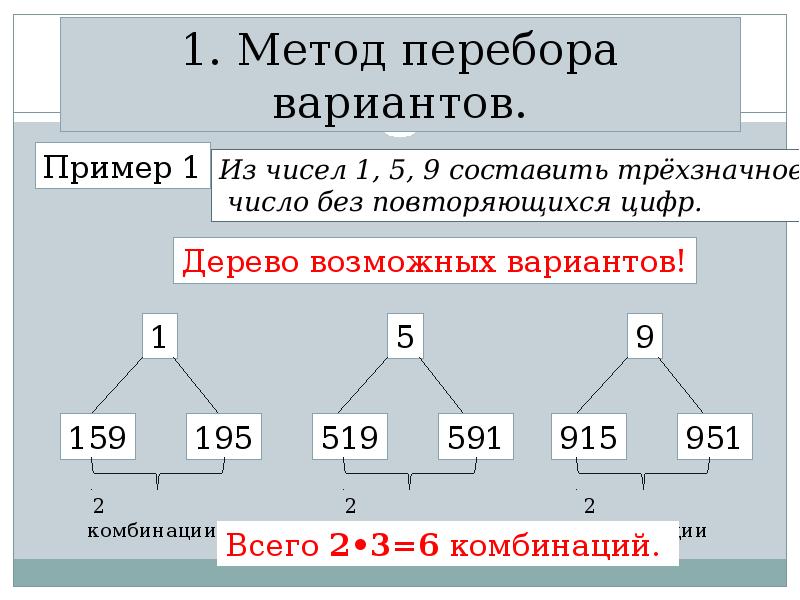
Сколькими способами классный руководитель может расставить девочек по одной на каждом из трёх этажей школы?
Решение
1 способ (перебор возможных вариантов): ОВК; ОКВ; ВОК; ВКО; КОВ; КВО.
2 способ (дерево событий):
Классный руководитель
О
3 ЭТАЖ
В
К
2 ЭТАЖ
К
О
В
К
В
О
1 ЭТАЖ
К
В
О
О
К
В
Задача
При встрече 4 приятеля обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Решение. Назовём приятелей А; В; С и D .
Составим схему
А
В
D
С
Ответ: 6 вариантов
№ 645.
Запишите все двузначные числа, в записи которых используются только цифры 1; 2 и 3 (цифры могут повторятся)
Решение .
Двузначное число ( цифры могут повторятся )
Первая цифра 1 2 3
Вторая цифра 1 2 3 1 2 3 1 2 3
Варианты чисел: 11; 12; 13; 21; 22; 23; 31; 32; 33.
Ответ: 9 чисел
Задача. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0; 1 и 2?
Решение . Двузначное число (цифры не могут повторятся)
Первая цифра 1 2
Вторая цифра 0 2 0 1
Варианты числа: 10; 12; 20; 21
Ответ: 4 числа
Задача. Запишите все 3-хзначные числа, в записи которых используются только цифры 3; 4 и 6 ( цифры не могут повторятся )
Решение . трёхзначное число (цифры не могут повторятся)
Первая цифра 3 4 6
Вторая цифра 4 6 3 6 3 4
Третья цифра 6 4 6 3 4 3
Назовите числа:
Ответ: 6 чисел
Задача.
У ослика Иа-Иа есть 3 надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько есть вариантов и Иа-Иа?
шарики
друзья
Винни-Пух
красный
красный
Пятачок
зелёный
Кролик
зелёный
жёлтый
зелёный
жёлтый
жёлтый
жёлтый
жёлтый
зелёный
красный
красный
красный
зелёный
зелёный
жёлтый
красный
Решение.
Ответ: 6 вариантов
Задача. В футбольном турнире участвовали команды 5 «А», 5 «Б» и 5 «В» классов. Сколько существует способов распределения 1-го и 2-го мест среди этих команд?
Решение.
Команды 5 «А» 5 «Б» 5 «В»
1 место + — —
2 место — + —
2 место — — +
Значит: если 5 «А» займёт 1 место, то — 2 варианта
Аналогично, если 5 «Б» займёт 1 место, то — 2 варианта
если 5 «В» займёт 1 место, то ещё — 2 варианта
Ответ: 6 спос.
Решить самостоятельно
Задача. Запишите все 3-хзначные числа, в записи которых используются только цифры 4; 7 и 0 ( цифры не могут повторятся )
Ответ: ??? чисел
Решить самостоятельно
Задача. Сколько различных трёхзначных чисел можно составить из цифр (цифры могут повторяться):
а) 1 и 2 б) 0 и 1
Ответ: ??? чисел
Источники
Шаблон создан на основе клипарта рамки
- https://img-fotki.yandex.ru/get/4124/39663434.8ee/0_ace13_53b91bc7_XL.png
И возможностей программы Microsoft PowerPoint 2016
Шаблон презентации подготовила учитель русского языка и литературы Тихонова Надежда Андреевна , г. Костанай
А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Математика: 5 класс: учебник для учащихся общеобразовательных организаций, — 2-е изд.
, перераб. – М.:Вентана-Граф, 2016
Не сбрасывайте их со счетов – помогаем учащимся успешно решать комбинаторные задачи |
Элиз Локвуд, ответственный редактор Орегонского государственного университета
Введение
Решение задач на счет — одно из моих любимых занятий. Мне нравится задача осмысления проблемы, работа по правильному моделированию того, что я пытаюсь посчитать, и тот факт, что я могу рассуждать об удивительно больших числах. Однако я не всегда так относился к решению задач на счет. На протяжении большей части моей математической карьеры счет был загадкой — набором малопонятных формул и уравнений, от которых я просто страдал. Будучи студентом, я изо всех сил пытался понять разницу между порядком, имеющим значение или не имеющим значения, что представляют соответствующие факториалы в запутанных формулах и почему меня должно волновать, сколько фулл-хаусов можно выбрать из колоды карт. Мои учителя в то время, возможно, разделяли чувства, хорошо переданные Аннином и Лаем: «Учителей математики часто спрашивают: «Какая самая сложная тема для преподавания?» Наш ответ — учить учащихся считать» (2010, стр.
403). .
В какой-то момент во время обучения в аспирантуре (благодаря влиятельному профессору, который любил считать), я свернул за угол и стал больше интересоваться пониманием счета. Многократно практикуясь, я начал улучшать свои способности решать задачи на счет. С тех пор я сосредоточил свои исследовательские интересы на том, чтобы узнать все, что я могу, о счете студентов бакалавриата: что они делают, когда подходят к задачам счета, почему у них возникают трудности и как мы можем помочь им решать такие задачи более эффективно.
Модель комбинаторного мышления учащихся
В этом посте я представляю модель комбинаторного мышления учащихся, которая помогла мне разобраться в счетной деятельности учащихся. Я также предлагаю примеры, иллюстрирующие аспекты модели, и заканчиваю конкретными рекомендациями по обучению учащихся решению задач на счет.
Модель (первоначально представленная в Локвуде, 2013 г., а затем уточненная в Локвуде, Суинъярде и Каумане, 2015 г.
) состоит из трех компонентов: формул/выражений, процессов подсчета и наборов результатов, а также взаимосвязей между этими компонентами ( см. рис. 1 ниже). 94)\). Процессы подсчета относятся к фактическим пошаговым процедурам, в которых кто-то участвует (мысленно или физически) при решении задачи подсчета. Это может включать в себя применение принципа умножения или внедрение разбивки случаев. Набор из исходов для данной задачи относится к желаемым исходам этой проблемы — элементам, которые фактически подсчитываются. Эти результаты могут быть каким-то образом закодированы (например, в виде строк чисел или букв), и этот компонент может состоять из различных способов кодирования и структурирования результатов.
В качестве простого примера для разработки этих компонентов и выделения взаимосвязей между формулами/выражениями, процессами счета и наборами результатов рассмотрим следующую задачу: Сколько последовательностей из трех букв состоит из букв a, b, c, d, e, f могут быть образованы, если повторение не допускается и мы должны включать букву e? (Эта проблема была представлена в Tucker, 2002).
Прежде чем решать задачу, мы можем подумать, как будут выглядеть результаты. Это трехбуквенные последовательности (так, abe отличается от eab ), которые содержат букву e, где повторение не разрешено (такие результаты, как abc или aaa , не допускаются). Чтобы подсчитать все такие последовательности, трехэтапный процесс подсчета для решения задачи будет заключаться в том, чтобы сначала выбрать позицию, в которой должны стоять и (есть 3 варианта), а затем выбрать, какая из 5 оставшихся букв ( a, b, c, d, f ) может перейти в следующую доступную позицию, а затем выбрать, какая из 4 оставшихся букв (четырех, которые ранее не были выбраны) может перейти в последнюю доступную позицию. Этот процесс дает формулу/выражение \(3 \cdot 5\cdot 4\), что равно 60.
Важно отметить, что описанный выше процесс подсчета структурирует результаты особым образом. В частности, он группируется в соответствии с расположением и , как следует из следующего списка результатов на рисунке 2:
Рисунок 2.
Одна организация набора результатов
приводят к различным структурам множества результатов. Например, даже если это может быть не столь элегантное решение, другим процессом может быть организация результатов в соответствии с первой буквой. В частности, мы начинаем с выбора того, какая буква будет первой, и если это не e мы рассматриваем два случая: поместить e на вторую позицию (затем прокручивая оставшиеся буквы в третьей позиции) и затем помещая e на третью позицию (затем прокручивая оставшиеся буквы во второй позиции). позиция). Если e — это первая буква, мы циклически перебираем каждую из оставшихся букв для второй и третьей позиции. Таким образом, мы могли бы рассматривать последовательности с разными соответствующими первыми буквами, в результате чего результаты были бы структурированы, как на рисунке 3. Выражение, отражающее этот процесс, имеет вид \(5 \cdot 2 \cdot 4 + 1\cdot 5 \cdot 4\), что также равно 60. Смысл этого примера в том, что разные способы структурирования или организации набора результатов могут отражать разные соответствующие процессы подсчета, и, наоборот, разные процессы подсчета могут привести к разным способам организации результатов.
Рисунок 3. Альтернативная организация набора результатов
Итак, зачем нам эта модель и эти компоненты? Я утверждаю, что очень важно, чтобы учащиеся сосредоточились на наборе результатов (Lockwood, 2014) и, в частности, на размышлениях о взаимосвязи между процессами подсчета и наборами результатов. Есть несколько причин, почему эти отношения так важно понять. Во-первых, если учащиеся не настроены на набор результатов (и вместо этого сосредотачиваются в первую очередь на процессах счета и формулах/выражениях), то правила, определяющие, какую формулу использовать, становится труднее анализировать. Подсчет может стать упражнением в простом манипулировании формулами без четкого понимания того, что подсчитывается. Кроме того, некоторые распространенные ошибки, такие как пересчет, трудно обнаружить и исправить без четкого понимания результатов и того, как процессы подсчета связаны с этими результатами. В качестве примера того, почему эта взаимосвязь важна, рассмотрим следующую аналогичную задачу, связанную с последовательностями из трех букв (также найденную в Tucker, 2002): Сколько 3-буквенных последовательностей, составленных из букв a, b, c, d, e, f, можно составить, если мы должны включить букву e, и повторение букв разрешено?
Здесь общий процесс подсчета следующий: Сначала поместите e в одну из трех позиций.
Затем для каждого размещения и мы можем утверждать, что, поскольку повторение разрешено, теперь мы можем поместить любую из оставшихся 6 букв в оставшиеся две позиции. Этот процесс предлагает формулу/выражение \(3 \cdot 6 \cdot 6\). Этот процесс подсчета, кажется, имеет смысл, и действительно, это очень распространенная реакция среди студентов. Однако это неверный ответ, так как этот процесс слишком много раз подсчитывает некоторые результаты. Чтобы увидеть это, мы должны внимательно рассмотреть результаты и, в частности, то, как результаты генерируются и организуются в процессе подсчета.
Давайте подумаем о следующем: предположим, что на первом этапе процесса мы поместили и на третью позицию, а затем на оставшихся этапах выбора одной из 6 букв, которые должны быть на оставшихся двух позициях, мы выбрал и , а затем и . Это дает пароль eae . Однако рассмотрим другой способ завершения этого процесса: мы могли бы сначала поместить e на первую позицию, а затем на этапе 6 \(\cdot\) 6 мы могли бы выбрать и , а затем и .
Это тоже генерирует пароль eae . Способы завершения процесса не находятся в однозначном соответствии с количеством желаемых результатов, и поэтому этот процесс приводит к пересчету.
Если учащийся не понимает, что существует взаимосвязь между процессами подсчета и результатами, как он или она может знать, когда они пересчитывают, не говоря уже о том, чтобы быть готовыми рассмотреть и исправить этот пересчет? Проблемы со счетом сложны, и может быть много разумно звучащих процессов. Без обоснования этого в наборе результатов может быть трудно сказать, может ли (и почему) данный процесс переоценить.
Практические выводы
Проблема пересчета — лишь один пример того, почему важны все три компонента модели и почему мы должны побуждать учащихся рассматривать наборы результатов и то, как они соотносятся с процессами подсчета. В свете этого ниже я предлагаю несколько советов по обучению счетам (особенно для студентов старших курсов, хотя тот же совет можно применить и к обучению счету на любом уровне).
1) Предложите учащимся сосредоточиться на наборе результатов. Основной вывод моего исследования на данный момент состоит в том, что есть ценность в том, чтобы учащиеся сосредоточились на наборе результатов. Есть несколько практических способов сделать это. Во-первых, в широком смысле учителя должны стремиться рассматривать счет как деятельность по определению мощности набора, в частности, набора желаемых результатов, указанных в задаче на подсчет. Хотя это кажется рудиментарным, у нас есть свидетельства того, что учащиеся не всегда рассматривают счет таким образом — вместо этого счет может быть вопросом сопоставления формул, слепого угадывания типов задач и т. д. Например, когда их спрашивают о проблеме порядка в проблема, один из моих студентов однажды сказал: «Я не знаю, я как бы схожу с ума из-за тех, которые конкретно не говорят, что порядок имеет значение или не имеет значения». По иронии судьбы, если бы студенты были более настроены на наборы результатов, я считаю, что это помогло бы им в их стремлении найти заданный тип задачи или применить формулы.
Возможно, если бы мы всегда поощряли учащихся формулировать характер того, что они считают, задавая такие вопросы, как «Что вы пытаетесь считать?». Ваши результаты более уместно моделировать как наборы вещей или их расположение? — учащиеся могут быть более склонны рассматривать счет как деятельность, связанную с результатами. Этот подход к счету, ориентированный на множество, изложен в Lockwood (2014), а также упоминается в Hadar & Hadass (19).81), Мамона Даунс и Даунс (2004 г.) и Батанеро, Наварро-Пелайо и Годино (1997 г.).
Во-вторых, есть еще один способ, с помощью которого учащиеся могут активно работать с результатами: предложить учащимся составить частичные списки результатов. Появляется все больше свидетельств того, что фактическое участие в составлении списков является полезной стратегией для студентов (English, 1991; Halani, 2012), и даже была продемонстрирована статистическая значимость (Lockwood & Gibson, в печати). Таким образом, практический совет заключается в том, чтобы учащиеся участвовали в составлении списка.
В некоторых случаях перечисление действительно может предложить ответ на задачу счета, и, более того, это помогает учащимся понять, что такое результат. Например, рассмотрим задачу домино, в которой говорится: Домино — это маленькая тонкая прямоугольная плитка с точками на одной из широких граней. Это лицо разделено на две половины, и на каждой из этих половинок может быть от 0 до 6 точек. Предположим, вы хотите сделать набор костяшек костяшек (т. е. по одному из всех возможных костяшек костяшек). Сколько различимых доминошек вы бы сделали для полного набора? В этой задаче я видел, как студенты перед перечислением предлагают ответ типа \(7! \cdot 7!\), что не имеет особого смысла в контексте задачи. Решая подобную задачу, учащиеся могут понять природу результатов, которые мы хотим считать различимыми. Кроме того, стоит отметить, что частичное перечисление также полезно, особенно в задаче, в которой результаты могут быть трудно увидеть/признать похожими. Частичный список помогает, потому что, опять же, он может сориентировать учащихся в отношении того, что считается, и часто учащиеся могут экстраполировать более общее решение или стратегию даже из неполного списка.
2) Подчеркните взаимосвязь между процессами подсчета и наборами результатов. По мере того, как учащиеся будут заниматься составлением списков, идея о наличии связи между их процессами счета и их набором результатов должна укрепляться. Как мы отмечали выше, эта взаимосвязь может быть ключевой, помогая учащимся обнаруживать и решать проблемы порядка и пересчета, которые являются двумя распространенными трудностями, с которыми сталкиваются учащиеся. Также важно отметить, что не обязательно преуменьшать значение выражений и формул, потому что они являются важными аспектами счета, обеспечивающими упрощенные способы эффективного решения задач. Проблема в том, что мы склонны придавать им слишком большое значение, и учащиеся рассматривают их просто как формулу для запоминания, а не как обобщение и/или формализацию процесса подсчета, который имеет смысл и фактически каким-то образом структурирует набор результатов. На практике подчеркивание этой взаимосвязи может заключаться в том, чтобы давать учащимся задания, связанные с перечислением, или давать им задачи, не связанные с простым применением формулы.
Хорошими примерами являются задача домино и задачи с последовательностями из трех букв, а также следующая задача Language Book (также адаптированная из Tucker, 2002): Y У вас есть 5 разных испанских книг, 6 разных французских книг и 4 разных японских книги. Сколькими способами можно выбрать две книги на разных языках?
3) Напомните учащимся, что задачи на счет — это весело и дают прекрасную возможность для критического мышления. Поскольку не существует четко прописанных алгоритмов для решения каждой задачи (в отличие от решения страницы, полной задач на интегрирование по частям), учащиеся могут испытывать трудности со счетом. Тем не менее, учителя должны стараться разделять мнение о том, что счет на самом деле представляет собой интеллектуальную задачу и может доставлять удовольствие. Прекрасным примером этого являются недавние видеоролики, в которых учащиеся математического класса средней школы пытаются решить задачу на счет (https://www.youtube.com/watch?v=SrWt_XvWLUk).
Эти дети не беспокоятся о формулах или получении правильного ответа — они заняты критическим мышлением и решением проблем и, кажется, получают от этого удовольствие!
Для старшекурсников рассмотрите следующую задачу: Предположим, вы хотите надеть 8 одинаковых белых носков и 8 одинаковых красных ботинок на своего домашнего осьминога, у которого 8 различимых ног. Вы можете делать это в любом порядке, главное, чтобы для любой ноги носок был впереди ботинка. Сколькими способами можно надеть обувь и носки на осьминога? Если учащимся будет предоставлено время и пространство для размышлений и изучения счета как забавной возможности для решения задач, учащимся может быть удобнее заниматься результатами, а не просто пытаться применить заученную, но не совсем понятую формулу.
Ссылки:
Аннин С.А. и Лай К.С. (2010). Распространенные ошибки при подсчете задач. Учитель математики, 103(6), 402-409.
Батанеро, К., Наварро-Пелайо, В., и Годино, Дж.
(1997). Влияние неявной комбинаторной модели на комбинаторное мышление учащихся средней школы. Образовательные исследования по математике, 32, 181–199.
English, LD (1991). Комбинаторные стратегии для детей младшего возраста. Образовательные исследования по математике, 22, 451-47.
Хадар, Н., и Хадасс, Р. (1981). Путь к решению комбинаторных задач усеян ловушками. Образовательные исследования по математике, 12, 435-443.
Халани, А. (2012). Способы мышления учащихся о наборах решений перечислительной комбинаторики: категория одометра. В электронных материалах Пятнадцатой группы специальных интересов MAA по исследованиям в области математического образования для студентов. (стр. 59-68) Портленд, Орегон: Портлендский государственный университет.
Локвуд, Э. (2013). Модель комбинаторного мышления учащихся. Журнал математического поведения, 32, 251–265. Дои: 10.1016/j.jmathb.2013.02.008.
Локвуд, Э. (2014). Комплексно-ориентированный подход к решению задач на счет.
Для изучения математики, 34 (2), 31-37.
Локвуд Э. и Гибсон Б. (в печати). Комбинаторные задачи и список результатов: изучение продуктивного списка среди студентов бакалавриата. Чтобы появиться в образовательных исследованиях по математике.
Локвуд, Э., Суинъярд, К.А., и Коман, Дж. С. (2015). Шаблоны, наборы результатов и комбинаторное обоснование: два студента заново изобретают формулы счета. Международный журнал исследований в области математического образования бакалавриата, 1 (1), 27–62. Дои: 10.1007/s40753-015-0001-2.
Махер, К.А., Пауэлл, А.Б., и Аптегроув, Э.Б. (ред.). (2011). Комбинаторика и рассуждение: представление, обоснование и построение изоморфизмов. Нью-Йорк: Спрингер.
Мамона-Даунс, Дж. и Даунс, М. (2004). Реализация приемов решения задач: построение биекций для задач перечисления. Образовательные исследования по математике, 56, 235-253.
Такер, А. (2002). Прикладная комбинаторика (4-е изд.). Нью-Йорк: Джон Уайли и сыновья.
Эта запись была размещена в Практики оценивания, Практики в классе, Исследования и помечена как комбинаторная модель, комбинаторика, счет, формулы, результаты.
Добавьте постоянную ссылку в закладки.
Мир математики – Mathigon
Введение
Леонард Эйлер (1707 – 1783)
Комбинаторика— это раздел математики, в котором считают — и мы обнаружим много интересных примеров «вещей», которые вы можете посчитать.
Первые комбинаторные задачи изучались древними индийскими, арабскими и греческими математиками. Интерес к этому предмету возрос в 19-м и 20-м веках вместе с развитием теории графов и таких проблем, как теорема о четырех цветах. Некоторые из ведущих математиков включают Блеза Паскаля (1623–1662), Якоба Бернулли (1654–1705) и Леонарда Эйлера (1707–1783).
Комбинаторика имеет множество приложений в других областях математики, включая теорию графов, кодирование и криптографию, а также вероятность.
Факториалы
Комбинаторикаможет помочь нам подсчитать количество порядков из , в которых что-то может произойти. Рассмотрим следующий пример:
В классе V.
CombA1 учеников и V.CombA1 стульев, стоящих в ряд. В скольких различных порядках ученики могут сесть на эти стулья? Перечислим возможности – в этом примере V.CombA1 разных учеников представлены V.CombA1 разными цветами стульев.
Есть {2: 2, 3: 6, 4: 24, 5: 120}[V.CombA1] различных возможных порядков. Обратите внимание, что количество возможных заказов очень быстро увеличивается по мере увеличения числа учеников. С 6 учениками есть 720 различных возможностей, и перечислить их все становится непрактично. Вместо этого нам нужна простая формула, которая говорит нам, сколько заказов на n человек сидят на n стульях. Тогда мы можем просто заменить 3, 4 или любое другое число на n , чтобы получить правильный ответ.
Предположим, у нас есть V.CombB1 стульев, и мы хотим разместить V.CombB1==1?’один ученик’:V.CombB1==2?’два ученика’:V.CombB1==3?’три ученика. ‘:V.CombB1==4?’четыре ученика’:V.CombB1==5?’пять учеников’:V.CombB1==6?’шесть учеников’:’семь учеников’ на них. { 7: ‘На первый стул могут сесть 7 учеников. Тогда есть 6 учеников, которые могут сесть на второй стул. Есть 5 вариантов для третьего стула, 4 варианта для четвертого стула, 3 варианта для пятого стула, 2 варианта для шестого стула и только один вариант для последнего стула.’,
6: «На первый стул могут сесть 6 учеников. Тогда есть 5 учеников, которые могут сесть на второй стул. Есть 4 варианта для третьего стула, 3 варианта для четвертого стула, 2 варианта для пятого стула и только один вариант для последнего стула.’,
5: «На первый стул могут сесть 5 учеников. Тогда есть 4 ученика, которые могут сесть на второй стул. Есть 3 варианта выбора третьего стула, 2 варианта выбора четвертого стула и только один вариант выбора последнего стула.
‘,
4: «На первый стул могут сесть 4 ученика. Тогда есть 3 ученика, которые могут сесть на второй стул. Есть 2 варианта выбора третьего стула и только один вариант выбора последнего стула.’,
3: «На первый стул могут сесть 3 ученика. Затем есть 2 ученика, которые могут сесть на второй стул. Наконец, на третьем стуле остался только один ученик.’,
2: «Есть 2 ученика, которые могут сесть на первый стул. Далее на втором стуле остается только один ученик.’,
1: «Это только один вариант для одного стула».}[V.CombB1] Всего
возможности. Для упрощения записи математики используют «!» называется факториалом. Например, 5! («пять факториалов») — это то же самое, что 5 × 4 × 3 × 2 × 1. Выше мы только что показали, что существует n ! возможности заказать n объектов.
Упражнение
Решение
Сколькими способами 23 ребенка могут сесть на 23 стула на уроке математики? Если у вас 4 урока в неделю, а в году 52 недели, сколько лет потребуется, чтобы освоить все различные возможности? Примечание: Возраст Вселенной составляет около 14 миллиардов лет.
Для 23 детей, чтобы сидеть на 23 стульях есть 23! = 25 852 016 738 884 800 000 000 возможностей (это число слишком велико для отображения на экране калькулятора). Перепробование всех возможностей заняло бы
23,4 × 52 = 124 288 542 000 000 000 000 лет.
Это почти в 10 миллионов раз больше текущего возраста Вселенной!
Перестановки
Приведенный выше метод требовал, чтобы у нас было столько учеников, сколько стульев, на которых можно сидеть. Но что делать, если стульев не хватает?
Сколько существует различных возможностей для любого Math.min(V.CombC1,V.CombC2) из V.CombC1 учеников сесть на Math.min(V.CombC1,V.CombC2) стульев? Обратите внимание, что Math.max(0,V.CombC1-V.CombC2) останется в силе, что нам не нужно включать при перечислении возможностей.
Давайте начнем снова, перечислив все возможности:
attr(‘src’,’resources/Combinatorics/’+V.CombC1+’P’+(Math.min(V.CombC1,V.CombC2))+’@2x.png’).attr(‘width’,(V.CombC1==1&&(Math.min(V.CombC1,V.CombC2))==1)?29:(V.CombC1==2&&(Math.min(V.CombC1,V.CombC2))==1)?92:(V.CombC1==2&&(Math.min(V.CombC1,V.CombC2))==2)?156:(V.CombC1==3&&(Math.min(V.CombC1,V.CombC2))==1)?154:(V.CombC1==3&&(Math.min(V.CombC1,V.CombC2))==2)?250:(V.CombC1==3&&(Math.min(V.CombC1,V.CombC2))==3)?336:(V.CombC1==4&&(Math.min(V.CombC1,V.CombC2))==1)?216:(V.CombC1==4&&(Math.min(V.CombC1,V.CombC2))==2)?480:(V.CombC1==4&&(Math.min(V.CombC1,V.CombC2))==3)?532:586)»>
Чтобы найти простую формулу, подобную приведенной выше, мы можем думать об этом очень похожим образом. ‘Есть ученики ‘+V.CombC1+’, которые могли сесть на первый стул. ‘+
(((Math.min(V.CombC1,V.CombC2))==2||(Math.min(V.CombC1,V.CombC2))==3||(Math.min(V.CombC1,V .CombC2))==4)?’Тогда есть ‘+(V.CombC1-1)+’ учеников, которые могли бы сесть на второй стул.
‘:»)+
(((Math.min(V.CombC1,V.CombC2))==3||(Math.min(V.CombC1,V.CombC2))==4)?’Тогда есть ‘+(V.CombC1 -2)+’ ученики, которые могли сесть на третий стул. ‘:»)+
(((Math.min(V.CombC1,V.CombC2))==4)?’На последнем стуле остался один ученик. ‘:»)+
((V.CombC1-(Math.min(V.CombC1,V.CombC2))==1||V.CombC1-(Math.min(V.CombC1,V.CombC2))==2||V. CombC1-(Math.min(V.CombC1,V.CombC2))==3)?’Нас не волнуют оставшиеся ‘+(V.CombC1-V.CombC2)+’ дочерние элементы, оставшиеся стоять. ‘:’ ‘) Всего
возможности. Опять же, мы должны подумать об обобщении этого. Мы начинаем, как и с факториалов, но останавливаемся до того, как достигнем 1. На самом деле мы останавливаемся, как только достигаем количества студентов без стульев. При размещении 7 студентов на 3 стульев их становится
7 × 6 × 5 = 7 × 6 × 5 × 4 × 3 × 2 × 17 × 6 × 5 × 4 × 3 × 2 × 1 = 7 !4! = 7 !( 7 – 3 )!
возможности, так как 4 × 3 × 2 × 1 аннулируют друг друга.
Опять же, для этого есть более простое обозначение: 7 Р 3 . Если мы хотим разместить n объектов на m позиций, то есть
n P m = n !( n – m )!
возможности. P означает « p перестановок», так как мы подсчитываем количество перестановок (порядков) объектов. Если m и n такие же, как были в задаче в начале статьи, то имеем
n P n = n !( n – n )! = n !0!.
Чтобы понять это, мы определяем 0! = 1. Теперь n P n = n ! как и следовало ожидать от нашего решения первой проблемы.
Упражнение
Решение
К сожалению, вы не можете вспомнить код своего четырехзначного замка. Вы только знаете, что не использовали ни одну цифру более одного раза.
Сколько разных способов нужно попробовать? Что вы можете сказать о безопасности этих замков?
Имеется 10 цифр (0, 1, …, 9), каждая из которых встречается не более одного раза. Количество порядков этих цифр равно 10 P 4 = 5040. Тестирование такого количества комбинаций заняло бы очень много времени, поэтому замки с 4 цифрами очень безопасны.
Комбинации
Перестановки используются, когда вы выбираете объекты и заботитесь об их порядке — например, о порядке детей на стульях. Однако в некоторых задачах вам не важен порядок, и вы просто хотите знать, сколько существует способов выбрать определенное количество объектов из большего набора.
В магазине есть пять разных футболок, которые вам нравятся, красного, синего, зеленого, желтого и черного цветов. К сожалению, у вас есть только достаточно денег, чтобы купить три из них. Сколькими способами можно выбрать три футболки из пяти понравившихся?
Здесь нас не волнует порядок (неважно, покупаем ли мы сначала черную, а затем красную или сначала красную, а затем черную), только количество комбинаций футболок.
Возможности
, всего их 10. Если бы мы рассчитали 5 P 3 = 60, мы бы дважды посчитали некоторые возможности, как показано в следующей таблице:
С перестановками каждую комбинацию из трех футболок считаем 6 раз, потому что их 3! = 6 способов заказать три футболки. Чтобы получить количество комбинаций из количества перестановок, нам нужно просто разделить на 6. Пишем
5 C 3 = 5 P 33! = 606 = 10,
Здесь C означает « c комбинаций». В общем, если мы хотим выбрать r объектов из общего числа n есть
n C r = n P r r ! = n ! р ! ( n – r )!
различных комбинации. Вместо n C r математики часто пишут n C r = ( n r ), как дробь в скобках, но без черты между ними.
(Чтобы упростить набор текста, мы продолжим использовать первое встроенное обозначение.)
Упражнения
Решения
(a) В вашем классе 10 детей, но вы можете пригласить только 5 на свой день рождения. Сколько различных комбинаций друзей вы могли бы пригласить? Объясните, следует ли использовать комбинации или перестановки.
(б) На вечеринке 75 человек. Все пожимают всем руку один раз. Как часто в целом пожимают руки? Подсказка: Сколько человек участвует в рукопожатии?
(a) Количество комбинаций друзей, которых вы можете пригласить, равно 10 C 5 = 252. Мы использовали комбинации, потому что не имеет значения в каком порядке мы приглашаем друзей, на каких мы приглашаем.
(b) Вы хотите найти количество всех возможных пар гостей вечеринки. Это просто 75 C 2 = 2775. (Много рукопожатий!)
Комбинаторика и треугольник Паскаля
Рассчитаем некоторые значения n C r .
Начинаем с 0 C 0. Затем находим 1 C 0 и 1 C 1. Далее 2 C 0, 2 C 1 и 2 C 2. Затем 3 90 007 С 0 , 3 C 1, 3 C 2 и 3 C 3. Запишем все эти результаты в таблицу:
| 0 С 0 = 1 | |||||||||||
| 1 С 0 = 1 | 1 С 1 = 1 | ||||||||||
| 2 С 0 = 1 | 2 С 1 = 2 | 2 С 2 = 1 | |||||||||
| 3 С 0 = 1 | 3 С 1 = 3 | 3 С 2 = 3 | 3 С 3 = 1 | ||||||||
| 4 С 0 = 1 | 4 С 1 = 4 | 4 С 2 = 6 | 4 С 3 = 4 | 4 С 4 = 1 | |||||||
| 5 С 0 = 1 | 5 С 1 = 5 | 5 С 2 = 10 | 5 С 3 = 10 | 5 С 4 = 5 | 5 С 5 = 1 | ||||||
Это и есть треугольник Паскаля, который мы исследовали в статье о последовательностях.
Его можно легко создать, заметив, что любая ячейка является суммой двух ячеек выше. В треугольнике Паскаля скрыты бесчисленные закономерности и числовые последовательности.
Теперь мы также знаем, что r -е число в n -й строке также задается как n C r (но мы всегда должны начинать счет с 0, поэтому первая строка или столбец на самом деле является нулевой строкой). Если мы применим то, что мы знаем о построении треугольника Паскаля, к нашим комбинациям, мы получим
( н р ) + ( п р + 1) «=» ( n + 1 r + 1) .
Это известно как Личность Паскаля . Вы можете получить его, используя определение n C r в терминах факториалов, или вы можете думать об этом следующим образом:
Мы хотим выбрать r + 1 объектов из набора n + 1 объектов. Это точно так же, как пометить один объект из n + 1 для обозначения X и либо выбрать X плюс r других (из оставшихся n), либо не выбрать X и r + 1 других ( из оставшихся n).
Многие задачи по комбинаторике имеют простое решение, если правильно подумать, и очень сложное решение, если просто попробовать использовать алгебру…
Stars and Bars
Solution
Пример
Зеленщик на рынке хранит большое количество n различных видов фруктов. Сколькими способами можно составить мешок из r фруктов? Обратите внимание, что r может быть меньше, равно или больше, чем n .
Обратите внимание, что при r ≤ n существует n C r способов выбрать по одному фрукту каждого вида. Однако нам также разрешено брать более одного фрукта каждого вида, например, два яблока, одну клубнику и один банан.
Мы можем представить любой правильный выбор фруктов с помощью цепочки звездочек и полос, как показано в этом примере:
| ★★★ | | | ★★ | | | | | ★★ | | | ★ | |
| 3 типа 1 | 2 типа 2 | 0 типа 3 | 2 типа 4 | 1 тип 5 |
Всего имеется r звездочек (представляющих r фруктов, которые нам разрешено брать) и n – 1 полоска (делящих n различных видов фруктов).
Получается r + n – всего 1 место. Любой заказ r звездочек и n – 1 батончиков соответствует ровно одному действительному набору фруктов.
Теперь мы можем применить наши комбинаторные инструменты: есть r + n – 1 место, и мы хотим выбрать n – 1 из них в качестве баров (все остальные – звезды). Что есть ровно ( r + n – 1) C ( n – 1) возможности сделать это!
Предположим, есть пять видов фруктов, и мы хотим взять десять штук. Из того, что мы подсчитали выше, имеется
(10 + 5 – 1) C (5 – 1) = 14 C 4 = 24 024
возможности. Подумайте об этом в следующий раз, когда пойдете за покупками!
Комбинаторика и вероятность
Комбинаторика имеет множество приложений в теории вероятностей. Вы часто хотите найти вероятность одного конкретного события, и вы можете использовать уравнение
P ( X ) = вероятность того, что произойдет X = количество исходов, при которых произойдет X , общее количество возможных исходов
Вы можете использовать комбинаторику, чтобы вычислить «общее количество возможных исходов».
Вот пример:
Четверо детей, которых зовут А, В, С и D, произвольно сидят на четырех стульях. Какова вероятность того, что А сядет на первый стул?
Мы уже показали, что всего есть 24 способа сесть на четыре стула. Если вы вернетесь к нашему решению, вы также обнаружите, что А сидит на первом стуле в шести случаях. Поэтому
P (A сидит на первом стуле) = количество исходов, где A сидит на первом стуле, общее количество возможных исходов = 624 = 14,
Этот ответ был ожидаем, так как каждый из четырех детей с равной вероятностью сядет на первый стул. Но в других случаях все не так однозначно…
Упражнения
Решения
(a) Почтальон должен доставить четыре письма в четыре разных дома на улице. К сожалению, дождь стер адреса, поэтому он просто раздает их случайным образом, по одной букве на дом. Какова вероятность того, что каждый дом получит нужную букву? (☆ Какова вероятность того, что каждый дом получит неправильную букву?)
(b) В лотерее нужно угадать 6 номеров из 49.