Программа кружка «Учимся решать комбинаторные задачи.» 1 класс Истомина Н.Б. | Материал (1 класс) на тему:
РЕШЕНИЕ КОМБИНАТОРНЫХ ЗАДАЧ
Пояснительная записка
Рабочая программа учебного курса «Решение комбинаторных задач» для 1 класса составлена на основе федерального государственного образовательного стандарта, с учетом авторской программы по математике Н. Б. Истоминой и адаптирована к возможностям учащихся класса.
Основная цель программы — создать условия для формирования у учащихся приемов умственной деятельности (анализ, синтез, сравнение, абстрагирование), для развития произвольного внимания и образного мышления и для усвоения тех способов, которые входят в содержание программы по математике в начальной школе.
Задачи:
- прививать интерес к математике;
- расширять кругозор учащихся в различных областях элементарной математики;
- расширять математические знания в области однозначных чисел;
- учить применять математическую терминологию; делать доступные выводы и обобщения, обосновывать собственные мысли.

Общая характеристика учебного курса.
Комбинаторика – один из разделов дискретной математики, который приобрел большое значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике, кибернетике.
Элементы теории вероятностей, в частности элементы комбинаторики, на современном этапе являются составной частью всего курса математики, начиная с начальной школы.
Данная программа составлена в соответствии с логикой построения начального курса математики; результатами психологических и методических исследований, связанных с решением комбинаторных задач младшими школьниками; различными видами соединений (комбинаций), которые связаны с размещениями, перестановками, сочетаниями.
В практической деятельности человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Приходится выбирать из некоторого конечного множества совокупности объектов его подмножества, обладающие тем или иным свойством, подсчитывать, сколько различных комбинаций можно составить из конечного числа элементов, принадлежащих данной совокупности, располагать эти элементы в определенном порядке.
Приходится выбирать из некоторого конечного множества совокупности объектов его подмножества, обладающие тем или иным свойством, подсчитывать, сколько различных комбинаций можно составить из конечного числа элементов, принадлежащих данной совокупности, располагать эти элементы в определенном порядке.
С комбинаторными вычислениями приходится иметь дело представителям многих специальностей: прорабу при распределении между рабочими различных видов работ, диспетчеру при составлении графика движения. Завуч школы, составляя расписание учебных занятий, использует разные комбинации, шахматист из различных комбинаций выбирает наилучшую и т.д.
В этих задачах речь идет о тех или иных комбинациях. Решение большинства комбинаторных задач основано на двух основных законах комбинаторики, которые называют правилом суммы и правилом произведения.
Комбинаторные задачи учащиеся1-2 классов сначала решают способом перебора (хаотичного или системного), а затем с помощью таблиц. Эти способы не требуют введения в программное содержание начального курса математики новых понятий, то есть не перегружают младших школьников дополнительной информацией.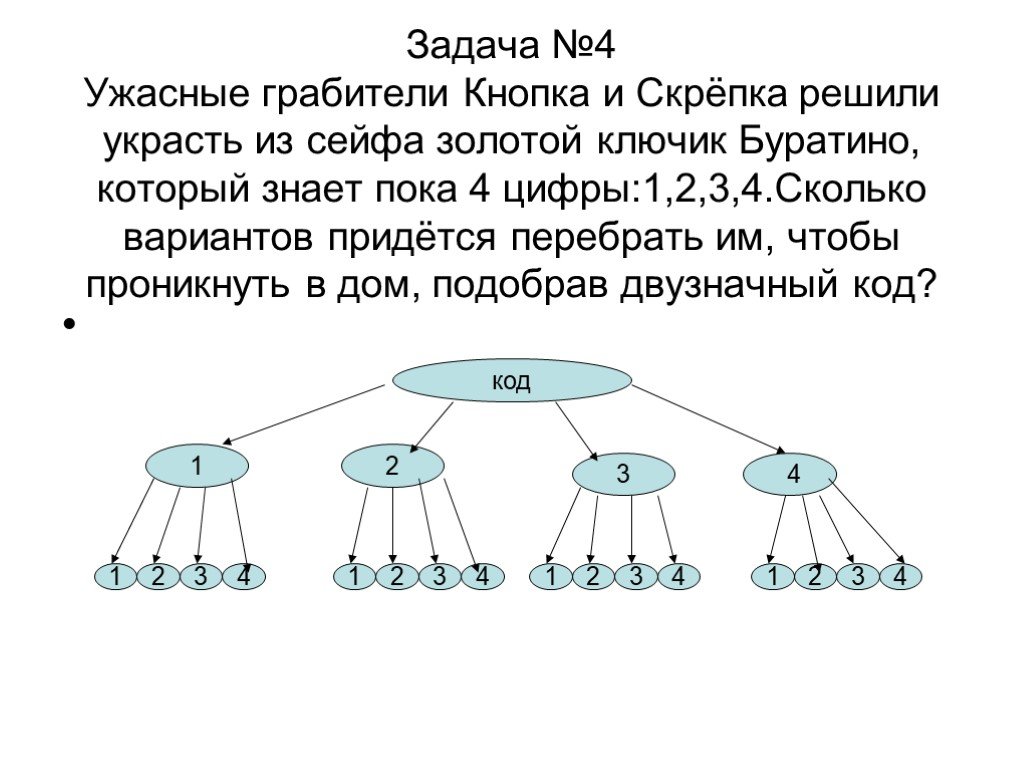 Термин «комбинаторные задачи» детям не разъясняется. Представление о содержании этого понятия сложится у них в процессе обучения.
Термин «комбинаторные задачи» детям не разъясняется. Представление о содержании этого понятия сложится у них в процессе обучения.
Не менее важным фактором реализации данной программы является и стремление развить у учащихся умения самостоятельно работать, думать, решать творческие задачи, а также совершенствовать навыки аргументации собственной позиции по определенному вопросу. Содержание программы соответствует познавательным возможностям младших школьников и предоставляет им возможность работать на уровне повышенных требований, развивая учебную мотивацию.
Ценностные ориентиры курса.
- Математика является важнейшим источником принципиальных идей для всех естественных наук и современных технологий, дальнейшего изучения данного предмета, для выявления и развития математических способностей учащихся и их способности к самообразованию.
- Математическое знание, в частности решение комбинаторных задач – это особый способ коммуникации:
- наличие знакового (символьного) языка для описания и анализа действительности;
- участие математического языка как своего рода «переводчика» в системе научных коммуникаций, в том числе между разными системами знаний;
- использование математического языка в качестве средства взаимопонимания людей с разным житейским, культурным, цивилизованным опытом.

Таким образом, в процессе обучения математике осуществляется приобщение подрастающего поколения к уникальной сфере интеллектуальной культуры.
- Овладение различными видами учебной деятельности в процессе обучения математике является основой изучения других учебных предметов, обеспечивая тем самым познание различных сторон окружающего мира.
- Успешное решение математических (логических и комбинаторных) задач оказывает влияние на эмоционально – волевую сферу личности учащихся, развивает их волю и настойчивость, умение преодолевать трудности, испытывать удовлетворение от результатов интеллектуального труда.
Место учебного предмета в учебном плане.
В учебном плане школы на изучение программы учебного курса в рамках кружка «Решение комбинаторных задач» в 1-4 классах отводится по 34 часа в год (1 час в неделю).
Планируемые результаты освоения программы.
Личностные результаты:
- Определять и высказывать под руководством педагога самые простые общие для всех людей правила поведения при сотрудничестве.

- В предложенных педагогом ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, при поддержке других участников группы и педагога.
Метапредметные результаты :
Регулятивные УУД:
- Определять и формулировать цель деятельности с помощью учителя.
- Проговаривать последовательность действий.
- Учиться высказывать своё предположение (версию) на основе работы с иллюстрацией рабочей тетради.
- Учиться работать по предложенному учителем плану.
- Учиться отличать верно выполненное задание от неверного.
- Учиться совместно с учителем и другими учениками давать эмоциональную оценку деятельности товарищей.
Познавательные УУД:
- Ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя.
- Делать предварительный отбор источников информации: ориентироваться в тетради.
- Добывать новые знания: находить ответы на вопросы, используя свой жизненный опыт и информацию, полученную от учителя.

- Перерабатывать полученную информацию: делать выводы в результате совместной работы всего класса.
- Преобразовывать информацию из одной формы в другую; находить и формулировать решение задачи с помощью простейших моделей (предметных, рисунков, схематических рисунков, схем).
- Использовать знаково-символические средства.
Коммуникативные УУД:
- Донести свою позицию до других: оформлять свою мысль в устной и письменной речи (на уровне одного предложения или небольшого текста).
- Слушать и понимать речь других.
- Учиться выполнять различные роли в группе (лидера, исполнителя).
Предметные результаты:
- описывать признаки предметов и узнавать предметы по их признакам;
- выделять существенные признаки предметов;
- сравнивать между собой предметы;
- обобщать, делать несложные выводы;
- классифицировать предметы;
- давать определения тем или иным понятиям;
- выявлять функциональные отношения между понятиями;
- владеть терминологией;
- выявлять закономерности и проводить аналогии.

- классифицировать числа по одному или нескольким основаниям, объяснять свои действия;
- распознавать одну и ту же информацию, представленную в разной форме — (таблицы, схемы).
Основное содержание курса «Решение комбинаторных задач» во втором классе (34 часа).
Развитие внимания.
Дорисуй, нарисуй, раскрась. Найди закономерность. Выбираем основание для классификации. Проверка результатов для классификации. Выбираем нужный ответ. Делим объекты на классы по заданному основанию.
Родовое и видовое отличие.
Развиваем наблюдательность. Родовое и видовое отличие. Задачи на смекалку. Сравнение.
Развитие памяти и воображения. связаны с размещениями, перестановками, сочетаниями.
Сравнение. Развиваем память и внимание. Вставь нужную букву, цифру. Развиваем воображение.
Комбинаторные задачи.
Выбор комбинаций. Решаем комбинаторные задачи. Развиваем логику мышления. Обобщаем изученное.
Тематическое планирование
№ | Тема | Кол-во часов | Дата | Характеристика деятельности учащихся |
1-2 | Дорисуй, нарисуй, раскрась | 2 | Учатся ориентироваться в тетради; описывать признаки предметов. Знать основные цвета. | |
3 | Развиваем внимание | 1 | ||
4 | Найди закономерность | 1 | Учатся отличать элемент объекта от целого; выделять существенные признаки объекта; определять и формулировать цель деятельности. Использовать знаково-символические средства. Оформлять свою мысль в устной речи. Делать выводы о результатах работы класса. | |
5 | Выбирать основание для классификации | 1 | ||
6-7 | Проверка результатов классификации | 2 | ||
8 | Выбираем нужный цвет | 1 | Уметь выбирать нужный цвет. Учатся классифицировать объекты по данным требованием. Делать выводы, оценивать свою работу и арботу одноклассников. Знать основные цвета | |
9-10 | Делим объекты на классы по заданному основанию | 2 | ||
11-12 | Развиваем наблюдательность | 2 | ||
13 | Задачи на раскрашивание | 1 | Учатся выбирать основание для классификации. Сравнивать, классифицировать объекты. Выявлять функциональные отношения между понятиями; находить и формулировать решение задачи с помощью простейших моделей. Выполнять простейшие рассуждения, используя информацию, данную на рисунке, схеме Преобразовывать информацию, данную в табличной форме в текстовую. | |
14 | Родовое и видовое отличие | 1 | ||
15-16 | Задачи на смекалку | 2 | ||
17-18 | Сравнение | 2 | ||
19-20 | Развиваем память и внимание | 2 | ||
21-22 | Вставь нужные буквы | 2 | ||
23-24 | Развиваем воображение | 2 | Уметь работать по предложенному учителем плану; преобразовывать информацию из одной формы в другую. | |
25-26 | Выбор комбинаций | 2 | ||
27-28 | Решаем комбинаторные задачи | 2 | ||
29-30 | Развиваем логику мышления | 2 | ||
31-32 | Обобщаем изученное | 2 | ||
33 | Чему мы научились | 1 |
Материально-техническое обеспечение учебного процесса.
- Н. Б. Истомина, Е. П. Виноградова. «Учимся решать комбинаторные задачи». Рабочая тетрадь 1-2 класс. Смоленск, из-во «Ассоциация XXI век», 2013г.
- Агаркова Н. В. Нескучная математика. 1 – 4 классы. Занимательная математика. Волгоград: «Учитель», 2007
- Агафонова И. Учимся думать. Занимательные логические задачи, тесты и упражнения для детей 8 – 11 лет. С. – Пб,1996
- Лавриненко Т. А. Задания развивающего характера по математике. Саратов: «Лицей», 2002
- Сухин И. Г. Занимательные материалы. М.: «Вако», 2004
- Шкляров Т. В. Как научить вашего ребёнка решать задачи. М.: «Грамотей», 2004
- Узорова О. В., Нефёдова Е. А. «Вся математика с контрольными вопросами и великолепными игровыми задачами. 1 – 4 классы. М., 2004
Комбинаторные задачи по математике для 3 класса.
Задачи по математике 3 класс
MAT-ZADACHI.RU
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна.
 Часть 2
Часть 2 - Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты. 3 класс.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
Задача 1
- 1) Впиши в квадраты недостающие цифры от 1 до 9, чтобы получились законченные выражения.

- 2) Впиши недостающие цифры от 0 до 20.
Решение:
- 1)
- 2)
Задача 2
Составь замкнутые цепочки, впиши нужные числа от 0 до 20. Найди ключевые числа.
Решение:
Задача 3
- Расставь указанные цифры внутри пустых кружков в звездах так, чтобы при сложении на каждой прямой линии получалась указанная сумма.
Решение:
На странице использован материал из книги «Примеры по математике. Счет в пределах 1000. Первый уровень сложности.». Автор О. В. Узорова и Е. А. Нефедова.
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
[PDF] Комбинаторика и развитие комбинаторного мышления у детей.

- title={Комбинаторика и развитие детского комбинаторного мышления},
автор = {Лин Д. Инглиш},
год = {2005}
}
- Лин Д. Инглиш
- Опубликовано в 2005 г.
- Образование
Эта глава начинается с изучения некоторых элементарных идей комбинаторики и того, как они способствуют развитию у детей начальных представлений о вероятности и навыков решения задач. Затем рассматриваются различные типы комбинаторных задач и соответствующие трудности, которые они представляют для детей. Обзор исследований, посвященных комбинаторному мышлению детей, представлен во второй половине главы. Глава завершается рассмотрением способов увеличения числа детей…
View Via Publisher
Web.Archive.org, поддерживающие маленьких детей для разработки комбинаторных рассуждений
- Люсия Zapata-Cardona
Психология
- 2018
Цель этой главы.
 с комбинаторными задачами и представить некоторые стратегии учителей для поддержки детского комбинаторного мышления. The…
с комбинаторными задачами и представить некоторые стратегии учителей для поддержки детского комбинаторного мышления. The…Предположение и доказательство как подход к активному мышлению и обсуждению со сверстниками в комбинаторном классе
- Yun Chen, Yi-Chi Chang
Образование
- 2015
Введение и цели Преподавание и обучение комбинаторике Хотя комбинаторика играет важную роль в изучении вероятностей, для многих студентов и учителей комбинаторика не более чем …
Детская конструкция мультипликативного принципа в комбинаторном мышлении
- Ронначай Панапой
Образование
- 2013
Принцип умножения, один из фундаментальных принципов счета, играет решающую роль в изучении комбинаторики. Целью данного исследования было исследование операций, схем и…
Процессы комбинаторного мышления учащихся при решении математических задач
Комбинаторное мышление – это способ мышления при решении комбинаторных задач.
 Комбинационные задачи – одна из самых сложных задач для решения учащимися. Это исследование направлено на анализ…
Комбинационные задачи – одна из самых сложных задач для решения учащимися. Это исследование направлено на анализ…Перечисление всех возможных результатов: анализ работы учащихся
- A. Savard, L. DeBlois
Образование
- 2013
Разнообразие контекстов в изучении теории вероятностей может предоставить учащимся возможности для изучения разума в условиях неопределенности. Такого рода рассуждения могут помочь учащимся развить критическое мышление…
Комбинаторная и пропорциональная задача: поиск интуитивных стратегий в начальном образовании
- Мария Рикарт, Ассумпта Эстрада
Образование
Математика
- 2022
Развитие вероятностного мышления в школе требует развития комбинаторного и пропорционального мышления. По этой причине 190 учащихся шестых классов начальной школы (11–12 лет) без…
СПОСОБНОСТИ ДЕТЕЙ ДОМАШНЕГО САДА В РЕШЕНИИ КОМБИНАТОРНЫХ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ КОМПЬЮТЕРНЫХ МИКРОМИРОВ И МАНИПУЛЯТИВОВ
- Г.
 Фессакис, С. Кафусси
Фессакис, С. Кафусси Психология
- 2009
Изучение возможностей детей дошкольного возраста при решении задач на получение комбинаций одного или двух из набора четырех предметов с повторением для понимания влияния особенностей микромира на их выполнение .
Исследование мышления учащихся при ознакомлении с формальной теорией комбинаторики в 12 классе
- Томас Перрин
Образование
- 2006
Это исследование изучает математическое мышление учащихся при знакомстве с формальной теорией комбинаторики. Он определяет, как учащиеся понимают формальную теорию и модифицируют свое математическое мышление и…
Роль и связь между систематизацией и представлением при работе маленьких детей над комбинаторной задачей
РЕФЕРАТ Эта статья посвящена систематизации и представлению, которые маленькие дети спонтанно используют, работают над комбинаторной задачей.
 В этой статье документы от 123 детей…
В этой статье документы от 123 детей…Классификация стратегий, используемых старшеклассниками в изоморфных комбинаторных задачах
Комбинаторика играет важную роль в школьной математике. Эта тема неоднократно упоминалась в литературе по математическому образованию (Fischbein & Gazit, 1988; English, 2005; Lesh & Heger, 2001; Muter…
ПОКАЗЫВАЕТСЯ 1–10 ИЗ 51 ССЫЛОК
- Lyn D. English
Образование, психология
- 1991
Детям в возрасте от 4 лет 6 месяцев до 9 лет 10 месяцев индивидуально давалась серия новых заданий, включающих формирование различных комбинаций двух элементов, выбранных из …
Влияние имплицитной комбинаторной модели на комбинаторное мышление учащихся средней школы
- К. Батанеро, Вирджиния Наварро-Пелайо, Дж. Годино
Образование
- 1997
Элементарные комбинаторные задачи можно разделить на три различные комбинаторные модели (выбор, разделение и распределение).
 Основная цель данного исследования состояла в том, чтобы определить влияние…
Основная цель данного исследования состояла в том, чтобы определить влияние…Детские стратегии решения двумерных и трехмерных комбинаторных задач.
- Lyn D. English
Психология
- 1993
В исследовании изучались стратегии, которые дети в возрасте от 7 до 12 лет спонтанно применяют для решения новых комбинаторных задач. Детям индивидуально вводили набор из шести…
Развитие рекурсивного мышления в комбинаторике с использованием манипулятивных и вычислительных технологий.
- С. Абрамович, А. Пипер
Образование
- 1996
Энн Пипер в настоящее время преподает геометрию в средней школе Вестминстерских школ в Атланте, штат Джорджия. Недавно она окончила Университет Джорджии со степенью магистра математического образования. Текущий…
Рискованная стратегия, чтобы получить M & Ms
- S. Nisbet, Graham A. Jones, C.A. Thornton, C. Langrall
Социология
- 2000
Понимание и анализ эпизода обучения, в котором двое детей 4-х лет взаимодействуют друг с другом и учителем во время игры.
 вероятностная игра с участием шоколада M и Ms — это…
вероятностная игра с участием шоколада M и Ms — это…Возможности обработки информации и проблема горизонтального декаляжа: демонстрация с использованием комбинаторных логических задач.
- М. Скардамалия
Психология
- 1977
СКАРДАМАЛИЯ, МАРЛЕН. Способность обработки информации и проблема горизонтального декаляжа: демонстрация с использованием задач комбинаторного мышления. РАЗВИТИЕ ДЕТЕЙ, 1977, 48, 28-37. Сила…
Вероятностное мышление учащихся в процессе обучения.
- Graham A. Jones, C. Langrall, C.A. Thornton, A.T. Mogill
Education
- 1999
В этом исследовании мы оценили мышление учащихся 3-го класса в отношении учебной программы. Учебная программа была основана на исследовательской структуре, которая включала…
Анализ арифметики для преподавания математики
- Г. Лейнхардт, Ральф Т. Патнэм, Розмари А. Хаттруп
Образование
- 1992
Содержание Предисловие Дж.
 Т. Соудер, Осмысление чисел в школьной математике. К.С. Фьюсон, Исследования по обучению и обучению сложению и вычитанию целых чисел. P. Nesher, Solving…
Т. Соудер, Осмысление чисел в школьной математике. К.С. Фьюсон, Исследования по обучению и обучению сложению и вычитанию целых чисел. P. Nesher, Solving…Комбинаторная математика: практические исследования
- Bharath Sriraman, Lyn D. English
Математика
- 2004
В этой статье мы представляем последствия и предложения по использованию комбинаторной математики в классе посредством обзора и синтеза многочисленных исследований. Последствия этих…
Мышление и письмо студентов в контексте вероятности
- Тодд М. Джонсон, Грэм А. Джонс, К. А. Торнтон, К. Ланграл, Эми Роус
Образование, психология
- 1998
В ответ на потребность в исследованиях, посвященных обучению и письму по математике, в этом исследовании изучались изменения в вероятностном мышлении и письме учащихся во время учебной программы, которая…
Улучшение комбинаторных действий у детей 9 лет
Целью исследования было определение условий совершенствования комбинаторных действий у детей 9 лет (учащиеся 3 класса 9 лет начальной школы).
 Оригинальная образовательная программа «Комбинация-2» может стать условием совершенствования комбинаторных действий. Предполагалось создать такие условия. Программа включает 30 видов нестандартных заданий внеклассного содержания. Каждый тип задач имел три структурных варианта задач: найти ответ, найти вопрос и найти часть начальных условий. Решение этих задач требует комбинаторных действий. Контрольную группу составили 91 ребенок, экспериментальная группа — 96 человек. Эти дети приняли участие в 30 групповых занятиях по 30 недель (еженедельно, с сентября по май). Исследование показало, что занятия «Комбинация-2» способствуют совершенствованию комбинаторных действий у детей. В дальнейших исследованиях планируется определить, насколько программа «Комбинация-2» способствует совершенствованию комбинаторных действий у детей 10 лет.
Оригинальная образовательная программа «Комбинация-2» может стать условием совершенствования комбинаторных действий. Предполагалось создать такие условия. Программа включает 30 видов нестандартных заданий внеклассного содержания. Каждый тип задач имел три структурных варианта задач: найти ответ, найти вопрос и найти часть начальных условий. Решение этих задач требует комбинаторных действий. Контрольную группу составили 91 ребенок, экспериментальная группа — 96 человек. Эти дети приняли участие в 30 групповых занятиях по 30 недель (еженедельно, с сентября по май). Исследование показало, что занятия «Комбинация-2» способствуют совершенствованию комбинаторных действий у детей. В дальнейших исследованиях планируется определить, насколько программа «Комбинация-2» способствует совершенствованию комбинаторных действий у детей 10 лет.Там Метин
___
- Бржеховский, Й., Пржигонская, Й. (2017). Комбинаторные задачи по математике для начальной школы. 16-й
Конференция прикладной математики.
 Applimat. Журнал прикладной математики и инженерии,
206-214.
Applimat. Журнал прикладной математики и инженерии,
206-214. - Бржеховский, Й., Пржигонска, Й. (2018). Умение учащихся начальных классов решать комбинаторные задачи. В 17-я конференция по прикладной математике. Источник: Аплимат (стр. 127-136). 13 сентября 2019 г. полученное из http://evlm.stuba.sk/APLIMAT2018/proceedings/Papers/0127_Brehovsky_Prihonska.pdf
- Давыдов В. В. (2008). Лекции по общей психологии. Москва: Академия.
- Айзенберг М.М. и Заславский О. (2003). Совместное решение задач в комбинаторике: взаимосвязь между процессами управления и успешными решениями. Журнал математических Поведение, 22(4), 389-403. https://doi.org/10.1016/j.jmathb.2003.09.001
- English, LD (1991). Комбинаторные стратегии детей младшего возраста. Педагогические занятия по математике, 22(5), 451-474. https://doi.org/10.1007/BF00367908
- English, LD (1993). Детские стратегии решения двух- и трехмерных комбинаторных задач.
Журнал исследований в области математического образования, 255-273.
 https://doi.org/10.2307/749347
https://doi.org/10.2307/749347 - English, LD (2005). Комбинаторика и развитие детского комбинаторного мышления. В Изучение вероятности в школе (стр. 121-141). Спрингер, Бостон, Массачусетс. https://doi.org/10.1007/0- 387-24530-8_6
- Фишбейн, Э., и Гроссман, А. (1997). Схемы и интуиции в комбинаторных рассуждениях. Образовательный исследования по математике, 34 (1), 27-47.
- Герцог, М., Элерт, А., и Фриц, А. (2017). Kombinatorikaufgaben в der dritten Grundschulklasse. Журнал für Mathematik-Didaktik, 38(2), 263-289. https://doi.org/10.1007/s13138-017-0118-8
- Hidayati, YM, Sa’dijah, C., & Qohar, SA (2019). Комбинаторное мышление для решения проблем Комбинаторика в типе выбора. Международный журнал обучения, преподавания и образования Исследования, 18 (2). https://doi.org/10.26803/ijlter.18.2.5
- Хёвелер, К. (2016). Детские комбинаторные стратегии счета и их связь с математическими
Принципы счета. In Makalah disajikan dalam 13-й Международный математический конгресс
Образование Гамбург (стр.
 231-245). Дортмунд: ТУ Дортмунд. 1 сентября 2019 г. получено из
https://www.mathematik.tu-dortmund.de/sites/karinahoeveler/download/TSG17_PA_Hoeveler.pdf
231-245). Дортмунд: ТУ Дортмунд. 1 сентября 2019 г. получено из
https://www.mathematik.tu-dortmund.de/sites/karinahoeveler/download/TSG17_PA_Hoeveler.pdf - Хёвелер, К. (2017). Детские комбинаторные стратегии счета и их связь с обычными математические принципы счета. В Преподавании и изучении дискретной математики по всему миру: Учебный план и исследования (стр. 81–9).2). Спрингер, Чам. https://doi.org/10.1007/978-3-319-70308-4_6
- Инхельдер, Б., и Пиаже, Дж. (1969). Психология ребенка. Нью-Йорк: Основные книги.
- Крекич-Пинтер, В., Иванович, Дж., Наместовский, Ж., и Майор, Л. (2015). Стратегия и методы решения Комбинаторные задачи в начальном обучении математике. Международный журнал модерна Образовательные исследования, 2(6), 77-87. 30 августа 2019 г. получено из http://article.aascit.org/file/pdf/9100785.pdf
- Крпец, Р. (2014). Развитие комбинаторных умений младших школьников через
Организация наборов элементов. ACTA MATHEM ATICA 17, 103. 9 сентября 2019 г.
 получено из
http://www.nmk.fpv.ukf.sk/2014/proceedings/13_krpec_fulltext.pdf
получено из
http://www.nmk.fpv.ukf.sk/2014/proceedings/13_krpec_fulltext.pdf - Maher C.A., Yankelewitz D. (2011). Представления как инструменты построения аргументов. В комбинаторике и Рассуждение. Представление, обоснование и построение изоморфизмов (стр. 17-25). Дордрехт, Спрингер Нидерланды. https://doi.org/10.1007/978-94-007-0615-6_3
- Палмер, Х., и ван Боммель, Дж. (2016). Изучение роли представлений, когда маленькие дети решают задачу. комбинаторная задача. ИКТ в математическом образовании: будущее и реалии, 47. 08 сентября 2019 г. получено из http://ncm.gu.se/media/smdf/Published/No11_Madif10/047056_madif_001_palmer.pdf
- Палмер, Х., и ван Боммель, Дж. (2018). Роль и связь между систематизацией и представление, когда маленькие дети работают над комбинаторной задачей. Европейское раннее детство Журнал исследований в области образования, 26 (4), 562–573
- Поддьяков А. Н. (2011). Многовариантные объекты для стимуляции комбинаторной деятельности детей раннего возраста.
 Экспериментирование и причинно-экспериментальное мышление. Психология в России, 4, 397.
https://doi.org/10.11621/pir.2011.0027
Экспериментирование и причинно-экспериментальное мышление. Психология в России, 4, 397.
https://doi.org/10.11621/pir.2011.0027 - Темникова М. (2018). Комбинаторные математические задачи в обучении по математике для 1-4 классов. Европейский научный журнал, 2, 46-55. https://doi.org/10.19044/esj.2018.c5p18
- Ван Боммель, Дж., и Палмер, Х. (2017). Бумага или цифра: Исследование по комбинаторике в дошкольном классе. В NORMA17 Восьмая Северная конференция по математическому образованию, Стокгольм, 30 мая – 2 июня 2017 г. Svensk forskning forskning-SMDF. 13 сентября 2019 г.полученное из http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1181427&dswid=7604
- Ван Боммель, Дж., и Палмер, Х. (2018). Развивать у детей понимание комбинаторной задачи. используя дуэт цифровых и физических артефактов. Ранние годы, 1-14 лет. https://doi.org/10.1080/09575146.2018.1501553
- Уайт, Х. (1984). Развитие комбинаторного мышления: роль когнитивных способностей. Журнал
генетической психологии, 145(2), 185-193.
 https://doi.org/10.1080/00221325.1984.10532266
https://doi.org/10.1080/00221325.1984.10532266 - Зак А. (2004). Мышление младшего школьника. св. Петербург: содействие.
- Зак А. (2016). Развитие авторского мышления у младших школьников. мышления младших школьников]. Москва: Библио-Глобус.
___
АПА ЗАК А (2020). Совершенствование комбинаторных действий у детей 9 лет. İlköğretim Online (электроника), 19(1), 324 — 332. 10.17051/ilkonline.2020.644570 Чикаго Зак Анатолий Совершенствование комбинаторных действий у детей 9 лет. İlköğretim Online (elektronik) 19, №1 (2020): 324 — 332. 10.17051/ilkonline.2020.644570 MLA ZAK Анатолий Совершенствование комбинаторных действий у детей 9 лет. İlköğretim Online (электроника), том 19, № 1, 2020, сс.0345 ЗАК А Совершенствование комбинаторных действий у детей 9 лет.  İlköğretim Online (электронный). 2020; 19(1): 324 — 332. 10.17051/ilkonline.2020.644570
İlköğretim Online (электронный). 2020; 19(1): 324 — 332. 10.17051/ilkonline.2020.644570Ванкувер ЗАК А Совершенствование комбинаторных действий у детей 9 лет. İlköğretim Online (электронный). 2020; 19(1): 324 — 332. 10.17051/ilkonline.2020.644570 IEEE ЗАК А «Совершенствование комбинаторных действий у детей 9 лет». İlköğretim Online (электроника), 19, сс.324 — 332, 2020. 10.17051/ilkonline.2020.644570 ИСНАД ЗАК, Анатолий. «Совершенствование комбинаторных действий у детей 9 лет». İlköğretim Online (электроника) 19/1 (2020), 324-332. 13.3b 682
Саидаки Дигер Макалелер
Выводы из различных реализаций личностно-ориентированного подхода
Севинч ТУНАЛИ
Понимание учителями естественных наук средней школы природы науки: исследование методом q
Гюнкут МЕШИ, Уильям В.





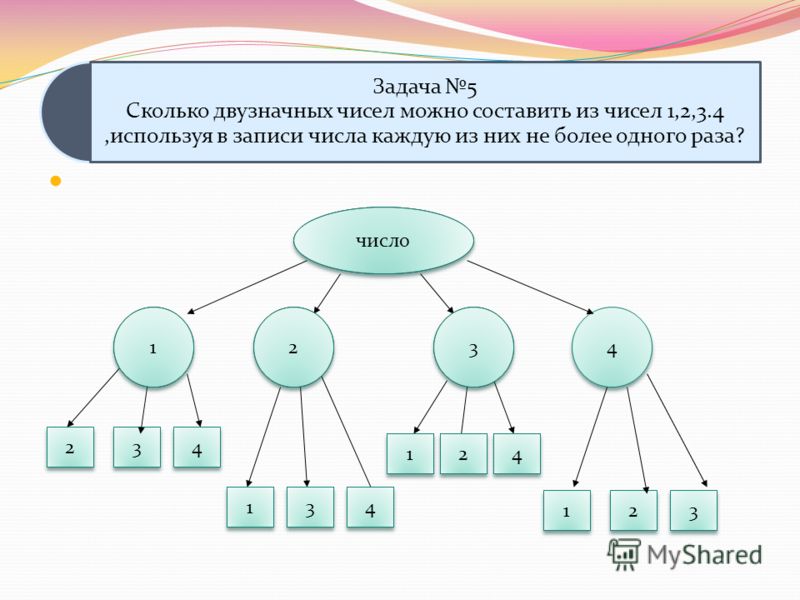


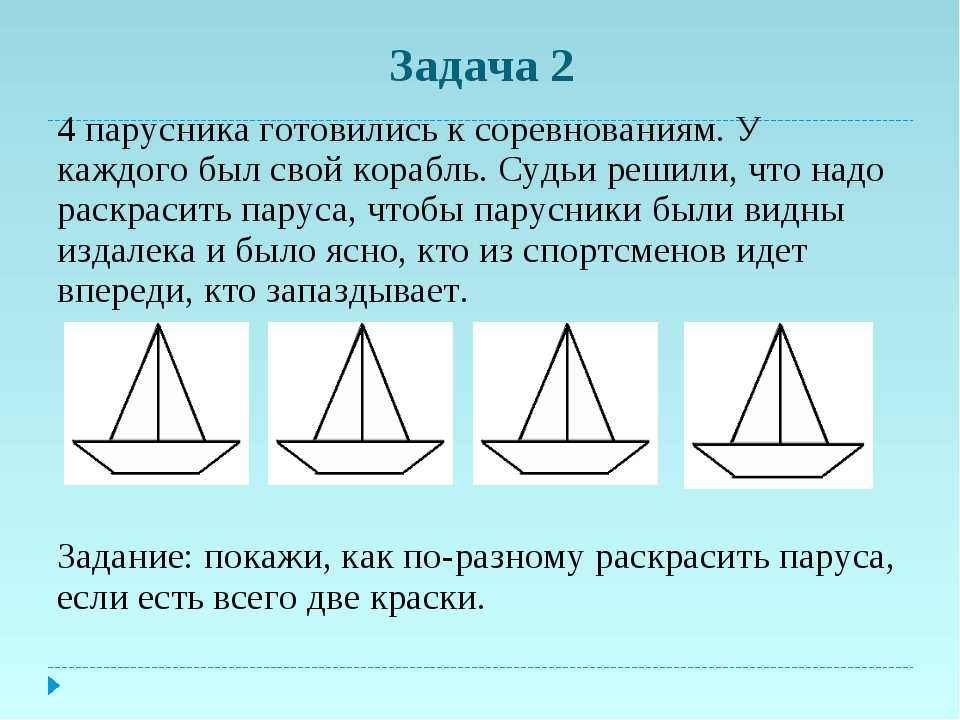
 Сравнивать, классифицировать объекты. Оформлять свою мысль в устной и письменной речи. Делать выводы о результатах работы класса.
Сравнивать, классифицировать объекты. Оформлять свою мысль в устной и письменной речи. Делать выводы о результатах работы класса. Часть 2
Часть 2