Комбинаторные задачи в начальной школе: Решение комбинаторных задач в начальной школе

Решение комбинаторных задач в начальной школе

Решение комбинаторных задач в начальной школе

 

Комбинаторика – раздел дискретной математики, изучающий всевозможные сочетания и расположения предметов.

 

Цели:         1. Понимание того, что в задаче на перебор вариантов целесообразно следовать логике перебора, а не хаотично.

                   2. Познакомить с инструментом перебора вариантов, деревом возможности.

                   3. Развивать вариативное мышление.

                   4. Закреплять вычислительные навыки.

 

Процесс обучения школьников решению комбинаторных задач таит в себе большие развивающие возможности: на их основе совершенствуются приемы умственной деятельности, формируется важная для человека способность комбинировать, определяющая развитие комбинаторного мышления. Комбинаторное мышление, тесно связанное со становлением умственных операций и представляющее собой активизацию мыслительной деятельности « в направлении поиска тех или иных преобразований» (О.

С.Медведева), в свою очередь, взаимосвязано с теоретическим мышлением, считающимся основным «новообразованием» младшего школьного возраста  (Л.С.Выготский, В.В.Давыдов).

 

Подготовительный период

(свойства предметов, отношения).

 

1. Следы от НЛО. Витя и Вика обнаружили в поле странные следы. Они сразу догадались. Что ночью здесь приземлились НЛО. Но дети поспорили: с одной планеты прилетели НЛО или с разных? Разрешите спор Вити и Вики. (Рис. 1)

Чтобы помочь ученикам справиться с заданием, проводится беседа:

— Что надо определить, чтобы ответить на вопрос задания? (Одинаковые следы или разные)

— Как вы считаете? Ваши предложения? Чем они похожи? (По 4 кружка 4 цветов)

— Но чем же все-таки различаются следы? (Кружки строятся в разном порядке)

Учитель предлагает проследить, как «путешествуют» кружки одного цвета в следах. Ученики приходят к выводу, что если последовательно поворачивать «следы» по кругу, то получится один и тот же рисунок.

При обнаружении этой ситуации ученики сравнивают, обобщают, анализируют и устанавливают отношения между предметами.

 

2. «Парусники». 4 парусника готовились к соревнованиям. У каждого спортсмена был свой белый корабль. Судьи решили, что надо раскрасить паруса, чтобы парусники были видны издалека, и было ясно, кто из спортсменов идет впереди, кто запаздывает. Покажите, кА по-разному раскрасили паруса, если были всего 2 краски. (Рис.2.)

Основная трудность, которая возникает у школьников при раскрашивании – это догадаться, что весь парус можно закрасить одним цветом. В этой ситуации можно задать вопрос: «Обязательно каждый парус надо закрасить двумя красками? Как еще по-другому можно закрасить оставшиеся?» (Рис.3).

 

Перестановка из двух элементов.

 

          Далее идет работа над понятиями «выше», «ниже», «наверху», «внизу», «слева», «справа» и вводится понятие перестановки. Учитель сообщает, что порядок расположения предметов называется перестановка. Сначала переставляются 2 элемента. (Рис.4)

Дети делают вывод, что существует 2 способа расположения предметов.

 

Перестановка из трех элементов по два.

 

Теперь ученики при выполнении другого задания смогут сразу определить число комбинаций, если они будут составлены без повторений из трех элементов по два.

Из трех букв А, У, Х можно составить 6 слогов, где слог состоит из двух букв, буквы не повторяются

 

         АУ             УА             ХА

         АХ             УХ             ХУ

 

Перестановки из трех элементов.

 

Далее ребятам предлагается игра «Электричка». Сначала 2, а потом 3 девочки меняются местами.

 

         ТК              \\       ТКЛ           КТЛ           ЛКТ

         КТ              \\       ТЛК           КЛТ           ЛТК

 

Деи проговаривают алгоритм получения новых перестановок: один элемент фиксируется, а два других переставляются.

На 13-м уроке рассматривается перестановка 3-х элементов, здесь есть подсказка, и дети её замечают. Один цвет фиксируется 2 раза наверху, остальные дети меняют. (Рис.5)

Учитель предлагает учащимся определить

— какой прямоугольник расположен выше красного?

— ниже красного?

— какой ниже синего, но выше красного?

— как изменить расположение прямоугольников, чтобы красный находился ниже синего, но выше зеленого?

Такая же работа проводится над всеми столбиками, кроме последнего.

— Можно ли раскрасить последний столбик как-нибудь по другому?

Ребята вспоминают и закрепляют алгоритм перестановки.

В последующих заданиях дети самостоятельно разукрашивают 2,3,4,5 столбиков. А потом – С\Р над всем заданием. Игры: «Светофор», «Поясок», «Бусинки».

«Картины»

Художник написал 3 картины и сделал для них рамки. (Рис. 6)

Помоги ему найти лучший способ расположения картин на стене.

 

Состав числа в пределах 10.

Смысл действий сложения и вычитания.

 

Большинство задач этого этапа основывается на знании состава однозначного числа – на умении представить число разными способами в виде суммы других чисел, причем соблюдается принцип перевода предметных действий на язык математических символов и наоборот.

1. «Чашки». Помоги расставить 5 чашек на 3 полки разными способами так, чтобы на каждой полке стояли чашки.

 

                   1 2 2                     1+2+2

                   2 1 2                     2+1+2

                   2 2 1                     2+2+1

 

                   3 1 1                     3+1+1

                   1 3 1                     1+3+1

                   1 1 3                     1+1+3

 

Вывод: от перестановки слагаемых сумма не меняется.

 

2. Запиши значения выражений 2+1, 3-1, 3-2.

Какие цифры использованы для записи чисел? Запиши все возможные перестановки этих цифр, без повторов. Подчеркни ту запись, которая обозначает отрезок чисел, стоящих по порядку, в обратном порядке.

 

         3 2 1                     2 1 3                     1 2 3

         3 1 2                     2 3 1                     1 3 2

 

3. Состав чисел в пределах 20.

а) составь все возможные суммы из двух чисел, используя лишь числа 5,6,7 (порядок слагаемых не принимается во внимание)

 

5 + 5, 5 + 6, 5 + 7, 6 + 6, 6 + 5, 6 + 7, 7 + 5, 7 + 6, 7 + 7

 

б) составь все возможные разности из этих же чисел.

 

         6 – 6, 6 – 5,          7 – 7, 7 – 6, 7 – 5,          5 – 5

 

                   Перестановки из 4,5,6… элементов

 

Во 2 классе рассматриваются случаи перестановки 4,5,6 элементов, где первые 1,2,3 соответственно элементы фиксируются, а остальные 3 переставляются:

«Раскрась флаги».

Задача учителя показать и познакомить детей с эффективными инструментами систематического перебора – таблицами и графами. Эта работа поможет создать мотивацию для изучения дерева возможностей.

 

                   з  з \\    к  к  к

з  к \\

з  к  к к  з  к к  к  з

к  з\\

з  к  к к  з  к к  к  з

к  к\\

з  з  к з  к  з к  з  з

 

Двузначные и трехзначные числа.

 

1.Запишите числа: 22,24,26,   42,44,46,   62,64,66.

По какому правилу все эти числа собраны в одну группу? По каким признакам можно разбить эти числа на две группы?

— в записи чисел 22,24,26 использованы цифры 2,3,6

— в этих числах по 2 дес. , в записи каждого числа цифра 2

— в записи чисел 42,44,46 использованы цифры 2,4,6

— в этих числах по 4 дес., в записи каждого числа цифра 4

— в записи чисел 62.64,66 использованы цифры 2,4,6

— в этих числах по 6 дес., в записи каждого числа цифра 6

— Итак, по какому правилу записали все числа?

В записи двузначных чисел использовали цифры 2,4,6.

— На какие две группы разбиваются эти числа?

22,44,66 – записи использована одна цифра

24,26,42,46,62,64 – в записи разные цифры.

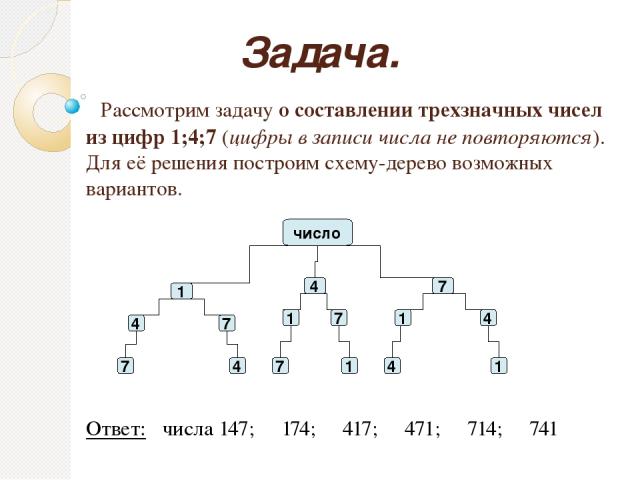
2. Какие трехзначные числа можно составить из цифр 7,0,9, если

а) цифры в записи числа не повторяются?

                            7  0  9                   9  0  7

                            7  9  0                   9  7  0

4 перестановки, т.к. трехзначное число не может начинаться с 0.

         Дети должны усвоить мысль о том. Что перебор вариантов выгодно осуществлять в определенном порядке. Каждую цифру надо фиксировать  по очереди в разряде сотен.

б) цифры в записи числа могут повторяться?

«7»             «9»             «7 и 0»                «7 и 9»                 «9 и 0» \\ 9,7,0

                                                                    9 и 7

777             999                770                     779                        990

                                         707                     797                        909

                                         700                     799                        900

                                                                    977

                                                                    997

                                                                    979

— найди наименьшее трехзначное число

— подчеркни наибольшее трехзначное число

— найди число, в котором: 70 дес. 7 ед.,  7 дес. 99 ед..

— какое число подходит к схеме

                             ?

·        * * * + * = * * *

          Итак, при выполнении только одного задания задействуется весь комплекс мыслительных операций.

         Кроме того, в процессе выполнения этого задания школьники повторяют устную и письменную нумерацию, работают над их разрядным составом, обращают внимание на поместное значение цифр, постоянно различают понятия «число» и «цифра». Можно сделать вывод, что систематическое использование комбинаторных задач при изучении тех или иных математических понятий одновременно будет способствовать реализации развивающих и образовательных функций курса «Математика в начальной школе».

 

Таблицы, графы. Дерево возможностей.

 

1. Три поросенка Ниф-Ниф, Нуф-Нуф и Наф-Наф решили построить себе домики. Выбрали три прекрасных места: у реки, на озере и на горе. Найди все возможные варианты их размещения с помощью таблицы. (Рис. 7)

2. Однажды встретились пятеро друзей. Каждый, здороваясь, пожал каждому руки. Сделай график и определи, сколько рукопожатий было сделано. (Рис.8)

3. Дерево возможностей — ветки растут и сверху и снизу. Дети являются творцами создания веточек у дерева. На их глазах точка превращается в дерево возможностей.

 

Сосчитай, сколько слов содержится в заклинании волшебника, если слова начинаются с букв Ш, Ц. Второй буквой могут быть О, И, Е. А оканчиваться слова могут буквами Р, К, Х. (Рис. 9)

 

                   ШОР                   ШИР                   ШЕР
                   ШОК                  ШИК                  ШЕК
                   ШОХ                  ШИХ                  ШЕХ

                   ЦОР                    ЦИР                    ЦЕР
                   ЦОК                    ЦИК                    ЦЕК
                   ЦОХ                    ЦИХ                    ЦЕХ

                   2 * 3 * 3 = 18 вариантов.

         Таким образом, при решении  комбинаторных задач активизируется мыслительная деятельность учащихся. Ученики, анализируя условие, выделяют определенные части, составляют нужные комбинации. Задействуется такая мыслительная операция, как анализ – процесс расчленения целого на части, выделения отдельных элементов в объекте. С другой стороны, в процессе синтеза, или соединения элементов, сторон объектов в целое, учащиеся определяют, что сначала можно составить определенную комбинацию.

На примерах хорошо видно, что при поиске ответа на поставленный вопрос ученики не смогут обойтись без наблюдения и сравнения.

Если младшие школьники не будут специально, с определенной целью воспринимать информацию, заключенную в задаче, то вряд ли смогут решить её. Сравнение – процесс выделения  признаков, свойств объектов и установления сходства и различия между ними – позволяет ученикам при составлении чисел избежать повторов. Составит все возможные числа на основе сходства и различия.

Систематическое использование комбинаторных задач в обучении – эффективно для формирования у учащихся базовых математических знаний, умений, навыков.

 

ЛИТЕРАТУРА:

1.     Е.Е.Белокурова «Обучение решению комбинаторных задач с помощью таблиц и граф».

2.     Л.Г.Петерсон «Математика 1,2,3 кл.».

3.      Л.Г.Петерсон «Методические рекомендации».

4.     С.В.Солнышко «Использование комбинаторных задач при обучении первоклассников математике».

 

 

Решение комбинаторных задач в начальной школе. | Методическая разработка (2, 3, 4 класс) на тему:

 «Комбинаторные задачи и способы их решения»

Проблема, над которой я работала в последние годы —  это «Комбинаторные задачи и способы их решения». Слайд 2            

Учитывая возрастные особенности младших школьников, комбинаторные задачи решаются бесформульным методом на основе рассуждений учащихся, составлением графов, размещением, таблиц, дерева решений.

Сегодня я попытаюсь показать, как можно решать комбинаторные задачи, имея минимум знаний по комбинаторике. Слайд 3

Что же такое комбинаторика?

Комбинаторика — это раздел  математики,  в котором    исследуются и

решаются задачи выбора элементов из   исходного множества и расположения   их   в некоторой комбинации, составляемой    по    заданным правилам.  Слайд 4  

Предлагаю вам следующую задачу, которая часто встречается в курсе математики начальной школы.

Из цифр 1,2,3,4,5,6 составить все возможные трехзначные числа.

Скажите, пожалуйста,  расположение цифр в записи числа будет играть  роль? Слайд 5

 При такой постановке вопроса мы должны рассмотреть случаи:

1) когда цифры в записи числа повторяются

2) когда цифры в записи числа не повторяются. Слайд  6

Рассмотрим первый случай, когда цифры повторяются.

Отметим место каждой цифры звездочкой. Сколько цифр претендует на первое место? На второе место? На третье?

6 х 6 х 6 =216         Слайд 7          

Рассмотрим второй случай, когда цифры не повторяются.    Слайд 8          

Отметим место каждой цифры звездочкой. Сколько цифр претендует на первое место? На второе место? На третье?

        6 х 5 х 4 =120      

Используя это условие задачи можно составить большое количество задач, изменяя формулировку вопроса: например составьте четное количество трехзначных чисел,  кратных 5, так чтобы цифры в записи числа не повторялись

        Таким образом, не меняя условия задачи, мы можем составлять большое количество задач с учетом того материала, который изучается на уроке.

 Такой вид комбинаторной задачи называется размещением.

        Следующим способом решение комбинаторных задач  бесформульным методом является таблица. Предлагаю решить следующую задачу.

   Для начинки пирогов бабушка решила смешать два продукта. Сколько различных пирогов может испечь бабушка, если для начинки у нее есть картофель, грибы,  яблоки, мясо.   Слайд 9        

Составим таблицу по строкам и столбцам распределим наши продукты. Теперь я прошу вас, не задумываясь о совместимости продуктов заполнить нашу таблицу. Слайд 10    

Рассмотрим получившуюся таблицу. Обратите внимание на диагональ. Слайд 11  

Здесь произошло объединение двух одинаковых продуктов. Что вы предлагаете? (Использовать можно, но конечный продукт не будет достигнут.)  Слайд 12  

Исключаем диагональ. Слайд 13  

Рассмотрим сочетание продуктов выше и ниже диагонали. Что вы можете сказать? (одинаковое сочетание)

Слайд 14  Исключим либо верхнюю, либо нижнюю часть.

• Сколько вариантов решений осталось 6. С математической точки зрения 6 вариантов являются решением, а если опираться на жизненный опыт, то понятно не все начинки могут быть использованы для пирога. Говорят о вкусах не спорят!

Когда нам необходимо составить комбинацию, в которой более двух элементов удобно пользоваться древом решений.

         Перечислите все возможные варианты обедов из трех блюд (одного первого, одного второго, одного третьего) В меню имеется два первых блюда – щи, борщ, три вторых – рыба, гуляш, плов два третьих – компот, чай.   Слайд 15  

Сколько всего вариантов у вас получилось? (12)

Как вы посчитали?

Слайд 16,  17, 18.

Итак, предлагаю решить следующую задачу:

« 5 финалистов конкурса «Учитель года», решили обменяться впечатлениями о конкурсе и позвонили между собой. Сколько звонков будет сделано?»   Слайд 19  — 26

Убедимся в истинности ваших суждений.

 Сколько звонков сделает 1 финалист?

Сколько звонков сделает 2 финалист?

Сколько звонков сделает 3 финалист?

Сколько звонков сделает 4 финалист?

Сколько звонков сделает 5 финалист?

Сколько звонков будет сделано?

Таким образом, решение непростой задачи свелось к тому, что появилась картинка, называемая графом и для того, чтобы ее решать достаточно пересчитать ребра графов.

Эту задачу можно решать и аналитическим способом. Давайте рассуждать

1 сделает 4 звонка

2 – 3 звонка,

3 -2 звонка, 4 – 1 звонок

        4+3+2+1= 10

А теперь сделаем итог:  на сколько, вы,  имея минимум знаний по комбинаторике, научились их решать:        

        Решите следующую задачу. Сколько существует вариантов размещения 5 финалистов конкурса «Учитель года» на три призовых. Слайд  27      

 (цифры в записи числа не повторяются)

 5х4х3х2х1=120   Слайд  28      

В начальном курсе математики рассматриваются только четыре вида комбинаций:

Размещение с повторением

                  Размещение без повторения

                  Сочетание

                  Перестановка                      Слайд  29        

Ни один из перечисленных видов не обременен формулой подсчета вариантов. Любую комбинаторную задачу можно решить путем рассуждений, что я вам  предложила.

Умение составлять комбинации по определенным признакам, классифицировать их лежит в основе разнообразнейших сфер человеческой деятельности. Поэтому вариативность – качество необходимое людям разных специальностей: учителю, составляющему расписание, конструктору программу, биологу ит.д. Вариативность играет важную роль в творчестве.

Я хочу закончить свое выступление словами Анри  Пуанкаре

знаменитого французского математика, философа:

 «Творчество, конечно, состоит не в том, чтобы составить бесконечные комбинации, а в том, чтобы создавать полезные, а таких не особенно много. Творить – это значит различать, выбирать» Слайд 30

«Комбинаторные задачи

и способы их решения»

учитель начальных классов

МКОУ «СОШ №3» ИМРСК

Колесникова Татьяна Николаевна

ноябрь 2015 год

Способы решения комбинаторных задач | Начальная школа

Автор: Вивдюк Мария Ананьевна

Организация: МАОУ СОШ №1 Им. М.А. Погодина

Населенный пункт: Мурманская область, г. Полярный

План-конспект дистанционного занятия с учащимися 4 класса в режиме реального времени с использованием функции демонстрации рабочего стола для просмотра презентации

Краткая аннотация

Ключевым направлением данного занятия является формирование математической компетентности учащихся как одной из тенденций формирования основ функциональной грамотности. Урок имеет коммуникативно-деятельностную направленность, способствует становлению у детей учебной самостоятельности, интереса к изучению математики. Содержание учебного материала способствует развития комбинаторного мышления, соответствует возрастным особенностям учащихся, принципам научности, доступности, связи с жизнью и практической направленности обучения. Урок спроектирован в соответствии с ФГОС НОО: применение диалоговых форм общения, эмоционального стимулирования и поощрения, наглядных пособий, осуществление обратной связи с помощью рефлексии. Создание благоприятной рабочей обстановки и психологического настроя способствуют повышению интереса учащихся к работе. Общение с детьми строится на принципах сотрудничества и взаимопонимания. Организация совместной деятельности способствуют осознанию общей цели, установлению коммуникации и взаимопонимания, взаимопомощи и сотрудничества посредством ведения диалога.

Предмет Математика Занятие по курсу внеурочной деятельности общеинтеллектуаль-ного направления «Решение комбинаторных задач»

Учитель Вивдюк Мария Ананьевна

Класс 4

Тема занятия «Способы решения комбинаторных задач».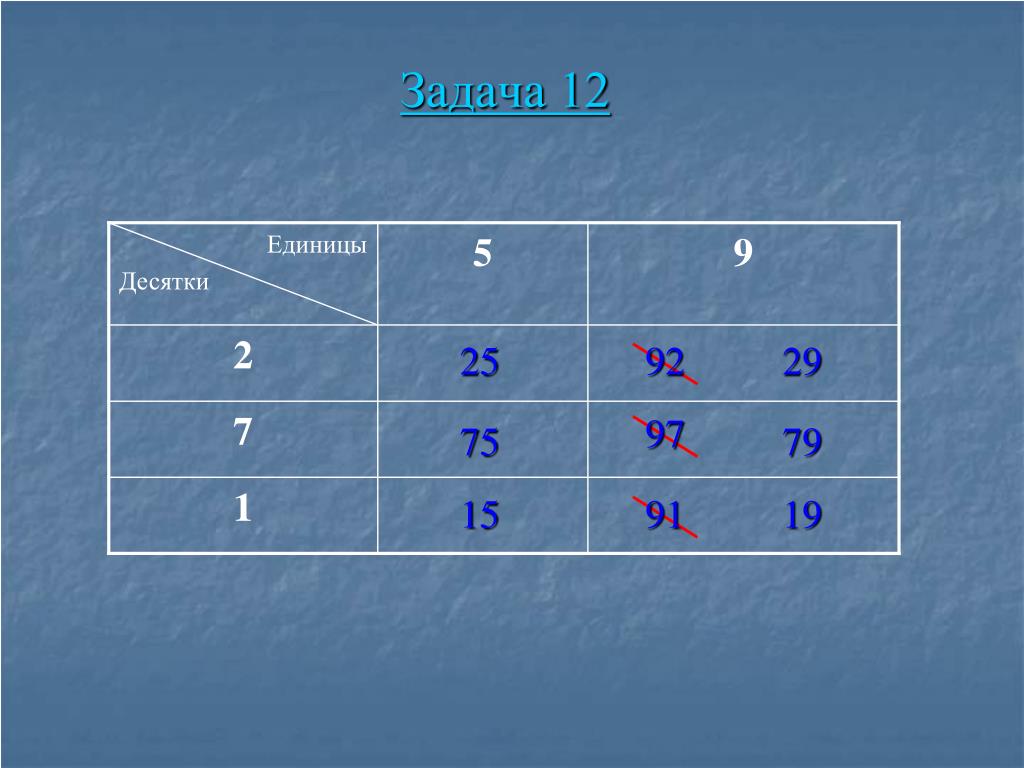

Тип занятия Открытия новых знаний

Цель Познакомить с понятием «комбинаторика», научить решать комбинаторные задачи, имея минимум знаний по комбинаторике, развивать умение сопоставить и сравнить факты, делать самостоятельные выводы, развивать творческую самостоятельность учащихся, сообразительность, любознательность, творческое мышление посредством решения нестандартных задач, формировать интерес к предмету; воспитание чувства ответвенности за результаты своей работы и учёбы, обеспечить формирование универсальных учебных действий.

Планируемые результаты

Предметные:

уметь решать простые комбинаторные.

Метапредметные:

Личностные: самоопределение, положительное отношение к учебной деятельности, высказывать свою точку зрения, смыслообразование, самооценка на основе критерия успешности, адекватное понимание причин успеха/неуспеха учебной деятельности.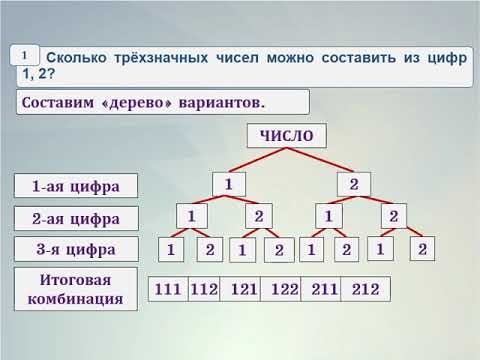

Познавательные: анализ объектов с целью выделения признаков, подведение под понятие, структурирование знаний, поиск необходимой информации, выдвижение гипотез, их обоснование, построение логической цепи рассуждения, осознанное и произвольное построения, понимание текстов, доказательство, речевого высказывания. обобщение, выполнение действий по плану, рефлексия способов и условий действий, контроль и оценка процесса и результатов деятельности.

Регулятивные:

фиксация затруднения, саморегуляция в ситуации затруднения, контроль способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона, планировать своё действие в соответствии с поставленной задачей и условия-ми её реализации, познавательная инициатива, волевая саморегуляция, контроль, коррекция, оценка.

Коммуникативные:

выражение своих мыслей, аргументация своего мнения, учет разных мнений, участие в диалоге, осознание ответственности за общее дело, самоопределение, использование критериев для обоснования своих суждений, выражение своих мыслей с достаточной точностью и полнотой, формирование своего мнения.

Техники и технологии

технология развивающего обучения «Технология деятельностного метода обучения», при которой ребенок не получает знания в готовом виде, а добывает их сам в процессе собственной учебно-познавательной деятельности;

технология на основе гуманно-личностной ориентации педагогического процесса «Педагогика сотрудничества». Данная технология реализует демократизм, равенство, партнёрство в субъектных отношениях педагога и ребёнка. Учитель и учащиеся совместно вырабатывают цели, содержание занятия, дают оценки, находясь в состоянии сотрудничества, сотворчества;

технология ведения проблемно-диалогического обучения, которая позволяет учащимся самостоятельно открывать знания;

«Технология применения информационно-компьютерных средств в предметном обучении», целью которой является формирование умений работать с информацией, развитие коммуникативных способностей, подготовка личности «информационного общества»

План-конспект дистанционного занятия

Тема: Способы решения комбинаторных задач.

Код доступа: https://cloud.mail.ru/public/c8HG/UcN7uSw9p

Цель: познакомить с понятием «комбинаторика», научить решать комбинаторные задачи, имея минимум знаний по комбинаторике, развивать умение сопоставить и сравнить факты, делать самостоятельные выводы, развивать творческую самостоятельность учащихся, сообразительность, любознательность, творческое мышление посредством решения нестандартных задач, формировать интерес к предмету; воспитание чувства ответственности за результаты своей работы и учёбы.

Оборудование: мультимедийная установка.

Время проведения занятия: 45 минут, во второй половине дня, во внеурочное время.

Количество учащихся: 10-16 человек.

Презентация к занятию: Код доступа: https://cloud.mail.ru/public/LFCh/BzFGXbqYs

Ход занятия

1. Организационный момент. Ознакомление с темой и целью занятия.

Учитель. Здравствуйте, ребята. Сегодня на занятии мы продолжим учиться решать комбинаторные задачи. Я попытаюсь показать вам, как можно решать комбинаторные задачи, имея минимум знаний по комбинаторике.

1. Понимание проблемной ситуации и осмысление проблемы.

Просмотр видеоурока. Код доступа: https://youtu.be/Q9pcmLfC2yI

(Сценарий видеоурока. Код доступа: https://cloud.mail.ru/public/MhEL/6gSv6unV6 )

Учитель. — Что же такое комбинаторика? Для чего она нужна нам?

Дети. Комбинаторика – это раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам. Решение комбинаторных задач не обременено формулой подсчета вариантов. Любую комбинаторную задачу можно решить путем рассуждений. Оказывается, что комбинаторика встречается часто в нашей жизни. Стоит обратить на это внимание. Можно провести исследования в этой области науки. Будет интересно.

1. Изучение нового материала. Решение задач.

Задача 1.

Из цифр 1,2,3,4,5,6 составить все возможные трехзначные числа.

Учитель. Предлагаю вам решить следующую задачу, которая часто встречается в курсе математики начальной школы.

Учитель. Скажите, пожалуйста, расположение цифр в записи числа будет играть роль? Дети. И да, и нет.

Учитель. При такой постановке вопроса мы должны рассмотреть случаи:

1) когда цифры в записи числа повторяются

2) когда цифры в записи числа не повторяются.

Рассмотрим первый случай, когда цифры повторяются.

Отметим место каждой цифры звездочкой.

1. Учитель. — Сколько цифр претендует на первое место?

Дети Шесть.

Учитель. — На второе место?

Дети Шесть.

Учитель. — На третье?

Дети Шесть.

Учитель. А теперь умножим количество цифр, которые претендуют на каждое из трёх мест.

6 х 6 х 6 =216

Учитель. Сколько можно составить трёхзначных чисел, когда в записи числа цифры повторяются?

Дети 216 цифр.

1. Учитель. Рассмотрим второй случай, когда цифры не повторяются.

Отметим место каждой цифры звездочкой.

Учитель. — Сколько цифр претендует на первое место?

Дети Шесть.

Учитель. — На второе место?

Дети Пять.

Учитель. — На третье?

Дети Четыре.

6 х 5 х 4 =120

Учитель. А теперь умножим количество цифр, которые претендуют на каждое из трёх мест.

— Сколько можно составить трёхзначных чисел, когда в записи числа цифры не повторяются?

Дети 120 цифр.

Учитель. Используя это условие задачи, можно составить большое количество задач, изменяя формулировку вопроса.

Дети составляют задачи.

Мини-вывод таким образом, не меняя условия задачи, мы можем составлять большое количество задач с учетом того материала, который изучается на уроке.

Такой вид комбинаторной задачи называется размещением.

Задача 2.

Для начинки пирогов бабушка решила смешать два продукта. Сколько различных пирогов может испечь бабушка, если для начинки у нее есть картофель, грибы, яблоки, мясо.

Учитель. Следующим способом решения комбинаторных задач является таблица. Предлагаю решить следующую задачу.

Составим таблицу по строкам и столбцам распределим наши продукты. Теперь я прошу вас, не задумываясь о совместимости продуктов заполнить нашу таблицу.

Рассмотрим получившуюся таблицу. Обратите внимание на диагональ.

Здесь произошло объединение двух одинаковых продуктов.

— Что вы предлагаете?

Дети. Использовать можно, но конечный продукт не будет достигнут.

Учитель Исключаем диагональ. Рассмотрим сочетание продуктов выше и ниже диагонали.

— Что вы можете сказать?

Дети Одинаковое сочетание продуктов.

Учитель. Исключим либо верхнюю, либо нижнюю часть.

— Сколько вариантов решений осталось

Дети 6.

Учитель. С математической точки зрения 6 вариантов являются решением, а если опираться на жизненный опыт, то понятно не все начинки могут быть использованы для пирога. Говорят, на вкус и цвет, товарищей нет.

Мини-вывод таким образом, комбинаторные задачи такого вида просто решаются с помощью таблицы.

Задача 3.

Перечислите все возможные варианты обедов из трех блюд (одного первого, одного второго, одного третьего). В меню имеется два первых блюда – щи, борщ, три вторых – рыба, гуляш, плов, два третьих – компот, чай.

Учитель. — Какие способы решения нестандартных задач вам ещё известны?

Дети (отвечают)

Учитель. Ваня не назвал ещё один способ решения комбинаторных задач, который называется древо решений. Задачи такого вида решаются с помощью. рисования т.н. дерева.

А мы продолжаем наше общение и рассмотрим этот способ решения комбинаторных задач.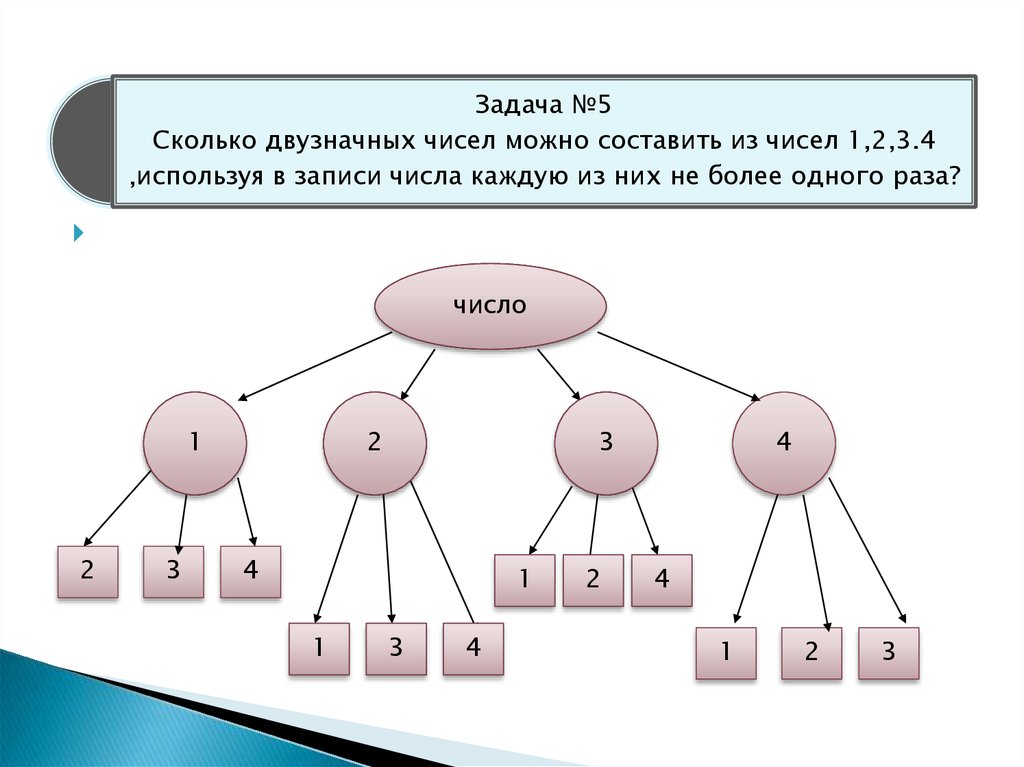

Учитель. — Сколько всего вариантов у вас получилось?

Дети 12

Учитель. — Как вы посчитали?

Дети отвечают

Учитель Вам самостоятельно надо решить комбинаторную задачу, которую вы получили по электронной почте.

Задача 4.

5 финалистов конкурса «Ученик года — 2020», решили обменяться впечатлениями о конкурсе и позвонили между собой. Сколько звонков будет сделано?

Учитель Ребята, предлагаю вам решить следующую комбинаторную задачу, используя граф. Представьте себе, что вы – участники самого престижного ученического конкурса «Ученик года – 2020».

Дети рассуждают после прочтения задачи.

Учитель. Убедимся в истинности ваших суждений.

— Сколько звонков сделает 1 финалист?

Дети 4

Учитель -Сколько звонков сделает 2 финалист?

Дети 3

Учитель — Сколько звонков сделает 3 финалист?

Дети 2

Учитель — Сколько звонков сделает 4 финалист?

Дети 1

Учитель — Сколько звонков сделает 5 финалист?

Дети нисколько, так как ему уже все конкурсанты позвонили.

Учитель — Сколько звонков будет сделано?

Дети 10 звонков.

Учитель Мини-вывод. Таким образом, решение непростой задачи свелось к тому, что появилась картинка, называемая графом и для того, чтобы ее решить, достаточно пересчитать ребра графов.

Учитель

Эту задачу можно решать и аналитическим способом. Давайте рассуждать

4+3+2+1= 10 (раз)

1. Выводы.

Учитель А теперь подведём итог занятия.

— Назовите способы решения комбинаторных задач.

Учитель. Ни один из перечисленных видов не обременен формулой подсчета вариантов. Любую комбинаторную задачу можно решить путем рассуждений, что я вам предложила.

1. Рефлексия.

Учитель Ребята, полученная информация пригодится вам в жизни? Где? Каким образом?

Дети На уроках математики при решении нестандартных задач; буду помогать своим одноклассникам решать такие задачи; уверен, что справлюсь с такими заданиями на олимпиаде по математике; приму участие в дистанционных олимпиадных конкурсах по математике; текстовые задачи по математике решаю плохо, а комбинаторные задачи можно решать без арифметических действий, поэтому нравиться комбинаторика; буду сам искать комбинаторные задачи в Интернет-сети и пытаться их решать; интересно и др.

Учитель Успехов вам и до свидания.

 

Приложения:

1. file0.docx.. 31,7 КБ
2. file1.ppt.zip.. 1,9 МБ

Опубликовано: 16.02.2021

Журнал образования одаренных молодых ученых » Подача заявки » Уровень комбинаторного мышления при решении математических задач

Подробнее

Основной язык	Английский
Субъекты	Образование и исследования в области образования
Дата публикации	Сентябрь 2020
Раздел журнала	Навыки мышления
Авторы	Юлия Мафтуха ХИДАЯТИ> (основной автор) Университет Мухаммадия Суракарта 0000-0003-0842-0897 Индонезия Абдул НГАЛИМ> Университет Мухаммадия Суракарта 0000-0001-9196-3918 Индонезия Сутама СУТАМА> Университет Мухаммадия Суракарта 0000-0002-9006-8388 Индонезия Зайнал АРИФИН> Университет Мухаммадия Суракарта 0000-0002-0945-0943 Индонезия Заеналь АБИДИН> Университет Мухаммадия Суракарта 0000-0003-1102-430X Индонезия Эка РАХМАВАТИ> Университет Мухаммадия Суракарта 0000-0003-0484-2937 Индонезия
Поддерживающее учреждение	Университет Мухаммадия Суракарта
Дата публикации	15 сентября 2020 г.
Опубликовано в выпуске	2020 год, Том 8, Выпуск 3

Укажите

Бибтекс	@научная статья {jegys751038, journal = {Журнал для образования одаренных молодых ученых}, эйссн = {2149-360X}, адрес = {editorjegys@gmail. com}, издатель = {Genç Bilge Yayıncılık}, год = {2020}, громкость = {8}, число = {3}, страницы = {1231 — 1243}, дои = {10.17478/jegys.751038}, title = {Уровень комбинаторного мышления при решении математических задач}, ключ = {цитировать}, автор = {Хидаяти, Юлия Мафтуха и Нгалим, Абдул и Сутама, Сутама и Арифин, Зайнал и Абидин, Заенал и Рахмавати, Эка} }
АПА	Хидаяти, Ю. М. , Нгалим, А. , Сутама, С. , Арифин, З. , Абидин, З. и Рахмавати, Э. (2020). Уровень комбинаторного мышления при решении математических задач . Журнал для образования одаренных молодых ученых , 8 (3) , 1231-1243 гг. DOI: 10.17478/jegys.751038
“Article Title.” Journal Name Volume Number (Year Published): Page Numbers. Medium.»> ГНД	Хидаяти, Ю.М. , Нгалим, А. , Сутама, С. , Арифин, З. , Абидин, З. , Рахмавати, Э. «Уровень комбинаторного мышления при решении математических задач» . Журнал образования одаренных молодых ученых 8 (2020 г. ) ): 1231-1243
Чикаго	Хидаяти, Ю.М. , Нгалим, А. , Сутама, С. , Арифин, З. , Абидин, З. , Рахмавати, Э. «Уровень комбинаторного мышления при решении математических задач».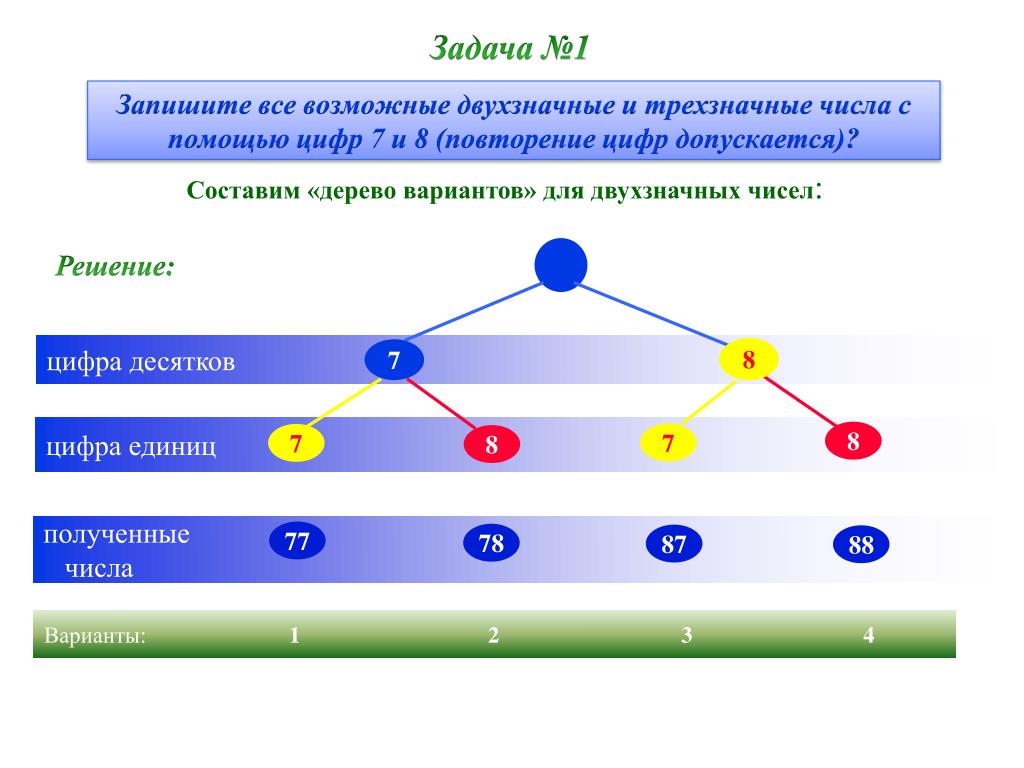 Журнал образования одаренных молодых ученых 8 (2020 г.) ): 1231-1243
РИС	ТЫ — ДЖУР Т1 — Уровень комбинаторного мышления при решении математических задач AU — Юлия Мафтуха Хидайати, Абдул Нгалим, Сутама Сутама, Зайнал Арифин, Заэнал Абидин, Эка Рахмавати 1 год – 2020 год ПГ — 2020 N1 — doi: 10.17478/jegys.751038 DO — 10.17478/jegys.751038 T2 — Журнал образования одаренных молодых ученых JF — Журнал ДЖО — ДЖОР СП — 1231 ЭП-1243 ВЛ — 8 ИС — 3 СН — -2149-360X M3 — doi: 10.17478/jegys.751038 UR — https://doi.org/10.17478/jegys.751038 Y2 — 2020 Скорая помощь —
Примечание	%0 Журнал образования одаренных молодых ученых Уровень комбинаторного мышления при решении математических задач %A Юлия Мафтуха Хидаяти , Абдул Нгалим , Сутама Сутама , Зайнал Арифин , Заеналь Абидин , Эка Рахмавати %T Уровень комбинаторного мышления при решении математических задач %D 2020 Журнал %J для образования одаренных молодых ученых %Р-2149-360X %V 8 %N 3 %R doi: 10. 17478/jegys.751038 %U 10.17478/jegys.751038
ИСНАД	Хидаяти, Юлия Мафтуха , Нгалим, Абдул , Сутама, Сутама , Арифин, Зайнал , Абидин, Заэнал , Рахмавати, Эка . «Уровень комбинаторного мышления при решении математических задач». Журнал для образования одаренных молодых ученых 8 / 3 (сентябрь 2020 г. ): 1231-1243 . https://doi.org/10.17478/jegys.751038
АМА	Хидаяти Ю. М. , Нгалим А. , Сутама С. , Арифин З. , Абидин З. , Рахмавати Э. Уровень комбинаторного мышления при решении математических задач. ДЖЕГИС. 2020; 8(3): 1231-1243 гг.
Ванкувер	Хидаяти Ю. М. , Нгалим А. , Сутама С. , Арифин З. , Абидин З. , Рахмавати Э. Уровень комбинаторного мышления при решении математических задач. Журнал для образования одаренных молодых ученых. 2020; 8(3): 1231-1243 гг.
IEEE	Ю. М. Хидаяти , А. Нгалим , С. Сутама , З. Арифин , З. Абидин и Э. Рахмавати , «Уровень комбинаторного мышления при решении математических задач», Журнал по обучению одаренных молодых ученых , об. 8, нет. 3, стр. 1231-1243, сентябрь 2020 г., doi:10.17478/jegys.751038

112 Комбинаторные задачи — из летней программы AwesomeMath

112 Комбинаторные задачи (мягкая обложка) дает учащимся возможность начать изучение некоторых вводных и промежуточных тем комбинаторики, увлекательной и доступной области математики, сосредоточенной вокруг (среди другие вещи) считая различные предметы и наборы. Мы включили главы, в которых представлены инструменты для решения задач на счет, методы проверки и многое другое, чтобы дать учащимся прочную основу для дальнейшего развития. Единственными предпосылками являются хорошие знания арифметики, немного базовой алгебры и любовь к изучению математики.

Авторы

• Влад Матей и Элизабет Рейланд

Предметы

• Комбинаторика

Сведения о книге

• Мягкая обложка:  196 страниц
• Издатель: XYZ Press (2016)
• Язык: Английский
• ISBN-10: 0996874526
• ISBN-13: 978-0996874526

Я искал книгу по комбинаторике, в которой обсуждались бы темы, часто встречающиеся на математических олимпиадах, и эта книга с честью прошла тест. Он предлагает четкое и исчерпывающее решение любой проблемы. Глава, посвященная индукции, была особенно полезна, так как давала четкое и краткое объяснение как нормальной, так и сильной индукции. Я быстро освоился после прочтения этой главы. Глава об инвариантах тоже была довольно хороша; обычно довольно сложно определить инвариант, но примеры, представленные в этой главе, были хорошо мотивированы.

Кристал Х. (Калифорния)

Как человек, который хотел улучшить свои навыки в комбинаторике с предолимпиадного до олимпийского уровня, я подумал, что эта книга очень хорошо подходит для этой цели. В частности, мне очень понравился раздел о счете несколькими способами. Хотя представленная идея была довольно простой по своей природе, мне нравилось читать примеры, так как они были очень нестандартными и помогали увидеть технику в более общем свете. Например, пример доказательства тождества с функцией пола был очень поучительным, поскольку я никогда не знакомился с комбинаторной идеей подсчета точек решетки, что делало чтение решения очень информативным; Я думал, что это было чрезвычайно элегантно, и это добавило еще одну идею в мой набор инструментов комбинаторики. Мне также понравился раздел об инвариантах, так как в нем подробно объясняется мотивация этой техники и то, как она применяется в задачах комбинаторики, связанных с играми и алгоритмами. Часто я читал решения таких проблем на других ресурсах и понятия не имел, как бы я сам нашел эти решения. Тем не менее, я считаю, что эта глава определенно дала достаточно объяснений того, как такие элегантные решения могут быть найдены самостоятельно, что я оценил. Наконец, мне очень понравился раздел по комбинаторной геометрии. При подготовке к олимпиаде я часто застревал на задачах, сочетающих идеи геометрии и комбинаторики, но я так и не нашел подходящих ресурсов, которые освещали бы идеи комбинаторной геометрии в информативной и интуитивно понятной форме. Этот раздел был именно тем, что я искал, так как в начале в нем были изложены основные идеи и приемы, а затем перешли непосредственно к рабочим примерам с подробными и мотивированными решениями, которые я нашел очень полезными и эффективными. Я подумал, что обсуждение выпуклости было очень полезным для целей этой главы, так как я никогда не понимал, что такое выпуклость, пока не прочитал эту часть. Было предоставлено достаточно теории, лежащей в основе выпуклости, и это помогло мне понять, что происходит в решениях приведенных примеров. Кроме того, я думал, что примеры, представленные в этом разделе, были достаточно сложными, а также интересными и нестандартными. Было действительно приятно читать решения этих примеров, поскольку они методично анализировали проблему и демонстрировали силу обсуждаемой математики, применяя идеи очень красивыми способами. В целом, я думаю, что эту книгу было очень приятно читать, и опыт работы над проблемами в конце был чрезвычайно полезным, а решения к ним были написаны с учетом правильной аудитории. Задачи в конце включали правильный баланс между вычислительными задачами и доказательствами, и я обнаружил, что работа над ними в моем собственном темпе помогла мне преодолеть разрыв между предолимпиадной комбинаторикой и олимпийской комбинаторикой.

Чад Л. (Мэриленд)

В этой книге используется множество изящных способов четкого объяснения идей и концепций таким образом, чтобы это было понятно большинству людей. В книге также представлено множество альтернативных решений, которые стоит изучить, особенно когда они экономят ваше время, например решения, использующие дополнительный счет. В книге также объясняется, когда и когда не следует использовать определенные концепции, иногда с помощью наглядных пособий, таких как таблицы. Объясняя, почему работает тот или иной метод, эта книга не упускает деталей так, как это делают другие книги при доказательстве биномиальной теоремы. Кроме того, вводные задачи, приведенные позже в главе 15, очень хорошо отражают то, что вы, вероятно, увидите на математических тестах на более сложном конце спектра, потому что большинство из них разнообразны интересными способами, которые иногда требуют некоторого творческого подхода. Если у меня есть какие-то сомнения или я действительно не понимаю, как закончить задачу, решения в конце очень просты, и я часто ловлю себя на мысли, почему я не понимал, что то или иное можно сделать.

Ронгуи П. (Калифорния)

Книга «112 комбинаторных задач — от AMSP» — отличная книга, посвященная решению задач. В каждой главе книги представлены важные формулы и множество примеров, подтверждающих содержание. Одной из глав, которая оказалась особенно полезной, была «Индукция», так как в ней не только излагалась основная идея, но и подробно объяснялась правильность каждого шага, а также меры предосторожности, которые необходимо соблюдать при использовании индукции. Примеры начинаются с очень простого вопроса, который ясно показывает этапы индукции, и задачи постепенно становятся более сложными и уникальными, разветвляясь на множества, комбинаторные игры, а также на сильную индукцию для доказательства более сложных формул. Сама формула полезна во многих доказательствах, но подробные пояснения к ней уменьшили количество ошибок в моих решениях.

Джин Ф. (Калифорния)

«Я учусь в седьмом классе. Когда меня выбрали в AMSP в прошлом году, я решил пройти курс математических расчетов с доказательствами. Эта книга очень помогла мне понять основные понятия, чтобы подготовиться к летней программе. В книге была действительно хорошая теория для объяснения концепций и множество задач для практики Благодаря этой книге мне очень понравился AMSP, и он стал лучшим курсом, который я когда-либо проходил.

Мне еще нужно решить сложные задачи из книги. Это, несомненно, лучшая книга по комбинаторике для каждого ученика, стремящегося к соревнованиям.

Анш А. (Канада)

Эта книга дает мне полезные знания и методы решения комбинаторных задач. Уроки этой книги собраны из разных источников и помогают мне получить подробные и достаточные математические задачи, которые я и мои ученики могут использовать для расширения своих знаний. Меня очень впечатлила глава 14: Вероятности и вероятностный метод. Эта глава удивляет меня массой нового и интересного, чего я раньше никогда не открывал, ее содержание редко упоминается в нашей программе по математике.

Хун Т. (Вьетнам)

«Эта книга действительно потрясающая. Мои любимые главы — это комбинаторная геометрия и вероятностный метод, которые довольно сложно понять, читая другую книгу. дает моим студентам преимущество решать современные задачи комбинаторики, которые имеют тенденцию быть комбинаторной геометрией. Для вероятностных методов, это дает фундаментальные знания о таком методе, новые аспекты проблемы комбинаторики и новые инструменты для решения комбинаторных задач.Довольно трудно найти такая книга, которая охватывает эту тему, и эта книга подходит мне в этом отношении».

Юккрид Н. (Таиланд)

Это отличная книга для изучения комбинаторики, от основ до продвинутых знаний. Он охватывает многие комбинаторные темы, которые можно было бы протестировать в AMC или AIME. Теоремы объясняются очень хорошо, а примеры точно соответствуют темам. Это значительно улучшило мое понимание комбинаторики.

Манронг Дж. (Флорида)

Изучая 112 комбинаторных задач, вы изучаете основы счета и теории вероятностей на начальном уровне. Вы начинаете с изучения способов решения вычислительных задач, затем переходите к изучению доказательств, необходимых на Олимпиаде. Раньше я плохо разбирался в этом предмете, но после прочтения этой книги я узнал гораздо больше по этому предмету. Я бы порекомендовал эту книгу всем, кто начинает соревноваться в математике, поскольку все, что вам нужно в качестве предварительного условия, — это знание основ арифметики.

Шрирам К. (Канзас)

Комбинаторика — Дениз Гаскинс, Давайте поиграем в математику

Posted on 1 февраля 2017 г. 7 августа 2019 г. by Denise Gaskins

Я хочу рассказать вам историю. Все любят истории, верно? Но в основе моей истории лежит признание, которое, боюсь, шокирует многих читателей.

Люди предполагают, что, поскольку я преподаю математику, веду блоги о математике, даю советы по математике на интернет-форумах и провожу семинары по обучению математике — поскольку я все это делаю, я должен быть хорош в математике.

Примените логику к этому утверждению.

Вывод просто недействителен.

Продолжить чтение Признание: я плохо разбираюсь в математике

Опубликовано в Классы 5+, Математические монстры, ГоловоломкиTagged Комбинаторика, Математика, Ошибки, Решение задач, Головоломки, Обучение18 комментариев

Опубликовано 19 октября 2011 г. 30 октября 2019 г. Дениз Гаскинс

фото Энни Пилон через flickr

Мы продолжаем наши уроки счета — и в очередной раз Киттен доказывает, что она думает не так, как я. На самом деле, ее решение настолько элегантно, что я думаю, что у нее могло бы быть будущее как у математика. В конце концов, каждому начинающему писателю нужна дневная работа, верно?

Если бы я только мог убедить ее отказаться от мысли, что она ненавидит математику…

Перестановки с осложнениями

Сколько из возможных различных расположений 1-6 имеют 1 слева от 2?

— Математический конкурс для средней школы, Дж. Баттерсон

Продолжить чтение Больше, чем один способ решить эту проблему, снова

Опубликовано в Классы 5+, Головоломкипомеченный Комбинаторика, Соревнования по математике для средней школы, Средняя школа, Более чем одним способом, Моя семья, Принцесса Котенок, Решение задач, Словесные задачи11 комментариев

Опубликовано 24 августа 2011 г. 30 октября 2019 г. Дениз Гаскинс

Фото Эйрика Ньюта через flickr.

В ленивом настроении «Я не хочу ходить в школу» Принцесса Киттен была готова остановиться после трех математических задач. Мы правильно поняли два из них, но последний подсчитывал способы покраски куба в черно-белый цвет, и мы забыли посчитать варианты сплошного цвета.

Для моей дочери-перфекционистки одной ошибки было достаточно, чтобы уйти. Она прислонилась ко мне головой, пока мы сидели вместе на диване, и сказала: «Мы закончили. Сделано, сделано, сделано». Если бы она могла, то начала бы мурлыкать — один из самых манипулятивных звуков, известных человечеству. Я мягкое прикосновение. Кто может заниматься математикой, когда есть котенок, которого можно потискать?

от tanjila ahmed через flickr

Тем не менее, мне удалось втиснуть еще одну головоломку. Я взял свой маркер для белой доски и начал писать:

DONE
DOEN
DNOE
DENO
DNEO
ONED
ODNE

Продолжить чтение Больше, чем один способ решить эту проблему

Опубликовано в Классы 5+, ГоловоломкиTagged Комбинаторика, Соревнование по математике для средней школы, Средняя школа, Ошибки, Более чем одним способом, Моя семья, Принцесса Котенок, Решение задач, Словесные задачиОставить комментарий

Опубликовано 8 августа 2011 г. 30 октября 2019 г. Дениз Гаскинс

Фото Джорджа Парриллы с flickr.

Киттен жаловался, что некоторые математические программы повторяют одни и те же задачи снова и снова с большими числами: «Они не становятся сложнее, они просто становятся длиннее. Это скучно!»

Итак, мы вытащили уроки счета из конкурсной математики для средней школы. [Настоятельно рекомендуемая книга!] Киттен не любит соревноваться, но ей нравится изучать новые идеи, и книга Баттерсон дает ей множество таких идей, хорошо организованных и ясно объясненных.

Сегодняшней темой был основной принцип счета. Это был обзор, легкий-легкий. Задачи были слишком простыми, пока…

Пиццы в Mario’s бывают трех размеров, и у вас есть выбор из 10 начинок, которые можно добавить к пицце. Вы можете заказать пиццу с любым количеством начинок (до 10), в том числе и с нулевым. Сколько вариантов пиццы в Mario’s?

[В книге было сказано 9 начинок, но я бегло просмотрел/перефразировал вслух и неправильно прочитал. ]

• Можете ли вы найти ответ?

Продолжить чтение (Математическая) проблема с пиццей

Опубликовано в Классы 5+, ГоловоломкиTagged Книги, Комбинаторика, Соревнование по математике для средней школы, Средняя школа, Ошибки, Более чем одним способом, Моя семья, Принцесса Котенок, Решение задач, Словесные задачи6 комментариев

Опубликовано 11 мая 2009 г. 22 марта 2018 г. Дениз Гаскинс

[Фотографии Ragged Squares Quilt использованы с разрешения Crazy Mom Quilts.]

Я знаю, что другие учителя делали математические лоскутные одеяла, но я никогда не пробовала это делать ни на одном из своих занятий. Тем не менее, это изображение привлекло мое внимание и практически умоляло превратить его в урок математики для моего элементарного математического клуба.

Я подумал, по крайней мере, о двух способах, которыми я мог бы воспользоваться, но держу пари, что если мы объединим наши мозги, мы сможем придумать еще более творческие идеи. Так вот вопрос, аля Дэн Мейер:

• Что можно с этим сделать?

Как можно использовать это изображение в качестве трамплина для занятий математикой? Какие вопросы вы бы задали? Какие концепции вы бы попытались донести? Что бы вы последовали за ним? Прокомментируйте, пожалуйста!

Другие фотографии доступны…

Продолжить чтение Одеяло: что с этим делать?

Опубликовано в Деятельность, Средний элементарный Метки Деятельность, Комбинаторика, Геометрия, Головоломки8 комментариев

Опубликовано 16 января 2009 г. 21 мая 2022 г. Дениз Гаскинс

Искусство решать задачи Люди недавно объявили о своей новой программе Alcumus, которая предлагает онлайн-уроки по различным математическим темам, включая вероятность и комбинаторику, которые в большинстве учебников по математике освещаются плохо, если вообще освещаются.

Обновление за октябрь 2011 г.:

В настоящее время Alcumus дополняет наши учебники «Введение в алгебру», «Введение в счет и теорию вероятностей», «Введение в теорию чисел» и «Предварительную алгебру», а также онлайн-курсы «Алгебра 1», «Алгебра 2», «Введение в счет и вероятность», «Введение в теорию чисел» и «Предварительная алгебра 1». . Мы ожидаем дальнейшего расширения тем в Alcumus.

— Информационная страница AoPS Alcumus

Я регистрирую всех своих учеников MathCounts. Если вы учитесь на дому, мы будем рады, если вы присоединитесь к нам!

Продолжить чтение Бесплатная онлайн-математика для средней школы и старше

Опубликовано в Классы 5+UpTagged Комбинаторика, Средняя школа, Математический клуб, Математика, Средняя школа, Вероятность12 комментариев

Опубликовано 13 октября 2008 г. 22 июня 2021 г. Дениз Гаскинс

[Фотография выше от ThunderChild tm.]

Последние пару недель в Математическом клубе мы учились считать. Моя новая группа студентов MathCounts никогда не слышала о комбинаторике, поэтому мы начали с самого начала:

• Подсчет и вероятность I, Кеоне Хон
• Подсчет и вероятность Джейсона Баттерсона

Продолжить чтение Математический клуб: счет 101

Опубликовано в Алгебра и не только, Классы 5+, Головоломкипомеченный Комбинаторика, Средняя школа, Математический клуб, Математика, Средняя школа, Вероятность6 комментариев

Опубликовано 16 апреля 2008 г. 27 марта 2022 г. Дениз Гаскинс

Фото: peigianlong.

Вот головоломка от Just a Substitute Teacher:

Запись в плане урока: «Раздайте пакеты с рабочими листами и попросите учащихся сшить их перед началом. Они знают, что делать».

Звучит достаточно просто! Четыре пронумерованных листа, всего восемь страниц, печатные лицевая и оборотная стороны. Что может пойти не так?

Знаете ли вы, сколько возможных комбинаций из четырех листов бумаги можно сшить?

Продолжить чтение Эксперименты с заменой учителя с комбинаторикой

Опубликовано в Классы 5+, ГоловоломкиTagged Занятия, Комбинаторика, Кооператив в домашнем обучении, Математический клуб, MathCounts, Головоломки, Обучение1 Комментарий

Опубликовано 8 декабря 2007 г. 21 мая 2022 г. Дениз Гаскинс

Большая часть подготовки к олимпиаде по математике состоит из рабочих партий и большого количества старых тестовых задач. Однако иногда я составлял лист с советами, в котором резюмировал тему, которую мои ученики плохо запоминали.

Продолжить чтение Советы по математике

Опубликовано в Классы 5+UpTagged Комбинаторика, Геометрия, Раздаточные материалы, Математический клуб, Математика, Средняя школа, Вероятность9 комментариев

Опубликовано 25 июля 2007 г. 13 мая 2022 г. Дениз Гаскинс

В первом разделе «Творческого решения задач по школьной математике» Джорджа Ленхнера, сразу после обязательного поклона Джорджу Полиа (см. третью цитату здесь), Лехнер ставит эту задачу. Если вы видели это раньше, наберитесь терпения — его идея была намного больше, чем просто подсчет блоков.

Деревянный куб со стороной 3 см по ребрам окрашен в красный цвет. Окрашенный куб затем разрезают на кубики размером 1 см, как показано выше. Сколько кубиков со стороной 1 см не имеют красной краски ни на одной из граней?

И затем он бросает вызов нам как учителям:

У вас есть идеи по расширению задачи?
Если да, то запишите их.

Это удачно расположено в конце правой страницы, и я смог удержаться, чтобы не начать читать дальше. Я составил список из 15 других вопросов, которые можно было бы задать — некоторые из них будут использованы в будущих историях об Александрии Джонс.