 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Степень числа. Квадрат и куб числа. 5-й класс
Степень числа. Квадрат и куб числа. 5-й класс- Трофимова Елена Иозасовна, учитель математики, информатики и классный руководитель
Разделы: Математика, Конкурс «Презентация к уроку»
Класс: 5
ЦЕЛЬ: Изучение новых понятий степени числа, научить находить, используя таблицы значение квадрата и куба числа.
ЗАДАЧИ:
- Образовательная: Научиться находить квадрат куб числа;
- Развивающая: Развивать познавательную активности, пространственного воображения, самостоятельной работы, творческих способностей; Развивать логическое мышление на уроках математики.

- Воспитательная: Воспитание интереса к предмету, умение работать в коллективе, культуре общения.
ОБОРУДОВАНИЕ: Презентация к уроку – мультимедийное оборудование, раздаточный материал таблица квадрата и куба числа, справочный материал.
| Содержание урока | Мультимедийное сопровождение |
| Ι. ОРГАНИЗАЦИОННЫЙ МОМЕНТ. | |
| – Здравствуйте ребята, садитесь. – Сегодня на уроке мы рассмотрим новые для вас понятия: степень числа, основание степени, показатель степени, научимся возводить число в квадрат, в куб и закрепим на конкретных примерах. |
Слайд 35 |
– Подготовительный этап к изучению новых понятий. – Рассмотрим пример и пишем в тетрадь (объясняет учитель) |
Слайд 36 |
| ΙΙ. АКТУАЛИЗАЦИЯ ЗНАНИЙ. | |
| – Пример рассматривает ученик, решая у доски с комментирование. | Слайд 37 |
| ΙΙI. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА. |
|
| – Мы подошли к интересному моменту нашего урока (учитель поясняет запись на слайде) – А теперь можно записать в тетрадь и запомнить. |
Слайд 38 |
| – А вот теперь можно закрепить то что мы с вами разобрали. – Примеры на закрепления основных понятий. – Затем проверка (следующий слайд) |
Слайд 39 |
– Понятие квадрата числа, объясняет учитель, дети записывают формулу в тетради. – Для облегчения возведения числа в квадрат, существует таблица квадратов первых 10 натуральных чисел. – Учитель раздаёт таблички, дети вклеивают себе в тетрадь. – И закрепляют навыки использования данной таблицы. – Понятие куба числа, пытается учитель вывести формулу с помощью учеников, дети записывают формулу в тетради. – Учитель раздаёт таблички, дети вклеивают себе в тетрадь. – И закрепляют навыки использования данной таблицы. |
Слайды 41-44 |
| – Учитель даёт определения (первой степени числа) – Закрепляют понятие на примерах и также приводят свои примеры. |
Слайд 45 |
| ΙV. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА: | |
| – Учащиеся отвечают на вопросы «профессора математических наук» | Слайд 46 |
Работа по учебнику. – Откройте стр. 100 №657. |
Слайд 47 |
| ФИЗКУЛЬТМИНУТКА | |
| Руки вверх на плечи, вниз (3 раза) Головою влево вправо, вперёд назад (3 раза) Туловище движется влево вправо, вперёд назад (3 раза) Стали мы теперь бодрее, будем думать мы быстрее! (Хором) |
Слайды 90-93 |
| – Повторение мать учения. – Молодцы ребята, справились с заданием |
Слайд 53 |
| V. САМОСТОЯТЕЛЬНАЯ РАБОТА. | |
| – Молодцы ребята, справились с заданием, результаты на следующем уроке. | Слайд 54 |
VI. ИТОГ УРОКА ИТОГ УРОКА |
|
| – Вопросы на закрепления: «Задаёт профессор математических наук»
1.
Что такое квадрат числа?
|
Слайд 55 |
| VIΙ. ДОМАШНЕЕ ЗАДАНИЕ. | |
| – Вы сегодня познакомились с новыми понятиями, дома ещё раз по учебнику прочитаете, выучите формулы, которые нам помогали при решении заданий. | |
| – Молодцы ребята! Спасибо за урок! | Слайд 58 |
Степень числа 5 класс Как найти степень
Степень числа 5 класс
Как найти степень числа. • Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 пишут 46 и произносят «четыре в шестой степени». 4 • 4 • 4 • 4 = 46
Выражение 4 в степени 6 • 4 — основание степени; • 6 — показатель степени.
• В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:
Запомните! • Запись an читается так: «а в степени n» или «n-ая степень числа a». • Исключение составляют записи: • a 2 — её можно произносить как «а в квадрате»; • a 3 — её можно произносить как «а в кубе».
Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».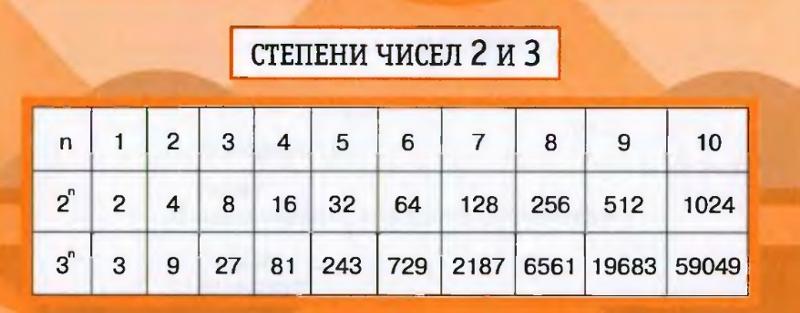
• Конечно, выражения выше можно читать и по определению степени: • a 2 — «а во второй степени»; • a 3 — «а в третьей степени».
• Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0). • • Степенью числа «а» с показателем n = 1 является само это число: a 1 = a • Любое число в нулевой степени равно единице. a 0 = 1 • Ноль в любой натуральной степени равен нулю. 0 n = 0 • Единица в любой степени равна 1. 1 n = 1
• Выражение 00 (ноль в нулевой степени) считают лишённым смыслом. • (-32)ст0 = 1 • 0 ст253 = 0 • 1 ст4 = 1 • При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.
• При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени. • Пример. Возвести в степень. • 5 ст3 = 5 • 5 = 125 • 2. 5 ст2 = 2. 5 • 2. 5 = 6. 25
Возведение в степень отрицательного числа 5 класс
Запомните! • Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.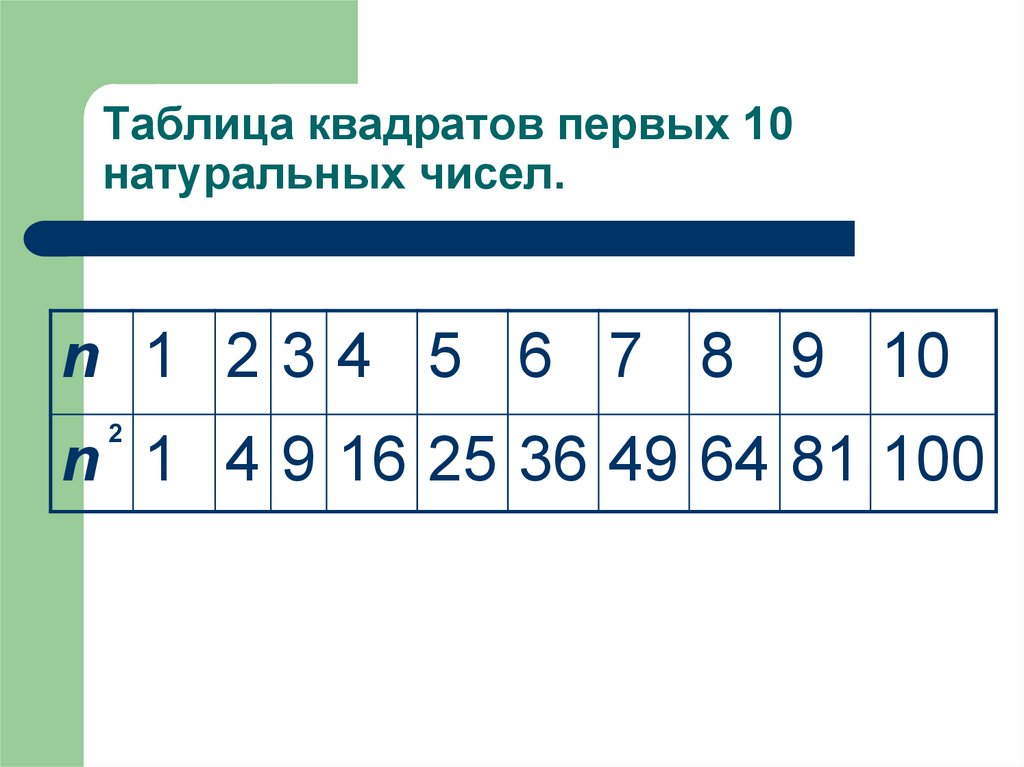
• При возведении в степень положительного числа получается положительное число. • При возведении нуля в натуральную степень получается ноль.
• При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел. • Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.
• Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.
Запомните! • Отрицательное число, возведённое в чётную степень, есть число положительное. • Отрицательное число, возведённое в нечётную степень, число отрицательное.
Пример 2 • (- 3)ст2 = 2 • (- 3) = 2 • 9 = 18 — 5 • (- 2)ст3 = — 5 • (- 8) = 40
• При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (5)ст4 и -5 ст4 это разные выражения. Результаты возведения в степень данных выражений будут разные.
• Вычислить (- 5)ст4 означает найти значение четвёртой степени отрицательного числа. • (- 5)ст4 = (- 5) • (- 5) = 625
• В то время как найти -5 ст4 означает, что пример нужно решать в 2 действия: • Возвести в четвёртую степень положительное число 5. 5 ст4 = 5 • 5 • 5 = 625 • Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание). -5 ст4 = — 625
Обратите внимание! • • • Вычислить: — 6 ст2 — (- 1)ст4 6 ст2 = 6 • 6 = 36 -6 ст2 = — 36 (- 1)ст4 = (- 1) • (- 1) = 1 — (- 1)ст4 = — 1 — 36 — 1 = — 37
Порядок действий в примерах со степенями. 5 класс
5 класс
• Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Запомните! • В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание. • Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.
Пример • Вычислить:
• Для облегчения решения примеров полезно знать и пользоваться таблицей степеней.
Спасибо за внимание!
Выражение чисел
Цель обучения
- Научиться правильно выражать числа.
Величины состоят из двух частей: числа и единицы измерения. Число говорит «сколько». Важно уметь правильно выражать числа, чтобы количества можно было правильно передать.
Стандартная записьПрямое выражение числа. является прямым выражением числа. Такие числа, как 17, 101,5 и 0,00446, выражаются в стандартных обозначениях. Для относительно небольших чисел подходят стандартные обозначения. Однако для очень больших чисел, таких как 306 000 000, или для очень маленьких чисел, таких как 0,000000419, стандартная запись может быть громоздкой из-за количества нулей, необходимых для размещения ненулевых чисел в нужной позиции.
Научное обозначениеВыражение числа с использованием степеней 10. является выражением числа с использованием степеней 10. Степени 10 используются для выражения чисел, которые имеют много нулей:
| 10 0 | = 1 |
| 10 1 | = 10 |
| 10 2 | = 100 = 10 × 10 |
| 10 3 | = 1000 = 10 × 10 × 10 |
| 10 4 | = 10 000 = 10 × 10 × 10 × 10 |
и так далее. Приподнятое число справа от 10, указывающее количество множителей 10 в исходном числе, является показателем степени. Приподнятое число справа от 10 указывает количество множителей 10 в исходном числе.. (Научную запись иногда называют показательная запись .) Значение показателя степени равно количеству нулей в числе, выраженном в стандартной записи.
Приподнятое число справа от 10, указывающее количество множителей 10 в исходном числе, является показателем степени. Приподнятое число справа от 10 указывает количество множителей 10 в исходном числе.. (Научную запись иногда называют показательная запись .) Значение показателя степени равно количеству нулей в числе, выраженном в стандартной записи.
Небольшие числа также могут быть выражены в экспоненте, но с отрицательными показателями:
| 10 −1 | = 0,1 = 1/10 |
| 10 −2 | = 0,01 = 1/100 |
| 10 −3 | = 0,001 = 1/1000 |
| 10 −4 | = 0,0001 = 1/10 000 |
и так далее. Опять же, значение показателя степени равно количеству нулей в знаменателе соответствующей дроби. Отрицательный показатель степени означает, что десятичное число меньше единицы.
Отрицательный показатель степени означает, что десятичное число меньше единицы.
Число выражается в экспоненциальном представлении путем написания первой отличной от нуля цифры, затем десятичной точки и остальных цифр. Часть числа в научной записи, умноженная на степень 10, называется коэффициентом. Часть числа в научной записи, умноженная на степень 10. Затем определите степень 10, необходимую для преобразования этого числа в степень исходное число и умножить записанное число на соответствующую степень 10. Например, чтобы написать 79,345 в экспоненциальном представлении,
79 345 = 7,9345 × 10 000 = 7,9345 × 10 4
Таким образом, число в научной записи равно 7,9345 × 10 4 . Для небольших чисел используется тот же процесс, но показатель степени 10 отрицательный:
0,000411 = 4,11 × 1/10 000 = 4,11 × 10 −4
Обычно лишние нули в конце или начале числа не включаются. (См. рис. 2.1 «Использование экспоненциальной записи».)
(См. рис. 2.1 «Использование экспоненциальной записи».)
Пример 1
Выразите эти числа в экспоненциальном представлении.
- 306 000
- 0,00884
- 2 760 000
- 0,000000559
Решение
- Число 306 000 равно 3,06 умножить на 100 000 или 3,06 умножить на 10 5 . В экспоненциальном представлении это число равно 3,06 × 10 5 .
- Число 0,00884 равно 8,84, умноженному на 1/1000, что равно 8,84, умноженному на 10 9.0019 −3 . В научной записи это число равно 8,84 × 10 −3 .
- Число 2 760 000 равно 2,76 умножить на 1 000 000, что равно 2,76 умножить на 10 6 . В научной записи число записывается как 2,76 × 10 6 . Обратите внимание, что мы опускаем нули в конце исходного числа.
- Число 0,000000559 равно 5,59 умножить на 1/10 000 000, что равно 5,59 умножить на 10 −7 .
 В научной записи число записывается как 5,59.× 10 −7 .
В научной записи число записывается как 5,59.× 10 −7 .
Проверьте себя
Выразите эти числа в экспоненциальном представлении.
- 23 070
- 0,0009706
Ответы
- 2,307 × 10 4
- 9,706 × 10 −4
Другой способ определить степень числа 10 в экспоненциальном представлении — подсчитать, на сколько знаков нужно переместить десятичную точку, чтобы получить числовое значение от 1 до 10. Количество знаков равно степени 10. Это число положительное, если вы переместите десятичную точку вправо, и отрицательное, если вы переместите десятичную запятую влево:
56↖4,9↖30↖20↖1=5,69 × 1040,0↗10↗20↗30↗42↗58=2,8 × 10−5
Многие химические величины выражаются в научных обозначениях. При выполнении расчетов может потребоваться ввести число в экспоненциальном представлении в калькулятор. Убедитесь, что вы знаете, как правильно ввести число в экспоненциальном представлении в свой калькулятор. Различные модели калькуляторов требуют разных действий для правильного ввода экспоненциальной записи. Если вы сомневаетесь, немедленно обратитесь к инструктору. (См. рис. 2.2 «Научная запись в калькуляторе».)
Убедитесь, что вы знаете, как правильно ввести число в экспоненциальном представлении в свой калькулятор. Различные модели калькуляторов требуют разных действий для правильного ввода экспоненциальной записи. Если вы сомневаетесь, немедленно обратитесь к инструктору. (См. рис. 2.2 «Научная запись в калькуляторе».)
Key Takeaways
- Стандартная нотация обычно выражает число.
- В научной записи число выражается коэффициентом, умноженным на степень 10.
- Степень 10 положительна для чисел больше 1 и отрицательна для чисел от 0 до 1.
Упражнения
Выразите эти числа в экспоненциальном представлении.
- 56,9
- 563 100
- 0,0804
- 0,00000667
Выразите эти числа в экспоненциальном представлении.

- −890 000
- 602 000 000 000
- 0,0000004099
- 0,000000000000011
Выразите эти числа в экспоненциальном представлении.
- 0,00656
- 65 600
- 4 567 000
- 0,000005507
Выразите эти числа в экспоненциальном представлении.
- 65
- −321,09
- 0,000077099
- 0,000000000218
Выразите эти числа в стандартной записи.
- 1,381 × 10 5
- 5,22 × 10 −7
- 9,998 × 10 4
Выразите эти числа в стандартной записи.

- 7,11 × 10 −2
- 9,18 × 10 2
- 3,09 × 10 −10
Выразите эти числа в стандартной записи.
- 8,09 × 10 0
- 3,088 × 10 −5
- −4,239 × 10 2
Выразите эти числа в стандартной записи.
- 2,87 × 10 −8
- 1,78 × 10 11
- 1,381 × 10 −23
Эти числа не записаны в правильной научной нотации. Перепишите их так, чтобы они были в правильном научном представлении.

- 72,44 × 10 3
- 9 943 × 10 −5
- 588 399 × 10 2
Эти числа не записаны в правильной научной нотации. Перепишите их так, чтобы они были в правильном научном представлении.
- 0,000077 × 10 −7
- 0,000111 × 10 8
- 602 000 × 10 18
Эти числа не записаны в правильной научной нотации. Перепишите их так, чтобы они были в правильном научном представлении.
- 345,1 × 10 2
- 0,234 × 10 −3
- 1800 × 10 −2
Эти числа не записаны в правильной научной нотации.
 Перепишите их так, чтобы они были в правильном научном представлении.
Перепишите их так, чтобы они были в правильном научном представлении.- 8 099 × 10 −8
- 34,5 × 10 0
- 0,000332 × 10 4
Запишите эти числа в экспоненциальном представлении, сосчитав количество знаков, на которое переместилась десятичная точка.
- 123 456,78
- 98 490
- 0,000000445
Запишите эти числа в экспоненциальном представлении, сосчитав количество знаков, на которое переместилась десятичная точка.
- 0,000552
- 1 987
- 0,00000000887
Воспользуйтесь калькулятором, чтобы вычислить эти выражения.
 Выразите окончательный ответ в правильном научном представлении.
Выразите окончательный ответ в правильном научном представлении.- 456 × (7,4 × 10 8 ) = ?
- (3,02 × 10 5 ) ÷ (9,04 × 10 15 ) = ?
- 0,0044 × 0,000833 = ?
Воспользуйтесь калькулятором, чтобы вычислить эти выражения. Выразите окончательный ответ в правильном научном представлении.
- 98 000 × 23 000 = ?
- 98 000 ÷ 23 000 = ?
- (4,6 × 10 −5 ) × (2,09 × 10 3 ) = ?
Воспользуйтесь калькулятором, чтобы вычислить эти выражения. Выразите окончательный ответ в правильном научном представлении.
- 45 × 132 ÷ 882 = ?
- [(6,37 × 10 4 ) × (8,44 × 10 −4 )] ÷ (3,2209 × 10 15 ) = ?
Воспользуйтесь калькулятором, чтобы вычислить эти выражения.
 Выразите окончательный ответ в правильном научном представлении.
Выразите окончательный ответ в правильном научном представлении.- (9,09 × 10 8 ) ÷ [(6,33 × 10 9 ) × (4,066 × 10 −7 )] = ?
- 9 345 × 34,866 ÷ 0,00665 = ?
Ответы
- 5,69 × 10 1
- 5,631 × 10 5
- 8,04 × 10 −2
- 6,67 × 10 −6
- 6,56 × 10 −3
- 6,56 × 10 4
- 4,567 × 10 6
- 5,507 × 10 −6
- 138 100
- 0,000000522
- 99 980
- 8.
 09
09 - 0,00003088
- −423,9
- 8.
- 7,244 × 10 4
- 9,943 × 10 −2
- 5,88399 × 10 7
- 3,451 × 10 4
- 2,34 × 10 −4
- 1,8 × 10 1
- 1,2345678 × 10 5
- 9,849 × 10 4
- 4,45 × 10 −7
- 3,3744 × 10 11
- 3,3407 × 10 −11
- 3,665 × 10 −6
- 6,7346 × 10 0
- 1,6691 × 10 −14
Объяснение урока: Степени и показатели степени для рациональных чисел
В этом объяснении мы научимся определять основание и показатель степени в формулах степени, записывать их в экспоненциальном и
расширенные формы и оценивают простые степени.
Начнем с того, что вспомним, что многократное умножение можно представить в виде степени. Например, 2 определяется как произведение пяти двоек следующим образом. 2=2×2×2×2×2.раз
Мы называем 2 основанием и 5 показателем степени. Мы можем распространить это определение на общие рациональные базисы. В этом случае, если 𝑛 — натуральное число, а 𝑎𝑏 — рациональное число, то 𝑎𝑏 будет продуктом 𝑛 множества 𝑎𝑏.
Например, мы можем оценить 12, найдя произведение трех половин как следует: 12=12×12×12=1×1×12×2×2=18.
Точно так же мы можем вычислить −23 повторным умножением, как показано: −23=−23×−23×−23×−23=(−2)×(−2)×(−2)×(−2)3×3×3× 3=1681.
Мы можем проследить тот же процесс в обратном порядке. Допустим, мы хотим записать 278 в показательная форма. Мы можем разложить числитель и знаменатель на простые числа следующим образом: 278=3×3×32×2×2.
Затем мы можем разделить умножение, как показано:
3×3×32×2×2=32×32×32.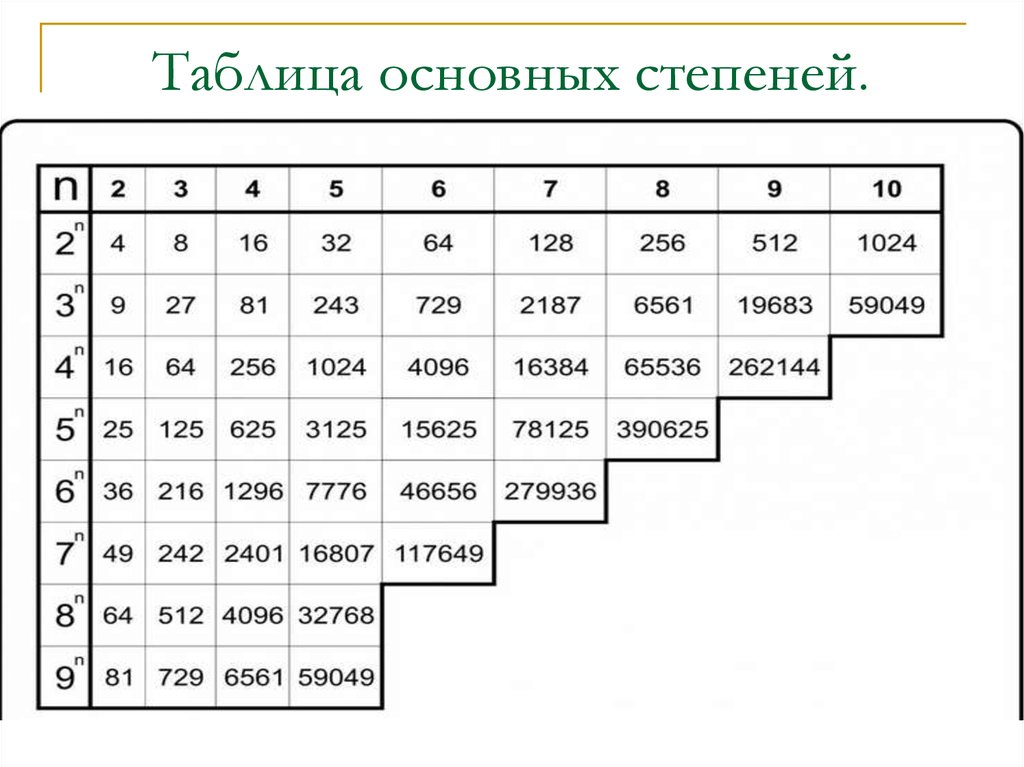
Мы видим, что 278 — это произведение трех партий по 32, поэтому мы можем написать это в экспоненциальной форме 32×32×32=32.
Таким образом, 278=32.
Давайте теперь рассмотрим несколько примеров со степенями рациональных чисел.
Пример 1: Понимание полномочий
Какую терминологию мы используем для описания числа 12 в выражении 12 и 5 в выражении 12?
Ответ
Напомним, что выражение вида 𝑎 называется экспоненциальным выражением или 𝑛-я степень 𝑎. Мы называем 𝑎 основанием выражения и 𝑛 показатель степени или степени.
В выражении 12 заметим, что 12 – это число, которое берется в степень, а 5 — это сама сила. Следовательно, 12 называется основание выражения, а 5 — показатель степени выражения.
В следующем примере мы упростим выражение, переписав его в экспоненциальной форме.
Пример 2. Запись числового выражения в виде экспоненты
Что такое 411×411×411×411×411×411×411?
- 411
- 411
- 411
- 711
- 2811
.
 знаменатели. Это дало бы нам
411×411×411×411×411×411×411=4×4×4×4×4×4×411×11×11×11×11×11×11.
знаменатели. Это дало бы нам
411×411×411×411×411×411×411=4×4×4×4×4×4×411×11×11×11×11×11×11.Тем не менее, варианты указаны как силы. Таким образом, вместо вычисления этих выражений мы можем упростить их напоминая, что многократное умножение можно переписать как возведение в степень.
В частности, произведение 7 лотов из 411 можно записать, подняв 411 в степени 7.
Мы видели, что положительные целые степени можно рассматривать как многократное умножение основания. В общем, если 𝑎𝑏∈ℚ и 𝑛 — натуральное число, мы имеем 𝑎𝑏=𝑎𝑏×𝑎𝑏×⋯×𝑎𝑏.кратно
Мы можем оценить правую часть уравнения, умножив числители и знаменатели по отдельности следующим образом: 𝑎𝑏 = 𝑎𝑏 × 𝑎𝑏 × ⋯ × 𝑎𝑏 = 𝑎 × 𝑎 × ⋯ × 𝑎𝑏 × 𝑏 × ⋯ × 𝑏 𝑏 = 𝑎𝑏.Times
Другими словами, мы можем возвести рациональное число в целочисленную положительную степень, возведя его числитель и знаменатель до показатель отдельно.
Например, мы видели, что 12=12×12×12=18. Вместо этого мы могли бы оценить это, возведя в куб числитель и знаменатель:
12=12=18.
Вместо этого мы могли бы оценить это, возведя в куб числитель и знаменатель:
12=12=18.
Формально этот результат можно записать следующим образом.
Свойство: Степени рациональных чисел
Поскольку степень положительного целого числа рационального основания определяется повторным умножением, мы можем показать, что если 𝑛 — натуральное число и 𝑎𝑏∈ℚ, то 𝑎𝑏=𝑎𝑏×𝑎𝑏×⋯×𝑎𝑏=𝑎𝑏.times
Другими словами, мы можем возвести числитель и знаменатель в степень по отдельности.
В следующем примере мы оценим степень, в которой основание рационально.
Пример 3. Вычисление рациональных чисел, возведенных в степень
Найдите значение −65 и дайте ответ в простейшей форме.
Ответ
Мы можем вычислить это выражение двумя способами. Начнем с того, что напомним, что возведение в степень определяется повторением
умножение. Таким образом, −65 является произведением 3 лотов
−65, как показано:
−65=−65×−65×−65.
Мы можем умножить числители и знаменатели по отдельности, чтобы получить −65×−65×−65=(−6)×(−6)×(−6)5×5×5=−216125.
Мы также можем вычислить это выражение, вспомнив общий результат для степеней рациональных чисел. В целом, если 𝑛 — натуральное число и 𝑎𝑏∈ℚ, то 𝑎𝑏=𝑎𝑏.
Следовательно, −65=−65=(−6)5=−216125.
В нашем следующем примере мы вычислим экспоненциальное выражение, включающее несколько экспоненциальных множителей.
Пример 4. Вычисление числового выражения с использованием степеней
Оцените выражение 23×65÷45, представив ответ в виде дроби в простейшей форме.
Ответ
Чтобы оценить это выражение, нам сначала нужно вспомнить, что порядок операций говорит нам начинать со степеней. Затем мы вспоминаем, что если 𝑛 — натуральное число и 𝑎𝑏∈ℚ, тогда 𝑎𝑏=𝑎𝑏.
Следовательно, мы можем оценить каждую степень следующим образом:
23=23=827,65=65=3625,45=45=256625.
Мы можем подставить эти значения в выражение, чтобы получить 23×65÷45=827×3625÷256625.
Далее нам нужно вычислить самые внутренние скобки. Мы делаем это, умножая числители и знаменатели отдельно. У нас есть 827×3625=8×3627×25.
Мы можем отметить, что и 36, и 27 делятся на 9 для упрощения. 8×3627×25=8×9×49×3×25=8×43×25=3275.
Подстановка этого значения в выражение дает 827×3625÷256625=3275÷256625.
Теперь мы можем вспомнить, что деление на дробь равносильно умножению на ее обратную величину. Это дает 3275÷256625=3275×625256.
Затем мы можем упростить это выражение, разложив его на множители следующим образом: 3275×625256=32×62575×256=32×(25×25)(25×3)×(32×8)=253×8=2524.
В следующем примере мы найдем выражение для объема куба по заданному выражению для длины его стороны.
Пример 5. Решение текстовой задачи с использованием степени рациональных чисел
Найдите выражение для объема заданного куба, длина стороны которого равна 2𝑥5.
Ответ
Начнем с того, что вспомним, что объем куба определяется длиной стороны куба. Итак, если куб имеет сторону длина 𝑎, то его объем равен 𝑎×𝑎×𝑎=𝑎. В этом случае сторона длина равна 2𝑥5, поэтому его объем определяется кубом этого выражения: 2𝑥5.
Мы можем упростить это, записав произведение полностью. Находим произведение 3 лотов 2𝑥5, чтобы получить 2𝑥5=2𝑥5×2𝑥5×2𝑥5=(2𝑥)×(2𝑥)×(2𝑥)5×5×5.
Вспомним, что для умножения одночленов нужно умножить коэффициенты и добавить полномочия общих переменных. Таким образом, (2𝑥)×(2𝑥)×(2𝑥)5×5×5=2×2×2×𝑥125=8𝑥125.()
В нашем последнем примере мы вычислим алгебраическое выражение, используя результаты для степеней рациональных чисел.
Пример 6. Вычисление алгебраического выражения с использованием степеней
Если 𝑥=32 и 𝑦=−45, найдите значение 𝑥𝑦−𝑥𝑦, давая ответ в виде дроби в простейшей форме.
Ответ
Сначала мы подставляем данные значения в выражение, чтобы получить
𝑥𝑦−𝑥𝑦=32−45−32−45.
Теперь мы хотим оценить степени, вспомнив, что если 𝑛 — натуральное число и 𝑎𝑏∈ℚ, то 𝑎𝑏=𝑎𝑏.
Итак, 32=32=94,−45=(−4)5=−64125.
Теперь мы можем подставить эти значения в выражение, чтобы получить 32−45−32−45=94−45−32−64125.
Теперь мы можем вычислить каждое произведение, перемножая числители и знаменатели по отдельности. Мы получаем 94−45−32−64125=−9×44×5−3×(−64)2×125.
Мы можем отменить общий множитель 4 в первом члене и 2 во втором члене, чтобы получить −9×44×5−3×(−64)2×125=−95−3×(−32)125.
Тогда мы можем упростить −95−3×(−32)125=−95+96125.
Наконец, нам нужно переписать обе дроби, чтобы они имели один и тот же знаменатель, чтобы сложить их вместе. Заметим, что 5
коэффициент 125 , поэтому 125 является наименьшим общим кратным знаменателей. Переписав первый член так, чтобы
знаменатель 125 и сложение двух дробей дает нам
−95+96125=−9×255×25+96125=−225125+96125=−225+96125=−129125.
Заметим, что в числителе и знаменателе нет общих множителей, поэтому дальше просто нельзя.
Следовательно, 𝑥𝑦−𝑥𝑦=−129125.
Давайте закончим повторением некоторых важных моментов из этого объяснения.
Ключевые моменты
- В выражении вида 𝑏 мы называем 𝑏 основанием, а 𝑛 степень или экспонента. Мы можем прочитать это выражение как 𝑏, возведенное в 𝑛-ю степень. сила.
- Мы определяем положительные целые степени повторным умножением, известным как расширенная форма. В общем, если 𝑎𝑏∈ℚ и 𝑛 — натуральное число, то 𝑎𝑏 является продуктом 𝑛 многих 𝑎𝑏. 𝑎𝑏=𝑎𝑏×𝑎𝑏×⋯×𝑎𝑏.кратно
- В общем, мы можем оценить мощность рационального числа, оценив мощность числителя и знаменатель отдельно. Если 𝑛 — натуральное число и 𝑎𝑏∈ℚ , то 𝑎𝑏=𝑎𝑏.
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.


 В научной записи число записывается как 5,59.× 10 −7 .
В научной записи число записывается как 5,59.× 10 −7 .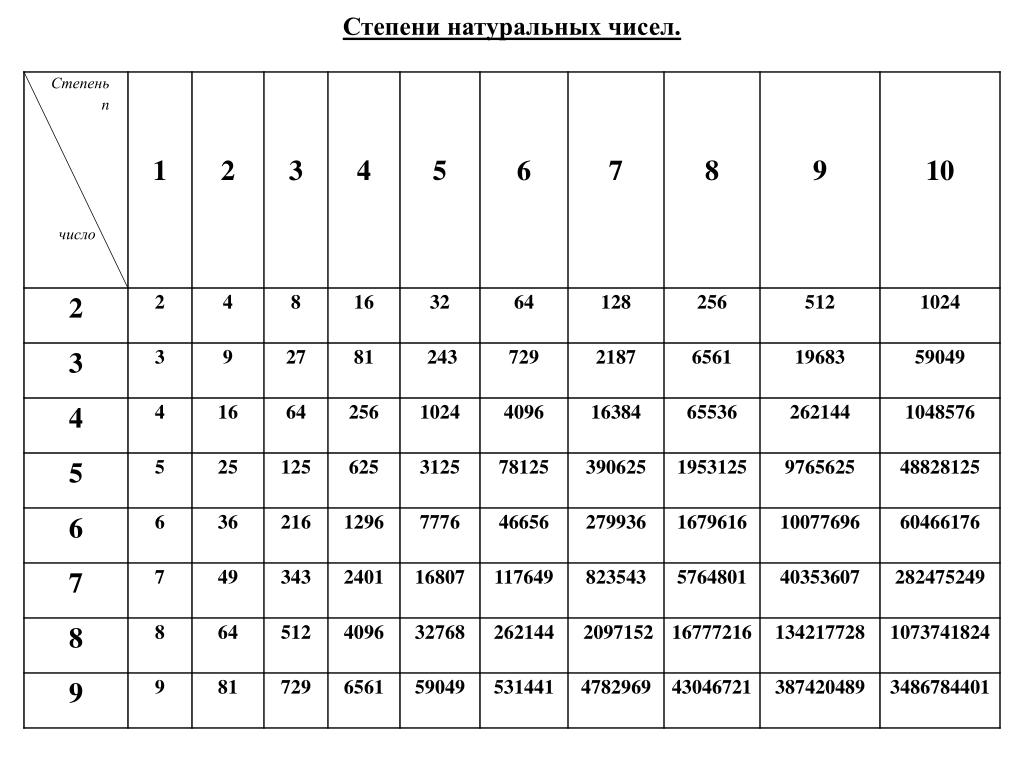


 Перепишите их так, чтобы они были в правильном научном представлении.
Перепишите их так, чтобы они были в правильном научном представлении. Выразите окончательный ответ в правильном научном представлении.
Выразите окончательный ответ в правильном научном представлении. Выразите окончательный ответ в правильном научном представлении.
Выразите окончательный ответ в правильном научном представлении.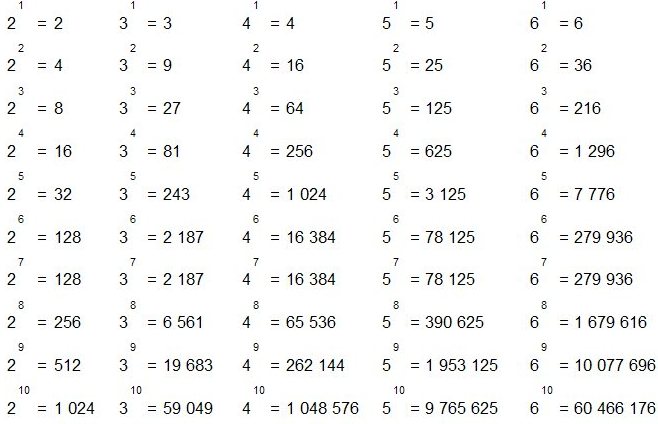 09
09