|
1.Понятие комплексного числа. 2.Тригонометрическая форма комплексного числа.
|
|||||||||||||||||||||||||||||
| 19 20 21 22 23 24 25 26 27 | |||||||||||||||||||||||||||||
1.Понятие комплексного числа.
Выражение вида z = x + iy называется комплексным числом. Число х называется действительной частью комплексного числа z и обозначается Re(z), число y — мнимой частью комплексного числа z и обозначается Im(z). Числа z = x + iy и z1 = x — iy называются сопряженными. Если равны действительные и мнимые части комплексного числа, то они называются равными т.е. z1 = z2 или x1 + iy1 = x2 + iy2. Операции над комплексными числами. |
|||||||||||||||||||||||||||||
1. Сумма (разность) комплексных чисел. z1+z2 = x1+x2+i(y1+y2). 2. Произведение комплексных чисел. z1z2 = (x1x2 — y1y2) + i(x1y2 + x2y1). отсюда i² = (0 + i1)(0 + i1) = (0 -1) + i(0 + 0) = -1. 3. Деление двух комплексных чисел. |
|||||||||||||||||||||||||||||
Рассмотрим на плоскости декартову прямоугольную систему координат Oxy. Каждому комплексному числу Z = x + iy ставится в соответствие единственная точка плоскости z(xy). Плоскость Oxy, где каждая точка отождествлена с комплексным числом, называется комплексной. Координатные оси Ox и Oy, на которых расположены действительные и мнимые числа, называются действительной и мнимой осями. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
2.Тригонометрическая форма комплексного числа.До любой точки комплексной плоскости из начала координат можно провести вектор определенной длины r. Число r называется модулем комплексного числа z и обозначается |z|. |
|||||||||||||||||||||||||||||
Угол ϕ, образованный между вектором и осью Ox, называется аргументом комплексного числа z и обозначается Arg z. ϕ = Arg z = arg z + 2kπ где 0≤ argz < 2π Таким образом: x = r cos ϕ, y = r sin ϕ. Следовательно, комплексное число z = x + iy можно представить как: |
|||||||||||||||||||||||||||||
Представление комплексного числа в такой форме, где r = |z| ≥ 0, ϕ = Arg z, называется тригонометрической формой комплексного числа. |
|||||||||||||||||||||||||||||
| Пример. | |||||||||||||||||||||||||||||
| 19 20 21 22 23 24 25 26 27 | |||||||||||||||||||||||||||||
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
6.
 1: Комплексные числа — Математика LibreTexts
1: Комплексные числа — Математика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14531
- Кен Каттлер
- Университет Бригама Янга via Lyryx
Исходы
- Понять геометрическое значение комплексного числа как точки на плоскости.
- Докажите алгебраические свойства сложения и умножения комплексных чисел и примените эти свойства. Поймите действие взятия сопряженного комплексного числа.
- Знать абсолютное значение комплексного числа и способы его нахождения, а также его геометрическое значение.
Хотя действительные числа очень эффективны, они недостаточны для решения таких уравнений, как \(x^2+1=0\), и здесь на помощь приходят комплексные числа. 2 = -1\), и определить комплексные числа как числа вида \(z = a + bi\), где \(a\) и \(b\) — действительные числа. Мы называем это стандартной формой или декартовой формой комплексного числа \(z\). Затем мы ссылаемся на \(a\) как на действительная часть \(z\) и \(b\) как мнимая часть \(z\). Оказывается, такие числа не только решают приведенное выше уравнение, но и фактически решают любой многочлен степени не ниже 1 с комплексными коэффициентами. Это свойство, называемое основной теоремой алгебры, иногда называют \(\mathbb{C}\) алгебраически замкнутым. Гауссу обычно приписывают доказательство этой теоремы в 1797 г., но многие другие работали над ней, а первое полностью правильное доказательство принадлежит Аргану в 1806 г.
2 = -1\), и определить комплексные числа как числа вида \(z = a + bi\), где \(a\) и \(b\) — действительные числа. Мы называем это стандартной формой или декартовой формой комплексного числа \(z\). Затем мы ссылаемся на \(a\) как на действительная часть \(z\) и \(b\) как мнимая часть \(z\). Оказывается, такие числа не только решают приведенное выше уравнение, но и фактически решают любой многочлен степени не ниже 1 с комплексными коэффициентами. Это свойство, называемое основной теоремой алгебры, иногда называют \(\mathbb{C}\) алгебраически замкнутым. Гауссу обычно приписывают доказательство этой теоремы в 1797 г., но многие другие работали над ней, а первое полностью правильное доказательство принадлежит Аргану в 1806 г.
Точно так же, как вещественное число можно рассматривать как точку на прямой, комплексное число \(z = a + bi\) можно рассматривать как точку \(\left( a,b\right)\) на плоскости чья координата \(x\) равна \(a\) и чья координата \(y\) равна \(b. \). Например, на следующем рисунке точка \(z = 3+2i\) может быть представлена как точка на плоскости с координатами \(\left( 3,2\right).\)
\). Например, на следующем рисунке точка \(z = 3+2i\) может быть представлена как точка на плоскости с координатами \(\left( 3,2\right).\)
Сложение комплексных чисел определяется следующим образом. \[\left( a+bi\right) +\left( c+di\right) =\left( a+c\right) +\left( b+d\right)i\nonumber \]
Это дополнение обладает всеми обычными свойствами, как показывает следующая теорема.
Теорема \(\PageIndex{1}\): свойства сложения комплексных чисел
Пусть \(z,w,\) и \(v\) — комплексные числа. Тогда выполняются следующие свойства.
- Коммутативный закон сложения \[z+w=w+z\номер\]
- Аддитивный идентификатор \[z+0=z\номер \]
- Существование аддитивной инверсии \[\begin{array}{l} \mbox{Для каждого} \; z\in \mathbb{C}, \mbox{существует}\; -z\in \mathbb{C} \mbox{ такое, что}\; z+\left( -z\right) =0 \\ \mbox{На самом деле, если } z=a+bi, \mbox{ тогда } -z=-a-bi. \конец{массив}\номер\] 9{2}bd \\ &=\left( ac-bd\right) +\left( ad + bc \right)i \end{выровнено}\]
Рассмотрим следующие примеры.

Пример \(\PageIndex{1}\): умножение комплексных чисел
- \((2-3i)(-3+4i) = 6+17i\)
- \((4-7i)(6-2i) = 10-50i\)
- \((-3+6i)(5-i) = -9+33i\)
Ниже приведены важные свойства умножения комплексных чисел.
Теорема \(\PageIndex{2}\): свойства умножения комплексных чисел 9{-1}=1\номер\]
- Распределительный закон \[z\left( w+v\right) =zw+zv\nonnumber\]
Вы можете проверить некоторые из этих утверждений. Действительные числа также удовлетворяют вышеуказанным аксиомам, и вообще любая математическая структура, удовлетворяющая этим аксиомам, называется полем. Есть много других областей, в частности, даже конечные области, особенно полезные для криптографии, и причина для определения этих аксиом заключается в том, что линейная алгебра — это все о полях, и мы можем делать почти все в этом предмете, используя любое поле. Хотя здесь наибольший интерес представляют знакомые поля действительных чисел, обозначаемые как \(\mathbb{R}\), и поля комплексных чисел, обозначаемые как \(\mathbb{C}\).
Важной конструкцией, относящейся к комплексным числам, является комплексное сопряжение, обозначаемое горизонтальной чертой над числом, \(\overline{z}\). Он определяется следующим образом.
Определение \(\PageIndex{1}\): сопряженное комплексное число
Пусть \(z = a+bi\) — комплексное число. Тогда сопряженное из \(z\), записанное \(\overline{z}\), задается выражением \[\overline{a+bi}= a-bi\nonumber\]
Геометрически действие сопряжение — это отражение заданного комплексного числа по оси \(x\). Алгебраически он меняет знак мнимой части комплексного числа. Следовательно, для действительного числа \(a\), \(\overline{a} = a\). 9{2}\конец{выровнено}\]
Обратите внимание, что в произведении нет мнимой части, поэтому умножение комплексного числа на его сопряженное дает действительное число.
Теорема \(\PageIndex{3}\): свойства сопряженного
Пусть \(z\) и \(w\) — комплексные числа. Тогда выполняются следующие свойства сопряжения. 2}i.\end{выровнено}\] 9{1/2}\номер\]
2}i.\end{выровнено}\] 9{1/2}\номер\]
Также из определения, если \(z=a+bi\) и \(w=c+di\) два комплексных числа, то \(\left\vert zw\right\vert =\left\vert z\ right\vert \left\vert w\right\vert .\) Найдите минутку, чтобы убедиться в этом.
Неравенство треугольника является важным свойством модуля комплексных чисел. Здесь представлены две полезные версии, хотя первая официально называется неравенством треугольника.
Предложение \(\PageIndex{1}\): Неравенство треугольника
Пусть \(z,w\) — комплексные числа.
Следующие два неравенства выполняются для любых комплексных чисел \(z,w\): \[\begin{array}{l} \left| г+ш\вправо| \leq\влево| г\право| +\влево| ш\право| \\ \влево| \влево| г\право| -\влево| ш\право| \право| \leq\влево| г-в\вправо| \end{array}\nonumber\] Первый называется Неравенство Треугольника .
- Доказательство
Пусть \(z=a+bi\) и \(w=c+di\). Сначала обратите внимание, что \[z \overline{w}=\left( a+bi\right) \left(c-di\right) =ac+bd+\left(bc-ad\right)i\nonumber\] и т.
 д. \(\left\vert ac+bd\right\vert \leq \left\vert z\overline{w}\right\vert =\left\vert z\right\vert \left\vert w\right\vert .\ ) 9{2}\номер\]
д. \(\left\vert ac+bd\right\vert \leq \left\vert z\overline{w}\right\vert =\left\vert z\right\vert \left\vert w\right\vert .\ ) 9{2}\номер\]Взяв квадратный корень, мы имеем, что \[\left\vert z+w\right\vert \leq \left\vert z\right\vert +\left\vert w\right\vert\nonumber\] так что это подтверждает неравенство треугольника.
Чтобы получить второе неравенство, напишите \[z=z-w+w,\;w=w-z+z\nonumber\] и, таким образом, по первой форме неравенства мы получим оба: \[\left\vert z\right\vert \leq \left\vert z-w\right\vert +\left\vert w\right\vert ,\;\left\vert w\right\vert \leq \left\vert z-w\right\vert + \left\vert z\right\vert\nonumber\]
Следовательно, как \(\left\vert z\right\vert -\left\vert w\right\vert\), так и \(\left\vert w\right\vert -\left\vert z\right\vert\ ) не больше, чем \(\left\vert z-w\right\vert\). Это доказывает вторую версию, потому что \(\left\vert \left\vert z\right\vert -\left\vert w\right\vert \right\vert\) является одним из \(\left\vert z\right\ vert -\left\vert w\right\vert\) или \(\left\vert w\right\vert -\left\vert z\right\vert\).

С этим определением важно отметить следующее. Вы можете потратить время, чтобы проверить это замечание. 9{2}}. \номер\]
Таким образом, расстояние между точкой на плоскости, определяемой упорядоченной парой \(\left( a,b\right)\) и упорядоченной парой \(\left( c,d\right)\), равно \(\left | z-w\right|\), где \(z\) и \(w\) только что описаны.
Например, рассмотрим расстояние между \(\left( 2,5\right)\) и \(\left( 1,8\right) .\) Пусть \(z=2+5i\) и \(w =1+8i,\) \(z-w=1-3i\), \(\left( z-w\right) \left( \overline{z-w}\right) =\left( 1-3i\right) \left( 1+3i\right) = 10\), поэтому \(\left\vert z-w\right\vert =\sqrt{10}\).
Вспомните, что мы ссылаемся на \(z=a+bi\) как на стандартную форму комплексного числа. В следующем разделе мы рассмотрим другую форму, в которой мы можем выразить комплексное число.
Эта страница под названием 6.1: Комплексные числа распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- комплексно-сопряженный
- комплексные номера
- источник@https://lyryx.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра - неравенство треугольника
Понимание реальных и сложных чисел в алгебре
Ключевые члены
o Реальное число
o Комплексное число
o Натуральное число
o Rational
O Irrative Number
O Rational
Orration Number
o Rational
Orranative
o Rational
Ordative
o
o Распространенность
o Идентичность
o Обратное
Цели
o Изучите, каковы набор реальных чисел
o Узнайте некоторые из основных подмножества реальных чисел
o Знай свойства реальных чисел и почему они применимы
и реальные и реальные и реальные и реальные и реальные и реальные и реальные и реальные и реальные и реальные и реальные и
и Комплексные числа Числа, с которыми мы имеем дело в реальном мире (игнорируя любые сопутствующие им единицы, такие как доллары, дюймы, градусы и т. На приведенной выше иллюстрации, конечно, показана только часть числовой строки (было бы невозможно показать ее целиком), и помечены только определенные числа (–1, 0, 1 и т. д.). Таким образом, действительным числом может быть 8, 4,357, -3/5, π, 9.0365 или любой другой подобный номер. Конкретное представление, будь то дробь, десятичная дробь или другое представление, не имеет значения. Возможно, лучший способ описать действительное число — определить числа, которые не являются действительными числами. Бесконечность (∞) — это , а не — действительное число, хотя оно больше любого заданного действительного числа; также не является действительным числом, так как не существует числа, квадрат которого равен –1. В качестве краткого отступления давайте определим мнимое число 9.0365 (так называемый, потому что не существует эквивалентного «настоящего числа») с использованием буквы i ; затем мы можем создать новый набор чисел, называемый комплексными числами. Комплексное число — это любое число, включающее и . Таким образом, 3 i , 2 + 5,4 i и –π i — комплексные числа. (На самом деле действительные числа являются подмножеством комплексных чисел — любое действительное число r можно записать как r + 0 i , что является комплексным представлением.) Комплексные числа — важная часть алгебры, и они имеют отношение к таким вещам, как решения полиномиальных уравнений. Символ часто используется для набора комплексных чисел. Подмножества действительных чисел Действительные числа включают диапазон явно различных чисел: например, числа без десятичных знаков, числа с конечным числом десятичных разрядов и числа с бесконечным числом знаков. Сначала дети изучают «счетные» числа: 1, 2, 3 и т. д. Формально они называются 9.0069 натуральных чисел , а множество натуральных чисел часто обозначают символом . Если мы добавим к этому набору число 0, мы получим целых чисел . Помимо положительных чисел, есть и отрицательные числа: если мы включим в набор отрицательные значения каждого целого числа, то получим так называемые целых чисел . Набор целых чисел часто обозначается символом . В дополнение к целым числам множество действительных чисел также включает дробные (или десятичные) числа. Между любыми двумя целыми числами существует бесконечное число дробных значений. Рассмотрим, например, 1 и 2; между этими числами находятся значения 1,1, 1,11, 1,111, 1,1111 и т. д. Очевидно, мы могли бы добавить столько дополнительных знаков после запятой, сколько пожелаем. Хотите узнать больше? Почему бы не пройти онлайн-курс по алгебре? Давайте рассмотрим эти подмножества действительных чисел: Натуральные числа, = Целые числа Целые числа, Рациональные числа, Иррациональные числа Комплексные числа, Практическая задача: Определите, какие из следующих чисел принадлежат : {0, i , 3,54, , ∞}. Решение: Если число можно записать как , где a и b — целые числа, то это число рационально (т. е. оно находится в множестве ). Обратите внимание на следующее: Таким образом, каждое из этих чисел рационально. Число и мнимое, поэтому оно не принадлежит к реальным числам. Точно так же ∞ не является действительным числом; i и ∞ поэтому не входят в набор . Свойства действительных чисел Теперь, когда вы знаете немного больше о действительных числах и некоторых их подмножествах, мы можем перейти к обсуждению некоторых свойств действительных чисел (и операций над действительными числами). Хотя некоторые свойства очевидны, они, тем не менее, полезны для обоснования различных шагов, необходимых для решения задач или доказательства теорем. Одним из свойств является то, что умножение и сложение действительных чисел являются коммутативными. Коммутативность утверждает, что порядок умножения или сложения двух чисел не влияет на результат. Мы можем записать это символически ниже, где x и y — два действительных числа (обратите внимание, что . можно использовать вместо для обозначения умножения): Представьте, что у вас есть группа из x бананов и группа из y бананов; не имеет значения, как вы их сложите, общее количество бананов всегда будет одинаковым: либо x + y , либо y + x . Точно так же, если у вас есть прямоугольник с длиной x и шириной y , не имеет значения, умножаете ли вы x на y или y на x ; площадь прямоугольника всегда одинакова, как показано ниже. Другим свойством, подобным коммутативности, является ассоциативность. Ассоциативность утверждает, что порядок сложения трех чисел или порядок их умножения не влияет на результат. Если рассматривать действительные числа x , y и z , то Напомним, что операции в круглых скобках выполняются перед теми, которые находятся вне круглых скобок. Распределимость — еще одно свойство действительных чисел, которое в данном случае относится к комбинации умножения и сложения. Это свойство выражено ниже. Мы можем понять это свойство, снова взглянув на группы бананов. Предположим, например, что у нас есть 3 группы по 6 бананов и 3 группы по 5 бананов. Если мы объединим эти группы один к одному (одна группа из 6 бананов с одной группой из 5), мы получим 3 группы по 11 бананов. Последние два свойства, которые мы обсудим, — тождественность и инверсия. Свойство identity просто утверждает, что сложение любого числа x с 0 дает просто x , а умножение любого числа x на 1 равно x . Свойство инвертирует для вещественного числа x :0046 Обратите внимание, что обратное свойство тесно связано с тождеством. Эти свойства сами по себе могут показаться немного эзотерическими. Хотя, если их полностью вырвать из контекста, они могут показаться менее чем полезными, оказывается, что вы будете использовать их регулярно, даже если вы явно не признаете это в каждом случае. Практическая задача: Определите свойство действительных чисел, которое оправдывает каждое равенство: a + i = i + a ; ; 5 r + 3 s — (5 r + 3 s ) = 0. Solution: In the first case, a + i = i + a , равенство явно подтверждается коммутативностью. Второе равенство также можно записать в следующем виде: 92 = -1j2=-1. Комплексные числа часто встречаются в математике и
техники, особенно в таких темах, как обработка сигналов. Традиционно многие пользователи и библиотеки (например, TorchAudio) имеют
обрабатывал комплексные числа, представляя данные в тензорах с плавающей запятой с формой (…, 2) (…, 2) (…, 2), где последний
размерность содержит действительные и мнимые значения. Тензоры сложных dtypes обеспечивают более естественный пользовательский интерфейс при работе с комплексными числами. Операции по
комплексные тензоры (например, Примечание Спектральные операции в поддержке модуля torch.fft
родные комплексные тензоры. Предупреждение Сложные тензоры — это бета-функция, которая может быть изменена. Мы поддерживаем два сложных типа dtype: torch.cfloat и torch.cdouble Примечание Тип dtype по умолчанию для сложных тензоров определяется типом dtype с плавающей запятой по умолчанию.
Если тип dtype с плавающей запятой по умолчанию равен torch.float64 , то комплексные числа выводятся как
иметь dtype torch.complex128 , в противном случае предполагается, что они имеют dtype torch.complex64 . Все фабричные функции, кроме Пользователи, которые в настоящее время работали над отсутствием сложных тензоров с реальными тензорами формы (…,2)(…,2)(…,2)
могут легко переключаться, используя сложные тензоры в своем коде, используя Доступ к действительным и мнимым значениям комплексного тензора можно получить с помощью Примечание При доступе к атрибутам real и imag память не выделяется, а обновления на месте
Тензоры real и imag обновят исходный комплексный тензор. Так же
возвращенные реальных и изображений тензоров не являются смежными. Угол и абсолютные значения комплексного тензора можно вычислить с помощью Многие операции линейной алгебры, такие как  д.), обычно являются действительными числами. А действительное число — это любое число, которое можно поместить на числовую прямую, простирающуюся до бесконечности как в положительном, так и в отрицательном направлениях. Эта числовая строка проиллюстрирована ниже числом 4,5, отмеченным в качестве примера закрытой точкой. Набор действительных чисел часто обозначается символом
д.), обычно являются действительными числами. А действительное число — это любое число, которое можно поместить на числовую прямую, простирающуюся до бесконечности как в положительном, так и в отрицательном направлениях. Эта числовая строка проиллюстрирована ниже числом 4,5, отмеченным в качестве примера закрытой точкой. Набор действительных чисел часто обозначается символом 
 десятичные знаки. Давайте рассмотрим некоторые подмножества действительных чисел, начиная с самых основных.
десятичные знаки. Давайте рассмотрим некоторые подмножества действительных чисел, начиная с самых основных. Множество действительных чисел делится на два принципиально разных типа чисел: рациональные числа и иррациональные числа. А рациональное число — это число, которое может быть эквивалентно выражено в виде дроби , где a и b оба являются целыми числами, а b не равно 0. Таким образом, рациональные числа включают целые числа, а также конечные десятичные дроби и повторяющиеся десятичные дроби (например, 0,126126126). Символ часто используется для обозначения набора рациональных чисел. Иррациональное число , с другой стороны, является неповторяющимся десятичным числом без завершения. Множество действительных чисел полностью состоит из рациональных и иррациональных чисел.
Множество действительных чисел делится на два принципиально разных типа чисел: рациональные числа и иррациональные числа. А рациональное число — это число, которое может быть эквивалентно выражено в виде дроби , где a и b оба являются целыми числами, а b не равно 0. Таким образом, рациональные числа включают целые числа, а также конечные десятичные дроби и повторяющиеся десятичные дроби (например, 0,126126126). Символ часто используется для обозначения набора рациональных чисел. Иррациональное число , с другой стороны, является неповторяющимся десятичным числом без завершения. Множество действительных чисел полностью состоит из рациональных и иррациональных чисел.
 Помните: переменные — это просто неизвестные значения, поэтому они действуют так же, как числа, когда вы складываете, вычитаете, умножаете, делите и т. д.
Помните: переменные — это просто неизвестные значения, поэтому они действуют так же, как числа, когда вы складываете, вычитаете, умножаете, делите и т. д.


torch.mv() , torch.matmul() ), вероятно, будут быстрее и эффективнее использовать память
чем операции над тензорами с плавающей запятой, имитирующие их. Операции с комплексными числами в PyTorch оптимизированы
использовать векторизованные инструкции по сборке и специализированные ядра (например, LAPACK, cuBlas).
Создание сложных тензоров
>>> x = torch.randn(2,2, dtype=torch.cfloat)
>>> х
тензор([[-0,4621-0,0303j, -0,2438-0,5874j],
[0,7706+0,1421j, 1,2110+0,1918j]])
torch.linspace() , torch.logspace() и torch. ,
поддерживается для комплексных тензоров. arange()
arange() Переход от старого представления
факел.view_as_complex() и torch.view_as_real() . Обратите внимание, что эти функции не копируют и не возвращают
представление входного тензора. >>> x = torch.randn(3, 2)
>>> х
тензор([[ 0,6125, -0,1681],
[-0,3773, 1,3487],
[-0,0861, -0,7981]])
>>> y = torch.view_as_complex(x)
>>> г
тензор ([0,6125-0,1681j, -0,3773+1,3487j, -0,0861-0,7981j])
>>> torch.view_as_real(y)
тензор([[ 0,6125, -0,1681],
[-0,3773, 1,3487],
[-0,0861, -0,7981]])
Доступ к действительным и мнимым
вещественных и изображение .
>>> у.реал
тензор ([ 0,6125, -0,3773, -0,0861])
>>> у.имаг
тензор ([-0,1681, 1,3487, -0,7981])
>>> y.real.mul_(2)
тензор ([ 1,2250, -0,7546, -0,1722])
>>> г
тензор([ 1,2250-0,1681j, -0,7546+1,3487j, -0,1722-0,7981j])
>>> y.real.stride()
(2,)
Угол и абс
torch.angle() и факел.abs() . >>> x1=torch.tensor([3j, 4+4j])
>>> x1.abs()
тензор([3.0000, 5.6569])
>>> x1.угол()
тензор ([1,5708, 0,7854])
Линейная алгебра
torch.matmul() , torch.



 Из значения ϕ = Arg z выделяется главное значение arg z, которое кратно 2π.
Из значения ϕ = Arg z выделяется главное значение arg z, которое кратно 2π.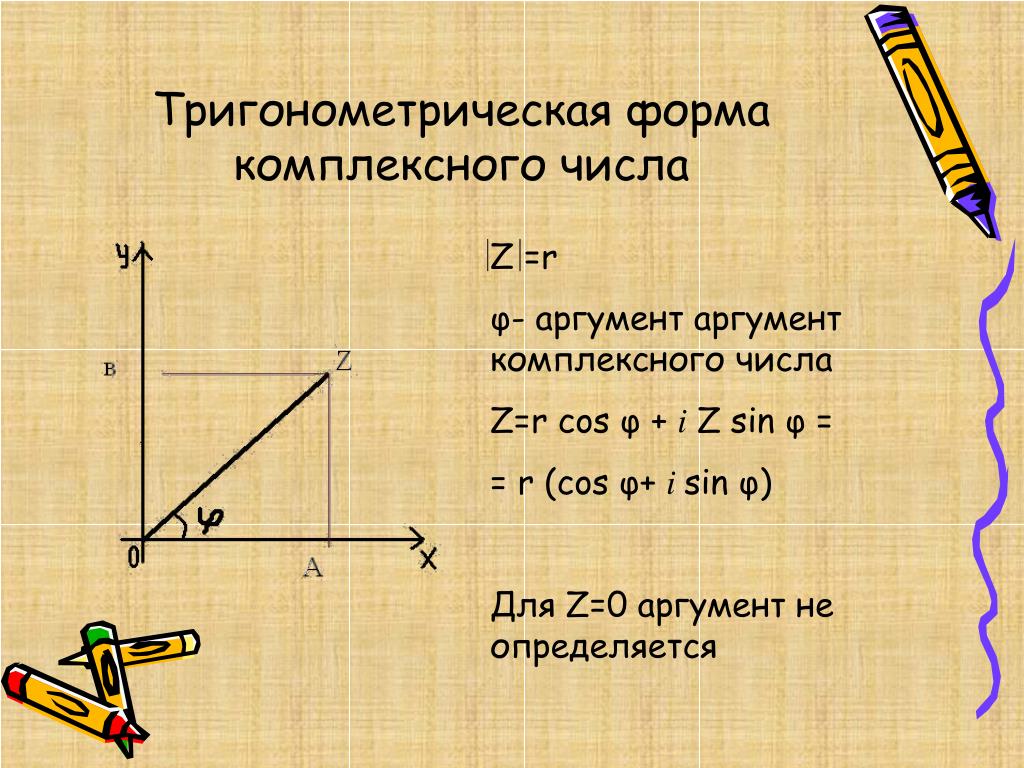
 д. \(\left\vert ac+bd\right\vert \leq \left\vert z\overline{w}\right\vert =\left\vert z\right\vert \left\vert w\right\vert .\ ) 9{2}\номер\]
д. \(\left\vert ac+bd\right\vert \leq \left\vert z\overline{w}\right\vert =\left\vert z\right\vert \left\vert w\right\vert .\ ) 9{2}\номер\]
 com/first-course-linear-алгебра
com/first-course-linear-алгебра