Комплексной плоскости изобразить множество точек: Решение задач по математике | Комплексные числа. множества в комплексной плоскости

Изобразите на рисунке множество точек z комплексной плоскости, удовлет… — Учеба и наука

Лучший ответ по мнению автора

18. 10.18 Лучший ответ по мнению автора

Другие ответы

Ответ в чате 18. 10.18

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1

Решено

вычислить скалярное произведение векторов m и n, если m=a + 2b — c, n=2a — b. /a/=2. /b/=3. угол между а и b равен 60 градусов. с перпендикулярно а, с перпендикулярно b

Решено

2. Задана функция y = x2 + 4x + 3. Постройте его график и с помощью графика найдите: а) промежутки, в которых график возрастает; б) промежутки в

Решено

В треугольнике АВС В1-середина АС, точка А1 лежит на стороне ВС так, что ВА1 : А1С = 1 : 2. Используя векторы, докажите, что середина ВВ1 лежит на прямой АА1.

Решено

постройте график функции y=x-8x+13 a) значения y = 1.5 b) значения х, при которых y = 2 с) нули функции промежутки в которых y 0 и в которых y

Пользуйтесь нашим приложением

4.4. 4.5.

5. Решить квадратное уравнение:

5.1. .5.2. .

5.3. .5.4.

6. Найти все значения корней и построить их на комплексной плоскости:

6.1. .6.2. .6.3.

7. Решить уравнения:

7.1. .7.2. .7.3. .

7.4. .7.5. .7.6.

8. Выполните арифметические действия над комплексными числами Изобразите найденные числа на комплексной плоскости.

9. Изобразить на рисунке множества точек z комплексной плоскости, удовлетворяющих условию:

9.1. .9.2. .

9.3. .9.4.

Дополнительные задания

Д-1. Найти действительную и мнимую части комплексных чисел:

Д-1.1. .Д-1.2. .Д-1.3.

Д-2. Найти модуль и главное значение аргумента комплексных чисел:

Д-2.1. .Д-2.2. .

Д-3. Выполните арифметические действия над комплексными числами. Изобразите найденные числа на комплексной плоскости:

Д-3.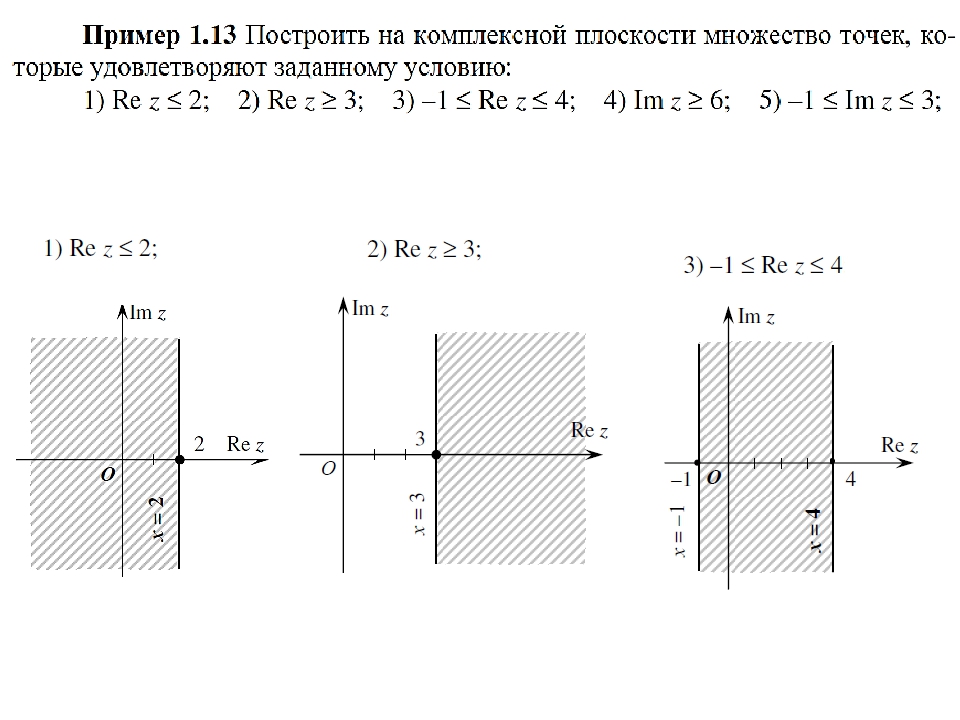 1. .Д-3.2. .

Д-3.3.

Д-4. Изобразить множество всех точек комплексной плоскости, удовлетворяющих данным неравенствам

Д-4.1. .Д-4.2.

Д-5. Изобразить область, заданную неравенствами

Д-6. Замкнутое множество, изображенное на рисунке, задать системой неравенств

Д-7. Выполнить действия. Результат представить в алгебраической форме:

Д-7.1. .Д-7.2.

Д-8. Решить уравнения:

Д-8.1. .Д-8.2.

Д-9. Решить систему уравнений

Итоговый самоконтроль

С-1. Как расположены комплексно-сопряженные числа в комплексной плоскости?

С-2. Определите модуль числа

С-3. Чему равно значение ?

С-4. Что собой представляет множество точек комплексной плоскости, для которых:

С-4.1. .С-4.2. .С-4.3. .

С-4.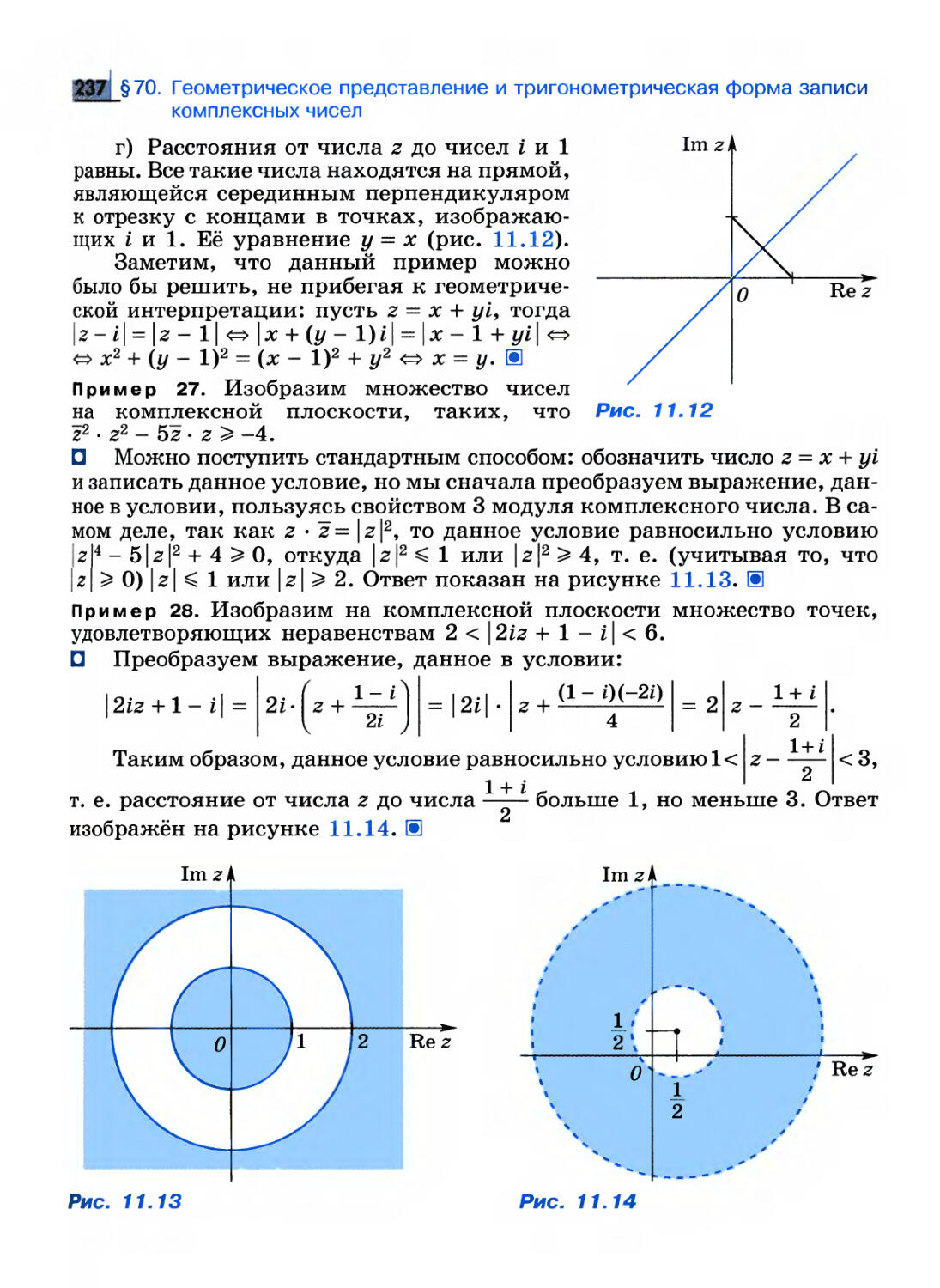 4.

.С-4.5. ?

С-5. Где расположены действительные числа, мнимые числа в комплексной плоскости?

С-6. Следующие комплексные числа изобразить векторами и записать в тригонометрической и показательной формах, отметить на рисунке модуль и аргумент.

С-6.1. .С-6.2. .С-6.3.

С-7. Представить в алгебраической форме числа

С-7.1. .С-7.2.

С-8. Представить в тригонометрической форме комплексные числа:

С-8.1. .С-8.2. .

С-8.3.

C-9. Найти наибольшее и наименьшее значения , если

С-10. При каких значениях икомплексные числаи:

С-10.1. Равны? С-10.2. Сопряжены?

С-11. Могут ли быть сопряженными: два действительных числа? два чисто мнимых? действительное и мнимое число?

С-12. Пусть Чему равен?

С-13. Какое из чисел больше: или?

С-14. Найти действительные решения уравнения:

С-14.1. .С-14.2.

С-15. Вычислить

С-16. Изобразить на комплексной плоскости множество точек , удовлетворяющих условию

С-16.1. .С-16.2.

С-17. Найти и, если:

С-17.1. .С-17.2.

С-18. Доказать справедливость тождества:

С-18.1. .С-18.2.

С-19. Дано Найтии

С-20. При каких действительных значениях ичислаибудут сопряженными?

С-21. Может ли сумма квадратов двух комплексных чисел быть отрицательной?

Объяснение урока: Диаграмма Аргана | Nagwa

В этом объяснении мы узнаем, как идентифицировать комплексные числа, нанесенные на диаграмму Аргана, и узнаем их геометрические свойства.

Одна из самых удивительных особенностей комплексных чисел заключается в том, что они вводят геометрическую интерпретация знакомых арифметических операций.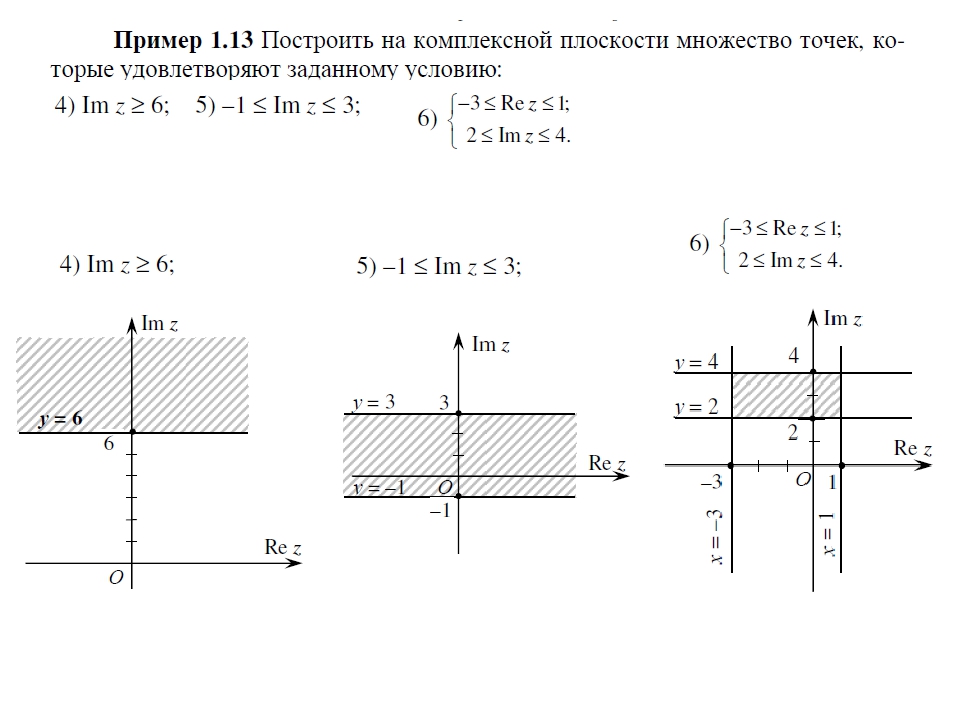 Работая с чисто действительными числами, мы могли бы выразить их на одномерной числовой прямой. Такое мышление дало нам дополнительные представление об их свойствах. Принимая во внимание, что с введением 𝑖 мы можем добавить второе измерение и рассматривать комплексные числа как точки на плоскости, мы обнаружим, что визуализация комплексных чисел таким образом даст нам дополнительное понимание их характеристики.

Определение: Диаграмма Аргана

Комплексные числа могут быть представлены геометрически на двумерной плоскости с двумя перпендикулярные оси, представляющие действительную и мнимую части числа соответственно. Комплексное число 𝑧=𝑥+𝑦𝑖 представлено точкой (𝑥,𝑦) в декартовых координатах. Этот самолет называют комплексная плоскость, плоскость Аргана или диаграмма Аргана.

Начнем с простого примера, где мы определим декартовы координаты комплексного числа на диаграмме Аргана.

Пример 1: Координаты комплексных чисел на диаграмме Аргана

Если число 𝑍=8+𝑖 представлено на диаграмме Аргана точки 𝐴, определите декартовы координаты этой точки.

Ответ

Из определения диаграммы Аргана мы знаем, что комплексное число 𝑧=𝑎+𝑏𝑖 будет представлено точкой с декартовыми координатами (𝑎,𝑏).

Следовательно, 𝑍 будет представлен точкой 𝐴(8,1).

В следующем примере мы идентифицируем комплексные числа и их сопряженные числа по диаграмме Аргана.

Пример 2. Представление комплексных чисел на диаграмме Аргана

Семь комплексных чисел 𝑧, 𝑧, 𝑧, 𝑧, 𝑧, 𝑧 и 𝑧 представлены на Аргане. диаграмма.

1. Какое из комплексных чисел равно −3+2𝑖?
2. Какое комплексное число представлено 𝑧?
3. У какого комплексного числа действительная и мнимая части равны?
4. Какие два комплексных числа являются сопряженной парой? Какова их геометрическая отношение?

Ответ

Часть 1

Согласно определению диаграммы Аргана комплексное число −3+2𝑖 будет представлен точкой (−3,2). Считая эти координаты с плоскости, мы находим, что −3+2𝑖=𝑧.

Часть 2

Начнем с считывания координат 𝑧 с диаграммы Аргана в виде (−4,−1), которые по определению представляют собой комплекс число −4−𝑖. Следовательно, 𝑧=−4−𝑖.

Часть 3

На прямой будет лежать комплексное число с равными действительными и мнимыми частями 𝑥=𝑦. Проводя эту линию на диаграмме Аргана, мы находим, что только один числа лежит на этой строке: 𝑧.

Часть 4

Напомним, что комплексное сопряжение 𝑧=𝑎+𝑏𝑖 равно 𝑧=𝑎−𝑏𝑖. Следовательно, мы могли бы построить 𝑧 в точке (𝑎, 𝑏), а мы могли бы построить 𝑧 в точке (𝑎, −𝑏). Следовательно, точки, представляющие комплексное число и его сопряженное имеют одинаковое 𝑥-значение, но противоположные 𝑦-значения. Смотрящий на приведенной нами диаграмме мы видим только две пары точек с одинаковыми 𝑥-координаты: 𝑧 и 𝑧 и 𝑧 и 𝑧. Учитывая 𝑧 и 𝑧, получаем, что 𝑦-координата 𝑧 равно 3, тогда как 𝑦-координата 𝑧 равно −2. Следовательно, эти два не являются комплексом сопряженная пара, тогда как, учитывая 𝑧 и 𝑧, мы найти, что 𝑦-координата 𝑧 равна 3 и 𝑦-координата 𝑧 равна −3. Следовательно, они представляют собой комплексно-сопряженную пару. Кроме того, мы видим, что как сложный сопряженная пара, точки 𝑧 и 𝑧 связаны соотношением отражение на действительной оси (𝑥-оси).

Используя диаграммы Аргана, мы можем геометрически интерпретировать сложение комплексных чисел. Для двоих комплексные числа 𝑧=𝑎+𝑏𝑖 и 𝑧=𝑐+𝑑𝑖, их сумма можно выразить как 𝑧+𝑧=(𝑎+𝑐)+(𝑏+𝑑)𝑖. Если мы построим эти числа на диаграмме Аргана мы нанесли бы точки (𝑎,𝑏), (𝑐,𝑑) и (𝑎+𝑐,𝑏+𝑑). Рассмотрение этих моментов предполагает некоторые своего рода эквивалентность между комплексными числами и векторами. Это действительно так, и для количество операций с комплексными числами, считая их векторами в матрице Аргана. схема на самом деле наиболее информативна. В частности, для сложения и вычитания мы можем рассмотрим два комплексных числа 𝑧 и 𝑧, чтобы представлены векторы с компонентами (𝑎,𝑏), (𝑐,𝑑) соответственно. Таким образом, добавление комплексные числа можно интерпретировать как сложение векторов. Например, сложение комплексных чисел 1+2𝑖 и 3+𝑖 по правилу параллелограмма можно представлено следующим образом.

В следующем примере мы вычислим сложение двух комплексных чисел, используя показанный выше графический подход.

Пример 3. Нахождение суммы двух комплексных чисел, представленных в аргане Диаграмма

Используя показанную диаграмму Аргана, найдите значение 𝑧+𝑧.

Ответ

Одним из способов сложения комплексных чисел, данных на диаграмме Аргана, является считывать значения и добавлять их алгебраически. Напомним, что точка (𝑎,𝑏) на диаграмме Аргана представляет собой комплексное число 𝑎+𝑏𝑖. Таким образом, находим выражения для 𝑧 и 𝑧 путем определения точек.

Мы видим, что 𝑧 находится в (2,3), поэтому 𝑧=2+3𝑖, а 𝑧 находится в точке (−4,−3), поэтому 𝑧=−4−3𝑖.

Теперь мы можем складывать числа, складывая их действительные и мнимые компоненты соответственно: 𝑧+𝑧=(2+3𝑖)+(−4−3𝑖)=(2−4)+(3−3)𝑖=−2+0𝑖=−2.

Таким образом, ответ равен −2.

Кроме того, отметим, что если мы построим −2 как точка (−2,0) на диаграмме, это один из концов диагонали параллелограмма, противоположные вершины которого равны 𝑧 и 𝑧.

Только что увидев, как сложение комплексных чисел может быть представлено с помощью закона параллелограмма на диаграмме Аргана, мы можем задаться вопросом, как другие геометрические конструкции соответствуют операциям с комплексными числами. Для Например, как насчет середины между двумя комплексными числами? Давайте рассмотрим эту идею на следующем примере.

Пример 4. Нахождение середины двух комплексных чисел, нарисованных на аргане Диаграмма

Какое комплексное число лежит на середине 𝑧 и 𝑧 на заданной комплексной плоскости?

Ответ

Существуют различные способы найти среднюю точку между двумя точками. доступны для нас. Один из способов заключается в использовании Формула середины отрезка. Конкретно, для заданных конечных точек (𝑥,𝑦) и (𝑥,𝑦), середина является 𝑥+𝑥2,𝑦+𝑦2.

Из диаграммы Аргана видно, что 𝑧 имеет координаты (−2,7) и 𝑧 имеет координаты (6,−3). Поэтому, используя формулу, их середина −2+62,7+(−3)2=42,42=(2,2).

Напомним, что точка (𝑎,𝑏) на диаграмме Аргана представляет собой комплексное число 𝑎+𝑏𝑖. Таким образом, комплекс число, лежащее посередине 𝑧 и 𝑧 равно 2+2𝑖.

Давайте рассмотрим значение ответа на последний пример. Читая точки с диаграммы Аргана, мы можем видеть, что 𝑧 и 𝑧 расположен в координатах (−2,7) и (6,−3) соответственно, а значит, равны 𝑧=−2+7𝑖,𝑧=6−3𝑖.

Если рассматривать их сумму, то 𝑧+𝑧=(−2+6)+(7−3)𝑖=4+4𝑖.

Обратите внимание, что это двойное 2+2𝑖, что было средней точкой, которую мы рассчитали. На самом деле это общее свойство это относится к середине любых двух чисел на комплексной плоскости.

Свойство: Середина комплексных чисел

Середина отрезка между двумя комплексными числами 𝑧 и 𝑧 на диаграмме Аргана соответствует к комплексному числу 𝑧, заданному формулой 𝑧=𝑧+𝑧2.

Далее исследуем геометрические отношения между точками на диаграмме Аргана и их соответствующим комплексом аналоги в следующем примере.

Пример 5. Нахождение умножения комплексного числа на диаграмме Аргана вещественным числом

Используя приведенную ниже диаграмму Аргана, найдите значение −2𝑧.

Ответ

Нас просят найти что −2𝑧 задан 𝑧 на диаграмме Аргана, которую мы можем определить, найдя комплексное число, на которое ссылается 𝑧, и умножение его на −2.

Напомним, что точка с координатами (𝑎,𝑏) на диаграмме Аргана относится к комплексному числу 𝑎+𝑏𝑖. Так как 𝑧 находится в точке (1,−2), это означает, что 𝑧=1−2𝑖.

Теперь мы можем умножить это число на -2, чтобы найти новое число: −2𝑧=−2(1−2𝑖)=−2(1)−2(−2𝑖)=−2+4𝑖.

Хотя это и не требуется, мы можем изобразить результат умножения из предыдущего вопроса на диаграмме.

Интерпретируя это геометрически, мы видим, что расстояние от происхождение было удвоено, но в противоположном направление. Это соответствует расширению точки с масштабный коэффициент −2 с центром в начале координат. В качестве альтернативы мы можем думайте об этом как о вращении на 𝜋 радиан вокруг начала координат с последующим расширением с масштабным коэффициентом 2. Это концепция, которую мы можно обобщить.

Свойство: умножение на действительные числа на диаграмме Аргана

Если комплексное число 𝑧 умножается на действительное число 𝑐, это соответствует расширению с масштабным коэффициентом 𝑐 с центром в начале координат на диаграмме Аргана.

Теперь обратим внимание на геометрическую интерпретацию умножения на 𝑖.

Пример 6. Нахождение квадранта, в котором комплексное число лежит на аргане Диаграмма

Рассмотрим комплексное число 𝑧=5+3𝑖. Если 𝑖𝑧 представлено на диаграмме Аргана точка 𝐴, в каком квадранте плоскости Аргана находится 𝐴 ложь?

Ответ

Самый простой способ решить эту проблему — начать с расчет 𝑖𝑧 напрямую: 𝑖𝑧=𝑖(5+3𝑖)=5𝑖+3𝑖=−3+5𝑖.

Теперь нарисуем это на диаграмме Аргана (вместе с исходной точка для справки). Напомним, что число 𝑎+𝑏𝑖 соответствует точке (𝑎,𝑏) на диаграмма Аргана. Таким образом, мы нанесем точки (5,3) и (−3,5) для 𝑧 и 𝑖𝑧 соответственно.

Используя соглашение о том, что верхний правый квадрант является первым квадрант, и продолжая движение против часовой стрелки, мы можем видите, что наша точка 𝐴 (т. е. точка, представляющая 𝑖𝑧) лежит во втором квадранте.

Дадим геометрическую интерпретацию преобразования из предыдущего примера. На диаграмме Аргана мы видим, что точка осталась на том же расстоянии от начала координат, но угол ее с реальной осью изменился. В частности, исходная точка была повернута вокруг начала координат на угол 𝜋2 радиана (положительно, так как это вращение против часовой стрелки). Это качество справедливо для общих случаев.

Свойство: Умножение на 𝑖 на диаграмме Аргана

Если комплексное число 𝑧 умножается на 𝑖, это соответствует вращению (против часовой стрелки) на 𝜋2 о начало на диаграмме Аргана.

Кстати, мы можем видеть, как это связано с предыдущим свойством умножение на действительные числа. Если комплекс число умножается на 𝑖 дважды, это то же самое, что умножение на 𝑖=−1. Используя определение, данное ранее, это будет расширением с коэффициентом масштабирования -1. Эквивалентно, используя наше новое определение, это будет два оборота на 𝜋2 (или один оборот на 𝜋), что в конечном итоге имеет тот же эффект.

Давайте вспомним основные вещи, которые мы узнали из этого объяснения.

Ключевые точки

• Комплексные числа можно интерпретировать как точки или векторы на диаграмме Аргана.
• Многие операции с комплексными числами можно интерпретировать геометрически.

Операция	Геометрическая интерпретация
Добавление 𝑧 = 𝑎+𝑏𝑖	Перевод от Vector (𝑎, 𝑏)
Сознание 9017.0171
Умножение на действительное число 𝑐	Расширение с центром в начале координат с масштабным коэффициентом 𝑐
Умножение на 𝑖 происхождение

Комплексные числа и полярные координаты

Давным-давно математики погрузились в свое воображение и изобрели совершенно новый набор чисел. Им нужны были эти числа, чтобы решить некоторые математические задачи — задачи, в которых встречается квадратный корень из отрицательного числа.

Такие области, как инженерия, электричество и квантовая физика, используют мнимые числа в своих повседневных приложениях. Мнимое число в основном представляет собой квадратный корень из отрицательного числа. Мнимая единица , обозначается как i, является решением уравнения i ² = –1.

Комплексное число может быть представлено в виде a + bi, , где a и b — действительные числа, а i обозначает мнимую единицу. В комплексном числе a + bi, a называется действительной частью, а b называется мнимой частью. Действительные числа можно рассматривать как подмножество комплексных чисел, имеющих вид a + 0 i. Когда a равно нулю, тогда 0 + bi записывается просто как bi и называется чисто мнимым числом.

Как выполнять операции с комплексными числами и строить графики

Комплексные числа в виде a + bi можно изобразить на комплексной координатной плоскости . Каждое комплексное число соответствует точке ( a , b ) на комплексной плоскости. Действительная ось — это прямая на комплексной плоскости, состоящая из чисел, имеющих нулевую мнимую часть: a + 0 i. Каждое действительное число соответствует уникальной точке на действительной оси. Мнимая ось — это прямая на комплексной плоскости, состоящая из чисел, имеющих нулевую действительную часть: 0 + би. На рисунке показано несколько примеров точек на комплексной плоскости.

График комплексных чисел.

Сложение и вычитание комплексных чисел — это еще один пример сбора подобных терминов: вы можете складывать или вычитать только действительные числа, а складывать или вычитать — только мнимые числа.

При умножении комплексных чисел вы СЛОМАЕТЕ два двучлена. Все, что вам нужно сделать, это помнить, что воображаемая единица определяется так, что i ² = –1, поэтому каждый раз, когда вы видите i ² в выражении замените его на –1. Имея дело с другими степенями i, обратите внимание на следующую закономерность:

.

Так продолжается вечно, повторяя в цикле каждую четвертую силу. Чтобы найти большую степень i, , а не считать бесконечно, поймите, что схема повторяется. Например, чтобы найти i ²⁴³ , разделите 4 на 243, и вы получите 60 с остатком 3. Шаблон повторится 60 раз, и тогда у вас останется 3, так что i ²⁴³ = i ²⁴⁰ × i ³ = 1 × i ³ i 9019, то есть – 9019.

Сопряжение комплексного числа a + bi равно a – bi и наоборот. Когда вы умножаете два комплексных числа, которые являются сопряженными друг с другом, вы получаете чистое действительное число:

( a + bi )( a – bi ) = A ² — ABI + ABI — B ² I ²

Combining Like Tempsing Like Tempsing Like Tempsing Like Tempsing Like Tempsing Like Tempsing Like Tempsing Like Tempsing Like Tempsing Like Tempsing Like Tempsing Like Like Tempsicing Like Tempsing Like Tempsing Like Tempsip ² – b ² (–1) = a ² + b ²

Помните, что абсолютные значения представляют собой столбцы, представляющие действительное числовое расстояние. В случае комплексного числа | а + би| представляет собой расстояние от точки до начала координат. Это расстояние всегда равно длине гипотенузы прямоугольного треугольника, проведенного при соединении точки с осями х и у .

При делении комплексных чисел числитель и знаменатель умножаются на сопряженное. Если задействован квадратный корень числа, то вы будете рационализировать знаменатель.

В общем случае задача на деление комплексных чисел выглядит так:

Вокруг столба: как построить график полярных координат

До сих пор ваш опыт построения графиков мог быть ограничен прямоугольной системой координат . Прямоугольная система координат получила такое название, потому что она основана на двух числовых линиях, перпендикулярных друг другу. Пришло время развить эту концепцию и ввести полярных координат.

В полярных координатах каждая точка расположена вокруг центральной точки, называемой полюсом , и названной ( r ,n θ ). r — это радиус, а θ — это угол, образованный между полярной осью (представьте, что использовал как положительную ось x ) и отрезком, соединяющим точку с полюсом (что использовал как источник).

В полярных координатах углы обозначаются либо в градусах, либо в радианах (или в обоих). На рисунке показана полярная координатная плоскость.

Круговое построение графиков в плоскости полярных координат.

Обратите внимание, что точка на плоскости полярных координат может иметь более одного имени. Поскольку вы движетесь по кругу, вы всегда можете прибавить или вычесть 2π к любому углу и оказаться в одной и той же точке. Это важная концепция при графическом отображении уравнений в полярных формах, поэтому в этом обсуждении она будет хорошо освещена.

Если и радиус, и угол положительны, угол движется против часовой стрелки. Если радиус положительный, а угол отрицательный, точка движется по часовой стрелке.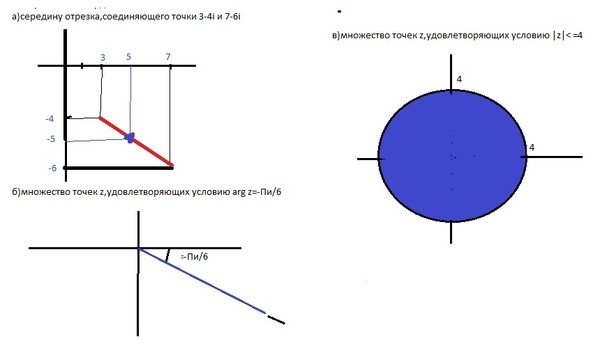 Если радиус отрицательный, а угол положительный, сначала найдите точку, в которой оба значения положительны, а затем отразите эту точку на полюсе. Если и радиус, и угол отрицательные, найдите точку, в которой радиус положительный, а угол отрицательный, а затем отразите ее на полюсе.

Переключение на полярную и обратно

Вы можете использовать как полярные, так и прямоугольные координаты для обозначения одной и той же точки на координатной плоскости. Иногда проще написать уравнение в одной форме, чем в другой, поэтому это должно познакомить вас с вариантами выбора и с тем, как переключаться с одной формы на другую. На этом рисунке показано, как определить взаимосвязь между этими двумя не такими уж разными методами.

Прямоугольный треугольник показывает взаимосвязь между прямоугольными и полярными координатами.

Немного тригонометрии прямоугольного треугольника и теорема Пифагора:

Полярные уравнения Когда вам дадут уравнение в полярном формате и попросят построить его график, вы всегда можете воспользоваться методом «подключи и пыхни»: выберите значения для θ из единичного круга, который вы так хорошо знаете, и найдите соответствующее значение r . У полярных уравнений есть различные типы графиков, и их легче изобразить, если у вас есть общее представление о том, как они выглядят.

спираль Архимеда

r = aθ дает график, образующий спираль. a — это константа, умножающая угол. Если и положительны, спираль движется против часовой стрелки, как и положительные углы. Если a отрицательно, спираль движется по часовой стрелке.

Кардиоидная

Вы можете узнать слово кардиоида , если вы когда-либо тренировались и делали кардио. Это слово относится к сердцу, и когда вы рисуете кардиоидную диаграмму, она действительно выглядит как сердце. Кардиоиды записываются в форме ИЛИ.

Уравнения косинуса — это сердечки, которые указывают влево или вправо, а уравнения синусов открываются вверх или вниз.

Роза

Роза под любым другим названием — это… полярное уравнение. Если r = a sin bθ или r = a cos bθ , то графики выглядят как цветы с лепестками.