Комплексные числа примеры тригонометрическая форма: Комплексные числа, примеры с решением

2=-1$ .

Рассмотрим некоторую точку $M(a,b)$ комплексной плоскости. Введем полярную систему координат следующим образом:

• полюс полярной системы координат будет совпадать с началом координат комплексной плоскости, т.е. точкой $O(0;0)$;
• полярная ось будет совпадать с положительным направлением оси $Ox$ .

Обозначим полярные координаты рассматриваемой точки М через $r$ и $\varphi$,

где $r \ge 0$ (рис. 1).

Рис. 1

Связь координат двух систем задается следующими равенствами:

$a=r \cos \varphi $, $b=r \sin \varphi $

Подставим приведенные выше равенства в запись заданного комплексного числа в виде $z=a+bi$ и получим

$$z=r \cos \varphi + i \cdot r \sin \varphi$$

или

$$z=r(\cos \varphi + i \cdot \sin \varphi)$$

Определение 2

Запись некоторого комплексного числа $z$ в виде $z=r(\cos \varphi + i \cdot \sin \varphi)$ называется тригонометрической формой записи, при этом число $r$ — модуль данного комплексного числа $z$ , $\varphi$ — аргумент данного комплексного числа $z$ .

2}} \end{cases} \end{equation*}$$

Примечание 1

Аргумент вещественных чисел равен соответственно:

• 0 для положительного числа;
• $\pi$ для отрицательного числа.

Примечание 2

Аргумент чисто мнимых чисел равен соответственно:

$ \frac {\pi}{2} $ с положительной мнимой частью;

$ \frac {3\pi}{2} $ с отрицательной мнимой частью.

Примечание 3

Аргумент некоторого комплексного числа $z$ считается:

положительным $( \varphi >0)$ при отсчете против часовой стрелки от положительного направления оси $Ox$;

отрицательным $( \varphi

Примечание 4

Аргумент некоторого комплексного числа $z$ определяется не однозначно, а с точностью до слагаемого $2 \pi k$, где $k \in Z$.

Пример 1

Представить в тригонометрической форме заданные комплексные числа, для которых: 1) $r=0, \varphi=5 \pi$ ; 2) $r=10, \varphi= \frac {\pi}{2}$ ; 3) $r= \sqrt {2}, \varphi =- \frac {\pi} {3}$ ; 4) $r=3, \varphi = 0$.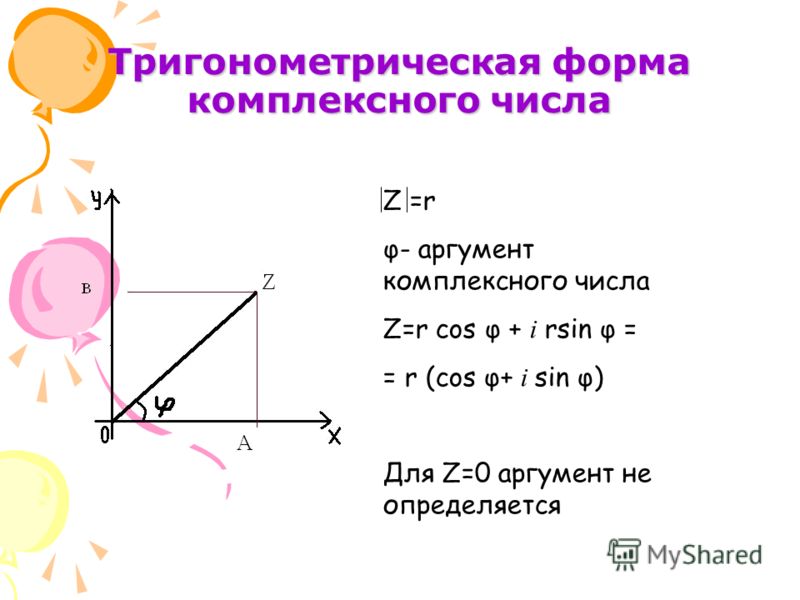

Решение:

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos \varphi + i \cdot sin \varphi)$.

Для $r=0, \varphi=5 \pi$ получаем комплексное число $z=0 \cdot (cos5 \pi + i \cdot sin 5 \pi)$.

Для $r=10, \varphi = \frac {\pi}{2}$ получаем комплексное число $z=10 \cdot (cos \frac {\pi}{2} + i \cdot sin \frac {\pi} {2}$.

Для $r= \sqrt {2}, \varphi=- \frac {\pi}{3}$ получаем комплексное число $z= \sqrt {2} \cdot (cos (- \frac {\pi}{3}) + i \cdot (- \frac {\pi}{3}))$.

Для $r=3, \varphi=0$ получаем комплексное число $z=3 \cdot (cos0+i \cdot sin0)$.

Определение 3

Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:

• $a$ — вещественная (действительная) часть, обозначение Re$z=a$;
• $b$ — мнимая часть, обозначение Im $z=b$.

Алгоритм 1

Чтобы комплексное число $z$, записанное в алгебраической форме, привести к тригонометрической форме записи, необходимо выполнить следующее:

• вычислить модуль и аргумент;
• подставить полученные значения в выражение $z=r(cos \varphi + i \cdot sin \varphi)$. {\pi \cdot i}$.

  Решение:

  Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos \varphi + i \cdot sin \varphi)$.

  1) Определим значения модуля и аргумента: $r=3, \varphi = \frac {\pi}{3}$.

  Запись числа в тригонометрической форме имеет вид: $z=3 \cdot (cos \frac {\pi}{3} + i sin \frac {\pi}{3})$.

  2) Определим значения модуля и аргумента: $r=6, \varphi = \pi$.

  Запись числа в тригонометрической форме имеет вид: $z=6 \cdot (cos \pi + i sin \pi)$.

  Вывод

  Таким образом, можно сделать вывод о том, что в каком бы виде не было записано комплексное число $z$, его всегда можно представить в тригонометрической форме записи $z=r \cdot (cos \varphi + i sin \varphi)$.

  Содержание

  Тема 18 тригонометрическая форма комплексного числа. Действия над комплексными числами в тригонометрической форме конспект 18.

  Любое комплексное число (кроме нуля) можно записать в тригонометрической форме:, где– этомодуль комплексного числа, а–аргумент комплексного числа. Изобразим на комплексной плоскости число. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что:

  Напоминаю, модулем комплексного числа

  называется расстояние от начала координат до соответствующей точки комплексной плоскости.

  Модуль комплексного числа стандартно обозначают:или

  По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедливадля любыхзначений «а» и «бэ».

  Аргументом комплексного числаназываетсяугол междуположительной полуосьюдействительной осии радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:.

  Аргумент комплексного числа стандартно обозначают:или

  Из геометрических соображений получается следующая формула для нахождения аргумента: .Внимание!Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.

  Эти случаи мы тоже разберем.

  Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.

  Пример 1

  Представить в тригонометрической форме комплексные числа: ,,,.

  На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа:

  Запомним намертво, модуль – длина(которая всегданеотрицательна), аргумент –угол.

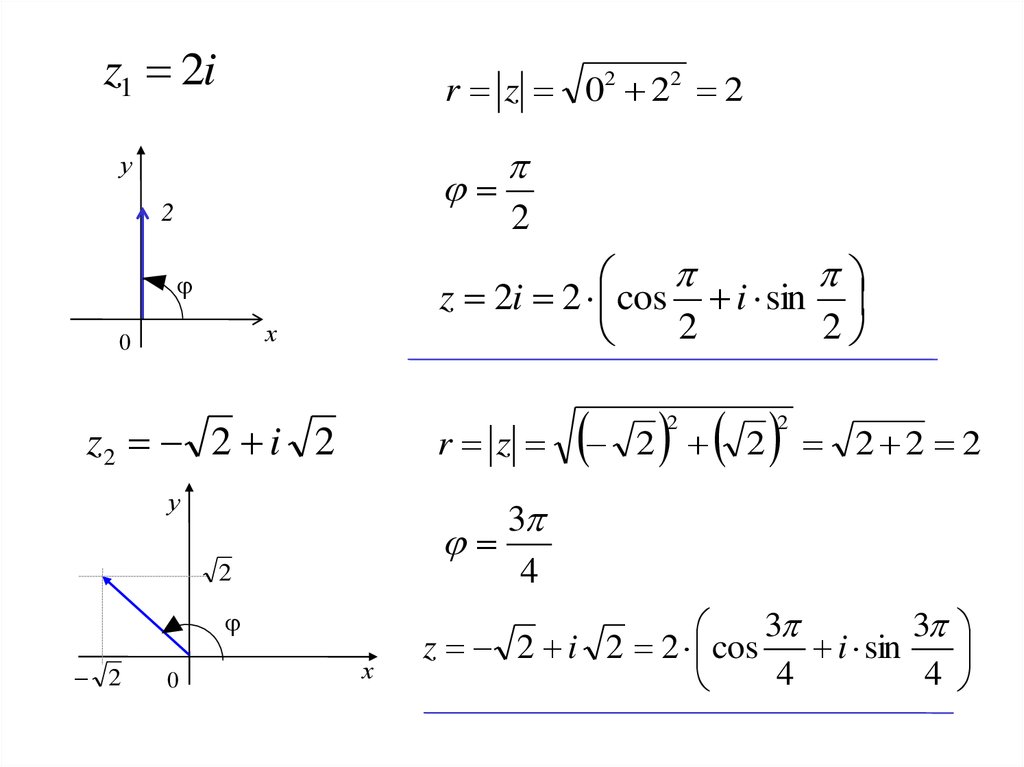
  1) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:.

  Ясно, как день, обратное проверочное действие:

  2) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме:.

  Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

  3) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме:.

  Проверка:

  4) И четвёртый интересный случай. Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:.

  Аргумент можно записать двумя способами: Первый способ: (270 градусов), и, соответственно:. Проверка:

  18.2 ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ

  Частное комплексных чисел

  Произведение комплексных чисел

  Возведение комплексных чисел в степень

  формула Муавра

  Пример 2

  найти.

   

  Тогда, по формуле Муавра:

  Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря,  нужно избавиться от лишних оборотов. Один оборот составляетрадиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе:оборотов, в данном случае можно убавить один оборот:. Надеюсь всем понятно, чтои– это один и тот же угол.

  Таким образом, окончательный ответ запишется так:

  Любители стандартов везде и во всём могут переписать ответ в виде: (т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).

  Хотя – ни в коем случае не ошибка.

  ПРАКТИКУМ 18

  ЗАДАНИЕ N 1Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

  Решение:Для представления комплексного числа в тригонометрической форме записи необходимо найти его модуль и аргумент. Используя формулу, где– действительная, а– мнимая часть комплексного числа, получим:По формуламинайдем аргументкомплексного числа. Обращаем внимание, что под аргументомпонимается его главное значение, то есть значение, удовлетворяющее условиюТак кактоЗная, что тригонометрическая форма комплексного числа имеет видполучим:

  ЗАДАНИЕ N 2Тема: Тригонометрическая форма комплексного числаПроизведение комплексных чиселиравно …

  Решение:Воспользуемся формулой:Получим:

  ЗАДАНИЕ N 3Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

  Решение:Для представления комплексного числа в тригонометрической форме записи необходимо найти его модуль и аргумент.

  Заметим, что мнимая часть данного комплексного числа равна нулю, поэтомуТочка, изображающая это число, принадлежит положительной части действительной оси, значит,Зная, что тригонометрическая форма комплексного числа имеет видполучим:

  ЗАДАНИЕ N 4Тема: Тригонометрическая форма комплексного числаЧастноекомплексных чиселиравно …

  Решение:Воспользуемся формулой:Получим:

  ЗАДАНИЕ N 5Тема: Тригонометрическая форма комплексного числаСтепень комплексного числаравна …

  Решение:Согласно формуле Муавранаходим:

  САМОСТОЯТЕЛЬНАЯ РАБОТА 18

  ЗАДАНИЕ N 1Тема: Тригонометрическая форма комплексного числаСтепень комплексного числаравна …

  ЗАДАНИЕ N 2Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

  ЗАДАНИЕ N 3Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

  ЗАДАНИЕ N 4Тема: Тригонометрическая форма комплексного числаЧастноекомплексных чиселиравно …

  ЗАДАНИЕ N 5Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

   ЗАДАНИЕ N 6Тема: Тригонометрическая форма комплексного числаЧастноекомплексных чиселиравно …

  ЗАДАНИЕ N 7Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

   

  ЗАДАНИЕ N 8Тема: Тригонометрическая форма комплексного числаСтепень комплексного числаравна …

  ЗАДАНИЕ N 9Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

  ЗАДАНИЕ N 10Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

  ЗАДАНИЕ N 11Тема: Тригонометрическая форма комплексного числаЧастноекомплексных чиселиравно …

  ЗАДАНИЕ N 12Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

  ЗАДАНИЕ N 13Тема: Тригонометрическая форма комплексного числаТригонометрическая форма комплексного числаимеет вид …

  ЗАДАНИЕ N 14Тема: Тригонометрическая форма комплексного числаПроизведение комплексных чиселиравно …

  \circ}$$.

  Если мы запишем два комплексных числа в тригонометрической форме, мы получим:

  $$z_1=|z_1|\cdot[\cos(\alpha)+i \cdot\sin(\alpha)]$$

  $$z_2 =|z_2|\cdot[\cos(\beta)+i \cdot\sin(\beta)]$$

  Когда мы делаем продукт, у нас есть:

  $$$ \displaystyle \begin{array}{ рл} z_1\cdot z_2 =& |z_1|\cdot[\cos(\alpha)+i \cdot\sin(\alpha)] \cdot |z_2|\cdot[\cos(\beta)+i \cdot\sin( \бета)] \\ =& |z_1|\cdot |z_2|\cdot [\cos(\alpha)\cdot\cos(\beta)-\sin(\alpha)\cdot\sin(\beta) \\ &+ \ i\cdot (\cos(\alpha)\cdot\sin(\beta)+\sin(\alpha)\cdot\cos(\beta)) ] \end{массив} $$$ 9\circ}$$$

  и это последние два способа выражения результата в тригонометрической форме.

  Следовательно, из предыдущего определения можно сказать, что модуль произведения двух комплексных чисел равен произведению модулей множителей, а аргумент произведения равен сумме аргументов. Это тот же результат, что и в полярной форме.

  Заметим, что произведение двух сопряженных комплексных чисел является действительным числом, так как сумма аргументов равна нулю. 9\circ$$ (если мы их добавим).

  Для двух комплексных чисел всегда существует третье число, называемое частным, которое при умножении на второе (не равное нулю) дает произведение, равное первому числу. Используя свойства произведения, мы видим, что частное будет числом, модуль которого является частным модулей, а какой аргумент будет разностью двух аргументов, как и в полярной форме. Вот почему мы собираемся использовать следующую формулу для решения частных:

  9\circ i}$$$

  Тригонометрическая форма – определение, пример и объяснение

  Мы можем записывать комплексные числа через $r$ и $\theta$. Эта форма называется тригонометрической формой и является важной формой комплексных чисел, потому что гораздо легче найти корни и степени комплексных чисел, когда они находятся в их тригонометрических формах.

  Тригонометрическая форма комплексных чисел содержит расстояние координаты комплексного числа от начала координат и угол, образованный действительной осью, а также отрезок, соединяющий комплексное число и начало координат.

  Мы часто используем тригонометрическую форму комплексных чисел, чтобы проиллюстрировать их как величины с расстоянием и направлением. Когда мы хотим найти степени и корни комплексных чисел, их также легче найти, когда комплексные числа представлены в тригонометрической форме.

  В этой статье мы узнаем следующее:

  • Два важных компонента комплексных чисел в тригонометрической или полярной форме.
  • Преобразование комплексных чисел из стандартной формы в тригонометрическую.
  • Нахождение частного и произведения двух комплексных чисел в тригонометрических формах.

  Давайте продолжим и углубимся в определение комплексных чисел в тригонометрических формах.

  Что такое тригонометрическая форма?

  Тригонометрическая форма комплексных чисел также называется полярной формой комплексных чисел. Поэтому обязательно проверьте свои знания о полярных формах.

  Тригонометрическая форма комплексного числа содержит модуль $r$ и аргумент $\theta$, представляющий комплексное число. Общая тригонометрическая форма комплексных чисел: $r(\cos\theta + i\sin\theta)$.

  Из графика видно, как были получены тригонометрические или полярные формы комплексных чисел. Поскольку $a = r \cos\theta$ и $b = r \sin\theta$, $a + bi = r(\cos \theta + i\sin \theta)$.

  Отсюда $r$ представляет модуль, а $\theta$ показывает угол (или аргумент), образованный $r$ и действительной осью.

  Эти два компонента являются важными при представлении комплексных чисел в тригонометрической форме.

  Как записать комплексные числа в тригонометрической форме? 9{\circ})$ в полярной или тригонометрической форме.

  Мы можем использовать аналогичный процесс при записи других комплексных чисел в их соответствующих тригонометрических формах, поэтому обязательно попробуйте приведенный выше пример самостоятельно?

  Как умножать и делить комплексные числа в тригонометрической форме?

  Мы также можем умножать и делить комплексные числа в тригонометрической форме. 2\sin \theta_1  \sin \theta_2)]\\&= (r_1r_2)[(\cos \theta_1\cos \theta_2) + (\cos \theta_1i\sin\theta_2) + (i\sin\theta_1\cos \theta_2)+ -\sin \theta_1  \sin \theta_2] \\&=(r_1r_2)[(\cos \theta_1\cos \ theta_2-\sin \theta_1  \sin \theta_2) + i(\cos \theta_1\sin\theta_2 + \sin\theta_1\cos \theta_2) ]\\&=(r_1r_2)[\cos(\theta_1 + \theta_2) + i(\cos \theta_1\sin\theta_2 + \sin\theta_1\cos \theta_2) \\&=(r_1r_2)[(\cos \theta_1\cos \theta_2-\sin \theta_1  \sin \theta_2) + i \sin (\theta_1 + \theta_2) ] \end{выровнено}$

  Мы можем применить аналогичный процесс, чтобы вывести формулу для отношения $z_1$ и $z_2$. Но мы оставим это для вас, чтобы вы могли попробовать сами. ( Подсказка : используйте метод ФОЛЬГИ и разностные свойства синуса и косинуса).

  На данный момент имеем $\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} [\cos(\theta_1 – \theta_2) + i\sin(\theta_1 – \theta_2)]$.

  Это означает, что нам не нужно преобразовывать комплексное число в тригонометрической форме в стандартную форму, чтобы найти их произведение или частное. 9{-1} \dfrac{b}{a}\phantom{x}\end{aligned}$

  Мы также научились умножать и делить два комплексных числа в тригонометрической форме. Для двух комплексных чисел $z_1 = r_1(\cos\theta_1 + i\sin\theta_1)$ и $z_2 = r_2(\cos\theta_2+ i\sin\theta_2)$ произведение и частное будут такими, как показано ниже:

  • $z_1 z_2 = r_1r_2 [\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)]$
  • $\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} [\cos(\theta_1 – \theta_2) + i\sin(\theta_1 – \theta_2)]$

  Давайте воспользуемся этими свойствами для решения некоторых примеров, показанных ниже. Обязательно просматривайте наш раздел сводки всякий раз, когда вы чувствуете, что застряли на элементе!

  Пример 1

  Изобразите следующие комплексные числа на комплексной плоскости, затем найдите соответствующие им модули и аргументы.

  а. $-4 + 4i$
  б. 6i$
  гр. $4\sqrt{3} – 4i$

  Решение

  Давайте изобразим три комплексных числа на одной комплексной плоскости.

  No related posts.