Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит… Оснащения врачебно-сестринской бригады. Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Интересное: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей. Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция | ⇐ ПредыдущаяСтр 2 из 3Следующая ⇒ Прямая на плоскости и в пространстве. 2.3. Виды самостоятельной работы студентов. Самостоятельная работа студентов предполагает изучение теоретического материала и выполнение контрольной работы. 3. Рекомендуемая литература. Основная литература: 1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. Учебник для вузов. -М: ФИЗМАТЛИТ, 2005. -304с. 2. Владимирский Б.М., Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс: Учебник для бакалавров. –СПб.: Изд-во «Лань», 2008. -960с. ISBN: 978-5-8114-0445-2 (http://e.lanbook.com/books/element.php?pl1_id=634). 3. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия. –М.: Велби: Проспект, 2007. 4. Мышкис А.Д. Лекции по высшей математике: учебное пособие. –СПб. 5. Шипачев В.С. Высшая математика. Учебник для вузов. -М. Высшая школа, 2005. -479 с. 6. Шипачёв В.С. Задачи по высшей математике: Учеб. пособие для вузов. – М.: Высш. шк., 2005. -304с. Дополнительная литература:
4. Методические указания по изучению дисциплины. В процессе изучения данной дисциплины студенты должны сначала изучить теоретический материал и выработать навыки решения типовых задач, используя рекомендованную литературу, а затем выполнить по одной контрольной работе в каждом из семестров обучения (задания для контрольной работы приведены в разделе 5. При выполнении контрольной работы необходимо придерживаться указанных ниже правил: 1.Контрольная работа должна быть выполнена студентом в отдельной ученической тетради с полями не менее 3 см для замечаний преподавателя. 2. На обложке тетради указываются: название дисциплины; номер варианта и номера решаемых задач; Ф.И.О. студента, выполнившего работу, его номер группы и номер зачетной книжки; Ф.И.О. преподавателя, проверяющего работу (образец оформления обложки приведён в Приложении 6.4).3.Номер варианта соответствует номеру студента в списке группы. 4.Номера решаемых задач выбираются из ТАБЛИЦЫ НОМЕРОВ ВЫПОЛНЯЕМЫХ ЗАДАНИЙ (Приложение 6.5). 5.Условия задач переписываются полностью, без сокращения слов, после чего приводится их подробное решение (чертежи можно выполнять аккуратно от руки). В конце решения приводится ответ. 6.В работу должны быть включены все задачи, указанные в задании, строго по порядку номеров. 7.Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу с исправлениями на повторную проверку. 8.Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления. 9.Работа может быть выполнена заново в случае выявления серьёзных замечаний и ошибок. 10.В конце тетради рекомендуется оставлять несколько чистых страниц для дополнений и исправлений. После проверки контрольная работа предъявляется к защите. На защите студент должен показать свое умение решать задачи, подобные тем, что имеются в его контрольной работе. Образец решения типового варианта контрольной работы приведён в Приложении 6.
5. Материалы для контроля знаний студентов. Итоговой формой контроля знаний является экзамен (зачёт) в конце первого семестра обучения. На экзамене (зачёте) студент должен показать знание теоретических основ курса в объёме вопросов, приведённых в разделе 5.2и умение решать задачи, подобные тем, что имеются в его контрольной работе. Задания для контрольной работы. 1 – 10.Вычислить определитель: а)непосредственным разложением по строке; б)непосредственным разложением по столбцу. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11 – 20. 11. , 12. , 13. 15. , 16. , 17. , 18. , 19. , 20. , .
21 – 30. Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31–40.Найти общее решение системы линейных уравнений методом Гаусса: 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41 – 50. Требуется:а)найтисобственные числа и векторы матрицы ; б)исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра). 41. а) б) 42. а) б) 43. а) б) 44. а) б) 45. а) б) 46. а) б) 47. а) б) 48. а) б) 49. а) б) 50. а) б) 51 – 60.Даны векторы . Показать, что векторы образуют базис и найти координаты вектора в этом базисе. 51. 52. 53. 54. 55. 56. 57. 59. 60.
61 – 70.Даны векторы . Требуется: а)найти векторы и ; б)вычислить скалярное произведение ; в)найти проекцию вектора на направление вектора ; г)найтивекторное произведение и его модуль . 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71-80.Даны вершины треугольника .Требуется найти: а)длину стороны ;б)уравнение стороны ; в)уравнение медианы ,проведённой из вершины ; г)уравнение высоты , проведённой из вершины ; д)длину высоты ; е)площадь треугольника .Сделать чертёж. 71. . 72. 73. 74. 75. 76. 77. 78. 79. 80. 81 – 90.Даны вершины пирамиды . а)длины ребер и ;б)угол между ребрами и ; в)площадь грани ; г)объем пирамиды ; д)уравнение плоскости грани ; е)длину высоты пирамиды. 81. 82. 83. 84. 85. 86. 87. 88. 89. 90. 91–100.Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её. 91. 92. 93. 94. 95. 96. 97. 98. 99. 100. 101-110.Даны комплексные числа , , . 101. , , . 102. , , . 103. , , . 104. , , . 105. , , . 106. , , . 107. , , . 108. , , . 109. , , . 110. , , . 111-120.Дано алгебраическое уравнение . Требуетсянайти все корни алгебраического уравнения на множестве комплексных чисел. 111. . 112. . 113. . 114. . 115. . 116. . 117. . 118. . 119. . 120. . Вопросы к экзамену (зачёту). Раздел. Линейная алгебра. 1. Понятие матрицы. 2. Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу) и их свойства. Линейная комбинация матриц. 3. Определители 2-ого и 3-егопорядка, их вычисление. Основные свойства определителей. 4. Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по элементам строки или столбца. 5. Понятие системы линейных уравнений (СЛУ). Частные виды СЛУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛУ. 6. Решение, множество решений СЛУ. Совместность, несовместность, определённость, неопределённость, эквивалентность СЛУ. Элементарные преобразования СЛУ, их основное свойство. 7. Теорема Крамера (о разрешимости СЛУ порядка ). Формулы Крамера для решения СЛУ, условия их применимости. 8. Метод Гаусса решения СЛУ, условия его применимости. Базисные и свободные переменные. Нахождение общего решения СЛУ. Частные решения СЛУ. 9. Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы. 10. Матричные уравнения и их решение. Матричная форма записи СЛУ. Матричный способ (метод обратной матрицы) решения СЛУ и условия его применимости. 11. Однородные СЛУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛУ. 12. Понятие линейной независимости и зависимости частных решений однородной СЛУ. Фундаментальная система решений (ФСР), её нахождение. Представление общего решения однородной СЛУ через ФСР. 13. Минор -ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛУ (теорема Кронеккера-Капелли). 14. Понятие -мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). 15. Скалярное произведение арифметических векторов. Длина вектора и угол между векторами. Понятие ортогональности векторов. 16. Система векторов и её линейная комбинация. Понятие линейной зависимости и независимости системы векторов. Теорема о необходимом и достаточном условиях линейной зависимости системы векторов. 17. Понятие векторного пространства ,евклидова пространства . Базис, канонический базис, ранг . Разложение вектора в по векторам его базиса, координаты вектора. Теорема о единственности разложения вектора в данном базисе. 18. Понятие ортогональной системы векторов, ортогонального базиса. Нахождение координат вектора в ортогональном базисе. 19. Понятие оператора, линейного оператора. Матрица линейного оператора. Сумма (разность) операторов, произведение оператора на число, произведение оператора на оператор, обратный оператор. 20. Понятие собственного числа и собственного вектора оператора. Характеристическое уравнение. 21. Понятие квадратичной формы. Матрица квадратичной формы. Вырожденная, невырожденная, каноническая, нормальная квадратичная форма. Закон инерции квадратичных форм. 22. Понятие знакоопределённости квадратичной формы. Главные миноры матрицы квадратичной формы. Критерии знакоопределённости квадратичной формы.
Раздел. Векторная алгебра и аналитическая геометрия. 23. Понятие геометрического вектора. Равенство векторов. Противоположный вектор. Орт вектора. Графические правила сложения, вычитания, умножения вектора на число. Проекция вектора на вектор. 24. Коллинеарность и компланарность векторов. Базис и канонический базис плоскости ; базис и канонический базис пространства . Координаты вектора. 25. Понятие декартовой системы координат в . Радиус-вектор, координаты точки. Вычисление длины и направляющих косинусов вектора; координат вектора, заданного двумя точками; расстояния между точками. 26. 27. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты векторов. Вычисление угла между векторами. Условие ортогональности векторов. 28. Векторное произведение векторов, его геометрический смысл и свойства. Выражение векторного произведения через координаты векторов. Условие коллинеарности векторов. 29. Смешанное произведение векторов, его геометрический смысл и свойства. Выражение смешанного произведения через координаты векторов. Условие компланарности векторов. 30. Понятие линии на плоскости. Общее уравнение линии и его нахождение по известному геометрическому свойству её точек. Окружность и её уравнение. 31. Прямая линия на плоскости и её общее уравнение. Нормальный и направляющий векторы прямой. Нахождение уравнения прямой, проходящей через точку перпендикулярно вектору. 32. Каноническое уравнение прямой; уравнение прямой, проходящей через две точки; уравнение прямой с угловым коэффициентом; уравнение прямой в отрезках. Расстояние от точки до прямой на плоскости. Угол между прямыми на плоскости и его вычисление, условия и ½½ прямых. 33. Понятие поверхности. Общее уравнение поверхности, его нахождение по известному геометрическому свойству её точек. Сфера и её уравнение. 34. Плоскость и её общее уравнение. Нормальный вектор плоскости и его нахождение. Уравнение плоскости, проходящей через точку перпендикулярно вектору. Построение плоскости. 35. Уравнение плоскости, проходящей через три точки; уравнение плоскости в отрезках. Расстояние от точки до плоскости. Угол между плоскостями и его вычисление, условия и ½½ плоскостей. 36. Понятие линии в пространстве и её общее уравнение. Понятие прямой линии в пространстве и её общее уравнение. Направляющий вектор прямой и его нахождение. 37. Каноническое уравнение прямой в пространстве; уравнение прямой, проходящей через две точки; параметрические уравнения прямой. 38. Угол между двумя прямыми в пространстве, между прямой и плоскостью и их вычисление, условия и ½½ двух прямых, прямой и плоскости. Точка пересечения прямой и плоскости. 39. Кривая 2-ого порядка на плоскости и её общее уравнение. Классификация кривых 2-ого порядка. Приведение уравнения кривых к каноническому виду. 40. Эллипс. Каноническое уравнение эллипса. Построение эллипса. Вершины, полуоси, фокусы, эксцентриситет, общее геометрическое свойство точек эллипса. 41. Гипербола. Каноническое уравнение гиперболы. Построение гиперболы. Вершины, полуоси, фокусы, эксцентриситет, асимптоты, общее геометрическое свойство точек гиперболы. 42. Парабола. Каноническое уравнение параболы. Построение параболы. Вершина, фокус, эксцентриситет, директриса, общее геометрическое свойство точек параболы. 43. Сфера. Эллипсоид. Канонические уравнения и графики. 44. Гиперболоиды (однополостной и двуполостной). Канонические уравнения и графики. 45. Параболоиды (эллиптический и гиперболический). Канонические уравнения и графики. 46. Цилиндры (эллиптический, гиперболический, параболический), их уравнения и графики. ⇐ Предыдущая123Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… |
Контрольная работа № 6 (1 час) Вариант 1
а), б).
а) середину отрезка, соединяющего точки ; б) множество точек z, удовлетворяющих условию в) множество точек z, удовлетворяющих условию .
____________________________________________________________ 6. Решите уравнение . ___________________________________ 7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям: Контрольная работа № 6 (1 час) Вариант 2
а), б).
а) середину отрезка, соединяющего точки ; б) множество точек z, удовлетворяющих условию в) множество точек z, удовлетворяющих условию .
ческой форме: а), б).
____________________________________________________________ 6. ___________________________________ 7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям: Контрольная работа № 6 (1 час) Вариант 3
а) середину отрезка, соединяющего точки ; б) множество точек z, удовлетворяющих условию в) множество точек z, удовлетворяющих условию .
____________________________________________________________ 6. Решите уравнение . ___________________________________ 7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям: Контрольная работа № 6 (1 час) Вариант 4
а) середину отрезка, соединяющего точки ; б) множество точек z, удовлетворяющих условию в) множество точек z, удовлетворяющих условию .
ческой форме: а), б).
____________________________________________________________ 6. Решите уравнение . ___________________________________ 7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям: Контрольная работа № 6 (1 час) Вариант 5
а) точки пересечения отрезка, соединяющего точки , с координатными осями; б) множество точек z, удовлетворяющих условию в) множество точек z, удовлетворяющих условию .
ческой форме: а), б).
____________________________________________________________ 6. Решите уравнение . ___________________________________ 7. Дана точка . Изобразите множество точек для которых выполняются условия: Контрольная работа № 6 (1 час) Вариант 6
а) точки пересечения отрезка, соединяющего точки , с координатными осями; б) множество точек z, удовлетворяющих условию в) множество точек z, удовлетворяющих условию .
ческой форме: а), б) .
____________________________________________________________ 6. Решите уравнение . ___________________________________ 7. Дана точка . Изобразите множество точек для которых выполняются условия: | |||
| Контрольная работа по теме «Координатная плоскость» Отметьте на координатной плоскости точки А(6; 1) и в (-2; -3). Проведите отрезок ав. Найдите координаты точки пересечения отрезка… | Контрольная работа №2. Корень п-ой степени Вариант Вычислите : 10. 0,3 Вычислите > Решите уравнение = 3 х. Решите систему Вариант 2 Вычислите | ||
| Контрольная работа №2 «Линейное выражение» Длина отрезка ас=60 см. Точка в взята на отрезке ас так, что длина отрезка ав в 4 раза больше длины отрезка вс. Найдите длину отрезка… | Контрольная работа по теме «Деление десятичных дробей» Вариант 1 №1. (1 балл) Вычислите 53,2: 0,1 Товарный поезд был в пути 3 часа.  За первый час он проехал 40,5км, за второй – 40км, за третий – 39,2км. Найдите среднюю скорость… За первый час он проехал 40,5км, за второй – 40км, за третий – 39,2км. Найдите среднюю скорость… | ||
| Контрольная работа №1 Тема: Векторы (на 20 мин) Изобразите систему координат Oxyz и постройте точку а (1; –2; –4). Найдите расстояния от этой точки до координатных плоскостей | Контрольная работа по алгебре №1 а 10 -1 Действительные числа. Вариант 2 Вычислите: а б | ||
| Контрольная работа по теме «Компьютер и информация» 6 класс (10-15 мин) Вариант 1 Переведите число из десятичной системы счисления в двоичную Отметьте и последовательно соедините на координатной плоскости точки, координаты которых приведены в двоичной системе счисления…. | Контрольная работа №3. Вариант 1 Изобразите схематически график функции и перечислите ее свойства: а) б) Докажите, что функция f(x) = 4x tgx является нечётной | ||
| Контрольная работа Отметьте и последовательно соедините на координатной плоскости точки, координаты которых приведены в двоичной системе счисления | Контрольная работа Отметьте и последовательно соедините на координатной плоскости точки, координаты которых приведены в двоичной системе счисления | ||
| Контрольная работа №6 «Формулы» вариант 1 Вычислите: а) (53 + 132) : 21; б) 180 94 47 700 : 45 + 4946 Найдите объём прямоугольного параллелепипеда, измерения которого равны 4 м, 3 м и 5 дм |
Как комплексные числа используются в реальной жизни?
Комплексное число получается из-за корней любого n-го уравнения. Если уравнение имеет действительные корни, все в порядке, иначе уравнение может иметь корни, отличные от действительных, означает, что корни, которые не являются реальными в этой путанице корней, которые не являются реальными комплексными числами, рождаются. Если уравнение n-й степени имеет действительные корни, а также комбинацию действительных и мнимых корней. Эти комбинации действительных и мнимых корней мы назвали комплексными числами.
Если уравнение имеет действительные корни, все в порядке, иначе уравнение может иметь корни, отличные от действительных, означает, что корни, которые не являются реальными в этой путанице корней, которые не являются реальными комплексными числами, рождаются. Если уравнение n-й степени имеет действительные корни, а также комбинацию действительных и мнимых корней. Эти комбинации действительных и мнимых корней мы назвали комплексными числами.
Комплексные числа
Комплексные числа имеют форму a+ib, которую также называют общей формой комплексных чисел. В форме a+ib a — действительная часть комплексного числа, b — мнимая часть комплексного числа, а i определяется как √(-1). Есть много форм комплексных чисел. Они есть,
- Общая форма (Z = a + ib).
- Полярная форма (Z = r(cosθ + isinθ)).
- Экспоненциальная форма (Z = re iθ ).
Общая форма комплексного номера
Комплексное число имеет общую форму, которая выглядит как Z=a+ib, где a — действительная часть, b — мнимая часть, а i называется йотой, что равно √(-1). Полярная форма комплексного числа мнимая часть, а i называется йотой, что равно √(-1).
Полярная форма комплексного числа мнимая часть, а i называется йотой, что равно √(-1).
Экспоненциальная форма комплексного числа
Комплексное число имеет экспоненциальную форму, которая выглядит как Z=reiθ, где eiθ также может быть записано как cosθ+isinθ, что в конце выглядит как полярная форма.
Примечание: Мы также можем преобразовывать общую форму в полярную, экспоненциальную наоборот, также можем преобразовывать полярную форму в общую, экспоненциальную форму наоборот, а также можем преобразовывать экспоненциальную форму в общую, полярную форму наоборот наоборот Теперь нам нужно обсудить, где эти комплексные числа полезны в реальной жизни.
Комплексные числа в реальной жизниКомплексные числа используются во многих областях реальной жизни. Ниже приведены наиболее важные случаи использования комплексных чисел, а также дано их правильное объяснение.
- Комплексный номер используется в электронике.

- Комплексное число используется в электромагнетизме.
- Комплексное число используется для упрощения неизвестных корней, если корни не являются действительными для квадратных уравнений.
- Комплексные числа используются в вычислительной технике.
- Комплексный номер используется в машиностроении и гражданском строительстве.
- Комплексные числа используются в системах управления.
- Комплексные числа в электронике
В электронике мы привыкли представлять общую форму комплексного числа в цепи, имеющей напряжение и ток. В электронике схема в основном основана на токе и напряжении. Эти два элемента складываются в одно комплексное число. Z = V+ iI представляет собой комплексное представление цепи, имеющей как ток, так и напряжение, где V — часть действительной оси, а I — часть мнимой оси, так что мы можем увидеть сравнение как V, так и I, представляя в виде комплексного числа в электронике. Иногда в цепях RC или RLC, если мы хотим объединить два элемента, скажем, например, резистор и катушку индуктивности, мы можем записать это как R + jX L , а также в случае представления комплексных чисел резистора и конденсатора R + j X c , где X L = jwL и X c = 1/jwc.
- Комплексные числа в электромагнетизме
В электромагнетизме основными элементами являются электрическое поле и магнитное поле. Эти элементы представлены в виде комплексных чисел, где действительное число или действительная ось представлены электрическим полем, магнитное поле представлено мнимой частью мнимой оси.
- Комплексные числа для нахождения корней квадратного уравнения
Квадратное уравнение используется для нахождения корней уравнения. Если квадратное уравнение имеет действительные корни, то все в порядке. Если квадратное уравнение не может найти действительные корни, то говорят, что корни не являются действительными корнями, называемыми мнимыми корнями. Мнимые корни можно найти по формуле (-b + √(b 2 – 4ac))/2a, (-b – √(b 2 – 4ac))/2a – два комплексных мнимых корня, если квадратное уравнение не может в состоянии найти настоящие корни. В этом приложении мы можем использовать комплексные числа.
- Комплексные числа, используемые в вычислительной технике
В информатике данные играют важную роль. Данные нельзя увидеть визуально, потому что они представлены в виде CSV-файлов. Эти данные файла CSV можно увидеть с помощью методов визуального представления в информатике. Это визуальное представление находится только на реальной оси и воображаемой оси, поэтому комплексные числа используются для представления данных в визуальном формате для компьютерных технологий. В 2D-изображениях мы также можем использовать комплексные числа. Вращение точки, имеющей действительную и мнимую части, и перемещение точки на двумерном изображении представляет собой комплексное число.
- Комплексные числа в машиностроении и строительстве
В машиностроении и строительстве основное внимание уделяется проектированию автомобилей и зданий. Чтобы сделать это, мы должны использовать концепции 2D-проектирования, которые в основном зависят только от комплексных чисел. Повороты также используются в рисовании, поскольку точка представлена только комплексным числом.
Повороты также используются в рисовании, поскольку точка представлена только комплексным числом.
- Комплексные числа в системах управления
Системы управления Требуется преобразование системы во временной области в частотную, что должно быть выполнено с использованием преобразования Лапласа. При этом полюса и нули системы адресуются с помощью комплексной плоскости, имеющей действительную и мнимую оси. Это причина и использование комплексного числа, используемого в системе управления.
Примеры задач
Задача 1: Решите квадратное уравнение X 2 + 5X + 3 = 0 и проверьте, являются ли корни мнимыми или нет?
Решение. квадратного уравнения = (-b + √(b 2 – 4ac))/2a, (-b – √(b 2 – 4ac))/2a
= (-5 + √25 – 4 × 3 × 3)/2 × 3, (-5 – √25 – 4 × 3 × 3)/2 × 3
= (-5 + √25 – 36)/6, (-5 – √25 – 36)/6
= (-5 + √-11)/6, (-5 – √-11)/6
= (-5+i 3,3)/6, (-5-i 3,3)/6
= -0,83 + i 0,55, -0,83 – i 0,55
0,55 представлены в виде a+ib и a-ib, поэтому они являются комплексными числами. Корни квадратных уравнений могут быть комплексными числами. В этом приложении для нахождения корней квадратных уравнений используются комплексные числа.
Корни квадратных уравнений могут быть комплексными числами. В этом приложении для нахождения корней квадратных уравнений используются комплексные числа.
Задача 2: Рассчитайте импеданс RC-цепи, если резистор имеет сопротивление 2 Ом, а конденсатор имеет емкость 4 фарад в цепи, которые включены последовательно и частота f = 1 кГц?
Решение:
Учитывая, что r = 2 Ом
C = 4 Farads
Импеданс Z = R + X C , где x C = 1/JWC
Z = R + (1 (1/ /j(2 × π × f × C)
Подставив R, f, C в приведенное выше уравнение, мы получим импеданс RC-цепи
Z = 2-j(1/ 2 × 3,14 × 1 × 4)
Z = 2 – j(1/6,28 × 4)
Z = 2 – j(0,0398)
Импеданс Z = 2 – j(0,0398), который также представлен только в виде комплексных чисел. Вот почему комплексные числа используются при расчете импеданса цепи.
Задача 3: Если z 1 = 2 + 5i и z 2 = 7 + 9i. Вычислить z 1 × z 2 ?
Вычислить z 1 × z 2 ?
Решение:
Учитывая, что Z 1 = 2 + 5i и z 2 = 7 +
Z 1 × Z 2 = (4 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + 5I) (7 + + 9i)
= 14 + 18i + 35i + (i 2 ) × 45
= 14 + 53i – 145
= -31 + 53i.
z 1 × z 2 в виде комплексного числа (a + ib) = -31 + 53i.
Задача 4: Если Если z 1 = 5,5 + 5i и z 2 = 7,7 + 7i. Вычислить z 1 + z 2 ?
Solution:
Given that z 1 = 5 + 5i and z 2 = 7 + 7i
z 1 + z 2 = 5.
5 + 5i + 7.7 + 7i
= 13,2 + 12i
z 1 + z 2 в виде комплексного числа (a + ib) = 12 + 12i.
Задача 5: Если Если z 1 = 6 + 5i и z 2 = 6 + 7i. Вычислить z 1 – z 2 ?
Решение:
Учитывая, что z 1 = 6 + 5i и z 2 = 6 + 7i
z 1 — z 2 = 6 + 5i — 6 + 7i
2 = 0 + 12i
z 1 – z 2 , которое представляет собой комплексное число (a + ib) = 0 + 12i.
Задача 6: Если Если z 1 = 1 + 5i и z 2 = 2 + 5i. Вычислить z 1 /z 2 ?
Решение:
Учитывая, что z 1 = 1 + 5i и z 2 = 2 + 5i
z 1 /z 2 = 1 + 5i /2 + 5i
/z Умножить и разделить на 2 – 5i
z 1 /z 2 = 1 + 5i × (2 – 5i)/(2 – 5i)(2 + 5i)
z 1 /z 2 = (2 – 5i + 10i + 25)/(4 + 25)
z 1 /z 2 = (27 + 5i)/29
z 07 / 30073 41 2 = 0,93 + i 0,17
z 1 /z 2 в виде комплексного числа (a + ib) = 0,93 + i 0,17.
Задача 7: Как представить комплексное число 9+10 i в двумерной комплексной плоскости?
Решение:
Учитывая, что комплексное число a + ib = 9 + 10i.
Где a = 9 и b = 10, что означает, что действительная часть равна 9, а мнимая часть оси равна 10. , и поддерживает все стандартные математические операции и элементарные функции для них. Преобразование и продвижение определены таким образом, что операции с любой комбинацией предопределенных числовых типов, будь то примитивные или составные, ведут себя должным образом.
Глобальная константа
imсвязана с комплексным числом i , представляющим главный квадратный корень из -1. (Использование математическихiили инженерныхjдля этой глобальной константы было отклонено, поскольку они являются такими популярными именами индексных переменных.) Поскольку Julia позволяет сопоставлять числовые литералы с идентификаторами в качестве коэффициентов, этой привязки достаточно, чтобы обеспечить удобный синтаксис для комплексные числа, похожие на традиционные математические обозначения: 92 -2 + 0им юлия> 1 + 3/4им 1.0 — 0.75im
Обратите внимание, что
3/4im == 3/(4*im) == -(3/4*im), так как буквальный коэффициент связывает сильнее, чем деление.Предусмотрены стандартные функции для работы со сложными значениями:
julia> z = 1 + 2im 1 + 2им julia> real(1 + 2im) # действительная часть z 1 julia> imag(1 + 2im) # мнимая часть z 2 julia> conj(1 + 2im) # комплексное сопряжение z 1 - 2им julia> abs(1 + 2im) # абсолютное значение z 2.23606797749979julia> abs2(1 + 2im) # квадрат абсолютного значения 5 julia> angle(1 + 2im) # фазовый угол в радианах 1.1071487177940904Как обычно, абсолютное значение (
абс) комплексного числа равно его расстоянию от нуля.abs2дает квадрат абсолютного значения и особенно полезен для комплексных чисел, поскольку позволяет избежать извлечения квадратного корня.angleвозвращает фазовый угол в радианах (также известный как функция аргумент или аргумент ). Полный спектр других элементарных функций также определен для комплексных чисел:юлия> sqrt(1im) 0,7071067811865476 + 0,7071067811865475им юлия> sqrt(1 + 2im) 1,272019649514069 + 0,7861513777574233им юлия> cos(1 + 2im) 2,0327230070196656 - 3,0518977991517997им юлия> exp(1 + 2im) -1,1312043837568135 + 2,4717266720048188им юлия> sinh(1 + 2im) -0,48905625937 + 1,4031192506220405imОбратите внимание, что математические функции обычно возвращают действительные значения при применении к действительным числам и комплексные значения при применении к комплексным числам.
Например,
sqrtведет себя по-разному при применении к-1по сравнению с-1 + 0im, хотя-1 == -1 + 0im:julia> sqrt(-1) ОШИБКА: DomainError с -1.0: sqrt вернет сложный результат только при вызове со сложным аргументом. Попробуйте sqrt (комплекс (x)). Трассировки стека: [...] юлия> sqrt(-1 + 0im) 0.0 + 1.0imОбозначение буквенных числовых коэффициентов не работает при построении комплексного числа из переменных. Вместо этого умножение должно быть явно записано:
юлия > а = 1; б = 2; а + б*им 1 + 2imОднако это , а не . Вместо этого используйте более эффективную
комплексную функциюдля создания комплексного значения непосредственно из его действительной и мнимой частей:julia> a = 1; б = 2; комплекс (а, б) 1 + 2imЭта конструкция позволяет избежать операций умножения и сложения.
InfиNaNраспространяются через комплексные числа в действительной и мнимой частях комплексного числа, как описано в разделе «Специальные значения с плавающей запятой»:юлия> 1 + инф*им 1.0 + Инф*им Юлия> 1 + NaN*im 1.0 + NaN*im
Джулия имеет рациональный тип числа для представления точных отношений целых чисел. Рационалы строятся с помощью оператора
//:julia > 2//3 2//3Если числитель и знаменатель рационального числа имеют общие делители, они приводятся к наименьшим слагаемым, так что знаменатель неотрицательен:
julia> 6//9 2//3 юлия>-4//8 -1//2 юлия> 5//-15 -1//3 юлия>-4//-12 1//3Эта нормализованная форма отношения целых чисел уникальна, поэтому равенство рациональных значений можно проверить, проверив равенство числителя и знаменателя. Стандартизированный числитель и знаменатель рационального значения можно извлечь с помощью функций
числителяизнаменателя:julia> numerator(2//3) 2 юлия> знаменатель(2//3) 3Прямое сравнение числителя и знаменателя, как правило, не требуется, поскольку стандартные арифметические операции и операции сравнения определены для рациональных значений:
юлия> 2//3 == 6//9 истинный юлия> 2//3 == 9//27 ЛОЖЬ юлия> 3//7 < 1//2 истинный юлия > 3//4 > 2//3 истинный юлия> 2//4 + 1//6 2//3 юлия> 5//12 - 1//4 1//6 юлия> 5//8 * 3//12 5//32 юлия> 6//5 / 10//7 21//25Рациональные числа можно легко преобразовать в числа с плавающей запятой:
julia> float(3//4) 0,75Преобразование рациональных чисел в числа с плавающей запятой соблюдает следующее тождество для любых целых значений
aиb, за исключением случаяа == 0иб == 0:юлия > а = 1; б = 2; julia> isequal(float(a//b), a/b) trueДопустимо построение бесконечных рациональных значений:
julia> 5//0 1//0 юлия> х = -3//0 -1//0 Юлия> typeof(x) Rational{Int64}Попытка построить
NaNрациональное значение недействительна:julia> 0//0 ОШИБКА: ArgumentError: неверный рациональный: ноль (Int64) // ноль (Int64) Трассировки стека: [.

 Плоскость. Классификация кривых второго порядка, приведение к каноническому виду, построение. Комплексные числа, действия над ними. Нахождение корней алгебраических уравнений на множестве комплексных чисел.
Плоскость. Классификация кривых второго порядка, приведение к каноническому виду, построение. Комплексные числа, действия над ними. Нахождение корней алгебраических уравнений на множестве комплексных чисел. : Лань, 2009. -640с.
: Лань, 2009. -640с. В., Репин А.Ю. Практическое руководство к решению задач по высшей математике. Линейная алгебра, векторная алгебра, аналитическая геометрия, введение в математический анализ, производная и её приложения: Учебное пособие. –СПб.: Изд-во «Лань», 2009. -320с. ISBN: 978-5-8114-0751-4. (http://e.lanbook.com/books/element.php?pl1_id=374).
В., Репин А.Ю. Практическое руководство к решению задач по высшей математике. Линейная алгебра, векторная алгебра, аналитическая геометрия, введение в математический анализ, производная и её приложения: Учебное пособие. –СПб.: Изд-во «Лань», 2009. -320с. ISBN: 978-5-8114-0751-4. (http://e.lanbook.com/books/element.php?pl1_id=374). 1).
1). Контрольные работы, содержащие не все задания, а также задачи не своего варианта, не зачитываются.
Контрольные работы, содержащие не все задания, а также задачи не своего варианта, не зачитываются. 1.
1. , 14. ,
, 14. , 

 Требуется найти:
Требуется найти: Требуется: а)вычислить , , , ; б)представить комплексное число в тригонометрической форме, вычислить и результат представить в алгебраической форме.
Требуется: а)вычислить , , , ; б)представить комплексное число в тригонометрической форме, вычислить и результат представить в алгебраической форме. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.
Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.
 Линейная комбинация векторов.
Линейная комбинация векторов. Нахождение собственных чисел и векторов оператора.
Нахождение собственных чисел и векторов оператора.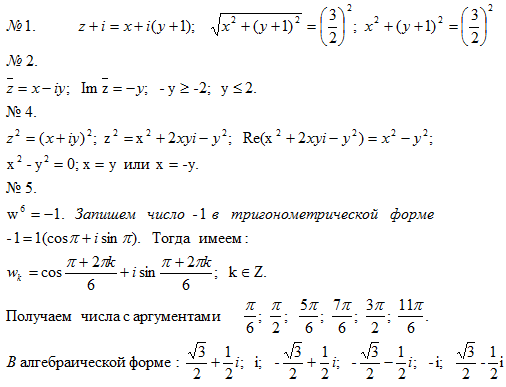 Преобразования прямоугольных декартовых систем координат на плоскости (параллельный перенос, поворот, зеркальное отражение). Связь между собой координат произвольной точки в старой и новой системах координат.
Преобразования прямоугольных декартовых систем координат на плоскости (параллельный перенос, поворот, зеркальное отражение). Связь между собой координат произвольной точки в старой и новой системах координат. Построение прямой.
Построение прямой. Приведение общего уравнения к каноническому.
Приведение общего уравнения к каноническому.
 doc
doc Найдите остаток от деления на 11 числа 437. Запишите периодическую дробь 0,(87) в виде обыкновенной дроби
Найдите остаток от деления на 11 числа 437. Запишите периодическую дробь 0,(87) в виде обыкновенной дроби
 Решите уравнение .
Решите уравнение .

