Конус площадь боковой поверхности: Площадь поверхности и объём конуса — урок. Геометрия, 11 класс.

Содержание

Конус. Площадь боковой поверхности конуса

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

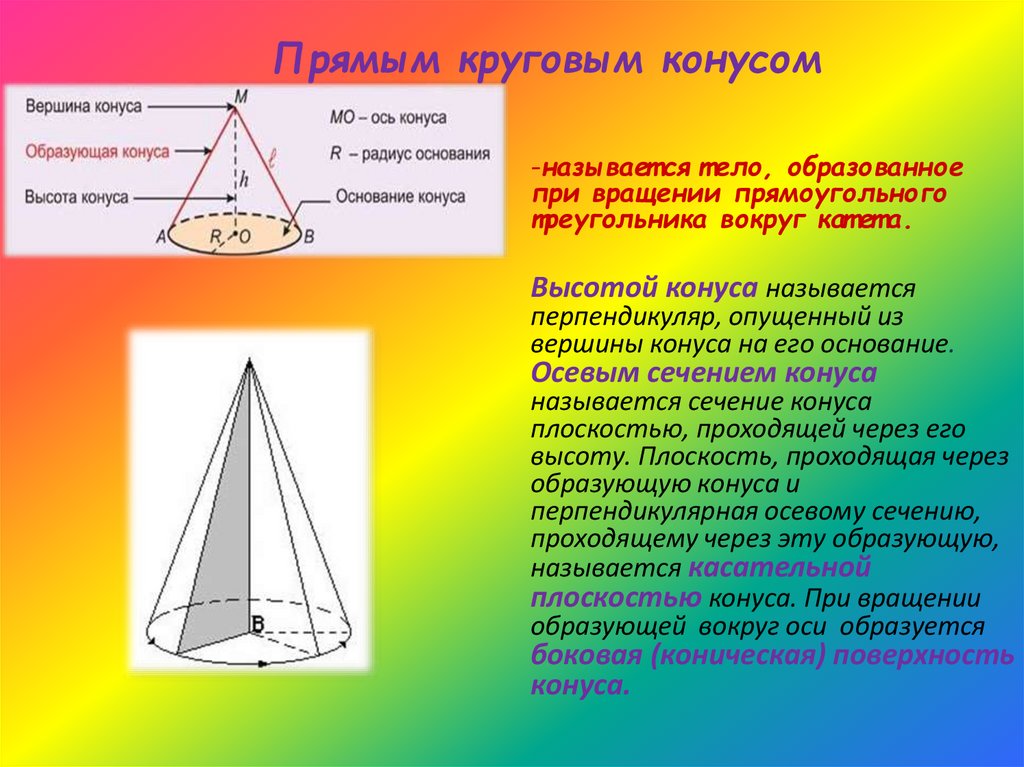
Конус
Конус может быть получен
вращением прямоугольного
треугольника вокруг одного из его
катетов.
На рисунке изображен конус,
полученный вращением
прямоугольного треугольника АВС
вокруг катета АВ.
При этом боковая поверхность
конуса образуется вращением
гипотенузы АС, а основание —
вращением катета ВС.

Смотреть анимацию
Рассмотрим окружность L с центром
О и прямую ОР, перпендикулярную к
плоскости α этой окружности.
Через точку Р и каждую точку
окружности проведем прямую.
Поверхность, образованная этими
прямыми, называется конической
поверхностью, а сами прямые —
образующими конической
поверхности.
Точка Р называется вершиной, а
прямая ОР — осью конической
поверхности.
Тело, ограниченное конической поверхностью и
кругом с границей L, называется конусом.
РМК — конус
Круг называется основанием конуса,
вершина конической поверхности —
вершиной конуса, отрезки
образующих, заключенные между
вершиной и основанием —
образующими конуса, а образованная
ими часть конической поверхности —
боковой поверхностью конуса.
Ось конической поверхности
называется осью конуса, а ее отрезок,
заключенный между вершиной и
основанием — высотой конуса.
Все образующие конуса равны друг

другу.

Р – вершина конуса
РМ – образующая конуса
РО – высота конуса (ось)
Круг L – основание конуса
МО – радиус основания
Наклонный конус
В школьном курсе геометрии мы
будем рассматривать только
прямые круговые конусы
(называя их просто конусы), хотя
бывают и другие.
Если ось конуса не
перпендикулярна
основанию, то такой конус
называется наклонным.

8. Наклонный конус

Сечения конуса
Если секущая плоскость проходит
через ось конуса, то сечение
представляет собой равнобедренный
треугольник, основание которого —
диаметр основания конуса, а боковые
стороны — образующие конуса.
Это сечение называется осевым.
АВС – осевое сечение

9. Сечения конуса

Сечения цилиндра
Если секущая плоскость
перпендикулярна к оси конуса,
то сечение конуса представляет
собой круг с центром О1,
расположенным на оси конуса.
Радиус этого круга, можно найти из
подобия треугольников AOM и AO1M1:

10.

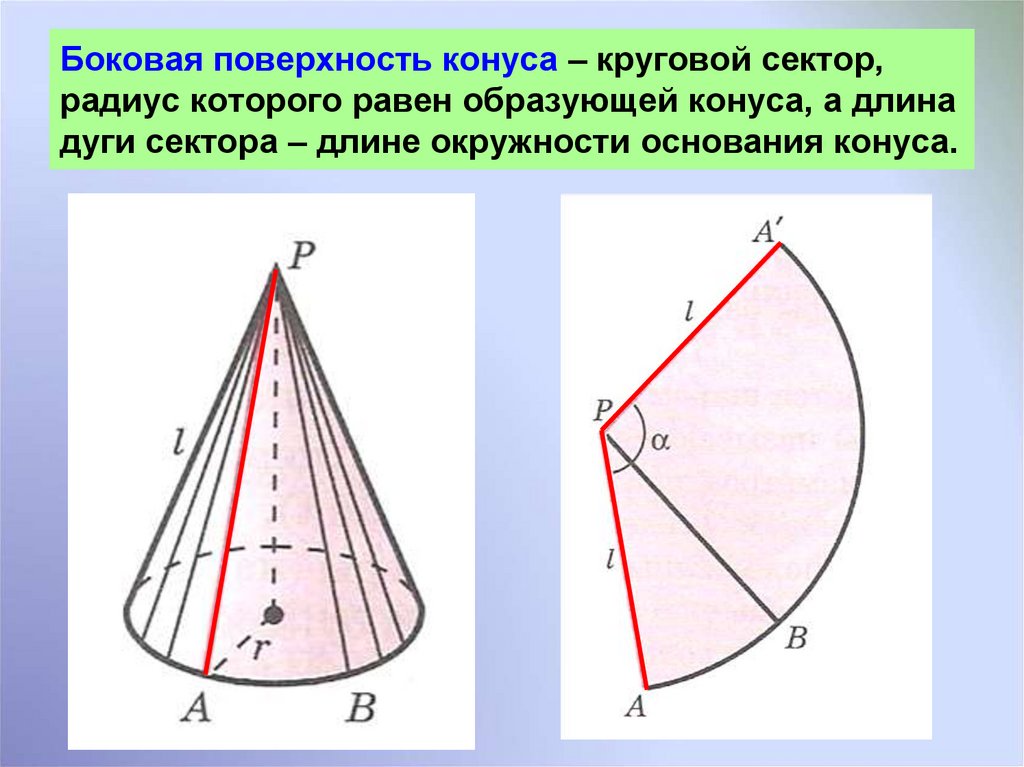
Сечения цилиндраПлощадь боковой поверхности конуса
Боковую поверхность конуса,
как и боковую поверхность
цилиндра, можно развернуть на
плоскость, разрезав ее по одной
из образующих.
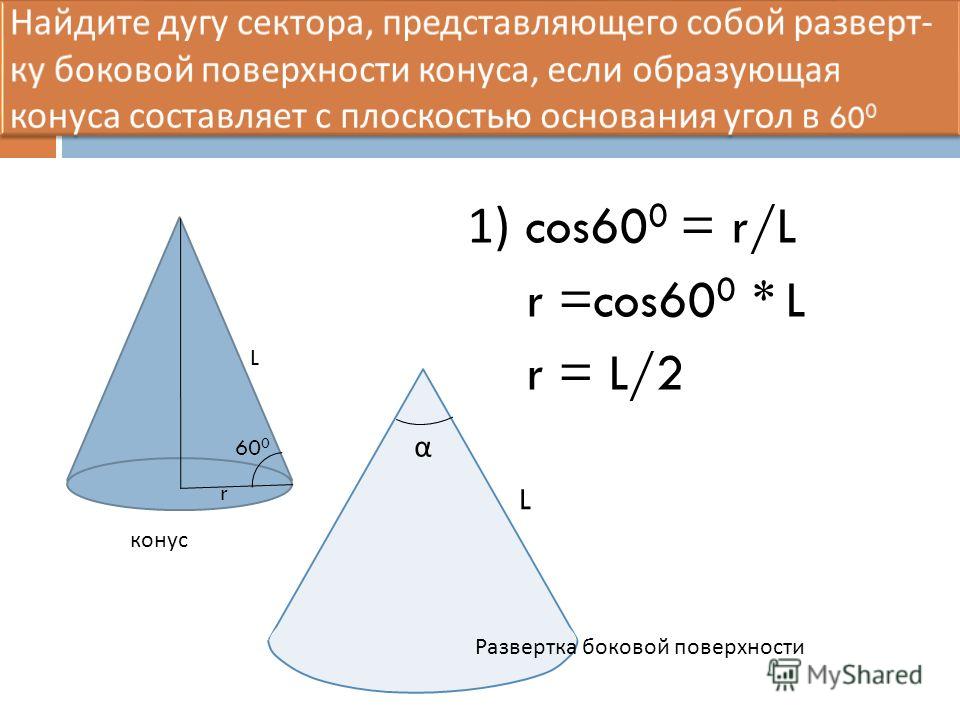
Разверткой боковой
поверхности конуса является
круговой сектор, радиус
которого равен образующей
конуса, а длина дуги сектора
равна длине окружности
основания конуса.

11. Площадь боковой поверхности конуса

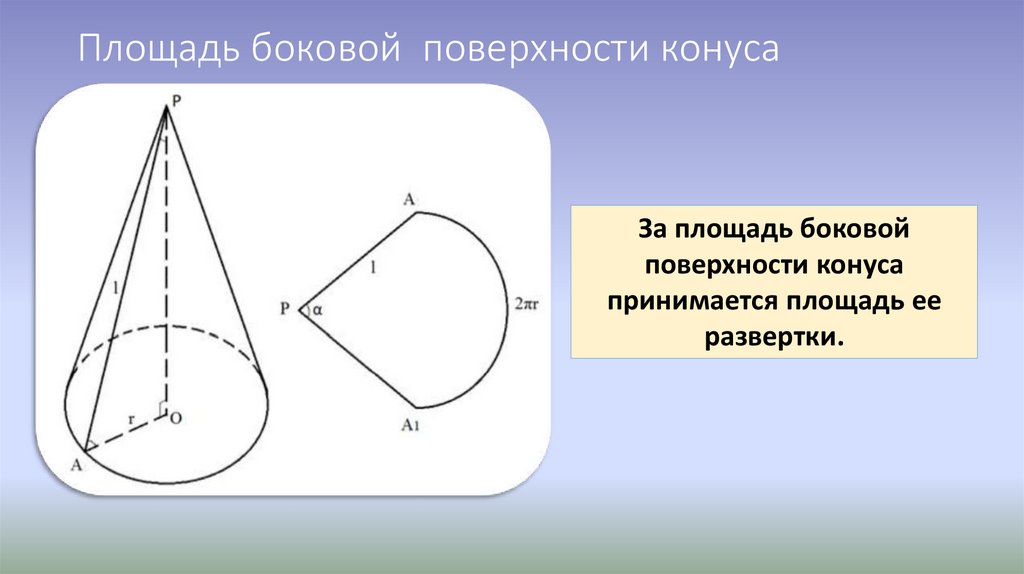
Площадь боковой поверхности конуса
За площадь боковой
поверхности конуса
принимается площадь ее
развертки.

12. Площадь боковой поверхности конуса

Площадь боковой поверхности конуса
Выразим площадь боковой поверхности конуса через его образующую l и радиус
основания r.
Если сектору S соответствует угол α, то
Найдем угол α, чтобы подставить в полученную формулу.
Составим пропорцию, связывающую угол и дугу, на которую
он опирается.
Подставим полученную дробь в формулу и найдем S.

13.

Площадь боковой поверхности конусаПлощадь боковой поверхности конуса

14. Площадь боковой поверхности конуса

Площадь полной поверхности конуса
Площадью полной поверхности конуса
называется сумма площадей боковой
поверхности и основания.
Так как площадь основания равна πr2,
то для вычисления площади полной
поверхности конуса получаем
формулу:

15. Площадь полной поверхности конуса

Конус в природе
Потухший вулкан
Маелифелл в
Исландии.

16. Конус в природе

Конус в архитектуре
Это аноморфозное зеркало-конус
ученого Джона Далтона и
архитектора Эндрю Комптона
можно увидеть рядом с Музеем
Науки и Промышленности в
Манчестере, Великобритания.

18. Конус в архитектуре

Испания — Валенсия — Город искусств и наук Пирамида али некий Конус

19. Конус в архитектуре

Список источников содержания и
иллюстраций
• Геометрия: учеб. для 10 — 11 кл. для общеобразовательных учреждений: базовый и профильный
уровни /Л.

С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: «Просвещение», 2008-2014
• http://liceum-6-tmb.narod.ru/teacher/material/matem/metod/metod.files/image242.jpg
• http://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38183/272983a0_f319_0130_2dc3_220
00a1c9e18.jpg
• http://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38193/0d251990_f32f_0130_97fc_2200
0a1d011d.jpg
• http://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38178/22adbad0_f319_0130_2dbe_220
00a1c9e18.jpg
• http://d3mlntcv38ck9k.cloudfront.net/content/konspekt_image/38179/23960320_f319_0130_2dbf_220
00a1c9e18.jpg
• http://egemaximum.ru/wp-content/uploads/2013/08/ch2.jpg
• https://lh5.googleusercontent.com/hpd3quMjyXM/T0y139a4zLI/AAAAAAAAIoc/wnlfMp38YWQ/s1600/konus_vraschenie.gif

21. Список источников содержания и иллюстраций

• http://www.fresher.ru/manager_content/images/pobeditelikonkursa-fotografij-dikoj-prirody-2012/big/12.jpg
• https://yandex.

ru/images/search?text=%D0%BA%D0%BE%D0%B
D%D1%83%D1%81%20%D0%B2%20%D0%BF%D1%80%D0%B8%
D1%80%D0%BE%D0%B4%D0%B5&noreask=1&img_url=http%3A
%2F%2Frpp.nashaucheba.ru%2Fpars_docs%2Frefs%2F166%2F16
5527%2Fimg8.jpg&pos=2&rpt=simage&lr=213
• http://darga.do100verno.com/blog/302/18489/
• http://www.fotodom.ru/image/Z000-0761.html
• http://velikol.ru/dostc/%D0%9C%D0%BE%D1%83%20%D1%81%
D0%BE%D0%B2%D0%B5%D1%82%D1%81%D0%BA%D0%B0%D1
%8F%20%D1%81%D0%BE%D1%88%20%D0%B3%D0%B5%D0%B
E%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%
D1%81%D0%BA%D0%B8%D0%B5%20%D1%84%D0%B8%D0%B3
%D1%83%D1%80%D1%8B.%20%D0%A0%D0%B0%D0%B1%D0%
BE%D1%82%D1%83c/main.html

English Русский Правила

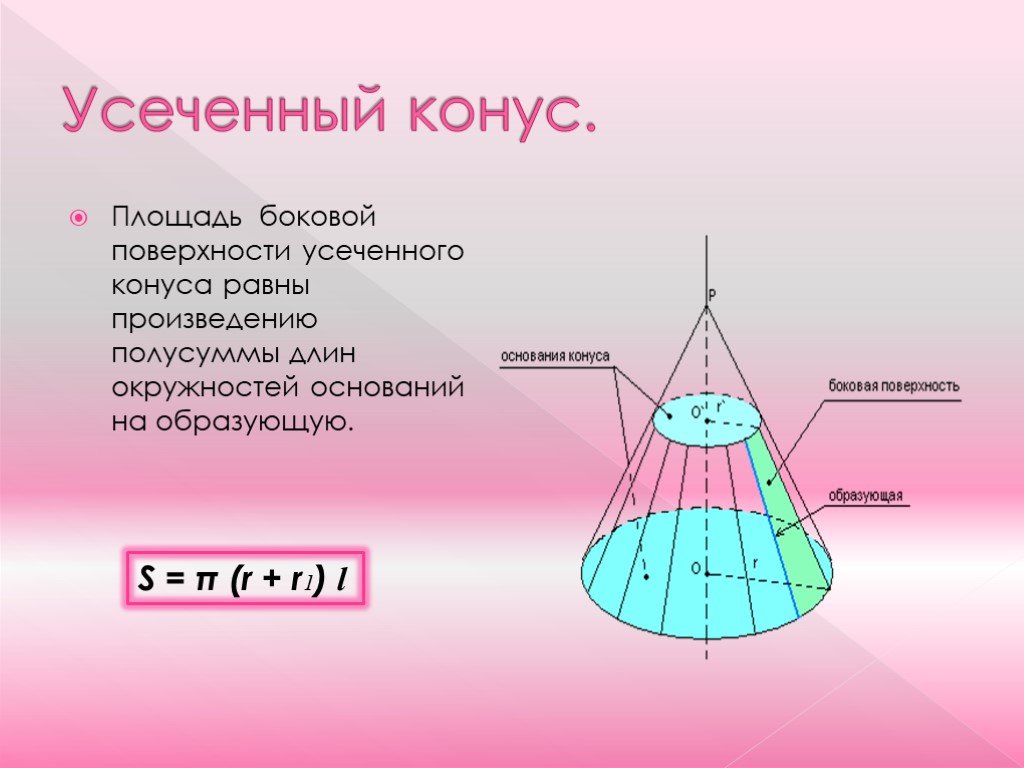
Площадь поверхности усеченного конуса

Площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса.

Пусть Р – вершина конуса, из которого получен усеченный конус, АА1-одна из образующих

Усеченного конуса О и О1 – центры оснований.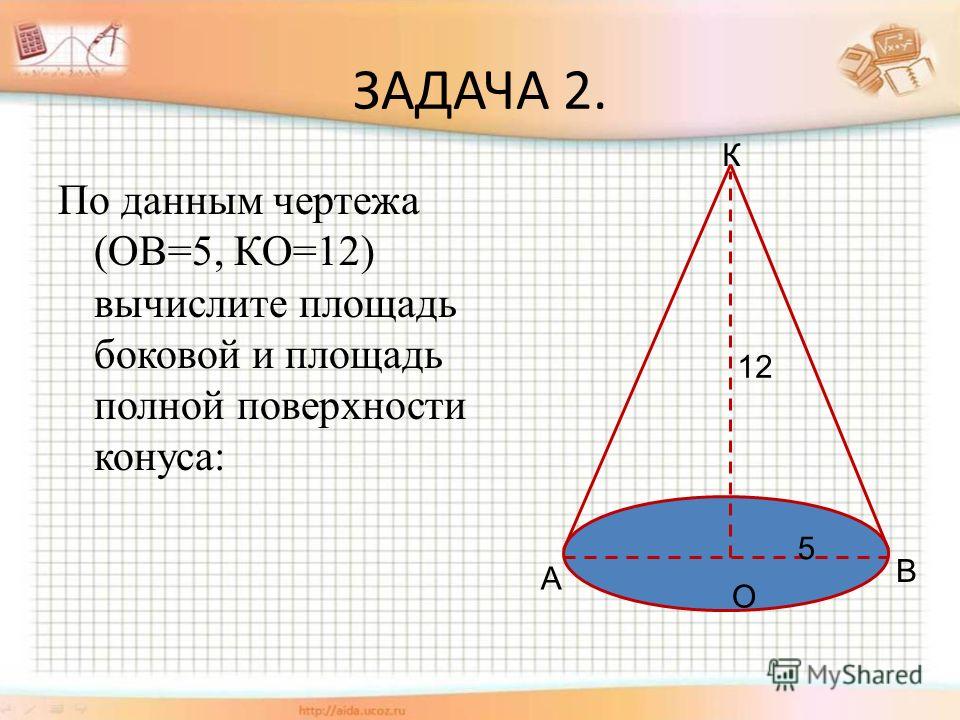 Используя формулу Sбок для конуса получаем

S бок = πr*PA-πr1*PA1=πr(PA1+AA1)- πr1PA1, отсюда, учитывая, что AA1=L, находим

Sбок =πrL +π (r — r1)PA1

Выразим РА1 через L1, r и r1. Прямоугольные треугольники РО1А1 и РОА подобны, так как имеют общий острый угол Р и поэтому PA1/PA=r/r1 или PA1/PA1+L=r/R1. Получаем PA1=Lr1/R-r1. S=πrL + (π(r-r1)Lr1)/r-r1=πrL+πr1L=πL(r+r1)

Sбок =πL(r+r1)

2. Площадь полной поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и оснований

Sполн = S1+S2+Sбок=πL(r+r1)+ πR²+πr²

Обьем усеченного конуса

Объем усеченного конуса равен разности объемов полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса.. Обьем усеченного конуса V, высота которого равна h, а площади оснований S и S1 вычисляется по формуле

V=1/3h(S+S1+√S*S1)

рисунок 8 рисунок 9

Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащей эту образующую

За величину боковой поверхности конуса (полного или усеченного) принимается предел, к которому стремится боковая поверхность вписанной в этот конус правильной пирамиды (полной или усеченной), когда число сторон правильного многоугольника, вписанного в основание, неограниченно увеличивается (и, следовательно, площадь каждой боковой грани неограниченно убывает).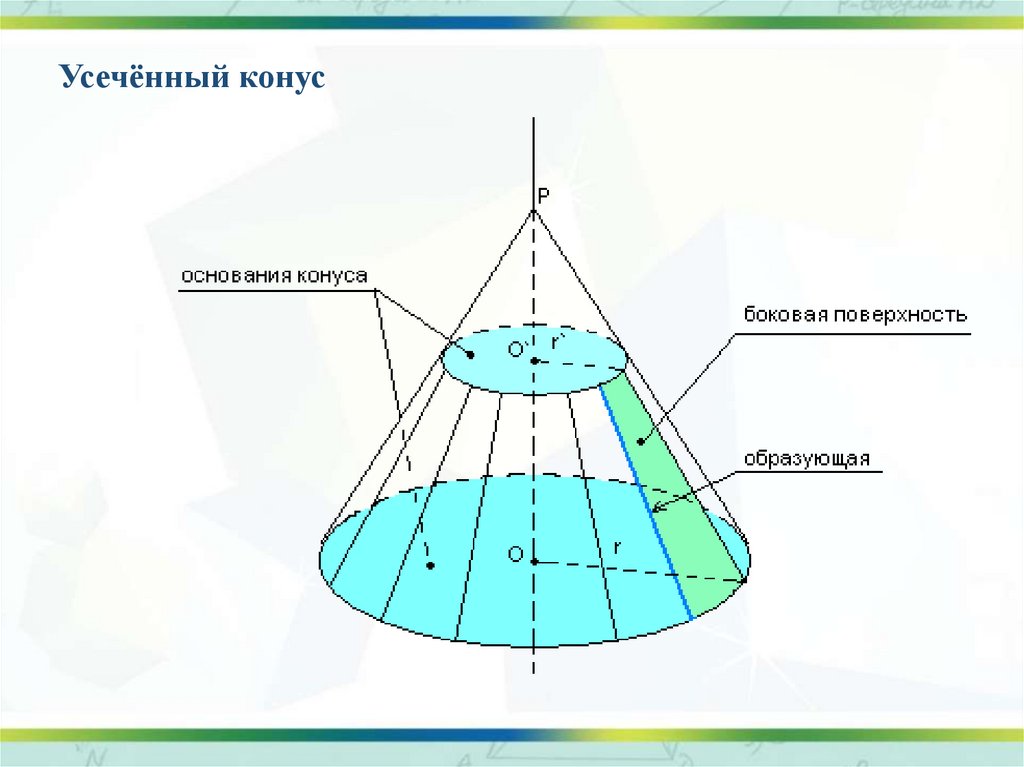

Теорема. Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

В пишем в конус какую-нибудь правильную пирамиду. Пусть p — длина периметра основания, l — длина апофемы пирамиды,

L — образующая конуса. Предположим, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр p будет стремиться к пределу, принимаемому за длину окружности основания C, а апофема l будет иметь пределом образующую конуса, значит боковая поверхность вписанной пирамиды, равная , будет стремиться к пределу. Этот предел и принимается за величину боковой поверхности конуса, то есть .

Чтобы получить полную поверхность конуса, достаточно приложить к боковой поверхности площадь основания: .

Теоремы:. Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность — по окружности с центром на оси конуса.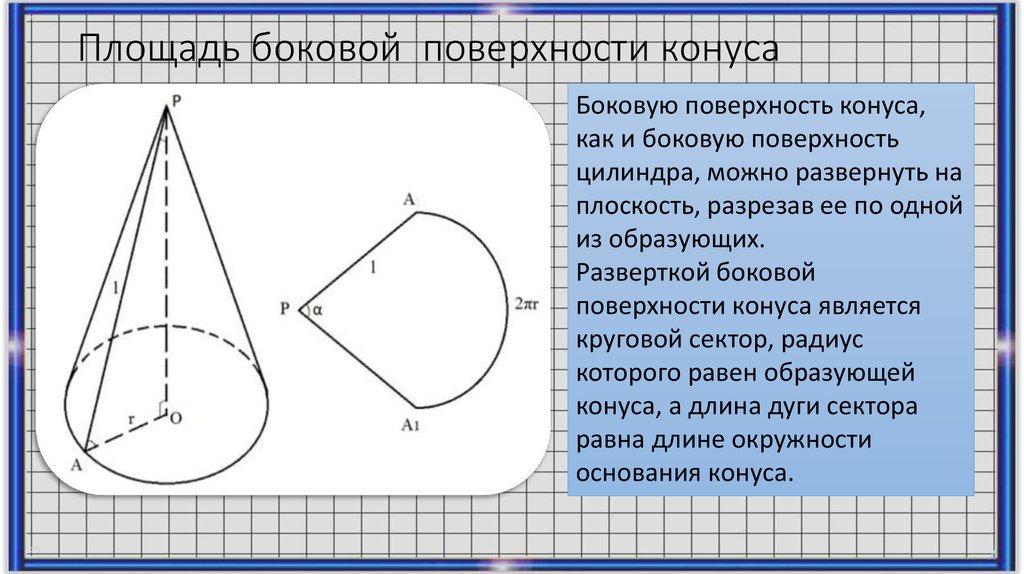 Доказательство. Пусть — плоскость, параллельная плоскости основания конуса и пересекающая конус (рис.5). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость с плоскостью основания, совмещает сечение конуса плоскостью с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса.

Теорема доказана.

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Теоремы: 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Боковая поверхность усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

Доказательство.

В пишем в усеченный конус какую-нибудь правильную усеченную пирамиду. Пусть p — периметр нижнего основания, — периметр верхнего, l — длина апофемы пирамиды,

L — образующая усеченного конуса. При неограниченном возрастании числа боковых граней вписанной пирамиды периметры p и стремятся к пределам, принимаемым за длины окружностей оснований C и , а апофема l имеет пределом образующую L => величина боковой поверхности вписанной пирамиды, равная , будет стремиться к пределу . Этот предел и принимается за величину боковой поверхности усеченного конуса, то есть .

Чтобы получить полную поверхность усеченного конуса, достаточно приложить к боковой поверхности сумму площадей двух оснований: .

Следствие:

Если в трапеции , от вращения которой получается конус, провести среднюю линию BC, то => => .

Площадь боковой поверхности усеченного конуса с меньшим радиусом \[{{r}_{2}}\] и большим радиусом \[{{r}_{1}}\] равна (a) \[ \pi \left( {{r}_{2}}-{{r}_{1}} \right)h\](b) \[\pi \left( {{r}_{2}}+ {{r}_{1}} \right)h\](c) \[\pi \left( {{r}_{2}}-{{r}_{1}} \right)l\] (d) \[\pi \left( {{r}_{2}}+{{r}_{1}} \right)l\]

Дата последнего обновления: 01 апреля 2023 г.

•

Всего просмотров: 309.3k

•

Просмотров сегодня: 3.84k

Ответить

Подтверждено

309,3 тыс.+ просмотров

Подсказка: предположим, что усеченная пирамида имеет форму конуса. Усеченный конус можно рассматривать как удаление конуса с меньшим радиусом от конуса с большим радиусом. Чтобы вычислить площадь боковой поверхности усеченного конуса, вычтите площадь боковой поверхности конуса меньшего радиуса из площади боковой поверхности конуса большего радиуса.

Полный пошаговый ответ:
Нам нужно найти площадь боковой поверхности данного усеченного конуса, меньший радиус которого равен \[{{r}_{1}}\], а больший радиус равен \[{{r} _{2}}\]. Высота данного усеченного конуса равна h, а наклонная высота равна l.
Примем расширение данной усеченной части в виде конуса. Мы можем получить усеченный конус, удалив конус меньшего радиуса из конуса большего радиуса.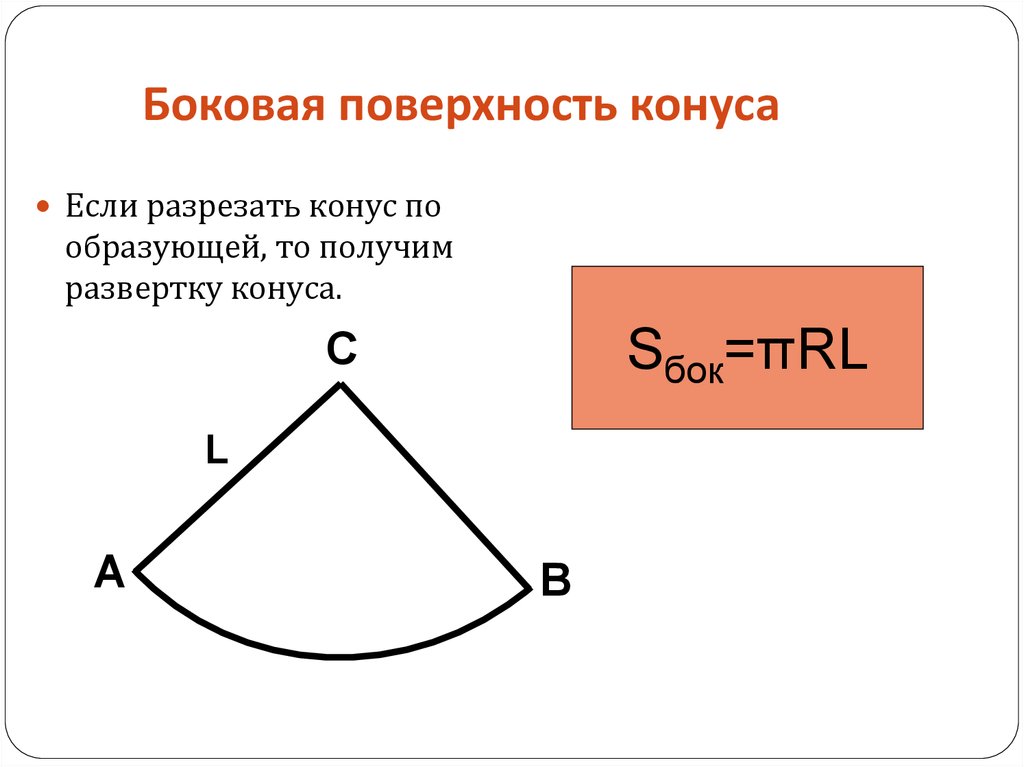 Следовательно, площадь боковой поверхности усеченного конуса получается путем вычитания площади боковой поверхности конуса меньшего радиуса из площади боковой поверхности конуса большего радиуса.
Предположим, что усеченный конус вытянут в виде конуса в вершине O. Предположим, что высота OP этого конуса равна \[{{h}_{1}}\], а наклонная высота OA равна \[{{l}_ {1}}\], как показано на рисунке.

Так как \[OP\bot PA\] и \[OQ\bot QB\], мы видим, что PA параллелен QB. Таким образом, имеем \[\angle OAP=\angle OBQ\]. Итак, имеем \[\cos \left( \angle OAP \right)=\cos \left( \angle OBQ \right)…..\left( 1 \right)\]
Сначала рассмотрим конус образован треугольником \[\vartriangle OPA\]. Высота этого конуса равна \[{{h}_{1}}\, наклонная высота равна \[{{l}_{1}}\], а радиус равен \[{{r}_{1}}. \]. Поскольку конус имеет прямой угол в точке P, мы имеем \[\cos \left( \angle OAP \right)=\dfrac{основание}{гипотенуза}=\dfrac{AP}{OA}=\dfrac{{{r }_{1}}}{{{l}_{1}}}. ….\left( 2 \right)\].
Теперь рассмотрим треугольник \[\vartriangle OQB\]. Высота этого конуса равна \[{{h}_{2}}\, наклонная высота равна \[{{l}_{2}}\], а радиус равен \[{{r}_{2}}. \]. Поскольку конус имеет прямой угол в точке Q, мы имеем \[\cos \left( \angle OBQ \right)=\dfrac{основание}{гипотенуза}=\dfrac{QB}{OB}=\dfrac{{{r }_{2}}}{{{l}_{1}}+l}…..\left( 3 \right)\].
Подставив уравнения (2) и (3) в уравнение (1), получим \[\dfrac{{{r}_{1}}}{{{l}_{1}}}=\dfrac{{{ r}_{2}}}{{{l}_{1}}+l}\].
Упрощая приведенное выше уравнение, мы имеем \[{{r}_{1}}\left( l+{{l}_{1}} \right)={{r}_{2}}{{l}_ {1}}\].
\[\begin{align}
& \Rightarrow {{r}_{2}}{{l}_{1}}=l{{r}_{1}}+{{r}_{1} }{{l}_{1}} \\
& \Rightarrow {{l}_{1}}\left( {{r}_{2}}-{{r}_{1}} \right) =l{{r}_{1}} \\
& \Rightarrow {{l}_{1}}=\dfrac{l{{r}_{1}}}{{{r}_{2} }-{{r}_{1}}} \\
\end{align}\]
Таким образом, имеем \[{{l}_{1}}=\dfrac{l{{r}_{1 }}}{{{r}_{2}}-{{r}_{1}}}…..\left( 4 \right)\].
Теперь мы вычислим площадь боковой поверхности усеченного конуса. Мы можем найти площадь боковой поверхности усеченного конуса, вычитая площадь боковой поверхности конуса с меньшим радиусом из конуса с большим радиусом.
Мы знаем, что площадь боковой поверхности конуса с радиусом r и высотой наклона l равна \[\pi rl\].
Площадь боковой поверхности конуса с радиусом \[{{r}_{1}}\] и наклонной высотой \[{{l}_{1}}\] равна \[\pi {{r}_{1 }}{{l}_{1}}\].
Площадь боковой поверхности конуса с радиусом \[{{r}_{2}}\] и наклонной высотой \[{{l}_{1}}+l\] равна \[\pi {{r}_ {2}}({{l}_{1}}+l)\].
Таким образом, площадь боковой поверхности усеченного конуса \[=\pi {{r}_{2}}({{l}_{1}}+l)-\pi {{r}_{1}}{{ л}_{1}}\].
Мы можем переписать боковую поверхность усеченного конуса как \[\pi {{l}_{1}}\left( {{r}_{2}}-{{r}_{1}} \right)+\ пи л{{г}_{2}}\].
Подставив уравнение (4) в приведенное выше выражение, мы получим площадь боковой поверхности усеченного конуса \[=\pi \left( l{{r}_{1}} \right)+\pi l{{r}_{ 2}}=\pi l\left( {{r}_{1}}+{{r}_{2}} \right)\].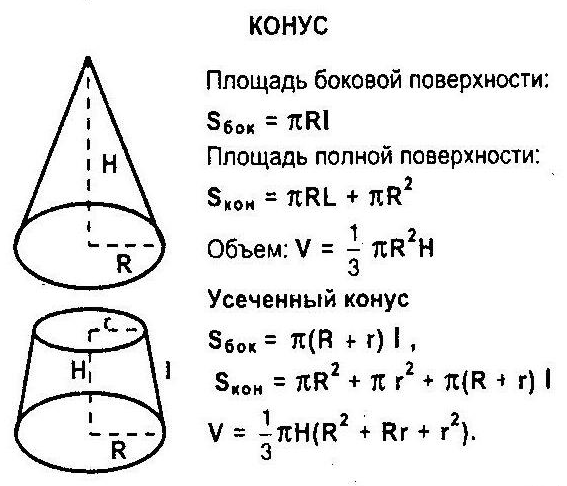
Следовательно, площадь боковой поверхности усеченного конуса равна \[\pi l\left( {{r}_{1}}+{{r}_{2}} \right)\], где l — наклонная высота усеченного конуса, \[{{r}_{1}}\] — меньший радиус усеченного конуса, а \[{{r}_{2}}\] — больший радиус усеченного конуса, что является вариантом (d).

Примечание. Усеченная часть — это часть твердого тела, расположенная между одной или двумя пересекающими его параллельными плоскостями. Прямое усечение представляет собой параллельное усечение прямого конуса. Усеченный конус называется круглым, если он имеет круглые основания. Высота усеченного конуса — это перпендикулярное расстояние между плоскостями двух оснований. При расчете площади боковой поверхности усеченного конуса вы также можете записать площадь усеченного конуса через высоту и радиус. Используйте функцию синуса, чтобы связать высоту усеченного конуса с наклонной высотой и радиусом двух его оснований.

Недавно обновленные страницы

Если abc являются pthq-м и r-м терминами GP, то left fraccb математика класса 11 JEE_Main

Если pthqth и r-й термин GP являются abc соответственно, математика класса 11 JEE_Main

Если любые четыре последовательных коэффициенты любого класса 11 maths JEE_Main

Если A1A2 являются двумя AM между двумя числами a и b class 11 maths JEE_Main

Если pthqthrth и sth члены AP находятся в GP, то p class 11 maths JEE_Main

Один корень уравнения cos x x + frac12 0 лежит в классе 11 maths JEE_Main

Если abc являются pthq-м и r-м членами GP, то слева fraccb class 11 maths JEE_Main

Если pthq-й и r-й члены GP равны abc соответственно математика класса 11 JEE_Main

Если abcdare любые четыре последовательных коэффициента любой математики класса 11 JEE_Main

Если A1A2 — два AM между двумя числами a и b, математика класса 11 JEE_Main

Если pthqthrth и sth члены AP находятся в GP, то р класс 11 математика JEE_Main

Один корень уравнения cos x x + frac12 0 лежит в классе 11 по математике JEE_Main

Трендовые сомнения

Калькулятор конуса | Вычислить площадь поверхности, объем, наклонную высоту конуса

Конус представляет собой трехмерную геометрическую фигуру, имеющую круглое основание, соединенное с точкой изогнутой стороной.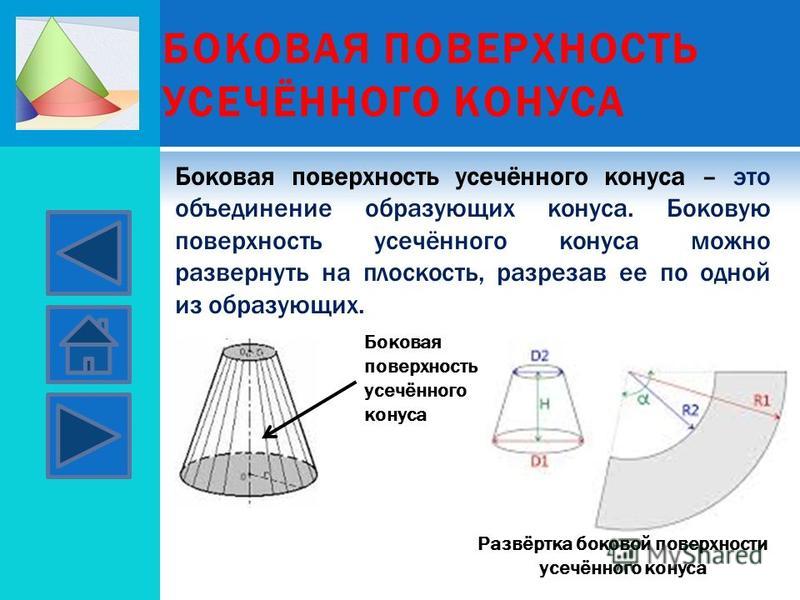

Заостренный конец конуса называется вершиной, а плоская поверхность называется основанием конуса.

Калькулятор конуса: Если вам нужна помощь в определении площади поверхности конуса, объема, высоты или любых других размеров, воспользуйтесь нашим калькулятором. Инструмент удобен для пользователя и отображает точный вывод вместе с шагами, чтобы вы могли легко изучить тему. Введите известные параметры конуса во входные сегменты калькулятора и нажмите кнопку расчета, чтобы проверить вывод.

Выбрать калькулятор конуса

радиус r =

cmmkminmiydftmm

высота h =

cmmkminmiydftmm

Пусть pi π =

Ответ

радиус	г =
длина стороны	ч =
высота наклона	с =
объем	В =
площадь боковой поверхности	Д =
площадь основания	Б =
общая площадь поверхности	А =

С точки зрения Пи №
объем	В =
площадь боковой поверхности	Д =
площадь основания	Б =
общая площадь поверхности	А =

Здесь приведены основные формулы для вычисления площади поверхности, объема, высоты, радиуса и наклонной высоты конуса.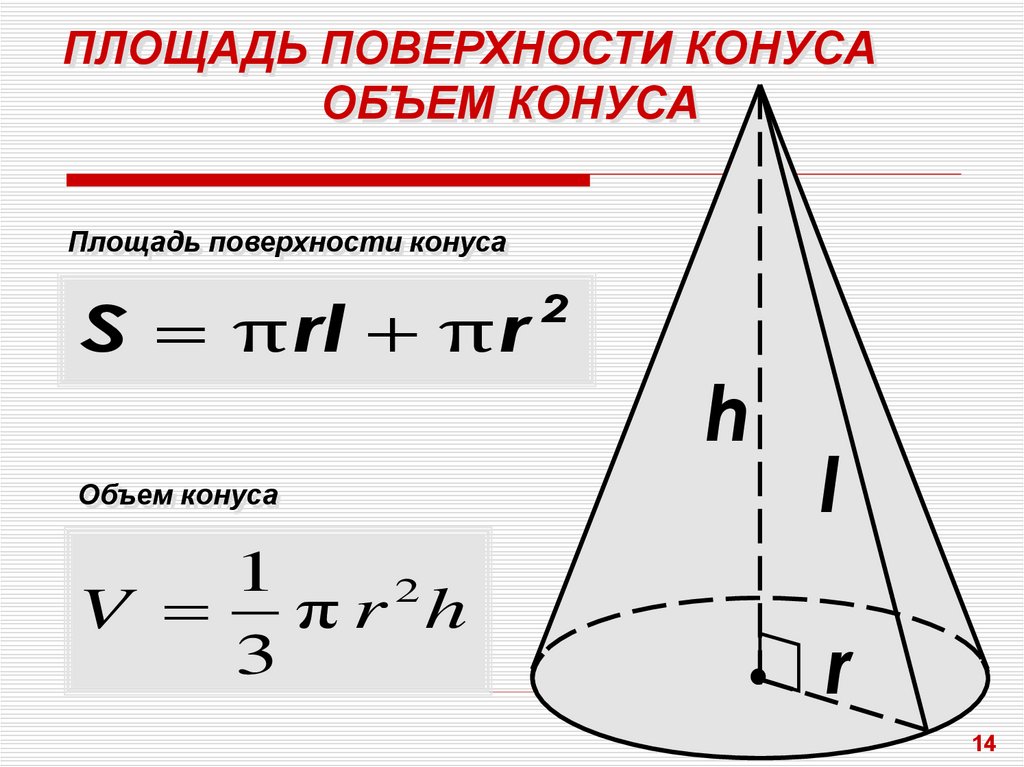

Объем конуса Формула:

Объем V = (1/3)πr²h

Наклонная высота конуса Формула:

Наклонная высота s = √(r² + h²)

Площадь боковой поверхности конуса Формула:

Площадь боковой поверхности L = πrs = πr√(r² + h²)

Площадь базовой поверхности конуса Формула:

Площадь основания B = πr²

Суммарная площадь поверхности конуса Формула:

Общая площадь поверхности A = L + B
= πrs + πr² = πr(s + r) = πr(r + √(r² + h²))

Расчет конуса:

Используйте эти дополнительные формулы, чтобы легко узнать неизвестные параметры конуса с меньшими вычислениями.

Если известны радиус, наклонная высота конуса, то

Высота h = √(s² — r²)
Объем V = (1/3)πr²(√(s2 — r²))
Площадь боковой поверхности L = πrs
Площадь базовой поверхности B = πr²
Общая площадь поверхности A = πrs + πr²

Если известны радиус, площадь боковой поверхности конуса, то

Наклонная высота s = L / (πr)
Высота h = √(s² — r²)
Объем V = (1/3)πr²ч
Площадь базовой поверхности B = πr²
Общая площадь поверхности A = L + πr²

Если известны высота, наклонная высота конуса, то

Радиус r = √(s² — h²)
Площадь боковой поверхности L = πrs = πr√(r² + h²)
Объем V = (1/3)πr²ч
Площадь базовой поверхности B = πr²
Общая площадь поверхности A = L + B = πrs + πr²

Если радиус конуса, объем конуса дан, то

Высота h = (3 * v) / (πr2)
Наклонная высота s = √(r² + h²)
Площадь боковой поверхности L = πrs = πr√(r² + h²)
Площадь базовой поверхности B = πr²
Общая площадь поверхности A = L + B = πrs + πr²

Если известны радиус и общая площадь поверхности конуса, то

Наклонная высота s = [A — (πr2)] / (πr)
Высота h = √(s2 — r2)
Объем V = (1/3)πr²h

Если даны объем, высота конуса, то

Rdaius r = √[ (3 * v) / (π * h) ]
Наклонная высота s = √(r² + h²)
Площадь боковой поверхности L = πrs = πr√(r² + h²)
Площадь базовой поверхности B = πr²
Общая площадь поверхности A = L + B = πrs + πr²

Если известны наклонная высота, площадь боковой поверхности конуса, то

Радиус r = L / (π * с)
Высота h = √(s² — r²) 90 196
Площадь базовой поверхности B = πr²
Общая площадь поверхности A = L + B = L + πr²

Если известны радиус и высота конуса, то

Наклонная высота s = √(r² + h²)
Объем V = (1/3)πr²ч
Площадь базовой поверхности B = πr²
Площадь боковой поверхности L = πrs = πr√(r² + h²)
Общая площадь поверхности A = L + B = πrs + πr² = πr(s + r) = πr(r + √(r² + h²))

Где r – радиус конуса

h – высота

s – наклонная высота

V – объем

B – площадь основания

L – площадь боковой поверхности

A – общая площадь поверхности конуса

Конус твердое тело, имеющее круглое основание и единственную вершину, называемую вершиной. Если вершина находится над центром основания, конус называется прямым. Мы все знаем, что вычисление размеров конуса немного сложнее по сравнению с другими формами. Взгляните на подробную пошаговую процедуру, которая помогает определить объем конуса, радиус, общую площадь поверхности, высоту наклона и высоту.

Объем конуса:

Проверьте радиус и высоту конуса из вопроса.
Возведите радиус в квадрат и умножьте его на π, высоту.
Разделите результат на 3, чтобы получить объем.

Высота наклона конуса:

Получить высоту, радиус конуса.
Возведение в квадрат радиуса и высоты.
Добавьте квадраты значений и примените к результату квадратный корень, чтобы найти наклонную высоту.

Радиус конуса:

Процесс 1:

Запишите высоту наклона вниз, высоту конуса.
Вычесть квадрат высоты из квадрата длины стороны.
Примените квадратный корень к результату, чтобы найти радиус.

Процесс 2:

Проверить объем, высоту конуса.
Трижды разделить объем на π, умноженное на высоту
Примените квадратный корень к выходным данным, чтобы получить радиус.

Процесс 3:
- Получите площадь боковой поверхности, наклонную высоту конуса.
- Разделите площадь боковой поверхности на произведение π и наклонной высоты.

Площадь боковой поверхности конуса:

Запишите высоту наклона конуса, радиус.
Получите произведение π, радиуса и наклонной высоты, чтобы получить площадь боковой поверхности.

Площадь основания конуса:

Получите радиус конуса.
Возведите радиус в квадрат и умножьте его на π, чтобы проверить площадь базовой поверхности.

Высота конуса:

Процесс 1:

Проверить высоту наклона, радиус конуса из вопроса.
Вычтите квадрат наклонной высоты и квадрат радиуса.
Примените квадратный корень к полученному значению, чтобы получить высоту.

Процесс 2:

Найти объем, радиус конуса.
Получите произведение π на квадрат радиуса.
Разделите три раза объем на результат, чтобы проверить высоту.

Суммарная площадь поверхности конуса:

Рассчитайте боковую площадь основания для заданных значений.
Добавьте площадь боковой поверхности, площадь основания, чтобы проверить общую площадь поверхности.

Пример 1: Вычислите объем круглого конуса, высоту, высоту наклона, площадь основания и общую площадь поверхности. Если радиус конуса 5 мм, а площадь боковой поверхности 176 мм³.

Решение:

Учитывая, что

Площадь боковой поверхности конуса L = 176 мм³

Радиус конуса r = 5 мм * 5)

= 176 / (3,14 * 5)

= 176 / 15,7 = 11,21 мм

Высота h = √(s² — r²)

h = √((11,21)² — 5²)

3 (125,664 — 25) = √(100,664)

= 10,03 мм

Объем V = (1/3)πr²h

V = (1/3) * π * 5² * 10,03

= (1/3) * 3,14 * 25 * 10,03

= 787,35 / 3 = 262,45 мм 30

Площадь базовой поверхности B = πr²

B = π * 52

= 3,14 * 25 = 78,5 мм²

. Площадь поверхности A = L + πr²

A = 176 + 78,5 = 254,5 мм³

∴ Радиус кругового конуса 5 мм, высота 10,03 мм, высота наклона 11,21 мм, объем 262,45 мм³, площадь боковой поверхности 176 мм³, площадь базовой поверхности составляет 78,5 мм², а общая площадь поверхности составляет 254,5 мм³.

Пример 2: Круглый конус имеет радиус 12 см и высоту 18 см. Найдите площадь боковой поверхности конуса, площадь основания, общую площадь поверхности, объем и наклонную высоту?

Решение:

Учитывая, что

Радиус конуса r = 12 см

Высота h = 18 см

Площадь боковой поверхности L = πr√(r² + h²)

π2 L2 900 * √(12² + 18²)

= π * 12√(144 + 324)

= π * 12√(468) = 3,14 * 12 * 21,63

= 815.14 cm³

Base Surface Area B = πr²

= π * 12² = π * 144

= 3.14 * 144 = 452.16 cm²

Total Surface Area A = L + B

= 452.16 + 815.14

= 1267,3 см³

Наклонная высота Объем s = √(r² + h²)

s = √(12² + 18²)

= √(144 + 324)

= √20 см3 30 ² = 21,60 (1/3)πr²h

В = (1/3) * π* 12² * 18

= (1/3) * π* 144 * 18

= (1/3) * π* 2592 = (2592π/3)

= 864 π = 864 * 3,14

= 2712,96 см³

∴ Радиус кругового конуса 12 мм, высота наклона 21,6 см² 18 см, объем 2712,96 см³, площадь боковой поверхности 815,14 см³, площадь основания 452,16 см², общая площадь поверхности 1267,3 см³.

Наш веб-сайт Areavolumecalculator.com предоставляет бесплатные инструменты калькулятора, которые помогут вам решить сложные задачи, связанные с геометрией, или перепроверить любую концепцию после урока.

1. Как найти объем прямого кругового конуса?

Формула для расчета объема прямого круглого конуса: (1/3)πr²h. Подставьте значения радиуса и высоты в эту формулу и выполните вычисления, чтобы получить результат.

2. Как найти недостающий радиус конуса?

Существует несколько способов найти радиус отсутствующего конуса на основе имеющихся у вас параметров. Если известны объем и высота конуса, радиус будет равен √[(3 * v) / (π * h)]. Если у вас есть площадь боковой поверхности и высота наклона, то радиус равен L / (π * s), иначе √(s² — h²), где s — высота наклона, а h — высота.

3. Как найти вес конуса?

Чтобы узнать вес конуса, вы должны знать радиус, высоту и среднюю плотность.