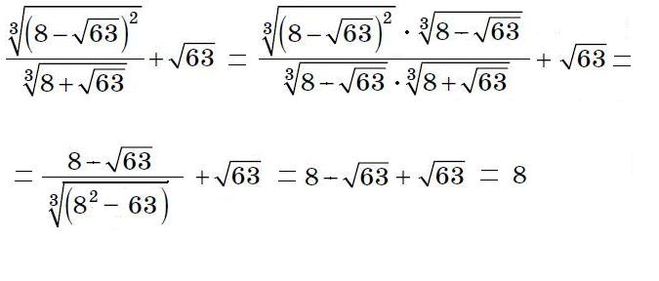Вычислитель корней онлайн: Калькулятор корней онлайн

Содержание

§ Извлечь корень из числа онлайн. Калькулятор

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную
Площадь
Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола

Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое
Чётные и нечётные функции

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Человек наиболее живёт в то время, когда он чего-нибудь ищет. Ф.М. Достоевский

на главную

Введите тему

Поддержать сайт

←Вернуться в «Калькуляторы онлайн»

Инструкции к калькулятору

Введите число и степень корня и нажмите «Извлечь корень».

Важно!

Калькулятор расчета корней онлайн может служить лишь для проверки ваших вычислений.

Научиться находить квадратный, кубический или корень любой другой степени можно самостоятельно в уроке квадратный корень.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:


Отправить

Калькулятор Квадратного Корня — Mathcracker.

Com

Инструкции: Используйте этот калькулятор квадратного корня, чтобы уменьшить и вычислить любое выражение, включающее корни/радикалы, показывая все шаги. Пожалуйста, введите выражение квадратного корня, которое вы хотите упростить.

Подробнее об этом калькуляторе квадратного корня

Этот калькулятор позволяет упростить и вычислить любое допустимое выражение квадратного корня, показывая все шаги. Вам нужно предоставить допустимое выражение, включающее радикалы. Например, это может быть что-то вроде «sqrt(1/2 + 1/3)» или что-то более сложное, например, «sqrt((1/3+1/4)/(1/3+1/5))». .

Как только вы предоставите допустимое выражение с квадратными корнями, все, что вам нужно сделать, это нажать на кнопку «Рассчитать», и вам будут предоставлены пошаговые расчеты.

Выражения квадратного корня обычно можно упростить, когда в них задействовано умножение, но часто их невозможно упростить дальше. Например, что-то вроде $\sqrt 2 + \sqrt{3}$ нельзя упростить дальше, но что-то вроде $\sqrt 2 \cdot \sqrt{8}$ мы, безусловно, можем упростить:

\[\sqrt 2 \cdot \sqrt{8} = \sqrt{2 \cdot 8}= \sqrt{16} = 4\]

Формула квадратного корня

Есть несколько правил или основных формул, которые необходимы для упростить радикальные выражения . Эти правила — все, что необходимо для сокращения любого квадратного корня, следуя приоритетам PEMDAS для операций.

Как упростить радикалы? Этот калькулятор, упрощающий радикалы, сначала попытается максимально упростить сторону радикальных выражений, а затем, если возможно, постарается уменьшить радикальное выражение.

Правила упрощения квадратного корня

Правило 1 : Это главное правило: $\sqrt x \cdot \sqrt{y} = \sqrt{x y}$
Правило 2 : Следствие предыдущего правила, но полезно иметь его как отдельное правило: $\sqrt{x \cdot y} = |x|$
Правило 3 : Еще одно главное правило: $\frac{\sqrt x}{\sqrt{y}} = \sqrt{\frac{x}{y}}$

Мы могли бы добавить в список больше правил, но все остальные вытекают из этих. Когда дело доходит до правил алгебры, лучше иметь глубокое понимание нескольких правил, чем слабое владение многими правилами.

Как упростить квадратные корни и радикалы?

Не всегда возможно упростить квадратные корни, но часто можно сделать хоть какое-то упрощение. В общих чертах, вы будете использовать Правило 1 для группировки (или разгруппировки) выражений под корнем.

И вы будете использовать Правило 2, чтобы удалить радикалы из подходящих терминов. Вот и все, что вам нужно. Остальное практика.

Каковы шаги для упрощения квадратных корней?

Шаг 1: Определите корневое выражение и оцените, есть ли у вас один или несколько радикалов.
Шаг 2: Если у вас есть более одного радикала, вы можете сгруппировать их, которые перемножаются друг с другом, используя Правило 1. Вы можете сгруппировать их под одним радикалом.
Шаг 3: Если есть разделение радикалов, можно использовать Правило 3, чтобы сгруппировать их под одним радикалом.

Шаг 4: После того, как вы воспользовались Правилом 1 или 3, чтобы максимально сгруппировать радикалы, вы используете Правило 2, поэтому посмотрите, какую часть выражения можно убрать из радикала.

В конечном счете игра групповая и потенциальная "отмена" подкоренной части выражения (если не всей) числителя на знаменатель дроби). 2} = |1| = 1 \) , по правилу 2.

Калькулятор квадратного корня дроби

Вопрос в том, могу ли я использовать те же правила для калькулятора квадратного корня для дробей? Ответ: абсолютно. Идея точно такая же, сгруппировать радикалы, которые умножаются друг на друга, и потенциал убрать радикал из части выражения.

При работе с дробями выражение, скорее всего, тоже будет дробью, и вы будете иметь дело с упрощения в числителе и знаменатель все тот же.

Это радикальный калькулятор?

В самом деле. Радикальный калькулятор относится к тому, который проводит и упрощает операции внутри радикала, который совпадает с корнем. Итак, квадратный корень — это особый тип радикала, есть кубические корни, корни четвертой степени и т. д., и все они являются радикалами.

С помощью этого калькулятора вы можете вычислить все виды радикалов, так что это радикальный решатель а также это решатель квадратного корня, в зависимости от аргумента, который он предоставляет.

Пример: вычисление квадратного корня

Можете ли вы упростить квадратный корень из 5.

Отвечать: Во-первых, мы видим, что 5 не имеет множителей, а так как у нас есть только один радикал с числом без множителей, то мы заключаем, что $\sqrt 5$ нельзя еще больше упростить. 2} = |5| = 5\]

чем завершается расчет.

Пример: упрощение квадратного корня

Можете ли вы упростить квадратный корень из 10.

Отвечать: Во-первых, мы видим, что у 10 есть делители, поскольку $10 = 2 \cdot 5$ и поскольку у нас есть только один радикал, мы можем писать $\sqrt{10} = \sqrt{5 \cdot 2}$, но это не упрощение, а расширение. Ни 5, ни 2 не имеют множителей, и их нельзя записать в виде квадрата, чтобы применить правило 2, которое указывает, что мы не можем упростить это выражение дальше. 2} = 10 \sqrt 3\]

чем завершается расчет.

Другие полезные калькуляторы алгебры

Если вам нужно работать в более общих условиях, вы можете использовать это упростить выражение , который будет обрабатывать общие выражения и будет вам общим упрощенным калькулятором с шагами.

Для дробей вы можете использовать наш калькулятор смешанных дробей или калькулятор правильной дроби , но это будет зависеть от того, что вам нужно вычислить.

Калькулятор квадратного корня

Базовый калькулятор

Поделись этим калькулятором и страницей

Калькулятор Используйте

Используйте этот калькулятор, чтобы найти главный квадратный корень и корни действительных чисел. Входными данными для подкоренного числа x могут быть положительные или отрицательные действительные числа. Ответ также скажет вам, вошли ли вы в идеальный квадрат.

Ответ покажет вам комплексные или мнимые решения для квадратных корней из отрицательных действительных чисел. См. также Simplify Radical Expressions Calculator для упрощения радикалов вместо поиска дробных (десятичных) ответов.

Квадратные корни, нечетные и четные:

Для любого положительного действительного числа существует 2 возможных корня. Положительный корень и отрицательный корень. Дан номер х , квадратный корень из х — это число a такое, что а ² = х . Квадратные корни — это специализированная форма нашего общего калькулятор корней.

«Обратите внимание, что любое положительное действительное число имеет два квадратных корня, один положительный и один отрицательный. Например, квадратные корни из 9 равны -3 и +3, поскольку (-3) ² = (+3) ² = 9. Любое неотрицательное действительное число x имеет уникальный неотрицательный квадратный корень r; это называется главный квадратный корень ………. Например, главный квадратный корень из 9sqrt(9) = +3, а другой квадратный корень из 9 равен -sqrt(9) = -3. В обычном использовании, если не указано иное, «квадратный корень» обычно означает главный квадратный корень.»[1].

Калькулятор идеального квадрата

Этот калькулятор также сообщит вам, является ли введенное вами число идеальным квадратом или нет. Полный квадрат — это число x , где квадратный корень из x представляет собой число a , такое что a ² = x и a является целым числом. Например, 4, 9 и 16 являются полными квадратами, поскольку их квадратные корни, 2, 3 и 4, соответственно, являются целыми числами.

Пример квадратных корней:

Второй корень из 81, или 81 радикал 2, или квадратный корень из 81 записывается как $$ \sqrt[2]{81} = \sqrt[]{81} = \pm 9 $$.
Корень второй степени из 25, или радикал 2 из 25, или квадратный корень из 25 записывается как $$ \sqrt[2]{25} = \sqrt[]{25} = \pm 5 $$.
Второй корень из 100, или 100 радикал 2, или квадратный корень из 100 записывается как $$ \sqrt[2]{100} = \sqrt[]{100} = \pm 10 $$.
Второй корень из 10, или 10 радикал 2, или квадратный корень из 10 записывается как $$ \sqrt[2]{10} = \sqrt[]{10} = \pm 3,162278 $$.

Для расчета степени дроби используйте наш калькулятор Дробные показатели.

Каталожные номера

[1] Вайсштейн, Эрик В. «Квадратный корень». От MathWorld — Веб-ресурс Wolfram. Квадратный корень

Дополнительное чтение о квадратных корнях:

At Math is Fun: квадратный корень

Подписаться на калькуляторSoup:

бесплатный калькулятор квадратных корней | Математические вкусности

Форма поиска

Поиск

Работа с квадратными корнями — захватывающая тема для студентов-математиков, но они могут оказаться сложными. Начинающие математики часто полагаются на предположения, например, ошибочно принимают квадрат 3 за 6 только потому, что 6 кажется 3, считая дважды. Но возведение в квадрат подразумевает умножение, а не сложение. Когда мы возводим 3 в квадрат (или умножаем 3 само на себя), мы получаем 9— квадратный корень из 9 равен 3.

Квадратные корни не должны быть сложной темой. На самом деле легко запомнить таблицу идеальных квадратов и произвести впечатление на учителя. Но работа с несовершенными квадратами — или теми числами, квадратные корни которых содержат дроби или десятичные дроби — не всегда может быть такой простой. Вот тут и приходит на помощь наш бесплатный онлайн-калькулятор квадратного корня.

Как пользоваться нашим бесплатным онлайн-калькулятором квадратного корня

Как и некоторые другие наши калькуляторы, этот бесплатный онлайн-калькулятор квадратного корня чрезвычайно прост в использовании. В калькуляторе всего четыре части:

Числовое поле
Кнопка расчета
Кнопка очистки
Поле квадратного корня

Чтобы найти квадратный корень с помощью нашего бесплатного онлайн-калькулятора квадратного корня:

Нажмите ОЧИСТИТЬ, чтобы обновить калькулятор.
Введите значение, квадратный корень которого вы хотите найти, в числовое поле.
Щелкните ВЫЧИСЛИТЬ.
Ваш ответ появится в поле квадратного корня.
Нажмите ОЧИСТИТЬ, чтобы начать заново и найти другое значение.

Номер:
Квадратный корень:

Другие калькуляторы

Что такое квадратный корень?

Квадратный корень относится к любому числу, которое дает вам исходное число как произведение при умножении на себя. Квадратные корни, выраженные символом «√», принадлежат к семейству показателей степени. Квадраты и корни являются специальными показателями. Любой квадрат x — это просто x, возведенный в степень ½, или x1/2.

Пример

Например, когда вас спрашивают о квадратном корне из 16, вы ищете число, которое даст вам произведение 16 при умножении на себя. Это число равно 4, потому что 4, умноженное на 4 — или возведенное в степень 2 (математически выраженное как 42), — равно 16. 16 1/2 равно 4.

Работа с идеальными квадратами целые числа. Ниже приведены наиболее распространенные способы нахождения квадратных корней из этих идеальных квадратов.

Повторное вычитание

Вычитание последовательных нечетных чисел (1, 3, 5, 7 и т. д.), начиная с 1, из числа, квадратный корень которого вы пытаетесь найти, пока не получите 0.

Например:

9 — 1 = 8
8 — 3 = 5
5 — 5 = 0

Вы выполнили 3 вычитания из 0. Квадратный корень из 9 равен 3.

Факторизация простых чисел

Этот метод состоит из четырех шагов. Давайте пройдемся по каждому из них, чтобы найти квадратный корень из 144.

Разложите число 144 на простые множители.
No related posts.

Вычислитель корней онлайн: Калькулятор корней онлайн | umath.ru