Примеры решения дифференциала функции с ответами
Алгоритм решения дифференциала функции
Теорема
Дифференциалом функции называется произведение её производной и дифференциала независимой переменной
Для вычисления дифференциалов используются свойства дифференциалов, а также таблица их значений.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Примеры решения дифференциала функции
Пример 1
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 2
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 3
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 4
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
В этом примере квадратный корень извлекается из суммы . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 5
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 6
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 7
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
По правилу вычисления производной от дроби, получаем:
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 8
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
Функция является сложной, поэтому процесс нахождения производной будет происходить в два этапа.
Обозначим . Исходная функция примет следующий вид:
Найдём её производную по таблице основных тригонометрических функций:
Далее найдём производную :
Производная сложной функции будет равна произведению и :
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 9
Пример 9
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.
Данная функция является сложной, т.к. подкоренным выражением является функция синус.
Найдём производную данной функции, как произведение производных корня и синуса:
Окончательно получаем:
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Пример 10
Задача
Найти дифференциал функции
Решение
Найдём производную данной функции.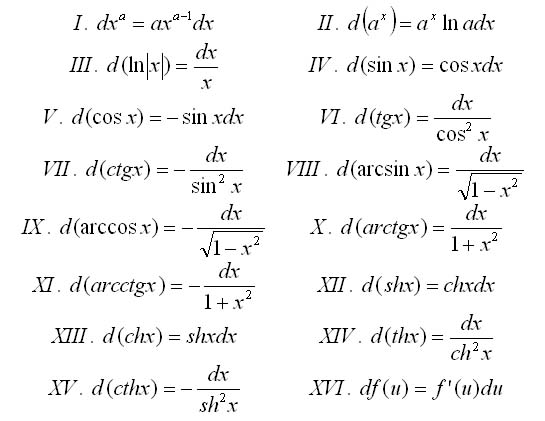
Процесс нахождения произвоной данной функции будет происходить в три этапа: на первом этапе требуется определить производную функции косинус, на втором – производную от корня, на третьем – производную от дроби подкоренного выражения.
Найдём производную
По таблице производных определяем, что
Т.к. аргумент косинуса сам является функцией от , то необходимо найти его производную по :
Подкоренное выражение является дробью, поэтому необходимо также найти производную этой дроби :
Перемножая найденные производные, получаем окончательный результат:
Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :
Ответ
Средняя оценка 3 / 5. Количество оценок: 1
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
6163
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ § 1. Действительные числа. § 2.  Абсолютная величина действительного числа§ 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11. Сравнение бесконечно малых Упражнения к главе II ГЛАВА III.  n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23.  x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных  Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  Формула Чебышева§ 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
1Как рассчитать гандикап для гольфа в 2020 году
Если вы новичок в гольфе или начинаете относиться к своим партиям более серьезно, понимание вашего гандикапа в гольфе является необходимостью.
Гольф-гандикапы — это число, которое представляет способности игрока в гольф на основе результатов его предыдущего раунда игры в гольф. Он служит для сравнения вашей игры с другими игроками в гольф. Для мужчин гандикап в гольфе обычно составляет от нуля до двадцати восьми, а для женщин — от нуля до тридцати шести.
Знать свой гандикап необходимо, если игрок хочет участвовать в турнирных форматах. Ваш гандикап — великий уравнитель. Многие турниры форматируют свою игру таким образом, что для подсчета очков в раунде используется гандикап игроков. Это увеличивает конкуренцию и дает игрокам, которые могут быть не самыми сильными игроками в гольф, шанс ощутить вкус победы. Но это приводит нас к нескольким важным вопросам. Каков ваш гандикап и, что более важно, как вы его рассчитываете?
Новые изменения в расчете гандикапа были введены в 2020 году, поэтому мы рассмотрим, что такое гандикап, как рассчитать свой гандикап и какие правила изменились на 2020 год.
История гандикапов в гольфе
Гольф-гандикап появился более 100 лет назад и с тех пор действует.
В предыдущие годы это было известно как практическое ограничение, в котором участвовали три стороны: судья и два игрока. Позже, в 1850 году, они изменили название на гандикап.
Теперь ваш гандикап используется для оценки вашего уровня мастерства на основе вашего счета по сравнению с номинальным раундом поля. Гандикапы используются в больших и малых турнирах. От схватки с друзьями до клубных чемпионатов.
Что означает ваш гандикап
По сути, чем ниже ваш гандикап в гольфе, тем выше ваш уровень мастерства. Игрок с гандикапом 5 означает, что среднее значение предыдущих раундов этого игрока было на 5 больше номинала (критерии изменились с 5 раундов на 3 раунда, начиная с 2020 г.). Гандикапы часто используются для оценки того, как игрок выступил по сравнению с его средним уровнем игры, в отличие от прямого матча один на один. Гандикапы позволяют игрокам соревноваться и выигрывать у более талантливых игроков в гольф в зависимости от того, как каждый из них играл в тот день.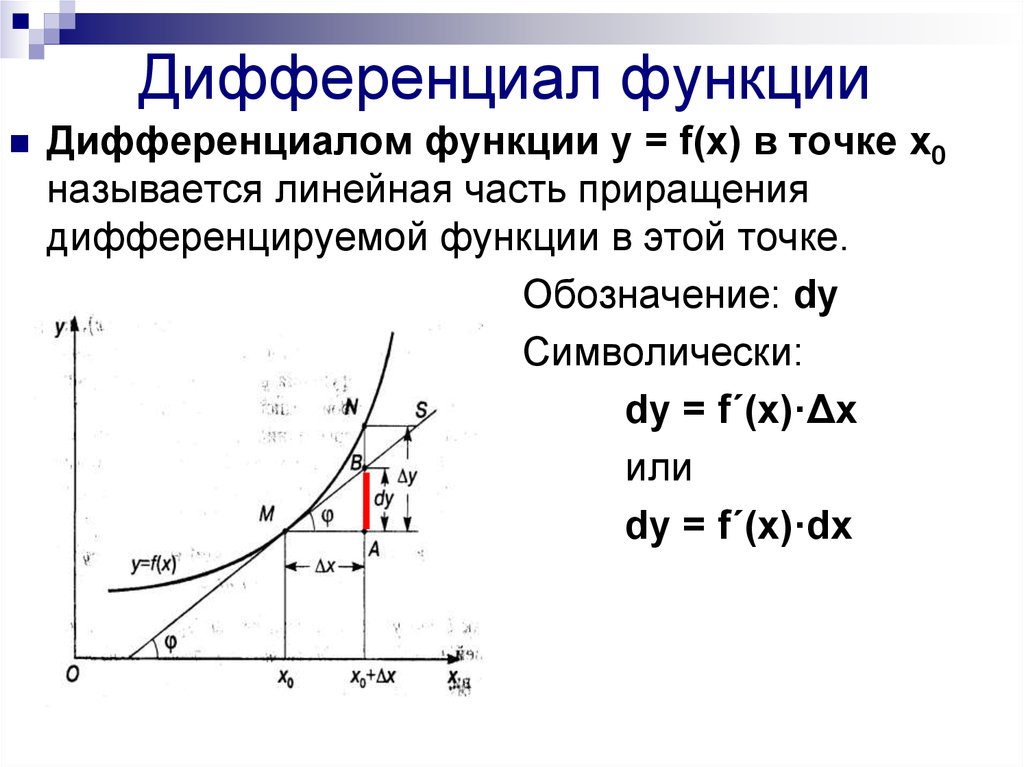
Например, предположим, что вы и ваш друг собираетесь играть на поле с 18 лунками с номиналом 72. Ожидается, что ваш друг с гандикапом в гольф, равным шести, сделает 78 ударов, или на шесть больше номинала. Ожидается, что вы и ваш гандикап на двенадцать ударов сделаете 84 удара, еще 12 больше номинала. Короче говоря, ваш гандикап — это количество ударов сверх номинала, которое вы должны сделать в ходе 18-луночного раунда. В этом сценарии предположим, что вы стреляете 82, а ваш друг стреляет 80. Технически, ваш друг стрелял в нижнем раунде, но поскольку вы включили гандикапы (вам -2, а вашему другу +2), вы на самом деле победитель!
Как рассчитать гандикап для гольфа в 2020 году
Если вы никогда не играли в гольф, вашего гандикапа в гольф не существует. Когда вы будете готовы создать свой гандикап для гольфа, начните с отслеживания результатов на 9 и 18 лунках. Результаты должны быть записаны в оценочной карточке и должны быть подписаны двумя людьми: вами и партнером, сопровождающим вас на игре в гольф.
Подписи необходимы, чтобы свести к минимуму коррупцию и сделать ваши результаты реальными и действительными.
Количество очков, необходимое для получения показателя гандикапа
По состоянию на январь 2020 г. для получения индекса гандикапа необходимо предоставить результаты трех 18-луночных матчей. Это можно сделать из комбинации патронов с 9 и 18 отверстиями; индекс гандикапа будет пересматриваться в начале и середине каждого месяца (1-го и 15-го числа). Это изменение требует, чтобы вы представили только три счета на 18 лунках. Пересмотр вашего гандикапа будет производиться ежедневно до тех пор, пока вы не обновите свой третий счет на 18 лунках до полуночи.
Изменения в расчете гандикапа для гольфа на 2020 год
До 2020 года расчет гандикапа гольф-поля производился по следующей формуле: Индекс гандикапа X Рейтинг сложности / 113
Расчет на 2020 год выполняется по новой формуле: Индекс гандикапа X (рейтинг сложности/113) + (рейтинг поля-пар)
.
Обратите внимание на изменения; новая формула включает рейтинг курса минус номинал. Эти изменения были сделаны для удобства игроков, играющих с разных площадок-ти. Поскольку они играют с разными критериями, необходимо сделать распределение гандикапов более справедливым.
Изменения 2020 года вводят новые правила определения гандикапов, и они представляют собой удары, которые игроки получают на соревнованиях. Таким образом, новая формула для игровых гандикапов – это гандикап поля X надбавка на гандикап. Это новое изменение вводит два новых правила для определения гандикапов, а именно: вам будет разрешено использовать гандикапы поля для корректировки ваших очков, и, во-вторых, игровые гандикапы будут использоваться для целей чистой конкуренции.
Формула расчета гандикапа поля
Вы можете подписаться на несколько приложений или программ, которые рассчитают ваш гандикап за вас, но если вам нравится делать что-то по старинке, вот полная разбивка по расчету вашего собственного гандикапа поля.
Расчет гандикапа основан на нескольких элементах. Некоторые из этих элементов включают рейтинг склона, гандикап поля и скорректированные валовые баллы. Другие факторы, которые можно учитывать, включают индекс гандикапа игры, связанный с ним дифференциал гандикапа, а также рейтинг поля.
Шаг 1. Вам необходимо преобразовать общий балл в скорректированный общий балл.
Чтобы получить скорректированные валовые баллы, используйте равноправный контроль ударов USGA. Используйте ESC вниз, регулируя отдельные 18-луночные счета, чтобы создать гандикап для гольфа. Согласно ESC, вы ограничены максимальным количеством ударов, которые вы можете ввести в данную лунку. Максимум можно получить из таблицы ниже
Гандикап поля | Максимальный балл |
Девять или меньше | Двойная тележка |
10-19 | 7 |
20-29 | 8 |
30-39 | 9 |
40 и выше | 10 |
Шаг 2: Рассчитайте разницу в гандикапе для каждого результата
Было бы лучше, если бы вы использовали эту формулу для расчета разницы форы.
Дифференциал гандикапа = (Скорректированный общий балл — рейтинг поля) X 113 / Рейтинг уклона поля.
Рейтинг поля – это просто количество очков, набранных новым игроком в гольф на обычном поле в нормальных игровых условиях. Рейтинг сложности — это рейтинг 113 для трассы, основанный на стандартной сложности.
Шаг 3: Выберите наименьший гандикапный дифференциал
Выберите лучший или самый низкий дифференциал гандикапа. Если вы ввели более 20 баллов, для расчета будут использованы 10 лучших дифференциалов ваших 20 самых последних баллов.
Шаг 4: Расчет среднего наименьшего значения из разностей
Если у вас есть 10 доступных дифференциалов гандикапа, рассчитайте среднее значение для 3 самых низких HD. Для 15 HD рассчитайте среднее значение для 6 самых низких оценок. Когда у вас будет не менее 20 оценок, всегда используйте 10 лучших из последних 20 оценок.
Шаг 5: Умножение среднего значения разницы гандикапов на 96%
Пятый шаг включает в себя определение среднего из чистых дифференциалов гандикапа путем умножения среднего дифференциала на 0,96.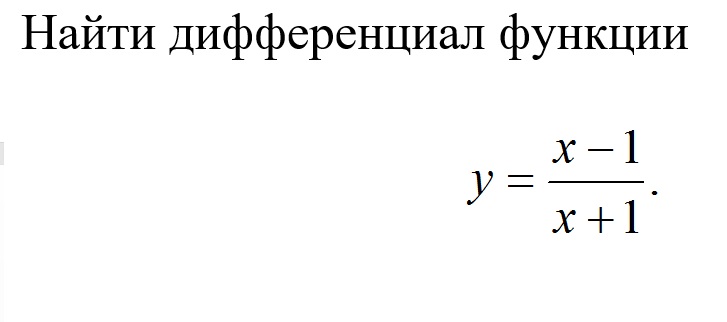
Шаг 6: Усечение, удаление числа до значения справа от десятых долей
Не округляйте числа в баллах. USGA заявляет, что максимальное число по умолчанию из любого индекса гандикапа в матче по гольфу должно составлять 40,4 для женщин и 36,4 для мужчин, если игра проводится на поле с 18 лунками. 9-луночное поле должно быть 18,2 у мужчин и 20,2 у женщин. Например, если среднее дифференциального гандикапа равно 13,196 после умножения на 0,96, усеченное значение будет 13,1.
Шаг 7: Расчет гандикапа курса
Гандикап поля — это количество ударов, которые игрок получает на определенном поле.
Гандикап поля = Индекс гандикапа X Рейтинг сложности/113 + (Рейтинг поля-Пар)
Пример: Этот расчет гандикапа поля предполагает 12,7 и уклон поля 115
Гандикап поля = 12,7 x 115 / 113 = 12,92 = 13
Как улучшить свой гандикап
Теперь, когда вы знаете свой гандикап в гольфе и полны решимости улучшить его, что вам нужно? Вот несколько советов, которые помогут вам улучшить свой гандикап:
- Улучшите свой замах.
Улучшите свой замах, тренируясь рано и часто. Если вам нужна профессиональная помощь, обратите внимание на персональные уроки гольфа в гольф-клубе Everglades. - Убедитесь, что ваша экипировка идеальна. Плохо подобранная экипировка может повлиять на вашу игру и увеличить риск получения травмы.
- Подтолкните себя — Всегда стремитесь устанавливать новые рекорды каждый раз, когда играете.
Улучшите свой замах, тренируясь рано и часто. Если вам нужна профессиональная помощь, обратите внимание на персональные уроки гольфа в гольф-клубе Everglades.Что такое надбавка за смену и как ее рассчитать?
Хотя ночная смена (также известная как ночная смена) может предоставить некоторые неожиданные льготы и гибкость, многие работодатели считают, что это может быть проблемой, чтобы заполнить эти поздние вечерние и ранние утренние временные интервалы. Кроме того, нехватка рабочей силы и растущий спрос на работников добавляют дополнительные трудности в усилия по найму для предприятий, которые полагаются на этот тип талантов. Даже для компаний, где ночные графики могут не быть нормой, часто может возникнуть необходимость в том, чтобы сотрудники подрабатывали в праздничные и выходные дни, что иногда называют третьей сменой.
Краткие факты о надбавках за смену
- Работодатели могут предлагать надбавки за смену для поощрения работников, работающих в смены, которые традиционно менее желательны.
- Работодатели могут устанавливать свои собственные правила в отношении того, когда и сколько выплачивается надбавка за смену.
- Надбавки за смену обычно представляют собой процент от обычной ставки заработной платы работника.
- Законодательство не требует, чтобы работодатель использовал разницу в сменах при наборе персонала в эти менее востребованные графики.
Реальность такова, что нестандартные рабочие часы не всегда находятся в верхней части списка желаний сотрудника. Таким образом, предложение надбавки за смену — и связанная с ней возможность дополнительной заработной платы — может помочь привлечь таланты, не позволяя вашим нынешним сотрудникам задаваться вопросом, зеленее ли трава в другом месте.
Прежде чем мы углубимся в детали, рассмотрим следующий сценарий в качестве примера, когда работодатель может предложить надбавку за смену.
Знаете ли вы?
Помимо надбавки за смену в виде процента от их почасовой ставки или процента от заработной платы, работодатели также могут предложить единовременную выплату за работу в третью смену.
Брэндон Перри, консультант по продуктам для расчета заработной платы OnPay
Уверенная работа с цифрами
OnPay вселила в нас уверенность в том, что мы можем с легкостью вести отчетность по заработной плате и связанным с ней налогам. Как занятый владелец бизнеса, знание того, что расчет заработной платы осуществляется правильно и вовремя, является облегчением. От адаптации и оплаты наших сотрудников до подачи отчетов о заработной плате — это отличный сервис и очень доступный!
— Тереза Эриксон, The Hope Bar LLC
Как рассчитать разницу между сменами?
Расчет надбавок за смену прост, если ваш сотрудник регулярно работает в смену, в которую предусмотрена надбавка. Например, Джо работал 40 часов в неделю в третью смену, что дает разницу в 15%.
Его заработок будет рассчитываться следующим образом:
- Обычная заработная плата: 40 часов x 35 долларов в час = 1400,00 долларов
- Дифференциал переключения: 35 долларов США в час x 15% = 5,25 долларов США в час в дополнение к обычной оплате
- 40 часов x 5,25 USD = 210,00 USD
- 1400 долл. США + 210 долл. США = 1610,00 долл. США
Общий чек Джо составит 1610,00 долларов.
Было бы немного сложно, если бы Джо работал только в одну ночную смену в течение недели. Используя приведенную выше разницу между сменами, мы рассчитали бы заработную плату Джо следующим образом:
- Обычная заработная плата: 40 часов x 35 долларов в час = 1400,00 долларов
- Разница между сменами (для одной ночной смены): 8 часов x 5,25 долл. США = 42,00 долл. США
- 1400 долл. США + 42 долл. США = 1442,00 долл. США
США = 1442,00 долл. США
Общий чек Джо составит 1442,00 доллара.
Поскольку Джо отработал 8 часов в третью смену, он получает 8-часовую надбавку к оплате, в результате чего его премиальная ставка составляет 40,25 доллара в час за смену.
Расчет сверхурочных с учетом разницы смен
Что произойдет, если Джо сделает все возможное? Джо работал в общей сложности 48 часов в неделю; его обычные 8 часов в день в дневную смену и в 8-часовую ночную смену в его обычный выходной день.
Подсчитаем зарплату Джо.
- Обычная оплата: 40 часов x 35 долларов = 1400,00 долларов
- Дифференциал смены: 8 часов x 5,25 долл. США = 42,00 долл. США
Теперь помните, что надбавка Джо за третью смену составляет 40,25 доллара. Поскольку он работал в субботу (обычно в выходной день), ему нужно будет платить за сверхурочную работу, используя его премиальную ставку.
Поскольку сверхурочное время рассчитывается по ставке, умноженной на 1,5% от обычной ставки, сверхурочное время Джо будет рассчитываться следующим образом:
- Ставка за сверхурочную работу: 40,25 долл. США x 1,5% = 60,38 долл. США
Далее мы рассчитаем сверхурочные Джо:
- Оплата сверхурочных: 8 часов x 60,38 долл. США = 483,04 долл. США
Наконец, мы добавим оплату за сверхурочную работу к регулярному графику оплаты Джо:
- Обычная оплата: 40 часов x 35 долларов США = 1400,00 долларов США
- Оплата сверхурочных: 8 часов x 60,38 долл. США = 483,04 долл. США
- 1400 долл. США + 483,04 долл. США = 1 883,04 долл. США
Итак, общий чек Джо за неделю составит 1883,04 доллара.
Совет для профессионалов:
Помните, что вы не обязаны предлагать своим сотрудникам надбавку за смену, но вы все равно обязаны оплачивать сверхурочную работу, даже если она приходится на смену, которая получает надбавку за смену.
Итог: разница между сменами может помочь при подборе персонала в сложных графиках
Если вы ведете бизнес, выходящий за рамки обычного 9к 5 графику работы, вы можете рассмотреть возможность предложения разницы смен. Этот небольшой прирост в оплате может помочь вам привлечь качественных сотрудников, которые готовы работать меньше оптимального количества часов. В то время как предложение надбавки за смену повысит ваши расходы на заработную плату, взамен вы получите более стабильную рабочую силу, более высокую производительность и меньше времени (и денег), затрачиваемых на набор сотрудников, что делает его вполне оправданным для многих работодателей.
Обратите внимание, что все материалы в этой статье предназначены только для образовательных целей и не являются налоговой или юридической консультацией. Вам всегда следует обращаться к квалифицированному налоговому, юридическому или финансовому специалисту в вашем районе для получения исчерпывающей налоговой или юридической консультации.