Графический метод решения задач линейного программирования
- Когда нужен графический метод?
- Теоретические основы графического метода
- Схема решения задач линейного программирования графическим методом
- Примеры решения задач графическим методом
- Решить задачи графическим методом самостоятельно, а затем посмотреть решения
- Продолжаем решать задачи графическим методом вместе
На этом уроке будем знакомиться с графическим методом решения задач линейного программирования, то есть, таких задач, в которых требуется найти такое решения системы линейных уравнений и (или) неравенств (системы ограничений), при котором функция цели — линейная функция — принимает оптимальное значение.
Ввиду того, что наглядность графического решения достигается лишь на
плоскости, мы можем познакомиться с графическим представлением задачи только в двумерном
пространстве. Это представление пригодно для системы ограничений-неравенств с двумя
переменными или для систем уравнений, в которых число переменных на 2 превышает число
уравнений, то есть число свободных переменных равно двум.
Поэтому графический метод имеет такие узкие рамки применения, что о нём как об особом методе решения задач линейного программирования говорить нельзя.
Однако для выработки наглядных представлений о решениях задач линейного программирования графический метод представляет определённый интерес. Кроме того, он позволяет геометрически подтвердить справедливость теорем линейного программирования.
Итак, задача линейного программирования. Требуется найти неотрицательные значения переменных и , удовлетворяющих системе неравенств
при которых линейная форма принимает оптимальное значение.
Из теории и практики решения систем линейных неравенств известно, что множество всех решений данной системы, то есть множество
пар чисел и
, удовлетворяющих
системе, составляет многоугольник этой системы. Допустим, что это пятиугольник ABCDE (рисунок внизу).
Линейная форма графически означает семейство параллельных между собой прямых. При конкретном числовом значении F линейная форма изобразится в виде некоторой прямой. Каждую из прямых этого семейства принято называть линией уровня. На рисунке построена линия уровня (чёрного цвета, проходит через начало координат), соответствующая значению F =0.
Если исходную линию уровня передвигать вправо, то значение F при
этом возрастает. Нужное направление движения исходной линии уровня можно установить следующим
образом. Коэффициенты при переменных в уравнении прямой служат координатами вектора,
перпендикулярного этой прямой. Таким образом, получаем градиент — вектор
(на рисунке бордового цвета). Значения функции
Среди прямых упомянутого семейства параллельных прямых прямые mn (зелёного цвета) и MN (красного цвета), которые назовём опорными.
Опорными обычно
называют такие прямые, которые имеют с многоугольником ABCDE хотя бы одну общую точку,
и многоугольник ABCDE целиком лежит по одну сторону от этой прямой. Как видно из
чертежа, прямая mn является опорной, так как она касается многоугольника в точке A и многоугольник целиком лежит правее (или выше) этой прямой. Прямая MN также является опорной, так как имеет с многоугольником общую точку С и
многоугольник целиком лежит левее этой прямой.
Из основных теорем
линейного программирования известно, что линейная форма достигает максимального и
минимального значений в крайних точках многогранника решений. Это значит, что опорные
прямые mn и MN характеризуют экстремальные значения линейной формы (функции цели), то есть
в точках А и С линейная форма достигает оптимальных значений. В точке А, находящейся ближе к началу координат, функция цели достигает минимального
значения, а в точке С, находящейся дальше от начала координат, — максимального
значения.
1. Построить многоугольник решений системы неравенств.
2. Начертить из семейства прямых, соответствующих линейной форме, линию
равных значений функции цели. Для построения линии равных значений придадим F некоторое числовое значение. Во многих задачах удобно принять, что
Затем, откладывая на оси число , а на оси — число , найдём точки пересечения линии равных значений с осями координат. Прямая, проведённая через эти точки, и есть требуемая прямая.
3. Двигать прямую (или линейку) вдоль градиента — вектора
параллельно линии равных значений в сторону многоугольника решений до соприкосновения с
многоугольником решений. Если первая встреча с многоугольником решений произойдёт в крайней
точке с координатами ,
то в этой точке функция цели достигает минимального значения. Если первая встреча
произойдёт со стороной многоугольника, то данная функция цели достигает минимума во всех
точках этой стороны.
4. Двигаясь дальше, придём к некоторому опорному положению, когда прямая будет иметь одну общую точку с многоугольником решений. В этой точке функция цели достигает своего максимума.
5. Если первоначально построенная линия равных значений пересекает многоугольник решений, то функция цели достигает минимального значения в вершине многоугольника, расположенной ближе к началу координат, а максимального значения — в вершине, более удалённой от начала координат.
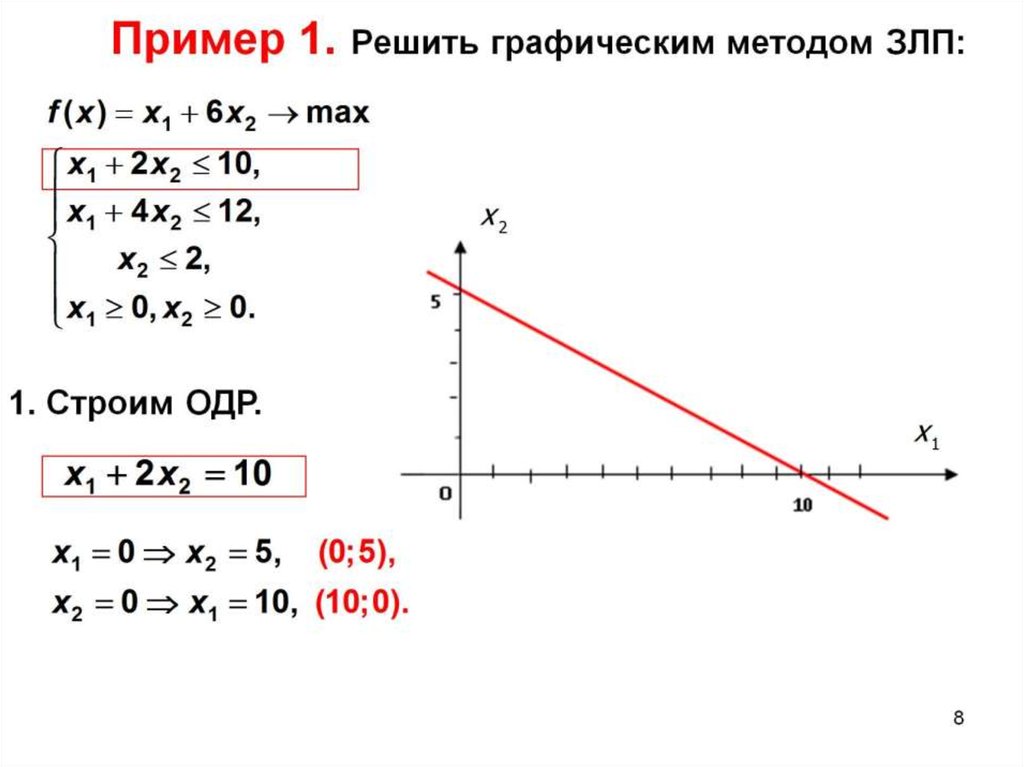
Пример 1. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Построим многоугольник решений. Для этого начертим граничные прямые. Из первого
неравенства запишем уравнение .
Это уравнение первой граничной прямой. Найдём точки пересечения этой прямой с осями
координат. При
из уравнения получим ,
при получим
. Это
значит, что первая прямая отсекает от осей координат отрезки
и .
Аналогично строим остальные граничные прямые. Вторая прямая от осей координат отсекает отрезки, равные 6. Третья прямая проходит параллельно оси , отсекая на оси отрезок, равный 2. Четвёртая прямая имеет уравнение . Она совпадает с осью .
Из рисунка ниже видно, что множество точек четырёхугольника ABDE удовлетворяет всем четырём неравенствам системы.
Следовательно, четырёхугольник ABDE является многоугольником решений системы (заштрихован вовнутрь).
Начертим линию равных значений функции цели. Приняв в равенстве F =1, получим, что эта линия отсекает отрезки 1 и 1/3 соответственно на оси и на оси . Проведём прямую через эти точки (на чертеже она чёрного цвета).
Двигая эту прямую параллельно самой себе в направлении градиента — вектора
(бордового цвета),
получим опорные прямые. Первая прямая (зелёного цвета) имеет с многоугольником общую точку A.
Здесь функция цели достигает минимума. Двигаясь дальше, придём к точке В.
Здесь максимум. Координаты точки В: (2, 4). Подставляя в функцию цели координаты
точки В, т. е. ,
,
получим максимальное значение функции цели: .
Нет времени вникать в решение? Можно заказать работу!
Пример 2. Решить графическим методом задачу линейного программирования, в которой требуется найти минимум функции при ограничениях
Решение. Многогранником решений является открытая область
Проведём линию равных значений функции цели при F =1, как в предыдущем примере (она опять чёрного цвета).
Из рисунка видно, что прямая ближайшнее от начала координат опорное
положение займёт в точке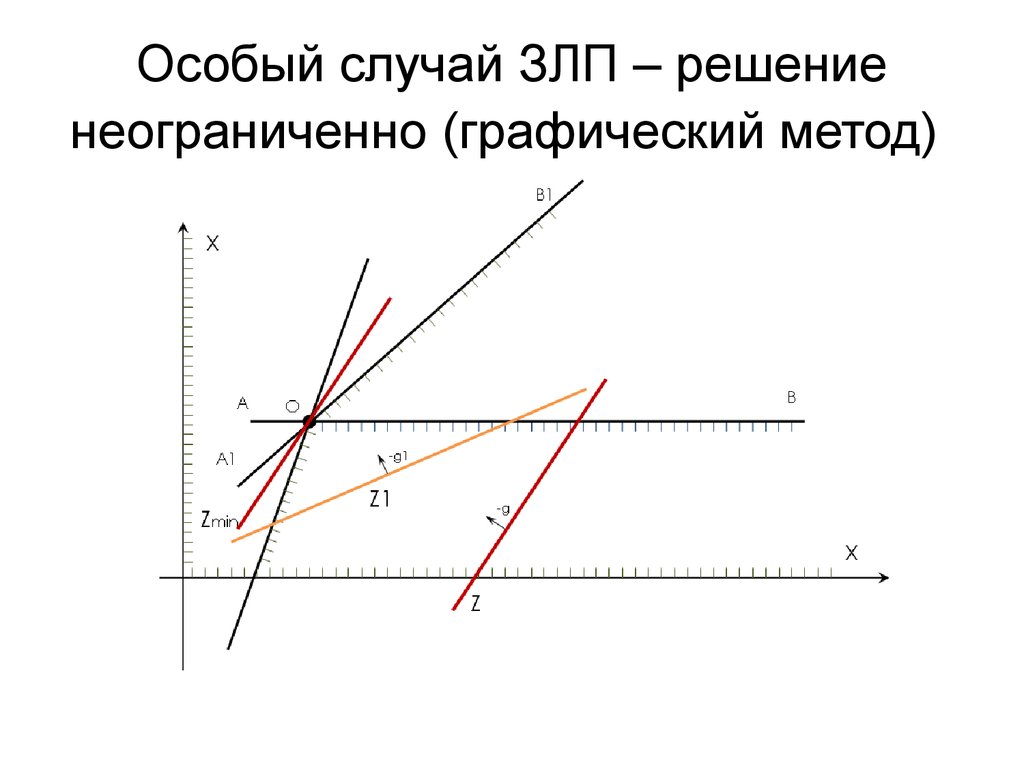 
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 3. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
где .
Правильное решение и ответ.
Пример 4. Решить графическим методом задачу линейного программирования, в которой требуется найти минимум функции при ограничениях
где .
Правильное решение и ответ.
До сих пор полученные выводы были основаны на том, что множество решений
задачи линейного программирования сконфигурировано так, что оптимальное решение конечно и
единственно. Теперь рассмотрим примеры, когда это условие нарушается. В этих примерах многоугольник
решений строится так, как показано в предыдущих примерах, остановимся же на признаках, которые
отличают эти исключительные примеры.
Пример 5. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. На рисунке изображены: неограниченная многогранная область решений данной системы ограничений, исходная линия уровня (чёрного цвета), вектор (бордового цвета), указывающий направление движения исходной линии уровня для нахождения максимума целевой функции.
Легко заметить, что функция F может неограниченно возрастать при заданной системе ограничений, поэтому можно условно записать, что .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 6. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение.
Изображённая на рисунке ниже область не содержит ни одной общей точки,
которая бы удовлетворяла всем неравенствам системы ограничений. То есть система ограничений противоречива
и не может содержать ни одного решения, в том числе и оптимального.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 7. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. Всем неравенствам системы ограничений удовлетворяют точки треугольника ABC, который и является областью решений. За исходную линию уровня взята прямая
(на рисунке ниже — чёрного
цвета), с тем чтобы она пересекала область решений. Как видно из рисунка, максимальное значение F = 8 достигается в точке С(8; 0).
При построении треугольника ABC не была использована прямая ,
соответствующая первому неравенству, хотя все точки треугольника удовлетворяют этому неравенству.
Таким
образом, этот пример отличается от предыдущих тем, что одно из неравенств системы ограничений оказалось
лишним.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 8. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. На рисунке ниже изображены область решений системы ограничений и линия уровня (чёрного цвета). Если передвигать линию уровня параллельно исходной в направлении вектора , то она выйдет из области решений не в одной точке, как это было в предыдущих примерах, а сольётся с прямой CD, которая является граничной линией области решений.
Все точки отрезка CD дают одно
и то же значение функции цели, которое и служит её оптимальным значением: .
Следовательно, имеется не одно, а бесчисленное множество оптимальных решений, совпадающих с точками
отрезка CD, в частности, с двумя угловыми точками C и D.
Этот пример показывает,
что в некоторых случаях единственность оптимального решения нарушается.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Напоследок следует заметить, что строить многогранник решений можно и другим способом, отличающимся о того, который мы рассматривали. А именно: можно не искать точки пересечения прямых с осями координат, а искать точки пересечения прямых. Для этого последовательно решаются системы из двух уравнений, так, чтобы решениями были точки пересечения всех прямых. Полученные точки и будут вершинами многогранника решений. Этот способ иногда бывает удобным в случаях, когда точки пересечения прямых с осями координат — дробные числа и, неправильно отложив точку пересечения, можно получить ошибку и в поиске точек пересечения самих прямых.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
Начало темы «Линейное программирование»
Задача и теоремы линейного программирования, примеры формулировки задач
Пример задачи линейного программирования: задача использования ресурсов, её графическое решение
Симплекс-метод решения задач линейного программирования: типичный пример и алгоритм
Симплекс-метод: случай, когда максимум целевой функции — бесконечность
Симплекс-метод: случай, когда система не имеет ни одного решения
Симплекс-метод: случай, когда оптимальное решение — не единственное
Двойственная задача линейного программирования
Решение задачи целочисленного программирования: методы и примеры
Решение транспортной задачи распределительным методом на примерах
Поделиться с друзьями
Графический метод — линейное программирование
Описание метода
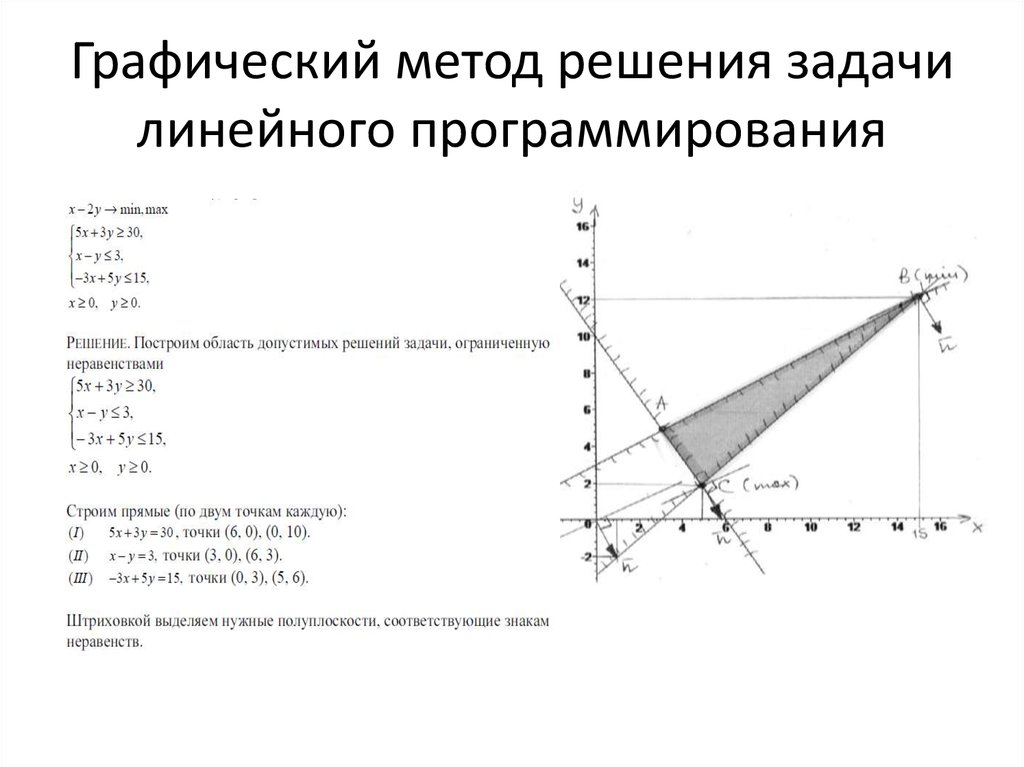
Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.
Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .
Построение области допустимых решений
Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.
Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку.
Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).
Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.
Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.
Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых.
Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.
Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).
Нахождение экстремума целевой функции
Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.
Теперь мы можем искать экстремум целевой функции
(1.1) .
Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР.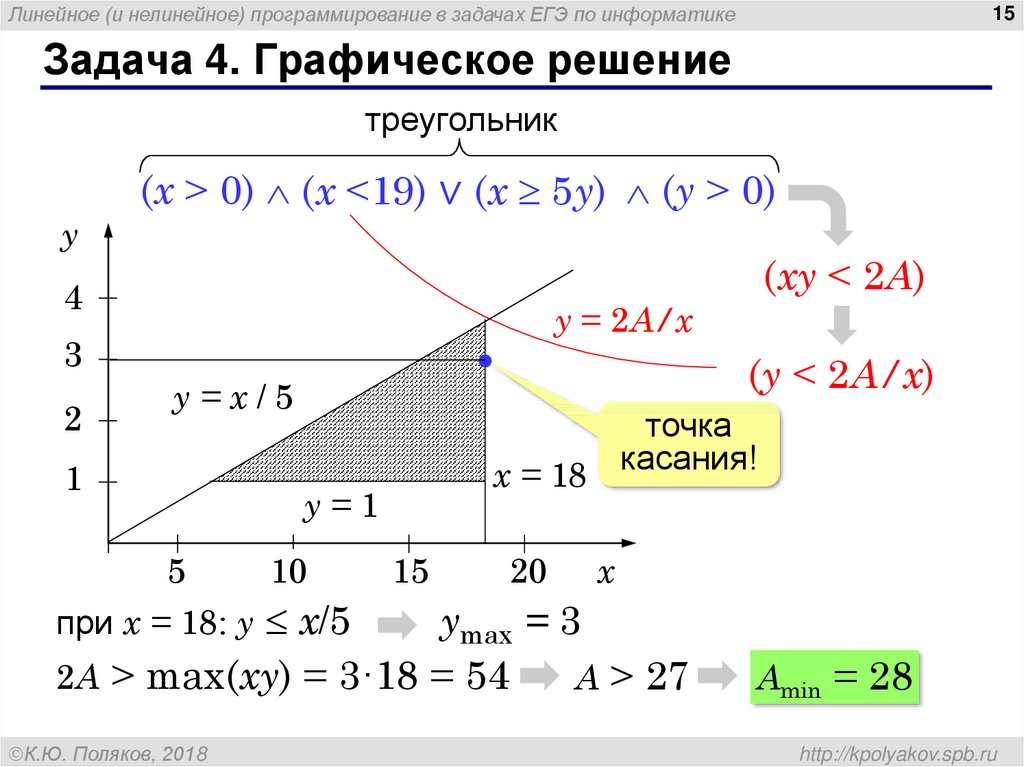
На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .
Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.
Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.
Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.
Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений.
Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .
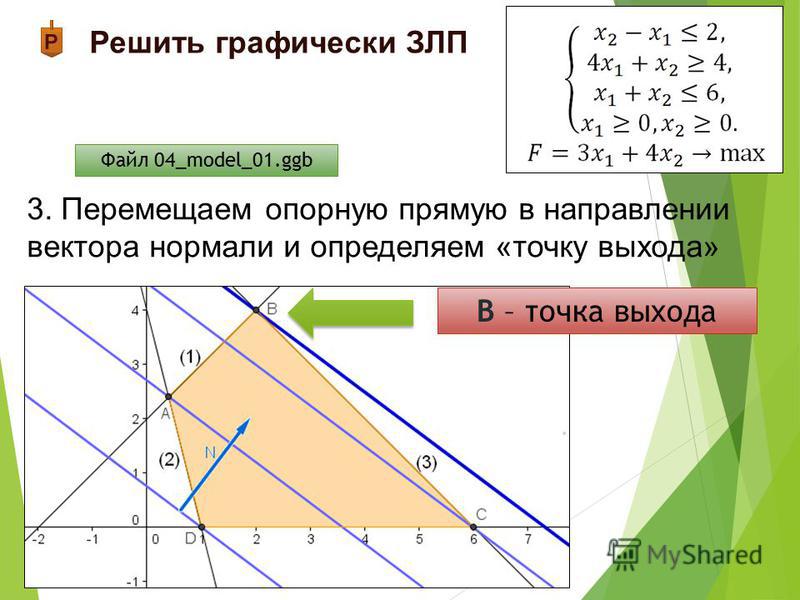
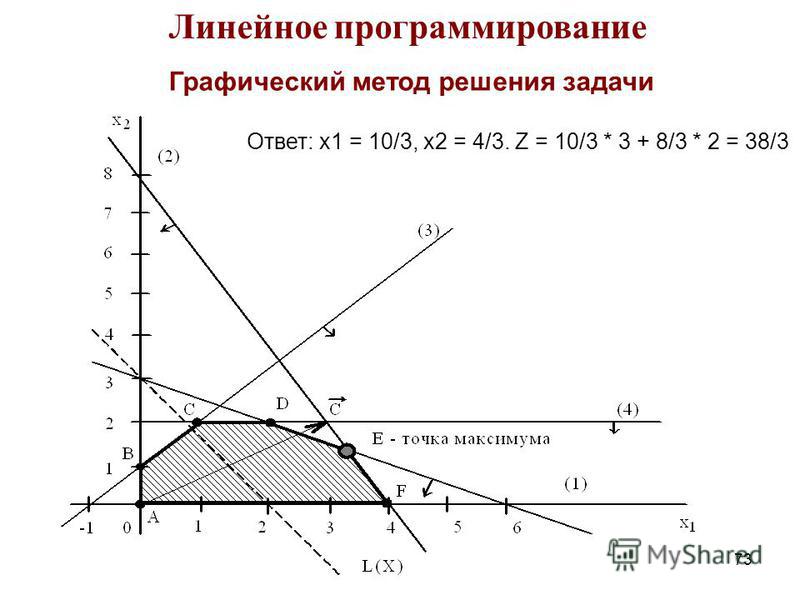
Пример решения задачи линейного программирования графическим методом
Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден. ед.
Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.
Решение
Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)
Тогда экономико-математическая модель задачи имеет вид:
Решаем графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).
Прямые и являются осями координат.
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.
Строим произвольную линию уровня целевой функции, например,
(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).
Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Решение задачи: ;
Ответ
.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.
Пример 2
Решить задачу линейного программирования графическим методом.
Решение
Решаем графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).
Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).
Строим прямую .
Строим прямую (ось абсцисс).
Область допустимых решений (ОДР) ограничена построенными прямыми.
Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.
Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Решение задачи: ;
Ответ
.
Пример отсутствия решения
Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.
Решение
Решаем задачу графическим методом.
Проводим оси координат и .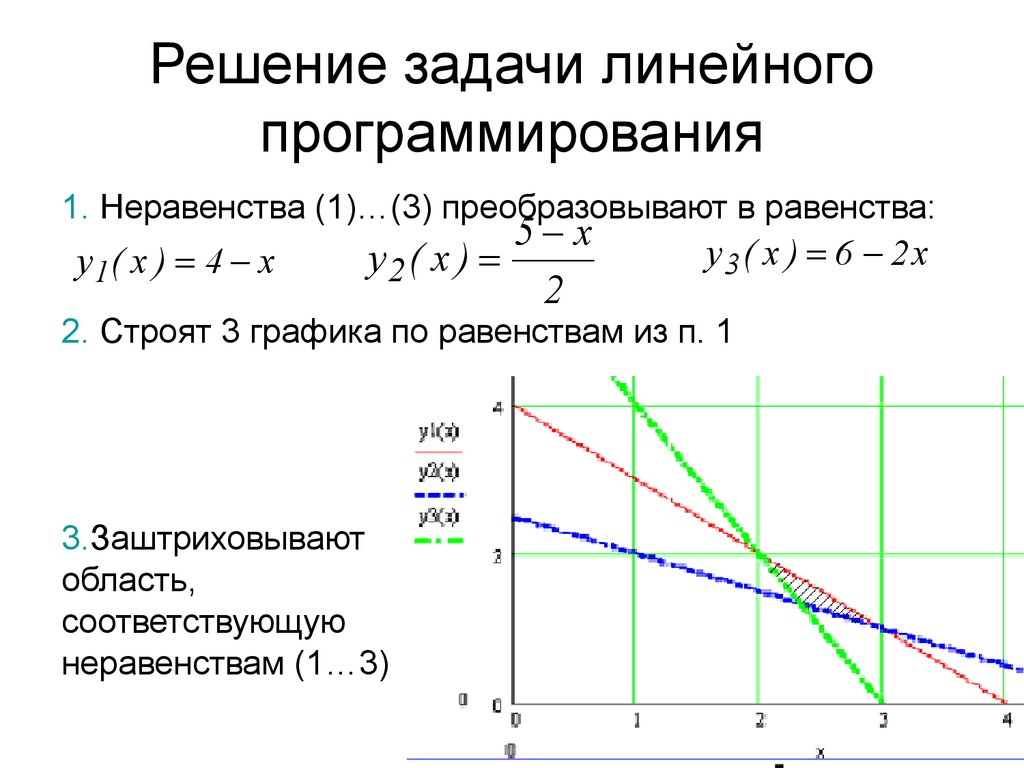
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).
Прямые и являются осями координат.
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.
Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .
Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE.
Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.
Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:
Ответ
Максимального значения не существует.
Минимальное значение
.
Графическое решение задач линейного программирования
Линейное программирование — самый простой способ оптимизации задачи. С помощью этого метода мы можем сформулировать реальную проблему в виде математической модели. С помощью линейного программирования мы можем решить огромное количество задач в различных областях, но обычно оно используется для задач, в которых мы должны максимизировать прибыль, минимизировать затраты или минимизировать использование ресурсов.
Типы задач линейного программирования
Существуют в основном три типа задач, основанных на линейном программировании. Они следующие:
Производственная задача: В задаче этого типа некоторые ограничения, такие как рабочая сила, единицы продукции в час, машино-часы, задаются в виде линейного уравнения. И мы должны найти оптимальное решение, чтобы получить максимальную прибыль или минимальные затраты.
Диетическая проблема: Такого рода проблемы, как правило, просты для понимания и имеют меньше переменных. Наша главная цель в этом виде проблемы состоит в том, чтобы свести к минимуму стоимость диеты и сохранить минимальное количество каждого компонента в рационе.
Транспортная задача: В этих задачах мы должны найти самый дешевый способ транспортировки, выбрав кратчайший маршрут/оптимизированный путь.
Некоторые часто используемые термины в задачах линейного программирования:
Целевая функция: Прямая функция формы Z = ax + by, где a и b являются постоянными, которая уменьшается или увеличивается, называется целевой функцией.
Например, если Z = 10x + 7y. Переменные x и y называются переменной решения.
Ограничения: Ограничения, которые применяются к линейному неравенству, называются ограничениями.
- Неотрицательные ограничения: x > 0, y > 0 и т. д.
- Общие ограничения: x + y > 40, 2x + 9y ≥ 40 и т. д.
Задача оптимизации: Минимизация переменных задачи линейного неравенства называется задачей оптимизации.
Допустимая область: Общая область, определяемая всеми заданными задачами, включая неотрицательное (x ≥ 0, y ≥ 0) ограничение, называется допустимой областью (или областью решения) задачи. Область, отличная от допустимой области, известна как недопустимая область.
Возможные решения: Эти точки внутри или на границе области представляют возможные решения проблемы. Любая точка вне сценария называется невозможным решением.
Оптимальное (наиболее возможное) решение: Любая точка в появляющейся области, которая обеспечивает правильное количество (максимум или минимум) целевой функции, называется оптимальным решением.
Теоремы задачи линейного программирования
Теорема 1: Пусть Y будет допустимой областью (выпуклым многоугольником) для задачи линейного программирования, т.е. Y = ax + by (целевая функция). Итак, когда Y имеет оптимальное значение (максимальное или минимальное), где x и y подчиняются ограничениям, описываемым линейными неравенствами, то это оптимальное значение возникает в угловых точках допустимой области, т. е. в вершинах.
Теорема 2: . Пусть Y — допустимая область задачи линейного программирования, т. е. Y = ax + by (целевая функция). Если X ограничено, то целевая функция Y имеет как максимальное, так и минимальное значение на X, и каждое из них происходит в угловой точке X.
ПРИМЕЧАНИЕ. должны учитывать самые внутренние точки пересечения всех уравнений. Мы можем решать задачи линейного программирования двумя разными методами:
Графическое решение задач линейного программирования
Угловая точка с помощью угловой задачи точечным методом необходимо выполнить следующие шаги:
Шаг 1: Создать математическую формулировку из данной задачи. Если не дано.
Шаг 2: Теперь постройте график, используя заданные ограничения, и найдите достижимую область.
Шаг 3: Найдите координаты допустимой области (вершин), которые мы получили из шага 2.
Шаг 4: Теперь оцените целевую функцию в каждой угловой точке допустимой области. Предположим, что N и n обозначают наибольшее и наименьшее значения этих точек.
Шаг 5: Если допустимая область ограничена, то N и n являются максимальным и минимальным значением целевой функции. Или, если допустимая область неограничена, то:
- N — максимальное значение целевой функции, если открытый полуплан получен по оси + by > N не имеет общих точек с допустимой областью.
В противном случае целевая функция не имеет решения. - n — минимальное значение целевой функции, если открытый полуплан получается по оси + by < n не имеет общих точек с допустимой областью. В противном случае целевая функция не имеет решения.
В противном случае целевая функция не имеет решения.Примеры:
Вопрос 1. Решите данные задачи линейного программирования графически:
Максимизируйте: Z = 8x + y
и ограничения:
x + y ≤ 40, +9 у ≤ 60,
x ≥ 0, y ≥ 0
Решение:
Шаг 1. Ограничения: 003
х ≥ 0, у ≥ 0
Шаг 2: Нарисуйте график, используя эти ограничения.
Здесь оба ограничения меньше или равны, поэтому они удовлетворяют области ниже (в направлении начала координат). Вы можете найти вершину допустимой области по графу или рассчитать, используя заданные ограничения:
x + y = 40 … (i)
2x + y = 60 … (ii)
Теперь умножьте уравнение (i) на 2, а затем вычтем оба уравнения (i) и (ii), мы получим
y = 20
Теперь подставим значение y в любое из уравнений, мы получим
x = 20
Итак, третья точка допустимая область (20, 20)
Шаг 3: Найти максимальное значение Z = 8x + y.
(0, 40) 40 (20, 20) 180 9020 Максимальное значение Z = 240 в точке x = 30, y = 0. (30, 0) 240
Сравните каждую точку пересечения графика, чтобы найти максимальное значениеВопрос 2. Для одного торта требуется 200 г муки и 25 г жира, а для другого вида торта требуется 100 г муки и 50 г жира Найдите максимальное количество тортов, которое можно приготовить из 5 кг муки. муки и 1 кг жира при условии, что в других ингредиентах, используемых при приготовлении лепешек, недостатка нет.
Решение:
Шаг 1. Создайте подобную таблицу для облегчения понимания (не обязательно).
Пол(г) Жир(г) Жмых первого сорта (х) 200 7 2173 Торт второго сорта (у) 100 50 Доступность 5000 1000 200x + 100y ≤ 5000 или 2x + y ≤ 50 25x + 50y ≤ 1000 или x + 2y ≤ 40 Кроме того, x > 0 и y > 0 Шаг 3: Создайте график, используя неравенство (помните, что оси x и y должны быть положительными)
Шаг 4: Найдите максимальное количество тортов ( Z) = х + у.
х у Z(x+y) 10 173 7 2 0 1973 7 2 7 2 7 77 20 20 10 30 8 2 , Z максимальна при координате (20, 10). Таким образом, максимальное количество тортов, которое можно испечь, равно Z = 20 + 10 = 30. Метод изо-затрат 25 0 25 Термин «изо-затраты» или «метод изо-прибыли» представляет собой комбинацию баллов, которая дает одинаковую стоимость /профит как любая другая комбинация на той же линии. Это делается путем построения линий, параллельных наклону уравнения.
Для решения задачи методом Изо-затрат необходимо выполнить следующие шаги:
Шаг 1: Создать математическую формулировку данной задачи.
Шаг 2: Теперь постройте график, используя заданные ограничения, и найдите допустимую область.
Шаг 3: Теперь найдите координаты допустимой области, которые мы получили из шага 2.
Шаг 4: Найдите подходящее значение Z (целевая функция) и нарисуйте линию этой целевой функции.
Шаг 5: Если целевая функция максимального типа, нарисуйте линию, параллельную линии целевой функции, и эта линия будет дальше всего от начала координат и имеет только одну общую точку с допустимой областью. Или, если целевая функция минимального типа, то нарисуйте прямую, параллельную прямой целевой функции, и эта линия является ближайшей к началу координат и имеет хотя бы одну общую точку с допустимой областью.
Шаг 6: Теперь получите координаты общей точки, которую мы нашли на шаге 5. Теперь эта точка используется для нахождения оптимального решения и значения целевой функции.
Примеры:
Вопрос 1. Решите данные задачи линейного программирования графически:
Максимизируйте: Z = 50x + 15y
3 900 02 5х + у ≤ 100,
x + y ≤ 50,
x ≥ 0, y ≥ 0
у ≤ 100,
х + у ≤ 50,
х ≥ 0, у ≥ 0
Шаг 1: Поиск точек
Мы также можем записать как
5x + y = 100 ….
x + y = 50 ….(ii)
Теперь мы находим точки
поэтому берем
eq(i), теперь в этом уравнении
Когда x = 0, y = 100
и когда y = 0, x = 20
Итак, точки (0, 100) и (20, 0)
Аналогично , в уравнении (ii)
Когда x = 0, y = 50
Когда y = 0, x = 50
Итак, точки (0, 50) и (50, 0)
Шаг 2: Теперь нанесите эти точки на график и найдите достижимую область.
Шаг 3: Теперь мы находим удобное значение Z (целевая функция)
Итак, чтобы найти удобное значение Z, мы должны взять lcm коэффициента 50x + 15y, т. е. 150. Итак, значение Z кратно 150, т. е. 300. Отсюда
50x + 15y = 300
Теперь найдем точки
Положим x = 0, y = 20
Положим y = 0, x = 6
нарисуйте линию этой целевой функции на графике:
Шаг 4: Поскольку мы знаем, что целевая функция является максимальным типом, мы рисуем линию, которая параллельна прямой целевой функции и находится дальше всего от начала координат и имеет только одну общую точку с допустимой областью.
Шаг 5: У нас есть общая точка (12,5, 37,5) с допустимой областью. Итак, теперь находим оптимальное решение целевой функции:
Z = 50x + 15y
Z = 50(12,5) + 15(37,5)
Z = 625 + 562,5
Z = 1187
Вопрос 2. Решить данные задачи линейного программирования графически:
Минимизировать: Z = 20x + 10y
9001: 9001 2 х + 2у ≤ 40,3x + y ≥ 30,
4x + 3y ≥ 60,
x ≥ 0, y ≥ 9
Дано:
x + 2y ≤ 40 ,
3х + у ≥ 30,
4x + 3y ≥ 60,
x ≥ 0, y ≥ 0
Шаг 1: Поиск точек + y = 30 ….(ii)
l3 = 4x + 3y = 60 ….(iii)
Теперь мы находим точки
Итак, мы берем уравнение (i), теперь в этом уравнении
Когда x = 0 , y = 20
и когда y = 0, x = 40
Итак, точки (0, 20) и (40, 0)
Аналогично, в уравнении (ii)
Когда x = 0, y = 30
Когда y = 0, x = 10
Итак, точки (0, 30) и (10, 0)
Аналогично, в уравнении (iii)
Когда x = 0, y = 20
Когда y = 0, x = 15
Итак, точки (0, 20) и (15, 0)
Шаг 2: Теперь нанесите эти точки на график и найдите допустимую область.
Шаг 3: Теперь мы находим подходящее значение Z (целевая функция)
Предположим, что z = 0 целевая функция на графике:
Шаг 4: Поскольку мы знаем, что целевая функция является минимальной, мы рисуем прямую, параллельную прямой целевой функции, ближайшую к началу координат и имеющую хотя бы одну общую точку с допустимой областью.
Эта параллельная линия касается допустимой области в точке A. Итак, теперь мы находим координаты точки A:
Как видно из графика в точке A линии l2 и l3 пересекаются, поэтому мы находим координату точки A путем решения этих уравнений:
l2 = 3x + y = 30 ….(iv)
l3 = 4x + 3y = 60 ….(v)
Теперь умножьте eq(iv) на 4 и eq(v) на 3, мы получим
12x + 4y = 120
12x + 9y = 180
Теперь вычтем оба уравнения, и мы получим координаты (6, 12)
Шаг 5: У нас есть общая точка (6, 12) с допустимой областью. Итак, теперь находим оптимальное решение целевой функции:
Z = 20x + 10y
Z = 20(6) + 10(12)
Z = 120 + 120
Z = 240
Графический метод линейного программирования | Упрощенный учет
Введение
Графический метод линейного программирования используется для решения задач путем нахождения самой высокой или самой низкой точки пересечения между линией целевой функции и допустимой областью на графике.
Этот процесс можно разбить на 7 простых шагов, описанных ниже .
Как и почему мы используем алгоритмы в…
Пожалуйста, включите JavaScript
Как и почему мы используем алгоритмы в программировании | Логика и алгоритмы программирования с использованием python?
Шаг 1: определение ограничений
Все ограничения, относящиеся к задаче линейного программирования, должны быть определены в виде неравенств.
Что такое неравенства?
Неравенства – это математические выражения, подобные уравнениям, за исключением одного отличия. В отличие от уравнений, в которых утверждается, что чему-то равно (например, x = y), неравенства выражают, что больше или меньше чего-то (например, x > y).
Неравенства обозначаются следующими символами:
> Больше
≥ Больше или равно< Меньше ≤ Меньше или равно
Шаг 2: Определите Целевая функция
Цель решения задачи выражается в виде математического уравнения.
Например, если цель состоит в том, чтобы максимизировать вклад от продажи Продуктов А и В с доходом на единицу 10 и 5 долларов соответственно, целевая функция должна быть:
10A + 5B = Максимальный вклад
Это означает, что цель решения проблемы состоит в том, чтобы максимизировать общий вклад бизнеса путем продажи оптимального сочетания продуктов A и B.
Задача с приведенным выше уравнением что мы не можем просто изобразить это на графике (как требуется на шаге 5). Чтобы обойти эту проблему, мы определяем случайное число вместо «Максимального вклада». Поскольку нам требуется только наклон (градиент) целевой функции, мы можем изобразить целевую функцию на графике, используя любое случайное значение вместо максимального вклада.
Используя предыдущий пример, целевую функцию можно переписать как:
10A + 5B = 100
Обратите внимание, что 100 выше — это просто случайное число. Вместо этого можно использовать любое другое значение.
Шаг 3: Нанесите ограничения на миллиметровую бумагу
Неравенства ограничений, определенные на шаге 1, следует нанести на график.
Вы можете построить ограничения таким же образом, как и уравнение.
Пример
Ограничение: 1A + 2B ≤ 100
Для того, чтобы отобразить приведенное выше ограничение на графике, вы можете преобразовать неравенство в уравнение:
1A + 2B = 100
Теперь вам нужны координаты любые 2 точки из приведенного выше уравнения.
Как найти координаты точки из уравнения?
Чтобы найти координаты, просто вставьте случайное значение для A или B. Решение уравнения после вставки случайных значений может быть использовано для нахождения значения другой координаты.
Например, мы можем найти значение B, когда A = 0, подставив ноль вместо A и решив уравнение следующим образом: = 100
2B = 100
B = 50Таким образом, координаты первой точки равны A = 0 и B = 90 8 , что может быть записано как 90 09 , 50).
Аналогично, вставка нуля в качестве значения B может дать нам значение A для второй точки следующим образом:
1A + 2(0) = 100
1A + 0 = 100
1A = 100
= 1 0 0Следовательно, координаты второй точки A = 100 и B = 0 или (100, 0).
После того, как вы определили координаты любых двух точек из уравнения, вы просто отмечаете их на графике и проводите через них прямую линию, как показано ниже.
Шаг 4: Выделите допустимую область на графике
После того, как вы нанесли неравенства ограничений на график, вам необходимо заштриховать область графика, которая находится за пределами ограничений, т. е. которая невозможна.
Например, ограничение 1A + 2B ≤ 100 будет заштриховано следующим образом:
Область на графике, которая лежит на или ниже предельной линии ограничения , допустима и поэтому не заштрихована.
Иногда бывает сложно понять, какую сторону ограничивающей линии закрасить. В таких случаях полезно рассмотреть, возможна ли конкретная комбинация (например, 0 единиц A, 0 единиц B) выше или ниже линии или не учитывать только это ограничение. Если комбинация выполнима, необходимо заштриховать противоположную сторону линии и наоборот.
Шаг 5: Нанесите целевую функцию на график
Линия целевой функции может быть нанесена на график так же, как и линии ограничения, за исключением того, что вы можете отличить ее от линий ограничения, например. нарисовав пунктирную линию вместо обычной линии.
Линия целевой функции 10A + 5B = 100 будет проведена следующим образом:
Рабочая
Точка A:
10(0) + 5B = 100
3 B = 902 0 100 0 0 0 0 0
(0, 20)
Точка B:
10(A) + 5(0) = 100 (10, 0)
Шаг 6: Найдите оптимальную точку
Оптимальная точка задачи линейного программирования всегда лежит в одной из угловых точек допустимой области графа.
Чтобы найти оптимальную точку, нужно провести линейкой по графику по градиенту целевой функции. Если цель состоит в том, чтобы максимизировать (например, вклад), вы должны сдвинуть линейку до точки в допустимой области, которая находится дальше всего от начала координат. И наоборот, если цель состоит в том, чтобы минимизировать (например, стоимость), вы должны сдвинуть линейку до точки в допустимой области, ближайшей к началу координат. В обоих случаях вы должны помнить о перемещении линейки по градиенту линии целевой функции.
Обратите внимание, что линейка параллельна пунктирной линии (т.е. линии целевой функции). Красная точка, отмеченная на графике (100, 0), — это последняя точка, которой касается линейка, оставаясь при этом в допустимой области, и, следовательно, это оптимальная точка.
Шаг 7: Найдите координаты оптимальной точки
В приведенном выше примере координаты оптимальной точки можно легко определить, поскольку точка лежит на оси X.
Сравните каждую точку пересечения графика, чтобы найти максимальное количество тортов, которые можно испечь.
Если не дано.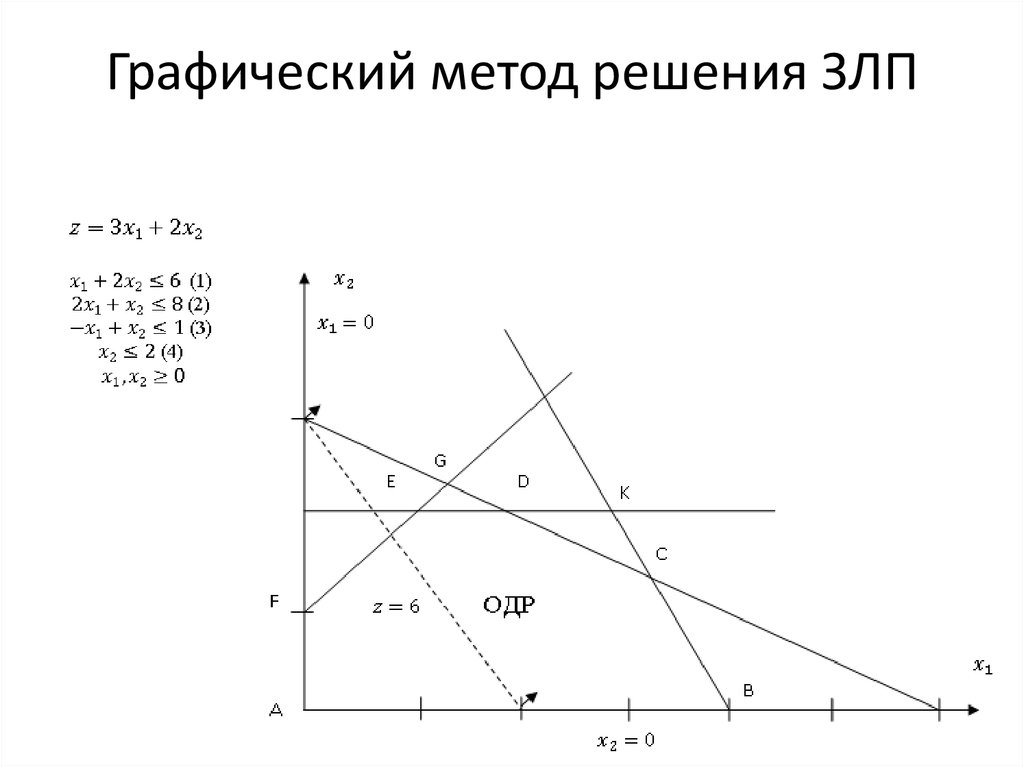
(i)
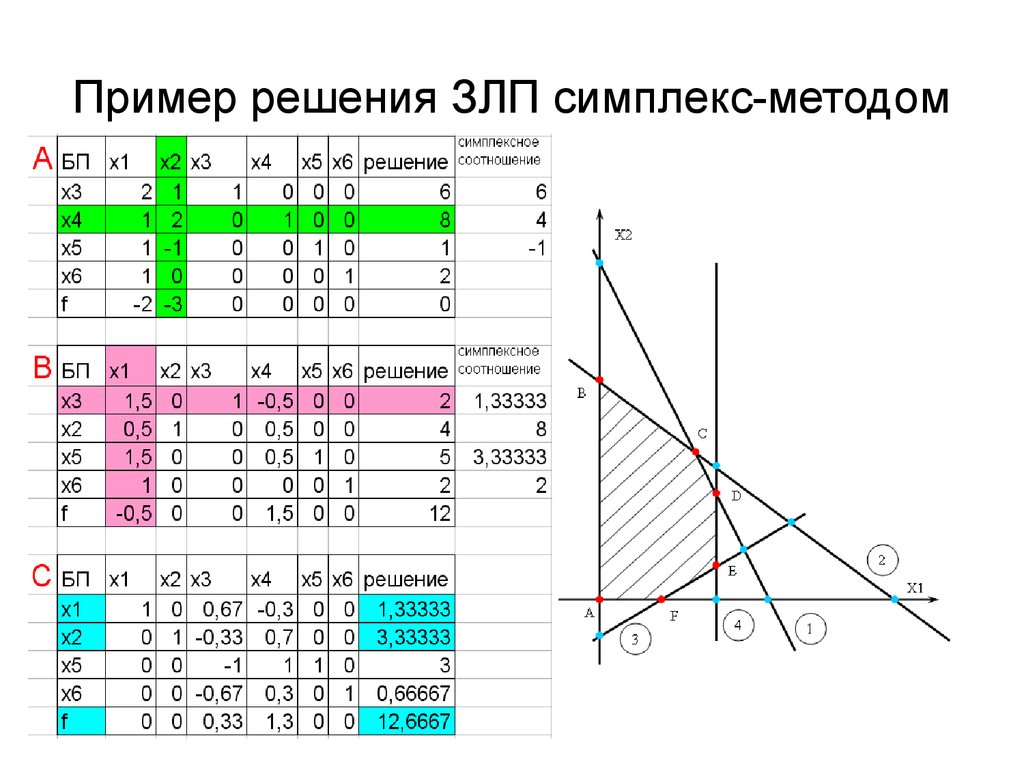
После того, как все линии ограничений будут одинаково заштрихованы, незаштрихованная часть графика будет представлять допустимую область.
