Конус площадь: Найдите площадь полной поверхности конуса если образующая наклонена к плоскости основания под углом 60 градусов…

Конус. Площади поверхностей. Объём

Урок 39. Подготовка к ЕГЭ по математике

В данном видеоуроке мы напомним, какое геометрическое тело называют конусом. Вспомним о сечениях конуса. Повторим формулы для вычисления площадей боковой и полной поверхностей конуса и его объёма. Поговорим об усечённом конусе.

Конспект урока «Конус. Площади поверхностей. Объём»

Напомним, что конус – это тело, полученное при вращении прямоугольного треугольника вокруг прямой, проходящей через один из его катетов.

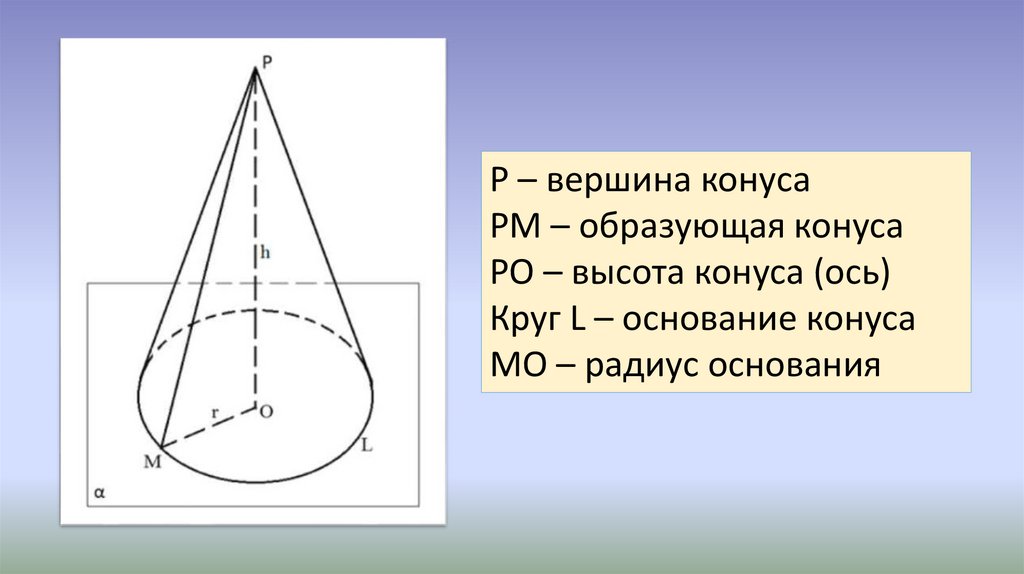
Назовём элементы конуса.

Осью конуса называется прямая вращения.

Основание конуса – круг радиуса , который равен катету треугольника вращения.

Радиус конуса  – это радиус его основания.

Вершина конуса – неподвижная вершина треугольника вращения.

Образующая конуса  – отрезок, соединяющий вершину конуса с любой точкой окружности основания. Все образующие конуса равны между собой.

Высота конуса  – перпендикуляр, опущенный из вершины конуса на плоскость его основания. Высота конуса совпадает с неподвижным катетом треугольника вращения.

В конусе радиус основания , высота  и образующая  связаны следующим соотношением:

.

Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса.

Осевым сечением конуса называется сечение конуса плоскостью, проходящей через его ось.

Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого – образующие, а основание – диаметр основания конуса.

Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав её по одной из образующих. Развёрткой боковой поверхности конуса является круговой сектор.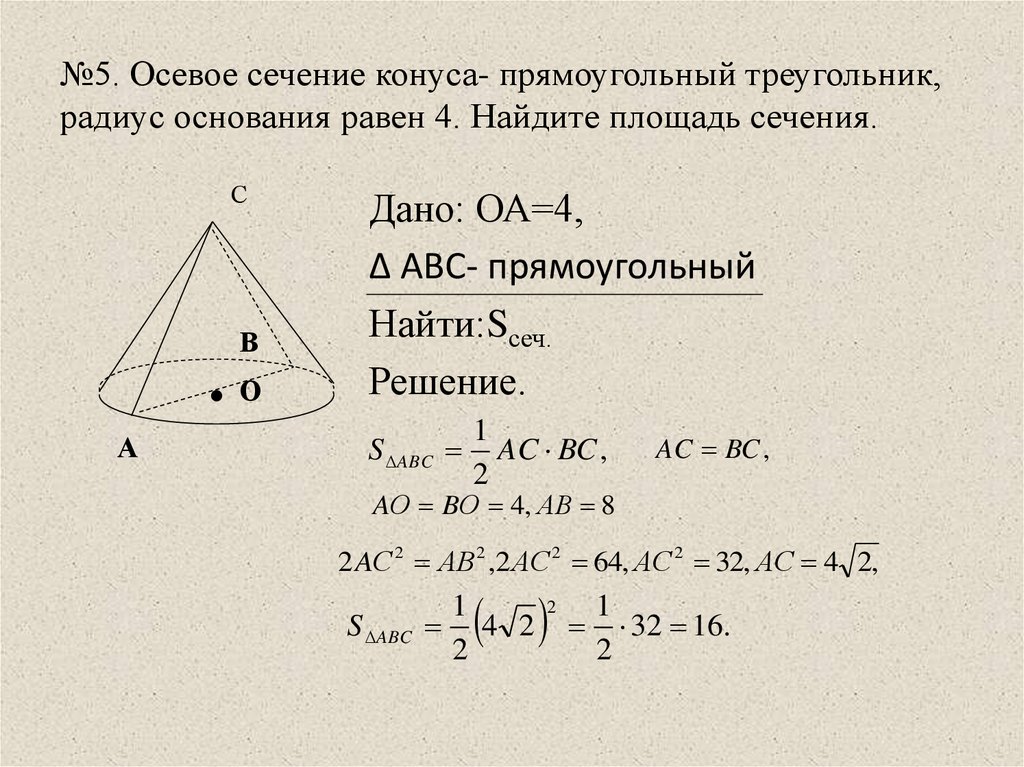

 ,

где  – радиус основания конуса,  – его образующая.

Объём конуса равен одной третьей произведения площади основания на высоту.

Тогда его можно вычислить по формуле:

,

где  – радиус основания конуса,  – его высота.

Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса. Эта плоскость разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая (нижняя) называется усечённым конусом.

Усечённым конусом называется часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. Усечённый конус имеет ось, высоту , радиусы оснований  и ,

образующую . Осевое сечение усечённого конуса – равнобедренная трапеция.

Площадь боковой поверхности усечённого конуса и объём усечённого конуса равен разности площадей боковых поверхностей и объёмов полного конуса и отсечённого.

,

Площадь боковой поверхности усечённого конуса можно найти по следующим формулам:

  ,  

Объём усечённого конуса можно вычислить по следующим формулам:

 ,

где  и  – площади оснований,  – высота усечённого конуса;

или ,

где  – высота усечённого конуса,  и  – радиусы верхнего и нижнего оснований.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. Радиус основания конуса равен  см, высота конуса равна  см. Найдите площадь боковой поверхности и объём конуса.

Решение.

Задача вторая. В конус вписана правильная треугольная пирамида с площадью основания  см² и углом наклона бокового ребра к основанию, равным . Найдите объём и площадь полной поверхности конуса.

Решение.

Задача третья. В равносторонний конус с радиусом основания, равным см, вписан прямоугольный параллелепипед в основании которого лежит квадрат, с высотой  см так, что одно его основание принадлежит основанию конуса, а вершины другого основания принадлежат боковой поверхности конуса. Найдите объём параллелепипеда. В ответе запишите значение .

Решение.

Задача четвёртая

. Длины радиусов оснований и образующей усечённого конуса равны соответственно  см,  см и  см. Вычислите его высоту.

Решение.

Предыдущий урок 38 Цилиндр. Площади поверхностей. Объём

Следующий урок 40 Шар и сфера, их сечения

Получите полный комплект видеоуроков, тестов и презентаций Подготовка к ЕГЭ по математике

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

формула объема, площади поверхностей и другое / Справочник :: Бингоскул

Конус – объемное тело, получаемое посредством вращения треугольника с углом 90° вокруг катета – его высоты.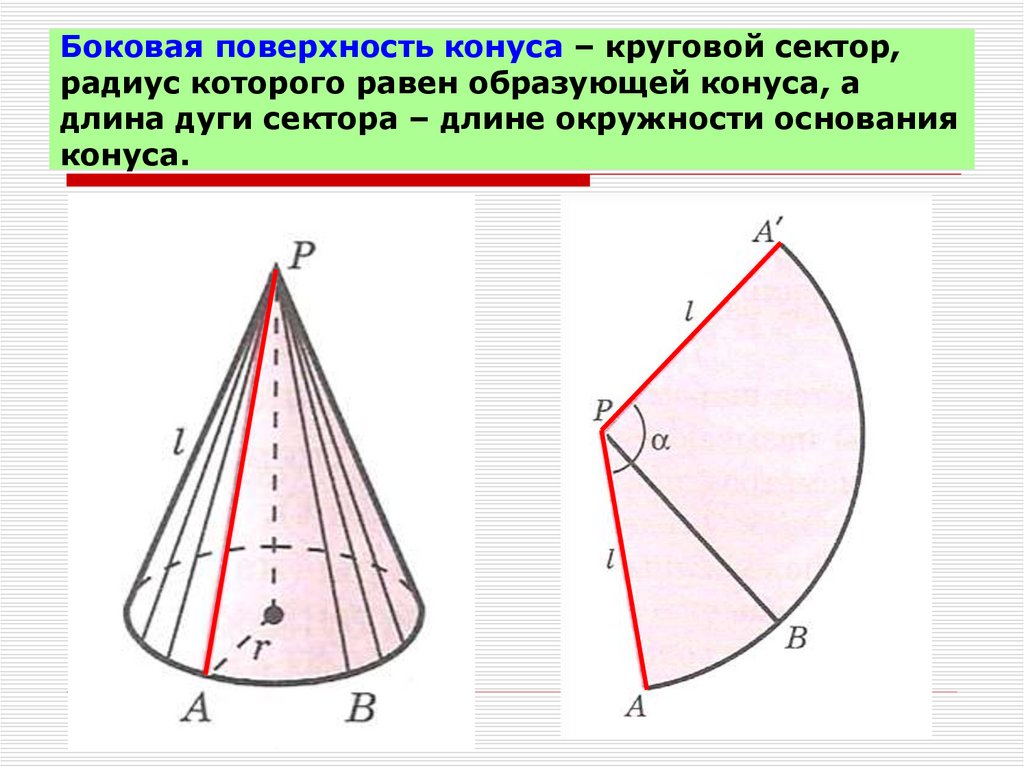 Расстояние от вершины до любой точки круга в основании тела называется образующей. Рассмотрим, как проводится расчет прямого и усеченного конусов: по каким формулам определяют их площади, объемы. 

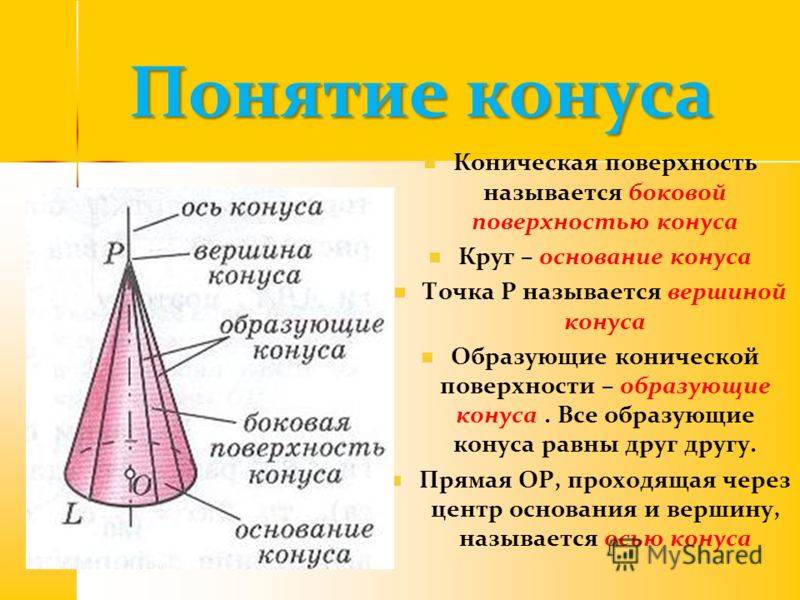
Понятие

Принципы образования геометрического тела просты. Представим две параллельные плоскости a и a1. С расположенной на первой точке перпендикуляр опускается на вторую. Точка на a1 – основание перпендикуляра, она является центром круга. Если соединить точку на плоскости a с каждой точкой круга на a1, получится конус. Основание перпендикуляра его – высота.

Второй вариант образования рассматриваемого геометрического тела: прямоугольный треугольник вращается вокруг катета по или против часовой стрелки. Катет, ставший осью, будет высотой конуса, лежащий в основании – диаметром нижней поверхности, гипотенуза – образующей.

Длина образующих одинакова, их совокупность называется боковой поверхностью. Квадрат длины образующей равняется сумме квадратов высоты и радиуса основания (из теоремы Пифагора): l² = h² + r². Отсюда 

Разновидности конусов

В геометрии насчитывают почти десяток типов конусов:

• Прямой круговой – нижняя грань представлена кругом – фигурой, имеющей центр симметрии. Ось, которая проходит от вершины к центру основания, перпендикулярна плоскости последнего.
• Наклонный либо косой – проекция вершины на нижнюю поверхность не совпадает с его центром.
• Круговой – с кругом в центре.
• Прямой – нижняя поверхность представлена кругом либо эллипсом. Центр нижней поверхности совпадает с проекцией вершины на неё.
• Гиперболический, параболический, эллиптический – опираются на соответствующие фигуры.
• Равносторонний – образующая равна диаметру нижней поверхности.
• Усеченный – ограниченный плоскостью, параллельной основанию. Располагается между ним и вершиной геометрического тела.
• Двойной – два одинаковых тела имеют общую вершину или основание и ось – проходит через оба тела.

Площадь

Под площадью подразумевают количество квадратов со стороной единица, помещающихся на определенной поверхности. 

Площадь прямого конуса определяется по формуле:

• основания – S_осн = πr²; r – радиус;
• боковой поверхности – S_бп = πrl; l – длина;
• полная – S = S_осн + S_бп = πr² + πrl = πr (r + l).

Пример:

• диаметр равен 12 см;
• длина образующей – 10 см.

Решение.

Радиус – это половина диаметра: 12/2 = 6 см.

Подставим значения в выражение: S = πr (r + l).

Получим: S = π * 6 *(6 + 10) = 96 π ≈ 301,584 см2.

Как вычислить площадь усеченного конуса

Формула площади боковой поверхности усеченного конуса отличается от используемой для вычисления прямого.

S_бп=πl(r + R).

Формула площади полной поверхности усеченного конуса:

S = S_бп + S₁ + S₂, здесь:

S₁ и S₂ – площади поверхностей усеченного конуса.

S₁ = πr², S₂ = πR².

Подставляем значения и упрощаем:

S = π(r² + (r + R)l + R².

Зная радиусы – 6 и 10 см, расстояние от вершины к лежащей на круге точке – 12 см найдём площадь граней.

S = π * (6² + (6 + 10) * 12 + 10²) = 328π ≈ 1030,4 см³.

Объем усечённого конуса

Объем – пространство, занимаемое геометрическим телом. Численное значение указывает на количество кубиков с гранью единица, помещающихся в конусе. Объем тела вычисляется как треть произведения площади основания на его высоту.

Основание – круг, его поверхность рассчитывается по формуле: S_осн = πr². После подстановки получим:

.

Пример: вычислить объем тела: r = 6 см, h = 9 см. Ставим значения в формулу, пошагово упрощаем выражение.

Если известен диаметр, разделите его на два: .

Вычислим объем усеченного конуса. Для понимания, от полного объема исходного тела нужно отнять значение отрезанного параллельной нижней грани плоскостью.

Формула объема усеченного конуса:

Высота

Существует несколько способов как найти высоту усеченного конуса. Какой подойдёт, зависит от исходных данных.

Когда даны радиусы оснований и объем, достаточно провести вычисления:

 

Для прямого при известном радиусе или диаметре оснований с образующей можно воспользоваться теоремой Пифагора:

Площадь поверхности конуса – формула, вывод, примеры

Площадь поверхности конуса – это площадь, занимаемая поверхностью конуса. Конус представляет собой трехмерную фигуру с круглым основанием. Это означает, что основание состоит из радиуса или диаметра. Расстояние между центром основания и самой верхней частью конуса (конечно, в случае с мороженым эта часть находится внизу) является высотой конуса. Мы можем найти площадь поверхности конуса двумя способами — полной площадью поверхности и площадью криволинейной поверхности конуса.

В этой статье мы узнаем, как вычислить площадь поверхности конуса. Общая площадь поверхности включает в себя как изогнутую, так и плоскую круглую площадь, тогда как площадь изогнутой поверхности включает площадь только изогнутой поверхности. Мы рассмотрим формулу и решим несколько примеров для лучшего понимания концепции.

1.	Какова площадь поверхности конуса?
2.	Площадь поверхности конуса Формула
3.	Изогнутая поверхность конуса
4.	Расчет площади поверхности конуса
5.	Часто задаваемые вопросы о площади поверхности конуса

Какова площадь поверхности конуса?

Площадь, занимаемая поверхностью/границей конуса, называется площадью поверхности конуса. Она всегда измеряется в квадратных единицах. Складывание множества треугольников и вращение их вокруг оси дает форму конуса. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой поверхности. Мы можем классифицировать конус как прямой круговой конус или наклонный конус. Вершина в прямом круглом конусе обычно находится вертикально над центром основания, тогда как вершина конуса в наклонном конусе не находится вертикально над центром основания.

Площадь поверхности конуса Формула

Поскольку конус имеет криволинейную поверхность, мы можем выразить площадь его криволинейной поверхности, а также общую площадь поверхности. Конус имеет два вида площади поверхности:

• Общая площадь поверхности
• Изогнутая поверхность

Если радиус основания конуса равен «r», а наклонная высота конуса равна «l», площадь поверхности конуса определяется как:

• Общая площадь поверхности, T = πr(r + л) квадратных единиц
• Площадь криволинейной поверхности, S = πrl квадратных единиц

Применяя теорему Пифагора о конусе, мы можем найти связь между площадью поверхности конуса и его высотой. Мы знаем, h ² + r ² = l ² , где h — высота конуса, r — радиус основания, а l — наклонная высота конуса.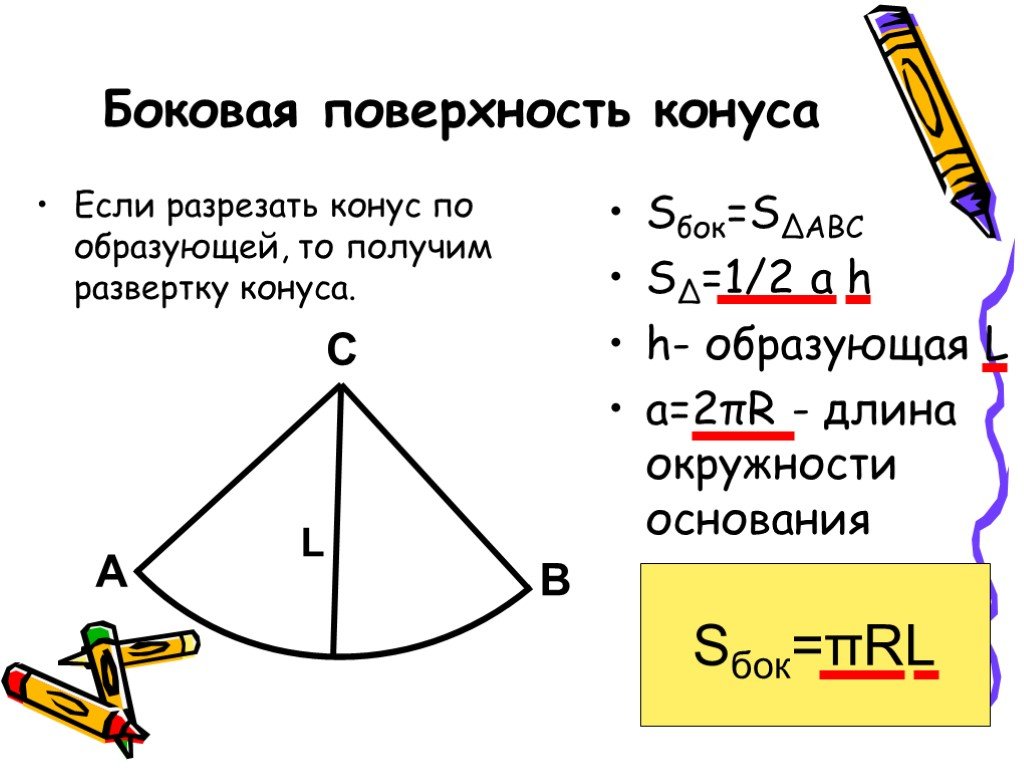
⇒ l = √(h ² + r ² )

Таким образом,

• Общая площадь поверхности по высоте может быть определена как T = πr(r + l) = T = πr(r + √(ч ² + р ² )).
• Площадь искривленной поверхности конуса по высоте может быть выражена как S = πrl = πr(√(h ² + r ² )).

Изогнутая поверхность конуса

Мы обсудили формулу для нахождения площади криволинейной поверхности конуса, теперь давайте разберемся в ее значении. Как и другие трехмерные фигуры, конус также имеет как плоские, так и криволинейные поверхности. Площадь изогнутой поверхности конуса относится только к изогнутой части конуса, отличной от круглого плоского основания. Чтобы найти площадь криволинейной поверхности конуса, мы умножаем радиус и наклонную высоту конуса на pi(π). Выведем формулу площади криволинейной поверхности конуса ниже.

Площадь криволинейной поверхности конуса Формула

Площадь криволинейной поверхности конуса может быть определена путем нахождения площади сектора по формуле

Площадь сектора (в пересчете на длину дуги) = (длина дуги × радиус)/ 2 = ((2πr) × l)/2 = πrl.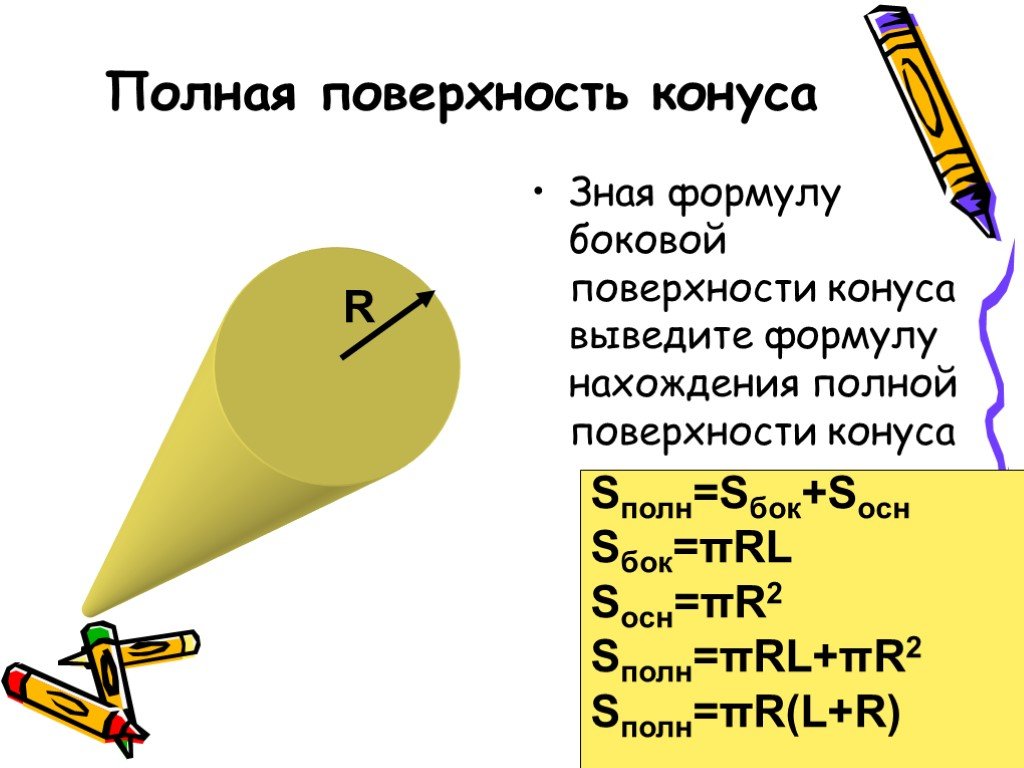

∴ Площадь криволинейной поверхности конуса, S = πrl единиц ² .

Расчет площади поверхности конуса

Возьмем конус высотой «h», радиусом основания «r» и высотой наклона «l». Чтобы определить площадь поверхности образования конуса, мы вырезаем конус из центра, который выглядит как сектор круга (плоская форма).

Общая площадь поверхности конуса = площадь основания конуса + площадь изогнутой поверхности конуса

⇒ Общая площадь поверхности конуса = πr ² + πrl = πr (r + l).

∴ Общая площадь поверхности конуса, T = πr (r + l) ед. криволинейная поверхность конуса.

Пример: Найдите общую площадь поверхности и площадь криволинейной поверхности конуса, радиус которого равен 7 дюймам, а наклонная высота равна 3 дюймам. (Используйте π = 22/7).

Мы знаем, что площадь полной поверхности конуса равна πr (r + l), а площадь боковой поверхности конуса равна πrl. Учитывая, что: r = 7 дюймов, l = 3 дюйма и π = 22/7.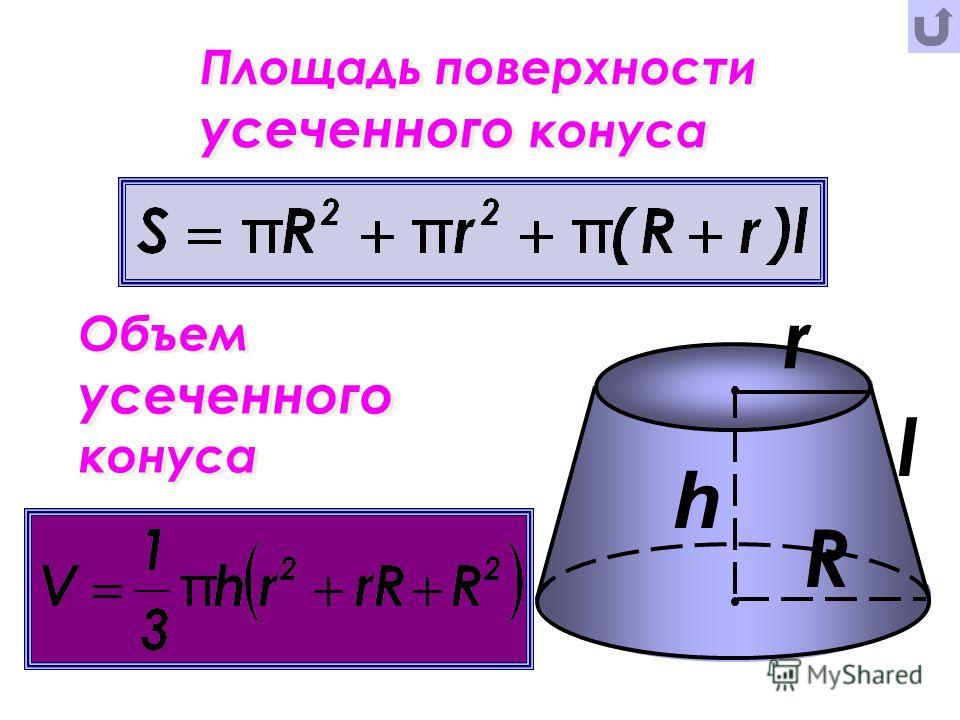

Таким образом, общая площадь поверхности конуса T = πr (r + l) = (22/7) × 7 × (7 + 3) = (22/7) × 7 × 10 = 22 × 10 = 220 в ² .

∴ Общая площадь поверхности конуса 220 ² .

Площадь криволинейной поверхности конуса, S = πrl = (22/7) × 7 × 3 = 66 в ² . ∴ Площадь изогнутой поверхности конуса составляет 66 дюймов ² .

Давайте рассмотрим еще несколько примеров площади поверхности конуса для более глубокого понимания.

Часто задаваемые вопросы о площади поверхности конуса

Какова площадь поверхности конуса?

Мера площади, занимаемой поверхностью конуса, называется площадью поверхности конуса. Существует два типа площади поверхности конуса, которые можно разделить на общую площадь поверхности и площадь криволинейной поверхности конуса.

Как найти площадь поверхности конуса?

Площадь поверхности конуса можно найти, выполнив следующие шаги:

• Шаг 1: Определите заданные значения радиуса, наклонной высоты и высоты конуса.
• Шаг 2: Используйте соответствующую формулу для расчета площади поверхности. Если необходимо найти общую площадь поверхности конуса, используйте формулу πr (r + l) квадратных единиц, а если нужно найти площадь криволинейной поверхности конуса, используйте формулу πrl квадратных единиц.
• Шаг 3: Упростите и запишите ответ в квадратных единицах.

Какова площадь криволинейной поверхности конуса?

Площадь криволинейной поверхности конуса известна как площадь криволинейной поверхности конуса. Формула для расчета площади криволинейной поверхности конуса: πrl, где «r» — радиус основания, а «l» — наклонная высота конуса. При этом мы не рассматриваем площадь основания конуса, имеющего форму круга.

Какова площадь криволинейной поверхности прямоугольного конуса?

Прямой круглый конус определяется как конус, осью которого является линия, соединяющая вершину и середину круглого основания. Таким образом, площадь криволинейной поверхности прямого круглого конуса определяется как πrl, где «r» — радиус основания, а «l» — наклонная высота. Что касается высоты, площадь криволинейной поверхности прямого круглого конуса определяется как πr(√(h ² + r ² )) где «h» — высота правильного круглого конуса.

Как найти площадь поверхности конуса с наклонной высотой и диаметром?

Общая площадь поверхности конуса с наклонной высотой и диаметром конуса может быть найдена по формуле T = π(D/2) ((D/2) + l), где D — диаметр, а l — наклонная высота. Площадь криволинейной поверхности конуса с наклонной высотой и диаметром можно найти по формуле S = π(D/2)l, где D — диаметр, а l — наклонная высота.

Как найти полную площадь поверхности конуса?

Полную площадь поверхности конуса можно найти, выполнив следующие шаги:

• Шаг 1: Проверьте значения, указанные в вопросе.
• Шаг 2: Подставьте значения радиуса и наклонной высоты в формулу πr (r + l). В случае, если наклонная высота не указана, мы записываем значение наклонной высоты через высоту конуса «h», подставляя l = √(h ² + r ² ), что дает значение, T = πr(r + √(h ² + r ² )) где «r» — радиус конуса, а «h» — высота конуса.
• Шаг 3: Теперь найдите значение общей площади поверхности.
• Шаг 4: Запишите окончательный ответ в квадратных единицах.

Как найти площадь криволинейной поверхности конуса?

Площадь криволинейной поверхности конуса можно найти, используя следующие шаги:

• Шаг 1: Запишите значения, указанные в вопросе.
• Шаг 2: Подставить значения радиуса и наклонной высоты заданного вопроса в формулу πrl. В случае, если наклонная высота не указана, мы записываем значение наклонной высоты через высоту конуса «h», подставляя l = √(h ² + r ² ), что дает значение S = πr√(h ² + r ² ), где «r» — радиус конуса, а «h» — высота конуса.
• Шаг 3: Теперь найдите значение площади криволинейной поверхности и запишите ответ в квадратных единицах.

Что произойдет с площадью поверхности конуса, если наклонную высоту и радиус основания удвоить?

Площадь поверхности конуса зависит от радиуса основания и его наклонной высоты.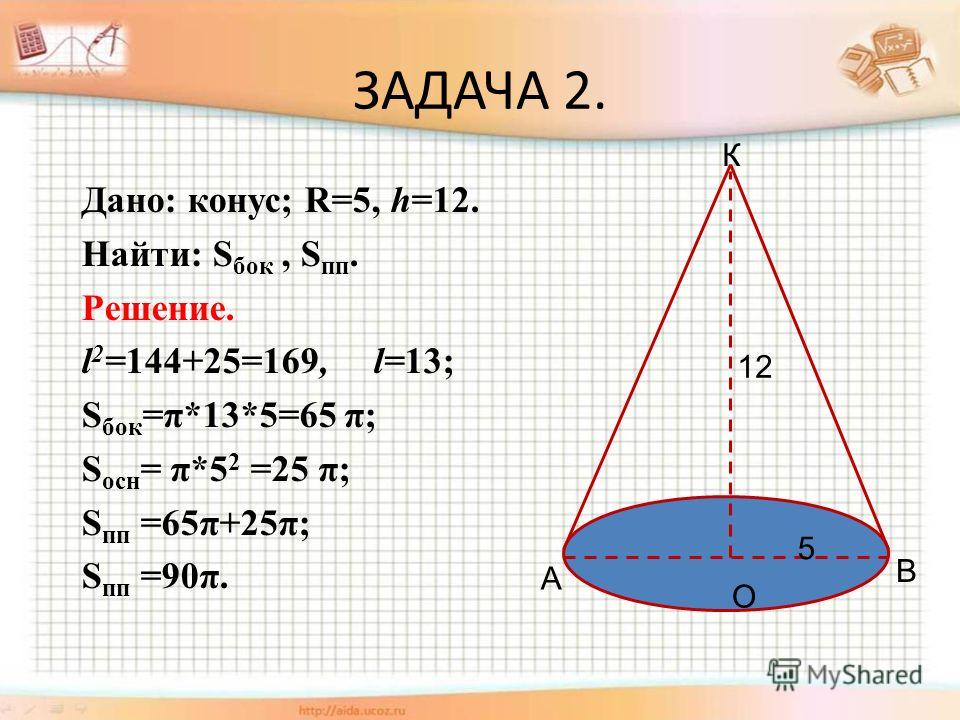 Таким образом, общая площадь поверхности и площадь криволинейной поверхности конуса увеличиваются в четыре раза, когда наклонная высота и радиус основания удваиваются как:

• Общая площадь поверхности = πr (r + l) = π(2r) (2r + 2l) = 4πr (r + l) = 4 × исходная общая площадь поверхности.
• Площадь криволинейной поверхности = πrl = π(2r)(2l) = 4πrl = 4 × исходная площадь криволинейной поверхности, где «r» — исходный радиус, а «l» — исходная наклонная высота конуса.

Диаграмма зависимости площади конуса | CarAudio.com

JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.

Бобб-самоубийца

Сбой SPLC

6 декабря 2010 г.

• #1

Модератор: Я думаю, вам следует прикрепить это или предложить другое название темы и прикрепить новую тему. Это уменьшит количество тем, которые спрашивают: «Сколько динамиков размера X нужно, чтобы сравнять площадь конуса динамиков размера nX?» а также, надеюсь, послужит кратким справочником даже для опытных пользователей.

ЭТИ ЦИФРЫ НЕ ТОЧНЫ! Я округлил почти все числа, а для диаграмм, сравнивающих громкоговорители X с громкоговорителями nX, я выбрал только те, которые были тесно связаны по площади конуса. Поскольку в моем калькуляторе нет функции числа Пи, я умножил квадрат радиуса на 3,14, что, как известно большинству из вас, достаточно близко. Эта таблица предназначена только для дает вам представление о том, насколько площадь конуса динамиков X похожа на динамики nX.

Как вы понимаете, я остановился на колонках обычного размера. Я не собираюсь включать такие динамики, как низкочастотный динамик Yamaha в форме уха, или какой-то одноразовый сабвуфер, такой как изготовленный на заказ MTX Thunder 1,000,000. Размеры, которые я выбрал, соответствуют размерам известных серийных динамиков (внезапно). Пожалуйста, дайте мне знать о том, что я пропустил, и я обновлю каждую категорию, чтобы включить их.

———————

Один динамик

Диаметр динамика | Площадь конуса динамика в квадратных дюймах

34″ —> 908

32″ —> 804

22″ —> 380

21″ —> 346

18″ —> 254

15″ —> 192

13,5″ —> 143

12″ —> 113

11 дюймов —> 95

10 дюймов —> 79

8″ —> 50

6×9 —> 42

6×8 —> 38

6,5″ —> 33

4×10 —> 31

5×7 —> 28

5,25″ —> 22

4″ —> 13

3,5″ —> 10

2″ —> 3

———————

Два динамика

Динамик X | Эквивалент динамиков 2X

3,5 дюйма —> 5,25″

4″ —> 5×7

5,25″ —> 6×9

5×7 —> 8″

6×8/6×9 —> 10 дюймов

8 дюймов —> 11 дюймов

10 дюймов —> 13,5″

11″ —> 15 дюймов

12 дюймов —> 18 дюймов

15 дюймов —> 22 дюйма

22 дюйма —> 32″

———————

Три динамика

X Speaker | Эквивалент 3X Speakers

2″ —> 3,5 дюйма

3,5 дюйма —> 5×7/4×10

4″ —> 6×8/6×9

5×7 —> 10″

4×10/6,5″ —> 11″

6×8 —> 12 дюймов

8 дюймов —> 13,5″

10″ —> 18 дюймов

12 дюймов —> 21″

18″ —> 32 дюйма

———————

Четыре динамика

Динамик X | Эквивалент 4 динамиков

2 дюйма —> 4 дюйма

3,5 дюйма —> 5×7/4×10

4″ —> 6×8/6×9

8″ —> 15 дюймов

10 дюймов —> 21 дюйм

11 дюймов —> 22 дюйма

15 дюймов —> 32 дюйма

 

Последнее редактирование модератором: 6 декабря 2010 г.

бенбенондатрак сказал:

когда я вижу маленькие подводные лодки, я просто думаю о девушке, 12 лет = подростки, 15 лет = мужчина, 18 = Кинг-Конг Мандинго Воин

Нажмите, чтобы развернуть…

Бобб-самоубийца

Сбой SPLC

6 декабря 2010 г.

• Автор темы
• #2

На этой диаграмме показано соотношение между сабвуферами неправильной формы и сабвуферами круглой формы. Возможно, вам известны треугольные и пятиугольные сабвуферы от Bazooka и Xtant соответственно, а 24-дюймовый квадратный сабвуфер — новый отбойный молоток MTX.

——————— —

Pentagon

Один сабвуфер

Диаметр конуса | Площадь конуса в квадратных дюймах

10″ —> 74

———————

Пятиугольник

Два сабвуфера

X Сабвуфер | Сабвуфер Circle Эквивалент 2 сабвуферов

10 дюймов —> 13,5 дюймов

———————

Pentagon

Три сабвуфера

X Сабвуфер | Сабвуфер Circle Эквивалент трех сабвуферов

10 дюймов —> 15 дюймов/18 дюймов (между двумя)

———————

Pentagon

Четыре сабвуфера

X Сабвуфер | Сабвуфер Circle Эквивалент 4-х сабвуферов

10 дюймов —> 18 дюймов/21 дюйм (между двумя)

———————

Треугольник

Один сабвуфер

Диаметр конуса | Площадь конуса в квадратных дюймах

10″ —> 48

12″ —> 86

———————

Треугольник

Два сабвуфера

X Сабвуфер | Сабвуфер Circle Эквивалент двух сабвуферов

10 дюймов —> 11 дюймов

12 дюймов —> 15 дюймов

———————

Треугольник

Три сабвуфера

X Сабвуфер | Сабвуфер Circle Эквивалент трех сабвуферов

10 дюймов —> 13,5 дюймов

12 дюймов —> 18 дюймов

———————

Треугольник

Четыре сабвуфера

X Сабвуфер | Сабвуфер Circle Эквивалент 4-х сабвуферов

10 дюймов —> 15 дюймов

12 дюймов —> 21 дюйм

———————

Квадрат

Один сабвуфер

Диаметр конуса | Площадь конуса в квадратных дюймах

8 дюймов —> 64

10 дюймов —> 100

12 дюймов —> 144

15 дюймов —> 225

18 дюймов —> 324

24″ —> 576

———————

Квадратный

Два сабвуфера

X Сабвуфер | Круглый сабвуфер Эквивалент 2X сабвуферов

8″ —> 12 дюймов/13,5 дюймов

10 дюймов —> 15 дюймов

12 дюймов —> 18 дюймов

15 дюймов —> 24 дюйма

———- ———-

Квадратный

Три сабвуфера

X Сабвуфер | Эквивалент сабвуфера Circle 3X Subwoofers

8 дюймов —> 15 дюймов

10 дюймов —> 18 дюймов/21 дюйм

———————

Square

Четыре сабвуфера

Сабвуфер X | Круглый сабвуфер Эквивалент 4 сабвуферов X

8″ —> 18 дюймов

10 дюймов —> 22 дюйма

12 дюймов —> 34″

———————

 

Последнее редактирование модератором: 6 декабря 2010 г.

benbenondatrack сказал:

когда я вижу маленькие подводные лодки, я просто думаю о девушке, 12 лет = подростки, 15 лет = мужчина, 18 = Кинг-Конг Мандинго Воин

Нажмите, чтобы развернуть…

CHEMMINS

CarAudio.com Veteran

6 декабря 2010 г.

• #3

2 15 значительно больше, чем 1 21″.

 

Каталожные номера:

kmarei, ge_off_me, AudioPipe, slim2fattycake, Louisiana_CRX, ARMed&Bangin, EXTREMECHEVYMAN, Dpc69ss, Psychoacoustics, Shinju, jonny101abc, snoopdan

 

ПОКУПКА SILVER TOP TRF MOTORS

 

 

RAM_Designs

Мастер SketchUp

6 декабря 2010 г.

• #4

хммм…

 

2500+ дизайнов с марта 2011 г.

​

Бобб-самоубийца

Сбой SPLC

6 декабря 2010 г.

• Автор темы
• #5

2 15 значительно больше, чем 1 21″.

Нажмите, чтобы развернуть…

Это был один из тех, о которых я сомневался. Разница составляет около 40 кубических дюймов, что составляет около 10% предельной погрешности. Я не думаю, что это будет слышно?

Спасибо за отзыв! Кто-нибудь еще не стесняйтесь помочь улучшить это!

 

бенбенондатрак сказал:

когда я вижу маленькие подводные лодки, я просто думаю о девушке, 12 лет = подростки, 15 лет = мужчина, 18 = Кинг-Конг Мандинго Воин

Нажмите, чтобы развернуть. ..

RAM_Designs

Мастер SketchUp

6 декабря 2010 г.

• #6

2 15 значительно больше, чем 1 21″.

Нажмите, чтобы развернуть…

И четыре 10-ки — это почти то же самое, что и одна 18-ка, а не одна 21-ка.

 

2500+ дизайнов с марта 2011 г.

​

CHEMMINS

CarAudio.com Veteran

6 декабря 2010 г.

• #7

А четыре 10-ки — это почти то же самое, что и одна 18-ка, а не одна 21-ка.

Нажмите, чтобы развернуть…

4 10 будет 314….. нет?

 

Каталожные номера:

kmarei, ge_off_me, AudioPipe, slim2fattycake, Louisiana_CRX, ARMed&Bangin, EXTREMECHEVYMAN, Dpc692) отнимите 3 дюйма от диаметра каждого НЧ-динамика нормального размера, так как у вас есть монтажное кольцо и подвес с каждой стороны, которые следует учитывать при поиске более точного представления о размере конуса. на НЧ-динамиках разного размера

 

Последнее редактирование модератором: 6 декабря 2010 г.

Более 2500 дизайнов с марта 2011 г.

​

1rockford1

Запрещено

6 декабря 2010 г.

• #9

, значит, 2 восьмерки такие же, как 1 12? собираюсь сделать 4 8s вместо моих 4 12s. похоже, мне не хватает площади конуса, я думаю,

 

согнутый боб над столом, широко открытый

ссылки: Loudaccent, kylecanthurdle (x2), Millertime1028(x4), sioner35, midnightg35x, BushJ311, Fender5 (x2), svarasnj, RetroAudioinc, nineball, wu501, BJ The Man, slivercookie, SPY, blackxj, solidcrowd, l4yfr4me x2, gbody805, dbeez, RAM_Designs, rachidfunaki, 5+ местных сделок,

Бобб-самоубийца

Сбой SPLC

6 декабря 2010 г.

• Автор темы
• #10

А четыре 10-ки — это почти то же самое, что и одна 18-ка, а не одна 21-ка.

Нажмите, чтобы развернуть…

79*4=316

18″=254

21″=346

 

бенбенондатрак сказал:

когда я вижу маленькие сабвуферы я просто думаю о девушке, 12 лет = подростки, 15 лет = мужчина, 18 = King Kong Mandingo Warrior 92) отнимите 3 дюйма от диаметра каждого НЧ-динамика нормального размера, так как у вас есть монтажное кольцо и окружность с каждой стороны, которые следует учитывать при поиске более точного представления о размере конуса. на НЧ-динамиках разного размера.

Нажмите, чтобы развернуть…

Хорошо, приятель, ты делаешь вещи слишком техническими //content. invisioncic.com/y282845/emoticons/smile.gif.1ebc41e1811405b213edfc4622c41e27.gif Как я сказал в заголовке, размеры не точно .

Вы ориентируетесь на площадь диффузора определенного сабвуфера, корзина которого измеряется как 8/10/12/15/18 дюймов. В моей таблице сравнивается ФАКТИЧЕСКАЯ площадь диффузора, поэтому она исключает угол, ширину объемного звучания и т. д.

Если бы я измерял по-твоему, мне пришлось бы помещать в эту таблицу каждую из когда-либо существовавших сабвуферов по отдельности Прости, бро, но у меня нет на это времени, лол

 

бенбенондатрак сказал:

когда я вижу маленькие сабвуферы я просто думаю о девушке, 12 лет = подростки, 15 лет = мужчина, 18 = King Kong Mandingo Warrior

Нажмите, чтобы развернуть…

Бобб-самоубийца

Сбой SPLC

6 декабря 2010 г.

• Автор темы
• #12

, значит, 2 8 такие же, как 1 12? собираюсь сделать 4 8 с вместо моих 4 12 с. похоже, мне не хватает площади конуса, я думаю

Нажмите, чтобы развернуть…

Нет :/ 2 8 с похоже на 11 дюймов. Предельная ошибка от 2 8 с до 1 12 составляет около 13%. Честно говоря, это не слышимая разница, но все же.

 

бенбенондатрак сказал:

когда я вижу маленькие подводные лодки, я просто думаю о девушке, 12 лет = подростки, 15 лет = мужчина, 18 = Кинг-Конг Мандинго Воин

Нажмите, чтобы развернуть…

Реакции:

1рокфорд1

1rockford1

Запрещено

6 декабря 2010 г.

• №13

Нет: / 2 8s похоже на 11 дюймов. Предельная ошибка от 2 8s до 1 12 составляет около 13%. Честно говоря, это не должно быть слышимой разницы, но все же.

Нажмите, чтобы развернуть…

, так что тогда я должен быть в порядке. Я собираюсь сделать 4 8s, настроить на 32 вместо 4 12s запечатанных. мощность будет такой же, я просто сделаю четыре сабвуфера с более низким среднеквадратичным значением, которые будут иметь мощность, близкую к номинальной мощности, тогда как мои 12 с примерно половиной номинальной мощности с моим текущим усилителем. спасибо, хорошо напиши, могу ли я добавить свою любовь

 

согнутый боб над столом, широко открытый

ссылки: Loudaccent, kylecanthurdle (x2), Millertime1028(x4), sioner35, midnightg35x, BushJ311, Fender5 (x2), svarasnj, RetroAudioinc, nineball, wu501, BJ The Man, slivercookie, SPY, blackxj, solidcrowd, l4yfr4me x2, gbody805, dbeez, RAM_Designs, rachidfunaki, 5+ местных сделок,

Бобб-самоубийца

Сбой SPLC

6 декабря 2010 г.

• Автор темы
• №14

, так что я должен быть в порядке. Я собираюсь сделать 4 8s, настроить на 32 вместо 4 12s запечатанных. мощность будет такой же, я просто сделаю четыре сабвуфера с более низким среднеквадратичным значением, которые будут иметь мощность, близкую к номинальной мощности, тогда как мои 12 с примерно половиной номинальной мощности с моим текущим усилителем. спасибо, хорошо напиши, могу ли я добавить свою любовь

Нажмите, чтобы развернуть…

Да, хорошая идея. Забавно покрасоваться перед всеми знакомыми любителями автозвука, а потом сказать им, что вы используете 8-е //content.invisioncic.com/y282845/emoticons/smile.gif.1ebc41e1811405b213edfc4622c41e27.gif

Спасибо! На это ушли часы за часами, так что я рад, что хоть кто-то это оценил…

 

бенбенондатрак сказал:

когда я вижу маленькие сабвуферы я просто думаю о девушке, 12 лет = подростки, 15 лет = мужчина, 18 = King Kong Mandingo Warrior

Нажмите, чтобы развернуть. ..

Бобб-самоубийца

Сбой SPLC

6 декабря 2010 г.

• Автор темы
• №15

Обновлен первый и второй посты, чтобы включить Jackhammer 22″ (первый пост), а также квадратные, пятиугольные и треугольные сабвуферы. Опять же, не стесняйтесь критиковать!

Завтра или когда у меня будет время, я пойду и отображать предельную ошибку для каждого сравнения эквивалентности.Кроме этого, я думаю, что это в значительной степени покрывает это!

 

бенбенондатрак сказал:

когда я вижу маленькие подводные лодки, я просто думаю о девушке, 12 лет = подростки, 15 лет = мужчина, 18 = Кинг-Конг Мандинго Воин

Нажмите, чтобы развернуть. ..

Делиться:

Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Электронная почта Делиться Связь

Предыдущая тема Следующая тема

Аналогичные резьбы

	Титул	Ответов	Дата
Е	Alpine Type R 12-дюймовый тканевый наконечник для конуса Advice	3	12 октября 2021 г.
А	ДЛЯ ПРОДАЖИ Focal 6W-4311b Pair W Cone Новый в коробке	0	7 июля 2021 г.
С	Подконус теплый	3	29 июня 2021 г.
	Длина порта превышает площадь?	14	9 ноября 2022 г.
	Строители в центральной части Флориды?	11	30 мая 2022 г.

• Е

  Alpine Type R 12″ Fabric Behind Cone Advice

  • Автор: ericberg
  • 12 октября 2021 г.

    No related posts.