Координатной плоскости: Координатная плоскость — урок. Алгебра, 7 класс.

Содержание

Координатная плоскость: что это такое? Как отмечать точки и строить фигуры на координатной плоскости?

Математика — сложная наука. Изучая его, нужно не только решать примеры и задачи, но и работать с различными фигурами и даже планами. Одна из наиболее часто используемых в математике — это плоская система координат. Детей учили работать с ней больше года. Поэтому важно знать, что это такое и как с ним правильно работать.

Давайте узнаем, что это за система, какие действия можно выполнять с ее помощью, а также узнаем ее основные особенности и характеристики.

Содержание

1 Определение понятия
2 Историческая справка
3 Примеры координатной плоскости
4 Оси координат
5 Четверти

6 Работа с координатной плоскостью
7 Правила построения плоскости
8 Отмечаем точку
9 Размещаем фигуру
10 Выводы

Определение понятия

Координатная плоскость — это плоскость, на которой определена определенная система координат. Эта плоскость определяется двумя прямыми линиями, пересекающимися под прямым углом. Начало координат находится в точке пересечения этих линий. Каждая точка на координатной плоскости определяется парой чисел, называемых координатами.

На школьном курсе математики школьники должны тесно работать с системой координат: строить на ней фигуры и точки, определять, к какой плоскости принадлежит конкретная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех характеристиках координат. Но сначала коснемся истории создания, а потом поговорим о том, как работать в координатной плоскости.

Историческая справка

Идеи создания системы координат были еще во времена Птолемея. Уже тогда астрономы и математики думали о том, как научиться определять положение точки на плоскости. К сожалению, тогда еще не было известной нам системы координат, и ученым пришлось использовать другие системы.

Первоначально они устанавливают точки, указывая широту и долготу. Долгое время это был один из самых распространенных способов отображения той или иной информации. Но в 1637 году Рене Декарт создал свою систему координат, которая позже была названа в честь великого «картезианского» математика».

После выхода в свет работы «Геометрия» система координат Рене Декарта получила признание в научных кругах.

Уже в конце 17 века понятие «координатная плоскость» получило широкое распространение в мире математики. Несмотря на то, что с момента создания этой системы прошло несколько столетий, она до сих пор широко используется в математике и даже в жизни.

Примеры координатной плоскости

Прежде чем мы поговорим о теории, вот несколько наглядных примеров координатной плоскости, чтобы вы могли ее представить. Система координат в основном используется в шахматах. На доске у каждого квадрата есть свои координаты: согласованная буква, вторая цифровая. С его помощью можно определить положение той или иной фигуры на доске.

Второй по яркости пример — всеми любимая игра «Морской бой». Вспомните, как во время игры вы вызываете координату, например B3, тем самым указывая, куда именно нужно прицелиться. При этом, размещая корабли, вы задаете точки на координатной плоскости.

Эта система координат широко используется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.

Оси координат

Как уже было сказано, в системе координат различают две оси. Поговорим о них немного, так как они имеют немалое значение.

Первая ось — абсцисса — горизонтальна. Он упоминается как (Бык). Вторая ось — это ордината, которая проходит вертикально через начало координат и обозначается как (Oy). Именно эти две оси образуют систему координат, разделяющую плоскость на четыре четверти. Начало координат находится в точке пересечения этих двух осей и принимает значение 0. Только если плоскость образована двумя осями, которые пересекаются перпендикулярно и имеют начало координат, это координатная плоскость.

Также обратите внимание, что каждая из осей имеет собственное направление. Обычно при построении системы координат принято указывать направление оси в виде стрелки. Также при построении координатной плоскости каждая из осей подписывается.

Четверти

Теперь несколько слов о таком понятии, как четверть координатной плоскости. План разделен двумя осями на четыре четверти. Каждому из них присвоен свой номер, при этом нумерация этажей — против часовой стрелки.

Каждый из микрорайонов имеет свои особенности. Следовательно, в первой четверти абсцисса и ордината положительны, во второй абсцисса отрицательна, ордината положительна, в третьей и абсцисса, и ордината отрицательны, в четвертой абсцисса положительна, а ордината отрицательный.

Запомнив эти особенности, вы легко сможете определить, к какому кварталу относится та или иная точка. Кроме того, эта информация может быть полезна, если вам нужно выполнить вычисления с использованием декартовой системы.

Работа с координатной плоскостью

Когда мы понимаем концепцию самолета и говорим о его помещениях, мы можем перейти к проблеме, как работать с этой системой, а также поговорить о том, как наносить на нее точки, координаты фигур. С точки зрения координат это не так сложно, как может показаться на первый взгляд.

В первую очередь строится сама система, на нее нанесены все важные обозначения. Итак, мы работаем напрямую с точками или фигурами. В этом случае даже при построении фигур сначала прорисовываются точки на плоскости, потом уже прорисовываются фигуры.

Далее мы поговорим более подробно о построении системы и непосредственном рисовании точек и фигур.

Правила построения плоскости

Если вы решили начать отмечать фигуры и точки на бумаге, вам понадобится координатная плоскость. На него наносятся координаты точек. Чтобы построить координатную плоскость, вам понадобится всего лишь линейка и ручка или карандаш. Сначала проводится горизонтальная абсцисса, затем вертикальная — ордината. Важно помнить, что оси пересекаются под прямым углом.

Кроме того, на каждой оси указано направление и они помечены с использованием общепринятых обозначений x и y. Точка пересечения осей также отмечена и подписана цифрой 0.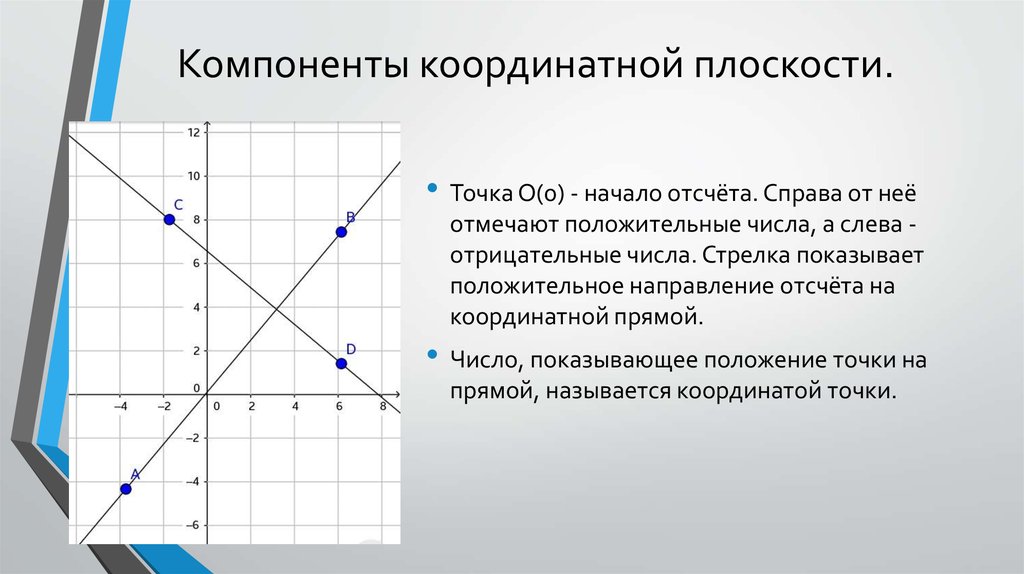

Следующий обязательный элемент — это маркировка. На каждой из осей в обоих направлениях отмечены и подписаны единицы-сегменты. Это сделано для того, чтобы потом с самолетом можно было работать с максимальным комфортом.

Отмечаем точку

Теперь поговорим о том, как нанести координаты точек на координатную плоскость. Это основы, которые вам нужно знать, чтобы успешно размещать различные фигуры на плоскости и даже отмечать уравнения.

При нанесении точек помните, как правильно записываются их координаты. Итак, обычно при указании точки в скобках пишут два числа. Первое число указывает координату точки по оси абсцисс, второе — по оси ординат.

Точка должна быть построена так. Сначала отметьте данную точку на оси Ox, затем отметьте точку на оси Oy. Далее из этих обозначений проведите воображаемые линии и найдите место их пересечения — это будет указанная точка.

Вам просто нужно отметить это и подписать. Как видите, все довольно просто и не требует особых навыков.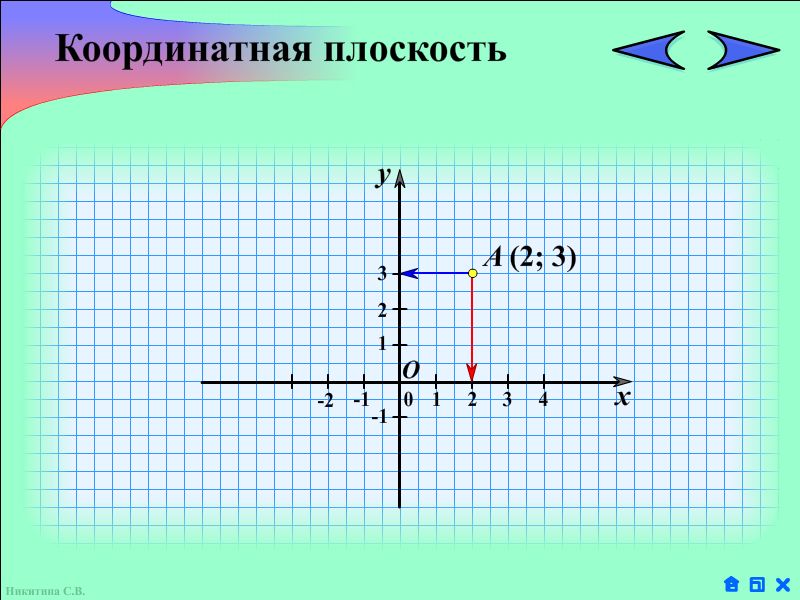

Размещаем фигуру

Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Чтобы построить любую фигуру на координатной плоскости, вам нужно знать, как размещать на ней точки. Если вы знаете, как это сделать, не так уж сложно разместить фигуру на плоскости.

Прежде всего, вам понадобятся координаты точек фигуры. Именно на них мы применим выбранные вами геометрические фигуры к нашей системе координат. Рассмотрите возможность рисования прямоугольника, треугольника и круга.

Начнем с прямоугольника. Применять довольно просто. Сначала на плоскости рисуются четыре точки, которые обозначают углы прямоугольника. Затем все точки соединяются последовательно друг с другом.

Рисование треугольника ничем не отличается. Единственное, что у него три угла, а это значит, что на плоскость нанесены три точки, которые обозначают ее вершины.

Что касается круга, здесь вы должны знать координаты двух точек. Первая точка — это центр круга, вторая — точка, указывающая его радиус. Эти две точки нарисованы на плоскости. Затем берется компас, измеряется расстояние между двумя точками. Точка компаса помещается в центр и описывается круг.

Как видите, здесь тоже нет ничего сложного, главное, чтобы у вас всегда были под рукой линейка и компас.

Теперь вы знаете, как рисовать координаты фигур. С точки зрения координат это не так сложно, как может показаться на первый взгляд.

Выводы

Итак, мы рассмотрели с вами одну из самых интересных и основных математических концепций, с которой приходится иметь дело каждому ученику.

Мы обнаружили, что координатная плоскость — это плоскость, образованная пересечением двух осей. С его помощью можно задавать координаты точек, наносить на них фигуры. Самолет разделен на микрорайоны, каждый из которых имеет свои особенности.

Главный навык, который следует развивать при работе с координатной плоскостью, — это умение правильно наносить на нее заданные точки. Для этого следует знать правильное положение осей, характеристики четвертей и правила, по которым задаются координаты точек.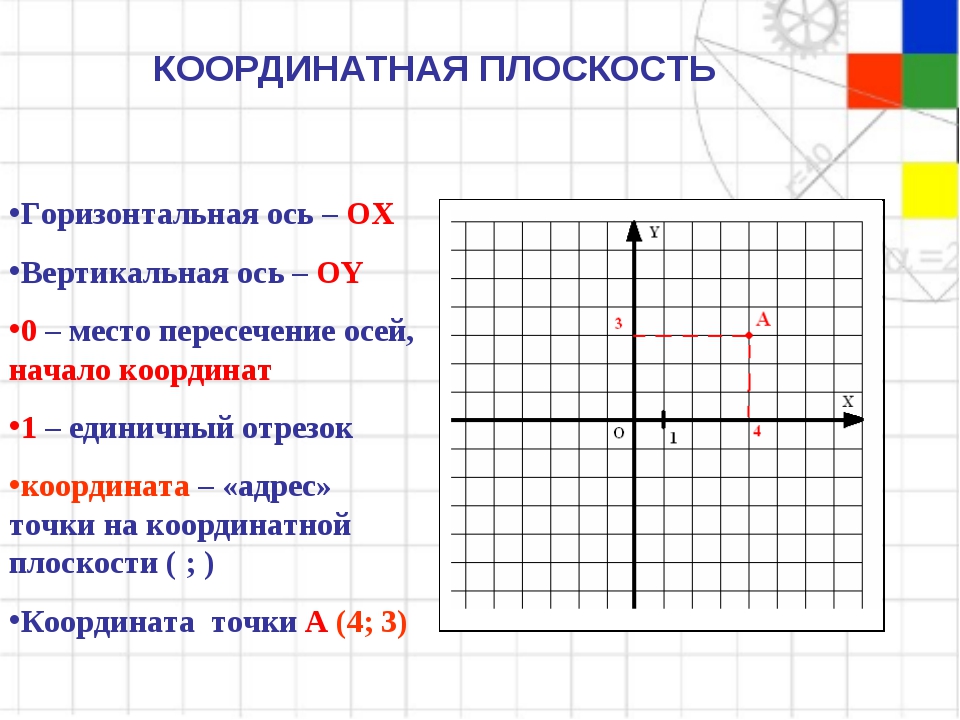

Надеемся, что представленная нами информация была доступной и понятной, а также что она была полезной для вас и помогла вам лучше разобраться в этой теме.

Предыдущая записьМеридиан нулевой: что это. Где проходит нулевой меридиан?
Следующая записьЛинейные алгоритмы — схема, структура и вычисление

Рекомендуем посмотреть

Adblock
detector

Математика. Основы геометрии: Уравнения прямых на координатной плоскости

Давайте рассмотрим такие функций, графики которых имеют вид прямых. Простоты ради, мы будем иметь дело с безразмерными величинами, а значит, в качестве осей у нас будут выступать простые числовые прямые, и все наши чертежи мы будем делать на обычной координатной плоскости.

Прямая, проходящая через начало координат

Построение графика по заданной функции

Пусть переменная \(y\) пропорциональна переменной \(x\) с коэффициентом пропорциональности \(k\):

\(y = k\,x. \)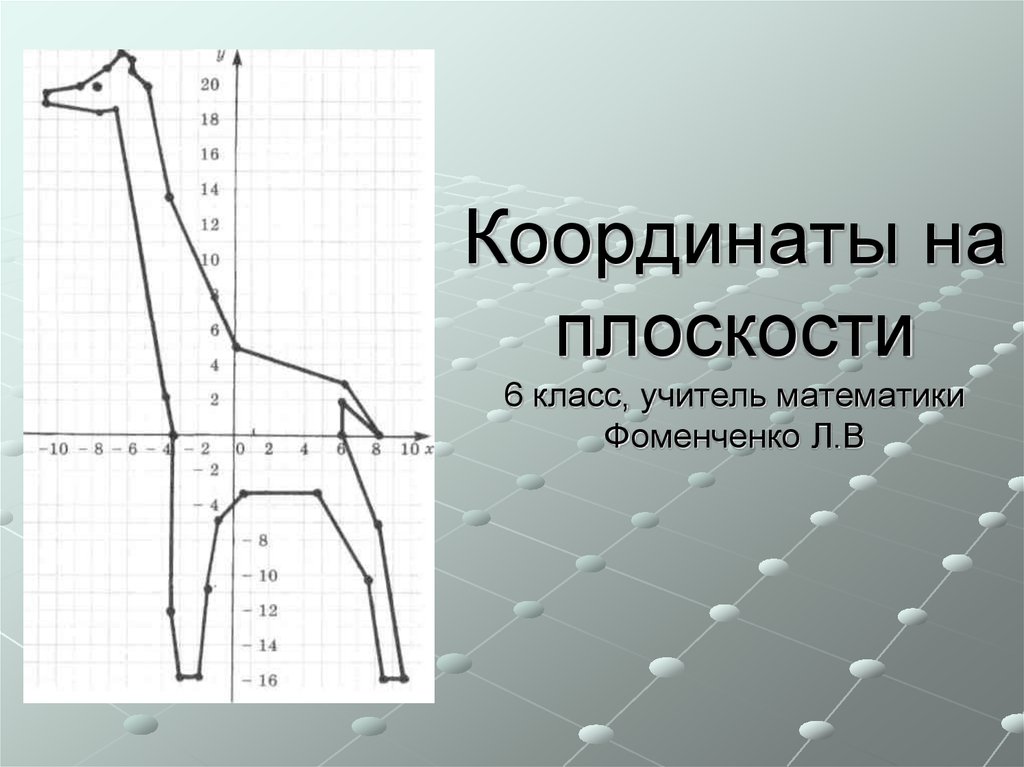

Давайте договоримся, что \(x\) здесь — это независимая переменная, а \(y\) — зависимая. Коэффициент \(k\) играет роль константы (параметра). В таких случаях говорят, что \(y\) является (однородной) линейной функцией от \(x\). Графиком этой функции, как мы хорошо знаем, является прямая, проходящая через начало координат \((0, 0)\). Для построения этой прямой нам достаточно определить еще какую-либо одну ее точку \((x_1, y_1)\). Для этого положим, например, \(x_1 = 1\). Тогда \(y_1 = k \cdot 1 = k\). Проводим через эту точку и начало координат прямую линию. Это и есть график функции \(y\) от \(x\). Так, по крайней мере, обстоит дело в теории, а на практике точку \((x_1, y_1)\) лучше брать настолько далеко от начала координат, насколько позволяет чертеж. В этом стучае прямую удается провести наиболее точно. Ниже приведен пример такого построения для функции \(y=\frac{1}{2} x\).

Восстановление функции по графику

Решим теперь обратную задачу.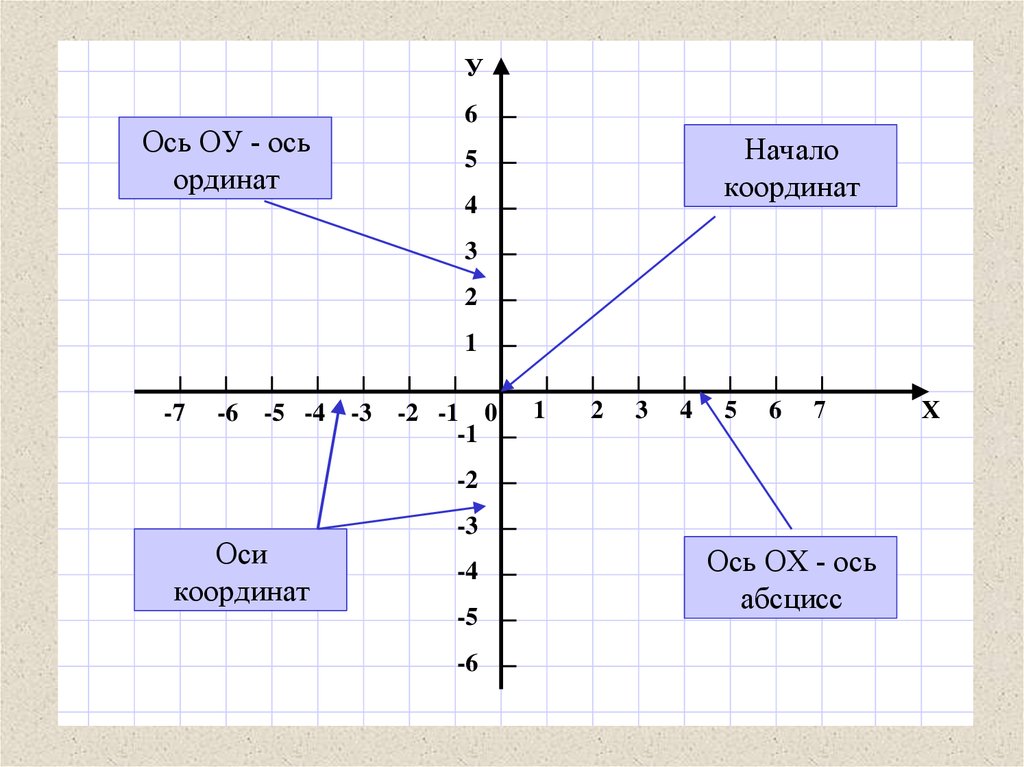 Пусть на координатной плоскости с осями \(x\) и \(y\) нам дана прямая, проходящая через начало координат. Спрашивается: графиком какой функции она является? При этом подразумевается, что функция должна быть задана в виде формулы, связывающей переменные \(x\) и \(y\). Такая формула носит название уравнения графика функции. В данном случае речь идет об уравнении прямой, проходящей через точку \((0,0)\).

Заранее ясно, что это уравнение имеет вид

\(y = k\,x.\)

От нас фактически только требуется найти значение константы \(k\). Для этого отметим на прямой произвольную точку, отличную от \((0,0)\), и определим ее координаты \((x_1, y_1).\) Эти координаты, очевидно, связаны соотношением

\(y_1 = k\,x_1.\)

Отсюда находим:

\(k = \cfrac{y_1}{x_1}.\)

При этом следует особо подчеркнуть, что константа \(k\) не зависит от выбора точки \((x_1, y_1).\) Какую бы точку на прямой мы не выбрали в качестве \((x_1, y_1),\) мы придем к одному и тому же значению \(k\).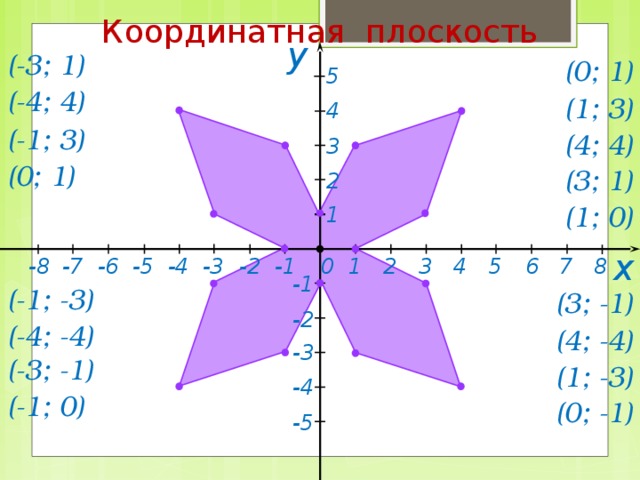 Таким образом,

\(y = \cfrac{y_1}{x_1} x.\)

Пример нахождения уравнения прямой приведен на следующем рисунке.

Отметим два особых случая. Во-первых, прямая может совпасть с осью \(x\). Тогда значение \(y\) остается постоянным и равным нулю на всем ее протяжении. Тем не менее наше общее решение остается в силе. При этом оказывается, что \(k = 0\) и переменную \(y\) можно всё еще формально считать функцией от \(x\):

\(y = 0 \cdot x.\)

Во-вторых, прямая может совпасть с осью \(y\). В этом случае в каждой ее точке \(x = 0\). Формула для константы \(k\) оказывается неприменимой, потому что число \(x_0\), стоящее в знаменателе, обращается в нуль. Приходится признать, что мы не можем подобрать такую функцию \(y\) от \(x\), которая имела бы подобный график. Разве что, мы можем теперь принять \(y\) за независимую переменную и формально рассматривать \(x\) как функцию от \(y{:}\)

\(x = 0 \cdot y.\)

Несложно убедиться, что всякая точка, лежащая на оси \(y\), удовлетворяет этому равенству. Заметим, что если бы мы захотели написать уравнение прямой, проходящей через начало координат, в самом общем виде, то мы могли бы это сделать так:

\(x_1 y = y_1 x.\)

Это соотношение между \(x\) и \(y\) остается справедливым в обоих рассмотренных частных случаях, однако выбор параметров не является однозначным, так как в качестве пары чисел \((x_1, y_1)\) можно взять координаты любой точки, принадлежащей прямой.

Произвольная прямая

Восстановление функции по графику

Начнем с обратной задачи. Пусть теперь на координатной плоскости дана произвольная прямая, не проходящая через начало координат. Вопрос нас будет интересовать всё тот же: графиком какой функции она является или, короче говоря, каково уравнение этой прямой?

Отметим на прямой две любые несовпадающие точки и обозначим их координаты через \((x_0, y_0)\) и \((x_1,y_1)\). Поместим в точку \((x_0, y_0)\) начало новой системы координат с осями \(x’\) и \(y’\), сонаправленными с соответствующими осями \(x\) и \(y\) старой системы.

Тогда координаты другой отмеченной точки в новой системе окажутся равны

\(\begin{pmatrix} x_1′ \\ y_1′ \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} — \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} = \begin{pmatrix} x_1 — x_0 \\ y_1 — y_0\end{pmatrix}.\)

Вообще, как мы знаем, новые («штрихованные») координаты любой точки связаны со старыми («нештрихованными») координатами соотношением

\(\begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} x — x_0 \\ y — y_0\end{pmatrix}.\)

Наша прямая проходит через начало координат новой системы, поэтому мы можем сразу же выписать ее уравнение в «штрихованных» переменных:

\(y’ = k\,x’,\) где \(k = \cfrac{y_1′}{x_1′}.\)

Переходя к «нештрихованным» переменным, получаем

\(y-y_0 = k \cdot (x — x_0),\) где \(k = \cfrac{y_1 — y_0}{x_1 — x_0},\)

или же

\(y-y_0 = \cfrac{y_1-y_0}{x_1-x_0} (x-x_0).\)

Что и решает поставленную задачу.

При желании, можно еще выразить функцию \(y\) от \(x\) в явном виде:

\(y = k\,x — k\,x_0 + y_0\)

или

\(y = k\,x + b,\) где \(b = — k\,x_0 + y_0. \)

Значения констант \(k\) и \(b\) не зависят от выбора точек \((x_0, y_0)\) и \((x_1,y_1)\). Какие бы точки на заданной прямой мы не взяли, мы всегда придем к одним и тем же значениям \(k\) и \(b\). Заметим, что из-за дополнительного слагаемого \(b\) переменные \(x\) и \(y\) не пропорциональны друг другу. Поэтому константа \(k\) называется теперь не коэффициентом пропорциональности, как это было раньше, а угловым коэффициентом. Название это происходит от того, что значение \(k\) тесно связано с углом наклона прямой по отношению к оси \(x\). Чем круче идет прямая, тем больше ее угловой коэффициент.

Константу \(b\) иногда называют свободным членом. Как легко видеть, переменная \(y\) равна \(b\) при \(x = 0\). Иными словами, \(b\) — это точка на оси \(y\), в которой эта ось пересекается с нашей прямой. Если \(b = 0\), то прямая проходит через начало координат, и мы возвращаемся к частному случаю, рассмотренному ранее.

Из наших рассуждений следует, что любая прямая на координатной плоскости может быть описана уравнением вида

\(y = k\,x + b\)

при подходящем выборе констант \(k\) и \(b\).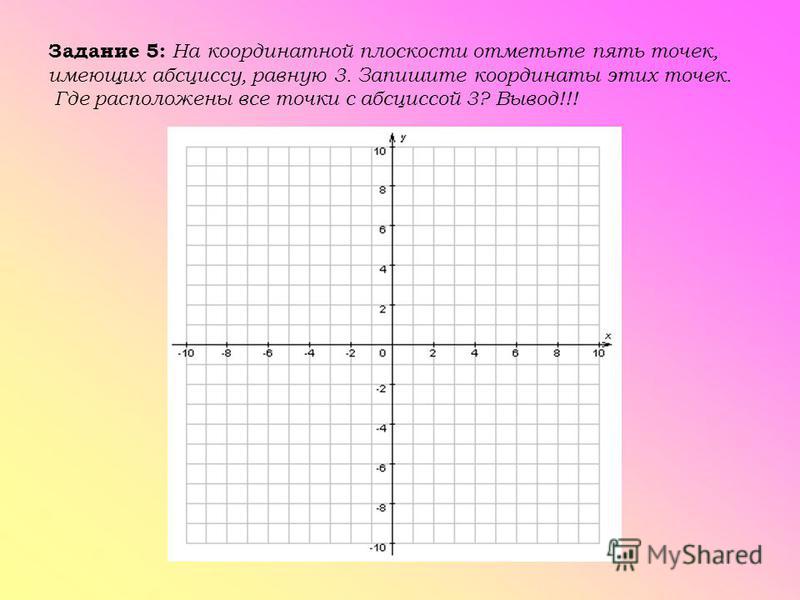 Единственным исключением является особый случай, когда в выражении для углового коэффициента \(k = \frac{y_1 — y_0}{x_1 — x_0}\) знаменатель обращается в ноль. Это происходит, если \(x_1 = x_0\). Это значит, что прямая перпендикулярна оси \(x\) (и соответственно параллельна оси \(y\)). При таких обстоятельствах \(x\) неизбежно утрачивает роль независимой переменной, но может формально рассматриваться как функция от \(y\):

\(x = 0 \cdot (y — y_0) + x_0.\)

В совершенно общем виде уравнение прямой можно написать следующим образом:

\((x_1-x_0) (y-y_0) = (y_1-y_0) (x-x_0).\)

При этом, однако, выбор двух пар параметров \((x_0, y_0)\) и \((x_1, y_1)\) (которые, по смыслу, являются координатами двух произвольных точек, лежащих на прямой) неоднозначен.

Построение графика по заданной функции

Теперь давайте выясним, как построить график неоднородной линейной функции \(y\) от \(x\), которая определяется как

\(y = k\,x + b,\)

где \(k\) и \(b\) — любые действительные числа. Как мы только что выяснили, к такому виду сводится уравнение произвольной прямой (при условии, что она не параллельна оси \(y\)). Строго говоря, это не исключает, что при некоторых значения параметров \(k\) и \(b\) график этой функции может отличаться от прямой линии. Давайте убедимся, что этого никогда не происходит. Перепишем данное нам уравнение следующим образом:

\((y — b) = k\cdot (x-0),\)

Если перейти в новую, штрихованную, систему координат с началом в точке \((0, b)\) и с осями \(x’\) и \(y’\), сонаправленными с соответствующими осями старой системы, то в новых координатах уравнение примет вид:

\(y’ = k\,x’.\)

Мы получим тогда не что иное, как уравнение пропорциональной зависимости, которое гарантировано задает прямую линию. Значит, и график неоднородной линейной функции

\(y = k\,x + b\)

представляет собой прямую линию при любых значениях параметров \(k\) и \(b\). Но для того, чтобы построить прямую, достаточно знать две ее произвольные точки \((x_0, y_0)\) и \((x_1, y_1)\).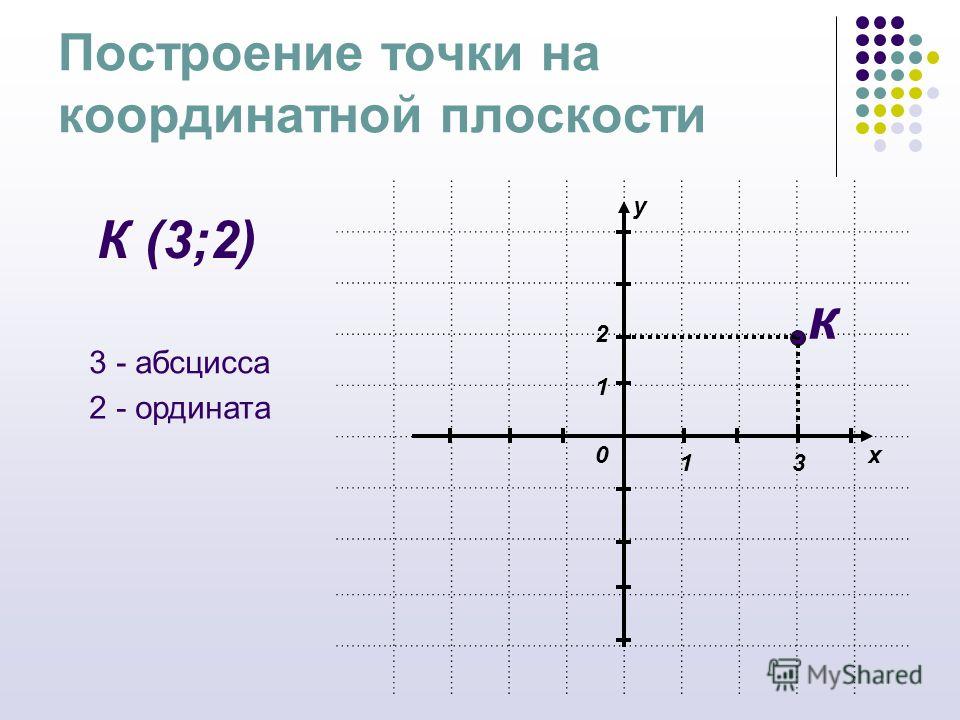 В качестве \(x_0\) и \(x_1\) можно взять, например, соответственно ноль и единицу. Тогда

\(y_0 = b\) (при \(x_0 = 0\)),
\(y_1 = k+b\,\) (при \(x_1 = 1\)).

Проводим прямую через точки \((x_0, y_0)\) и \((x_1, y_1)\) — и задача решена. На практике, впрочем, лучше брать такие точки, которые расположены друг от друга по возможности дальше, насколько позволяет чертеж. Пример графика неоднородной линейной функции со значением параметров \(k = \frac{1}{3}\) и \(b = 1\) представлен на следующем рисунке.

Конспект

\(1\). Линейная функция \(y = k\,x + b\) называется однородной при \(b = 0\) и неоднородной при \(b \ne 0.\) Ее график на координатной плоскости представляет собой прямую линию, которая строится по двум произвольным точкам.

\(2\). Уравнение прямой, проходящей через начало координат: \(y = \frac{y_1}{x_1} x,\) где \((x_1, y_1)\) — координаты произвольной точки, принадлежащей этой прямой \((x_1 \ne 0). \) Исключение: прямая совпадает с осью \(y\). Тогда уравнение прямой: \(x = 0.\)

\(3\). Уравнение произвольной прямой: \(y-y_0 = \frac{y_1-y_0}{x_1-x_0} (x-x_0),\) где \((x_0, y_0)\) и \((x_1, y_1)\) — координаты двух различных произвольных точек, принадлежащих этой прямой. Исключение: прямая проходит через точку \((x_0, y_0)\) параллельно оси \(y\). Тогда уравнение прямой: \(x = x_0\).

8 веселых и увлекательных занятий на координатной плоскости

Вы представляете или повторяете координатную плоскость со своими учениками? Ознакомьтесь с этими 8 забавными и увлекательными заданиями на координатную плоскость, которые я использовал на протяжении многих лет со своими студентами-алгебраистами, чтобы познакомить их с декартовой плоскостью.

Координатная плоскость Действия

border-color number-border-width.border-width»/> Координатная плоскость Игра с мухобойками
Объедините гигантскую координатную плоскость занавески для душа с парой мухобойок, чтобы получить увлекательную игру с координатной плоскостью и попрактиковаться в графическом построении упорядоченных пар.
Читать далее
Упражнение с полетом для построения графика упорядоченных пар
Я создал это упражнение с полетом, чтобы познакомить своих учеников с историей координатной плоскости и дать им столь необходимую им практику построения графика упорядоченных пар.
Подробнее
color»> Складные части координатной плоскости
Я был вдохновлен г-жой Хейли и ее чудесным блогом Journal Wizard на создание новых и улучшенных складных частей координатной плоскости!
Подробнее
Создание координатной плоскости душевой занавески
Я хочу поделиться с вами инструкциями по созданию моего нового любимого учебного пособия – координатной плоскости душевой занавески.
Подробнее
color number-background-color.background-color number-border-color.border-color number-border-width.border-width»/> Части магнитов для координатной плоскости
Я создал эти части магнитов для координатной плоскости для своего класса и хочу поделиться файлами с вами, чтобы вы также могли создать свой собственный набор.
Подробнее
Графический органайзер упорядоченных пар
Я создал этот графический органайзер с упорядоченными парами, чтобы рассмотреть координатную плоскость со своими студентами-алгебраистами. На самом деле я использовал его как со своими учениками по Алгебре 1, так и со студентами по Алгебре 2.
Подробнее
color»> Части графического органайзера на координатной плоскости
Я создал эти части графического органайзера на координатной плоскости несколько лет назад для подготовки к началу учебного года.
Подробнее
Координатная плоскость Складная
Я создал эту координатную плоскость, которую можно сложить, чтобы мои ученики по алгебре 2 могли вклеить ее в свои интерактивные тетради. Я использовал это как возможность просмотреть ключевые словарные термины, которые мы будем использовать в течение года при построении графиков уравнений.
Подробнее
Дополнительные ресурсы для обучения координатной плоскости
Опубликовано
Опубликовано: 25 сентября 2022 г. – Последнее обновление: 11 ноября 2022 г.
Графические уравнения и неравенства — Координатная плоскость
Графические уравнения и неравенства — Координатная плоскость — Первый взгляд
Дом | Учитель | Родители | Глоссарий | О нас
В В этом блоке мы будем изучать уравнения с двумя переменными. Координата плоскости является важным инструментом для работы с этими уравнениями.
No related posts.

Координатной плоскости: Координатная плоскость — урок. Алгебра, 7 класс.