Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5.  СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1.  ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ§ 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3.  КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4.  СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4.  СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. 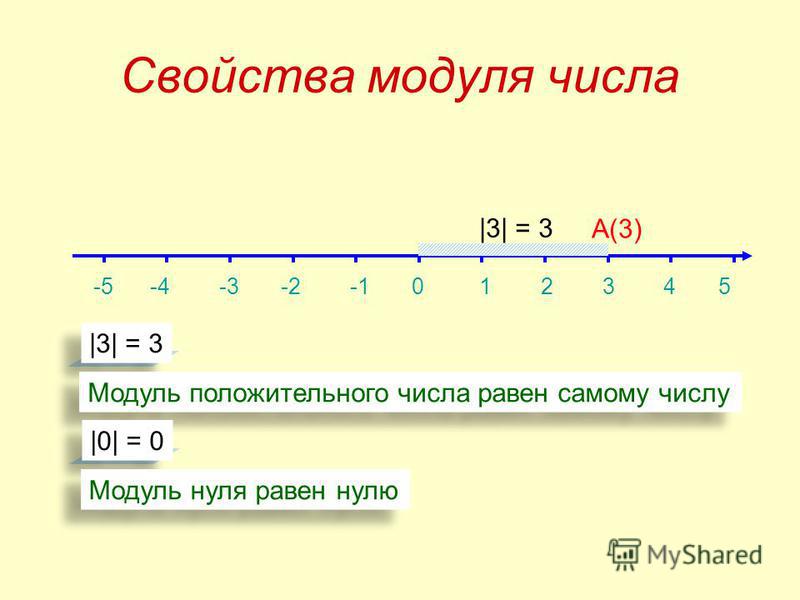 ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Модуль числа сравнение чисел. Модуль числа объяснение.
- Альфашкола
- Статьи
- Модуль числа (Часть 2)
Модуль абсолютная величина числа
КВАДРАТНЫЕ КОРНИ
Продолжение статьи Модуль числа (Часть 1)
\( (3)^2 = 9\)
\(b = 3\)
но!!!
\( (-3)^2 = 9 \) \(b = -3\)
Положительный квадратный корень квадрата числа равен этому числу.
2} = |a||b|\)
\( |-4| = |4| \)
\( |2*(-3)| = |-6| = 6 = |2|*|3| = 6\)
\( |5/4| = 5/4 = |5|/|4| = 5/4\)
Геометрическая интерпретация абсолютной величины
Где A и B-точки с координатами a и b. Расстояние между A и B
Если \(a\) и \(b\) являются точками на координатной линии с координатами A и b соответственно, то расстояние \( d\) между A и B
\( d = |b-a| \)
\(| x-a | < k (k>0)\)
Другая форма записи
-\(k < x-a < k \)
Пример 1. Решить неравенство
\( | x-3 |< 4 \)
записываем как:
\( -4 < х-3 < 4 \)
прибавляем \(3\) с обоих сторон:
\( -1 < x < 7 \)
Ответ: \( (-1,7)\)
Пример 2. Решить неравенство:
Решить \( |x+4 |≥ 2 \)
\( x+4 ≤ -2\)
\(х ≤ -6 х+4 ≥ 2\)
\(x≥ -2\)
Ответ: объединение из двух промежутков:
\( (-∞ , -6] ∪ [-2 , +∞ )\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа».
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Станислав Николаевич Перепада
Репетитор по математике
Стаж (лет)
Образование:
Челябинский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Владимир Николаевич Плехов
Репетитор по математике
Стаж (лет)
Образование:
Гомельский государственный университет им.
Ф. Скорины
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Андрей Александрович Якунин
Репетитор по математике
Стаж (лет)
Образование:
Петрозаводский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по олимпиадной математике
- Репетитор по английскому языку для подготовки к ЕГЭ
- Репетитор по разговорному английскому
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор для подготовки к ОГЭ по истории
- Репетитор для подготовки к ВПР по русскому языку
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор для подготовки к ЕГЭ по обществознанию
- Репетитор по информатике для подготовки к ЕГЭ
Похожие статьи
- Сложение смешанных дробей
- Медиана треугольника
- Корень
- Как сокращать дроби
- ЕГЭ по математике, базовый уровень.
Текстовые задачи (вариант 2) - Задачи на движение по воде
- 5 советов, как развить математические способности у ребенка
- Что такое снег, как появляется и зачем он нужен?
Текстовые задачи (вариант 2)Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Что такое 4 мод 4? (4 по модулю 4)
Вам нужно знать, что означает 4 по модулю 4? Может надо посчитать? В этом небольшом руководстве мы покажем вам, как точно вычислить мод числа. Вы также можете увидеть, что это называется модулем или модулем.
Хотите быстро научиться или показать учащимся, как считать 4 по модулю 4? Включи это очень быстрое и веселое видео прямо сейчас!
Так что же такое модуль или модуль? Проще говоря, по модулю — это математическая операция нахождения остатка при делении двух чисел.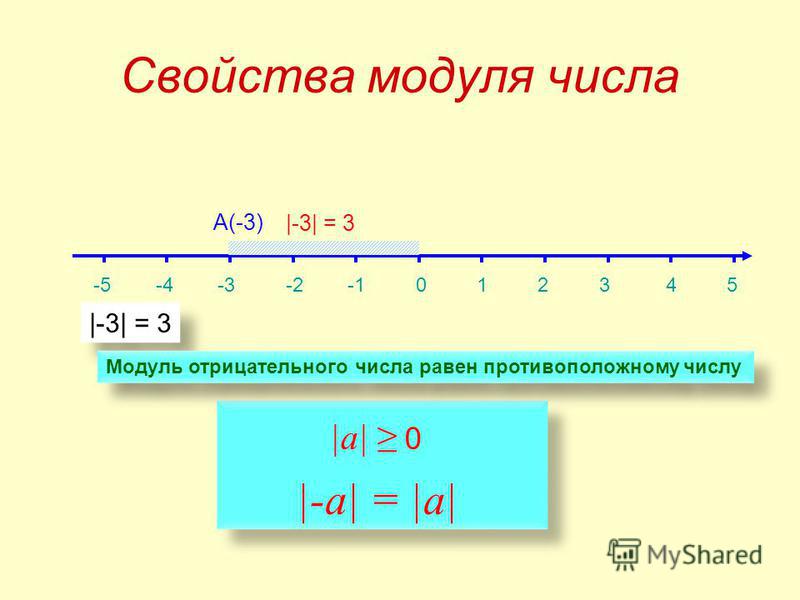
Если вы спрашиваете «что такое 4 мод 4?» тогда вам действительно нужно знать: «Каков остаток при делении 4 на 4?».
Существует множество причин, по которым вы хотели бы использовать модуль по модулю, в том числе проверка того, является ли число четным или нечетным, подсчет чего-либо определенное количество раз, и даже обычные часы в вашем доме будут использовать модуль для определения времени. .
Давайте рассмотрим два метода вычисления 4 по модулю 4. Мы назовем их методом по модулю и методом по модулю.
Примечание: первое число (4) называется Дивидендом, а второе число (4) называется Делителем. Когда вы делите дивиденд на делитель, ответ, который у вас остается, это частное. Это частное имеет целую числовую часть (называемую целым) и десятичную часть, которая называется дробной.
Метод по модулю
Сначала нужно разделить дивиденд на делитель:
4 / 4 = 1,00
Затем мы берем целую часть частного (1) и умножаем ее на делитель (4):
1 x 4 = 4
И, наконец, мы берем ответ на втором шаге и вычитаем его из Делимое для получения ответа на 4 по модулю 4:
4 — 4 = 0
Как видите, ответ на 4 по модулю 4 равен 0 .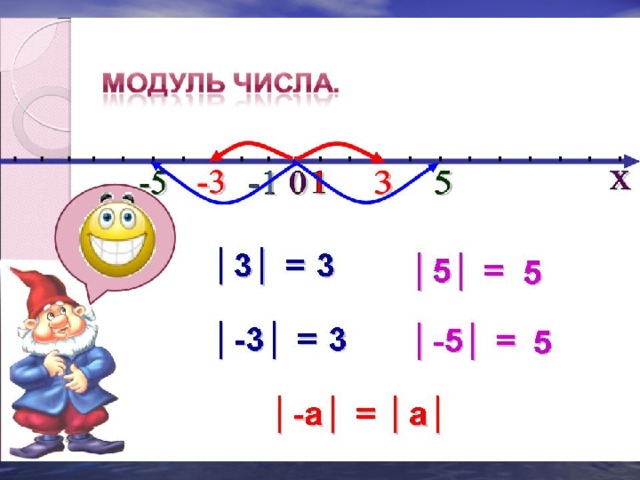
Модульный метод
Модульный метод требует, чтобы мы сначала выяснили, каково наибольшее общее кратное Делителя (4), которое равно или меньше Делимого (4).
Мы видим, что числа, кратные 4, равны 0, 4, 8, 12 и т. д. Наибольшее кратное, меньшее или равное 4, равно 4.
Итак, последний шаг в методе модуля здесь — вычесть делитель наибольшее кратное из Дивиденда и ответьте на вопрос «чему равно 4 по модулю 4?»:
4 — 4 = 0
Как мы видим, это тот же ответ, что и метод по модулю, и ответ равен 0 .
Надеюсь, вы поняли это краткое, но увлекательное путешествие по модулю и модульному методу вычислений. Если вам интересно, возьмите ручку и бумагу и сделайте пару таких упражнений сами, чтобы посмотреть, действительно ли вы чему-то научились.
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.
Мы очень ценим вашу поддержку!
«Что такое 4 мод 4?». VisualFractions.com . По состоянию на 30 января 2023 г. http://visualfractions.com/calculator/modulo/what-is-4-mod-4/.
«Что такое 4 мод 4?». VisualFractions.com , http://visualfractions.com/calculator/modulo/what-is-4-mod-4/. По состоянию на 30 января 2023 г.
Что такое 4 mod 4?. VisualFractions.com. Получено с http://visualfractions.com/calculator/modulo/what-is-4-mod-4/.
Калькулятор модуля
Хотите решать больше задач на модуль? Введите свои числа ниже и нажмите рассчитать.
Введите задачу по модулю
Следующий расчет по модулю
- Что такое 5 mod 4?
Модульная электрическая ярусная печь MODULO 4
Описание
Данная модель рассчитана на 4 противня на ярусе
Печи Modulo широко используются в кондитерских, пекарнях и магазинах и предназначены для выпекания самых разнообразных хлебобулочных изделий.
На выбор заказчика мы предлагаем Modulo в 7 моделях вместимости камеры: от 1 до 8 лотков размером 40×60 см.
Модульная конструкция позволяет спроектировать печь с максимальным количеством камер до 6, что обеспечивает полный диапазон мощностей от 1 до 48 противней размером 40×60 см. Независимо от его мощности каждый модуль Modulo может поставляться «по частям» и собираться на месте.
Передняя панель, а также корпус духовки изготовлены из полированной стали AISI 304, что обеспечивает эстетические преимущества и практические преимущества легкой очистки.
Каждая печь Modulo может быть оборудована камерой расстойки или подставкой.
Modulo снабжен электрическим подогревом; современные нагреватели
- в каждой камере могут включаться и выключаться отдельно для соответствия эффективности печи текущим производственным потребностям
- отдельный выбор температуры для верхней и нижней части однокамерной камеры для обеспечения идеального температурного режима для различных продуктов.
- отдельные парогенераторы, предназначенные для каждой камеры отдельно, чтобы ими можно было легко управлять непосредственно с панели управления
Более 20 лет опыта в производстве хлебопекарных печей позволили нам спроектировать печь Modulo, отличающуюся от других решений, прежде всего, увеличенным сроком службы, энергосбережением и, прежде всего, стабильной средой и ровными условиями выпечки.
- Каждая камера имеет профнастил, обеспечивающий большую жесткость конструкции и обеспечивающий трапециевидное гнездо для размещения нагревательных элементов.
- Каждый нагревательный элемент устанавливается отдельно; это решение защищает нагреватели от самопроизвольного выскальзывания во время цикла выпечки (предварительный нагрев/охлаждение)
- Каждый нагревательный элемент имеет специальное профилирование с левой и правой стороны, чтобы обеспечить расширенную зону нагрева по бокам камеры для равномерного пропекания
- Ни один из управляющих элементов Modulo, таких как контакторы, предохранители и реле, не размещен на стенках печи. Чтобы защитить эти хрупкие элементы от температурных воздействий, они были перемещены и установлены в одном электрическом ящике из нержавеющей стали. Кроме того, это облегчает контроль и техническое обслуживание печи.
- Обогреватели соединены силиконовой трубкой, обеспечивающей термостойкость, значительно превышающую реальную температуру в этих местах.
- В результате нашего ноу-хау мы внедрили специальное расположение нагревателей вдоль камеры, чтобы обеспечить превосходную однородность температуры.
- Каждая камера оснащена вентиляционными полосами, расположенными между боковыми стенками и подами печи, и это решение оказывает значительное влияние на выравнивание температуры и даже выпечку.
- Равномерное распределение пара обеспечивается задней листовой панелью с отверстиями для выхода пара
- Выпечка изделий осуществляется на противнях или непосредственно на керамических плитах повышенной гладкости.
- Лицевые части керамических плит оснащены нержавеющими маскировочными рамками для защиты от прямого попадания взрывчатых веществ. поднос.
- Формы духовки и стыки выровнены, что обеспечивает легкую очистку; система быстрой сборки двери из двойного закаленного стекла без инструментов позволяет также легко демонтировать ее.
- Полная изоляция печи изоляционной ватой средней или высокой плотности, в зависимости от места ее размещения + дополнительно экранирующий лист, отражающий тепло
- каждая духовка оснащена регулятором давления воды для обеспечения адекватной дозировки и контроля температуры пароварки и предотвращения перелива воды.
Чтобы защитить эти хрупкие элементы от температурных воздействий, они были перемещены и установлены в одном электрическом ящике из нержавеющей стали. Кроме того, это облегчает контроль и техническое обслуживание печи.
поднос.В зависимости от модели наши духовые шкафы оснащены прочными металлическими колесами, а модели меньшего размера – вращающимися колесами.
Каждая камера освещается галогенными лампами, а расстойная камера — светодиодными лампами.
По желанию заказчика наша печь Modulo может быть оснащена автоматическим блоком управления для программирования цикла выпечки. Процесс выпечки, т. е. температура, время, пропаривание, открытие/закрытие выпускной трубы, может осуществляться автоматически.