Свойства арифметического квадратного корня. Квадратный корень из степени. Преобразование выражений, содержащих
Тема 6: Квадратные корни
Урок 6: Свойства арифметического квадратного корня. Квадратный корень из степени. Преобразование выражений, содержащих квадратные корни
- Видео
- Тренажер
- Теория
Заметили ошибку?
Свойства арифметического квадратного корня. Квадратный корень из степени.
Арифметический квадратный корень обладает рядом свойств.
-
ab=ab (a,b≥0). Если a и b – неотрицательные числа, то корень из их произведения равен произведению корней.
Доказательство: воспользуемся определением квадратного корня.
(ab)2=ab
(ab)2=ab
Функция y=x2 при х≥0 принимает свои значения ровно один раз.

Следовательно, ab=ab, так как равны их квадраты.
Примеры:
36·25=36∙25=6∙5=30
Рассмотрим обобщение первого свойства: abc=abc при a,b,c≥0.
Корень из произведения неотрицательных множителей равен произведению корней этих множителей.
Примеры:
81·4·16=81416=9∙2∙4=72
0,01·8·50=0,01∙8∙2∙25=0,011625=0,1∙4∙5=2
-
ab=ab (a>0, b≥0). Если а – неотрицательное число, а b – положительное число, то корень из их отношения равен отношению корней.
Доказательство: воспользуемся определением квадратного корня.
ab2=ab
ab2=(a)2(b)2=ab
Функция y=x2 при х≥0 принимает свои значения ровно один раз.
Следовательно, ab=ab, так как равны их квадраты.

Примеры:
49=49=23
1916=2516=2516=54=114
-
a2n=anпри a≥0, n∈N
Доказательство: воспользуемся определением квадратного корня.
(a2n)2=a2n
(an)2=a2n
Функция y=x2 при х≥0 принимает свои значения ровно один раз.
Следовательно, a2n=an, так как равны их квадраты.
Примеры:
36=32∙3=33=27
x8=x2∙4=x4 при x≥0
Рассмотренные свойства широко используются в различных задачах.
Разберем пример:
132-122=(13-12)(13+12)=1∙25=5
Конечно, в данном примере можно было просто вычислить квадраты указанных чисел, а затем посчитать их разность. Однако подсчёт «в лоб» станет слишком трудным для больших чисел.
Рассмотрим одну из самых распространённых и грубейших ошибок, которую часто допускают при работе с квадратными корнями.

Утверждение а±b=a±b – НЕВЕРНО!
В качестве подтверждения рассмотрим следующий пример: 9+16=25=5, а 9+16=3+4=7. Как видим, применение неправильной формулы приводит к неправильным результатам.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим. 3-8Квадратный корень из 16 — Как найти квадратный корень из 16?
LearnPracticeDownload
Квадратный корень из 16 выражается как √16 в радикальной форме и как (16) ½ или (16) 0,5 в экспоненциальной форме. Квадратный корень из 16 равен 4. Это положительное решение уравнения x 2 = 16. Число 16 является полным квадратом.
Квадратный корень из 16 равен 4. Это положительное решение уравнения x 2 = 16. Число 16 является полным квадратом.
- Квадратный корень из 16: 4
- Квадратный корень из 16 в экспоненциальной форме: (16) ½ или (16) 0,5
- Квадратный корень из 16 в подкоренной форме: √16
| 1. | Чему равен квадратный корень из 16? |
| 2. | Является ли квадратный корень из 16 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 16? |
| 4. | Часто задаваемые вопросы о квадратном корне из 16 |
Что такое квадратный корень из 16?
Квадратный корень числа — это число, которое умножается само на себя, чтобы получить произведение. Для любых двух действительных чисел a и b
a 2 = b
a = √b
0919 .
Квадратный корень из 16 = √ 16
4 2 = 4 × 4 равно 16
Здесь 4 называется квадратным корнем из 16
.
16 — полный квадрат.
Таким образом, квадратный корень из 16 равен 4. Квадратный корень из 16 – это обратная операция возведения в квадрат 4 и -4 90 993.
4 × 4 = 16
(-4) × (-4) = 16
Является ли квадратный корень из 16 рациональным или иррациональным?
Рациональное число определяется как число, которое может быть выражено в виде частного или деления двух целых чисел, т. е. p/q, где q = 0. В предыдущем разделе мы схематически заметили, что квадратный корень из 16 равно 4 или (-4). Оба числа могут быть представлены в виде рационального числа, т. е. 4/1 и -(4/1) соответственно.
√ 16 = 4 = 4/1
Таким образом, квадратный корень из 16 является рациональным.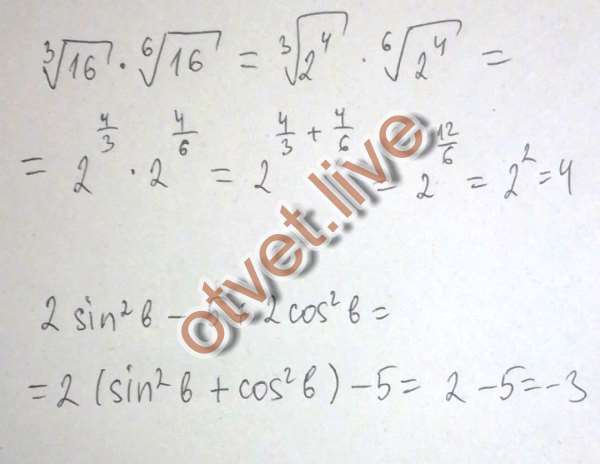
Итак, √ 16 — иррациональное число.
Как найти квадратный корень из 16?
Квадратный корень из 16 можно вычислить с помощью различных методов: простой факторизации и метода длинного деления. Давайте посмотрим, как это вычисляется с помощью простой факторизации:
Квадратный корень из 16 с помощью простой факторизации
Следующие шаги можно выполнить с помощью простой факторизации:
- Шаг 1. Определите простую факторизацию числа 16
. 16 = 2 × 2 × 2 × 2
16 = 2 × 2 90 920 - Шаг 2. Сгруппируйте простые множители, полученные для числа 16, попарно.
- Шаг 3. Выберите один фактор из каждой пары, и они могут быть записаны в виде:
- Шаг 4. Таким образом, следуя закону экспонент, получаем,
√16 = √ (2 × 2) 2
√16 = (4 2 ) ½ = 4
Теперь попробуем найти квадратный корень из 16 методом деления в большую сторону!
Квадратный корень из 16 на длинное деление
Вот шаги, которые необходимо выполнить, чтобы вычислить квадратный корень из 16:
- Шаг 1.
 Запишите 16, как показано на рисунке. Начните группировать число парами с правого конца. Для 16 оба числа будут сгруппированы под одной полосой.
Запишите 16, как показано на рисунке. Начните группировать число парами с правого конца. Для 16 оба числа будут сгруппированы под одной полосой. - Шаг 2. Найдите наибольшее число, которое при умножении само на себя даст 16 или меньшее число, ближайшее к 16. 4 – это необходимое число. 909:20
- Шаг 3. Выполнить деление делимого 16, используя 4 в качестве делителя.
- Шаг 4. Частное, полученное при делении в длинную сторону, равно квадратному корню из 16
Изучение квадратного корня с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 64
- Квадратный корень из 36
- Квадратный корень из 169
- Квадратный корень из 25
- Квадратный корень из 81
Аналитический центр:
- У Дженни есть квадратный стол площадью 16 квадратных дюймов. Она накрыла его скатертью площадью 25 квадратных дюймов.
 На сколько дюймов свисает ткань над столом с каждой стороны, если положить ее по центру?
На сколько дюймов свисает ткань над столом с каждой стороны, если положить ее по центру?
Важные примечания:
- Квадратный корень из 16 выражается как √ 16 в радикальной форме и как 16 1/2 в экспоненциальной форме.
- Квадратный корень числа является как отрицательным, так и положительным для одного и того же числового значения, т. е. квадратный корень из 16 будет равен 4. 909:20
Квадратный корень из 16 решенных примеров
Пример 1 : У Ноя есть мешок, наполненный кубиками. 9 из них зеленые и 7 оранжевые. Если она сложит их вместе, то сколько кирпичей будет с каждой стороны?
Решение
Всего кубов, использованных Ноем для создания квадратной поверхности = 9 + 7 = 16 кубов
Количество кубиков на каждой стороне квадрата = √ Всего кубов, необходимых для составления квадрата
Кубических кирпичей на каждой стороне куба = √16 = √ (4 × 4) = 4
Поскольку количество используемых кубов не может быть отрицательным, практически мы возьмем только положительное значение.
Следовательно, кирпичей на каждой стороне квадрата = 4 .Пример 2 : Джейк расположил 16 цветочных растений на квадратной клумбе. Он получил несколько дополнительных цветочных растений и попытался сохранить квадратную форму клумбы после их добавления. Если общее количество цветочных растений на новой грядке равно 36, сколько дополнительных растений добавляется в каждом ряду?
Раствор
Мы знаем, что каждая сторона квадрата = √Площадь
Мы будем использовать ту же концепцию, чтобы найти цветы в каждом ряду.
Мы пренебрегаем отрицательным значением квадратного корня, когда он практически неприменим. Поэтому мы не использовали значение — 4 в этом примере.
Для композиции из 36 цветов цветочные растения в каждом ряду = √36 = 6 цветов
Таким образом, дополнительные цветы, добавленные в каждом ряду = 6 — 4 = 2 цветка 90 907Пример 3: Если площадь равностороннего треугольника равна 16√3 в 2 .
 Найдите длину одной из сторон треугольника.
Найдите длину одной из сторон треугольника.Решение:
Пусть а будет длиной одной из сторон равностороннего треугольника.
⇒ Площадь равностороннего треугольника = (√3/4)a 2 = 16√3 в 2
⇒ а = ±√64 в
Поскольку длина не может быть отрицательной,
⇒ а = √64 = 2 √16
Мы знаем, что квадратный корень из 16 равен 4.
⇒ а = 8 в
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о квадратном корне из 16
Каково значение квадратного корня из 16?
Квадратный корень из 16 равен 4.
Почему квадратный корень из 16 является рациональным числом?
При разложении на простые множители 16, т.




 Запишите 16, как показано на рисунке. Начните группировать число парами с правого конца. Для 16 оба числа будут сгруппированы под одной полосой.
Запишите 16, как показано на рисунке. Начните группировать число парами с правого конца. Для 16 оба числа будут сгруппированы под одной полосой. На сколько дюймов свисает ткань над столом с каждой стороны, если положить ее по центру?
На сколько дюймов свисает ткань над столом с каждой стороны, если положить ее по центру?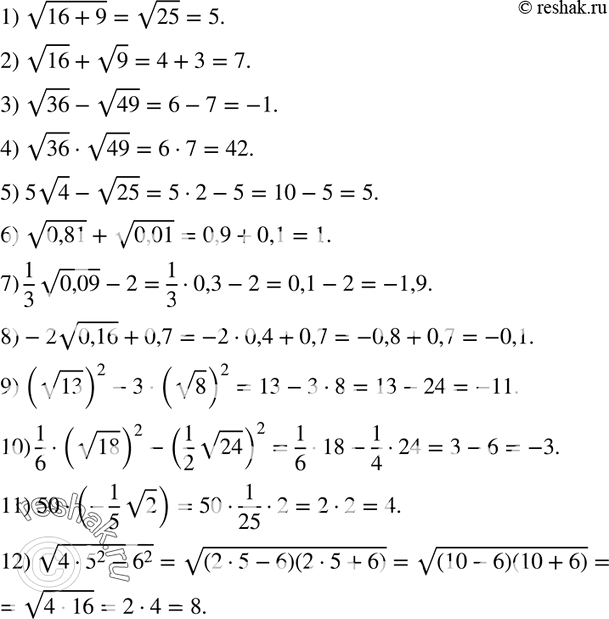
 Найдите длину одной из сторон треугольника.
Найдите длину одной из сторон треугольника.