Корень любой степени
Главная / i / t
Есть в математике такая операция – возведение числа в степень с натуральным показателем. Такая операция позволяет из числа 5 получить его квадрат равный 25, а из числа 3 четвертую степень этого числа равную 81:
52=5∙5=25
34=3∙3∙3∙3=9∙9=81
Но довольно часто возникает необходимость производить обратную операцию, например, выяснять какое число в квадрате будет равно 25. Мы уже изучали операцию обратную возведению в квадрат – извлечение квадратного корня.
Таким образом, есть прямая операция, позволяющая из числа 5 получить его квадрат 25; и обратная операция, с помощью которой можно из 25 назад получить число 5:
52=25
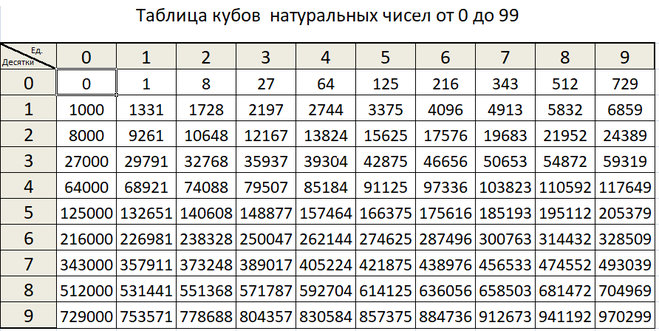
Но кроме операции возведения в квадрат, существует еще операция возведения в куб, и у нее тоже есть своя обратная операция – извлечение кубического корня, которую еще называют корнем третьей степени.
Чтобы извлечь кубический корень нужно подобрать такое число, куб которого равен подкоренному числу. Например, кубический корень из 8 равен двум, потому что два в кубе равно восьми:
23=2∙2∙2=8
Наряду с операцией обратной возведению в куб есть и операция обратная возведению в четвертую степень – это извлечение корня четвертой степени, в его основе тот же принцип – он равен неотрицательному числу, четвертая степень которого равна подкоренному числу. Так корень четвертой степени из 81 равен 3, потому что 3 в четвертой степени равно 81:
34=3∙3∙3∙3=9∙9=81
Но число 3 не единственное, четвертая степень которого равна 81, число −3 в четвертой степени тоже равно 81:
(−3)4=(−3)∙(−3)∙(−3)∙(−3)=9∙9=81
Поэтому, если выбор стоит между двумя такими вариантами, принято считать, что корнем из неотрицательного числа является только неотрицательное число.
Это не единственный нюанс, который обязательно надо учитывать. Познакомимся поближе с сутью такого понятия как обратная операция.
Вот шесть примеров применения прямой операции – возведение в четную степень, которая из чисел 1, 2, 3 и −1, −2, −3 позволяет получить числа 1, 16 и 729:
12 = 1 (−1)2 = 1
24 = 16 (−2)4 = 16
36 = 729 (−3)6 = 729
Заметим, что какое бы число мы не возводили в четную степень, всегда получаются неотрицательные.
Изобразим все шесть прямых операций в виде следующей диаграммы. Каждая красная стрелка символизирует прямую операцию – возведение в четную степень: красная стрелка идет от
Применение обратной операции к числам 1, 16 и 729 должно назад возвращать числа 1, 2, 3 и −1, −2, −3, если это возможно.
Тогда построим диаграмму, только с обратными операциями – извлечение корня четной степени, которые изображены синими стрелками, указывающими противоположное направление.
Кажется что, чтобы совершить обратную операцию нужно только перейти по синей стрелке, например, от 16. Вот только из 16 идут сразу две стрелки. Какую следует выбрать? Какое число 2 или −2 возвели в четвертую степень, чтобы получить 16? Выяснить это невозможно – оба числа в четвертой степени равны 16. Эта неопределенность и порождает все трудности.
Поэтому для однозначности принято считать, что корнем четной степени из положительного числа является только неотрицательное число. Стрелки, ведущие от чисел под корнем к отрицательному числу, изображены серым цветом – такие операции считаются недопустимыми в действительных числах и делать их нельзя. Значит, обратных операций будет уже только три:
К тому же, как видите, ни одна из синих стрелок не идет от отрицательных чисел −1, −16 и −729, потому что ни одна красная стрелка не вела к этим отрицательным числам, невозможно вернуться оттуда, куда невозможно прийти.
Поэтому в действительных числах и нельзя извлечь корень четной степени из отрицательного числа.
Теперь проведем такой же опыт, только уже с нечетными степенями. Вот шесть прямых операций с нечетными степенями:
23 = 8 (−2)3 = −8
35 = 243 (−3)5 = −243
47 = 16384 (−4)7 = −16384
Нарисуем на диаграмме красными стрелками каждую из этих прямых операций.
В отличие от предыдущей диаграммы с красными стрелками, здесь нет чисел, на которые показывают сразу две красные стрелки, благодаря этому не будет возникать неопределенности и обратные операции будут осуществимы для всех шести чисел.
Значит, можно извлечь корни из всех чисел и получить точно такие же числа, которые возводили в нечетную степень:
Совместим две диаграммы с синими стрелками, и тогда получим следующую картину.
Можно сделать вывод: из неотрицательного числа можно извлекать корень любой степени, а из отрицательного можно извлекать корень только нечетной степени.
Дадим же определения корню любой натуральной (кроме первой) степени из неотрицательного числа и корню нечетной степени из отрицательного числа.
Корнем n-й степени из неотрицательного числа a называется такое неотрицательное число, при возведении которого в степень n получится число a:
Корнем нечетной степени n из отрицательного числа a называется такое отрицательное число, при возведении которого в степень n получится a:
Например, корень пятой степени из 32 равен двум:
Потому что 2 в пятой степени равно 32:
25=2∙2∙2∙2∙2=32
Попробуем извлечь кубический корень из −27:
Известно ли нам число, куб которого равен
(−3)3 = (−3)∙(−3)∙(−3) = 9∙(−3) = −27
Значит, кубический корень из −27 равен −3:
Корень пятой степени из 3125 равен 5:
А корень седьмой степени из −128 равен −2:
Из нецелого числа тоже может извлекается корень:
1.
16=1.771561
Как и в случае с квадратным корнем, корень n-й степени может быть иррациональным числом, тогда возможно получить только его приближенное значение:
В таких случаях не пытаются извлекать корень или искать его приближенное значение, а оставляют его без изменений, т. к. это иррациональное число и больше ничего сделать не получится:
Очевидным должно быть, что и корень любой степени из нуля и единицы будут равны нулю и единице:
Как возвести корень в квадрат
Возведение числа в степень — это сокращенная форма записи операции многократного умножения, в котором все множители равны исходному числу. А извлечение корня означает обратную операцию — определение множителя, который должен быть задействован в операции многократного умножения, чтобы в ее результате получилось подкоренное число. Как показатель степени, так и показатель корня указывают на одно и то же — сколько сомножителей должно быть в такой операции умножения.
Вам понадобится
Если к числу или выражению требуется применить одновременно и операцию извлечения корня, и возведения его в степень, сведите оба действия в одно — в возведение в степень с дробным показателем. В числителе дроби должен стоять показатель степени, а в знаменателе — корня. Например, если нужно возвести в квадрат кубический корень, то две эти операции будут эквивалентны одному возведению числа в степень ⅔.
Если в условиях требуется возвести в квадрат корень с показателем степени, равным двойке, это задача не на вычисление, а на проверку ваших знаний. Воспользуйтесь способом из первого шага, и вы получите дробь 2/2, т.е. 1. Это значит, что результатом возведения в квадрат квадратного корня из любого числа будет само это число.
При необходимости возвести в квадрат корень с четным показателем степени, всегда есть возможность упростить операцию. Так как у двойки (числителя дробного показателя степени) и любого четного числа (знаменателя) есть общий делитель, то после упрощения дроби в числителе останется единица, а это значит, что возводить в степень при расчетах не требуется, достаточно извлечь корень с половинным показателем степени.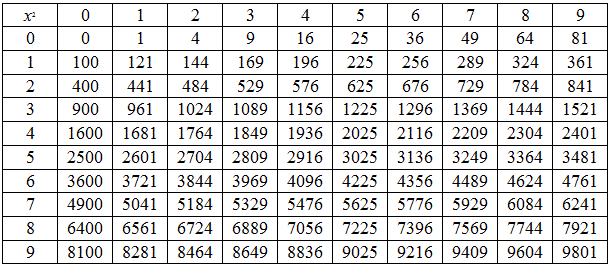
(2 / 5) = 14,1261725.
Как вырастить кристалы из медного купороса | Что такое натурализм | Как перевести см в литры |
Какие сказки написал Андерсен | Почему вымерли мамонты | Почему вода пенится |
Калькулятор квадратного корня, кубического корня, квадрата, куба и обратного числа
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дом Карта сайта Мастера преобразования Калькуляторы Закладки О Свяжитесь с нами Политика конфиденциальности Отказ от ответственности | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В математике квадрат — это результат умножения числа самого на себя. Куб числа — это его третья степень, а инверсия — это мультипликативная обратная или обратная величина числа. Квадратный корень из числа «X» — это число «Y», такое что «Квадрат Y» = «X», а кубический корень из числа «X» — это число «Y», такое, что «Куб из Y» = ‘ИКС’.
Найдите свой счастливый номер
..
Все права защищены.Как расширить кубический корень до комплексных чисел? — Новое для Джулии
СтивенСью
#1
Я могу найти квадратный корень из комплексных чисел, но не кубический корень
юлия> sqrt(1+2im)
1,272019649514069 + 0,7861513777574233им
юлия> cbrt(1 + 2im)
ОШИБКА: MethodError: нет метода, соответствующего cbrt(::Complex{Int64})
Ближайшие кандидаты:
cbrt(::BigFloat) в mpfr.jl:619
cbrt(::Float16) в math.jl:1125
cbrt(::Union{Float32, Float64}) в special/cbrt.jl:144
...
Трассировки стека:
[1] прицел верхнего уровня в REPL[2]:1
Итак, это моя попытка расширить кубический корень из комплексных чисел. Я делаю это правильно?
юлия> импорт База: cbrt
julia> cbrt(x::Complex{T}), где T = x^(one(T)/(one(T)+one(T)+one(T)))
cbrt (общая функция с 6 методами)
юлия> cbrt(1 + 2im)
1,2196165079717578 + 0,47171126778938893им
1 Нравится
4 июля 2020 г.
, 5:34
#2
А два других сложных корня?
1 Нравится
Tamas_Papp
#3
Думаю, cbrt можно расширить до комплексных чисел. Может, открыть тему? Тем временем 9(1/3)
аплавин
#5
Точно такая же ситуация, как и с sqrt :
a = комплекс(-1) кврт(а*а) == 1 кврт(а)*кврт(а) == -1
2 лайка
4 июля 2020 г.
, 16:13
#6
Я открыл вопрос: https://github.com/JuliaLang/julia/issues/36534 9(1//3) 0,7211247851537042 + 1,24
1 Нравится
4 июля 2020 г., 16:28
#7
Я не думаю, что есть очевидный выбор. Если вам нужен положительный вещественный корень для положительного вещественного входа, вы все еще в дыре. Если вы интегрируете контур вокруг начала координат, вы пересечете срез ветви и получите разные значения по мере увеличения аргумента. Итак, если z=r exp(im*theta) и cbrt(z) = r exp(im *theta/3), один проход по контуру не вернет вас туда, откуда вы начали. Все, что вы можете сделать, это правильно вести книги, когда вы проходите контур. 9(1/n) для n = 2, 3, …
2 лайка
СтивенСью