Урок. «Квадратные корни. Арифметический квадратный корень»
Урок № 3 § 12
Тема: Квадратные корни. Арифметический квадратный корень.
Цель урока:
Образовательная: ввести понятие квадратного корня. Дать учащимся свойства арифметического квадратного корня. Умение находить квадратные корни из чисел.
Развивающая: развитие устного счета при возведении в квадрат и при извлечении квадратного корня.
Воспитательная: воспитание трудолюбия и коллективизма.
Тип урока: урок усвоения новых знаний и умений
Оборудование: мел, доска, плакаты, карточки с заданием.
Х о д у р о к а
- Организационный момент.
— проверка готовности класса к уроку;
— проверка готовности учащихся к уроку;
— приветствие
— проверка Д.
З.
Анализ домашних заданий (устный опрос):
№ 356(1). Как найти координаты точек пересечения?
№ 354. Умение решать уравнение графически.
№ 372 и 373. Подготовка к новому материалу
2. Мотивация. Рациональные числа, с которыми мы ознакомились в предыдущих классах — это лишь малая часть множества чисел. На числовой прямой кроме рациональных ещё больше не рациональных чисел. Без знания этих чисел, без умения выполнять действия с ними невозможно в дальнейшем изучать математику и другие науки.
Рассказ учителя об исторической предпосылке возникновения понятия арифметического квадратного корня. Возникновение понятия «квадратного числа».
Вывешиваем плакат №1.
Древнегреческие математики представляли целые числа и любые величины, соизмеримые и несоизмеримые, геометрически, с помощью отрезков, прямоугольников и других фигур. Отсюда у них появились такие названия, как:
1) «плоские числа» для чисел вроде 6 = 2 • 3, 14 = 7 • 2, являющихся произведениями двух сомножителей и выражающих площадь прямоугольника, построенного на соответствующей паре отрезков;
2) «квадратные числа»: 4(= 2 • 2), 81 (= 9 • 9) и т.
д. Это название употребляется и поныне;
3) «телесные числа»: 24( = 2 • 3 • 4), 210( = 5 • 6 • 7) и т. д., являющиеся произведениями трех чисел и изображаемые с помощью параллелепипедов;
4) «кубические числа»: 8(=2 • 2 -2), 125(=5 • 5 • 5) и т.п.
Задание классу:
Представьте в виде квадрата числа
Это же задание формулируем по другому: «Какие числа удовлетворяют уравнениям
«Темринг» (к доске выходят три ученика, с каждого ряда по одному)
Задание: Найдите значение выражения, и записать на доске.
82 = 102 = 62 =
(-8)2 = (-10)2 = (-6)2 =
-82 = -102 = -62 =
Вопрос «как называются числа 82 и -82?» ( противоположными)
Эстафета 1
Ученики заполняют карточки, передавая друг другу (каждый заполняет только одну клетку).
а | 2 | 5 | 0,8 | 1,3 | -5 | |
а² |
|
|
|
|
|
|
а | 3 | 7 | 0,9 | 1,2 | -7 | |
а² |
|
|
|
|
|
|
а | 4 | 9 | 0,7 | 1,1 | -9 | |
а² |
|
|
|
|
|
|
3.
Подача нового материала.
Ещё в древности у египтян, из практической деятельности, возникла задача «Как, зная площадь поля квадратной формы, определить сторону?»
Пусть сторона квадрата х. Тогда х2 = S. Решим эту задачу с точки зрения математики. Зададим себе вопрос, например для уравнения х2 = 25, а каковы корни уравнения?
х1 = 5 т.к. 52 = 25, но и
х2 = -5 т.к. (-5)2 = 25.
5 и -5 называются квадратными корнями из числа 25;
7 и -7 называются квадратными корнями из числа 49;
0,3 и -0,3 называются квадратными корнями из числа 0,09 и т.п.
Даем определение квадратного корня из числа a.
Плакат 2.
Квадратным корнем из числа а называется число, квадрат которого равен а
Например:
Квадратным корнем из числа 81 есть числа 9 и -9,
так как 9² = 81 и (-9)² = 81.
Эстафета 2
Каждому ряду раздаем следующие карточки
Уравнение | х²=16 | х²=0,25 | х²=1,44 | х²=100 | х²= -9 | |
Корни уравнения | х1= х | х1= х2= | х1= х2= | х1= х2= | х1= х2= | х1= х2= |
Уравнение | х²=64 | х²=0,16 | х²=1,21 | х²=225 | х²= -16 | |
Корни уравнения | х 1=х2= | х1= х2= | х1= х2= | х1= х2= | х1= х2= | х1= х2= |
Неотрицательные корни этих уравнений принято называть арифметическим квадратным корнем из числа a.
Плакат 3.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а
Например:
— знак арифметического квадратного корня.
Выражение читают так: «квадратный корень из числа а ».
Знак арифметического квадратного корня впервые ввел в 1525 году немецкий математик Х.Рудольф.
Вводим знак радикала
И так = 10, т.к. 10 > 0 и 102 = 100.
= 4; = 12; =46; = 81.
Наименьшее число, которое может быть под корнем – это 0.
= 0
Арифметический квадратный корень из отрицательного числа не существует
— не определено
Практическая работа – как с помощью таблицы квадратов находить квадратные корни из чисел. Например:
= 81 = 810
= 8,1 = 8100
= 0,81 = ?
= 0,081 = ?
Последние два значения можно найти приближенно с помощью калькулятора.
Эстафета 3. Работа по нахождению арифметического квадратного корня из чисел.
а | 4 | 81 | 0,64 | 625 | 10,24 | |
|
|
|
|
|
|
a | 9 | 64 | 0,49 | 441 | 12,25 | |
|
|
|
|
|
|
а | 16 | 25 | 0,36 | 400 | 10,89 | |
|
|
|
|
|
|
4.
Динамическая пауза. ( Направлена на профилактику остеохондроза.)
Сесть на краешек стула.
Поднять руки, потянуться, напрячь мышцы.
Вытянуть руки перед грудью, потянуться.
Руки в стороны, потянуться, напрячь мышцы.
Обхватить себя руками, выгнуть спину.
Принять рабочее положение.
5. Закрепление материала.
Весь класс работает, в устной форме, с заданиями № 377, 378, 379(1,5,9,13).
Потом, всем классом, повторяем свойства арифметического квадратного корня.
Плакат 4
Из свойства арифметического квадратного корня имеем:
1) равенство = в имеет место, если
а) a 0 б) в2 = a;
2) если a < 0, то не имеет смысла.
6. Итоги урока. Рефлексия.
Оценивание результатов работы: устной, практической и с карточками.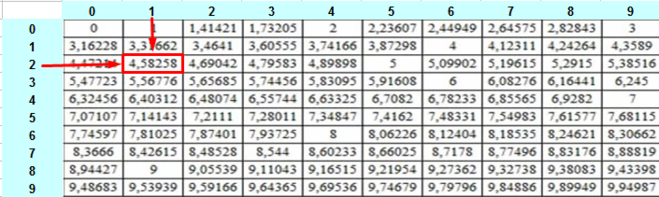
- Над какой темой мы сегодня на уроке работали?
- Трудным ли для тебя был материал урока?
- На каком из этапов урока было труднее всего, а на каком легче всего?
- Что нового ты узнал на уроке?
7. Домашнее задание § 12, № 380, 381, 382, 383.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Квадратный корень из 21 — Как найти квадратный корень из 21?
LearnPracticeDownload
Общее количество точек или сумма всех чисел на шестигранном кубике? Да – всего 21! Квадратный корень из числа получается путем возведения числа в половину степени.
В этой главе будет рассказано о том, как найти квадратный корень из 21 методом деления и методом среднего.
- Квадратный корень из 21: 4,582
- Площадь 21: 441
| 1. | Чему равен квадратный корень из 21? |
| 2. | Является ли квадратный корень из 21 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 21? |
| 4. | Часто задаваемые вопросы о квадратном корне из 21 |
Чему равен квадратный корень из 21?
- Квадратный корень из числа — это число, которое умножается на само себя, чтобы получить исходное число.
- √21= 4,582 × 4,582
- √21 = (21) ½ в экспоненциальной форме и √21 в простейшей радикальной форме.
Является ли квадратный корень из 21 рациональным или иррациональным?
- Число называется иррациональным, если оно не может быть выражено в виде отношения p/q, где q не равно 0.
- √21 = 4,58257569495584, что является неконечным десятичным числом. Таким образом √21 иррационально.
Как найти квадратный корень из 21?
Квадратный корень числа можно вычислить разными способами:
- Метод длинного деления
- Метод усреднения
√21 нельзя упростить дальше. Поэтому мы можем просто выразить это как √(7 × 3). Следовательно, мы не можем использовать метод простой факторизации для определения квадратного корня из 21.
Квадратный корень из 21 методом деления в длину
- Шаг 1: Запишите 21 как 21,000000. Теперь возьмите числа как пары справа. Слева у нас 21. Найдите число, которое при умножении само на себя дает 21 или меньше этого.
- Шаг 2: 4 × 4 = 16. Вычтите 16 из 21. Получите остаток как 5 и принесите одну пару нулей. Теперь новый дивиденд равен 500.
- Шаг 3: Умножьте частное 4 на 2. Получим 8. Получим 8 0 в качестве нового делителя. Выберите число, которое прибавлено к 80 и умножено на полученную сумму 500 или меньше.
- Шаг 4 : Мы находим, что 5, добавленное к 80, равно 85 и 85 × 5 = 425. Вычтите 425 из 500 и получите остаток как 75. Сократите следующую пару нулей. 7500 — это новый дивиденд.
- Шаг 5 : Умножьте частное 45 на 2. Получим 90. Получим 90 0 в качестве нового делителя. Выберите число, которое прибавлено к 900 и умножено на полученную сумму 7500 или меньше.
- Шаг 6: Мы находим, что 8 + 900 равно 908, а 908 × 8 = 7264. Вычтите 7264 из 7500 и получите остаток как 236. Сократите следующую пару нулей. 23600 — новый дивиденд.
- Повторяем процесс деления, пока не получим остаток.
- Таким образом, мы точно определили значение квадратного корня из 21 как 4,582.
Выберите число, которое прибавлено к 80 и умножено на полученную сумму 500 или меньше.Квадратный корень из 21 методом усреднения
- Значение √21 лежит между √16 и √25
- √16 < √21 < √25
- 4 < √21 < 5
- Делим 21 на 5. Получаем 21 ÷ 5 = 4,25
- Теперь найдите среднее значение частного и делителя на предыдущем шаге.
- ( 4,25 + 5 ) ÷ 2 = 9,25 ÷ 2 = 4,625
- √21 ≈ 4,625
- Таким образом, √21 лежит между двумя правильными квадратами, 4 и 5.
Получаем 21 ÷ 5 = 4,25Изучите квадратные корни с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 2
- Квадратный корень из 19
- Квадратный корень из 16
- Квадратный корень из 8
- Квадратный корень из 9
Важные примечания:
- √21 = 4,582 округлено до 3 знаков после запятой.
- √21 иррационально, так как это не идеальный квадрат.
- Используйте метод среднего, чтобы найти приблизительное значение √21, и метод деления, чтобы найти точное значение √21
Пример 1: Вычислить √21 + √28
Решение: √21 = √(7 × 3)
√28 = √(7 × 4)
90 906 √21 + √28 = √(7 × 3) + √(7 × 4)= √7 (3 + 4)
= √7 (7) = 7√7
√21 + √28 = 7√7
Пример 2 : Вычислить 3√12 ÷ 2√21
Решение:
3√12 = 3√(3 × 4) = 6√3
2√21 = 2 √(7 × 3) = 2 √7√3
3√12 ÷ 2√21 = 6√3 ÷ 2 √7√3
= 3√7
Пример 3 : Квадратный цветник имеет площадь 21 кв.
Какова длина одной стороны сада?Площадь = сторона × сторона кв. ед.
Сторона 2 = 21
Сторона = √21
Сторона = 4,582 единицы
Какова длина одной стороны сада?перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 21
Что такое квадратный корень из 21?
Таким образом, квадратный корень из 21 равен 4,58257569495584.
Является ли квадратный корень из 21 отрицательным 4,58257569495584?
Квадратный корень из 21 означает число, которое при умножении само на себя дает произведение равное 21.
√21 = √( 4,58257569495584 × 4,58257569495584), а также = √(- 4,58257569495584 × — 4,58257569495584)
Таким образом, отрицательное число 4,58257569495584 также является квадратным корнем из 21.