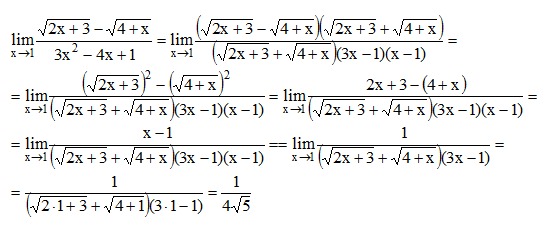Корень из 4 3x x: Решить ответ под корнем 4-3x =x

2

Показательные уравнения нестандартного вида

Показательные уравнения нестандартного вида

Пример №1

5^2x2-1-3*5^(x+1)(x+2)-2*5^6(x+1)=0

Раскроем скобки в показателях степеней:

5^2x2-1-3*5^x2+3x+2-2*5^6x+6=0

Вынесем 5^6x+6 за скобки:

5^6x+6*(5^2x2-6x-7-3*5^x2-3x-4-2)=0

5^6x+6=0

5^2x2-6x-7-3*5^x2-3x-4-2=0

Выражение 5^6x+6=0 не имеет решения, т.к. aⁿ≠0. Представим 5^2x2-6x-7 как 5^2(x2-3x-4)+1 и обозначим 5^x2-3x-4 переменной t. Получим:

5t²-3t-2=0

По теореме Виета получим корни:

t₁=1

t₂=-2/5

Корень t₂=-2/5 не будет удовлетворять уравнению, т. к. положительное число в любой степени больше нуля. Подставим вместо t — 5^x2-3x-4

5^x2-3x-4=1

Заметим, что 1=5⁰

5^x2-3x-4=5⁰

Приравниваем показатели:

x²-3x-4=0

D=9+16=25, D>0, следовательно, уравнение имеет два действительных корня:

x₁=(3-5)/2=-1

x₂=(3+5)/2=4

Ответ: x=-1 и x=4.

Пример №2

5^x/(√x+2)*0,2^4/(√x+2)=125^x-4*0,04^x-2

Напишем сразу ОДЗ: x≥0, т.к. D(√)=R+ U 0

Заметим, что 0,2^4/(√x+2)=5^{-1(4/(√x+2))}=5^-4/(√x+2); 125^x-4=5^3(x-4)=5^3x-12; 0,04^x-2=5

-2(x-2)=5^4-2x

Обозначим √x переменной t>0

5^t2/(t+2)*5^-4/(t+2)=5^3t2-12*5^4-2t2

Отметим, что t≠0, т. к. деление на 0 не определено. При умножении складываем показатели степеней:

5^(t2-4)/(t+2)=5^t2-8

Приравниваем показатели степеней

(t²-4)/(t+2)=t²-8

(t²-4) по формуле квадрат разности будет (t+2)*(t-2)

Упростим:

(t+2)*(t-2)/(t+2)=t²-8

Получим:

t-2=t²-8

Перенесем все члены в правую часть уравнения:

t²-t-6=0

D=1+24=25, D>0, следовательно, уравнение имеет два действительных корня.

t₁=(1+5)/2=3

t₂=(1-5)/2=-2

t₂=-2 не удовлетворяет уравнению, т.к. в случае 5^(t2-4)/(t+2)=5^t2-8 при t=-2 (t+2)=0, а деление на 0 не определено. Подставим вместо t — √x

√x=3

Возведем левую и правую часть уравнения в квадрат:

x=9

Ответ: х=9.

Пример №3

3*4^x+(1/3)*9^x+2=6*4^x+1-(1/2)*9^x+1

Перенесем 3*4^x в правую часть уравнения, а (1/2)*9^x+1 — в левую:

(1/3)*9^x+2+(1/2)*9^x+1=6*4^x+1-3*4^x

В левой части уравнения 9^x+1 вынесем за скобки, а в правой — 4^x :

9^x+1 * (1/3 * 9 + 1/2)=4^x * (6*4-3)

Сложив действия в скобках, получим:

7/2 * 9

x+1=4^x*21

Поделим левую и правую часть уравнения на 21/2 :

9^x+1 * 1/3=4^x*2

Заметим, что 9^x=3^2x,4^x=2^2x и 1/3=3^-1

3^2x+2*3^-1=2^x*2

Сложим показатели степеней при умножении:

3^2x+1=2^2x+1

3^2x+1=2^2x+1 лишь в том случае, если 2^x+1=0, т. к. любое число в нулевой степени — 1.

2x+1=0

2x=-1

x=-1/2

Ответ: x=-1/2

Пример №4

49^1+√x-2-344*7^√x-2=-7

Напишем сразу ОДЗ: x-2≥0, т.к. D(√)=R+ U 0, следовательно, x≥2

Представим 49^1+√x-2 как 7^2√x-2*49 и перенесем -7 в левую часть уравнения с противоположным знаком:

7^2*√x-2*49-344*7^√x-2+7=0

Обозначим 7^√x-2 переменной t>0, т.к. положительное число в любой степени больше нуля.

49t²-344t+7=0

D=118336-1372=116964, D>0, следовательно, уравнение имеет два действительных корня:

t₁=(344-342)/108=1/49

t₂=(344+342)/108=7

t₁=1/49 не удовлетворяет уравнению, т.к. t должно быть больше 0 . Подставим вместо t — 7^√x-2

7^√x-2=7

Приравниваем показатели:

√x-2=1

Возведем левую и правую часть уравнения в квадрат:

x-2=1

Перенесем -2 в правую часть уравнения с противоположным знаком:

x=3

Ответ: х=3

Пример №5

(0,25)^|x|*√(3)^2x2-8-(27/4)^|x|=0

Представим (0,25)^|x| как(1/4)

|x|, √(3)^2x2-8 как 3^x2-4, а (27/4)^|x| как 3^3|x|*(1/4)^|x|:

(1/4)^|x|*3^x2-4-3^3|x|*(1/4)^|x|=0

Вынесем (1/4)^|x| за скобки:

(1/4)^|x|*(3^x2-4-3^3|x|)=0

Получим:

(1/4)^|x|

3^x2-4-3^3|x|=0

(1/4)^|x| не удовлетворяет, т. к. любое положительное число в любой степени больше нуля.

Модуль раскроется в двух случаях:

A. a≥0

B. a<0.

Рассмотрим случай A:

3^x2-4-3^3x=0

Перенесем 3^3x в правую часть уравнения с противоположным знаком:

3

x²-4=3^3x

Приравниваем показатели:

x²-4=3x

Перенесем 3x в левую часть уравнения с противоположным знаком:

x²-3x-4=0

По теореме Виета получим корни:

x₁=4

x₂=-1

Корень t₂=-1 не будет удовлетворять уравнению, т.к. мы оговорили, что a≥0.

Рассмотрим случай B:

3^x2-4-3^-3x=0

Перенесем 3^-3x в правую часть уравнения с противоположным знаком:

3^x2-4=3^-3x

Приравниваем показатели:

x²-4=-3x

Перенесем 3x в левую часть уравнения с противоположным знаком:

x²+3x-4=0

По теореме Виета получим корни:

x₁=-4

x₂=1

Корень t₂=1 не будет удовлетворять уравнению, т.

к. мы оговорили, что a<0.

Ответ: х=4 и х=-4

Пример №6

(25^x2-5^x2)√-x=5^2x2+1-5^x2+1+20√-x-100

Напишем сразу ОДЗ: √-x≥0, т.к. D(√)=R+ U 0, следовательно, -x≥0, тогда x≤0.

Представим 25^x2 как 5^2x2:

(5^2x2-5^x2)√-x=5^2x2+1-5^x2+1+20√-x-100

Вынесем 5^x2, 20 и 5^x2+1 за скобки:

5^x2(5^x2-1)√-x=5^x2+1(5^x2-1)+20(√-x-5)

Перенесем 5^x2+1(5^x2-1)+20(√-x-5) в левую часть уравнения с противоположными знаками:

5^x2(5^x2-1)√-x — 5^x2+1(5^x2-1)-20(√-x-5)=0

Вынесем 5^x2(5^x2-1) за скобки:

5^x2(5^x2-1)(√-x-5)-20(√-x-5)=0

Вынесем (√-x-5) за скобки:

(√-x-5)(5^x2(5^x2-1)-20)=0

(√-x-5)=0

(5^x2(5^x2-1)-20)=0

Решим их по отдельности:

(√-x-5)=0

Перенесем -5 в правую часть уравнения с противоположным знаком:

√-x=5

Возведем левую и правую часть уравнения в квадрат:

-x=25

Домножим левую и правую часть уравнения на -1:

x=-25

(5^x2(5^x2-1)-20)=0

Раскроем скобки:

5^2x2-5^x2-20=0

5^x2 обозначим переменной t, тогда 5^2x2 будет t

2:

t²-t-20=0

Получили квадратное уравнение:

D=1+80=81, D>0, следовательно, уравнение имеет два действительных корня

t₁=(1+9)/2=1

t₂=(1-9)/2=-4

Корень t₂=-4 не будет удовлетворять уравнению, т. к. любое положительное число в любой степени больше нуля.

Подставим вместо t — 5^x2:

5^x2=1

Заметим, что 5⁰=1:

5^x2=5⁰

Приравним показатели:

x²=0

x=0

Ответ: x=0 и x=-25

Пример №7

(3-2√2)^x2-2x+2+(17+√288)^0,5*x2-x+1=6

Заметим, что (17+√288)^0,5*x2-x+1=(3+2√2)^{2(0,5*x2-x+1)}

(3-2√2)

x²-2x+2+(3+2√2)^{2(0,5*x2-x+1)}=6

Раскроем скобки в показателе степени 2(0,5*x²-x+1)

(3-2√2)^x2-2x+2+(3+2√2)^x2-2x+2=6

Введем подстановку: (3-2√2)^x2-2x+2 обозначим переменной t. А (3+2√2)^x2-2x+2 домножим на сопряженные и получим:

((3+2√2)^x2-2x+2*(3-2√2)^x2-2x+2)/(3-2√2)^x2-2x+2=(3²-2√2²)^x2-2x+2=(9-8)^x2-2x+2/(3-2√2)^x2-2x+2=1^x2-2x+2/(3-2√2)^x2-2x+2=1/(3-2√2)^x2-2x+2

Следовательно, 1/(3-2√2)^x2-2x+2=1/t:

t+1/t=6

Отметим, что t≠0, т. к. деление на 0 не определено. Домножим левую и правую часть на t:

t2+1=6t

Перенесем 6t в левую часть уравнения с противоположным знаком:

t2-6t+1=0

Решим квадратное уравнение:

D=36-4=32, D>0, следовательно, уравнение имеет два действительных корня. Отметим, что √32=4√2

t₁=(6+4√2)/2=3+2√2

t₂=(6-4√2)/2=3-2√2

Заменим t₁ на (3-2√2)^x2-2x+2

3+2√2=(3-2√2)^x2-2x+2

Домножим 3+2√2 на сопряженные и получим:

(3+2√2)*(3-2√2)/(3-2√2)=(9-8)/(3-2√2)=1/(3-2√2)

Следовательно:

1/(3-2√2)=(3-2√2)^x2-2x+2

Заметим, что 1/(3-2√2)=(3-2√2)^-1

Следовательно:

(3-2√2)^-1=(3-2√2)^x2-2x+2

Приравняв показатели, получим:

-1=x²-2x+2

Перенесем -1 в правую часть уравнения с противоположным знаком:

x²-2x+3=0

D=4-8=-4, D<0, следовательно, уравнение не имеет действительных корней

Заменим t₂ на (3-2√2)^x2-2x+2

3-2√2=(3-2√2)x2-2x+2

Приравняв показатели, получим:

1=x²-2x+2

Перенесем 1 в правую часть уравнения с противоположным знаком:

x²-2x+1=0

Сложив формулу, получим:

(x-1)²=0

Следовательно:

x-1=0

Перенесем -1 в правую часть уравнения с противоположным знаком. Получим:

x=1

Ответ: x=1

<< Назад ] [ Начало ] [ Вперед >>

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Квадратный корень из 43 — Как найти квадратный корень из 43?

LearnPracticeDownload

Квадратный корень из 43 выражается как √43 в радикальной форме и как (43) ^½ или (43) ^0,5 в экспоненциальной форме. Квадратный корень из 43, округленный до 8 знаков после запятой, равен 6,55743852. Это положительное решение уравнения x ² = 43.

• Квадратный корень из 43: 6,557438524302 909:20
• Квадратный корень из 43 в экспоненциальной форме: (43) ^½ или (43) ^0,5
• Квадратный корень из 43 в подкоренной форме: √43

1.	Что такое квадратный корень из 43?
2.	Является ли квадратный корень из 43 рациональным или иррациональным?
3.	Как найти квадратный корень из 43?
4.	Часто задаваемые вопросы о квадратном корне из 43

Что такое квадратный корень из 43?

Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число. Например, квадратный корень из 25 равен 5, так как 5 умножить на 5 дает 25, что делает его идеальным квадратом. Однако у вас также могут быть квадратные корни некоторых чисел, которые не дают целых чисел, например 43. Мы можем выразить квадратный корень из 43 разными способами:

• Десятичная форма: 6,557
• Радикальная форма: √43 909:20
• Форма экспонента: (43) ^1/2

Является ли квадратный корень из 43 рациональным или иррациональным?

• 43 — это число, которое не является полным квадратом, то есть не имеет натурального числа в качестве квадратного корня.
• Кроме того, его квадратный корень не может быть выражен как дробь формы p/q, что говорит нам о том, что квадратный корень из 43 является иррациональным числом.

Как найти квадратный корень из 43?

Поскольку мы пришли к выводу, что квадратный корень из 43 не является конечным, мы можем использовать только 2 метода для вычисления значения его квадратного корня 9.0907

• Метод длинного деления
• Метод оценки и приближения

Метод длинного деления

• Шаг 1: Начиная справа, мы соединим цифры 43, поставив над ними черту. Мы также соединяем 0 в десятичных дробях парами по 2 слева направо.
• Шаг 2: Задумайте число, квадрат которого меньше или равен 43. В этом случае это число будет 6.
• Шаг 3: Разделив 43 на 6 с частным равным 6, мы получим остаток 7.  909:20
• Шаг 4: Перетащите пару нулей вниз и закрасьте их рядом с 7, чтобы получить делимое 700. 
• Шаг 5: Делитель, в данном случае 6 удваивается и записывается ниже. Теперь у нас есть 12X в качестве нового делителя, и нам нужно найти значение X, при котором произведение 12X × X меньше или равно 700. В этом случае 125 — это требуемое значение 90 920.
• Шаг 6: Число 5 ставится в частном после запятой. Новый делитель для следующего деления будет 125 + 5 = 130. 909:20

Действуя таким же образом и повторяя шаг 4, мы можем вычислить остальные десятичные дроби.

Таким образом, квадратный корень из 43 = 6,557

Метод оценки и аппроксимации

Метод оценки дает приблизительный ответ и обычно имеет точность не более 1 знака после запятой. Тем не менее, это легко выполнить, как видно из ниже.

• Шаг 1: Найдите идеальный квадрат, который меньше и больше 43. В этом случае 6 и 7 будут работать, так как их квадраты равны 36 и 49..
• Шаг 2: Запись в терминах неравенства- 6 < √43 < 7 = 36 < 43 < 49
• Шаг 3: Умножьте на 100 и запишите в виде квадратных корней: √3600 < √4300 < √4900
• Шаг 4: Приблизиться к неравенству- √4225 < √4300 < √4356 = 65 < 10√43 < 66 = 6,5 < √43 < 6,6
• Шаг 5: Взяв среднее значение верхнего и нижнего пределов, получим (6,5 + 6,6)/2 = 6,55

Следовательно, мы можем оценить квадратный корень из 43 ≅ 6,55

Исследуйте Квадратный корень с помощью иллюстраций и интерактивных примеров

• Квадратный корень из 41
• Квадратный корень из 42
• Квадратный корень из 44
• Квадратный корень из 45
• Квадратный корень из 343

Наводящие вопросы

• Определите значение следующего:
  • √0,43
  • √4343
• Каковы корни числа -43? Также найдите значение квадрата отрицательного корня из -43. 909:20

Важные примечания

• Действительные корни √43 равны ± 6,557.
• В квадратном корне из четного числа, состоящего из n цифр, будет n/2 цифр.
• В квадратном корне из нечетного числа с n цифрами будет (n+2)/2 цифр.

 

1. Пример 1: Энди хочет вычислить длину стороны квадрата, который он сделал на уроке декоративно-прикладного искусства. Его площадь составляет 43 квадратных дюйма. Помогите ему найти длину, округлив до десятых.

   Решение:

   Чтобы найти сторону земли, нам нужно найти квадратный корень из 43. Квадратный корень равен √43 = 6,557.
   Следовательно, длина стороны сада составляет примерно 6,6 дюйма.

2. Пример 2: Какова длина окружности, площадь которой равна 43π дюймов ² ?

   Решение:

   Обозначим длину окружности через C, площадь через A и длину радиуса через r.
   С = 2πr
   А = πr ²
   43π = πr ²
   Упрощая, получаем, что r ²  = 43, откуда следует, что r = √43
   C = 2πr = 2π × √43 = 41,20 дюйма.

   Следовательно, длина окружности составляет около 41,20 дюйма.

3. Пример: Если площадь круга равна 43π в ² . Найдите радиус окружности.

   Решение:

   Пусть ‘r’ будет радиусом окружности.
   ⇒ Площадь круга = πr ² = 43π в ²
   ⇒ г = ±√43 в
   Поскольку радиус не может быть отрицательным,
   ⇒ г = √43
   Квадратный корень из 43 равен 6,557.
   ⇒ г = 6,557 в

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных эффектов.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о квадратном корне из 43

Каково значение квадратного корня из 43?

Квадратный корень из 43 равен 6,55743.