Матрицы для чайников и действия над ними: умножение, сложение, вычитание. Как решать, с чего начать

Содержание

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Линейная алгебра. (Вектора, матрицы) / / Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

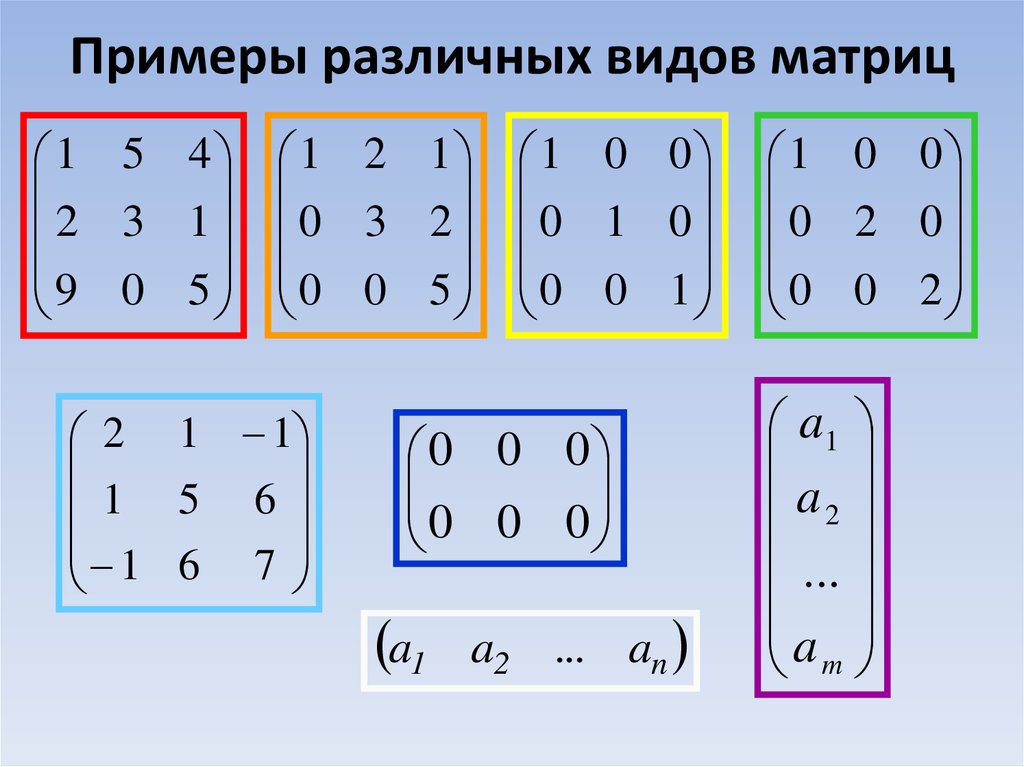
Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел — матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин «матрица» появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m — строк и n — столбцов.

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,…, a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,…,m; j=1,2,…,n)

Действия над матрицами.

1. Сложение матриц — поэлементная операция

2. Вычитание матриц — поэлементная операция

3. Произведение матрицы на число — поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент

с_ijматрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.

е.

Покажем операцию умножения матриц на примере

5. Возведение в степень

m>1 целое положительное число. А — квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A’

Строки и столбцы поменялись местами

Пример

Свойства опрераций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A’)’=A

(λA)’=λ(A)’

(A+B)’=A’+B’

(AB)’=B’A’

Виды матриц

1. Прямоугольные: m и n — произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) — во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2,…,m

j=1,2,…,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симметрическая матрица: m=n и a_ij=a_ji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A

Например,

10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a_ii=-a_ii)

Пример.

Ясно, A’=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji— комплексно — сопряженное к a_ji, т.е. если

A=3+2i, то комплексно — сопряженное Ã=3-2i)

Пример

Дополнительная информация от TehTab.ru:

Матрицы и действия над ними

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Тема 1. «Матрицы и действия над ними»

Основные понятия:
1. Определение матрицы
2. Виды матриц
3. Действия над матрицами
4. Перестановочные матрицы
завершить
1. Определение матрицы
Прямоугольная таблица чисел вида
à11
à
21
À
…
àm1
à12
à22
…
àm 2
… à1n
… à2 n
… …
… àmn
называется матрицей.
— элементы матрицы.
àij
Размер матрицы
Главная диагональ матрицы
Побочная диагональ матрицы
назад
2. Виды матриц
Прямоугольная
Квадратная
Нулевая
Единичная
Диагональная
Симметричная
Вырожденная
Равные
Треугольная
Квазитреугольная (ступенчатая или трапециевидная)
Матрица-строка или строчная матрица
Матрица-столбец или столбцевая матриц
назад
Матрица называется прямоугольной, если количество ее
строк не совпадает с количеством столбцов:
1
À
0
2
3
2
0
3
5
Матрица называется квадратной, если количество ее строк

совпадает с количеством столбцов:
7 45
À
1 0
назад
Матрица называется нулевой, если все ее элементы нулевые :
0 0 0
À
0 0 0
Квадратная матрица называется единичной, если элементы
по главной диагонали единицы, а остальные элементы
нулевые :
1 0 0
À 0 1 0
0 0 1
назад
Квадратная матрица называется диагональной, если
элементы по главной диагонали отличны от нуля, а
остальные элементы нулевые:
2 0 0
À 0 3 0
0 0 1
Квадратная матрица называется симметричной, если
относительно главной диагонали для всех ее элементов
выполняется условие
:
aij a ji
1 0 1
À 0 2 77
1 77 3
назад
Квадратная матрица называется вырожденной, если ее
определитель равен нулю.

Матрицы А и В (одинаковых размерностей) называются
равными, если aij :bij

1
À 13
2
3
0
7
1
B 13
2
3
0
7
назад
Квадратные матрицы вида
a1n
a11
или
a
0
n1
называются треугольными.
1 2 3
À 4 5 0
6 0 0
a11
0
1
0
À
0
0
a1n
ann
4
5 6 7
0 8 9
0 0 10 назад
2 3
Прямоугольная матрица вида
a11
0
0
a12
a1m
a22
a2 m
0
amm
a1n
a2 n
amn
называется квазитреугольной (ступенчатая или
трапециевидная)
1
À 0
0
2
1
0
3
2
2
3
1
0
3
3
1
1
0
5
назад
Матрица, состоящая из одной строки называется матрицейстрокой или строчной матрицей.
À 1 2 3 0
Матрица, состоящая из одного столбца называется
матрицей-столбцом или столбцевой матрицей
2
À 0
2
назад
Операции над матрицами
Линейные:
1) Сумма (разность) матриц;
2) Произведение матрицы на число.

Нелинейные:
1) Транспонирование матрицы;
2) Умножение матриц;
3) Нахождение обратной матрицы.
назад
Суммой (разностью) двух матриц одинаковой
размерности называется матрица, элементы которой
равны сумме (разности) соответствующих элементов
матриц слагаемых.
Например:
à11 à12 à13
b11 b12 b13
À
, B
à21 à22 à23
b21 b22 b23
à11 b11 à12 b12 à13 b13
A B
à21 b21 à22 b22 à23 b23
Пример
назад
Пример
2
À 0
4
3
5
4 , B 7
2
9
6
0
1
A B ?
A B ?
B A ?
Ответ
назад
Произведением матрицы на число называется матрица,
полученная из данной умножением всех ее элементов
на число.
Например:
à11 à12 à13
À
à21 à22 à23
à11 à12 à13
à21 à22 à23
Пример

назад
Линейные операции обладают следующими свойствами:
1) A B B A
2) A B C A B C
3) A 0 A
4) A A 0
5) 1 A A
6) A A
7) A B A B
8) A A A
Матрица, полученная из данной заменой каждой ее
строки столбцом с тем же номером, называется
матрицей, транспонированной относительно
данной.

Например:
à11 à12 à13
À
,
à21 à22 à23
à11 à21
T
A à12 à22
à
à
23
13
Свойства
назад
Умножение матриц определяется для согласованных
матриц.
Произведением матрицы Àm n àij на матрицу
Bn k bij называется матрица Cm k cij , для
которой cij ai1 b1 j ai 2 b2 j … ain bnj ,
т.е. каждый элемент матрицы С равен сумме
произведений элементов i-й строки матрицы А
на соответствующие элементы j-го столбца
матрицы В.
Например
Свойства
назад
Например:
b11
à11 à12 à13
b21
à21 à22 à23 b
31
à11 b11 à12 b21 à13 b31
à21 b11 à22 b21 à23 b31
Пример
назад
В случае, когда АВ=ВА, матрицы А и В называют
перестановочными или коммутативными.
Пример 1. Найти все перестановочные матрицы к матрице
1 2
À
0 3
Пример 2. Найти все перестановочные матрицы к матрице
2 4
À
1 0
назад
Ответ:
3
A B 7
6
7
A B 7
2
7
B A 7
2
9
4
10
3
4
8
3
4
8
назад
Пример
2
À 0
4
3
5
4 , B 7
2
9
6
0
1
2A ?
3 B ?
4B 7 A ?
Ответ
назад
Ответ:
4 6
2A 0 8
8 18
15 18
3B 21 0
6
3
34 3
4 B 7 A 28 28
20 59
назад
Свойства операции транспонирования:
1) A
T T
A
2) A B A B
T
T
T
3) A B B A
T
T
T
назад
Матрица А называется согласованной с
матрицей В, если число столбцов матрицы А
равно числу строк матрицы В:
Например:
1)
Àm n ,
Bn k
2)
À2 4 ,
B4 1
3)
Àm 2 ,
B2 k
назад
Пример
2
À 0
4
A B ?
3
1 2
4 , B
0 3
9
B A ?
A B ?
B A ?
A B ?
B AT ?
T
T
T
T
T
Ответ
назад
Ответ:
2
À 0
4
3
1 2
4 , B
0
3
9
2 5
A B 0 12
4 35
T
T
B A,
A B,
B A,
2
B A
5
T
T
0
12
A B
T
T
í åâî çì î æí î
4
35
назад
Свойства операции умножение матриц:
1.

Свойство сочетательности или ассоциативности
AB C A BC
2.
AB A B A B
3.
Свойство распределительности (дистрибутивности)
справа и слева относительно сложения матриц
A B C AC BC
C A B CA CB
назад
Решение (Пример 1):
a b
1) B
общий вид всех перестановочных матриц
c d
2) Применим определение перестановочных матриц
AB=BA:
1 2 a b a 2c b 2d
ÀB
3d
0 3 c d 3c
a b 1 2 a 2a 3b
BA
c d 0 3 c 2c 3d
Получаем: a 2c
3c
b 2d a 2a 3b
3d c 2c 3d
3) По определению равных матриц
a 2c a
a R
b 2d 2a 3b b a d
3c c
c 0
3d 2c 3d
d R
4) Общий вид всех перестановочных матриц
a a d
B
d
0
5) Проверка
назад
Ответ:
4c
a
B
c 2c a
d 2c 4c
или B
d
c
a
2d 2a
или B
0,5
d
0,5
a
d
назад
Спасибо за внимание!
(Тема следующей лекции «Определители»)

English Русский Правила

Руководство для начинающих по матрице решений в управлении проектами

Успех бизнеса заключается в принятии правильных решений в нужное время. Хорошие решения могут полностью решить или разрушить ваш бизнес, они могут либо направить вашу команду к правильному решению и достичь ваших целей, либо просто разбить вашу бизнес-машину с невосполнимыми потерями.

Итак, как вы принимаете эти решения? Бросить монетку? Бросить кости? Или просто довериться своей интуиции и следовать ей? Принятие решений является одной из наиболее важных частей хорошего бизнес-планирования, однако может быть довольно сложно понять, какой вариант является лучшим и какой из них следует использовать. Ключ в том, чтобы быть очень быстрым, не сомневаясь, принимая правильное решение.

Звучит как невыполнимая задача? Не волнуйтесь, даже если это немного хлопотно, мы разобьем его на более мелкие части, чтобы вам было очень легко понять и реализовать. С помощью матрицы решений вы можете удобно рассмотреть все за и против каждого решения, взвесить различные переменные и быстро и легко принять правильное решение.

Прежде чем мы узнаем все о матрице решений, важно знать, что это такое!

Что такое матрица решений?

Матрица решений — это тип значений, представленных в строках и столбцах, которые позволяют визуально сравнивать возможные решения, просто взвешивая переменные в зависимости от их важности. Это инструмент для тщательной оценки и выбора наилучшего из возможных вариантов.

Этот инструмент обычно используется, если вы путаетесь между несколькими вариантами и есть несколько вариантов, которые вы должны рассмотреть, чтобы принять окончательное решение. Существует несколько других названий матрицы решений, таких как матрица Пью, анализ сетки, теория полезности с несколькими атрибутами, а также матрица выбора проблемы и сетка решений.

Матрица решений не только помогает выбрать наилучший план действий для бизнеса, но также помогает расставлять приоритеты в задачах, решать проблемы и создавать аргументы для простой защиты уже принятого решения. Это наиболее полезно, когда вы ищете решение с логической и практической точки зрения, и у вас есть более одной переменной для взвешивания и сравнения. Чтобы создать такую матрицу, вы должны определить, какие критерии важны для окончательного выбора, а затем присвоить им вес для оценки.

Давайте проверим это с дополнительными подробностями и определим, когда вы должны и не должны использовать матрицу решений.

Рекомендуемое чтение:

Как использовать матрицу оценки рисков в управлении проектами?

Когда использовать матрицу решений, а когда нет?

Как обсуждалось выше, матрица решений не только помогает в принятии сложных решений, но также помогает расставить приоритеты задач и разработать решение для защиты решения, которое вы уже придумали. Однако вам не всегда нужно использовать матрицу решений.

Если ваши критерии оценки не ограничивают вас в выборе между двумя переменными, то матрица решений может быть не лучшим выбором. Например, это не позволит вам решить, в каком направлении должна двигаться ваша команда в предстоящем году, поскольку вещи, которые вы выбираете, несопоставимы. Вот несколько случаев, когда у вас должна быть матрица решений, например:

Сравнение нескольких вариантов или выбор между переменной
Сужение нескольких вариантов для выбора окончательного решения
Взвешивание множества важных факторов
Принятие решения с логической точки зрения, а не интуитивное чувство или эмоциональное/интуитивное решение.

Если вы считаете, что матрица принятия решений не соответствует ситуации в вашем бизнесе, узнайте о других формах подходов к принятию решений ниже.

Как создать матрицу решений?

Матрица решений помогает легко оценить лучший вариант между различными вариантами, основываясь на множестве факторов и их относительной важности. Вот шаги, необходимые для правильного создания матрицы решений.

1. Четко обозначьте проблему

Первый шаг — просто вставить решение, которое предполагается принять, или вопрос, который необходимо решить, в поле решения. Это утверждение должно быть четко определено и понятно каждому.

Давайте рассмотрим практический пример: вам нужно сделать выбор между ремонтом вашего старого офиса или просто переездом в новое обставленное здание. Задайте правильный вопрос и поместите его в поле решения для просмотра.

2. Определите все факторы принятия решений

На этом этапе вам необходимо провести мозговой штурм по критериям выбора решений, которые необходимо принять для этой матрицы. Короче говоря, необходимо ответить на все вопросы, какие факторы необходимы, чтобы помочь принять правильное решение? Или, каковы критические факторы успеха, которые должны быть соблюдены, чтобы принять решение?

В примере, приведенном на вышеупомянутом этапе, факторы, которые будут иметь огромное влияние на эти решения,

Как быстро мы сможем вернуть данные инвестиции? Чем раньше, тем лучше.
Каковы денежные потоки и как каждый из этих вариантов повлияет на денежные потоки компании в банке?
Всегда следите за временем — сколько времени теряется в каждом сценарии?

Этот набор критериев в процессе поможет вам определить наилучшее решение и избежать любой субъективности.

3. Добавить альтернативные варианты

Теперь пришло время добавить различные доступные варианты для их сравнения, другими словами, это решение существующей проблемы. В нашем примере у нас есть два варианта:

Переезд в новый офис
Реконструкция старого существующего офиса

4.

Создание матрицы решений

Матрица решений представляет собой сетку, в которой вы можете легко сравнить все существенные соображения между различными заданными вариантами. Естественно, вы даже можете построить эти матрицы решений с помощью nTask, это инструмент управления задачами и работой, который поможет вам организовать и выполнить работу в нескольких организациях и повысить эффективность и производительность в командах.

5. Присвойте вес каждому из ваших факторов принятия решения

Матрица рисков в nTask

Это основа любого решения, некоторые факторы всегда будут иметь более высокий приоритет по сравнению с другими переменными, по этой причине вам необходимо присвоить веса каждому из данные факторы. Каждому фактору принятия решения необходимо присвоить балл от 1 до 5, где 1 означает наименее важный при минимальной важности, а 5 — при максимальном приоритете.

Крайне важно не придавать каждому фактору принятия решения одинаковый вес, иначе анализ не будет проведен идеально и будет много лазеек, что затруднит принятие решения. Если вам трудно найти оценку, лучшим решением будет расширить шкалу от 1 до 10, чтобы оценить каждую переменную еще более тщательно.

6. Добавьте баллы для каждого из вариантов

Тот же процесс, который выполнялся ранее, теперь будет выполняться в отношении каждого из вариантов. Опять же, вы должны установить оценку от 1 до 5, и, если этого просто недостаточно, вы можете легко использовать шкалу от 1 до 10 для суммирования оценок.

Это фундаментально, потому что некоторые соображения важнее других. Вот почему вам нужно использовать взвешенную матрицу решений, чтобы определить лучший вариант для вас.

Умножьте взвешенные баллы

После того, как вы применили все свои рейтинговые шкалы и успешно присвоили вес каждому из соображений, умножьте вес на каждое из соображений. Это гарантирует, что более важным соображениям будет придан больший вес, что поможет выбрать лучшее агентство.

Примените взвешенную оценку к количеству альтернатив, выбранных вами для каждого из заданных вариантов.

Подсчитать общий балл

После того, как результаты были определены на основе всех факторов и для каждого из доступных вариантов, следующим шагом будет выбор победителя с наибольшим количеством очков.

Теперь, когда вы суммировали все оценки и соображения для каждой альтернативы, у вас должна быть четкая картина основанного на числах ответа, на который решение является лучшим.

Матрица решений Выводы

И последнее, но не менее важное: матрица решений упрощает измерение и взвешивание вариантов по сравнению с тем, что важно, и, прежде всего, делает это объективно и прагматично. Этот процесс устраняет всю сложность анализа, и решения гораздо легче принимать, когда все упрощается.

Проще говоря, матрица решений позволяет сосредоточиться на том, что действительно важно и что должно быть приоритетным. Также важно помнить, что матрица решений — не единственный доступный инструмент, например, иногда вам подойдет обычный список плюсов и минусов. Этот подход используется не только в управлении проектами, но и в повседневном жизненном цикле, чтобы принимать более обоснованные решения, избегая при этом всевозможных типичных предубеждений и осложнений, в которые время от времени впадают почти все мы.

Альтернативные матрицы принятия решений

Несмотря на то, что это может быть невероятно полезно для принятия бизнес-решений, описанная выше матрица решений не является единственным вариантом для оценки того, следует ли идти влево или вправо. Давайте взглянем на несколько других матриц, которые вы можете использовать для принятия решений.

1. SWOT-анализ

SWOT-анализ — это простой бизнес-инструмент, который используется для принятия решений на основе внутренних и внешних факторов компании. Это должно быть выполнено глубоко, с привлечением ключевых членов команды, которые имеют разные взгляды на бизнес, чтобы гарантировать, что анализ будет очень всесторонним.

SWOT-анализ состоит из четырех элементов, где сильные и слабые стороны — это внутренние факторы, которые вы можете легко контролировать, а возможности и угрозы — это отдельные факторы, которые необходимо контролировать.

2. Анализ силового поля

Для всех бизнес-лидеров, которые пытаются найти первопричину любой проблемы, обычно связанной с процессом или рабочим процессом, анализ силового поля поможет выявить причину и помочь в разработке решений . Чтобы провести анализ силового поля, вам нужно решить, каким будет желаемый результат, будь то цель, видение или лучшее понимание текущей ситуации.

Затем в параллельных столбцах нужно поставить цель и перечислить движущие и сдерживающие силы, противодействующие ей. Разработайте стратегию изменений, которые вам необходимо внести в эти силы, а затем расставьте приоритеты этих изменений по отношению к конечной цели.

Делать выводы теперь намного проще!

Принятие быстрых и разумных решений является неотъемлемой частью любой хорошей системы планирования проектов и управления проектами. Независимо от того, используете ли вы матрицу решений для принятия сложного или простого решения, эти вышеупомянутые инструменты помогут вам выбрать альтернативы между различными факторами и легко принять лучшее решение для вашей команды.

Итак, в следующий раз, когда вы окажетесь в ментальном блоке, не в состоянии решить и выбрать между двумя вариантами, вытащите свою матрицу и начните чередовать варианты. Освободитесь от обычно предвзятых решений менеджеров и заинтересованных сторон и принимайте власть только с логической точки зрения.

См. также:

Все, что вам нужно знать о S-Curve
Что такое Team App? – Все, что вам следует знать об этом
Руководство по матричной организационной структуре на 2022 год
4 квадранта матрицы управления временем
Полезное руководство по матрице прослеживаемости требований
Вся новая матрица рисков, настраиваемые поля рисков и многое другое
Что такое матрица Эйзенхауэра? Как им пользоваться
Что такое метод MoSCoW и как он помогает расставлять приоритеты?

r — model.matrix() с na.action=NULL?

Задавать вопрос

спросил 11 лет, 7 месяцев назад

Изменено 4 года, 9 месяцев назад

Просмотрено 17 тысяч раз

У меня есть формула и фрейм данных, и я хочу извлечь model. matrix() . Однако мне нужна результирующая матрица, чтобы включить NA, которые были найдены в исходном наборе данных. Если бы я использовал model.frame() для этого, я бы просто передал его na.action=NULL . Однако вывод, который мне нужен, имеет формат model.matrix() . В частности, мне нужны только переменные в правой части, мне нужно, чтобы на выходе была матрица (а не фрейм данных), и мне нужно преобразовать факторы в ряд фиктивных переменных.

Я уверен, что мог бы собрать что-то вместе, используя циклы или что-то в этом роде, но мне было интересно, может ли кто-нибудь предложить более чистое и эффективное обходное решение. Большое спасибо за ваше время!

Вот пример:

 dat <- data.frame(matrix(rnorm(20),5,4), gl(5,2))
дат[3,5] <- нет данных
имена(дата) <- c(буквы[1:4], 'факт')
ff <- a ~ b + факт
# Это опускает строку с отсутствующим наблюдением фактора
model.matrix(ff, dat)
# Это сохраняет NA, но дает мне фрейм данных и не разделяет фактор
model. frame(ff, dat, na.action=NULL)

Вот что я хотел бы получить:

 (Перехват) б факт2 факт3 факт4 факт5
1 1 0,7266086 0 0 0 0
2 1 -0,6088697 0 0 0 0
3 НП 0,4643360 НП НП НП НП
4 1 -1,1666248 1 0 0 0
5 1 -0,7577394 0 1 0 0
6 1 0,7266086 0 1 0 0
7 1 -0,6088697 0 0 1 0
8 1 0,4643360 0 0 1 0
9 1 -1,1666248 0 0 0 1
10 1 -0,7577394 0 0 0 1

r
матрица
нет

Предложение Джориса работает, но более быстрый и чистый способ сделать это — через глобальную настройку na.action. Параметр «Пропустить» позволяет нам сохранить NA из исходного набора данных.

Вариант 1: Пройти

Результирующая матрица будет содержать NA в строках, соответствующих исходному набору данных.

 вариантов (na.action='na.pass')
model.matrix(ff, dat)

Вариант 2: Пропустить

Результирующая матрица будет пропускать строки, содержащие NA.

 вариантов (na.action='na.omit')
model.matrix(ff, dat)

Вариант 3: Ошибка

Возникнет ошибка, если исходные данные содержат NA.

 вариантов (na.action='na.fail')
model.matrix(ff, dat)

Конечно, всегда будьте осторожны при изменении глобальных параметров, поскольку они могут изменить поведение других частей вашего кода. Осторожный человек может сохранить исходную настройку с чем-то вроде current.na.action <- options('na.action') , а затем изменить ее обратно после создания model.matrix.

Другой способ — использовать функцию model.frame с аргументом na.action=na.pass в качестве второго аргумента для model.matrix :

 > model.matrix(ff, model.frame(~ .,дат, на.экшен=на.пасс))
   (Перехват) б факт2 факт3 факт4 факт5
1 1 -1,3560754 0 0 0 0
2 1 2,5476965 0 0 0 0
3 1 0,4635628 НП НП НП НП
4 1 -0,2871379 1 0 0 0
5 1 2,2684958 0 1 0 0
6 1 -1,3560754 0 1 0 0
7 1 2,5476965 0 0 1 0
8 1 0,4635628 0 0 1 0
9 1 -0,2871379 0 0 0 1
10 1 2,2684958 0 0 0 1

model. frame позволяет установить соответствующее действие для na.action , которое сохраняется при вызове model.matrix .

Я наткнулся на более простое решение после просмотра ответов mattdevlin и Nathan Gould:

 model.matrix.lm(ff, dat, na.action = "na.pass")

model.matrix.default может не поддерживать аргумент na.action , но model.matrix.lm поддерживает!

(я нашел model.matrix.lm из предложений автозаполнения Rstudio — кажется, это единственный нестандартный метод для model.matrix , если вы не загрузили какие-либо библиотеки, добавляющие другие. Тогда я просто предположил, что это может поддерживать на.действие аргумент.)

Вы можете немного повозиться с объектом model.matrix , основываясь на именах строк:

 MM <- model. matrix(ff,dat)
MM <- MM[match(имена строк (dat), имена строк (MM)),]
MM["b"] <- dat$b
имена строк (MM) <- имена строк (дата)

что дает:

 > ММ
     (Перехват) б факт2 факт3 факт4 факт5
1 1 0,9583010 0 0 0 0
2 1 0,3266986 0 0 0 0
3 НП 1.4992358 НП НП НП НП
4 1 1,2867461 1 0 0 0
5 1 0,5024700 0 1 0 0
6 1 0,9583010 0 1 0 0
7 1 0,3266986 0 0 1 0
8 1 1,4992358 0 0 1 0
9 1 1,2867461 0 0 0 1
10 1 0,5024700 0 0 0 1

Кроме того, вы можете использовать контрасты() , чтобы сделать всю работу за вас. Построение матрицы вручную будет:

 продолжение <- контрастирует(dat$fact)[as.numeric(dat$fact),]
colnames(cont) <- вставить("факт",colnames(cont),sep="")
out <- cbind(1,dat$b,cont)
out[is.na(dat$fact),1] <- NA
colnames(out)[1:2]<- c("Перехват","b")
имена строк (исходящие) <- имена строк (данные)