Какие многолетники можно делить весной
Растущие на одном месте многолетние растения с каждым годом разрастаются и образуют густые куртины. От этого клумба выглядит менее декоративно, растения не так пышно цветут, из-за нехватки питательных веществ и пространства для развития.
Выходом из положения станет пересадка цветов, во время которой рекомендуется разделять корневую систему. Благодаря этому, весеннее деление многолетних цветов позволит омолодить и размножить культуру. А цветение станет более пышным и привлекательным.
Как часто необходимо выполнять пересадку
Тип корневой системы является определяющим фактором при выращивании и делении растения.
· Цветы с ползучей корневой системой, (многолетние астры, анемона, вербейник, чистец, стахис), способны расти на одном месте без омоложения до 8 лет. За время роста их корневая система разрастается в ширину, утолщается и при делении лучше использовать периферийные корневища.
Это стимулирует рост новых побегов, а выкопанные растения хорошо адаптируются на новом месте.
· Хоста, лилейник, пион имеют компактный корень, при правильной агротехнике растут в саду без деления до десяти лет. За этот период образуется плотный корень, разделить который можно при помощи острой лопаты.
· Флоксы имеют мочковатый корень, их требуется рассаживать каждые 4-5 лет. Цветок хорошо переносит размножение, а деленки быстро приживаются на новом месте.
· Растение со стержневым корнем (люпин, аквилегия, мак) болезненно переносят каждое внешнее вмешательство, но способны расти на одном месте до шести лет. Обновляют посадку, высаживая новые саженцы или при помощи корневых отпрысков.
Продолжительность выращивания культуры на одном месте может незначительно меняться в большую или меньшую сторону, в зависимости от состава почвы и прочих внешних факторов. Если вы стали замечать, что бутоны стали мельчать, стебли становятся тонкими, а листья мелкими, это значит пришло время обновить посадку.
Разбираемся, какие многолетники можно делить весной
Весна наилучшее время для деления и омоложения многих культур, к ним относятся:
· весеннецветущие – примула, камнеломка, фиалка, ясколка войлочная и др;
· зацветающие в летний период – гвоздика, лаванда, лилейник, хризантема, эхинацея, бузульник, кореопсис ланцевидный и др.;
· цветущие осенью – анемона японская, астра, гелениум, рудбекия, мискантус и др.
Деление многолетников весной выполняют как можно раньше, чтобы с приходом тепла цветок пошел в рост. Однако если луковицы цветов ранней весной начинают активно развиваться и расти, деление выполняют после цветения летом или осенью.
Процедуру выполняют в пасмурный день или после того как установится прохладная погода.
Рассмотрим, как выполнить весеннее деление многолетних цветов, пользующихся наибольшей популярностью.
Флоксы
Цветок делят после выкопки корневища.
Руками удаляют лишнюю землю и при помощи садового инструмента корень разрезают на несколько частей, чтобы на каждой части оставалось 5-6 побегов.
Сразу выполняют посадку отделенных частей, выбирая солнечный участок. А для успешной приживаемости выполняют регулярный полив и мульчирование поверхности.
Лилейник
Лилейники пользуются широкой популярностью у садоводов за неприхотливость и декоративность. При выращивании формируются толстые корни, которые можно разделить, не выкапывая растение. Для этого визуально отмечают отдельную розетку и острой лопатой отсекают растение.
Посадку на новое место выполняют вместе с комом земли, что обеспечивает успешную приживаемость. Если недостаточно опыта, деление можно выполнить после выкапывания растения. При посадке важно правильно выбрать новое место, а в посадочную лунку добавить перегной и минеральное удобрение для успешной приживаемости.
Лилейники можно размножать весной и осенью.
Высаженные осенью саженцы зацветают на следующий год.
Астры
Весной астру укореняют посредством побегов или выполняют черенкование. Деление корня позволит обновить кустарник. При этом необходимо удалить старые отростки, укоротить молодые. Деление выполняют так, чтобы на каждом корневище находилось не менее 4-5 стеблей.
Хризантемы
Посадки хризантем как и гелениума необходимо омолаживать каждые 3-4 года. Растение очень быстро разрастается, что сказывается на декоративности. При омоложении куст выкапывают и делят так, чтобы на каждой части оставалось не менее 4 стеблей. Посадку выполняют на расстоянии 40-50 см.
Анемона
Анемона при пересадке очень привередлива, трудно приживается после деления. Поэтому размножение выполняют корневыми отростками, что минимизирует стресс для материнского куста и обеспечивает успешную приживаемость саженца.
Пион
Хотя пион способен до десяти лет расти на одном месте, желая наблюдать обильное цветение без деления не обойтись.
При этом куст с корнем осторожно выкапывают, корни очищают от земли, отделяют части, имеющие не менее 3 почек. Одновременно срезают старые и подгнившие корни. Перед посадкой корни замачивают в растворе марганцовки.
Как делить многолетние цветы весной, чтобы не навредить
Омоложение выполняют до того как начнет расти зеленая масса. Если при делении планируется размножить растение, то выбирают побеги, расположенные на периферии основного куста. А место для их посадки готовят заблаговременно:
· создают посадочные лунки;
· при необходимости на дно насыпают измельченный щебень для отвода лишней влаги;
· сверху насыпают грунт с навозом, из расчета, чтобы смесь заполнила треть ямы.
Посадку можно выполнить в горшок, кадку, теплицу, а при благоприятных условиях посадить на постоянное место.
Если стоит сухая погода, за сутки растение поливают. Благодаря этому будет легче работать, а цветок испытает меньший стресс.
Стандартный процесс деления/размножения включает последовательные этапы:
· Выкапывание корневой системы. Для этого по периметру корня делают подкоп, а затем, за стебли внимают цветок из грунта.
· Если клубни расположены вблизи поверхности и новые растения растут отдельно от основного куста, их отделяют не выкапывая.
· Извлеченный корень освобождают от грунта, руками или при помощи острого ножа разделяют на части. Места деления засыпают измельченным углем, немного подсушивают.
· Деленки высаживают на новое место.
Уход за молодыми саженцами включает регулярный полив, удаление сорняков, рыхление и мульчирование грунта.
Пионы: размножение делением кустов в августе
Среди опытных цветоводов принято размножать пионы аккуратным делением куста. Размножение делением требует от садовода знаний и умений.
Чтобы пионы пышно цвели, их необходимо сажать на хорошо освещенном месте.
Фото: Сеть DIY
Август богат событиями – в конце лета происходит сбор урожая, отводки заготавливаются на зиму, размножаются пионы и другие многолетние цветы. Конечно, сами по себе пионы не размножаются — нужно приложить усилия, чтобы разделить старые кусты на несколько частей, а также высадить деленки на новое место. Именно о разделении пионеров и пойдет речь в этой статье.
Пионы – неприхотливая, долговечная и выносливая декоративная культура, способная расти на одном месте много лет, но даже пионы со временем нуждаются в пересадке, омоложении и размножении, чтобы сохранить первоначальные характеристики сорта.
Известно, что корневая система пионов очень мощная: мясистые корни достигают длины 40 см и толщины 60 мм. Именно в корневище пионы летом запасают питательные вещества, чтобы не погибнуть от истощения поздней осенью, зимой и ранней весной.
Чем старше кусты пиона, тем мощнее и объемнее становится корневище – корни становятся жесткими, частично отмирают, обрастают наростами и отростками, формируют почки возобновления.
Поэтому старые кусты пионов нужно выкапывать очень осторожно: корни легко ломаются, а глубина корней достигает 70 см, поэтому нужно очень постараться, чтобы не повредить корни при делении и пересадке.
Август, а точнее конец августа, лучшее время для размножения пионов делением корневища и пересадкой кустов на новое место. Если пересадить пионы в конце лета, кусты успеют прижиться на новом месте и успеют «заболеть» до наступления зимы, а значит, переживут холода с минимальными потерями.
Содержание
- Приступаем к делению кустов пионов
- Финал размножения пионов: посадка делёнок
- Как правильно посадить пионы
- Деление пионов весной и другие тонкости
Приступаем к делению кустов пионов
Перед делением кусты пиона необходимо обрезать на небольшой высоте. Фото: coffeepoint.club
Перед делением кусты пиона необходимо срезать на высоте 20 см от земли, а затем выкопать кусты штыковой лопатой на глубину до полуметра на расстоянии 25-30 см вокруг корневища, чтобы не повредить корни.
Когда работа по удалению почвы вокруг куста завершена, куст рыхлят с помощью подручных средств (монтировки, вил, прута, куска трубы) до оголения корневой системы от земли. Затем куст необходимо вынуть из земли и поставить на ровную поверхность, при этом пластиковой или деревянной лопаткой извлекают из земли корни, а затем подвои пиона промывают слабой струей воды.
Затем разрыхлите куст вилами или ломом, пока он полностью не освободится от земли, и осторожно извлеките его из земли.
Чтобы корни не ломались, перед делением куста необходимо просушить его в течение двух-трех часов в темном месте с хорошей вентиляцией. Корни станут гибкими и эластичными.
В первую очередь необходимо острым ножом или ножницами удалить загнившие и больные части корневища. Больные и поврежденные корни необходимо удалить до здоровой ткани, а срезы присыпать древесным углем.
Затем нужно подрезать толстые корни на 10-15 см под острым углом 45-60°. Удалив ненужную корневую массу, внимательно осмотрите корневище, чтобы определить, где корни соединяются с корневой шейкой и где образовались глазки.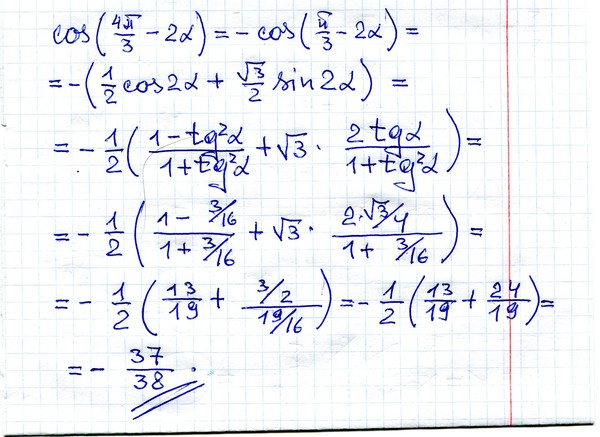
Чтобы корни были гибкими и не ломались при делении, корневище необходимо подсушивать в течение двух-трех часов. Фото: Южный пион
Затем приступают к делению куста пиона: кувалдой или молотком вбивают в центр клин и делят куст на 2-6 частей, в зависимости от возраста и размера старого куста. Их делят так, чтобы на каждой части было по три-пять здоровых, развитых почек и достаточное количество корешков.
Корневище пиона готово к разделению на несколько частей. Фото: Южный пион
Следует знать, что слишком маленькие деленки плохо укореняются, дольше болеют и хуже приживаются на новом месте. Поэтому не стоит делить его слишком мелко, в крайнем случае следует оставить для выращивания небольшие деленки пионов.
Затем в центр старого большого куста молотком вбивают клин и с его помощью куст разрывают на две и более частей. На каждой части должно быть по 3-5 хорошо развитых почек и достаточное количество корешков. Очень крупные и очень мелкие деления нежелательны, потому что растения из них хуже укореняются.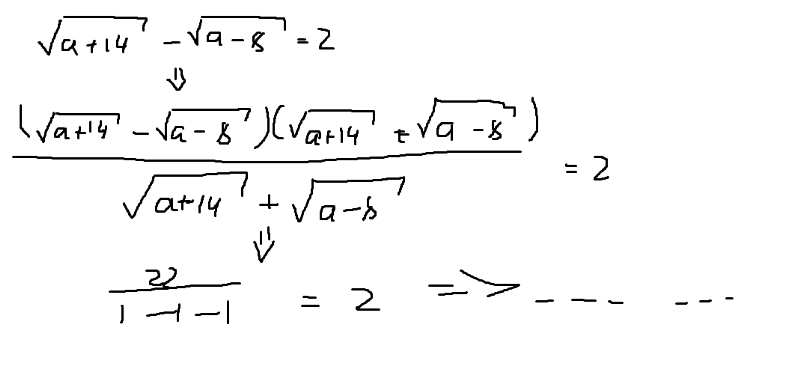
Но если получаются небольшие дивизии, их оставляют расти.
Финал размножения пионов: посадка делёнок
Мы уже писали, что для обильного цветения пионов необходимо, чтобы кусты росли на открытом солнечном месте, вдали от больших деревьев, построек и домов. Поэтому нужно 7 раз подумать, прежде чем приступать к посадке «новых» пионов, выбрать место расположения растений.
Пионы хорошо растут на глинистой почве, где нет застойных талых вод, богатых питательными веществами. Следует знать, что на песчаной почве кусты пиона вырастают много листвы, но мало цветков, а на глинистой почве цветки пиона крупные, но растения развиваются медленно.
Для предупреждения корневых гнилей необходимо дезинфицировать деленки в темно-розовом растворе марганцовки или в 1%-ном растворе медного купороса в течение получаса.
Посадочная яма для пионов имеет диаметр и глубину 50-60 см. Точный размер посадочной ямы определяют на месте: если почва тяжелая, размер ямы следует увеличить на 150-200 мм.
Расстояние между посадочными ямами около метра – 80-90 см.
Когда посадочные ямы готовы, их заполняют питательным грунтом, с добавлением 3-4 ведер перегноя или хорошо перепревшего навоза, по 1 стакану гранулированного суперфосфата и сульфата калия, 1-2 стакана золы. Удобрение тщательно перемешивают с почвой и оставляют в покое на 3-5 дней, а затем приступают к посадке пионов.
Глинистую почву следует разбавить речным песком, из расчета 2 ведра на посадочную лунку. Песчаную почву, наоборот, следует утяжелить 1-2 ведрами сухой, перемолотой, глины, а на дно посадочной ямы уложить слой глины толщиной 10 см.
Вообще дно посадочной ямы, предназначенной для пионов, настоятельно рекомендуется выложить толченым кирпичом или камнями, перемешанными с песком. Также полезно внести удобрения на дно и борта ямы. Затем яму заполняют на 2/3 приготовленной смесью, а верхнюю часть ямы (15-20 см от поверхности почвы) засыпают плодородной почвой.
Как правильно посадить пионы
Секрет правильной посадки пионов заключается в том, чтобы не заглубить корневую шейку и почки регенерации.
Поэтому перед посадкой в центре посадочной ямы необходимо сделать холмик из почвы и положить на него корни пиона. Затем корни необходимо тщательно засыпать землей, чтобы между корнями не было пустот. После посадки необходимо обильно полить высаженные растения. После полива корни станут несколько глубже.
Когда почва осядет, проверьте, чтобы корневая шейка находилась на одном уровне с землей, или не глубже 5 см, иначе пионы не будут цвести или цветут плохо.
Если перед посадкой посадочные лунки уже заполнены почвой, то высаживайте черенки так, чтобы почки были на уровне земли. В этом случае после усадки грунта в яме растения будут размещены на нужной глубине.
Посаженные кусты пионов могут зацвести на следующий год, если на материнском кусте были хорошо сформированные почки возобновления, но этого нельзя допускать для лучшего развития растений в будущем.
Следует знать, что небольшие деленки пионов, с 1-2 почками и слабыми корнями, могут зацвести только через 3-4 года после посадки.
Деление пионов весной и другие тонкости
При делении пионов весной растения образуют мало молодых поглощающих корней, плохо развиваются и болеют. Поэтому пересадкой и размножением пионов нужно заниматься только ранней весной, сразу после оттаивания почвы.
Многие цветоводы утверждают, что для размножения можно использовать и небольшие деленки пионов с одним бутоном. Спорить не буду, но дам способ размножения пионов небольшими деленками.
Подготовьте грядку с бороздками глубиной 10-12 см и поместите в бороздки небольшие пионы на расстоянии 20 см, обильно полейте теплой водой, замульчируйте и притените, чтобы укоренились. Записи будут следующей весной. За лето пионы окрепнут и уже в августе будут готовы к пересадке на постоянное место.
Желаю вам успехов в разведении и пересадке пионов!
- Об авторе
- Хотите связаться со мной?
Об авторе
Надежда Суворова
Главный редактор , vflore.
ru
Уже много лет я занимаюсь цветами. Несколько своих крупных оранжерей позволяют вдоволь экспериментировать. Сейчас я могу делиться с вами многим количеством идей связанных с цветами.
9.5 Деление квадратных корней — Элементарная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Разделить квадратный корень
- Рационализировать одночленный знаменатель
- Рационализировать двучленный знаменатель
Приготовься 9.12
Прежде чем начать, пройдите этот тест на готовность.
Найдите дробь, эквивалентную 5858, со знаменателем 48.
Если вы пропустили эту задачу, просмотрите пример 1.64.
Приготовься 9.13
Упрощение: (5)2(5)2.
Если вы пропустили эту проблему, просмотрите пример 9.48.
Приготовься 9.14
Умножить: (7+3x)(7−3x)(7+3x)(7−3x).
Если вы пропустили эту проблему, просмотрите пример 6.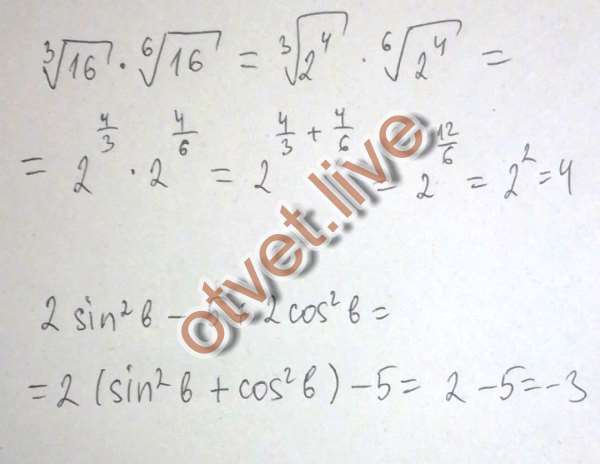
54.
Разделить квадратный корень
Мы знаем, что мы упрощаем дроби, удаляя множители, общие для числителя и знаменателя. Когда у нас есть дробь с квадратным корнем в числителе, мы сначала упрощаем квадратный корень. Тогда мы можем искать общие факторы.
Пример 9,60
Упрощение: 546546.
Решение
| 546546 | |
| Упростите радикальное. | 9·669·66 |
| Упрощение. | 366366 |
| Удалить общие множители. | 363·2363·2 |
| Упрощение. | 6262 |
Попробуй это 9.119
Упростить: 328328.
Попробуй это 9.120
Упрощение: 75157515.
Пример 9,61
Упрощение: 6-24126-2412.
Решение
| 6-24126-2412 | |
Упростите радикальное.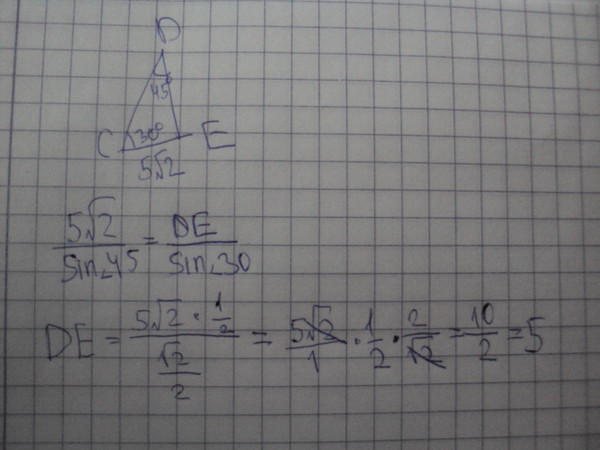 | 6-4·6126-4·612 |
| Упрощение. | 6-26126-2612 |
| Вынесите общий множитель из числителя. | 2(3−6)2·62(3−6)2·6 |
| Удалить общие множители. | 2(3−6)2·62(3−6)2·6 |
| Упрощение. | 3−663−66 |
Попробуй это 9.121
Упрощение: 8-40108-4010.
Попробуй это 9.122
Упрощение: 10-752010-7520.
Мы использовали частное свойство квадратных корней, чтобы упростить квадратные корни дробей. Частное свойство квадратных корней говорит
аб=аб,б≠0аб=аб,б≠0
Иногда нам нужно будет использовать частное свойство квадратных корней «в обратном порядке», чтобы упростить дробь с квадратными корнями.
аб=аб,б≠0аб=аб,б≠0
Мы перепишем частное свойство квадратных корней, чтобы увидеть оба пути вместе. Помните: мы предполагаем, что все переменные больше или равны нулю, поэтому их квадратные корни являются действительными числами.
Факторное свойство квадратных корней
Если a , b неотрицательные действительные числа и b≠0b≠0, то
аб=абандаб=абаб=абандаб=аб
Мы будем использовать частное свойство квадратных корней «в обратном порядке», когда дробь, с которой мы начинаем, представляет собой частное двух квадратных корней, и ни один подкоренный член не является полным квадратом. Когда мы записываем дробь одним квадратным корнем, мы можем найти общие множители в числителе и знаменателе.
Пример 9,62
Упрощение: 27752775.
Решение
| 27752775 | |
| Ни один из корней не является полным квадратом, поэтому перепишите, используя частное свойство квадратных корней. | 27752775 |
Удалите общие множители в числителе и знаменателе. | 3·93·253·93·25 |
| Упрощение. | 925925 |
| 3535 |
Попробуй это 9.123
Упрощение: 4810848108.
Попробуй это 9.124
Упрощение: 96549654.
Мы будем использовать свойство отношения показателей степени, aman=am-naman=am-n, когда у нас есть переменные с показателями степени в подкоренных.
Пример 9,63
Упрощение: 6y52y6y52y.
Решение
| 6y52y6y52y | |
| Ни один из корней не является полным квадратом, поэтому перепишите, используя частное свойство квадратных корней. | 6y52y6y52y |
| Удалить общие множители в числителе и знаменателе. | 2·3·y4·y2·y2·3·y4·y2·y |
| Упрощение. | 3y43y4 |
Упростите радикальное.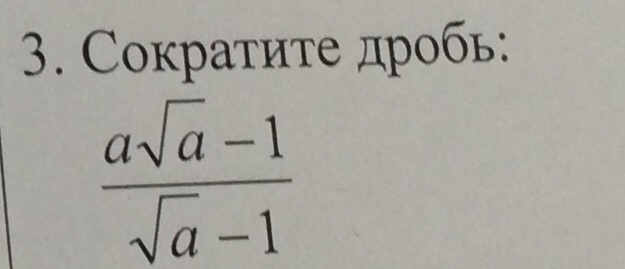 | y23y23 |
Попробуй это 9.125
Упрощение: 12р36р12р36р.
Попробуй это 9.126
Упрощение: 14p92p514p92p5.
Пример 9,64
Упрощение: 72x3162x72x3162x.
Решение
| 72x3162x72x3162x | |
| Перепишите, используя частное свойство квадратных корней. | 72x3162x72x3162x |
| Удалить общие множители. | 18·4·x2·x18·9·x18·4·x2·x18·9·x |
| Упрощение. | 4x294x29 |
| Упростите радикальное. | 2x32x3 |
Попробуй это 9.127
Упрощение: 50s3128s50s3128s.
Попробуй это 9.128
Упрощение: 75q5108q75q5108q.
Пример 9,65
Упрощение: 147ab83a3b4147ab83a3b4.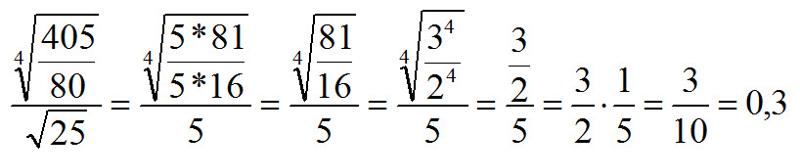
Решение
| 147ab83a3b4147ab83a3b4 | |
| Перепишите, используя частное свойство квадратных корней. | 147ab83a3b4147ab83a3b4 |
| Удалить общие множители. | 49b4a249b4a2 |
| Упростите радикальное. | 7b2a7b2a |
Попробуй это 9.129
Упрощение: 162x10y22x6y6162x10y22x6y6.
Попробуй это 9.130
Упрощение: 300м3н73м5н300м3н73м5н.
Рационализация знаменателя с одним членом
До того, как калькулятор стал инструментом повседневной жизни, таблицы квадратных корней использовались для нахождения приблизительных значений квадратных корней. На рис. 9.3 показана часть таблицы квадратов и квадратных корней. В этой таблице квадратные корни округляются до пяти знаков после запятой.
Рисунок 9.3 Таблица квадратных корней использовалась для нахождения приблизительных значений квадратных корней до того, как появились калькуляторы.
Если кому-то нужно было аппроксимировать дробь с квадратным корнем в знаменателе, это означало деление в длинное деление с пятизначным делителем. Это был очень трудоемкий процесс.
По этой причине был разработан процесс, называемый рационализацией знаменателя. Дробь с корнем в знаменателе преобразуется в эквивалентную дробь, знаменатель которой является целым числом. Этот процесс используется до сих пор и полезен и в других областях математики.
Рационализация знаменателя
Процесс преобразования дроби с корнем в знаменателе в эквивалентную дробь с целым знаменателем называется рационализацией знаменателя.
Квадратные корни чисел, которые не являются полными квадратами, являются иррациональными числами. Когда мы рационализируем знаменатель , мы записываем эквивалентную дробь с рациональным числом в знаменателе.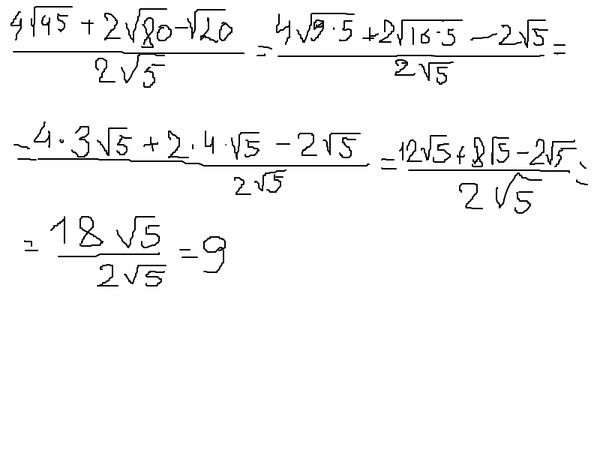
Давайте рассмотрим числовой пример.
Предположим, нам нужно приблизительное значение дроби.12Приближение с пятью десятичными знаками к 2 равно 1,41421,11,41421Без калькулятора, вы бы хотели выполнить это деление?1,414211,0Предположим, нам нужно приблизительное значение дроби. .41421.11.41421Вы бы хотели выполнить это деление без калькулятора?1.414211.0
Но мы можем найти дробь, эквивалентную 1212, умножив числитель и знаменатель на 22.
Теперь, если нам нужно приблизительное значение, мы делим 21,4142121,41421. Это намного проще.
Несмотря на то, что калькуляторы доступны почти везде, дробь с радикалом в знаменателе все же нуждается в рационализации. Он не считается упрощенным, если знаменатель содержит квадратный корень.
Аналогично, квадратный корень не считается упрощенным, если подкоренное число содержит дробь.
Упрощенные квадратные корни
Квадратный корень считается упрощенным, если
- в подкоренных числах нет множителей совершенного квадрата
- в подкоренной дроби нет дробей и
- нет квадратных корней в знаменателе дроби
Чтобы рационализировать знаменатель, мы используем свойство, что (a)2=a(a)2=a.
Если мы возведем в квадрат иррациональный квадратный корень, мы получим рациональное число.
Мы будем использовать это свойство для рационализации знаменателя в следующем примере.
Пример 9,66
Упрощение: 4343.
Решение
Чтобы рационализировать знаменатель, мы можем умножить квадратный корень сам на себя. Чтобы сохранить дробь эквивалентной, мы умножаем и числитель, и знаменатель на один и тот же коэффициент.
| 4343 | |
| Умножьте числитель и знаменатель на 3,3. | 4·33·34·33·3 |
| Упрощение. | 433433 |
Попробуй это 9.131
Упрощение: 5353.
Попробуй это 9.132
Упрощение: 6565.
Пример 9,67
Упрощение: −836−836.
Решение
Чтобы удалить квадратный корень из знаменателя, мы умножаем его сам на себя.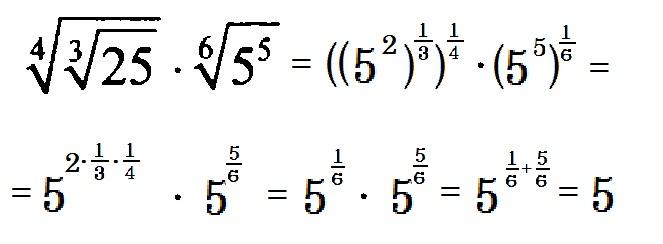
Чтобы сохранить эквивалентность дробей, мы умножаем и числитель, и знаменатель на 66.
| Умножьте числитель и знаменатель на 66. | |
| Упрощение. | |
| Удалить общие множители. | |
| Упрощение. |
Попробуй это 9.133
Упрощение: 525525.
Попробуй это 9.134
Упрощение: −943−943.
Всегда сначала упрощайте радикал в знаменателе, прежде чем рационализировать его. Таким образом, числа остаются меньше и с ними легче работать.
Пример 9,68
Упрощение: 512512.
Решение
| Дробь не является полным квадратом, поэтому перепишите, используя Частное свойство.  | |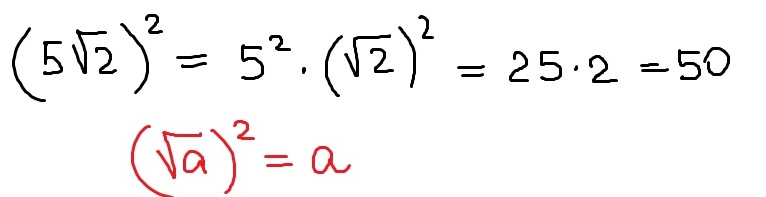
| Упростите знаменатель | |
| Рационализируйте знаменатель. | |
| Упрощение. | |
| Упрощение. |
Попробуй это 9.135
Упрощение: 718718.
Попробуй это 9.136
Упрощение: 332332.
Пример 9,69
Упрощение: 11281128.
Решение
| Переписать с использованием свойства Quotient. | |
| Упростите знаменатель. | |
| Рационализируйте знаменатель. | |
| Упрощение. | |
| Упрощение. |
Попробуй это 9.137
Упрощение: 327327.
Попробуй это 9.138
Упрощение: 10501050.
Рационализация двучленного знаменателя
Когда знаменатель дроби представляет собой сумму или разность с квадратными корнями, мы используем шаблон произведения сопряженных чисел для рационализации знаменателя.
(а−b)(a+b)(2−5)(2+5)a2−b222−(5)24−5−1(a−b)(a+b)(2−5)(2 +5)a2−b222−(5)24−5−1
Когда мы умножаем двучлен, содержащий квадратный корень, на сопряженный, произведение не имеет квадратных корней.
Пример 9,70
Упрощение: 44+244+2.
Решение
| Умножьте числитель и знаменатель на сопряженное значение знаменателя. | |
| Умножьте сопряженные числа в знаменателе. | |
| Упростите знаменатель. | |
Упростите знаменатель. | |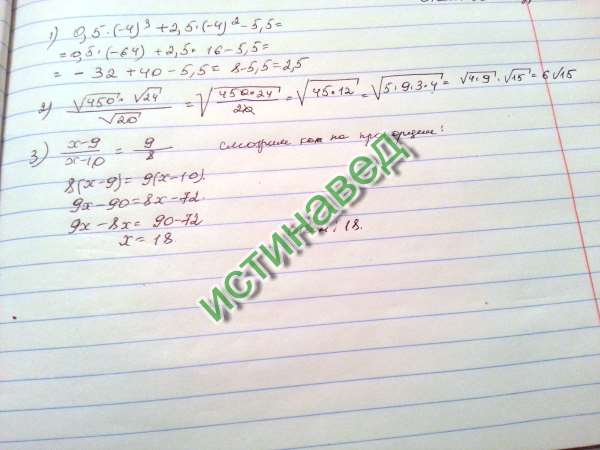
| Удалите общие множители из числителя и знаменателя. | |
| Мы оставили числитель в факторизованной форме, чтобы упростить поиск общих множителей после того, как мы упростили знаменатель. |
Попробуй это 9.139
Упрощение: 22+322+3.
Попробуй это 9.140
Упрощение: 55+355+3.
Пример 9,71
Упрощение: 52−352−3.
Решение
| Умножьте числитель и знаменатель на сопряженное значение знаменателя. | |
| Умножьте сопряженные числа в знаменателе. | |
| Упростите знаменатель. | |
| Упростите знаменатель. | |
Упрощение. |
Попробуй это 9.141
Упрощение: 31−531−5.
Попробуй это 9.142
Упрощение: 24−624−6.
Пример 9,72
Упрощение: 3u-63u-6.
Решение
| Умножьте числитель и знаменатель на сопряженное значение знаменателя. | |
| Умножьте сопряженные числа в знаменателе. | |
| Упростите знаменатель. |
Попробуй это 9.143
Упрощение: 5x+25x+2.
Попробуй это 9.144
Упрощение: 10y−310y−3.
Пример 9,73
Упрощение: x+7x−7x+7x−7.
Решение
Умножьте числитель и знаменатель на сопряженную часть знаменателя. | |
| Умножьте сопряженные числа в знаменателе. | |
| Упростите знаменатель. | |
| Мы не возводим числитель в квадрат. В факторизованной форме мы видим, что нет общих множителей, которые можно было бы удалить из числителя и знаменателя. |
Попробуй это 90,145
Упрощение: p+2p−2p+2p−2.
Попробуй это 9.146
Упрощение: q−10q+10q−10q+10.
Средства массовой информации
Получите доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практики разделения и рационализации.
- Разделение и рационализация
Раздел 9.5 Упражнения
Практика делает совершенным
Деление квадратного корня
В следующих упражнениях упрощайте.
317.
276276
318.
50105010
319.
729729
320.
24362436
321.
2−3282−328
322.
3+2793+279
323.
6+4566+456
324.
10−2002010−20020
325.
8012580125
326.
7220072200
327.
1287212872
328.
48754875
329.
ⓐ 8x62x28x62x2 ⓑ 200 м 598 м 200 м 598 м
330.
ⓐ 10y35y10y35y ⓑ 108n7243n3108n7243n3
331.
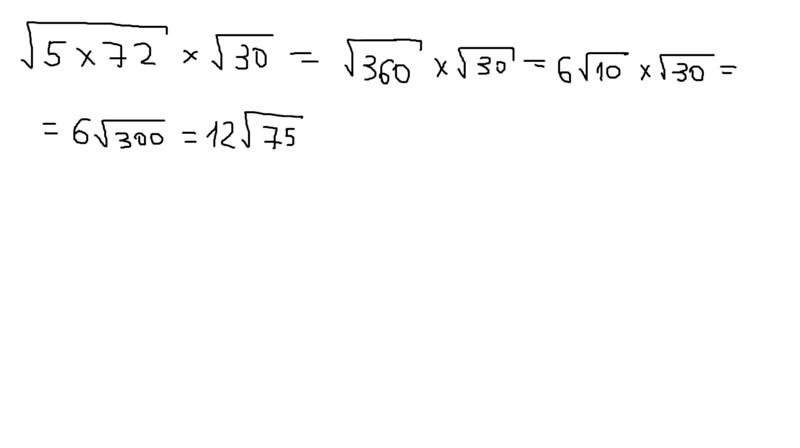
75р3108р75р3108р
332.
196q5484q196q5484q
333.
108p5q23p3q6108p5q23p3q6
334.
98рс102р3с498рс102р3с4
335.
320мн545м7н3320мн545м7н3
336.
810c3d71000c5d810c3d71000c5d
337.
98149814
338.
72187218
339.
5+125155+12515
340.
6-45126-4512
341.
9615096150
342.
28632863
343.
26y72y26y72y
344.
15x33x15x33x
Рационализация одночленного знаменателя
В следующих упражнениях упростите и рационализируйте знаменатель.
345.
106106
346.
8383
347.
6767
348.
4545
349.
313313
350.
10111011
351.
1031010310
352.
252252
353.
495495
354.
927927
355.
−923−923
356.
−836−836
357.
320320
358.
427427
359.
740740
360.
845845
361.
1917519175
362.
1719217192
Рационализация двучленного знаменателя
В следующих упражнениях упрощайте, рационализируя знаменатель.
363.
ⓐ 33+1133+11 ⓑ 81−581−5
364.
ⓐ 44+744+7 ⓑ 72−672−6
365.
ⓐ 55+655+6 ⓑ 63−763−7
366.
ⓐ 66+566+5 ⓑ 54−1154−11
367.
3м-53м-5
368.
5н-75н-7
369.
2x−62x−6
370.
7 лет+37 лет+3
371.
р+5р-5р+5р-5
372.
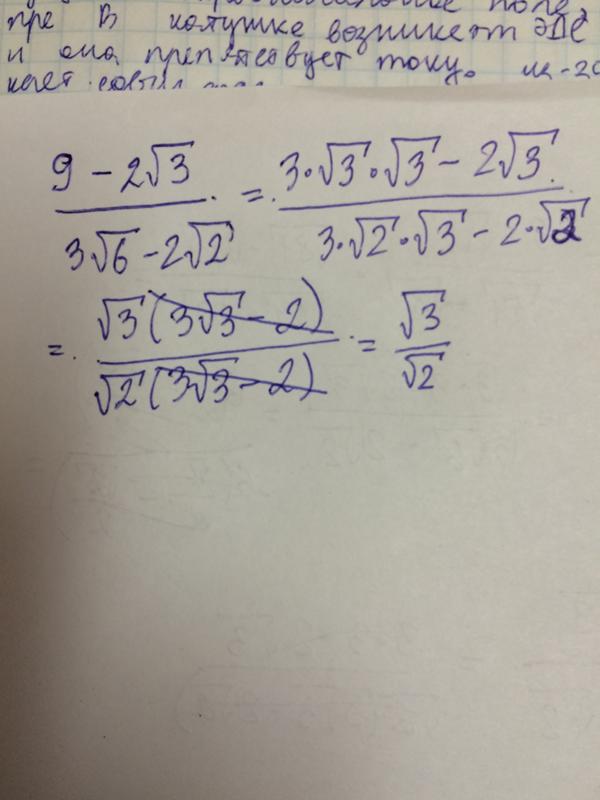
с-6с+6с-6с+6
373.
150x2y66x4y2150x2y66x4y2
374.
80p3q5pq580p3q5pq5
375.
155155
376.
358358
377.
854854
378.
12201220
379.
35+535+5
380.
204−3204−3
381.
2x−32x−3
382.
5 лет-75 лет-7
383.
х+8х-8х+8х-8
384.
м-3м+3м-3м+3
Математика на каждый день
385.
Комплект снабжения сбрасывается с самолета, летящего на высоте 250 футов.
Упростите 2501625016, чтобы определить, сколько секунд потребуется, чтобы комплект припасов достиг земли.
386.
Ракета сбрасывается в океан с самолета, летящего на высоте 1200 футов. Упростите 120016120016, чтобы определить, сколько секунд потребуется, чтобы вспышка достигла океана.
Письменные упражнения
387.
- ⓐ Упростите 273273 и объясните все свои шаги.
- ⓑ Упростите 275275 и объясните все свои шаги.
- ⓒ Чем отличаются два метода упрощения квадратных корней?
388.
- ⓐ Приблизительно получите 1212, разделив 11,41411,414 в длинное деление без калькулятора.
- ⓑ Рационализация знаменателя 1212 дает 22,22. Приблизительно получите 2222, разделив 1,41421,4142 в длинное деление без калькулятора.
- ⓒ Согласны ли вы с тем, что рационализация знаменателя облегчает вычисления? Почему или почему нет?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ После просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующему разделу? Почему или почему нет?
Квадратный корень из 5 — значение, метод расчета, примеры решений и часто задаваемые вопросы
Значение корня из 5, уменьшенное до 5 знаков после запятой, равно √5 = 2,23606. У него есть место с большим списком иррациональных алгебраических чисел. Он был отсортирован в свете из-за того, что квадратный корень из 5 не может быть описан как дробь и имеет бесконечное количество десятичных знаков. Кроме того, конкретное значение никогда не может быть найдено идеально. В математике квадратный корень из 5 представляется или записывается как √5.
Это положительное число, а также значение √5 при умножении на себя дает простое число 5. Чтобы отличить себя от отрицательного числа с теми же свойствами, оно называется главным корнем из 5.
Как найти квадратный корень из 5?
Этот вопрос может беспокоить вас уже довольно давно. Самый простой способ найти квадратный корень из любого числа — использовать метод деления. Как найти значение корня 5? Выполните шаги, указанные ниже:
Шаг 1. Первый шаг — сгруппировать цифры парами по два. Вы начинаете с единицы, которая находится в месте единицы, и двигаетесь к левой стороне для числа до десятичной точки. Для числа после запятой вы группируете первые два числа и двигаетесь вправо.
5. 00 00 00 00
Шаг 2. На этом шаге вам нужно будет выбрать наибольшее квадратное число, которое равно или меньше первой пары чисел. Теперь возьмите это число в качестве делителя и также запишите частное.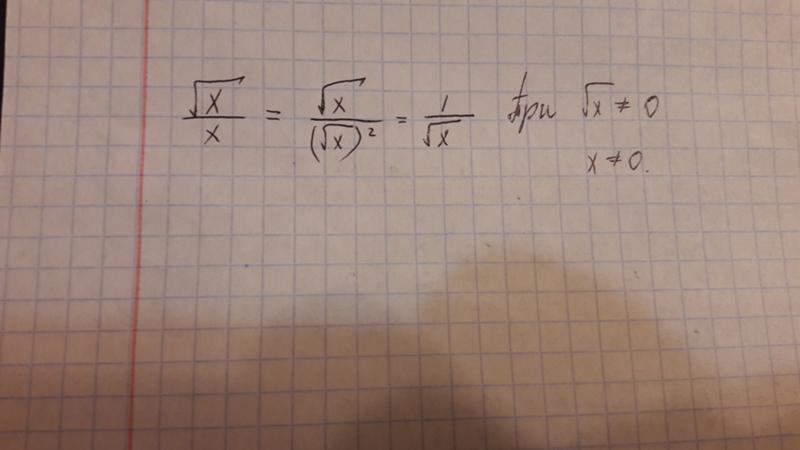
Шаг 3: Теперь вы вычитаете конечный продукт частного и делителя и частного из пары чисел или числа. Далее вы сбиваете следующую пару чисел.
Шаг 4: Теперь вам нужно вычислить делитель. Для этого вам нужно будет умножить предыдущее частное на 2, а затем выбрать новое число таким образом, чтобы цифра и новый делитель были меньше или равны новому делимому 9.0005
Шаг 5. Повторяйте шаги 2, 3 и 4, пока не будут исчерпаны все пары чисел. Итак, найденное вами частное — это квадратный корень. В случае значения под root 5 это делается так.
(Image will be uploaded soon)
| | 2.236 |
2 +2 | 5 . 00 00 00 4 |
42 + 2 | 1 00 — 84 |
443 + 3 | 16 00 — 13 29 |
4466 + 6 | 27100 — 26796 |
4452 | 304 |
Следовательно, квадратный корень из 5 = 2,236
Чему равен квадратный корень из 5?
Значение корня 5, уменьшенное до 5 знаков после запятой, равно 2,23606, и это просто упрощенная версия значения.
Кроме того, фактическое значение корня 5 может быть равно как минимум десяти миллиардам цифр.
Примеры вопросов
1. Используя метод деления, найдите квадратный корень из числа 784.
Решение:
| | 28 |
2 +2 | 784 4 |
48 | 384 — 384 |
| 0 |
Solution:
| | 73 |
7 +7 | 53 29 49 |
143 | 4 29 -4 29 |
| | 0 |
3.
Найдите квадратный корень 6604999.
Solution:
| | 257 |
2 +2 | 6 60 49 4 |
45 + 5 | 2 60 2 25 |
507 | 35 49 — 35 49 |
| | 0 |
Знаете ли вы?
5 не является полным квадратом, так как квадратный корень из 5 не является целым числом.
Квадратный корень из 5 в экспоненциальной форме можно записать как (5)½ или (5)0,5.
При решении задачи на квадратный корень из 5 желательно брать значение до 3 знаков после запятой.
Является ли квадратный корень из числа 5 рациональным или иррациональным числом?
Сначала давайте разберемся, что такое рациональные и иррациональные числа. Рациональное число — это число, которое можно записать в виде отношения любых двух целых чисел. Например, квадратный корень из 9 равен 3, что также можно записать как 3/1.
Принимая во внимание, что иррациональное число — это число, которое нельзя записать в виде отношения любых двух целых чисел. Итак, квадратный корень из 5, который эквивалентен 2,23 с точностью до двух десятичных значений, что является иррациональным числом.
Решенные примеры
1. Предположим, что стороны квадратной фоторамки имеют длину 2,33 м.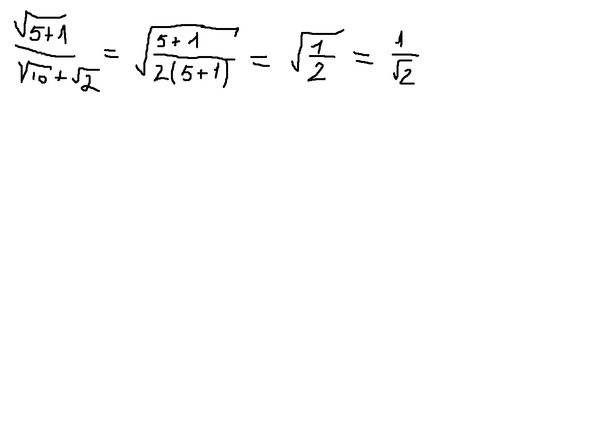
Узнайте площадь фоторамки и запишите ответ до ее ближайшего округления.
Анс. Длина стороны фоторамки = 2,33 м
Площадь квадрата = (сторона)2
Подставляя значение длины в приведенное выше уравнение, получаем,
Площадь фоторамки = (2,33)2= 5,4289 м2
Округлив, получим 5 м2
2. Площадь стены квадратной формы 25м2. Какова длина одной стороны стены? Чему равен периметр стены?
Анс. Площадь квадрата = (сторона)2
Подставляя значение площади стены получаем,
25 = (сторона)2
√25 = сторона = 5 метров.
Периметр квадрата = 4 х сторона
= 4 х 5 = 20 метров.
3. Каково значение 15√5?
Анс. 15√5 = 15 х 2,236 = 33,54101
4. Оцените следующие задачи:
1.
