Корень квадратный уравнения: Квадратные уравнения — урок. Алгебра, 8 класс.

alexxlab / / Разное

Содержание

Корни квадратного уравнения – примеры, формула нахождения

4.5

Средняя оценка: 4.5

Всего получено оценок: 328.

4.5

Средняя оценка: 4.5

Всего получено оценок: 328.

Решение квадратных уравнений весьма важно для решения практических задач по физике, так как многие формулы имеют старшую степень 2, в программировании и многих других смежных дисциплинах. Способов решить уравнение не так много, но чем больше уравнений вы решаете, тем быстрее и проще становится нахождение корней. Сегодня мы рассмотрим решение полных квадратных уравнений стандартной формы.

Квадратное уравнение

Квадратное уравнение – это уравнение, старшая степень которого равняется 2. Такое уравнение всегда имеет два корня, иногда эти корни совпадают, а иногда их нет среди действительных чисел. В последнем случае, мы пишем, что действительных корней нет.

В квадратном уравнении стандартной формы, есть три коэффициента:

  • а-первый коэффициент
  • в-второй коэффициент
  • с-свободный член уравнения.
    2*х+в*х+с=0$$ – где а,в,с – численные коэффициенты.

    Коэффициент а может равняться 1, тогда старший член записывается без чисел. Коэффициент при неизвестном равный 1 никогда не пишется, просто имеется в виду.

    Виды квадратного уравнения

    Квадратные уравнения бывают полные, где все коэффициенты имеют числовые значения, и неполные, где второй коэффициент или свободный член равен нулю.

    Если первый коэффициент равен 1, то уравнение называют приведенным и его можно решить двумя способами. Если а>1, способ решения только один.

    Способы нахождения корней квадратного уравнения

    Стандартный способ определения корней уравнения – через дискриминант. Этот способ работает с любым квадратным уравнением, вне зависимости от его вида и коэффициентов. Если перед нами приведенное квадратное уравнение, то можно воспользоваться теоремой Виета. Она требует некоторого опыта, но при определенном навыке ускоряет решение уравнения в несколько раз.

    Использование теоремы Виета позволяет не отвлекаться на промежуточные вычисления в задачах и легкие примеры, продолжая решать дальше.

    2+3х-10=0 $$– это уравнение приведенное, значит воспользуемся теоремой, обратной теореме Виета.

    $$x_1+x_2=-3$$

    $$x_1*x_2=-10$$

    Произведение чисел отрицательно, значит один из корней отрицателен. Причем отрицательный корень больше положительного на 3, так как результат сложения получился отрицательным. Начнем перебор и найдем корни квадратного уравнения для этого примера. Предположим, что один из корней равен 3, тогда:

    $$3-6=-3$$

    $$3*(-6)=-18$$ – не совпало.

    Попробуем 2:

    $$2-5=-3$$

    $$2*(-5)=-10$$

    Вот так, перебором и решается уравнение. Чем больше решенных примеров, тем быстрее подбор. Но неопытный ученик может решать этим способом очень долго. Поэтому на контрольных и экзаменах, если вы не уверены в себе, лучше использовать стандартный способ вычисления.

    Дискриминант

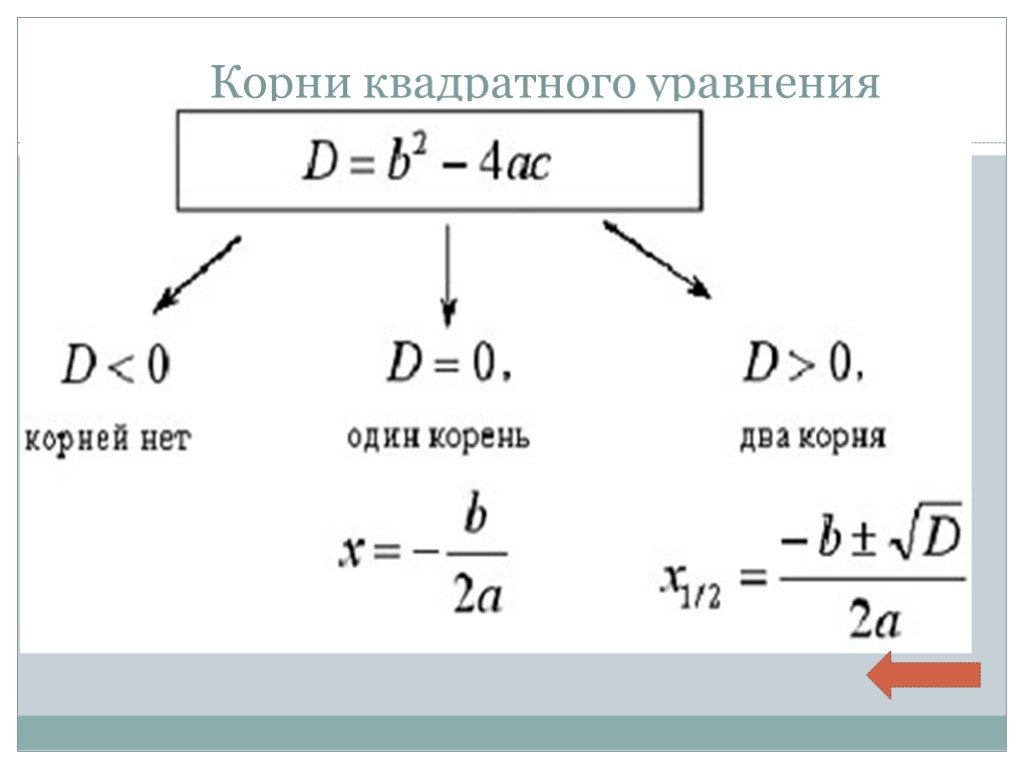
    Дискриминант это число, характеризующее уравнение. Корни квадратного уравнения равны:

    $$x_1= \frac{-b-\sqrt{D}}{2a}, x_1= \frac{-b+\sqrt{D}}{2a}$$,

    При этом дискриминант равен:

    $$D=b^2-4ac$$

    Имейте в виду, дискриминант может быть равен 0 и быть отрицательным. Но в первом случае, корни совпадают, а во втором – действительных корней нет.

    Что мы узнали?

    Мы узнали, как решаются квадратные уравнения. Привели два способа решения и сказали, в каком случае можно, а в каком нельзя пользоваться теоремой Виета. Привели формулу нахождения дискриминанта и решение через это значение.

    Тест по теме

    Доска почёта

    Чтобы попасть сюда — пройдите тест.

    • Патимат Кадиева

      4/5

    • Галина Садыкова

      5/5

    • Анастасия Петрова

      4/5

    Оценка статьи

    4.5

    Средняя оценка: 4.5

    Всего получено оценок: 328.

    А какая ваша оценка?

    Корень квадратного уравнения | это… Что такое Корень квадратного уравнения?

    Толкование

    Корень квадратного уравнения

    Квадратное уравнение — уравнение вида ax2 + bx + c = 0, где

    Содержание

    • 1 Уравнение с вещественными коэффициентами
      • 1. 1 Другие записи решений
      • 1.2 Приведённое квадратное уравнение
      • 1.3 Мнемонические правила
    • 2 Уравнение с комплексными коэффициентами
    • 3 Теорема Виета
    • 4 Разложение квадратного уравнения на множители
    • 5 См. также
    • 6 Ссылки

    Уравнение с вещественными коэффициентами

    Квадратное уравнение с вещественными коэффициентами может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта D = b2 − 4ac:

    • при D > 0 корней два, и они вычисляются по формуле
             (1)
    • при D = 0 корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях), кратности 2:
    • при D < 0 вещественных корней нет. Существуют два комплексных корня, выражающиеся той же формулой (1), либо (без использования извлечения корня из отрицательного числа) формулой

    Другие записи решений

    Вместо формулы (1) для нахождения корней можно использовать эквивалентное выражение

    где k = b / 2. Это выражение является более удобным для практических вычислений при чётном b, то есть для уравнений вида ax2 + 2kx + c = 0.

    Приведённое квадратное уравнение

    Квадратное уравнение вида x2 + px + q = 0, в котором старший коэффициент a равен единице, называют приведённым. В этом случае формула для корней (1) упрощается до

    Мнемонические правила

    • Из «Радионяни»:
      «Минус» напишем сначала,
      Рядом с ним p пополам,
      «Плюс-минус» знак радикала,
      С детства знакомого нам.
      Ну, а под корнем, приятель,
      сводится всё к пустяку:
      p пополам и в квадрате
      Минус несчастное прекрасное q.
    • Из «Радионяни» (другой вариант):
      p, со знаком взяв обратным,
      на два мы его разделим,
      и от корня аккуратно
      знаком «минус-плюс» отделим.
      А под корнем очень кстати
      половина p в квадрате
      минус q — и вот решенья,
      то есть корни уравненья.

    Уравнение с комплексными коэффициентами

    В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше ее вариантам, но различимыми является только два случая: нулевого дискриминанта (один корень) и ненулевого (два корня).

    Основная статья: Теорема Виета

    Сумма корней приведённого квадратного уравнения x2 + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:

    В общем случае (для неприведённого квадратного уравнения ax2 + bx + c = 0):

    Разложение квадратного уравнения на множители

    Если известны оба корня квадратного уравнения, его можно разложить по формуле

    В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

    См. также

    • Сведением к квадратному уравнению решается уравнение четвёртой степени (как в общем случае, так и в простейших: биквадратное уравнение, возвратное уравнение четвёртой степени).

    Ссылки

    • Решение квадратных уравнений онлайн [1],[2],[3]

    Wikimedia Foundation. 2010.

    Игры ⚽ Поможем написать реферат

    • Корень женьшеня
    • Корень квадратный

    Полезное


    Формула квадратного корня

    — Что такое формула квадратного корня? Примеры

    Формула квадратного корня помогает представить любое число в форме его квадратного корня. Квадратный корень из любого числа — это то значение, которое при умножении само на себя дает исходное число. Он представлен с помощью символа «√». Каждое число имеет два квадратных корня, один с положительным значением, а другой с отрицательным значением. Например, число 4 имеет два квадратных корня, -2 и 2. Это можно выразить как √4 = ±2. Это можно проверить следующим образом: (-2) × (-2) = 4 и 2 × 2 = 4. Давайте узнаем больше о формуле квадратного корня на этой странице.

    Что такое формула квадратного корня?

    Квадратный корень из любого числа дается как число, возведенное в степень 1/2. При вычислении квадратного корня любого числа мы берем как отрицательные, так и положительные значения в качестве квадратного корня после вычисления. Формула квадратного корня для полного квадрата даст в результате целое число. Квадратный корень из отрицательного числа никогда не может быть действительным числом.

    Формула квадратного корня

    Формула квадратного корня из числа x задается как формула для вычисления квадратного корня из x будет выглядеть так:

    √x = √(y × y) = y

    , где y — квадратный корень из любого числа x. Это также означает, что если значение y является целым числом, то x будет идеальным квадратом.

    Методы вычисления формул квадратного корня

    Хотя существуют различные методы, которые можно удобно использовать для получения идеальных квадратов, метод деления в длину можно использовать для любого числа, независимо от того, является ли оно идеальным квадратом или нет.

    • Метод многократного вычитания квадратного корня
    • Извлечение квадратного корня методом простой факторизации
    • Извлечение квадратного корня методом оценки
    • Извлечение квадратного корня методом деления в длину

    Давайте посмотрим на несколько решенных примеров, чтобы лучше понять формулу квадратного корня.

    Разбивайте сложные концепции с помощью простых визуальных средств.

    Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

    Запись на бесплатный пробный урок

    Примеры с использованием формулы квадратного корня

    Пример 1: Используя формулу квадратного корня, вычислите квадратный корень из 144.

    Решение:

    Чтобы найти квадрат корень 144 из простое разложение 144, мы получаем,

    144 = 2 × 2 × 2 × 2 × 3 × 3

    = (2 × 2 × 3) 2

    Используя формулу квадратного корня,

    √144 = ± ± [(2 × 2 × 3) 2 ] 1/ 2

    √144 = ±12

    Ответ: Квадратный корень из 144 = ±12

    Пример 2: Определите квадратный корень из 60. 2 Решение:

    Чтобы найти квадратный корень из 60 из простой факторизации 60, мы получаем,

    60 = 2 × 2 × 3 × 5

    = (2) 2 × 3 × 5

    Используя формулу квадратного корня,

    √60 = [( 2) 2 × 15 ] 1/ 2

    √60 = 2√15

    Ответ: Квадратный корень из 60 = 2√15

    Пример 3: Вычислите длину стороны квадрата, площадь которого равна 400 квадратных единиц.

    Решение:

    Найти: Длина стороны квадрата.

    Дано, площадь квадрата = 400 квадратных единиц

    Используя формулу квадратного корня или, точнее, формулу площади квадрата,

    Сторона = √(площадь) = √(сторона) 2

    = √400

    = 20 шт.

    Ответ: Длина стороны квадрата = 20 единицам

    Часто задаваемые вопросы о формуле квадратного корня

    Что такое формула квадратного корня в математике?

    В математике формула квадратного корня используется для представления любого числа в форме его квадратного корня, например, для любого числа x его квадратный корень будет выражен как √x = x 1/2

    Что такое Формула квадратного корня для отрицательных чисел?

    Мы знаем, что отрицательные числа не имеют действительных квадратных корней. Квадратные корни чисел, отличных от полного квадрата, считаются иррациональными числами. Главный квадратный корень любого отрицательного числа, скажем -x, равен: √(-x)= i√x, где i — квадратный корень из -1.

    Каковы применения формулы квадратного корня?

    Существует множество применений формулы квадратного корня.

    • Используется в алгебре и геометрии. Он служит основой для формулы корней квадратного уравнения; квадратичные поля и кольца целых квадратичных чисел.
    • Часто используется во многих физических законах.
    • Для расчета площадей, объемов и других формул измерения.
    • Широко используется плотниками, архитекторами и инженерами.

    Как написать формулу квадратного корня словами?

    На словах формула квадратного корня выражается следующим образом. Квадратный корень из любого числа — это число, возведенное в степень 1/2.

    Формула квадратного корня — GeeksforGeeks

    Алгебра — важная тема математики. Квадратный корень — это операция, которая используется во многих формулах и различных областях математики. Эта статья о квадратном корне и формуле квадратного корня. Квадратный корень из числа — это возведение числа в квадрат, которое дает исходное число. В этой статье обсуждаются несколько формул квадратного корня со своими проблемами.

    Квадратный корень 

    Квадратный корень из числа — это возведение числа в квадрат, которое дает исходное число. Это тот множитель числа, который при возведении в квадрат дает исходное число. Это значение мощности 1/2 от этого числа. Квадратный корень числа представлен как √ .

    Пример: Квадратный корень из 9 ⇒ √9 = ± 3         (-3) 2 = 9

    Число внутри квадратного корня называется радикалом, а символ квадратного корня называется радикалом.

    Методы нахождения квадратного корня числа

    В математике широко используются два метода нахождения квадратного корня числа. Они обсуждаются ниже.

    1. Метод простой факторизации
    2. Метод длинного деления

    Метод простой факторизации

    Простой факторизации — это метод, в котором число представляется в виде произведения простых чисел. Затем квадратный корень из числа штрафуется по заданному понятию.

    Чтобы найти квадратный корень, используя метод разложения на простые множители:

    Шаг 1: Представьте число в его простых множителях, используя метод разложения на простые множители.

    Шаг 2: Сформируйте пару одинаковых множителей.

    Шаг 3: Возьмите один множитель из каждой пары, а затем найдите произведение всех множителей, полученных путем взятия одного множителя из каждой пары.

    Шаг 4: Результатом является квадратный корень из числа.

    Пример метода простой факторизации:

    Метод простой факторизации для нахождения квадратного корня
     2     196       
     2       98
     7      49
     7       7 
            1
    Простые множители 196 = (2 × 2) × (7 × 7)
    Чтобы получить квадратный корень, возьмем произведение 2 из (2×2) и 7 из (7×7)

    Квадратный корень из 196 = 2×7 = 14

    Метод длинного деления

    Метод длинного деления — очень полезный метод для нахождения квадратного корня из числа. Квадратный корень из неполных квадратов, таких как 14, 15, 18 и т. д., можно найти с помощью метода деления в длинную сторону. Чтобы найти квадратный корень с помощью метода деления в длину, мы должны выполнить определенные шаги, которые описаны ниже.

    Шаги для нахождения квадратного корня числа с использованием метода деления в длинную сторону:

    Пример: Найдите квадратный корень из 256 с помощью метода деления в длинную сторону.

    Шаг 1. Разделите число на пары, начиная с одного места. Например, пары, начинающиеся с одного места:= 2 , 56

     

    Шаг 2. После разделения цифр на пары начните с самой левой пары или цифры. Наибольшее число, квадрат которого чуть меньше или равен первой паре или цифре, берется как делитель, а также как частное. В приведенном выше примере наибольшее число, квадрат которого чуть меньше 2, равно 1. Итак, делитель равен 1, а частное также равно 1. первую пару или цифру и перенесите следующую пару справа от напоминания, чтобы получить новый дивиденд. В приведенном выше примере 2 – 1 = 1, затем мы опускаем следующую пару, т.е. 56, и новое делимое становится 156.0003 Шаг 4. Теперь новый делитель получается путем сложения предыдущего делителя и предыдущей цифры частного и объединения его с подходящей цифрой, которая также берется в качестве следующей цифры частного, выбранной таким образом, чтобы произведение новый делитель, и эта новая цифра в частном равна или чуть меньше нового делимого. В приведенном выше примере предыдущий делитель равен 1, а предыдущая цифра частного равна 1, и их сложение дает 2, что является новым делителем. Теперь нам нужно выбрать цифру так, чтобы произведение нового делителя и новой цифры в частном было равно или меньше нового делимого, т. е. 26 — это новый делитель, а 6 — новая цифра, объединенная с предыдущей. частное. Текущее частное равно 16,9.0004

     

    Шаг 5. Повторяйте шаги 2, 3 и 4, пока не будут взяты все пары. Теперь полученное частное представляет собой квадратный корень из заданного числа. В приведенном выше примере взяты все пары, поэтому квадратный корень из числа 256 равен 16. 9 кв. Квадратный корень 1 1 √1 = 1 2 4 √2 = 1,414 9024 5 3 9 √3 = 1,732 4 16 √4 = 2 5 25 √5 = 2,236 6 36 9 0249 √6 = 2,4494 7 49 √7 = 2,645 8 64 √8 = 2,828 9 81 √9 = 3 10 9024 9 100 √10 = 3,162

    Формула квадратного корня

    Квадратный корень из числа имеет показатель 1/2. Формула квадратного корня используется для нахождения квадратного корня из числа.

    Формула квадратного корня:      √x = x 1/2

    Формула квадратного корня
    √x = x 1/2
    √x . √x = x
    x√y . x√y = x 2 y
    √(x × y) = √x × √y
    √( х/у) = √х/√у
    x / √y = (x / √y) × ( √y / √y) = (x . √y)/y  
    x. √y ± z. √y = (x ± z) √y

    x / (y + z. √p) = [x / (y + z√p)] × [(y – z√p)/ ( у – z√p)]

                          = [x(y – z√p)]/[y 2 – z 2 p]

    Рационализировать знаменателя путем умножения на [(y – z√p)/ (y – z √p)]

    x / (y – z. √p) = [x / (y – z√p)]×[(y + z√p)/ (y + z√p )]

                          = [x(y + z√p)]/[y 2 – z 2 p]

    9000 3 Рационализируйте знаменатель, умножив на [(y + z√p)/ (y + z√p)]

    Примеры задач

    Вопрос 1: Найдите сумму: 5√3 + 6√12

    Решение:

      5√3 + 6√12 = 5√3 + 6(√(4 × 3)

                                 √3 + 6 × 2√3

                                  = 5√3 + 12√3

                                      = 17√3

    Вопрос 2: Оцените:  √64 – √25

    Решение:

    √64 – √25 = √(8 × 8)  – √(5 × 5)

                             = 8 – 5 = 3

    Вопрос 3: Оцените: √63 / √ 28

    Решение:

     √63 / √28 = √(7 × 9)/ √(7 × 4)

                               = √[(7 × 9 )/ (7 × 4 )]

                              = √(9/4)

                              = √9 / √4 

                              = 3/2

    Вопрос 4.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *