| Дата: 20.11.2014 Таблица производных.Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств. Это знакомство позволит: Понимать суть несложных заданий с производной; Успешно решать эти самые несложные задания; Подготовиться к более серьёзным урокам по производной. Сначала — приятный сюрприз.) Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний! Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует. Приступим к знакомству?) Термины и обозначения.В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках. Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная. Дифференцирование — действие над функцией. Производная — результат этого действия. Так же, как, например, сумма — результат сложения. Или частное — результат деления. Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т. п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания. п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее. Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…) Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем. Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. 1. Таблица производных (формулы дифференцирования). 3. Производная сложной функции. Начнём по порядку. В этом уроке рассмотрим таблицу производных. Таблица производных.В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п. Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.) Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету… Рассмотрим несколько примеров: 1. Найти производную функции y = x 3 Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат: (x 3) » = 3·x 3-1 = 3x 2 Вот и все дела. Ответ: y» = 3x 2 2. Найти значение производной функции y = sinx в точке х = 0. Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция. По табличке находим синус и соответствующую производную: y» = (sin x)» = cosx Подставляем ноль в производную: y»(0) = cos 0 = 1 Это и будет ответ. 3. Продифференцировать функцию: Что, внушает?) Такой функции в таблице производных и близко нет. Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает… Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается! Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем: Ответ: y» = — sin x . Пример для продвинутых выпускников и студентов: 4. Найти производную функции: Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так: А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем: Вот и всё. Это будет ответ. Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования. |
Производная Содержание 1 Понятие производной 2 Алгоритм
Производная
Содержание 1. Понятие производной.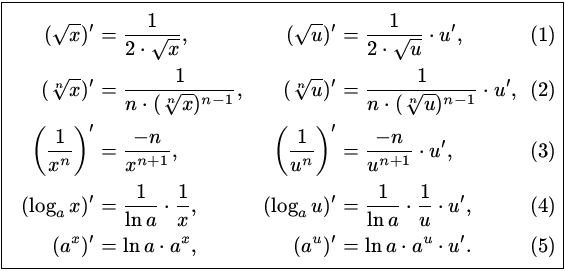 2. Алгоритм нахождения производной. 3. Примеры. 4. Таблица производных. 5. Физический смысл производной. 6. Правила нахождения производных. 7. Непрерывность функции. 8. Геометрический смысл производной.
2. Алгоритм нахождения производной. 3. Примеры. 4. Таблица производных. 5. Физический смысл производной. 6. Правила нахождения производных. 7. Непрерывность функции. 8. Геометрический смысл производной.
Понятие производной Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке х этого интервала называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю. ∆f f ′(x) = lim ∆x→ 0 ∆x Нахождение производной называют дифференцированием
Понятие производной у ∆f f ′(x) = lim ∆x→ 0 ∆x f(x 0) у = f(x) ∆f f(x 0 + ∆х) ∆х 0 х0 х0+ ∆х х
Алгоритм нахождения производной 1. Зафиксировать значение х0, найти f(x 0). 2. Дать аргументу х0 приращение ∆х, перейти в новую точку х0 + ∆х, найти f(x 0 + ∆х). 3. Найти приращение функции: ∆f = f(x 0 + ∆х) – f(x 0). ∆f 4. Составить отношение. ∆х ∆f 5. Вычислить lim. ∆x→ 0 ∆х 6. Этот предел и есть f ′(x 0).
Е Н А А я А
Примеры 1. Найти производную функции y = kx + b в точке хo
Примеры 2. Найти производную функции y = C (C – const) в точке хo
Примеры 3. Найти производную функции y = x 2 в точке хo
Примеры 4. Найти производную функции y = √x в точке хo
Примеры 4. Найти производную функции y = √x в точке хo
Примеры 5. Найти производную функции y = 1/x в точке хo
Примеры 5. Найти производную функции y = 1/x в точке хo
Таблица производных f (x) C f ′(x) 0 f (x) √x f ′(x) 1/(2√x) kx + b k ex ex x 2 2 x ax ax lna xn nxn– 1 tg x 1/cos 2 x 1/x – 1/x 2 ctg x – 1/sin 2 x sin x cos x ln x 1/x cos x – sin x loga x 1/(x lna)
Физический ( механический ) смысл производной Если прямолинейном движении путь s, пройденный точкой, есть функция от времени t, т. е. s = s(t), то скорость точки есть производная от пути по времени, т. е. v(t) = s′(t). Производная выражает мгновенную скорость в момент времени t.
е. v(t) = s′(t). Производная выражает мгновенную скорость в момент времени t.
Правила нахождения производной 1. Если функции u(x) и v(x) имеют в точке х производные, то их сумма u(x) + v(x) также имеет в этой точке производную, причем (u + v)′ = u′ + v′ 2. Если функция u(x) имеет в точке х производную и С – данное число, то функция С∙u(x) также имеет в этой точке производную, причем (Сu)′ = С∙u′
Правила нахождения производной 3. Если функции u(x) и v(x) имеют в точке х производные, то их произведение u(x) ∙ v(x) также имеет в этой точке производную, причем (u ∙ v)′ = u′∙v + u∙v′ 4. Если функция v(x) имеет в точке х производную и 1 v(x) ≠ 0, то функция также имеет в этой точке v(x) производную, причем v′ 1′ =– 2 v v ()
Правила нахождения производной 5. Если функции u(x) и v(x) имеют в точке х u(x) производные и v(x) ≠ 0, то функция также имеет v(x) в этой точке производную, причем u ′ u′v – uv′ v = v 2 ( )
Производная сложной функции (f(g(x)))′ = f′(g(x))∙g′(x) Примеры: 1. ((5 x – 3)3)′ = 3(5 x – 3)2∙(5 x – 3)′ = = 3(5 x – 3)2 ∙ 5 = 15(5 x – 3)2 2. (sin(4 x + 8))′ = cos(4 x + 8)∙(4 x + 8)′ = = cos(4 x + 8)∙ 4 = 4 cos(4 x + 8)
((5 x – 3)3)′ = 3(5 x – 3)2∙(5 x – 3)′ = = 3(5 x – 3)2 ∙ 5 = 15(5 x – 3)2 2. (sin(4 x + 8))′ = cos(4 x + 8)∙(4 x + 8)′ = = cos(4 x + 8)∙ 4 = 4 cos(4 x + 8)
Если функция имеет производную (дифференцируема) в точке х, то она непрерывна в этой точке.
【Как сделать】Что такое производная от 2 cos 2x
Последнее обновление: 2 февраля 2022 г. | Автор: Лерой Робертс
Чем отличается 2 от 2x?
Поскольку 2 постоянно относительно x , производная 2cos(2x) 2 cos ( 2 x ) относительно x равна 2ddx[cos(2x)] 2 d d x [ cos ( 2 x ) ] .
Как получить cos2x?
Как отличить 2sin2x?
youtube.com/embed/ZGhOG5ZNlzU?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Как отличить 4sin2x? 92). Вы помните домен и диапазон?
Cos2x равен 2cosx?
Раствор. cos2x и 2cosx и совершенно разные термины. 2cos x в два раза больше косинуса угла x . … cos2x — это косинус угла 2x.
Какая производная от Sin²x?
cos 2x
Производная от sin 2x равна cos 2x .
Что является производным от 5sin2x?
Поскольку 5 постоянно относительно x , производная 5sin(2x) 5 sin ( 2 x ) по x равна 93x равно 3 sin 2 x cosx. Мы можем оценить дифференцирование sin3x, используя цепное правило и первый принцип производных.
Является производной sin cos?
Производная функции синуса равна функции косинуса . т. е. производная от sin x по x равна cos x. Математически это записывается как d/dx(sin x) (или) (sin x)’ = cos x. 2x» src=»https://www.youtube.com/embed/7QbVam1vUX4?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>
2x» src=»https://www.youtube.com/embed/7QbVam1vUX4?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>
Как найти Cos2x при заданном sin2x?
Поскольку при использовании формулы суммы для косинуса получается cos 2x = cos 2 x – sin 2 x, у вас есть два дополнительных способа выразить это с помощью тождеств Пифагора: Вы можете заменить sin 2 x на ( 1 – cos 2 x) и упростить, чтобы получить cos 2x = 2 cos 2 x – 1. Вы можете заменить cos 2 х с (1 – sin 2 х) и упростить, чтобы получить cos 2x = 1 – 2 sin 2 х.
Как найти sin 2x Cos2x tan2x?
Как найти sin2x с учетом Sinx?
youtube.com/embed/5k5lqrFGTK8?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>10 1 График СИНАНСКИЙ И КОСИЗИНАЛЬНЫЙ ИСПОЛЬЗОВАНИЕ И УДАЛЕНИЕ Ответы
ALLBILDERVIDEOSSHOPPINGMAPSNEWSBücher
SUCOOPTION
10.1 Графический синус и косинус-предварительный калькулус
Precalculus.flipdmath.com-graphing-a-graphith-a-graphith-hraphtus—graphith-graphing-maraphing-maraphing-a-graphing-marphing-marphing-a-graphitus
.0005
Чтобы приобрести этот пакет уроков или уроки для всего курса, нажмите здесь. Практические решения. pc_10.1_solutions.pdf. Размер файла: 1125 кб.
[PDF] 10.1 Практика — построение графика синуса и косинуса Предварительное исчисление
precalculus.flippedmath.com › uploads › 1 › 1 › pc_10.1_solutions.pdf
10.1 Практика — построение графика синуса и косинуса. Предварительный расчет. Название: Решения. Для 1-3 определите амплитуду, период, частоту и вертикальное смещение каждого …
Предварительный расчет. Название: Решения. Для 1-3 определите амплитуду, период, частоту и вертикальное смещение каждого …
10.1 — График синуса и косинуса — Предварительный расчет
smacmathprecalculus.weebly.com › 101—график-…
главная · СУМКА BLIZZARD · Проход в зал · Обзор · Календарь · Содержание; Семестр 1; Семестр 2; Smacmath … 10.1 — График синуса и косинуса …
[PDF] 10.1 Корректирующее задание — Графический расчет синуса и косинуса
smacmathprecalculus.weebly.com › 1 › 2 fpc_10.1_ca_new_key.5
0.pdf
Корректирующее задание — Построение графика синуса и косинуса. Предварительный расчет. Для 1-6 определите данную информацию и нарисуйте график триггерной функции. 1) у = 3 потому что х.
[PDF] 10.1 Графики синуса и косинуса Название
schoolwires.henry.k12.ga.us › cms › lib › Centricity › Domain › 10.1…
10.1 Графики синуса и косинуса Название: Графики синуса и косинус выглядят как волны. Их называют синусоидами. • Родительские графики. = cos@f(0). И. 0. -1.
Их называют синусоидами. • Родительские графики. = cos@f(0). И. 0. -1.
[PDF] 10.1 Графики синуса и косинуса Название
schoolwires.henry.k12.ga.us › cms › lib › Centricity › Domain › 10.1…
Графики синуса и косинуса выглядят как … Для 1-3 определите амплитуду, период, частоту и вертикальное смещение каждого… 10.1 Применение и расширение.
Bilder
Alle anzeigen
Alle anzeigen
10-1 Graphing Sine and Cosine.pdf — Pre-Calculus 10.1…
and-Cosinepdf
Просмотр 10-1 Graphing Sine and Cosine.pdf из MATH 3516 в средней школе Ирвина. … 10.1 Применение и расширение1. Создайте asinefunction на основе …
Pre Calc — 10.1 Graph Sine and Cosine — YouTube
www.youtube.com › смотреть
21.10.2020 · Нужен репетитор? Нажмите на эту ссылку и получите первый сеанс бесплатно! https://gradegetter.com/sign-up …
Dauer: 21:46
Прислан: 21.10.2020
График синусоидальных и косинусных триггерных функций с преобразованиями .


 Вот они эти три кита:
Вот они эти три кита: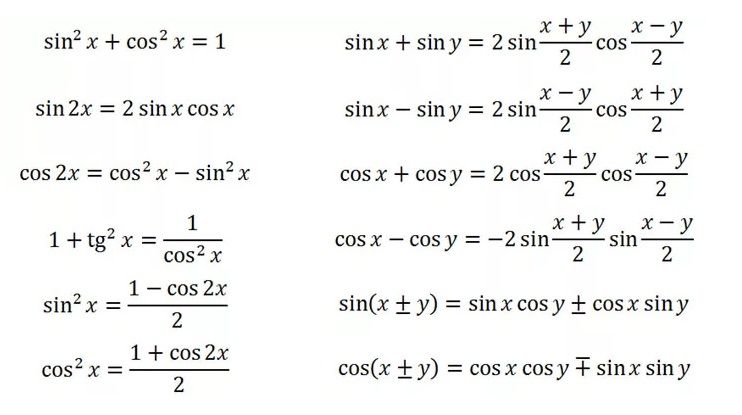
 Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
 По формуле косинуса двойного угла:
По формуле косинуса двойного угла: Запишем предел отношения приращения
функции к приращению аргумента при :
Запишем предел отношения приращения
функции к приращению аргумента при :









 Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
