Косинус 20 градусов равен: Косинус 20 равен чему? cos(20) = ?

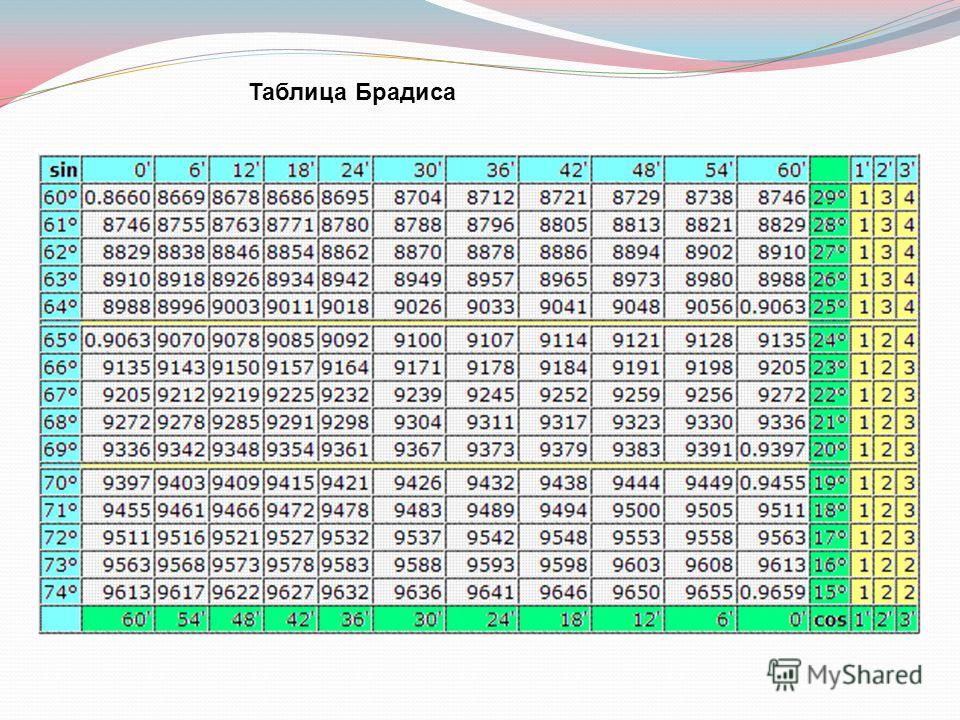
Тангенс 36 градусов : Чулан (М)

Sasha2	Тангенс 36 градусов 15.02.2011, 16:39
21/06/06 1721	Верно ли, что тангенс 36 градусов равен В учебнике дается другой ответ: Считал через сторону правильного 5-угольника, вписанного в единичную окружность. Тогда синус равен половине этой стороны, а косинус есть апофема. Сторона правильного 5-угольника, вписанного в единичную окружность, равна P.S. В ответе то же самое, только вместо (корень четвертой степени из двадцати) дается (корень квадратный из десяти).

caxap	Re: Тангенс 36 градусов 15.02.2011, 16:53
Заслуженный участник 07/01/10 2015	http://m. wolframalpha.com/input/?i=tan(Pi/5 ) (Могу предложить другой путь) Корни многочлена — это корни пятой степени из единицы, то есть . По теореме Виета, сумма всех корней равна нулю (коэффициент при нулевой), в частности равна нулю вещественная часть. Отсюда получаем уравнение относительно : . Находим , находим половинный угол, затем синус и тангенс.

Cute	Re: Тангенс 36 градусов 15.02.2011, 21:19
23/05/09 77	Sasha2 , преобразуйте выражение двумя способами: 1) по формуле бинома Ньютона; 2) по первой формуле Муавра. Далее приравняйте мнимые части двух записанных результатов, тогда получится однородное уравнение относительно и , которое легко приводится к алгебраическому уравнению относительно .

мат-ламер	Re: Тангенс 36 градусов 19.02.2011, 19:14
Заслуженный участник 30/01/09 5536	Ещё вариант — координаты правильного пятиугольника, вписанного в единичную окружность, можно найти, решая уравнение .

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 4 ]

Модераторы: Модераторы Математики, Супермодераторы

планиметрия. — Колпаков Александр Николаевич

Вопрос от Юлии:
Подскажите, как можно решить задачу: В треугольнике MNP угол M равен 40 градусов, угол N равен 20 градусов, а MN-NP=8. Найти длину биссектрисы, проведенной из вершины угла P. Задача взята из вступительной работы по математике в 8 класс физико — математического лицея.

Решение репетитора по математике к задаче про биссектрису (Колпаков А.Н.):

Пусть NP=x, MN=x+8. Очевидно, что . По теореме синусов имеем равенство:
Применим формулу синуса тройного угла:
. Сокращая на , после несложных преобразований получим, что
В треугольнике KNP снова по теореме синусов запишем:

Как и следовало ожидать, вся тригонометрия сокращается. Задача интересна тем, что имеет весьма красивое и простое решение (которое я показал) в противовес долгому и мучительному стандартному решению (через отрезок KN и теорему косинусов в треугольнике PKN).

Вопрос от Людмилы: Подскажите, как решить задачу: в равнобедренном треугольнике с углом альфа при основании высота, опущенная на основание, больше радиуса вписанного в треугольник круга на m. Основание треугольника равно? Спасибо.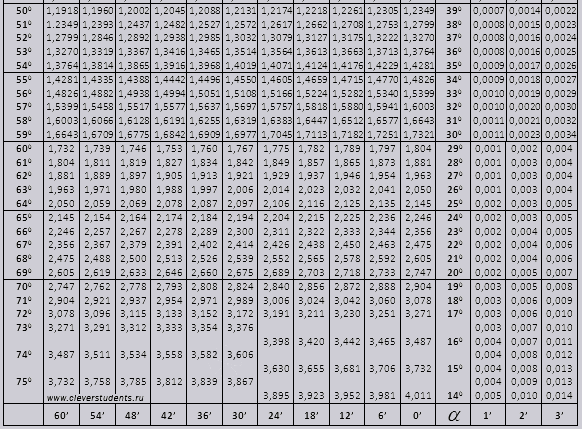
Задача про высоту и радиус. Решение репетитора по математике.(Колпаков А.Н. )
По техническим причинам вместо альфа будем использовать родной и любимый всеми математиками икс :). Пусть в треугольнике ABC угол  — угол при основании. Обозначим буквой N точку касания окружности с боковой стороной AB. Тогда и имеют два равных угла и . Поэтому . Так как высота больше радиуса на m, то BO=m. По определению косинуса острого угла в прямоугольном треугольнике имеем
Тогда . По определению тангенса острого угла A в прямоугольном треугольнике ABD имеем
Тогда

Вопрос репетитору по математике от Жанат:
Пожалуйста. Помогите решить задачу на площадь по геометрии. Прошу вас…
В треугольнике АВС AB=AC=13; AC=24. На его стороне АС дана точка D так, что CD=6. Найдите

Решение репетитора (Колпаков А.Н.).
Найдем сначала площадь всего треугольника ABC. Есть возможность действовать или по формуле Герона , или через высоту, проведенную к основанию. Дабы не усложнять рисунок дополнительной линией репетитор по математике работает с первым способом. Тогда  — полупериметр треугольника.
Воспользуемся известным фактом: при равных высотах отношение площадей двух треугольников равно отношению их оснований

Вопрос от Роберта:
Здравствуйте! Помогите пожалуйста решить задачу из типовых вариантов ЕГЭ под номером C4 (задача представлена ниже).Треугольник ABC вписан в окружность. Ее радиус равен 12 см. Известно, что BC=4cм и AB = 6 см . Найдите AC.
Репетитор по математике использует теорему Птолемея (А.Н. Колпаков)
Самое быстрое и красивое решение задачи дает редкая, но в некоторых ситуациях незаменимая теорема Птолемея. Она есть у меня в справочном отделе сайта: если четырехугольник вписан в окружность, то сумма произведений его сторон равна произведению его диагоналей. У нас никакого, казалось бы, четырехугольника нет. Построим его. Дополнительное построение репетитора по математике будет следующим: продлим радиус BO до пересечения его с дугой AC в точке К. Получим четырехугольник ABCK. Он вписан в окружность. Искомый отрезок AC — его диагональ. Очевидно, что BK=24 см. Так вписанные углы BAK и BCP опираются на диаметр, следовательно они прямые. По теореме Пифагора в треугольниках и находим катеты AK и CK и применяем:


Применяем терему Птолемея:


Сокращая на 24 получим окончательно:

Комментарий репетитора о применении теоремы Птолемея: на ЕГЭ можно использовать любой известный в математике факт, не обязательно соответствующий программе 5-11 класса. Надо только на него не забыть сослаться при оформлении. Если нужно школьное решение — можно действовать через поиск углов A и C (по формуле ). Найдя эти углы, применить теорему о сумме углов в треугольнике и через формулы приведения, удаляя «пи», найти косинус угла B по формуле . После этого AC легко находится по теореме косинусов. Но в таком случае мы получим не только более длинное решение, но и более громоздкое в плане вычислений.

Вопрос репетитору по математике от Светланы Ивановны:Уважаемый Александр Николаевич! Если Вам не трудно, помогите решить задачу: В трапеции АВСД сумма острых углов 90 градусов, меньшая диагональ ВД перпендикулярна основаниям ВС и АД.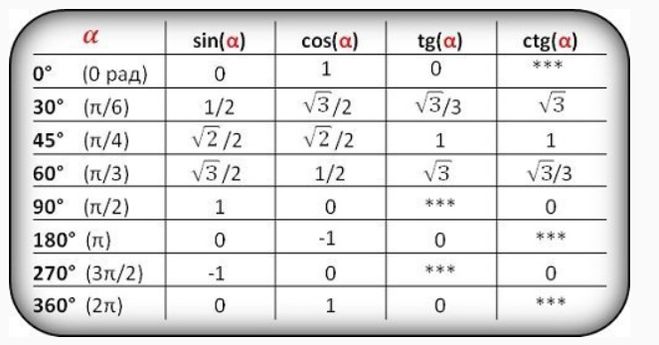 Найдите площадь трапеции, если основание АД = 2, СД = 18.
Репетитор о задаче с трапецией (А.Н. Колпаков)
Так как , то острыми будут углы A и C. Так как , то (по двум углам). Пусть BD=x, тогда составляя пропорцию из сторон подобных треугольников, получим , откуда BC=\frac{x}{2}[/math]. По теореме Пифагора в треугольнике BDC составим уравнение
У меня получился корень .
Тогда . После некоторых манипуляций с иррациональностями получаем в ответе .

Вопрос репетитору от Артема Иванова.Треугольник KLM подобен треугольнику NPR.Докажите,что отношение длин медиан,проведенных из K и N,равно коэффициенту подобия треугольников. Помогите, пожалуйста, задача с контрольной. Я ученик 8 класса. Не из России.
Репетитор по математике о задаче про медианы. Решение достаточно простое. Пусть коэффициент подобия треугольников равен k. Тогда . Так как и . Следовательно . Поскольку у подобных треугольников равны соответственные углы, то . Треугольники LKH и PNE будут подобны по двум пропорциональным сторонам и углу между ними, причем . Что и требовалось доказать.

Вопрос репетитору по математике от Тимерлана Селахова
Помогите с решениями этой задачи:

Решение (Колпаков А.Н.):
Треугольник ABD равнобедренный по определению (т.к. AB=DB по условию) и ВМ — медиана (т.к. АМ=DМ по условию). Следовательно ВМ — биссектриса и высота (по тереме о совпадении медианы с биссектрисой и высотой). Тогда и поэтому Так как и  — смежные углы, то

Вопрос от Тамины. Помогите найти площадь большого прямоугольника, разделенного на 12 квадратов, если площадь закрашенного квадрата равна 1 кв.см.

Задача про закрашенный квадрат. Решение репетитора по математике:

Очевидно, что площадь пяти нижних квадратов равна 8 и длина прямоугольника ABCD равна 4 см. Пусть BE=x, тогда NK=4-2x и соответственно NP=NM=2-x MH=x- (2-x)=2x-2. Так как в длине отрезка MP укладывается 3 длины квадрата со стороной 2х-2, то очевидно MP=3 (2x-2).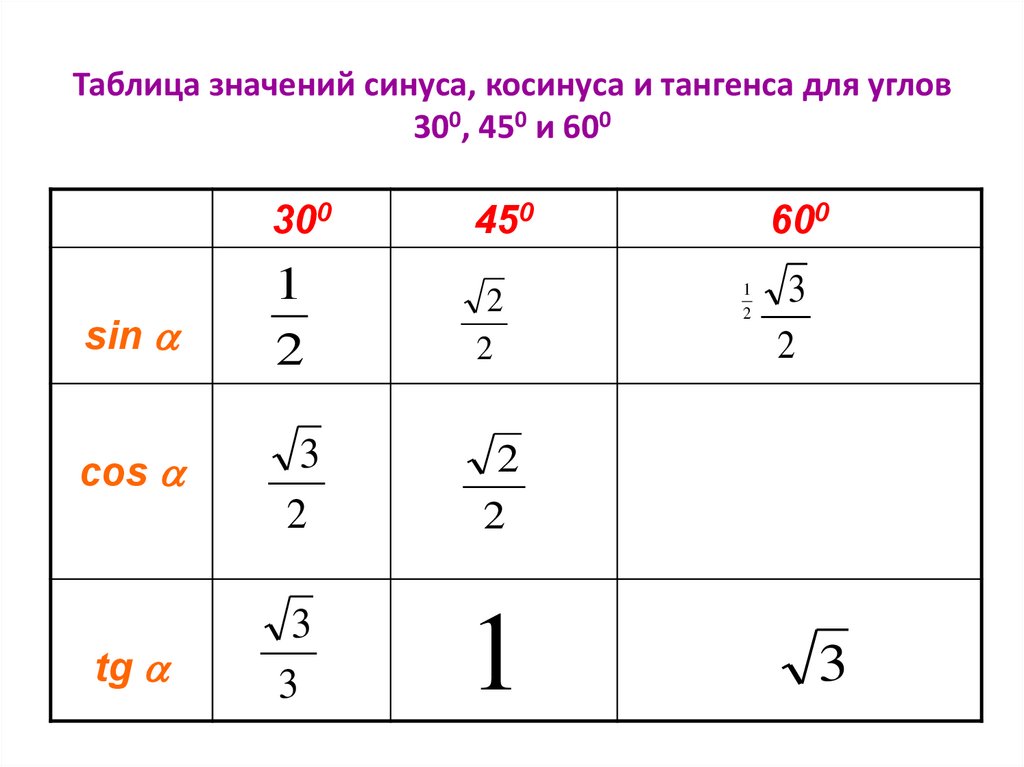 Учитывая, что MP=NK, получаем уравнение:
4-2x=3 (2x-2)
откуда x=1,25. Следовательно

Pages: 1 2

Cos 20 градусов — Найти значение Cos 20 градусов

LearnPracticeDownload

Значение cos 20 градусов равно 0,9396926. . . . Cos 20 градусов в радианах записывается как cos (20° × π/180°), т. е. cos (π/9) или cos (0,349065…). В этой статье мы обсудим способы нахождения значения cos 20 градусов на примерах.

• Cos 20°: 0,9396926. . .
• Cos (-20 градусов): 0,9396926. . .
• Cos 20° в радианах: cos (π/9) или cos (0,34 . . .)

Каково значение Cos 20 градусов?

Значение cos 20 градусов в десятичной системе равно 0,939692620. . .. Cos 20 градусов также можно выразить с помощью эквивалента заданного угла (20 градусов) в радианах (0,34906 . . .)

Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (пи/ 180°)
⇒ 20 градусов = 20° × (π/180°) рад = π/9 или 0,3490. . .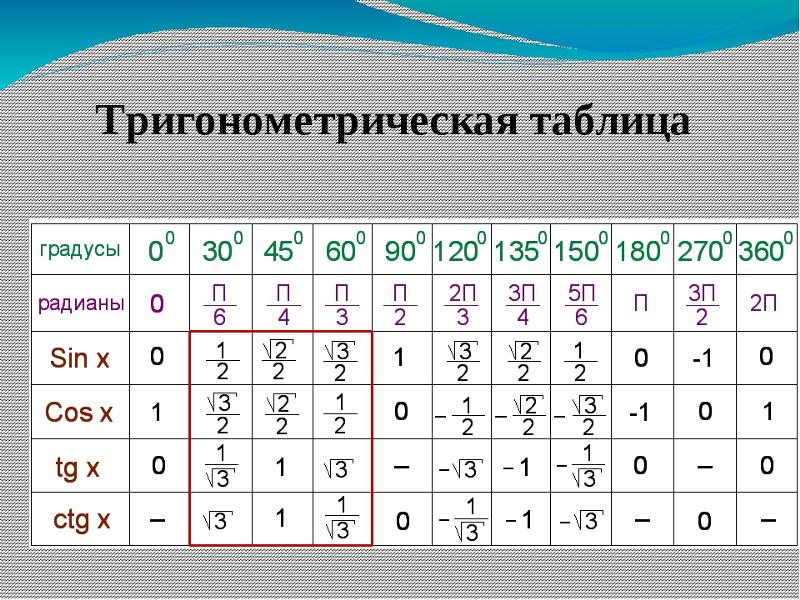
∴ cos 20° = cos (0,3490) = 0,9396926. . .

Объяснение:

Для cos 20 градусов угол 20° лежит между 0° и 90° (первый квадрант). Поскольку функция косинуса положительна в первом квадранте, значение cos 20° = 0,9396926. . .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 20° как cos 20 градусов = cos(20° + n × 360°), n ∈ Z.
⇒ cos 20° = cos 380° = cos 740° и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-20°) = cos(20°).

Методы определения значения косинуса 20 градусов

Функция косинуса положительна в 1-м квадранте. Значение cos 20° равно 0,93969. . .. Мы можем найти значение cos 20 градусов по:

• Используя тригонометрические функции
• Использование единичного круга

Cos 20° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить cos 20 градусов как:

• ± √(1-sin²(20°))
• ± 1/√(1 + tan²(20°))
• ± раскладушка 20°/√(1 + раскладушка²(20°))
• ±√(косек²(20°) — 1)/косек 20°
• 1/сек 20°

Примечание. Поскольку 20° лежит в 1-м квадранте, окончательное значение cos 20° будет положительным.

Мы можем использовать тригонометрические тождества для представления cos 20° как

• -cos(180° — 20°) = -cos 160°
• -cos(180° + 20°) = -cos 200°
• sin(90° + 20°) = sin 110°
• sin(90° — 20°) = sin 70°

Cos 20 градусов с использованием единичной окружности

Чтобы найти значение cos 20 градусов с помощью единичной окружности:

• Поверните ‘r’ против часовой стрелки, чтобы образовать угол 20° с положительной осью x.
• Cos 20 градусов равен координате x (0,9397) точки пересечения (0,9397, 0,342) единичной окружности и r.

Отсюда значение cos 20° = x = 0,9397 (приблизительно)

☛ Также проверьте:

• потому что 15 градусов
• , потому что 37 градусов
• потому что 90 градусов
• потому что 1170 градусов
• потому что 69 градусов
• потому что 16 градусов

Примеры использования Cos 20 градусов

1. Пример 1: Упростить: 8 (cos 20°/sin 110°)

   Решение:

   Мы знаем, что cos 20° = sin 110°
   ⇒ 8 cos 20°/sin 110° = 8 (cos 20°/cos 20°)
   = 8(1) = 8

2. Пример 2: Найдите значение cos 20°, если sec 20° равно 1,0641.

   Решение:

   Так как cos 20° = 1/сек 20°
   ⇒ cos 20° = 1/1,0641 = 0,9397

3. Пример 3. Найдите значение 2 cos(20°)/3 sin(70°).

   Решение:

   Используя тригонометрические тождества, мы знаем, что cos(20°) = sin(90° — 20°) = sin 70°.
   ⇒ cos(20°) = sin(70°)
   ⇒ Значение 2 cos(20°)/3 sin(70°) = 2/3

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Забронируйте бесплатный пробный урок

Часто задаваемые вопросы о Cos 20 Degrees

Что такое Cos 20 Degrees?

Cos 20 градусов — значение тригонометрической функции косинуса для угла, равного 20 градусам. Значение cos 20° составляет 0,9397 (приблизительно)

Каково значение Cos 20 градусов в пересчете на Cot 20°?

Мы можем представить функцию косинуса в терминах функции котангенса, используя тригонометрические тождества, cos 20° можно записать как cot 20°/√(1 + cot²(20°)).