⇐ Предыдущая12345678910Следующая ⇒ Кубическая парабола задается функцией . Вот знакомый со школы чертеж:
Область определения – любое действительное число: . Область значений – любое действительное число: . Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»: Функция не ограничена. На языке пределов функции это можно записать так: , Кубическую параболу тоже эффективнее строить с помощью Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что , то при вычислении уже не нужно ничего считать, автоматом записываем, что . Теперь немного поговорим о графиках многочленов. График любого многочлена третьей степени () принципиально имеет следующий вид:
Многочлены 4-ой, 6-ой и других четных степеней имеют график принципиально следующего вида:
График функции Выполним чертеж:
Область определения: . Область значений: . То есть, график функции полностью находится в первой координатной четверти. Функция не ограничена сверху . Или с помощью предела:При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело: На самом деле хочется разобрать еще примеры с корнями, например, , но они встречаются значительно реже.
⇐ Предыдущая12345678910Следующая ⇒
|
Сейчас я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде приходиться строить значительно чаще. Однако унывать не нужно, в других статьях я рассмотрю самые разнообразные функции и их графики, корни в том числе.
труда с производительностью 4 м ткани или 2 кг мяса…
..
..
Дробно-рациональная функция (задание №23 ОГЭ)
Дробно-рациональная функция — это функция вида , где f(x) и g(x) — некоторые функции.
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты
Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x — нечетная
Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная
Пример1 . Построим график функции , т.е. представим ее в виде : выделим целую часть дроби, разделив числитель на знаменатель, мы получим:
.
Итак, . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы вверх на 2 единицы.
При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.
Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3. Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т.
е. первую слева от точки пересечения асимптот, а вторую справа от нее):
x | -7 | -2 | -1 | 0 | 1 | 2 | 2,5 |
y | 1,5 | 1 | 0,75 | 0,33 | -0,5 | -3 | -8 |
x | 3,5 | 4 | 5 | 6 | 7 | 8 | 13 |
y | 12 | 7 | 4,5 | 3,33 | 3,25 | 3 | 2,52 |
Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы.
Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции изображен на рисунке 3.
Любую дробь можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.
Пример 2.
Построим график функции .
Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.
Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.
Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби относительно малы. Поэтому
.
Стало быть, горизонтальная асимптота – прямая у=3/2.
Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.
Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).
Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.
Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.
Найти область определения функции.
Разложить на множители квадратный трехчлен.
Сократить дробь.
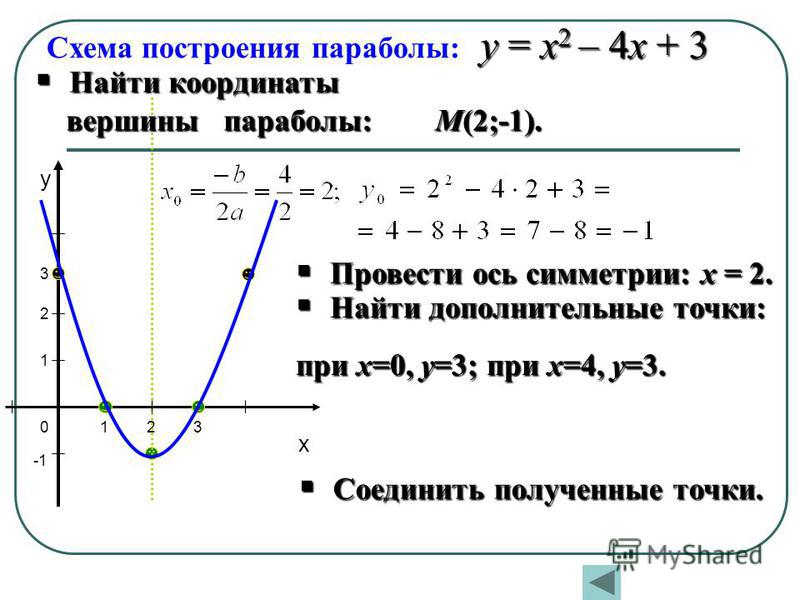
Построить график (параболу, гиперболу, кубическую параболу).
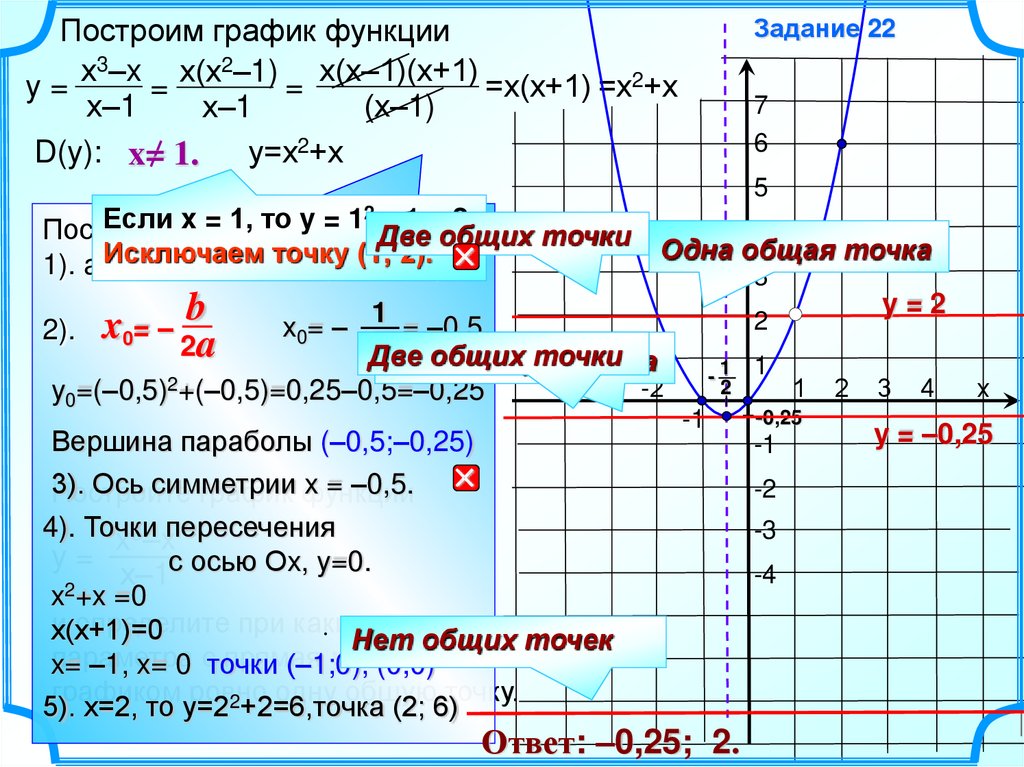
Исключить из графика точки, не входящие в область определения («выколотые» точки).
Найти значение функции в «выколотых» точках.
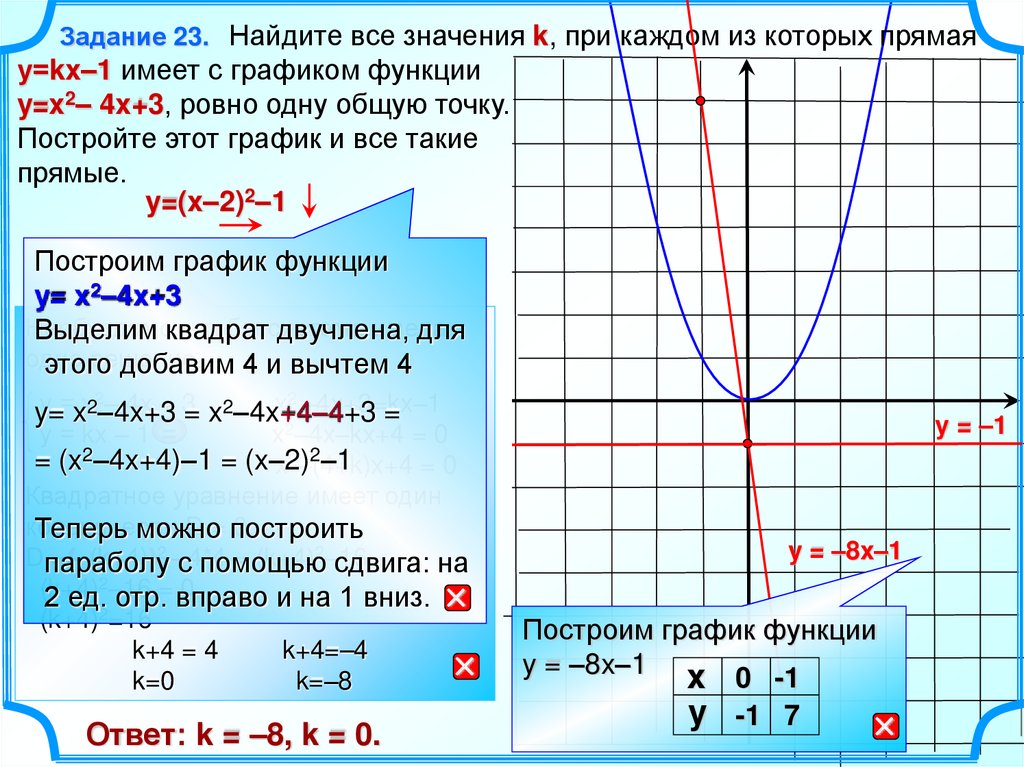
Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.
ЗАДАНИЕ
Построить график функции (D(y), на графике – выколотые точки):
Кубические функции | |
| Две точки с разными значениями x определяют линейную функцию (многочлен степени меньше или равной 1)  3Некоторые кубические функции имеют только один действительный корень (и два комплексно-сопряженных корня): РАССЛЕДОВАТЬ Нажав на флажок «Нули», вы можете увидеть нули кубической функции. Игра с красными точками или перевод графика вертикального перемещения фиолетового Вы можете видеть, как нули смешиваются вместе в двойном нуле или в тройном нуле. Все кубические функции (или кубические многочлены) имеют по крайней мере один действительный нуль (также называемый «корень»). Это следствие теоремы Больцано или Основная теорема алгебры. Любая кубическая функция имеет точку перегиба. Иногда кубическая функция имеет максимум и минимум. РАССЛЕДОВАТЬ Кубическая функция всегда имеет особую точку, называемую точкой перегиба. Некоторые кубические функции имеют один локальный максимум и один локальный минимум. В этом случае точка перегиба кубической функции находится «посередине». Нажав на флажок «Aux», вы увидите точку перегиба. Кубические функции с действительными или комплексными коэффициентами всегда имеют три корня (действительные или комплексные) (основная теорема алгебры): ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА Майкл Спивак, Расчет, третье издание, Publish-or-Perish, Inc. Том М. Апостол, Расчет, второе издание, John Willey and Sons, Inc. И.М. Гельфанд, Э.Г. Глаголева, Э. Э. Шноль, «Функции и графики», Dover Publications, Mineola, NY . БОЛЬШЕ ССЫЛОК |
Изменяя точки, вы можете видеть, что иногда максимум и минимум смешиваются вместе в
точка перегиба.Кубические функции и производная | |
| Кубическая функция — это полиномиальная функция степени 3. ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ Производную функции в точке можно определить как мгновенную скорость изменения или как наклон касательной к точке. график функции в этой точке. Мы можем сказать, что этот наклон тангенса функции в точке есть наклон функция. Наклон функции, вообще говоря, будет зависеть от x. Тогда, начиная с функции, мы можем получить новую функцию, производную от исходной функции. Процесс нахождения производной функции называется дифференцированием. Значение производной функции для любого значения x представляет собой наклон исходной функции в точке x. Чтобы найти производную в точке, мы можем провести касательную к графику кубической функции в этой точке: Но как мы можем провести касательную? Мы можем использовать увеличительное стекло!. Если мы посмотрим очень близко к точке на графике функции, мы увидим, что функция напоминает касательную. Эта касательная линия является наилучшей линейной аппроксимацией функции в этой точке: Затем мы можем провести параллельную прямую к этой касательной через значение x-1, и мы получим прямоугольный треугольник: Производная кубической функции является квадратичной функцией. Критическая точка – это точка, в которой касательная параллельно оси x, то есть наклон касательная в этой точке равна нулю. В следующем примере мы видим кубическую функцию с двумя критическими точками. Один из них является локальным максимумом, а другой локальный минимум. В этих точках производная функция (парабола) пересекает ось x: Эти критические точки — это точки, в которых функция перестает увеличиваться или уменьшаться (иногда их называют «стационарные точки»). В этих точках касательная горизонтальна. Для нахождения стационарных точек решаем квадратное уравнение: В этом случае решениями этого уравнения являются: Как мы уже знаем (квадратные функции), иногда квадратное уравнение не имеет действительных решений. (парабола не пересекает ось x). Тогда кубическая функция не имеет критических точек: Но у параболы всегда есть вершина. Вершина параболы связана с точкой кубической функции. Мы называем
это точка перегиба. Точка перегиба кубической функции — это единственная точка на графике, где изменяется вогнутость. Кривая изменяется от вогнутой вверх вогнутой вниз или наоборот Касательная кубической функции в точке перегиба пересекает график: Чтобы найти точку перегиба, мы можем вычислить вершину параболы: Это пример точки перегиба кубической функции без критических точек: Точка перегиба в этом случае также является точкой покоя (вершина производной касается оси x): Точки перегиба могут быть стационарными точками, но не локальными максимумами или локальными минимумами. Одна простая и интересная идея заключается в том, что когда мы переводим вверх и вниз график функции (мы добавляем или вычитаем число из исходной функции), производная не меняется. Причина очень интуитивная. Когда ты перемещайте фиолетовую точку, которую вы переводите, вверх и вниз по графику, и производная будет такой же: Важно отметить, что производная многочлена степени 1 является постоянной функцией (многочленом степени 0). |
