Sin 2 интеграл: ∫ Найти интеграл от y = f(x) = (sin(x)^2) dx ((синус от (х) в квадрате))

{1} frac{sin{left (2 x right )}}{3 cos{left (2 x right )} + 1}, dx$$

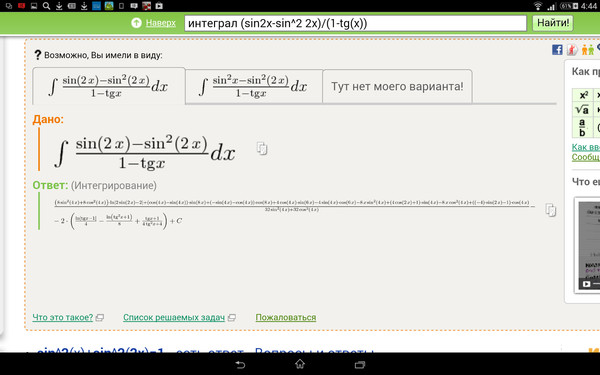
Подробное решение

Метод #1

1. пусть
   u = 2 x
   .

   Тогда пусть
   du = 2 dx
   и подставим
   du
   :

   int frac{sin{left (u right )}}{6 cos{left (u right )} + 2}, du

   1. пусть
      u = 6 cos{left (u right )} + 2
      .

      Тогда пусть
      du = – 6 sin{left (u right )} du
      и подставим
      – frac{du}{6}
      :

      int frac{1}{u}, du

      1. Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:

         int frac{1}{u}, du = – frac{1}{6} int frac{1}{u}, du

         1. Интеграл
            frac{1}{u}
            есть
            log{left (u right )}
            .$$

         Таким образом, результат будет: $$
         – frac{1}{6} log{left (u right )}
         $$

      Если сейчас заменить $$
      u
      ещё в:

      – frac{1}{6} log{left (6 cos{left (u right )} + 2 right )}
      $$

   Если сейчас заменить $$
   

   u
   ещё в:

   – frac{1}{6} log{left (6 cos{left (2 x right )} + 2 right )}

Метод #2

1. пусть
   u = 3 cos{left (2 x right )} + 1
   .

   Тогда пусть
   du = – 6 sin{left (2 x right )} dx
   и подставим
   – frac{du}{6}
   :

   int frac{1}{u}, du

   1. Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:

      int frac{1}{u}, du = – frac{1}{6} int frac{1}{u}, du

      1. Интеграл
         frac{1}{u}
         есть
         log{left (u right )}
         .$$

      Таким образом, результат будет: $$
      – frac{1}{6} log{left (u right )}
      $$

   Если сейчас заменить $$
   u
   ещё в:

   – frac{1}{6} log{left (3 cos{left (2 x right )} + 1 right )}

Добавляем постоянную интегрирования:

– frac{1}{6} log{left (6 cos{left (2 x right )} + 2 right )}+ mathrm{constant}

---

Ответ:

– frac{1}{6} log{left (6 cos{left (2 x right )} + 2 right )}+ mathrm{constant}

Ответ

1
/
|
| sin(2*x) log(3) log(-1/3 – cos(2)) log(4) pi*I
| ————– dx = – —— – —————— + —— – —-
| 1 + 3*cos(2*x) 6 6 6 6
|
/
0

$${{log 4}over{6}}-{{log left(-3,cos 2-1right)}over{6}}$$

Численный ответ

0. 2)

Решение задач, Высшая математика

Выполнил: user1504019

Так же вы можете купить уже выполненные похожие работы. Для удобства покупки работы размещены на независимой бирже. Подробнее об условиях покупки тут.

 

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х93(х) дх Исчисление Талина М. спросил 10.03.21 а) Объясните, почему замена u = sin(x) не поможет вычислить интеграл. b) Заметив, что sin 3 (x) = sin(x) • sin 2 (x), и используя тождество Пифагора, перепишите интеграл как произведение sin(x) и другой функции. c) Теперь объясните, почему замена u = cos(x) теперь помогает вычислить интеграл. d) Используйте свою работу в частях a), b) и c) для вычисления интеграла, тем самым найдя первообразную sin 3 (x) e) Используйте аналогичный подход для вычисления ∫ cos 3 ( х) дх. Подписаться І 1 Подробнее Отчет 1 ответ эксперта Лучший Новейшие Самый старый Автор: Лучшие новыеСамые старые Майкл К. ответил 12.03.21 Репетитор 5,0 (339) Кандидат наук по математике, физике и компьютерному репетиторству Об этом репетиторе › Об этом репетиторе › Итак, нас просят интегрировать sin 3 (x). Давайте попробуем сделать u-подстановку, чтобы посмотреть, сработает ли это… ∫sin 3 (x) * dx = ? Пусть: u(x) = sin(x) du = cos(x) * dx ∫sin 3 (x) * dx = ∫u 3 * du/cos(x) Как мы видим, это нам не поможет, так как у нас нет простого выражения для cos(x) через u(x). Но мы можем использовать теорему Пифагора, чтобы помочь нам с подходящей заменой с sin 2 (x) + cos 2 (x) = 1, ∫sin 3 (x) * dx = ∫sin(x) ) * грех 2 (x) * dx = ∫sin(x) * (1 — cos 2 (x)) * dx = ∫sin(x) * dx — ∫sin(x) * cos 2 (x) * dx Разбив исходный интеграл на две части, мы можем попытаться решить каждую часть по отдельности… Первый интеграл дает -cos(x) + C в качестве решения (с постоянной интегрирования из-за неопределенного интеграла) Ко второму интегралу можно применить u-подстановку… Пусть: u(x) = cos(x) du = -sin(x) * dx — ∫sin(x) * cos 2 (x) * dx = ∫u 2 du = u 3 /3 + C —> cos 3 (x)/3 + C Объединение двух частей дает —> ∫sin 3 (x) * dx = -cos(x) + cos 3 (x)/3 + C , где мы сложили два постоянных члена в один неизвестный постоянный член. Применим это понятие к другому интегралу —> ∫cos 3 (x) * dx ∫cos 3 (x) * dx = ∫cos(x) * cos 2 (x) * dx = ∫cos(x) * (1 — sin 2 (x)) * dx = ∫cos(x) * dx — ∫cos(x) * sin 2 (x) * dx Пусть u = sin(x) во втором интеграле du = cos(x) * dx ∫cos 3 (x) * dx = -sin(x) — sin 3 (x )/3 + C = -(sin(x) + sin 3 (x)/3) + C Голосовать за 0 Понизить Подробнее Отчет Все еще ищете помощь? Получите правильный ответ, быстро. Задайте вопрос бесплатно Получите бесплатный ответ на быстрый вопрос. Ответы на большинство вопросов в течение 4 часов. ИЛИ Найдите онлайн-репетитора сейчас Выберите эксперта и встретьтесь онлайн. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт