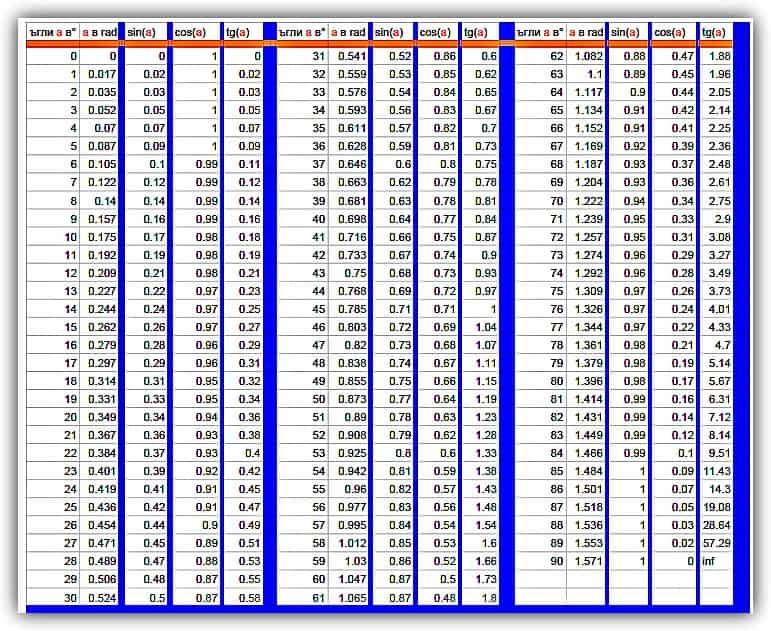
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.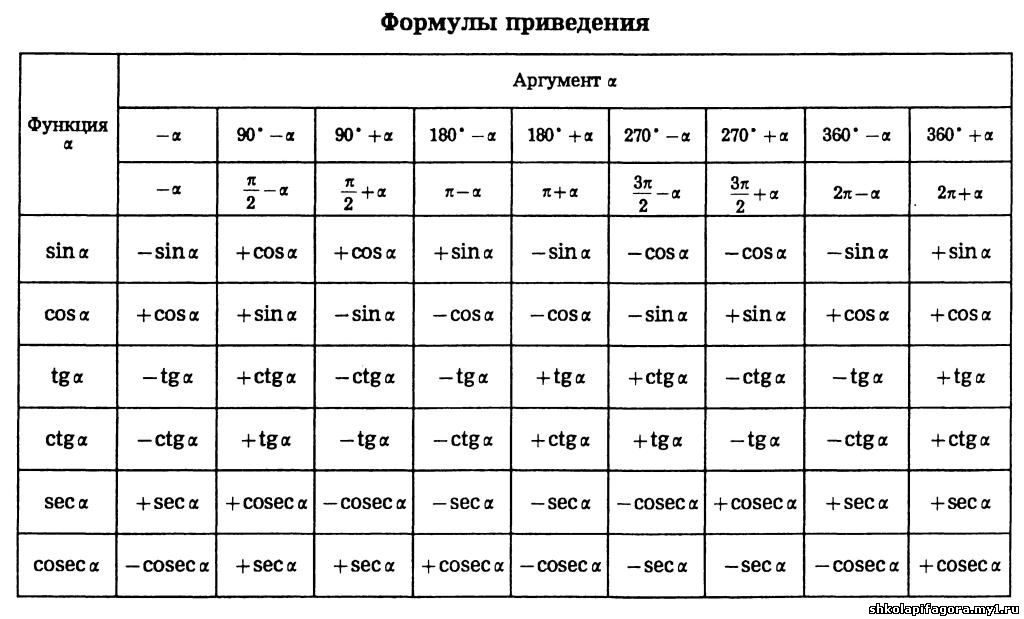 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.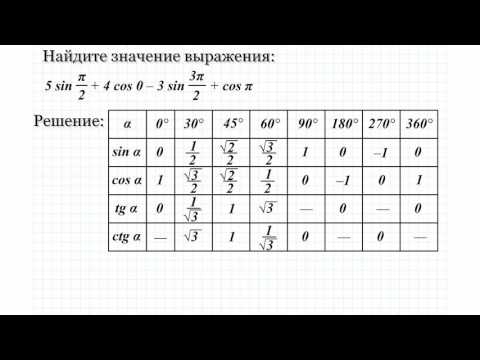 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.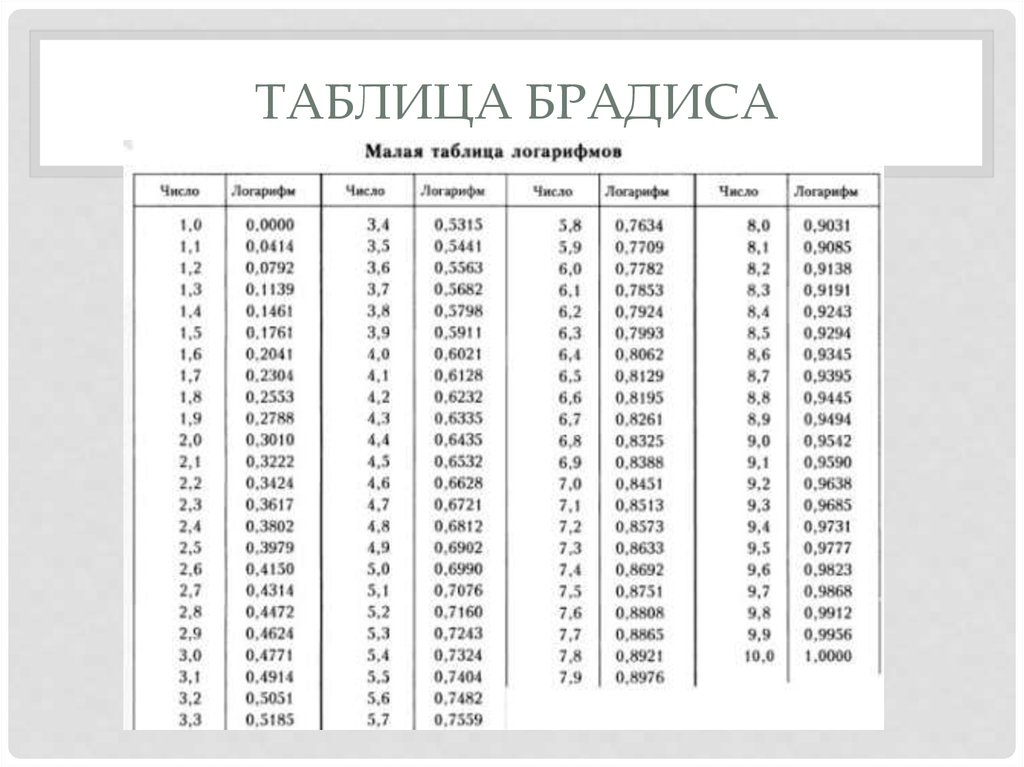 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| Найти точное значение | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
от 0 до 360 градусов
Таблица косинусов – это рассчитанные значения косинусов от 0 до 360 градусов. Она может быть полезна, если нужно будет выполнить определенные вычисления, в которых есть косинус какого-то угла, а под рукой не будет калькулятора.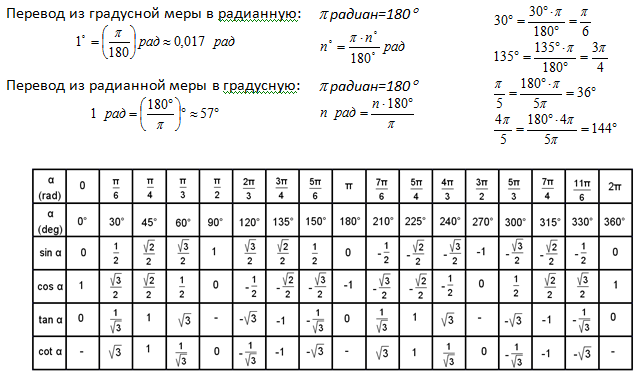
Пользоваться таблицей достаточно легко – находим градус и в столбце справа в той же строке будет указано соответствующее значение косинуса. Для удобства информация разделена на две части.
- Таблица косинусов от 0° до 180°
- Таблица косинусов от 181° до 360°
Таблица косинусов от 0° до 180°
| cos (0°) | 1 | ||||
| cos (1°) | 0,999848 | cos (61°) | 0,48481 | cos (121°) | -0,515038 |
| cos (2°) | 0,999391 | cos (62°) | 0,469472 | cos (122°) | -0,529919 |
| cos (3°) | 0,99863 | cos (63°) | 0,45399 | cos (123°) | -0,544639 |
| cos (4°) | 0,997564 | cos (64°) | 0,438371 | cos (124°) | -0,559193 |
| cos (5°) | 0,996195 | cos (65°) | 0,422618 | cos (125°) | -0,573576 |
| cos (6°) | 0,994522 | cos (66°) | 0,406737 | cos (126°) | -0,587785 |
| cos (7°) | 0,992546 | cos (67°) | 0,390731 | cos (127°) | -0,601815 |
| cos (8°) | 0,990268 | cos (68°) | 0,374607 | cos (128°) | -0,615661 |
| cos (9°) | 0,987688 | cos (69°) | 0,358368 | cos (129°) | -0,62932 |
| cos (10°) | 0,984808 | cos (70°) | 0,34202 | cos (130°) | -0,642788 |
| cos (11°) | 0,981627 | cos (71°) | 0,325568 | cos (131°) | -0,656059 |
| cos (12°) | 0,978148 | cos (72°) | 0,309017 | cos (132°) | -0,669131 |
| cos (13°) | 0,97437 | cos (73°) | 0,292372 | cos (133°) | -0,681998 |
| cos (14°) | 0,970296 | cos (74°) | 0,275637 | cos (134°) | -0,694658 |
| cos (15°) | 0,965926 | cos (75°) | 0,258819 | cos (135°) | -0,707107 |
| cos (16°) | 0,961262 | cos (76°) | 0,241922 | cos (136°) | -0,71934 |
| cos (17°) | 0,956305 | cos (77°) | 0,224951 | cos (137°) | -0,731354 |
| cos (18°) | 0,951057 | cos (78°) | 0,207912 | cos (138°) | -0,743145 |
| cos (19°) | 0,945519 | cos (79°) | 0,190809 | cos (139°) | -0,75471 |
| cos (20°) | 0,939693 | cos (80°) | 0,173648 | cos (140°) | -0,766044 |
| cos (21°) | 0,93358 | cos (81°) | 0,156434 | cos (141°) | -0,777146 |
| cos (22°) | 0,927184 | cos (82°) | 0,139173 | cos (142°) | -0,788011 |
| cos (23°) | 0,920505 | cos (83°) | 0,121869 | cos (143°) | -0,798636 |
| cos (24°) | 0,913545 | cos (84°) | 0,104528 | cos (144°) | -0,809017 |
| cos (25°) | 0,906308 | cos (85°) | 0,087156 | cos (145°) | -0,819152 |
| cos (26°) | 0,898794 | cos (86°) | 0,069756 | cos (146°) | -0,829038 |
| cos (27°) | 0,891007 | cos (87°) | 0,052336 | cos (147°) | -0,838671 |
| cos (28°) | 0,882948 | cos (88°) | 0,034899 | cos (148°) | -0,848048 |
| cos (29°) | 0,87462 | cos (89°) | 0,017452 | cos (149°) | -0,857167 |
| cos (30°) | 0,866025 | cos (90°) | 0 | cos (150°) | -0,866025 |
| cos (31°) | 0,857167 | cos (91°) | -0,017452 | cos (151°) | -0,87462 |
| cos (32°) | 0,848048 | cos (92°) | -0,034899 | cos (152°) | -0,882948 |
| cos (33°) | 0,838671 | cos (93°) | -0,052336 | cos (153°) | -0,891007 |
| cos (34°) | 0,829038 | cos (94°) | -0,069756 | cos (154°) | -0,898794 |
| cos (35°) | 0,819152 | cos (95°) | -0,087156 | cos (155°) | -0,906308 |
| cos (36°) | 0,809017 | cos (96°) | -0,104528 | cos (156°) | -0,913545 |
| cos (37°) | 0,798636 | cos (97°) | -0,121869 | cos (157°) | -0,920505 |
| cos (38°) | 0,788011 | cos (98°) | -0,139173 | cos (158°) | -0,927184 |
| cos (39°) | 0,777146 | cos (99°) | -0,156434 | cos (159°) | -0,93358 |
| cos (40°) | 0,766044 | cos (100°) | -0,173648 | cos (160°) | -0,939693 |
| cos (41°) | 0,75471 | cos (101°) | -0,190809 | cos (161°) | -0,945519 |
| cos (42°) | 0,743145 | cos (102°) | -0,207912 | cos (162°) | -0,951057 |
| cos (43°) | 0,731354 | cos (103°) | -0,224951 | cos (163°) | -0,956305 |
| cos (44°) | 0,71934 | cos (104°) | -0,241922 | cos (164°) | -0,961262 |
| cos (45°) | 0,707107 | cos (105°) | -0,258819 | cos (165°) | -0,965926 |
| cos (46°) | 0,694658 | cos (106°) | -0,275637 | cos (166°) | -0,970296 |
| cos (47°) | 0,681998 | cos (107°) | -0,292372 | cos (167°) | -0,97437 |
| cos (48°) | 0,669131 | cos (108°) | -0,309017 | cos (168°) | -0,978148 |
| cos (49°) | 0,656059 | cos (109°) | -0,325568 | cos (169°) | -0,981627 |
| cos (50°) | 0,642788 | cos (110°) | -0,34202 | cos (170°) | -0,984808 |
| cos (51°) | 0,62932 | cos (111°) | -0,358368 | cos (171°) | -0,987688 |
| cos (52°) | 0,615661 | cos (112°) | -0,374607 | cos (172°) | -0,990268 |
| cos (53°) | 0,601815 | cos (113°) | -0,390731 | cos (173°) | -0,992546 |
| cos (54°) | 0,587785 | cos (114°) | -0,406737 | cos (174°) | -0,994522 |
| cos (55°) | 0,573576 | cos (115°) | -0,422618 | cos (175°) | -0,996195 |
| cos (56°) | 0,559193 | cos (116°) | -0,438371 | cos (176°) | -0,997564 |
| cos (57°) | 0,544639 | cos (117°) | -0,45399 | cos (177°) | -0,99863 |
| cos (58°) | 0,529919 | cos (118°) | -0,469472 | cos (178°) | -0,999391 |
| cos (59°) | 0,515038 | cos (119°) | -0,48481 | cos (179°) | -0,999848 |
| cos (60°) | 0,5 | cos (120°) | -0,5 | cos (180°) | -1 |
Таблица косинусов от 181° до 360°
Перевести кВА и кВт: онлайн-калькулятор определения мощности ДГУ
При покупке дизельной электростанции первое, с чем сталкивается потребитель, – это выбор мощности ДГУ. В характеристиках производители всегда указывают две единицы измерения мощности.
В характеристиках производители всегда указывают две единицы измерения мощности.
Выбирая генератор или стабилизатор напряжения необходимо отличать полную потребляемую мощность (кВА) от активной мощности (кВт), которая затрачивается на совершение полезной работы.
Онлайн калькулятор перевода кВА в кВт:
кВА
кВт
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Мощность бывает полная, реактивная и активная:
- S – полная мощность измеряется в кВА (килоВольтАмперах)
Характеризует полную электрическую мощность переменного тока. Для получения полной мощности значения реактивной и активной мощностей суммируются. При этом соотношение полной и активной мощностей у разных потребителей электроэнергии может отличаться. Таким образом, для определения совокупной мощности потребителей следует суммировать их полные, а не активные мощности.
кВА характеризует полную электрическую мощность, имеющую принятое буквенное обозначение по системе СИ – S: это геометрическая сумма активной и реактивной мощности, находимая из соотношения: S=P/cos(ф) или S=Q/sin(ф).
- Q – реактивная мощность измеряется в кВар (килоВарах)
Реактивная мощность, потребляемая в электрических сетях, вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения).
- Р – активная мощность измеряется в кВт (килоВаттах)
Это физическая и техническая величина, характеризующая полезную электрическую мощность. При произвольной нагрузке в цепи переменного тока действует активная составляющая тока. Эта часть полной мощности, которая определяется коэффициентом мощности и является полезной (используемой).
Единый коэффициент мощности обозначается Сos φ.
Это коэффициент мощности, который показывает соотношение (потерь) кВт к кВА при подключении индуктивных нагрузок.
Распространенные коэффициенты мощности и их расшифровка(cos φ):
1 – наилучшее значение
0,95 – отличный показатель
0,90 – удовлетворительные значение
0,80 – средний наиболее распространенный показатель
0,70 – плохой показатель
0,60 – очень низкое значение
кВт характеризует активную потребляемую электрическую мощность, имеющую принятое буквенное обозначение P: это геометрическая разность полной и реактивной мощности, находимая из соотношения: P=S*cos(ф).
Говоря языком потребителя: кВт – нетто (полезная мощность), а кВа брутто (полная мощность).
1 кВт = 1.25 кВА
1 кВА = 0.8 кВт
Цены на дизельные электростанции:
Как перевести мощность кВА в кВт?
Чтобы быстро перевести кВА в кВт нужно из кВА вычесть 20% и получится кВт с небольшой погрешностью, которой можно пренебречь. Или воспользоваться формулой для перевода кВА в кВт:
Или воспользоваться формулой для перевода кВА в кВт:
P=S * Сos f
Где P-активная мощность (кВт), S-полная мощность (кВА), Сos f- коэффициент мощности.
К примеру, чтобы мощность 400кВА перевести в кВт, необходимо 400кВА*0,8=320кВт или 400кВа-20%=320кВт.
Как перевести мощность кВт в кВА?
Для перевода кВт в кВА применима формула:
S=P/ Сos f
Где S-полная мощность (кВА), P-активная мощность (кВт), Сos f- коэффициент мощности.
Например, чтобы мощность 1000 кВт перевести в кВА, следует 1000 кВт / 0,8= 1250кВА.
Комплекс ДГУ 3600 кВт (3 шт. по 1200 кВт) для ЦОДа крупнейшей в России компании межоператорского обмена интернет-трафиком ММТС-9
Февраль 2019 года
В феврале 2019 года компания «Техэкспо» обеспечила резервным электроснабжением АО «Московская междугородная телефонная станция №9» (АО «ММТС-9»).
 Это крупнейшая точка межоператорского обмена (пиринг) интернет-трафика в России. Здание АО «ММТС-9» оснащено системами бесперебойного электропитания, клим…
Это крупнейшая точка межоператорского обмена (пиринг) интернет-трафика в России. Здание АО «ММТС-9» оснащено системами бесперебойного электропитания, клим…Автономный генерирующий центр (АГЦ) из трех ДГУ общей мощностью 3600 кВт для складского комплекса Wildberries
Февраль 2020 года
ООО «Техэкспо» изготовило цельносварной контейнер размерами 8х9х3 м для трех ДГУ Perkins 1200 кВт, а также провело строительно-монтажные работы с прокладкой кабельной трассы
Немецкая ДГУ MTU единичной мощностью 2547 кВт в контейнере для газовой компании «НОВАТЭК»
Май 2019 года
В мае 2019 года компания «Техэкспо» поставила дизельную электростанцию ТЭ.
 2500С-Т 400-ЗРН мощностью 2500 кВт для «Делового центра Юг» в г. Новый Уренгой Ямало-Ненецкого АО. Дизель-генераторная установка контейнерного исполнения выполнена на базе двигателя MTU 20V4000G84F (Германия) и генератора …
2500С-Т 400-ЗРН мощностью 2500 кВт для «Делового центра Юг» в г. Новый Уренгой Ямало-Ненецкого АО. Дизель-генераторная установка контейнерного исполнения выполнена на базе двигателя MTU 20V4000G84F (Германия) и генератора …Дизельная электростанция мощностью 1 МВт напряжением 6,3 кВ для филиала АО «Гознак» в Санкт-Петербурге
Декабрь 2019 года
В декабре 2019 года мы завершили создание системы аварийного энергоснабжения на основе дизельной электростанции мощностью 1 МВт напряжением 6,3 кВ для филиала АО «Гознак» — Санкт-Петербургской бумажной фабрики. ДГУ позволяет поддерживать системы жизнеобеспечения фабрики и работу станков при отсу.
 ..
..
Число 63, 0x00003F, шестьдесят три
Энциклопедия чисел
Свойства натурального числа 63, 0x00003F, 0x3F:
Системы счисления Основные свойства Степени, корни
Тригонометрия Хэши, криптография Языки программирования
Дата и время Цвет по числу Интернет
Другие свойства
Рейтинг 8.6 из 10, оценок: 5.
Системы счисления, перевод в систему счисления
Десятичное число 63
- 63 в шестнадцатеричной системе счисления
- 3F
- 63 в двоичной системе счисления
- 111111
- 63 в восьмеричной системе счисления
- 77
Шестнадцатеричное число 3F
- 3F в десятичной системе
- 63
- 3F в двоичной системе
- 111111
- 3F в восьмеричной системе
- 77
Двоичное число 111111
- 111111 в десятичной системе
- 63
- 111111 в шестнадцатеричной системе
- 3F
- 111111 в восьмеричной системе
- 77
Восьмеричное число 77
- 77 в десятичной системе
- 63
- 77 в шестнадцатеричной системе
- 3F
- 77 в двоичной системе
- 111111
Основные арифметические и алгебраические свойства
- Число 63 на русском языке, number in Russian, число 63 прописью:
- шестьдесят три
- Четность
- Нечетное число 63
- Разложение на множители, делители числа 63
- 3, 3, 7, 1
- Простое или составное число
- Составное число 63
- Числа делящиеся на целое число 63
- 126, 189, 252, 315, 378, 441, 504, 567
- Число 63 умноженное на число два
- 126
- 63 деленное на число 2
- 31.
 5
5
- Список 8-ми простых чисел перед числом
- 61, 59, 53, 47, 43, 41, 37, 31
- Сумма десятичных цифр
- 9
- Количество цифр
- 2
- Десятичный логарифм 63
- 1.7993405494536
- Натуральный логарифм 63
- 4.1431347263915
- Это число Фибоначчи?
- Нет
- Число на 1 больше числа 63,
следующее число - число 64
- Число на 1 больше числа 63,
- Число на 1 меньше числа 63,
предыдущее число - 62
- Число на 1 меньше числа 63,
Степени числа, корни
- 63 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 3969
- 63 во второй степени (в квадрате)
- В третьей степени (в кубе, 63 в степени 3, x³) равно
- 250047
- Корень квадратный из 63
- 7.9372539331938
- Корень кубический из числа 63 =
- 3.9790572078964
Тригонометрические функции, тригонометрия
- Синус, sin 63 градусов, sin 63°
- 0.
 8910065242
8910065242
- Косинус, cos 63 градусов, cos 63°
- 0.4539904997
- Тангенс, tg 63 градусов, tg 63°
- 1.9626105055
- Синус, sin 63 радиан
- 0.16735570030281
- Косинус, cos 63 радиан
- 0.98589658158255
- Тангенс, tg 63 радиан равно
- 0.16974975208269
- 63 градуса, 63° =
- 1.0995574287564 радиан
- 63 радиан =
- 3609.6341093242 градуса, 3609.6341093242°
Контрольные суммы, хэши, криптография
- MD-5 хэш(63)
- 03afdbd66e7929b125f8597834fa83a4
- CRC-32, CRC32(63)
- 1997922972
- SHA-256 hash, SHA256(63)
- da4ea2a5506f2693eae190d9360a1f31793c98a1adade51d93533a6f520ace1c
- SHA1, SHA-1(63)
- a17554a0d2b15a664c0e73900184544f19e70227
- ГОСТ Р 34.
 11, GOST R 34.11-94, GOST(63)
11, GOST R 34.11-94, GOST(63) - a6f9b8c1975bd468c3be9976b86313e5fcbbb4dc002d9f9dc223dde59054e652
- ГОСТ Р 34.
- Base64
- NjM=
Языки программирования
- C++, CPP, C значение 63
- 0x00003F, 0x3F
- Delphi, Pascal значение числа 63
- $00003F
Дата и время
- 63-й день года
- 4 марта
- 63-й день високосного года
- 3 марта
- Конвертация UNIX timestamp 63 в дату и время
- UTC
- в Москве, Россия
- в Лондоне, Великобритания
- в Нью-Йорке, США
Интернет
- Конвертация в IPv4 адрес Интернет
- 0.0.0.63
- 63 в Википедии:
- 63
Другие свойства числа
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/63
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x3F
- Номер телефона
- 63
- Телефонный код страны
- +63 Филиппины
Цвет по числу 63, цветовая гамма
- html RGB цвет 63, 16-ричное значение
- #00003F — (0, 0, 63)
- HTML CSS код цвета #00003F
- .color-mn { color: #00003F; }
.color-bg { background-color: #00003F; }
Цвет для данного числа 63
Здесь вы можете изменить составляющую цвета для данного числа 63 или цвета 00003F:
Коэффициент для расчета установки компенсации реактивной мощности
Расчтетный (lействующий) коэффициент мощности без применения конденсаторных установок компенсации реактивнеой мощности
— Асинхронные двигатели (cos(ф) ~ 0. 7)
7)
— Асинхронные двигатели, при неполной загрузке (cos(ф) ~ 0.5)
— Выпрямительные электролизные установки (cos(ф) ~ 0.6)
— Электродуговые печи (cos(ф) ~ 0.6)
— Индукционные печи (cos(ф) ~ 0.2-0.6)
— Водяные насосы (cos(ф) ~ 0.8)
— Компрессоры (cos(ф) ~ 0.7)
— Машины, станки (cos(ф) ~ 0.5)
— Сварочные трансформаторы (cos(ф) ~ 0.4)
— Лампы дневного света (cos(ф) ~ 0.5-0.6)
Таблица расчета мощности конденсаторной установки компенсации реактивной мощности
Пример:
Активная мощность двигателя : P=20 кВт
Действующий cos φ = 0,6
Требуемый cos φ = 0,96
Коэффициент K из таблицы = 1,01
результат:
— требуемая реактивная мощность установки компенсации реактивной мощности УКРМ, кВАр:
Q = 20 х 1,01=20 кВАр (орентировочный расчет экономической составляющей, применения установки компенсации реактивной мощности УКРМ)
Текущий (действующий) | Требуемый (достижимый) cos (φ) | ||||||||||
| tan (φ) | cos (φ) | 0,80 | 0,82 | 0,85 | 0,88 | 0,90 | 0,92 | 0,94 | 0,96 | 0,98 | 1,00 |
| Коэффициент «k» | |||||||||||
| 3,18 | 0,30 | 2,43 | 2,48 | 2,56 | 2,64 | 2,70 | 2,75 | 2,82 | 2,89 | 2,98 | 3,18 |
| 2,96 | 0,32 | 2,21 | 2,26 | 2,34 | 2,42 | 2,48 | 2,53 | 2,60 | 2,67 | 2,76 | 2,96 |
| 2,77 | 0,34 | 2,02 | 2,07 | 2,15 | 2,23 | 2,28 | 2,34 | 2,41 | 2,48 | 2,56 | 2,77 |
| 2,59 | 0,36 | 1,84 | 1,89 | 1,97 | 2,05 | 2,10 | 2,17 | 2,23 | 2,30 | 2,39 | 2,59 |
| 2,43 | 0,38 | 1,68 | 1,73 | 1,81 | 1,89 | 1,95 | 2,01 | 2,07 | 2,14 | 2,23 | 2,43 |
| 2,29 | 0,40 | 1,54 | 1,59 | 1,67 | 1,75 | 1,81 | 1,87 | 1,93 | 2,00 | 2,09 | 2,29 |
| 2,16 | 0,42 | 1,41 | 1,46 | 1,54 | 1,62 | 1,68 | 1,73 | 1,80 | 1,87 | 1,96 | 2,16 |
| 2,04 | 0,44 | 1,29 | 1,34 | 1,42 | 1,50 | 1,56 | 1,61 | 1,68 | 1,75 | 1,84 | 2,04 |
| 1,93 | 0,46 | 1,18 | 1,23 | 1,31 | 1,39 | 1,45 | 1,50 | 1,57 | 1,64 | 1,73 | 1,93 |
| 1,83 | 0,48 | 1,08 | 1,13 | 1,21 | 1,29 | 1,34 | 1,40 | 1,47 | 1,54 | 1,62 | 1,83 |
| 1,73 | 0,50 | 0,98 | 1,03 | 1,11 | 1,19 | 1,25 | 1,31 | 1,37 | 1,45 | 1,63 | 1,73 |
| 1,64 | 0,52 | 0,89 | 0,94 | 1,02 | 1,10 | 1,16 | 1,22 | 1,28 | 1,35 | 1,44 | 1,64 |
| 1,56 | 0,54 | 0,81 | 0,86 | 0,94 | 1,02 | 1,07 | 1,13 | 1,20 | 1,27 | 1,36 | 1,56 |
| 1,48 | 0,56 | 0,73 | 0,78 | 0,86 | 0,94 | 1,00 | 1,05 | 1,12 | 1,19 | 1,28 | 1,48 |
| 1,40 | 0,58 | 0,65 | 0,70 | 0,78 | 0,86 | 0,92 | 0,98 | 1,04 | 1,11 | 1,20 | 1,40 |
| 1,33 | 0,60 | 0,58 | 0,63 | 0,71 | 0,79 | 0,85 | 0,91 | 0,97 | 1,04 | 1,13 | 1,33 |
| 1,30 | 0,61 | 0,55 | 0,60 | 0,68 | 0,76 | 0,81 | 0,87 | 0,94 | 1,01 | 1,10 | 1,30 |
| 1,27 | 0,62 | 0,52 | 0,57 | 0,65 | 0,73 | 0,78 | 0,84 | 0,91 | 0,99 | 1,06 | 1,27 |
| 1,23 | 0,63 | 0,48 | 0,53 | 0,61 | 0,69 | 0,75 | 0,81 | 0,87 | 0,94 | 1,03 | 1,23 |
| 1,20 | 0,64 | 0,45 | 0,50 | 0,58 | 0,66 | 0,72 | 0,77 | 0,84 | 0,91 | 1,00 | 1,20 |
| 1,17 | 0,65 | 0,42 | 0,47 | 0,55 | 0,63 | 0,68 | 0,74 | 0,81 | 0,88 | 0,97 | 1,17 |
| 1,14 | 0,66 | 0,39 | 0,44 | 0,52 | 0,60 | 0,65 | 0,71 | 0,78 | 0,85 | 0,94 | 1,14 |
| 1,11 | 0,67 | 0,36 | 0,41 | 0,49 | 0,57 | 0,63 | 0,68 | 0,75 | 0,82 | 0,90 | 1,11 |
| 1,08 | 0,68 | 0,33 | 0,38 | 0,46 | 0,54 | 0,59 | 0,65 | 0,72 | 0,79 | 0,88 | 1,08 |
| 1,05 | 0,69 | 0,30 | 0,35 | 0,43 | 0,51 | 0,56 | 0,62 | 0,69 | 0,76 | 0,85 | 1,05 |
| 1,02 | 0,70 | 0,27 | 0,32 | 0,40 | 0,48 | 0,54 | 0,59 | 0,66 | 0,73 | 0,82 | 1,02 |
| 0,99 | 0,71 | 0,24 | 0,29 | 0,37 | 0,45 | 0,51 | 0,57 | 0,63 | 0,70 | 0,79 | 0,99 |
| 0,96 | 0,72 | 0,21 | 0,26 | 0,34 | 0,42 | 0,48 | 0,54 | 0,60 | 0,67 | 0,76 | 0,96 |
| 0,94 | 0,73 | 0,19 | 0,24 | 0,32 | 0,40 | 0,45 | 0,51 | 0,58 | 0,65 | 0,73 | 0,94 |
| 0,91 | 0,74 | 0,16 | 0,21 | 0,29 | 0,37 | 0,42 | 0,48 | 0,55 | 0,62 | 0,71 | 0,91 |
| 0,88 | 0,75 | 0,13 | 0,18 | 0,26 | 0,34 | 0,40 | 0,46 | 0,52 | 0,59 | 0,68 | 0,88 |
| 0,86 | 0,76 | 0,11 | 0,16 | 0,24 | 0,32 | 0,37 | 0,43 | 0,50 | 0,57 | 0,65 | 0,86 |
| 0,83 | 0,77 | 0,08 | 0,13 | 0,21 | 0,29 | 0,34 | 0,40 | 0,47 | 0,54 | 0,63 | 0,83 |
| 0,80 | 0,78 | 0,05 | 0,10 | 0,18 | 0,26 | 0,32 | 0,38 | 0,44 | 0,51 | 0,60 | 0,80 |
| 0,78 | 0,79 | 0,03 | 0,08 | 0,16 | 0,24 | 0,29 | 0,35 | 0,42 | 0,49 | 0,57 | 0,78 |
| 0,75 | 0,80 | 0,05 | 0,13 | 0,21 | 0,27 | 0,32 | 0,39 | 0,46 | 0,55 | 0,75 | |
| 0,72 | 0,81 | 0,10 | 0,18 | 0,24 | 0,30 | 0,36 | 0,43 | 0,52 | 0,72 | ||
| 0,70 | 0,82 | 0,08 | 0,16 | 0,21 | 0,27 | 0,34 | 0,41 | 0,49 | 0,70 | ||
| 0,67 | 0,83 | 0,05 | 0,13 | 0,19 | 0,25 | 0,31 | 0,38 | 0,47 | 0,67 | ||
| 0,65 | 0,84 | 0,03 | 0,11 | 0,16 | 0,22 | 0,29 | 0,36 | 0,44 | 0,65 | ||
| 0,62 | 0,85 | 0,08 | 0,14 | 0,19 | 0,26 | 0,33 | 0,42 | 0,62 | |||
| 0,59 | 0,86 | 0,05 | 0,11 | 0,17 | 0,23 | 0,30 | 0,39 | 0,59 | |||
| 0,57 | 0,87 | 0,08 | 0,14 | 0,21 | 0,28 | 0,36 | 0,57 | ||||
| 0,54 | 0,88 | 0,06 | 0,11 | 0,18 | 0,25 | 0,34 | 0,54 | ||||
| 0,51 | 0,89 | 0,03 | 0,09 | 0,15 | 0,22 | 0,31 | 0,51 | ||||
| 0,48 | 0,90 | 0,06 | 0,12 | 0,19 | 0,28 | 0,48 | |||||
| 0,46 | 0,91 | 0,03 | 0,10 | 0,17 | 0,25 | 0,46 | |||||
| 0,43 | 0,92 | 0,07 | 0,14 | 0,22 | 0,43 | ||||||
| 0,40 | 0,93 | 0,04 | 0,11 | 0,19 | 0,40 | ||||||
| 0,36 | 0,94 | 0,07 | 0,16 | 0,36 | |||||||
| 0,33 | 0,95 | 0,13 | 0,33 | ||||||||
Cos 63 градуса — Найти значение Cos 63 градуса
LearnPracticeDownload
Значение cos 63 градуса равно 0,4539904. . . . Cos 63 градуса в радианах записывается как cos (63° × π/180°), то есть cos (7π/20) или cos (1,099557…). В этой статье мы обсудим способы нахождения значения cos 63 градусов на примерах.
. . . Cos 63 градуса в радианах записывается как cos (63° × π/180°), то есть cos (7π/20) или cos (1,099557…). В этой статье мы обсудим способы нахождения значения cos 63 градусов на примерах.
- Cos 63°: 0,4539904. . .
- Cos (-63 градуса): 0,4539904. . .
- Cos 63° в радианах: cos (7π/20) или cos (1,0995574 . . .)
Каково значение Cos 63 градуса?
Значение cos 63 градуса в десятичной системе равно 0,4539. . .. Cos 63 градуса также можно выразить с помощью эквивалента данного угла (63 градуса) в радианах (1,09955 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (пи/ 180°)
⇒ 63 градуса = 63° × (π/180°) рад = 7π/20 или 1,0995. . .
∴ cos 63 ° = cos (1,0995) = 0,4539904. . .
Объяснение:
Для cos 63 градуса угол 63° лежит между 0° и 90° (первый квадрант). Поскольку функция косинуса положительна в первом квадранте, значение cos 63° = 0,4539904. . .
. .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 63° как cos 63 градуса = cos(63° + n × 360°), n ∈ Z.
⇒ cos 63° = cos 423° = cos 783° и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-63°) = cos(63°).
Методы определения значения косинуса 63 градуса
Функция косинуса положительна в 1-м квадранте. Значение cos 63° составляет 0,45399. . .. Мы можем найти значение cos 63 градуса по:
- Используя тригонометрические функции
- Использование единичного круга
Cos 63° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 63 градуса как:
- ± √(1-sin²(63°))
- ± 1/√(1 + tan²(63°))
- ± кроватка 63°/√(1 + кроватка²(63°))
- ±√(косек²(63°) — 1)/косек 63°
- 1/сек 63°
Примечание. Поскольку 63° лежит в 1-м квадранте, окончательное значение cos 63° будет положительным.
Мы можем использовать тригонометрические тождества для представления cos 63° как
- -cos(180° — 63°) = -cos 117°
- -cos(180° + 63°) = -cos 243°
- sin(90° + 63°) = sin 153°
- sin(90° — 63°) = sin 27°
Cos 63 градуса с помощью единичной окружности
Чтобы найти значение cos 63 градуса с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 63° с положительной осью x.
- Косвенный угол 63 градуса равен координате x (0,454) точки пересечения (0,454, 0,891) единичной окружности и r.
Отсюда значение cos 63° = x = 0,454 (приблизительно)
☛ Также проверьте:
- потому что 18 градусов
- потому что 150 градусов
- потому что 75 градусов
- потому что 100 градусов
- потому что 81 градус
- потому что 17 градусов
Примеры использования Cos 63 градусов
Пример 1: Найдите значение cos 63°, если sec 63° равно 2,2026.

Решение:
Так как cos 63° = 1/сек 63°
⇒ cos 63° = 1/2,2026 = 0,454Пример 2: Упростить: 8 (cos 63°/sin 153°)
Решение:
Мы знаем, что cos 63° = sin 153°
⇒ 8 cos 63°/sin 153° = 8 (cos 63°/cos 63°)
= 8(1) = 8Пример 3: Найдите значение (cos² 31,5° — sin² 31,5°). [Подсказка: используйте cos 63° = 0,454]
Решение:
Используя формулу cos 2a,
(cos² 31,5° — sin² 31,5°) = cos(2 × 31,5°) = cos 63°
∵ косинус 63° = 0,454
⇒ (cos² 31,5° — sin² 31,5°) = 0,454
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Cos 63 Degrees
Что такое Cos 63 Degrees?
Cos 63 градуса — значение тригонометрической функции косинуса для угла, равного 63 градусам. Значение cos 63° равно 0,454 (приблизительно)
Как найти Cos 63° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 63° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(63°))
- ± 1/√(1 + tan²(63°))
- ± кроватка 63°/√(1 + кроватка²(63°))
- ± √(косек²(63°) — 1)/косек 63°
- 1/сек 63°
☛ Также проверьте: таблицу тригонометрии
Каково точное значение cos 63 градуса?
Точное значение для cos 63 градусов может быть задано с точностью до 8 знаков после запятой как 0,45399049.
Как найти значение Cos 63 градуса?
Значение cos 63 градуса можно рассчитать, построив угол 63° с осью x и затем найдя координаты соответствующей точки (0,454, 0,891) на единичной окружности. Значение cos 63° равно координате x (0,454). ∴ cos 63° = 0,454.
Значение cos 63° равно координате x (0,454). ∴ cos 63° = 0,454.
Каково значение Cos 63 градусов по отношению к Cot 63°?
Мы можем представить функцию косинуса в терминах функции котангенса, используя тригонометрические тождества, cos 63° можно записать как cot 63°/√(1 + cot²(63°)). Здесь значение ctg 63° равно 0,50952.
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
| 1 | Найдите точное значение | грех(30) | |
| 2 | Найдите точное значение | грех(45) | |
| 3 | Найдите точное значение | грех(30 градусов) | |
| 4 | Найдите точное значение | грех(60 градусов) | |
| 5 | Найдите точное значение | загар (30 градусов) | |
| 6 | Найдите точное значение | угловой синус(-1) | |
| 7 | Найдите точное значение | грех(пи/6) | |
| 8 | Найдите точное значение | cos(pi/4) | |
| 9 | Найдите точное значение | грех(45 градусов) | |
| 10 | Найдите точное значение | грех(пи/3) | |
| 11 | Найдите точное значение | арктический(-1) | |
| 12 | Найдите точное значение | cos(45 градусов) | |
| 13 | Найдите точное значение | cos(30 градусов) | |
| 14 | Найдите точное значение | желтовато-коричневый(60) | |
| 15 | Найдите точное значение | csc(45 градусов) | |
| 16 | Найдите точное значение | загар (60 градусов) | |
| 17 | Найдите точное значение | сек (30 градусов) | |
| 18 | Найдите точное значение | cos(60 градусов) | |
| 19 | Найдите точное значение | соз(150) | |
| 20 | Найдите точное значение | грех(60) | |
| 21 | Найдите точное значение | cos(pi/2) | |
| 22 | Найдите точное значение | загар (45 градусов) | |
| 23 | Найдите точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найдите точное значение | csc(60 градусов) | |
| 25 | Найдите точное значение | сек (45 градусов) | |
| 26 | Найдите точное значение | csc(30 градусов) | |
| 27 | Найдите точное значение | грех(0) | |
| 28 | Найдите точное значение | грех(120) | |
| 29 | Найдите точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найдите точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найдите точное значение | детская кроватка(30 градусов) | |
| 37 | Найдите точное значение | арккос(-1) | |
| 38 | Найдите точное значение | арктический(0) | |
| 39 | Найдите точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найдите точное значение | sin((5pi)/3) | |
| 43 | Найдите точное значение | sin((3pi)/4) | |
| 44 | Найдите точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найдите точное значение | грех(300) | |
| 46 | Найдите точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найдите точное значение | соз(0) | |
| 49 | Найдите точное значение | соз(135) | |
| 50 | Найдите точное значение | cos((5pi)/3) | |
| 51 | Найдите точное значение | соз(210) | |
| 52 | Найдите точное значение | сек (60 градусов) | |
| 53 | Найдите точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найдите точное значение | грех(135 градусов) | |
| 61 | Найдите точное значение | грех(150) | |
| 62 | Найдите точное значение | грех(240 градусов) | |
| 63 | Найдите точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найдите точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найдите точное значение | cos(150 градусов) | |
| 68 | Найдите точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найдите точное значение | сек(0) | |
| 71 | Найдите точное значение | cos((5pi)/6) | |
| 72 | Найдите точное значение | КСК(30) | |
| 73 | Найдите точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найдите точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найдите точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найдите точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт.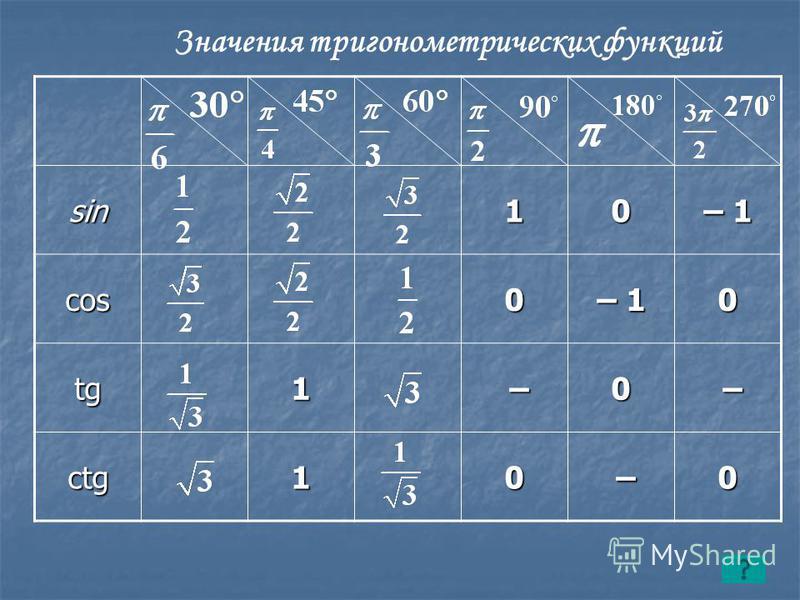 )/4 )/4 | |
| 79 | Найдите точное значение | sin((7pi)/4) | |
| 80 | Найдите точное значение | угловой синус(-1/2) | |
| 81 | Найдите точное значение | sin((4pi)/3) | |
| 82 | Найдите точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найдите точное значение | грех(135) | |
| 85 | Найдите точное значение | грех(105) | |
| 86 | Найдите точное значение | грех(150 градусов) | |
| 87 | Найдите точное значение | sin((2pi)/3) | |
| 88 | Найдите точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найдите точное значение | sin(pi/2) | |
| 91 | Найдите точное значение | сек(45) | |
| 92 | Найдите точное значение | cos((5pi)/4) | |
| 93 | Найдите точное значение | cos((7pi)/6) | |
| 94 | Найдите точное значение | угловой синус(0) | |
| 95 | Найдите точное значение | грех(120 градусов) | |
| 96 | Найдите точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найдите точное значение | соз(270) | |
| 98 | Найдите точное значение | sin((7pi)/6) | |
| 99 | Найдите точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Калькулятор — cos(-63) — Solumaths
Cos, расчет онлайн
Резюме:
Тригонометрическая функция cos вычисляет cos угла в радианах,
градусов или градианов.
cos online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить косинус , синус и касательная угла через одноименные функции.
Косинус тригонометрической функции отметил cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.
- Расчет косинуса
- Специальные значения косинуса
- Основные свойства
Вычисление косинуса угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, вы должны сначала
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 90, введите cos(90). возвращает 0.
Вычисление косинуса угла в градусах
Для вычисления косинуса угла в градианах необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 50, введите cos(50), после вычисления
возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения косинуса :
| cos(`2*pi`) | `1` | |||||
| cos(`pi`) | `-1` | |||||
| cos(`2 7 90 90`) | ||||||
| cos(`pi/4`) | `sqrt(2)/2` | |||||
| cos(`pi/3`) | `1/2` | |||||
| cos `) | `sqrt(3)/2` | |||||
| cos(`2*pi/3`) | `-1/2` | |||||
| cos(`3*pi/4`) | `-sqrt(2)/2` | |||||
| cos(`5*pi/6`) | `-sqrt(3)/2` | |||||
| cos(`0`) | `1` | cos(` pi`) | `1` | |||
| cos(`-pi`) | `-1` | |||||
| cos(`pi/2`) | `09` | 7 | 7 | `09` | 7 pi/4`) | `sqrt(2)/2` |
| cos(`-pi/3`) | `1/2` | |||||
| cos(`-pi/6`) | `sqrt(3)/2` | |||||
| cos(`-2*pi/3`) | `-1/2` | |||||
| cos(`-3*pi/4`) | `-sqrt(2)/2` | |||||
| cos(`-5*pi/6`) | `-sqrt(3)/2` |
`AA x в RR, k в ZZ`,
- `cos(-x)= cos(x)`
- `cos(x+2*k*pi)=cos(x)`
- `cos(pi-x)=-cos(x) `
- `cos(pi+x)=-cos(x)`
- `cos(pi/2-x)=sin(x)`
- `cos(pi/2+x)=-sin(x) )`
Производная косинуса равна -sin(x).
Первообразная косинуса равна sin(x).
Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с косинусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или же `2*cos(x)=sqrt(2)` с этапами расчета.
Синтаксис:
cos(x), где x — мера угла в градусах, радианах или градах.
Примеры:
cos(`0`), возвращает 1
Производная косинус :
Чтобы дифференцировать функцию косинуса онлайн,
можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса.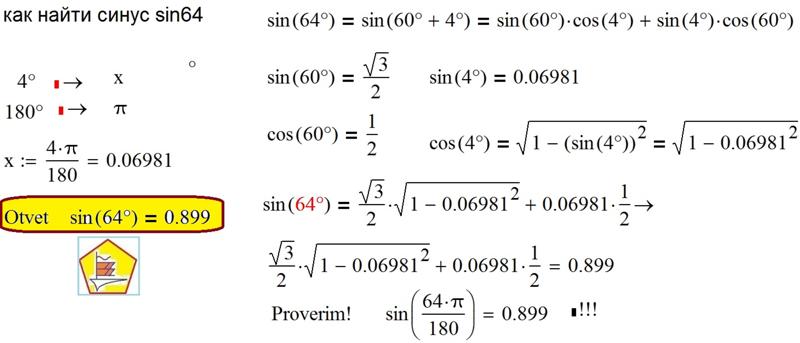
Первообразная косинуса :
Калькулятор первообразной позволяет вычислить первообразную функции косинуса.
Первопроизводная от cos(x) является первообразной(`cos(x)`)=`sin(x)`
Предельный косинус :
Калькулятор предела позволяет вычислить пределы функции косинуса.
предел cos(x) is limit(`cos(x)`)
Обратная функция косинуса :
обратная функция косинуса является функцией арккосинуса, отмеченной как arccos.
Графический косинус:
Графический калькулятор может отображать функцию косинуса в заданном интервале.
Свойство функции косинуса:
Функция косинуса является четной функцией.
Расчет онлайн с косинусом
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : грех. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции
Раздел 4.3: Тригонометрия прямоугольного треугольника
Результаты обучения
- Используйте прямоугольные треугольники для вычисления тригонометрических функций.

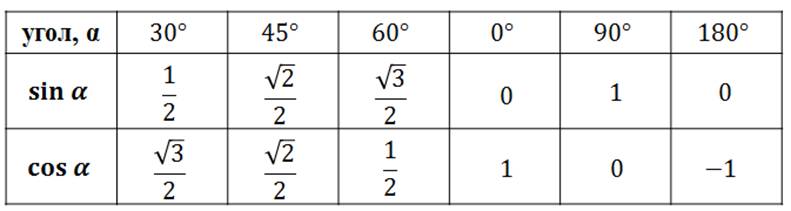
- Найдите значения функции для 30° (π/6), 45° (π/4) и 60° (π/3).
- Используйте кофункции дополнительных углов.
- Используйте определения тригонометрических функций любого угла.
- Используйте тригонометрию прямоугольного треугольника для решения прикладных задач.
Использование прямоугольных треугольников для вычисления тригонометрических функций
В предыдущих разделах мы использовали единичный круг для определения тригонометрические функции . В этом разделе мы расширим эти определения, чтобы их можно было применять к прямоугольным треугольникам. Значением функции синуса или косинуса [latex]t[/latex] является ее значение в [latex]t[/latex] радианах. Во-первых, нам нужно создать наш прямоугольный треугольник. На рисунке 1 показана точка на 90 005 единичной окружности 90 006 радиуса 1. Если мы опустим вертикальный отрезок из точки [латекс]\влево(х,у\вправо)\\[/латекс] на ось x , у нас есть прямоугольный треугольник, чья вертикальная сторона имеет длину [латекс]у[/латекс] и горизонтальная сторона имеет длину [латекс]х[/латекс]. Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника.
Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника.
Рис. =\frac{y}{1}=y[/latex]
Эти отношения по-прежнему применяются к сторонам прямоугольного треугольника, когда нет единичной окружности и когда треугольник не находится в стандартном положении и не отображается на графике с использованием [ латекс]\влево(х,у\вправо)[/латекс] координаты. Чтобы иметь возможность свободно использовать эти отношения, мы дадим сторонам более общие имена: вместо [латекс]х[/латекс] мы будем называть сторону между данным углом и прямым углом примыкающая сторона к углу [латекс]t[/латекс]. (Adjacent означает «рядом с».) Вместо [latex]y[/latex] мы будем называть сторону, наиболее удаленную от заданного угла, стороной , противоположной стороне от угла [latex]t[/latex]. И вместо [латекс]1[/латекс] мы будем называть сторону прямоугольного треугольника, противоположную прямому углу, гипотенузой .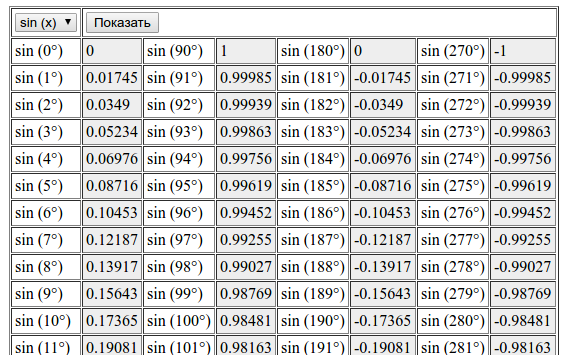 Эти стороны обозначены на рисунке 2.
Эти стороны обозначены на рисунке 2.
Рисунок 2. Стороны прямоугольного треугольника относительно угла [латекс]t[/латекс].
Понимание взаимоотношений прямоугольных треугольников
Дан прямоугольный треугольник с острым углом [latex]t[/latex],
[latex]\begin{align}&\sin \left(t\right)=\frac{ \text{напротив}}{\text{гипотенуза}} &\csc \left(t\right)=\frac{\text{гипотенуза}}{\text{напротив}}\\ &\cos \left(t\ справа) = \ frac {\ text {смежный}} {\ text {гипотенуза}} &\ sec \ left (t \ right) = \ frac {\ text {гипотенуза}} {\ text {смежный}} \\ &\ tan \left(t\right)=\frac{\text{напротив}}{\text{смежный}} &\cot \left(t\right)=\frac{\text{смежный}}{\text{напротив }}\end{выравнивание}[/latex]
Обычная мнемоника для запоминания этих отношений — Sohcahtoa, образованная из первых букв « S INE O PPOSITE более H Ypotenus Агент T находится между и напротив и .
Как: Зная длины сторон прямоугольного треугольника и один из острых углов, найдите синус, косинус и тангенс этого угла.

- Найдите синус как отношение противолежащего катета к гипотенузе
- Найдите косинус как отношение прилежащего катета к гипотенузе.
- Найдите тангенс отношения противолежащего катета к прилежащему.
Пример 1. Вычисление тригонометрической функции прямоугольного треугольника
Учитывая треугольник, показанный на рисунке 3, найдите значение [латекс]\cos \alpha[/латекс].
Рисунок 3
Показать решение
Попробуйте
Учитывая треугольник, показанный на рис. 4, найдите значение [латекс]\текст{sin}t[/латекс].
Рисунок 4
Показать решение
Взаимосвязь углов и их функции
При работе с прямоугольными треугольниками применяются одни и те же правила независимо от ориентации треугольника. Фактически, мы можем вычислить шесть тригонометрических функций любого из двух острых углов треугольника на рис.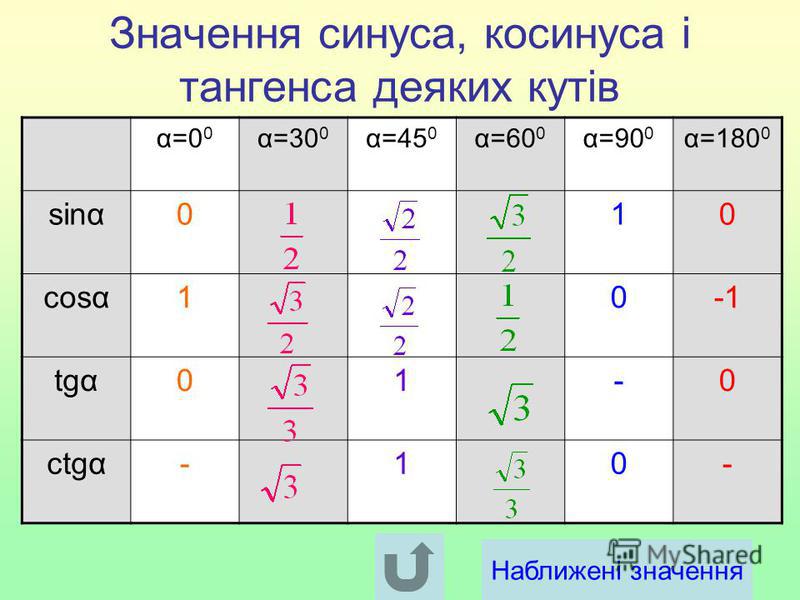 5. Сторона, противолежащая одному острому углу, является стороной, примыкающей к другому острому углу, и наоборот.
5. Сторона, противолежащая одному острому углу, является стороной, примыкающей к другому острому углу, и наоборот.
Рис. 5. Сторона, прилежащая к одному углу, противоположна другому.
Нас попросят найти все шесть тригонометрических функций для данного угла в треугольнике. Наша стратегия состоит в том, чтобы сначала найти синус, косинус и тангенс углов. Затем мы можем легко найти другие тригонометрические функции, потому что мы знаем, что обратная величина синуса является косекансом, обратная величина косинуса является секансом, а обратная величина тангенса является котангенсом.
Как: Имея длины сторон прямоугольного треугольника, вычислить шесть тригонометрических функций одного из острых углов.
- При необходимости начертите прямоугольный треугольник и обозначьте полученный угол.
- Определите угол, прилежащую сторону, сторону, противоположную углу, и гипотенузу прямоугольного треугольника.
- Найдите нужную функцию:
- синус как отношение противолежащего катета к гипотенузе
- косинус как отношение прилежащего катета к гипотенузе
- тангенс как отношение противоположной стороны к прилежащей стороне
- секанс как отношение гипотенузы к прилежащему катету
- косеканс как отношение гипотенузы к противолежащему катету
- котангенс как отношение прилежащей стороны к противолежащей стороне
Пример 2: вычисление тригонометрических функций углов, не находящихся в стандартном положении
Используя треугольник, показанный на рисунке 6, вычислите [латекс]\sin \alpha[/латекс], [латекс]\cos \альфа[/латекс], [ латекс]\тан \альфа[/латекс], [латекс]\сек \альфа[/латекс], [латекс]\csc \альфа [/латекс] и [латекс]\кот \альфа[/латекс].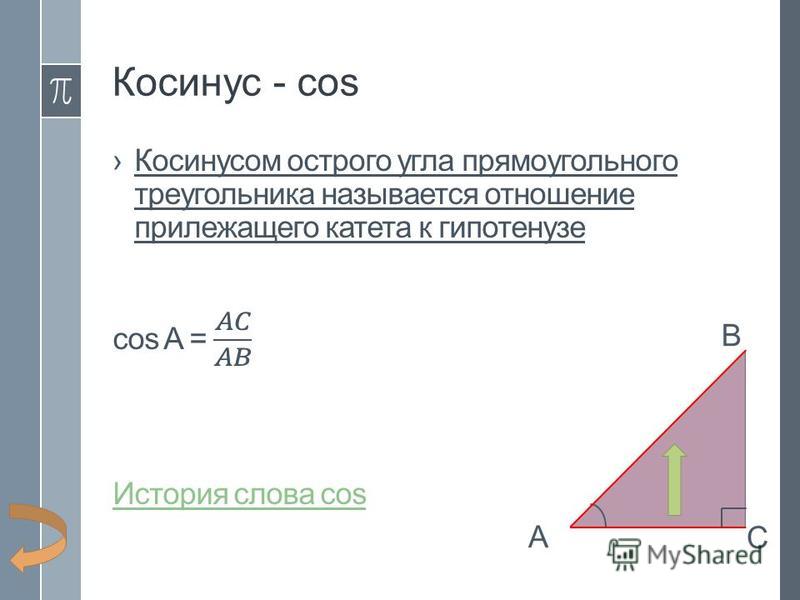
Рисунок 6
Показать решение
Попробуйте
Используя треугольник, показанный на рис. 7, оцените [латекс]\sin t[/латекс], [латекс]\cos t[/латекс], [латекс]\тангент[/латекс], [латекс ]\sec t[/latex], [латекс]\csc t[/латекс] и [латекс]\cot t[/латекс].
Рисунок 7
Показать решение
Попробуйте
Нахождение тригонометрических функций специальных углов с использованием длин сторон
Мы уже обсуждали тригонометрические функции, связанные с 9\circ [/latex] треугольник, который также может быть описан как [латекс]\frac{\pi }{4},\frac{\pi }{4},\frac{\pi }{2}[/latex ] треугольника, имеют длины в отношении [латекс]s,s,\sqrt{2}s[/латекс]. Эти отношения показаны на рисунке 8.
Рисунок 8. Длины сторон особых треугольников
Затем мы можем использовать отношения длин сторон для вычисления тригонометрических функций особых углов.
Как: Даны тригонометрические функции специального угла, вычислите их, используя длины сторон.
- Используйте длины сторон, показанные на рис. 8, для особого угла, который вы хотите оценить.
- Используйте соотношение длин сторон, соответствующее функции, которую вы хотите оценить.
Пример 3. Вычисление тригонометрических функций особых углов с использованием длин сторон
Найдите точное значение тригонометрических функций [латекс]\frac{\pi }{3}[/латекс], используя длины сторон.
Показать решение
Попробуйте
Найдите точное значение тригонометрических функций [латекс]\frac{\pi }{4}[/латекс], используя длины сторон. 9{\ circ} [/латекс]
Теперь, когда у нас есть эта таблица, мы можем использовать ее для нахождения точных значений тригонометрических выражений.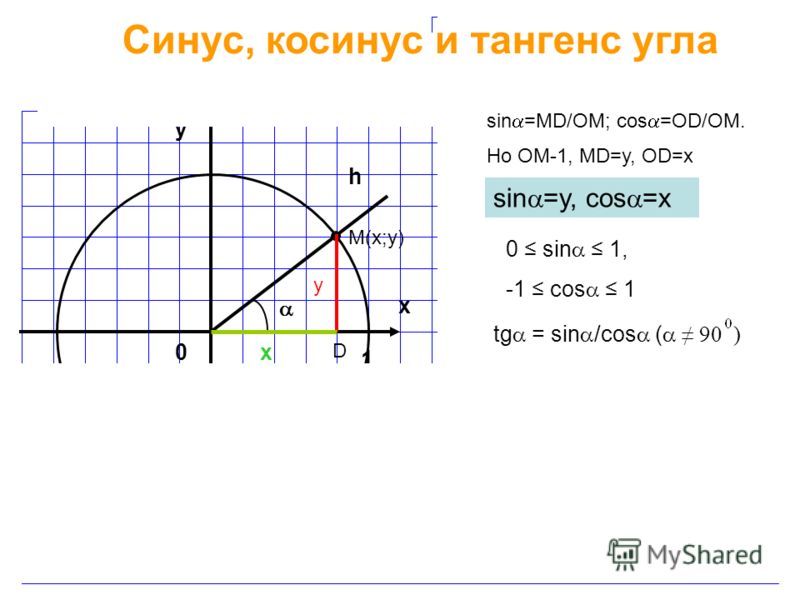 {2}\left(\frac{\pi}{6}\right)}[/latex], используя приведенную выше таблицу. 9\circ\right)[/latex], используя приведенную выше таблицу.
{2}\left(\frac{\pi}{6}\right)}[/latex], используя приведенную выше таблицу. 9\circ\right)[/latex], используя приведенную выше таблицу.
Показать решение
Использование равной кофункции дополнений
Если мы посмотрим на таблицу выше, мы заметим закономерность. В прямоугольном треугольнике с углами [латекс]\frac{\pi }{6}[/латекс] и [латекс]\frac{\pi }{3}[/латекс] мы видим, что синус [латекс] \frac{\pi }{3}[/latex], а именно [латекс]\frac{\sqrt{3}}{2}[/latex], также является косинусом [латекса]\frac{\pi }{ 6}[/latex], а синус [latex]\frac{\pi }{6}[/latex], а именно [latex]\frac{1}{2}[/latex], также является косинусом [латекс]\frac{\pi }{3}[/латекс].
[латекс]\begin{align} &\sin \frac{\pi }{3}=\cos \frac{\pi }{6}=\frac{\sqrt{3}s}{2s}=\ frac{\ sqrt {3}} {2} \\ &\ sin \ frac {\ pi} {6} = \ cos \ frac {\ pi} {3} = \ frac {s} {2s} = \ frac { 1}{2} \end{align}[/latex]
Рис. 9. Синус [latex]\frac{\pi }{3}[/latex] равен косинусу [latex]\frac{ \pi }{6}[/латекс] и наоборот.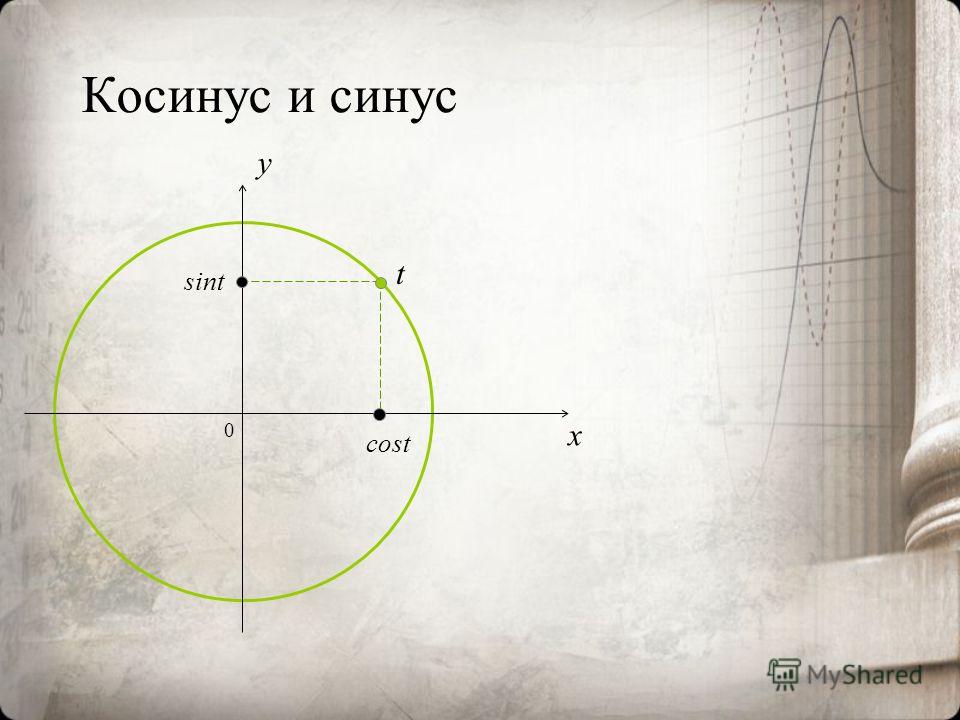
Этот результат не должен вызывать удивления, поскольку, как видно из рис. 9, сторона, противоположная углу [latex]\frac{\pi }{3}[/latex], также является стороной, примыкающей к [latex]\frac {\pi} {6}[/латекс], поэтому [латекс]\sin\left(\frac{\pi}{3}\right)[/latex] и [латекс]\cos\left(\frac{\ pi }{6}\right)[/latex] точно такое же отношение двух сторон, [latex]\sqrt{3}s[/latex] и [latex]2s[/latex]. Точно так же [латекс]\cos\left(\frac{\pi}{3}\right)[/latex] и [латекс]\sin\left(\frac{\pi}{6}\right)[/latex ] также имеют такое же соотношение, используя одни и те же две стороны, [латекс]s[/латекс] и [латекс]2с[/латекс].
Взаимосвязь между синусом и косинусом [latex]\frac{\pi }{6}[/latex] и [latex]\frac{\pi }{3}[/latex] также имеет место для двух острых углов в любом прямоугольном треугольнике, так как в любом случае отношение одних и тех же двух сторон составляет синус одного угла и косинус другого. Поскольку сумма трех углов треугольника равна [латекс]\пи [/латекс], а прямой угол равен [латекс]\фракция{\пи {2}[/латекс], оставшиеся два угла также должны составлять в сумме [латекс]\frac{\pi }{2}[/латекс]. Это означает, что прямоугольный треугольник может быть образован любыми двумя углами, сумма которых равна [латекс]\фракция{\пи }{2}[/латекс] — другими словами, любыми двумя дополнительными углами. Таким образом, мы можем констатировать тождество кофункции : Если любые два угла дополняют друг друга, то синус одного равен косинусу другого, и наоборот. Это тождество показано на рис. 10.
Это означает, что прямоугольный треугольник может быть образован любыми двумя углами, сумма которых равна [латекс]\фракция{\пи }{2}[/латекс] — другими словами, любыми двумя дополнительными углами. Таким образом, мы можем констатировать тождество кофункции : Если любые два угла дополняют друг друга, то синус одного равен косинусу другого, и наоборот. Это тождество показано на рис. 10.
Рис. 10. Кофунциональное тождество синуса и косинуса дополнительных углов
Используя это тождество, мы можем утверждать, не вычисляя, например, что синус [латекс]\фракция {\pi }{12}[/latex] равно косинусу [latex]\frac{5\pi }{12}[/latex], и что синус [latex]\frac{5\pi }{12 }[/latex] равен косинусу [latex]\frac{\pi }{12}[/latex]. Мы также можем утверждать, что если для некоторого угла [latex]t[/latex], [latex]\cos \text{ }t=\frac{5}{13}[/latex], то [latex]\sin \left(\frac{\pi }{2}-t\right)=\frac{5}{13}[/latex].
A Общее примечание: Идентичности кофункций
Идентичности кофункций в радианах перечислены в таблице ниже.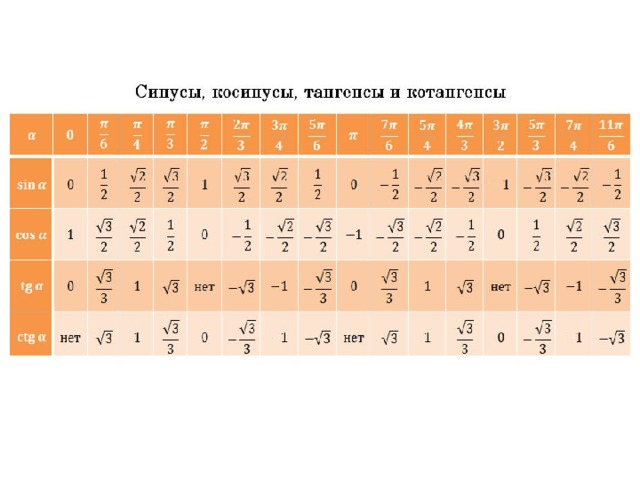
| [латекс]\cos t=\sin\left(\frac{\pi }{2}-t\right)[/latex] | [латекс]\sin t=\cos\left(\frac{\pi }{2}-t\right)[/latex] |
| [латекс]\tan t=\кроватка \влево(\frac{\pi} {2}-t\вправо)[/латекс] | [латекс]\кроватка т=\загар \влево(\фракция{\пи} {2}-т\вправо)[/латекс] |
| [латекс]\sec t=\csc \left(\frac{\pi }{2}-t\right)[/latex] | [латекс]\csc t=\sec\left(\frac{\pi }{2}-t\right)[/latex] |
Как: Зная синус и косинус угла, найти синус или косинус его дополнения.
- Чтобы найти синус дополнительного угла, найдите косинус исходного угла.
- Чтобы найти косинус дополнительного угла, найдите синус исходного угла.
Пример 5. Использование тождеств кофункций
Запишите следующее выражение в виде эквивалентного выражения косинуса: [латекс]\sin \left(\frac{5\pi}{12}\right)[/latex]. 9\circ\right)[/латекс].
Показать решение
youtube.com/embed/_gkuml—4_Q?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Использование тригонометрических функций
В предыдущих примерах мы вычисляли синус и косинус в треугольниках, для которых были известны все три стороны. Но настоящая сила тригонометрии прямоугольного треугольника проявляется, когда мы смотрим на треугольники, в которых мы знаем угол, но не знаем всех сторон.
Как: Зная прямоугольный треугольник, длину одной стороны и величину одного острого угла, найдите остальные стороны.
- Для каждой стороны выберите тригонометрическую функцию, у которой неизвестная сторона является либо числителем, либо знаменателем. Известная сторона, в свою очередь, будет знаменателем или числителем.
- Напишите уравнение, в котором значение функции известного угла равно отношению соответствующих сторон.
- Используя значение тригонометрической функции и известную длину стороны, найдите недостающую длину стороны.

Пример 7. Нахождение недостающих длин сторон с помощью тригонометрических соотношений
Найдите неизвестные стороны треугольника на рисунке 11.
Рисунок 11
Показать решение
Попробуйте
Прямоугольный треугольник имеет один угол [латекс]\frac{\pi }{3}[/латекс] и гипотенузу 20. Найдите неизвестные стороны и угол треугольника.
Показать решение
Попробуйте
Тригонометрия прямоугольного треугольника имеет множество практических применений. Например, возможность вычислить длины сторон треугольника позволяет найти высоту высокого предмета, не взбираясь на его вершину и не протягивая рулетку по его высоте. Мы делаем это, измеряя расстояние от основания объекта до точки на земле на некотором расстоянии, откуда мы можем смотреть на вершину высокого объекта под углом. Угол возвышения объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. Прямоугольный треугольник, создаваемый этим положением, имеет стороны, которые представляют собой неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол луча зрения, мы можем использовать тригонометрические функции для вычисления неизвестной высоты. Точно так же мы можем сформировать треугольник из вершины высокого объекта, глядя вниз. Угол наклона предмета ниже наблюдателя относительно наблюдателя — это угол между горизонталью и линией, проведенной от предмета к глазу наблюдателя. На рисунке ниже [латекс]\альфа[/латекс] представляет угол подъема и [латекс]\бета[/латекс] представляет угол депрессии .
Прямоугольный треугольник, создаваемый этим положением, имеет стороны, которые представляют собой неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол луча зрения, мы можем использовать тригонометрические функции для вычисления неизвестной высоты. Точно так же мы можем сформировать треугольник из вершины высокого объекта, глядя вниз. Угол наклона предмета ниже наблюдателя относительно наблюдателя — это угол между горизонталью и линией, проведенной от предмета к глазу наблюдателя. На рисунке ниже [латекс]\альфа[/латекс] представляет угол подъема и [латекс]\бета[/латекс] представляет угол депрессии .
Рисунок 12
Как: Имея высокий объект, косвенно измерьте его высоту.
- Сделайте набросок проблемной ситуации, чтобы отслеживать известную и неизвестную информацию.
- Отметьте измеренное расстояние от основания объекта до точки, где хорошо виден верх объекта.

- На другом конце измеренного расстояния посмотрите на верхнюю часть объекта. Измерьте угол, который линия взгляда образует с горизонтом. 9\circ [/latex], как показано на рисунке 13. Найдите высоту дерева.
Рисунок 13
Показать решение
Попробуй
Какой длины требуется лестница, чтобы добраться до подоконника на высоте 50 футов над землей, если лестница упирается в здание под углом [латекс]\frac{5\pi }{12}[/latex] ? Округлить до ближайшего фута.
Показать решение
Попробуйте
Обратная тригонометрическая функция на калькуляторе
9{-1}[/латекс]. Калькулятор вернет угол либо в радианах, либо в градусах, в зависимости от того, в каком режиме находится ваш калькулятор. \circ E[/latex] означает, что вы пойдете на север, а затем пойдете на 20 градусов на восток или вправо. На приведенном ниже рисунке показан пример того, как нарисованы подшипники. Как видите, каждый угол измеряется либо от N, либо от S, в зависимости от первой буквы направления. Подшипники НЕ нарисованы в стандартном положении, что означает, что они НЕ нарисованы от положительной оси X.
\circ E[/latex] означает, что вы пойдете на север, а затем пойдете на 20 градусов на восток или вправо. На приведенном ниже рисунке показан пример того, как нарисованы подшипники. Как видите, каждый угол измеряется либо от N, либо от S, в зависимости от первой буквы направления. Подшипники НЕ нарисованы в стандартном положении, что означает, что они НЕ нарисованы от положительной оси X. Теперь мы рассмотрим некоторые прикладные задачи, связанные с подшипниками и прямоугольными треугольниками.
Пример 9: Найдите азимут
Полуприцеп проходит 8 миль на восток, поворачивает направо и затем едет на юг еще 11 миль. Каков пеленг от начальной точки до текущего местоположения полуприцепа?
Показать решение
Попробуйте
Велосипедист проехал 7 миль на запад, повернул направо и проехал 4 мили на север. Каков пеленг от начальной точки до текущего положения велосипедиста? Округлите угол до одного десятичного знака.
 9\circ E[/latex] на 5 миль. Как далеко на восток и как далеко на юг находится бегун от исходной точки? Округлите свои ответы до ближайшей мили.
9\circ E[/latex] на 5 миль. Как далеко на восток и как далеко на юг находится бегун от исходной точки? Округлите свои ответы до ближайшей мили.Показать решение
Преобразование уклона в процентах в градусы
Уклон в процентах часто встречается на дорогах или тропах и является мерой крутизны. Например, если дорога имеет уклон 6 %, это означает, что дорога поднимается на 6 футов при горизонтальном расстоянии (пробеге) в 100 футов. Процентный уклон находится путем деления подъема на участок, как показано на рис. 14. Подъем и уклон также являются противоположными и смежными сторонами. Мы можем найти [латекс]\тета[/латекс], взяв арктангенс.
Рисунок 14
Чтобы вычислить градусное измерение процента, сначала преобразуйте процент в десятичную дробь, разделив ее на 100. Затем возьмите арктангенс этой десятичной дроби, и это даст угол в градусах. На самом деле это угол возвышения , который мы изучали ранее в этом разделе!
Практическое руководство.
 Преобразование процентов в градусы
Преобразование процентов в градусыУбедитесь, что ваш калькулятор находится в режиме градусов. Учитывая процентную градацию, угол [латекс]\тета[/латекс] можно рассчитать, используя: 9{-1}\left(\dfrac{\text{процент уклона}}{100}\right)[/latex]
Пример 11: Процент уклона в градусах
Филберт-стрит, самая крутая улица в Сан-Франциско, имеет 31,5% класса. Какой угол образует улица с горизонтальной линией, округленный до одного десятичного знака?
Показать решение
Попробуйте
Дорога имеет уклон 10,9%. Какой угол образует дорога с горизонтальной линией, округленный до одного десятичного знака?
Показать решение
Ключевые уравнения 9{-1}\left(\dfrac{\text{процентное содержание}}{100}\right)[/latex]
Ключевые понятия
- Тригонометрические функции можно определить как отношения длин сторон прямоугольного треугольника.

- Одинаковую длину сторон можно использовать для вычисления тригонометрических функций любого острого угла в прямоугольном треугольнике.
- Мы можем вычислить тригонометрические функции особых углов, зная длины сторон треугольников, в которых они встречаются.
- Любые два дополнительных угла могут быть двумя острыми углами прямоугольного треугольника.
- Если два угла дополняют друг друга, тождества кофункций утверждают, что синус одного равен косинусу другого и наоборот.
- Мы можем использовать тригонометрические функции угла, чтобы найти неизвестные длины сторон.
- Выберите тригонометрическую функцию, представляющую отношение неизвестной стороны к известной стороне.
- Тригонометрия прямоугольного треугольника позволяет измерять недоступные высоты и расстояния.
- Неизвестную высоту или расстояние можно найти, составив прямоугольный треугольник, в котором неизвестная высота или расстояние является одной из сторон, а другая сторона и угол известны.

- Подшипники измеряются либо от N, либо от S, в зависимости от первой буквы подшипника.
- Уклон в процентах может быть выражен в градусах, которые представляют собой угол возвышения.
Глоссарий
- смежная сторона
- в прямоугольном треугольнике, сторона между данным углом и прямым углом
- угол наклона
- угол между горизонталью и линией от объекта до глаза наблюдателя, при условии, что объект расположен ниже, чем наблюдатель
- угол возвышения
- угол между горизонталью и линией от объекта до глаза наблюдателя, при условии, что объект расположен выше наблюдателя
- противоположная сторона
- в прямоугольном треугольнике, сторона которого наиболее удалена от данного угла
- гипотенуза
- сторона прямоугольного треугольника, противоположная прямому углу
- %
- Соотношение роста по сравнению с тиражом, выраженное в процентах.
 Это мера крутизны.
Это мера крутизны.
Раздел 4.3. Домашнее задание. Упражнения
1. Для заданного прямоугольного треугольника обозначьте прилежащую сторону, противоположную сторону и гипотенузу указанного угла.
2. Когда прямоугольный треугольник с гипотенузой 1 помещен в единичную окружность, какие стороны треугольника соответствуют координатам x и y?
3. Тангенс угла сравнивает какие стороны прямоугольного треугольника?
4. Какая связь между двумя острыми углами в прямоугольном треугольнике?
5. Объясните тождество кофункции.
Для следующих упражнений оцените выражение. При необходимости рационализируйте знаменатель.
6. [латекс]\sin\frac{\pi}{4}\cos\frac{\pi}{4}-\tan\frac{\pi}{3}[/latex]
7. [ латекс]\sin\frac{\pi}{4}\cos\frac{\pi}{3}-\tan\frac{\pi}{4}[/latex] 9\circ \right)[/latex]
13. [латекс]\tan \left(\frac{\pi }{4}\right)=\cot \left(\text{__}\right)[/latex ]
В следующих упражнениях найдите длины недостающих сторон, если сторона [латекс]a[/латекс] противоположна углу [латекс]А[/латекс], сторона [латекс]b[/латекс] противоположна углу [ латекс]В[/латекс], а сторона [латекс]с[/латекс] — гипотенуза.

14. [латекс]\cos B=\frac{4}{5},a=10[/latex]
15. [латекс]\sin B=\frac{1}{2}, a=20 [/latex]
16. [латекс]\tan A=\frac{5}{12},b=6[/latex] 9{\circ }[/latex]
В следующих упражнениях используйте рисунок 14 для вычисления каждой тригонометрической функции угла [latex]A[/latex].
Рисунок 14
21. [латекс]\sin A[/латекс]
22. [латекс]\cos A[/латекс]
23. [латекс]\tan A[/латекс]
24. [латекс]\csc A[/latex]
25. [latex]\sec A[/latex]
26. [latex]\cot A[/latex]
В следующих упражнениях используйте рисунок 15 для вычисления каждой тригонометрической функции угла. [латекс]А[/латекс].
Рисунок 15
27. [латекс]\sin A[/латекс]
28. [латекс]\cos A[/латекс]
29. [латекс]\tan A[/латекс]
30. [латекс]\csc A[/latex]
31. [latex]\sec A[/latex]
32. [latex]\cot A[/latex]
В следующих упражнениях найдите неизвестные стороны данного треугольника.

33.
34.
35.
В следующих упражнениях используйте калькулятор, чтобы найти длину каждой стороны с точностью до четырех знаков после запятой. 9\circ [/латекс]. На какую высоту лестница достигает стены здания?
58. Установлено, что угол подъема на вершину здания в Нью-Йорке составляет 9 градусов от земли на расстоянии 1 мили от основания здания. Используя эту информацию, найдите высоту здания.
59. Установлено, что угол подъема на вершину здания в Сиэтле составляет 2 градуса от земли на расстоянии 2 миль от основания здания. Используя эту информацию, найдите высоту здания. 9\circ [/latex], как далеко я от основания дерева?
61. Автомобиль едет на запад 5 миль, поворачивает налево, а затем едет на юг 9 миль. Каков пеленг от начального положения автомобиля до его текущего положения? Округлите ответ до двух знаков после запятой.
62. Грузовик едет на восток 4 мили, поворачивает налево, а затем едет на север 6 миль.
 \circ E[/латекс] на 36 дюймов. Как далеко на восток и как далеко на север находится муравей от своего исходного положения? Округлите ответы до двух знаков после запятой. 9\circ W[/латекс] для 20 дюймов. Как далеко на запад и как далеко на юг находится паук от начальной точки? Округлите ответы до двух знаков после запятой.
\circ E[/латекс] на 36 дюймов. Как далеко на восток и как далеко на север находится муравей от своего исходного положения? Округлите ответы до двух знаков после запятой. 9\circ W[/латекс] для 20 дюймов. Как далеко на запад и как далеко на юг находится паук от начальной точки? Округлите ответы до двух знаков после запятой.65. Первоначально построен в 1901 году полковником Дж.В. Эдди, «Полет ангелов» в Лос-Анджелесе считается самой короткой в мире железной дорогой. Уравновешенные автомобили, управляемые тросами, преодолевают уклон 33% на 315 футов. Какой угол образует дорожка с горизонтальной линией, округленный до одного десятичного знака?
66. Участок Салуда является самым крутым уклоном магистральной железной дороги стандартной колеи в Соединенных Штатах. Между Мелроузом и Салудой, Северная Каролина, максимальная оценка составляет 4,9.% примерно на 300 футов. Какой угол образует дорожка с горизонтальной линией, округленный до одного десятичного знака?
Просмотр с использованием функций синуса, косинуса или тангенса для нахождения углов в прямоугольном треугольнике
Поиск
Учащийся находит углы прямоугольного треугольника с помощью синуса, косинуса или тангенса.

Рандомизировать вопросы случайных ответов
Если сторона a равна 3 дюймам, а сторона b равна 7 дюймам, какова мера угла A? Округлить до ближайшего целого числа.
- 25 градусов
- 23 градуса
- 67 градусов
- 90 градусов
Вопрос 1 из 10
Правильно!
Если сторона a равна 3 дюймам, а сторона b равна 7 дюймам, какова мера угла A? Округлить до ближайшего целого числа.
Правильный ответ
23 градуса
Объяснение:
Используя функцию касательной, угол A = tan -1 (3/7) = 23 0
Следующий вопрос
Вопрос 1 из 10
Неправильно
Если сторона a равна 3 дюймам, а сторона b равна 7 дюймам, какова мера угла A? Округлить до ближайшего целого числа.

Ваш ответ
Правильный ответ
23 градуса
Объяснение:
Используя функцию касательной, угол A = tan -1 (3/7) = 23 0
Следующий вопрос
Вопрос 1 из 10
Если сторона а равна 17 см, а сторона с равна 20 см, чему равен угол А? Округлить до целого числа.
58 градусов
59 градусов
90 градусов
42 градуса
Вопрос 1 из 10
Правильно!
Если сторона а равна 17 см, а сторона с равна 20 см, чему равен угол А? Округлить до целого числа.

Правильный ответ
58 градусов
Объяснение:
Мера угла A: угол A = sin -1 (17/20) = 58 0
Следующий вопрос
Вопрос 1 из 10
Неверно
Если сторона а равна 17 см, а сторона с равна 20 см, какова мера угла А? Округлить до целого числа.
Ваш ответ
Правильный ответ
58 градусов
Объяснение:
Мера угла A: угол A = sin -1 (17/20) = 58 0
Следующий вопрос
Вопрос 1 из 10
Чему равен угол B, если сторона a равна 10 футам, а сторона c равна 22 футам? Округлить до целого числа.

27 градусов
26 градусов
30 градусов
63 градуса
Вопрос 1 из 10
Правильно!
Чему равен угол B, если сторона a равна 10 футам, а сторона c равна 22 футам? Округлить до целого числа.
Правильный ответ
63 градуса
Объяснение:
Мера угла B = cos -1 (10/22) = 63 градуса
Следующий вопрос
Вопрос 1 из 10
Неверно
Чему равен угол B, если сторона a равна 10 футам, а сторона c равна 22 футам? Округлить до целого числа.

Ваш ответ
Правильный ответ
63 градуса
Объяснение:
Мера угла B = cos -1 (10/22) = 63 градуса
Следующий вопрос
Вопрос 1 из 10
Если сторона c равна 50 метрам, а сторона b равна 42 метрам, какова мера угла A? Округлить до ближайшего целого числа.
57 градусов
75 градусов
33 градуса
90 градусов
Вопрос 1 из 10
Правильно!
Если сторона c равна 50 метрам, а сторона b равна 42 метрам, какова мера угла A? Округлить до ближайшего целого числа.

Правильный ответ
33 градуса
Объяснение:
Угол A = cos -1 (42/50) = 33 0
Следующий вопрос
Вопрос 1 из 10
Неверно
Если сторона c равна 50 метрам, а сторона b равна 42 метрам, какова мера угла A? Округлить до ближайшего целого числа.
Ваш ответ
Правильный ответ
33 градуса
Объяснение:
Угол A = cos -1 (42/50) = 33 0
Следующий вопрос
Вопрос 1 из 10
Если сторона c равна 67 дюймам, а сторона b равна 20 дюймам, какова мера угла A? Чему равен угол В? Округлите ответы до ближайшего целого градуса.

угол А = 73 градуса; угол B = 17 градусов
угол А = 19 градусов; угол B = 71 градус
угол А = 17 градусов; угол B = 83 градуса
угол А = 19 градусов; угол B = 90 градусов
Вопрос 1 из 10
Правильно!
Если сторона c равна 67 дюймам, а сторона b равна 20 дюймам, какова мера угла A? Чему равен угол В? Округлите ответы до ближайшего целого градуса.
Правильный ответ
угол А = 73 градуса; угол B = 17 градусов
Объяснение:
Угол A = cos -1 (20/67) = 73 0 ; угол B = 90 0 — 73 0 = 17 0
Следующий вопрос
Вопрос 1 из 10
Неверно
Если сторона c равна 67 дюймам, а сторона b равна 20 дюймам, какова мера угла A? Чему равен угол В? Округлите ответы до ближайшего целого градуса.

Ваш ответ
Правильный ответ
угол А = 73 градуса; угол B = 17 градусов
Объяснение:
Угол A = cos -1 (20/67) = 73 0 ; угол B = 90 0 — 73 0 = 17 0
Следующий вопрос
Вопрос 1 из 10
Сторона b равна 8 метрам, а сторона a — 9 метрам. Чему равны углы А и В? Округлите ответы до целых чисел.
угол А = 42 градуса; угол B = 48 градусов
угол А = 48 градусов; угол B = 42 градуса
угол А = 45 градусов; угол B = 45 градусов
угол А = 90 градусов; угол B = 42 градуса
Вопрос 1 из 10
Правильно!
Сторона b составляет 8 метров, а сторона a — 9 метров.
 Чему равны углы А и В? Округлите ответы до целых чисел.
Чему равны углы А и В? Округлите ответы до целых чисел.Правильный ответ
угол А = 48 градусов; угол B = 42 градуса
Объяснение:
Угол A = тангенс -1 (9/8) = 48 0 ; Угол B = 90 0 — 48 0 = 42 0
Следующий вопрос
Вопрос 1 из 10
Неверно
Сторона b равна 8 метрам, а сторона a равна 9метров. Чему равны углы А и В? Округлите ответы до целых чисел.
Ваш ответ
Правильный ответ
угол А = 48 градусов; угол B = 42 градуса
Объяснение:
Угол A = тангенс -1 (9/8) = 48 0 ; Угол B = 90 0 — 48 0 = 42 0
Следующий вопрос
Вопрос 1 из 10
Если сторона b равна 17 км, а сторона c равна 21 км, каковы размеры углов A и B? Округлите до целых чисел.

угол А = 35 градусов; угол B = 55 градусов
угол А = 36 градусов; угол B = 54 градуса
угол А = 37 градусов; угол B = 53 градуса
угол А = 35 градусов; угол B = 90 градусов
Вопрос 1 из 10
Правильно!
Если сторона b равна 17 км, а сторона c равна 21 км, каковы размеры углов A и B? Округлите до целых чисел.
Правильный ответ
угол А = 36 градусов; угол B = 54 градуса
Объяснение:
Угол A = cos -1 (17/21) = 36 0 ; угол B = 90 0 — 36 0 = 54 0
Следующий вопрос
Вопрос 1 из 10
Неверно
Если сторона b равна 17 км, а сторона c равна 21 км, каковы размеры углов A и B? Округлите до целых чисел.

Ваш ответ
Правильный ответ
угол А = 36 градусов; угол B = 54 градуса
Объяснение:
Угол A = cos -1 (17/21) = 36 0 ; угол B = 90 0 — 36 0 = 54 0
Следующий вопрос
Вопрос 1 из 10
Если сторона a равна 12 дюймам, а сторона b равна 15 дюймам, какова мера угла A? Округлить до целого числа.
53 градуса
37 градусов
39 градусов
51 градус
Вопрос 1 из 10
Правильно!
Если сторона a равна 12 дюймам, а сторона b равна 15 дюймам, какова мера угла A? Округлить до целого числа.

Правильный ответ
39 градусов
Объяснение:
Угол A = tan -1 (12/15) = 39 0
Следующий вопрос
Вопрос 1 из 10
Неправильно
Если сторона a равна 12 дюймам, а сторона b равна 15 дюймам, какова мера угла A? Округлить до целого числа.
Ваш ответ
Правильный ответ
39 градусов
Объяснение:
Угол A = tan -1 (12/15) = 39 0
Следующий вопрос
Вопрос 1 из 10
Чему равен угол B? Округлить до целого числа.

34 градуса
56 градусов
90 градусов
44 градуса
Вопрос 1 из 10
Правильно!
Чему равен угол B? Округлить до целого числа.
Правильный ответ
44 градуса
Объяснение:
Угол B = cos -1 (50/70) = 44 0
Готово
Вопрос 1 из 10
Неверно
Чему равен угол B? Округлить до целого числа.

Ваш ответ
Правильный ответ
44 градуса
Объяснение:
Угол B = cos -1 (50/70) = 44 0
Готово
Вопрос 1 из 10
Вы правильно ответили на 5 из 10 вопросов.
50%
Начать сначала
Смотрите другие карточки и приложения, связанные с:
- уголок
- косинус
- прямоугольный треугольник
- синус
- тангенс
Вопрос 1 из 10
- Автор
- Мэри Рудник-Каун
- Опубликовано
- 21.

- Тригонометрические функции можно определить как отношения длин сторон прямоугольного треугольника.

 Это крупнейшая точка межоператорского обмена (пиринг) интернет-трафика в России. Здание АО «ММТС-9» оснащено системами бесперебойного электропитания, клим…
Это крупнейшая точка межоператорского обмена (пиринг) интернет-трафика в России. Здание АО «ММТС-9» оснащено системами бесперебойного электропитания, клим…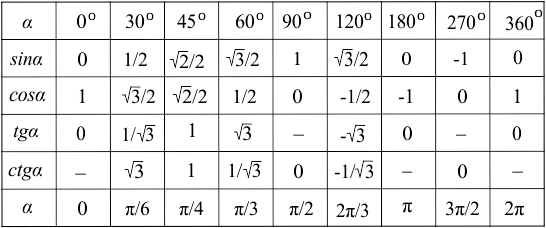 2500С-Т 400-ЗРН мощностью 2500 кВт для «Делового центра Юг» в г. Новый Уренгой Ямало-Ненецкого АО. Дизель-генераторная установка контейнерного исполнения выполнена на базе двигателя MTU 20V4000G84F (Германия) и генератора …
2500С-Т 400-ЗРН мощностью 2500 кВт для «Делового центра Юг» в г. Новый Уренгой Ямало-Ненецкого АО. Дизель-генераторная установка контейнерного исполнения выполнена на базе двигателя MTU 20V4000G84F (Германия) и генератора … ..
..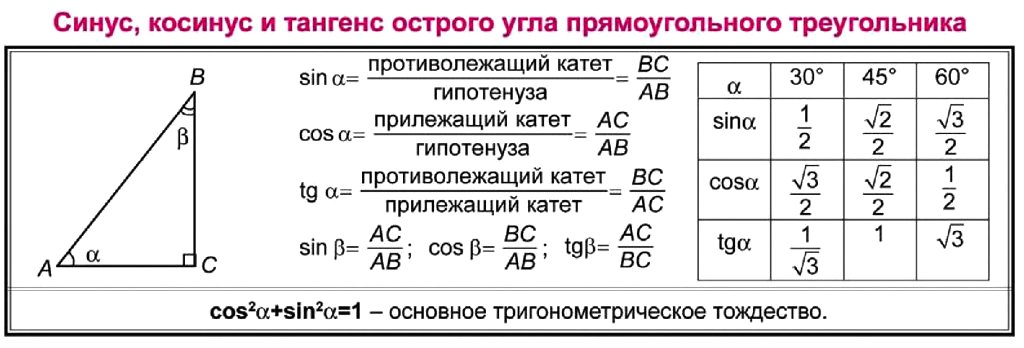 5
5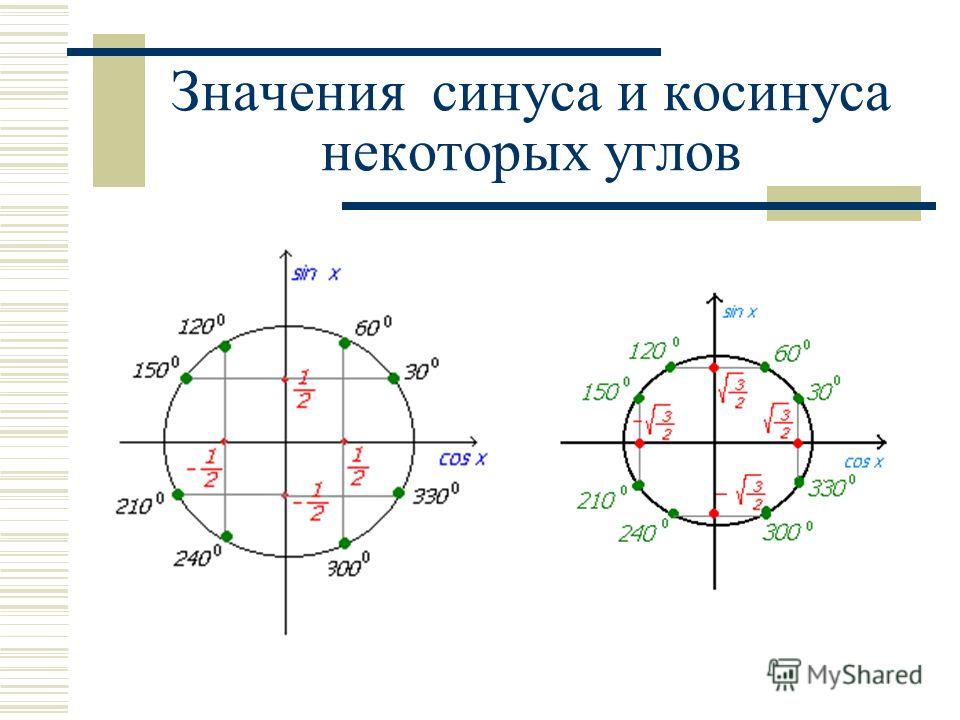 8910065242
8910065242 11, GOST R 34.11-94, GOST(63)
11, GOST R 34.11-94, GOST(63)
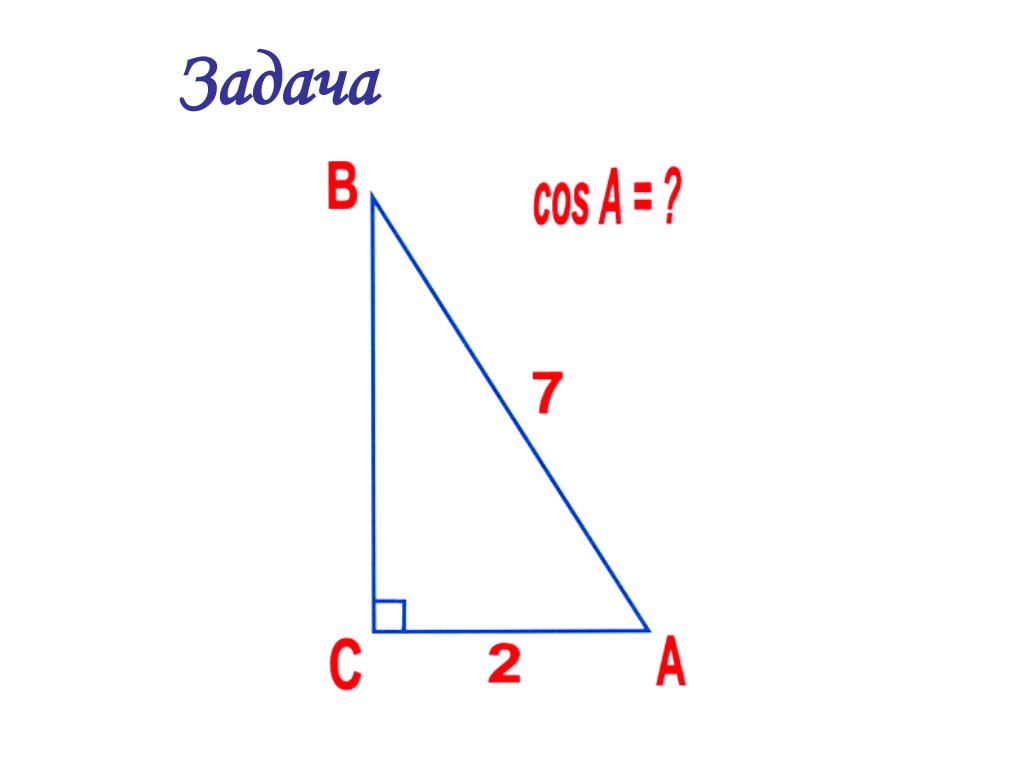 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.


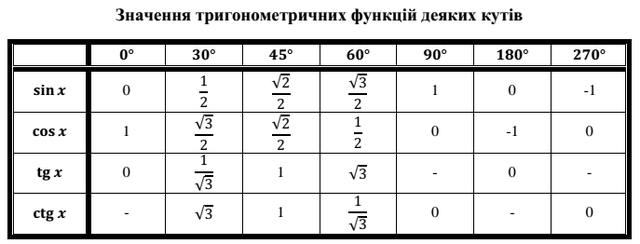 \circ E[/latex] означает, что вы пойдете на север, а затем пойдете на 20 градусов на восток или вправо. На приведенном ниже рисунке показан пример того, как нарисованы подшипники. Как видите, каждый угол измеряется либо от N, либо от S, в зависимости от первой буквы направления. Подшипники НЕ нарисованы в стандартном положении, что означает, что они НЕ нарисованы от положительной оси X.
\circ E[/latex] означает, что вы пойдете на север, а затем пойдете на 20 градусов на восток или вправо. На приведенном ниже рисунке показан пример того, как нарисованы подшипники. Как видите, каждый угол измеряется либо от N, либо от S, в зависимости от первой буквы направления. Подшипники НЕ нарисованы в стандартном положении, что означает, что они НЕ нарисованы от положительной оси X. 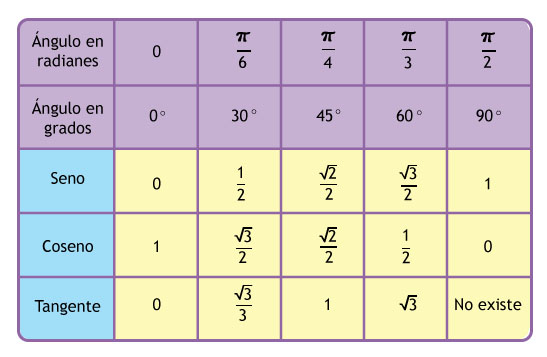 9\circ E[/latex] на 5 миль. Как далеко на восток и как далеко на юг находится бегун от исходной точки? Округлите свои ответы до ближайшей мили.
9\circ E[/latex] на 5 миль. Как далеко на восток и как далеко на юг находится бегун от исходной точки? Округлите свои ответы до ближайшей мили.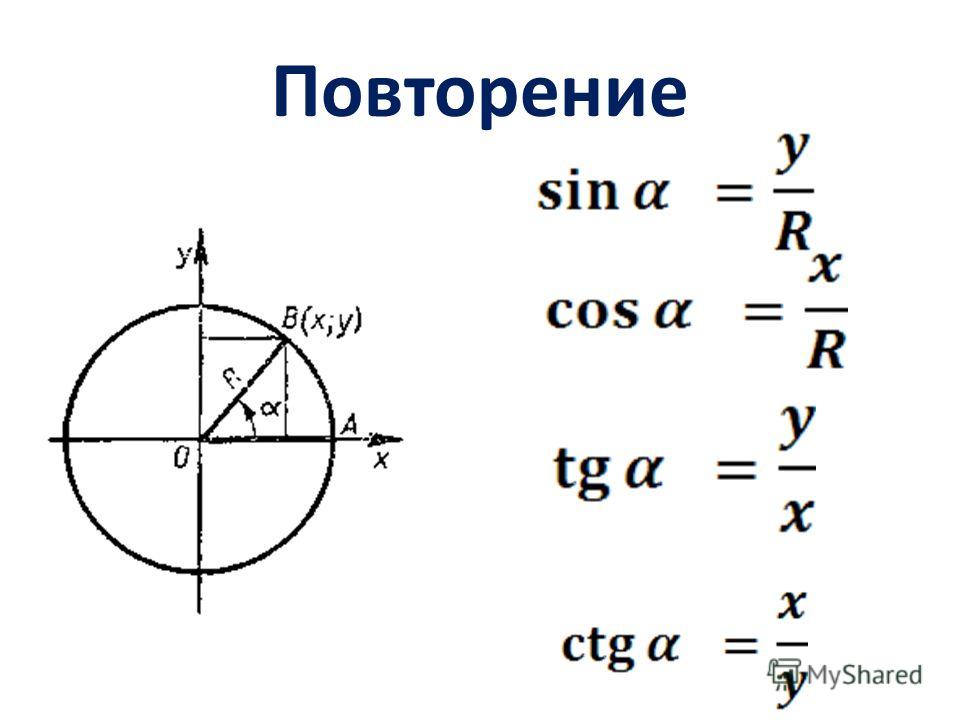 Преобразование процентов в градусы
Преобразование процентов в градусы

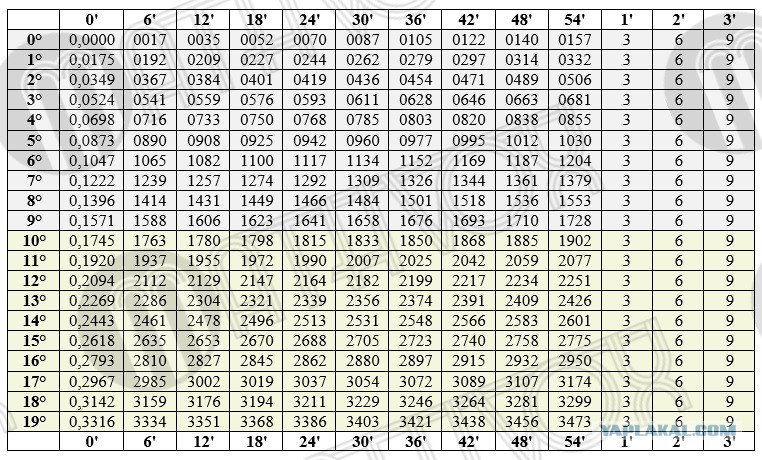 Это мера крутизны.
Это мера крутизны.
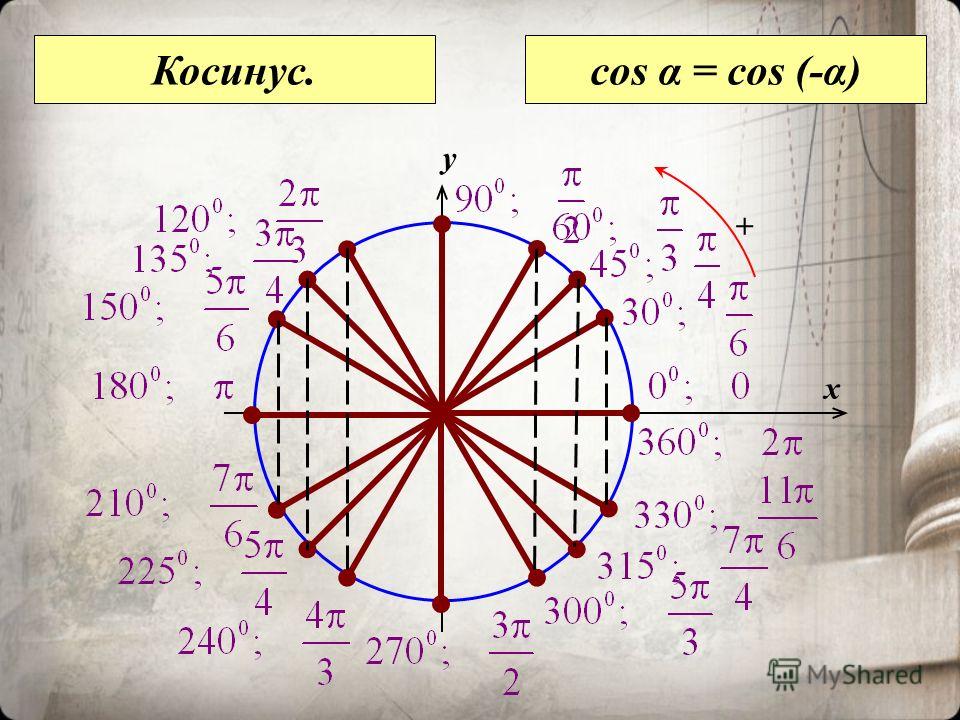
 \circ E[/латекс] на 36 дюймов. Как далеко на восток и как далеко на север находится муравей от своего исходного положения? Округлите ответы до двух знаков после запятой. 9\circ W[/латекс] для 20 дюймов. Как далеко на запад и как далеко на юг находится паук от начальной точки? Округлите ответы до двух знаков после запятой.
\circ E[/латекс] на 36 дюймов. Как далеко на восток и как далеко на север находится муравей от своего исходного положения? Округлите ответы до двух знаков после запятой. 9\circ W[/латекс] для 20 дюймов. Как далеко на запад и как далеко на юг находится паук от начальной точки? Округлите ответы до двух знаков после запятой.


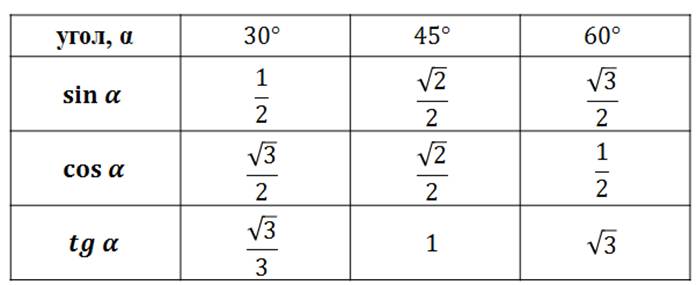
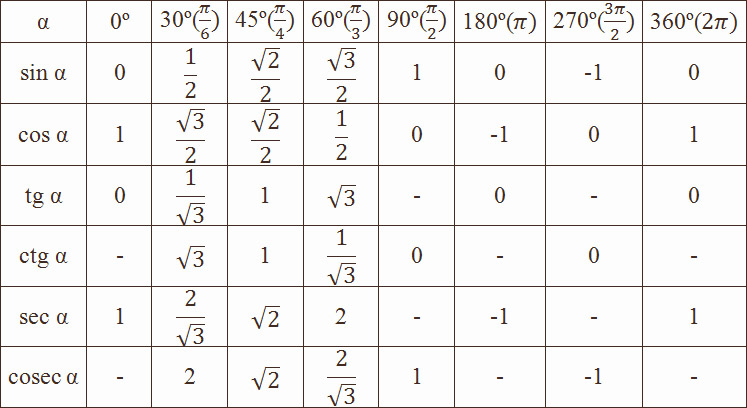


 Чему равны углы А и В? Округлите ответы до целых чисел.
Чему равны углы А и В? Округлите ответы до целых чисел.