Чему равен косинус 15° градусов
математика тригонометрия решение косинус
Только в сентябре: получи кредитку по акции с бонусом 2000р. и годом без % Получить карту
Как определить точное значение косинуса 15° градусов cos (15°)? Чему он равен?
Похвалить 0 Пожаловаться
3 ответа
Попробуем найти косинус 15 градусов путем решения задачи.
Допустим, у нас есть треугольник ACB, поделенные на равнобедренный тр. ADE, треугольник с 30, 60 и 90 градусов (BDE) и тр. BCD, у которого есть угол 15 градусов.
И нам известно, что равнобедренная сторона AE равна 1 сантиметру. Чтобы вычислить косинус 15 градусов, нам нужно найти размер сторон треугольника BCD.
ADE — равнобедренный треугольник, потому сторона DE равна AE = 1 см. AD легко найти по теореме Пифагора (прибавляем квадраты сторон AE и AD, вычитаем корень суммы) — длина стороны — это √2.
- ∠DBE = 30 гр.;
- соотношение сторон BE и BD — это cos 30 гр.
- табличное значение cos 30 — √3 поделить на 2;
- делаем вывод: BD = 2, BE = √3.
Поскольку углы CAE, CBA равны 45 гр., самый большой треугольник ABC тоже равнобедренный (стороны AC и BC одинаковые по размеру), можно применить теорему Пифагора:
Стороны большого треугольника найдены — осталось отыскать длину самой маленькой фигуры, в которой и есть нужный градус для вычисления косинуса. Принимаем CD за икс(это указано на иллюстрации выше). Находим значение переменной с помощью теоремы Пифагора. Для этого предположим, что икс плюс √2 равен квадратному корню из суммы квадратов двух других катетов, минус √2. Считаем:
Осталось совсем чуть-чуть! Делаем заключительное соотношение для вычисления косинуса:
Получается табличное значение cos 15:
Точное значение косинуса 15 гр. дуги
В нешкольных задачах используют точные цифры по таблице Брадиса. Если довести уравнение до конца получится следующее число:
Если довести уравнение до конца получится следующее число:
Смотрите также способы определить косинус 60 градусов и как найти cos 75.
Похвалить 3 Пожаловаться
Что такое косинус угла
Косинусом угла в прямоугольном треугольнике называется отношение длины противолежащего катета к длине гипотенузы.
На приведенном ниже рисунке для угла ‘х’ противолежащим катетом будет сторона ‘а’, а гипотенузой – сторона ‘с’. Таким образом, cos(х)=а/с.
Как вычислить значение cos(15°)
Рассмотрим несколько способов вычисления этого значения.
Первый способ – по математическим таблицам
По таблицам Брадиса или с помощью калькулятора: cos(15°)=0,9659.
Второй способ – используя тригонометрические выражения
1) Так как угол 15° равен половине 30°, то его косинус можно рассчитать по формуле половинного угла:
Известно, что косинус угла 30° определяется простым выражением:
Подставляя значение cos(30°) в предыдущую формулу получим:
2) Угол 15° также можно представить как разность между 60° и 45°. Тогда косинус 15° можно рассчитать по тригонометрической формуле:
Тогда косинус 15° можно рассчитать по тригонометрической формуле:
Значения косинусов и синусов углов 60° и 45° определяются простыми выражениями, подставляя которые в предыдущую формулу получим:
Третий способ – графически
Это наименее точный способ. Используя транспортир и линейку следует начертить прямоугольный треугольник произвольного размера, аналогичный показанному на рисунке. Затем с помощью линейки измерить длину сторон ‘а’ и ‘с’ треугольника и рассчитать их математическое отношение.
Похвалить 2 Пожаловаться
Определяем значение косинуса угла, равного 15 градусов, чтобы определить, рассмотрим треугольник.
Итак, косинус угла в прямоугольном треугольнике — отношение длины противолежащего катета к длине гипотенузы.
На нашем рисунке:
- неизвестный угол «α»;
- противолежащий катет сторона «а»;
- гипотенуза — «с».

Таким образом, cos(α)=а/с, определяем косинус угла в 15 градусов согласно таблице Брадиса: cos(15)=0,9659.
Таблица Брадиса — это таблица, которая поможет при вычислениях в решении задач как в школе (на математике, алгебре, геометрии и физике в старших классах), так и в вузах. На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов.
Итак, cos (15°)=0,966
Ознакомьтесь также:
- Чему равен косинус 90° градусов — cos(90°)?
- Чему равен косинус 180° градусов — cos(180°)?
- Чему равен косинус 330° градусов — cos(330°)?
Похвалить 0 Пожаловаться
Дать ответ и заработать:
Cимволов:
Вычислить и найти косинус онлайн
Пример решили: 87238 раз Сегодня решили: 0 раз
Введите градусы или радианы
Угол Градусы (°)Радианы (rad)
Вычисление косинуса
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
В прямоугольном треугольнике с острым углом α справедливо следующее соотношение:
 2 — 2 \cdot 16 \cdot 24 \cdot (-0.5) = 1216 $$
2 — 2 \cdot 16 \cdot 24 \cdot (-0.5) = 1216 $$Извлечем из полученного результата квадратный корень и возьмем положительное значение:
$$ c = \sqrt{1216} = 34,87 см $$
Ответ:
$$ с = 34,87 см $$
Посмотреть решение
Решение:
Скалярное произведение двух векторов равно произведению их модулей (длин) на косинус угла между ними $$ ab=│a│ \cdot │b│ \cdot \cos(ab) $$
Подставив, получим:
$$ ab=5 \cdot 7 \cdot \cos \left(\frac{\pi}{3} \right) = 5 \cdot 7 \cdot 0,5 = 17,5 $$
Ответ:
$$ ab = 17,5 $$
Посмотреть решение
Решение:
Работа силы находится по формуле
$$ A=F \cdot s \cdot cos(\alpha) $$, где $$ \alpha $$ – угол между векторами силы F и перемещения. 2
2
Синус, косинус и тангенс острого угла прямоугольного треугольника / Подобные треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Синус, косинус и тангенс острого угла прямоугольного треугольника
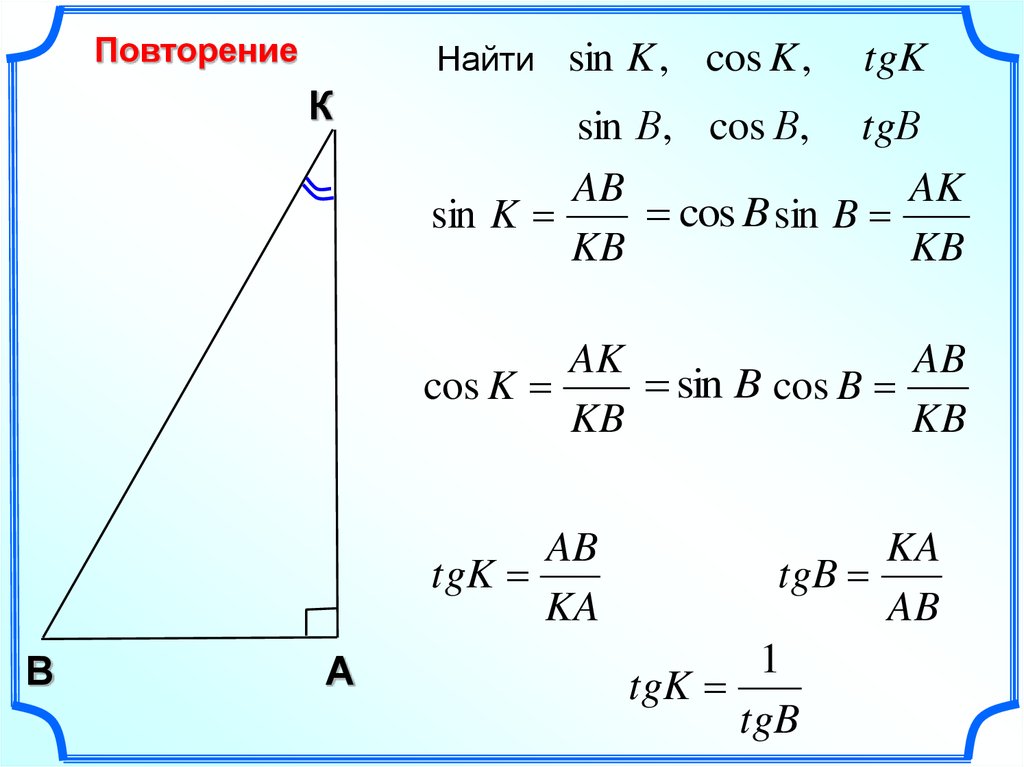
Рассмотрим прямоугольный треугольник АВС с прямым углом С:
Катет ВС этого треугольника является противолежащим углу А, а катет АС — прилежащим к этому углу.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Синус угла, который равен , обозначается символом , читается: «синус альфа».
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинус угла, который равен , обозначается символом , читается: «косинус альфа».
Косинус угла, который равен , обозначается символом , читается: «косинус альфа».
Тангенсом острого угла прямоугольного треугольника называется отношение
На рисунке
(1)
(2)
(3)
Из формул (1) и (2) получаем:
Сравнивая с формулой (3), находим:
(4)
Получили, что тангенс угла равен отношению синуса к косинусу этого угла.
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Дано: АВС, А1В1С1, С = С1 = 90 0, А = А1.
Доказать: sin A = sin A1, cos A = cos A1, tg A = tg A1.
Доказательство:
АВС А1В1С1 по первому признаку подобия треугольников (т.к. С = С1 = 900, А = А1). Из подобия треугольников следует пропорциональность сходственных сторон, поэтому мы можем записать:
Из этих равенств следует, что т.е. sin 
Мы получили, что синус, косинус и тангенс острого угла зависит только от величины этого угла.
Докажем основное тригонометрическое тождество:
Из формул (1) и (2) получаем
По теореме Пифагора , поэтому .
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 623, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 647, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 652, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 704, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1238, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1251, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1310, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Cos 0.
 75 чему равен угол. Косинус острого угла можно определить с помощью прямоугольного треугольника
75 чему равен угол. Косинус острого угла можно определить с помощью прямоугольного треугольникаВнимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»
Вот этот вывод:
Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое.
Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Почему почти? Об этом ниже.
Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов. )
)
Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)
И зачем тогда этот урок?! — спросите вы.
А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё . На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется…)
Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу . Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)
Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)
Итак, начнём. Для начала разобьём все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группа углов из семнадцати особых . Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:
Угол х(в градусах) | 0 | 90 | 180 | 270 | 360 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | 0 | -1 | 0 |
cos x | 1 | 0 | -1 | 0 | 1 |
tg x | 0 | не сущ.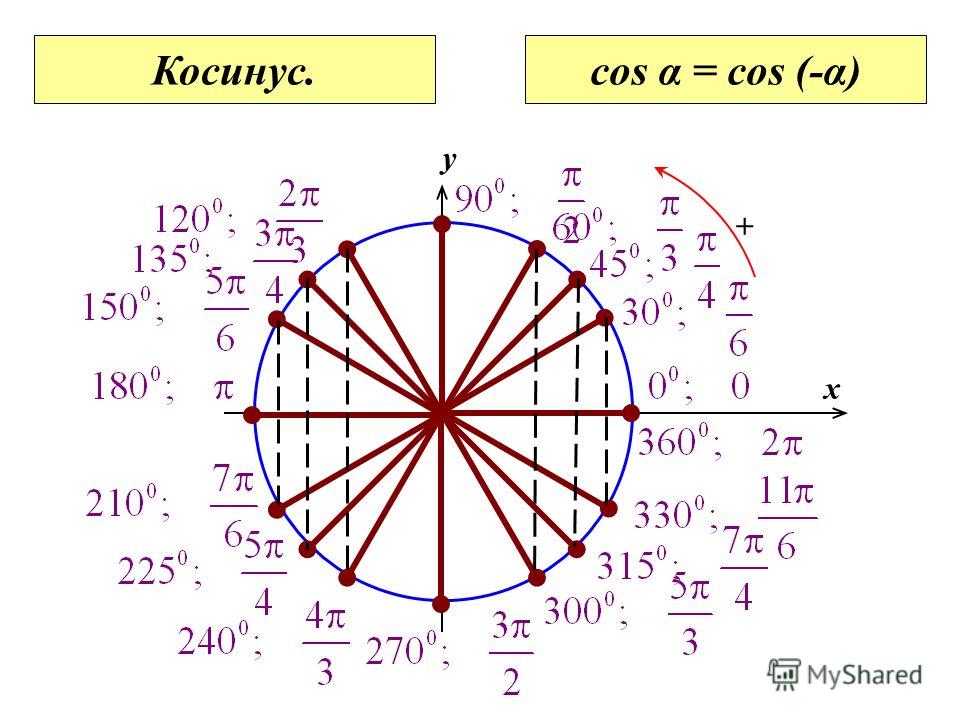 | 0 | не сущ. | 0 |
ctg x | не сущ. | 0 | не сущ. | 0 | не сущ. |
Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов. Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ.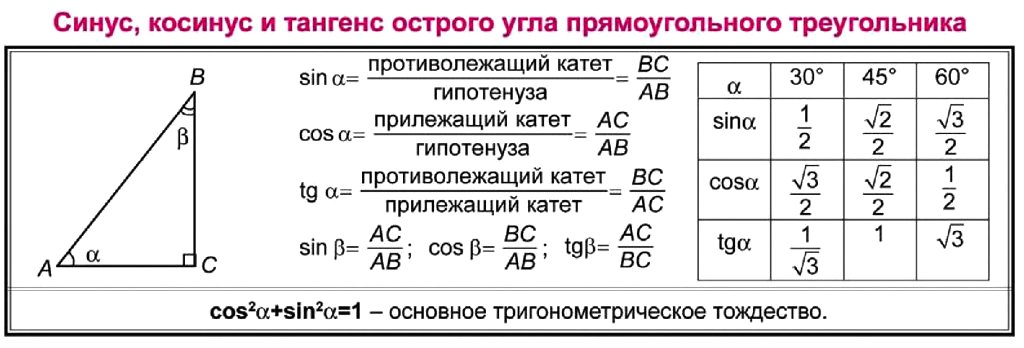 Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Вот и всё.
Вот и всё.
Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество.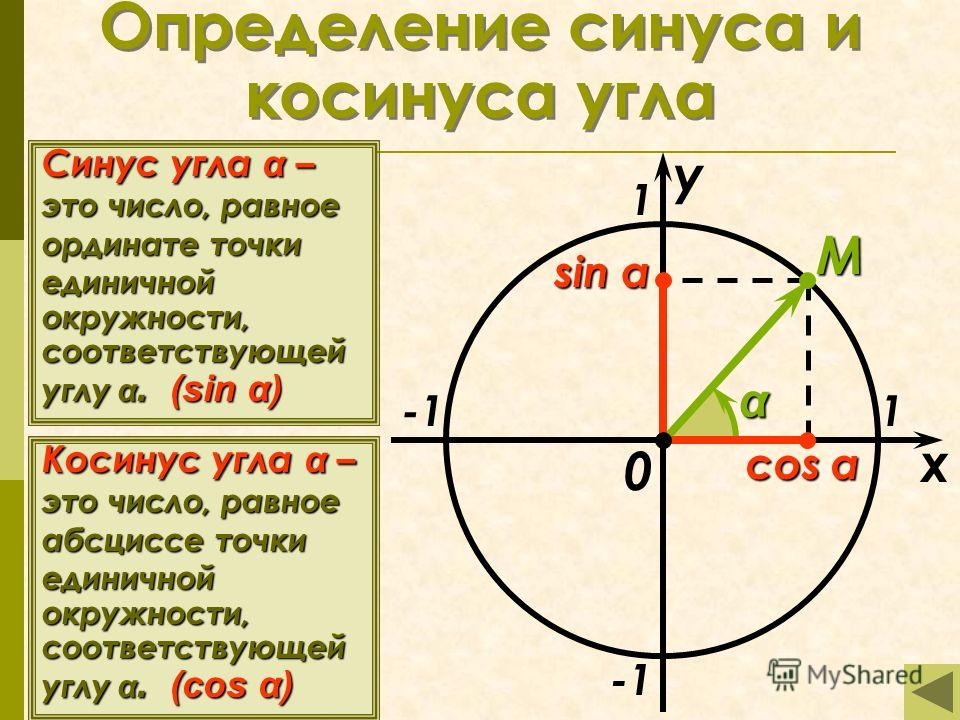 ..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол
вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол
Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.
Итак, с пятью углами из семнадцати — разобрались.
Вторая группа углов.
Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
Угол х(в градусах) | 0 | 30 | 45 | 60 | 90 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | |||
cos x | 1 | 0 | |||
tg x | 0 | 1 | не сущ. | ||
ctg x | не сущ. | 1 | 0 |
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же. Для углов 20, 50, 80 так бы не получилось…
Для углов 20, 50, 80 так бы не получилось…
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?
С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.
Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:
и многие другие, вы должны знать всё . °}=\)\(\frac{\sqrt{3}}{2}\)
°}=\)\(\frac{\sqrt{3}}{2}\)
\(\cos\)\(\frac{π}{3}\)
\(=\)\(\frac{1}{2}\)
\(\cos2=-0,416…\)
Аргумент и значение
Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.Пример :
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше \(0\) и меньше \(1\)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с : \(\frac{π}{2}\) , \(\frac{3π}{4}\) , \(-2π\).
Например, для числа \(\frac{π}{6}\)
— косинус будет равен \(\frac{\sqrt{3}}{2}\)
. А для числа \(-\)\(\frac{3π}{4}\)
он будет равен \(-\)\(\frac{\sqrt{2}}{2}\)
(приблизительно \(-0,71\)).
А для числа \(-\)\(\frac{3π}{4}\)
он будет равен \(-\)\(\frac{\sqrt{2}}{2}\)
(приблизительно \(-0,71\)).
Косинус для других часто встречающихся в практике чисел смотри в .
Значение косинуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ ), делаем также, но \(60°\) откладываем по часовой стрелке.
И, наконец, угол больше \(360°\) (угол КОС ) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по числовой (тригонометрической) окружности:
Там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от \(0\) до \(-1\), косинус будет иметь знак минус (II и III четверти – фиолетовая область). 2x}\)
2x}\)
— и синусом того же угла (или числа): формулой \(ctgx=\)\(\frac{\cos{x}}{\sinx}\)
Другие наиболее часто применяемые формулы смотри .
Функция \(y=\cos{x}\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной называется и обладает следующими свойствами:
Область определения – любое значение икса: \(D(\cos{x})=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos{x})=[-1;1]\)
— четная: \(\cos(-x)=\cos{x}\)
— периодическая с периодом \(2π\): \(\cos(x+2π)=\cos{x}\)
— точки пересечения с осями координат:
ось абсцисс: \((\)\(\frac{π}{2}\)
\(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\)\(\frac{π}{2}\)
\(+2πn;\) \(\frac{π}{2}\)
\(+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((\)\(\frac{π}{2}\)
\(+2πn;\)\(\frac{3π}{2}\)
\(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).
Косинус — что это такое
Обновлено 17 апреля 2022 Просмотров: 88 227 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое КОСИНУС.
Это слово, уверены, многим знакомо. Хотя бы потому что его проходят в школе. И многие наверняка точно определят, что это некий математический термин.
Но лишь единицы, которые действительно увлечены алгеброй и геометрией, вспомнят определение КОСИНУСА.
А между тем, без этих знаний не обойтись при сдаче ЕГЭ. Так что для старшеклассников это статья будет наиболее интересна. А для остальных – это хорошая возможность вспомнить подзабытые знания.
Косинус — это …
Со словом КОСИНУС школьники впервые знакомятся в 8 классе. И происходит это, когда проходят тему прямоугольных треугольников. Напомним, это такие треугольники, у которых две стороны пересекаются под прямым углом (90 градусов).
Выглядят они вот так:
У этого треугольника стороны АВ и ВС образуют между собой прямой угол. И напомним, по научному они называются КАТЕТАМИ. Этот термин имеет древнегреческие корни, произошло от «káthetos» и дословно переводится как «отвесный, опущенный, перпендикуляр».
И напомним, по научному они называются КАТЕТАМИ. Этот термин имеет древнегреческие корни, произошло от «káthetos» и дословно переводится как «отвесный, опущенный, перпендикуляр».
А линия АС, которая соединяет два катета между собой, как многие знают из школьного курса, называется ГИПОТЕНУЗА. Этот термин также родом из Древней Греции. Слово «ὑποτείνουσα» переводится как «натянутая».
К чему мы так подробно это рассказали? Ну, во-первых, никогда не бывает лишним освежить в памяти старые знания. А во-вторых, это имеет непосредственное отношение к нашей теме.
Косинус – это отношения прилежащего катета к гипотенузе.
Так звучит официальное определение КОСИНУСА. Но у внимательных читателей может возникнуть вопрос, а что такое «прилежащий катет»? И к чему он собственно «прилегает»?
Вопрос правильный. Дело в том, что КОСИНУС имеет прямое отношение к углам. А точнее, является их тригонометрической функцией. И в данном случае, надо просто понимать, о каком угле идет речь.
Вновь вернемся к нашему треугольнику АВС.
Если нам надо найти КОСИНУС угла с вершиной в точке А, то он будет равен отношению АC (прилежащий катет) к АB (гипотенуза). А если нужно найти КОСИНУС угла с вершиной в точке С, то для него прилежащим катетом будет уже СВ, и уже его надо соотносить с гипотенузой АС.
Вот так это будет выглядеть более наглядно:
И если описывать формулы для конкретного примера, то выглядеть они будут так:
История изучения
Всегда интересно, откуда взялось то или иное слово. И как раз у КОСИНУСА это весьма интересная история. Она начинается еще в IV веке, и связана с именем индийского астронома и математика Ариабхты.
Он ввел специальный термин, которым называл дугу. Это было слово «ардхаджива», образованное от «ардха» (половина) и «джива» (тетива лука).
Спустя 500 лет уже арабские математики решили заменить этот сложный для их произношения термин на привычное себе слово «джайб». В переводе оно обозначало «выпуклость».
И наконец, еще немного позднее европейцы стали переводить арабские математические тексты и встретили этот термин. Для них слово «джайб» также было чужеродным, поэтому они заменили его на латинское «Sinus», что в переводе означает «кривизна, изгиб».
А вот слово КОСИНУС – это производное от СИНУС. Оно возникло от выражения «completely sinus», что в переводе означает «дополнительный синус» или «синус дополнительной дуги».
Фактически уже тогда математики установили главную зависимость между синусом и косинусом. И выражается она в следующей формуле:
Таблица косинусов
Для каждого угла можно найти и рассчитать свой косинус.
Приведем самые популярные значения:
- 0 градусов – COS=1
- 30 градусов – COS=√3/2
- 45 градусов – COS=√2/2
- 60 градусов – COS=½
- 90 градусов – COS=0
- 180 градусов – COS=-1
- 270 градусов – COS=0
- 360 градусов – COS=-1
И еще одна важная зависимость. Если мы возьмем плоскость в 180 градусов:
В этом случае между углами α и β существует простая зависимость:
И тогда можно представить следующую формулу:
Данное утверждение будет верно при любых углах.
Вместо заключения
Есть еще две тригонометрические функции, которые широко используются в математике и изучаются в школе. Это ТАНГЕНС и КОТАНГЕНС.
Тангенс – это отношение противоположного катета к прилежащему. Также его можно представить как деление синуса на косинус.
Котангенс – это противоположная тангенсу функция, то есть отношение прилежащего катета к противолежащему. Или деление косинуса на синус.
Вот и все, что мы хотели рассказать про КОСИНУС.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo. ru
ru
Эта статья относится к рубрикам:
- Математика
Косинус — График, Значение, Период, Примеры
Косинус — одно из основных математических тригонометрических соотношений. Отношение длин стороны, прилежащей к углу, и гипотенузы прямоугольного треугольника называется функцией косинуса, которая изменяется при изменении угла. Он определяется в контексте прямоугольного треугольника для острых углов. Косинус используется для моделирования многих реальных сценариев — радиоволн, приливов и отливов, звуковых волн, музыкальных тонов, электрических токов.
Функция косинуса обозначается просто как cos x, где x — угол. В этой статье мы изучим основные свойства косинуса, его график, область определения и диапазон, производную, интеграл и разложение косинуса в степенной ряд. Cos x является периодической функцией и имеет период 2π.
| 1. | Что такое косинус? |
2. | Косинус Значение |
| 3. | График косинуса |
| 4. | Значения косинуса |
| 5. | Свойства функции косинуса |
| 6. | Косинусные тождества |
| 7. | Часто задаваемые вопросы о функции косинуса |
Что такое косинус?
Косинус или cos x — это периодическая функция в тригонометрии. Рассмотрим единичный круг с центром в начале координат плоскости. Переменная точка P движется по окружности этой окружности. Из рисунка видно, что P находится в первом квадранте, а OP образует острый угол x радиан с положительной осью x. PQ — перпендикуляр, опущенный из точки P на горизонтальную ось. Таким образом, треугольник образуется путем соединения точек O, P и Q, как показано на рисунке, где OQ — основание, а PQ — высота треугольника.
Следовательно, функция косинуса для приведенного выше случая может быть математически записана как:
cos x = OQ/OP, Здесь x — острый угол, образованный между гипотенузой и основанием прямоугольного треугольника.
Косинус Значение
Косинус можно определить как отношение длины основания к длине гипотенузы в прямоугольном треугольнике. Математически формула функции косинуса относительно сторон прямоугольного треугольника записывается как:
cos x = Смежная сторона/Гипотенуза = Основание/Гипотенуза, где x — острый угол между основанием и гипотенузой.
График косинуса
Как показано на изображении выше, мы отмечаем, что cos x = OQ/OP = OQ/1 = OQ. Поскольку x изменяется, значение косинуса изменяется с изменением длины OQ. Теперь изучим изменение функции косинуса в четырех квадрантах координатной плоскости.
Случай 1: Изменение OQ в первом квадранте.
Предположим, что изначально P находится на горизонтальной оси. Рассмотрим движение P на 90° или π/2 рад. На следующем рисунке показаны различные положения Q для этого движения. Ясно, что длина OQ уменьшилась от начального значения 1 (когда x равно 0 радианам) до конечного значения 0 (когда x равно π/2 радианам).
Случай 2: Изменение OQ во втором квадранте.
Теперь мы проверим положение P во втором квадранте, как мы делали это в первом квадранте, и проверим, как изменяется значение функции косинуса. P впоследствии перемещается из 9от 0° до положения 180°. В этой фазе движения длина или величина OQ увеличивается, а значение косинуса уменьшается со значения 0 при 90° до минимума -1 при 180°.
Случай 3: Изменение OQ в третьем квадранте.
Когда P перемещается из положения 180° в положение 270°, хотя длина или величина OQ уменьшается. Но поскольку направление вдоль отрицательной оси y, фактическое значение cos x увеличивается с -1 до 0. Таким образом, значение косинуса для угла x увеличивается.
Случай 4: Изменение OQ в четвертом квадранте.
Наконец, когда P перемещается из положения 270° в положение 360°, OQ увеличивается с 0 до 1 (снова). Длина или величина OQ увеличивается вместе с увеличением алгебраического значения OQ. Таким образом, значение функции косинуса для угла x увеличивается.
Таким образом, значение функции косинуса для угла x увеличивается.
Теперь мы можем изобразить это изменение на графике. Горизонтальная ось представляет входную переменную x как угол в радианах, а вертикальная ось представляет значение функции косинуса для x. Объединив реакцию изменения значения PQ для всех четырех квадрантов, мы получили полный график зависимости cos x от x для одного полного цикла от 0 до 2π радиан (от 0° до 360°). Полученный таким образом график показан ниже:
Значения косинуса
Мы изучаем значение функции косинуса для некоторых конкретных углов, так как их легко запомнить. Эти значения косинуса используются при решении различных математических задач. Некоторые из этих значений косинуса перечислены ниже в тригонометрической таблице:
| Градусы косинуса | Косинус радианы | Значение функции косинуса (cos x) |
|---|---|---|
| соз 0° | соз 0 | 1 |
| cos 30° | cos π/6 | √3/2 |
| cos 45° | cos π/4 | 1/√2 |
| cos 60° | cos π/3 | 1/2 |
| cos 90° | cos π/2 | 0 |
| cos 120° | cos 2π/3 | -1/2 |
| cos 150° | потому что 5π/6 | -√3/2 |
| cos 180° | потому что π | -1 |
| cos 270° | cos 3π/2 | 0 |
| cos 360° | потому что 2π | 1 |
Свойства функции косинуса
Свойства косинуса зависят от квадранта, в котором находится угол. Функция косинуса является специальной тригонометрической функцией и имеет множество свойств. Некоторые из них перечислены ниже:
Функция косинуса является специальной тригонометрической функцией и имеет множество свойств. Некоторые из них перечислены ниже:
- График cos x повторяется после 2π, что предполагает периодичность функции с периодом 2π.
- Cos x — четная функция, поскольку cos(−x) = cos x.
- Областью определения функции косинуса являются все действительные числа в диапазоне [-1,1]. 9{2n}}{(2n)!}\)
Идентичности функции косинуса
В тригонометрии есть несколько тождеств, связанных с функцией косинуса. Эти тождества очень полезны при решении различных математических задач. Некоторые из них перечислены ниже:
- cos x = 1/сек x
- Функция, обратная косинусу = cos -1 x = arccos x, где x лежит в [-1, 1]
- sin 2 х + cos 2 х = 1
- cos (x + y) = cos x cos y — sin x sin y
- cos (x — y) = cos x cos y + sin x sin y
- cos 2x = cos 2 x — sin 2 x = 2 cos 2 x — 1 = 1 — 2 sin 2 x
- Производная от cos x: d(cos x)/dx = -sin x
- Интеграл функции косинуса: ∫cos x dx = sin x + C, где C – постоянная интегрирования.

Связанные темы
- Синусоидальная функция
- Обратные тригонометрические соотношения
- Тригонометрическая таблица
- Тригонометрические соотношения
Важные замечания о функции косинуса
- Функция косинуса может быть математически записана как:
cos x = смежная сторона/гипотенуза = основание/гипотенуза - Функция косинуса — это периодическая функция с периодом 2π.
- Область определения cos x равна (−∞, ∞), а диапазон равен [−1,1].
Часто задаваемые вопросы о функции косинуса
Что такое косинус в тригонометрии?
Косинус угла является тригонометрической функцией. Отношение длин стороны, прилежащей к углу, и гипотенузы прямоугольного треугольника называется функцией косинуса, которая изменяется при изменении угла. Обычно его обозначают cos x, где x — угол между основанием и гипотенузой.
Каковы свойства косинуса?
Некоторые свойства функции косинуса: 9{2n}}{(2n)!}\)
Что означает косинус?
Косинус можно определить как отношение длины основания к длине гипотенузы в прямоугольном треугольнике. Он дает значение функции косинуса для угла x, обозначаемое как cos x.
Он дает значение функции косинуса для угла x, обозначаемое как cos x.
Что такое обратная тригонометрическая функция функции косинуса?
Обратная функция косинуса = cos -1 x = arccos x, где x лежит в [-1, 1]. Это функция, обратная косинусу, и произносится как «арккосинус» или «арккосинус».
Как записать функцию косинуса?
Функция косинуса может быть записана как cos x = Смежная сторона/Гипотенуза = Основание/Гипотенуза
Как выглядит график косинуса?
Кривая функции косинуса представляет собой кривую вверх-вниз, которая повторяется через каждые 2π радиан.
Что такое период функции косинуса?
Период функции — это когда функция имеет определенное горизонтальное смещение P, в результате чего получается функция, равная исходной функции, т. е. f(x+P) = f(x) для всех значений x в пределах домен ф. Период функции косинуса равен 2π.
Является ли функция косинуса четной или нечетной?
Функция f(x) является четной функцией, если f(-x) = f(x) для всех x, и нечетной, если f(-x) = -f(x) для всех x. Функция косинуса является четной функцией, потому что cos(−x) = cos x.
Функция косинуса является четной функцией, потому что cos(−x) = cos x.
Какое отношение косинуса?
Отношение косинуса равно отношению длины основания прямоугольного треугольника к длине гипотенузы.
Что такое область значений функции косинуса?
Областью определения функции косинуса являются все действительные числа, поскольку cos x определен для всех действительных чисел R.
Что такое диапазон Cos x?
Диапазон косинуса равен [-1, 1], поскольку значение cos x колеблется в пределах интервала [-1, 1], так как это периодическая функция и период, равный 2π.
Как найти косинус угла
Как найти косинус угла — ACT Math—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Обучение SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
Репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Мы открыты в субботу и воскресенье!
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Тригонометрия » косинус » Как найти косинус угла
Если , где и ,
то что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
В приведенном ниже треугольнике тангенс или противоположная сторона угла, деленная на прилежащую сторону угла. Согласно пифагорейцам
Согласно пифагорейцам
Теорема,
Таким образом, гипотенуза равна .
Косинус угла – это прилежащая сторона угла, деленная на гипотенузу треугольника, что дает нам .
Однако, поскольку равно , а когда находится между , положительное, а отрицательное. Таким образом отрицательно, что дает нам окончательный ответ .
Сообщить об ошибке
Что такое cos θ?
Возможные ответы:
Правильный ответ:
Объяснение:
cos = смежная/гипотенуза =
Чтобы получить радикал из знаменателя, умножьте:
Сообщить об ошибке
Каков косинус угла, образованного между осью и прямой проходящий с уклоном ? Округлить до сотых.
Возможные ответы:
Правильный ответ:
Объяснение:
Вам даже не нужно вычислять строку для этого вопроса. Все, что вам нужно сделать, это отметить, что вы можете сделать маленький прямоугольный треугольник с высотой и основанием , который вы получите из наклона линии. Итак, чтобы вычислить косинус, вам нужно будет найти гипотенузу, используя теорему Пифагора:
Все, что вам нужно сделать, это отметить, что вы можете сделать маленький прямоугольный треугольник с высотой и основанием , который вы получите из наклона линии. Итак, чтобы вычислить косинус, вам нужно будет найти гипотенузу, используя теорему Пифагора:
Итак, наш маленький треугольник выглядит так:
Косинусом будет прилежащая сторона, деленная на гипотенузу, :
или приблизительно .
Сообщить об ошибке
Чему равен угол с ?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку синус угла равен , это означает, что противоположная сторона треугольника равна , а гипотенуза равна . Автоматически вы знаете, что это особый прямоугольный треугольник 3-4-5 и что недостающая сторона равна 3. Если нет, вы также можете найти 3-ю сторону, применив теорему Пифагора. Это дает вам ответ 9 0005
Это дает вам ответ 9 0005
Сообщить об ошибке
Прямоугольный треугольник со сторонами , и . Что такое косинус ?
Возможные ответы:
Правильный ответ:
Объяснение:
SOHCATOA говорит нам об этом, а мы знаем, что гипотенуза — самая длинная сторона треугольника, . Наша смежная сторона будет другой стороной, имеющей в качестве вершины .
Таким образом, .
Сообщить об ошибке
Прямоугольный треугольник со сторонами , и . Что такое косинус ?
Возможные ответы:
Правильный ответ:
Объяснение:
SOHCATOA говорит нам об этом, а мы знаем, что гипотенуза — самая длинная сторона треугольника, . Наша смежная сторона будет другой стороной, имеющей в качестве вершины .
Наша смежная сторона будет другой стороной, имеющей в качестве вершины .
Таким образом, .
Сообщить об ошибке
Уведомление об авторских правах
Посмотреть репетиторов ACT по математике
Наоми
Сертифицированный репетитор
Earlham College, бакалавр искусств, математика. Университет Сент-Джозеф, магистр наук, образование.
View ACT Math Tutors
Sharif
Сертифицированный преподаватель
Университет Южной Флориды, главный кампус, бакалавр наук, клеточная и молекулярная биология.
View ACT Репетиторы по математике
Байрон
Сертифицированный репетитор
Университет штата Мичиган, бакалавр наук, математика. Университет Майами, магистр естественных наук, математика.
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Определениев кембриджском словаре английского языка
Строительными блоками формулы являются число пи, а также функции синуса и косинуса из тригонометрии.
Из журнала The New Yorker
Он изобрел инструменты для вычислений, навигации и геодезии, а также разработал концепции тригонометрии косинус и котангенс.
Из проводного
Я не думаю, что косинус и бром входят в описание работы.
Из ВРЕМЕНИ 907:25
Решениями этого дифференциального уравнения являются бетатронные колебания, то есть простые синусоидальные и косинусоидальные колебания.
Из Кембриджского корпуса английского языка
Эволюция косинус возмущений на границе раздела рассматривается без учета теплопроводности.
Из Кембриджского корпуса английского языка
Улучшение отношения сигнал/шум достигается за счет выборочного обнаружения известной частоты отклика с использованием квадратур (синус, косинус ) для получения информации об амплитуде и фазе.
Из Кембриджского корпуса английского языка
Совместный двигатель управляется для выполнения косинусного перемещения и измерения углового отклонения выходного фланца.
Из Кембриджского корпуса английского языка
А если бы был задан косинус , он использовал бы таблицу синусов, чтобы найти соответствующую дугу, а затем вычесть ее из девяноста градусов.
Из Кембриджского корпуса английского языка 907:25
Здесь usafe(k) вычисляется по закону косинусов.
Из Кембриджского корпуса английского языка
Значения амплитуды и фазы второй гармоники рассчитывались с использованием косинус , что приводит к фазовым значениям, соответствующим времени до положительного!
Из Кембриджского корпуса английского языка
Таким образом, в анализе выбора параметр сходства косинус играет жизненно важную роль для определения сходства с альтернативой ссылки или запроса.
Из Кембриджского корпуса английского языка
Здесь строки и столбцы помечены λ (или kr), чередующимися между косинусом и синусом.
Из Кембриджского корпуса английского языка
Кроме того, подобие косинуса эквивалентно скалярному произведению двух нормализованных векторов.
Из Кембриджского корпуса английского языка
Популярный косинус 9Мера 0722 использовалась для оценки сходства между двумя документами.
Из Кембриджского корпуса английского языка
Косинус страдает от вопиющего случая того, что мы назовем смещением против длины.
Из Кембриджского корпуса английского языка 907:25
Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Функция косинуса
Хотя функция синуса , вероятно, является самой известной из шести современных тригонометрических функций, функция косинуса занимает второе место. Действительно, функции синуса и косинуса очень тесно связаны между собой, как мы увидим (если вы не знакомы с функцией синуса, вы можете прочитать страницу, озаглавленную «Функция синуса»). Однако, в то время как современная функция синуса тесно связана с функция аккорда , используемая древними греками, функция косинуса не имеет эквивалента в греческой тригонометрии. На самом деле у греков не было других тригонометрических функций, кроме хорды. Тем не менее, они знали о связи между функциями синуса и косинуса, хотя и не в тригонометрическом смысле. То, как эти две функции соотносятся друг с другом, выражено в геометрических терминах теоремой Пифагора , которая определяет отношение между сторонами прямоугольного треугольника. Рассмотрим иллюстрацию ниже.
Однако, в то время как современная функция синуса тесно связана с функция аккорда , используемая древними греками, функция косинуса не имеет эквивалента в греческой тригонометрии. На самом деле у греков не было других тригонометрических функций, кроме хорды. Тем не менее, они знали о связи между функциями синуса и косинуса, хотя и не в тригонометрическом смысле. То, как эти две функции соотносятся друг с другом, выражено в геометрических терминах теоремой Пифагора , которая определяет отношение между сторонами прямоугольного треугольника. Рассмотрим иллюстрацию ниже.
Связь между синусом и косинусом
На схеме должно быть видно, что полухорда AD является одной из сторон прямоугольного треугольника ADC. Другой отрезок представляет собой отрезок CD , лежащий на биссектрисе хорды AB . Гипотенуза AC прямоугольного треугольника является радиусом окружности. На рисунке показан блок в виде круга 9.0722, который имеет радиус в одну единицу длины. Таким образом, длина полухорды, стягивающей центральный угол θ , будет иметь то же значение, что и синус угла θ . Точно так же длина отрезка, соединяющего середину хорды с центром окружности, будет иметь то же значение, что и косинус угла θ . Заметим, что для окружности произвольного радиуса r длина отрезка CD будет равна cos ( θ ) r . На всякий случай, если вы все еще немного не уверены в том, как все это работает, давайте вернемся к тому, как функции синуса и косинуса определяются с точки зрения прямоугольного треугольника.
На рисунке показан блок в виде круга 9.0722, который имеет радиус в одну единицу длины. Таким образом, длина полухорды, стягивающей центральный угол θ , будет иметь то же значение, что и синус угла θ . Точно так же длина отрезка, соединяющего середину хорды с центром окружности, будет иметь то же значение, что и косинус угла θ . Заметим, что для окружности произвольного радиуса r длина отрезка CD будет равна cos ( θ ) r . На всякий случай, если вы все еще немного не уверены в том, как все это работает, давайте вернемся к тому, как функции синуса и косинуса определяются с точки зрения прямоугольного треугольника.
Рассмотрим прямоугольный треугольник, показанный ниже. В любом прямоугольном треугольнике один из внутренних углов всегда будет девяносто градусов (90°). Так как внутренние углы в любом треугольнике всегда должны быть в сумме сто восемьдесят градусов (180°), два других внутренних угла должны быть равны острым углам (т. е. меньше девяноста градусов). Сторона, противоположная прямому углу, всегда является самой длинной стороной и называется гипотенузой . По отношению к любому из острых углов сторона, противоположная углу, называется , противоположной . Оставшаяся сторона (сторона, общая как для интересующего нас угла, так и для прямого угла) называется смежным .
е. меньше девяноста градусов). Сторона, противоположная прямому углу, всегда является самой длинной стороной и называется гипотенузой . По отношению к любому из острых углов сторона, противоположная углу, называется , противоположной . Оставшаяся сторона (сторона, общая как для интересующего нас угла, так и для прямого угла) называется смежным .
В треугольнике ABC sin ( θ ) = a / c и cos ( θ ) = b / c
В треугольнике ABC нас интересует угол θ . Мы использовали условное обозначение каждой вершины символом верхнего регистра, а сторону напротив каждой вершины соответствующим символом нижнего регистра. напротив по отношению к углу θ является стороной и . Смежное является стороной b , а гипотенуза является стороной c . Синус угла прямоугольного треугольника определяется как отношение длин противоположной стороны и гипотенузы. Таким образом, в треугольнике ABC синус угла θ задается как:
Синус угла прямоугольного треугольника определяется как отношение длин противоположной стороны и гипотенузы. Таким образом, в треугольнике ABC синус угла θ задается как:
| sin ( θ ) = | a |
| c |
Косинус угла прямоугольного треугольника определяется как частное длин прилежащего треугольника и гипотенузы. Таким образом, в треугольнике ABC косинус угла θ задается как:
| cos ( θ ) = | б |
| в | |
 Горизонтальный отрезок представляет косинус угла θ . Вы, наверное, также заметили тот факт, что относительно угла θ , катеты, соответствующие синусу и косинусу, также являются противоположной и смежной сторонами прямоугольного треугольника соответственно.
Горизонтальный отрезок представляет косинус угла θ . Вы, наверное, также заметили тот факт, что относительно угла θ , катеты, соответствующие синусу и косинусу, также являются противоположной и смежной сторонами прямоугольного треугольника соответственно. Синус и косинус — это отрезки единичной окружности.
Посмотрите на этот треугольник и подумайте о том, что мы знаем из теоремы Пифагора. В прямоугольном треугольнике квадрат гипотенузы всегда равен сумме квадратов двух других сторон. В этом случае, поскольку длина гипотенузы равна один (1), то квадрат гипотенузы тоже будет единицей. Отсюда можно сделать вывод, что сумма квадратов синуса и косинуса должна быть равна единице. Теперь имейте в виду, что для любого подобного треугольника (т. е. треугольника, в котором все углы одинаковы, а длины сторон находятся в одинаковой пропорции друг к другу) значения синуса и косинуса не изменятся , так как они относятся к отношениям сторон друг к другу независимо от их длин. Таким образом, из теоремы Пифагора мы выводим следующую связь между синусом и косинусом угла θ :
Таким образом, из теоремы Пифагора мы выводим следующую связь между синусом и косинусом угла θ :
sin 2 ( θ ) + cos 2 ( θ ) = 1
Из приведенного выше уравнения и рассмотрения представления синуса и косинуса в виде отрезков единичной окружности мы можем вывести некоторые другие интересные факты о взаимосвязи между синусом и косинусом. Прежде всего, мы можем перестроить уравнение, чтобы получить выражение для синуса угла через его косинус, и наоборот:
sin 2 ( θ ) = 1 — cos 2 ( θ )
cos 2 ( θ ) = 1 — sin 2 ( θ )
Теперь еще раз взглянем на диаграмму и подумаем, как бы все изменилось, если бы вместо угла θ нас интересовало нахождение синуса и косинуса другого острого угла, т. е. угла ABC . Линейный сегмент AC теперь становится напротив и по определению синус угла ABC . Отрезок до н.э. тем временем становится смежным и по определению косинусом угла ABC . Поскольку два острых угла в прямоугольном треугольнике дополняют друг друга (т. е. в сумме они должны давать девяносто градусов), мы можем вывести следующие соотношения между синусом и косинусом угла θ :
е. угла ABC . Линейный сегмент AC теперь становится напротив и по определению синус угла ABC . Отрезок до н.э. тем временем становится смежным и по определению косинусом угла ABC . Поскольку два острых угла в прямоугольном треугольнике дополняют друг друга (т. е. в сумме они должны давать девяносто градусов), мы можем вывести следующие соотношения между синусом и косинусом угла θ :
sin ( θ ) = cos (90° — θ )
cos ( θ ) = sin (90° — θ )
Следовательно, синус угла равен косинусу дополнения этого угла . По этой причине функция косинуса считается кофункцией функции синуса (вероятно, поэтому она называется косинусом ). Если вы читали страницу под названием «Функция синуса», то, возможно, помните, что каждая из трех основных тригонометрических функций ( синус , косинус и тангенс ) определяется как отношение двух сторон прямоугольного треугольника. Как мы видели выше, стороны помечены в соответствии с тем, как они относятся к интересующему нас острому углу, и хитрость состоит в том, чтобы запомнить , какие стороны использовать для вычисления значения любой из сторон. тригонометрическую функцию, которую мы хотим найти. Итак, просто напомню, вот еще раз (относительно) легко запоминающаяся мнемоника SOH-CAH-TOA , который должен напомнить вам, что:
Как мы видели выше, стороны помечены в соответствии с тем, как они относятся к интересующему нас острому углу, и хитрость состоит в том, чтобы запомнить , какие стороны использовать для вычисления значения любой из сторон. тригонометрическую функцию, которую мы хотим найти. Итак, просто напомню, вот еще раз (относительно) легко запоминающаяся мнемоника SOH-CAH-TOA , который должен напомнить вам, что:
S INE = O PPOSITE Более H YPOTENUSE
C OSINE = A DJACENT более H Ypotenus
К счастью, времена, когда приходилось использовать тригонометрические таблицы для нахождения косинуса угла (или угла, соответствующего заданному значению косинуса), давно прошли. Современные калькуляторы могут мгновенно произвести необходимые расчеты, если вы знаете, как правильно пользоваться калькулятором. Тем не менее, для тех, кто интересуется такими вещами, мы использовали Microsoft Excel для создания собственной таблицы косинусов для углов в диапазоне от ноль градусов (0°) до триста шестьдесят градусов (360°) с шагом в одну десятую градуса. Чтобы увидеть таблицу, нажмите здесь .
Тем не менее, для тех, кто интересуется такими вещами, мы использовали Microsoft Excel для создания собственной таблицы косинусов для углов в диапазоне от ноль градусов (0°) до триста шестьдесят градусов (360°) с шагом в одну десятую градуса. Чтобы увидеть таблицу, нажмите здесь .
Нахождение косинуса угла с помощью встроенного калькулятора, предусмотренного в Microsoft Windows , относительно просто. Предположим, мы хотим найти косинус угла семьдесят пять градусов (75°). Если он у вас есть, запустите встроенный калькулятор Microsoft Windows, нажав кнопку «Пуск» в Windows 7 и выбрав «Все программы»> «Стандартные»> «Калькулятор » (в других версиях Windows может потребоваться другая последовательность нажатий клавиш). Выберите научную версию калькулятора в меню View приложения. Чтобы найти косинус семидесяти пяти градусов с помощью калькулятора Windows, введите следующие нажатия клавиш (если у вас нет калькулятора Windows, используйте любой доступный калькулятор, который может выполнять триггерные функции):
Введите эти нажатия клавиш, чтобы найти косинус семидесяти пяти градусов.
Убедитесь, что калькулятор настроен на режим градусов (если только вы не планируете вводить значение угла в радианах или градах). Если вы правильно ввели нажатия клавиш, вы должны увидеть следующий экран:
Калькулятор отображает значение cos (75°)
Теперь давайте предположим, что вы хотите найти размер острого угла в прямоугольном треугольнике, сначала найдя частное прилежащего и гипотенузы (т.е. косинус угла ). Если у вас есть значения длин сторон треугольника, вы можете достаточно легко найти значение косинуса угла. Нахождение угла тогда просто случай применения функции арккосинуса (которая является обратной косинусу ) к результату. Найдем значение угла θ для прямоугольного треугольника, показанного ниже.
Мы хотим найти величину угла θ
Для угла θ стороны b и c являются прилежащим и гипотенузой соответственно. На самом деле мы можем найти размер угла за одну операцию на калькуляторе Windows. Мы делаем это, используя скобки во введенной последовательности клавиш, чтобы заставить калькулятор сначала найти частное смежного и гипотенузы (то есть косинус угла). Затем мы применяем функцию арккосинуса к результату. Вот последовательность клавиш для использования:
На самом деле мы можем найти размер угла за одну операцию на калькуляторе Windows. Мы делаем это, используя скобки во введенной последовательности клавиш, чтобы заставить калькулятор сначала найти частное смежного и гипотенузы (то есть косинус угла). Затем мы применяем функцию арккосинуса к результату. Вот последовательность клавиш для использования:
Введите эти нажатия клавиш, чтобы найти размер угла θ
Если вы правильно ввели комбинации клавиш, вы должны увидеть следующий экран:
Калькулятор отображает значение угла θ
Как и в случае функции синуса, мы можем применять функцию косинуса к углам больше девяноста градусов. Чтобы увидеть интерактивную демонстрацию того, как косинус изменяется при изменении размера угла, нажмите здесь (примечание: ваш браузер должен поддерживать Java, чтобы интерактивная страница работала). В демонстрации используется единичный круг , чтобы продемонстрировать, как значения косинуса изменяются в зависимости от угла поворота . Обратите внимание, что косинус представлен горизонтальной стороной прямоугольного треугольника. Вертикальный катет представляет собой полухорду, стягивающую интересующий нас центральный угол, а также представляет собой синус. Гипотенуза — это радиус окружности, а также конечная сторона e угла поворота ( начальная сторона является положительной осью x ).
В демонстрации используется единичный круг , чтобы продемонстрировать, как значения косинуса изменяются в зависимости от угла поворота . Обратите внимание, что косинус представлен горизонтальной стороной прямоугольного треугольника. Вертикальный катет представляет собой полухорду, стягивающую интересующий нас центральный угол, а также представляет собой синус. Гипотенуза — это радиус окружности, а также конечная сторона e угла поворота ( начальная сторона является положительной осью x ).
Когда угол поворота превышает девяносто градусов, прямоугольный треугольник переходит в новый квадрант. Приведенная ниже серия снимков экрана иллюстрирует этот момент (мы добавили номера квадрантов к снимкам экрана для ясности). Единичный круг имеет центр (показанный здесь как точка O) в начале декартовой системы координат и радиус в одну единицу. Таким образом, длина вертикального катета прямоугольного треугольника в любой точке равна абсолютной величине синуса центрального угла, опирающегося на полухорду. Точно так же длина горизонтального катета треугольника равна модулю косинуса центрального угла, опирающегося на полухорду.
Точно так же длина горизонтального катета треугольника равна модулю косинуса центрального угла, опирающегося на полухорду.
Косинус в квадранте I
Косинус в квадранте II
Косинус в квадранте III
Косинус в квадранте IV
Угол поворота в первом квадранте составляет сорок пять градусов (45°) и, следовательно, равен углу, образуемому полухордой. На втором скриншоте мы увеличили угол поворота на девяносто градусов до сто тридцать пять градусов (135°). Полухорда теперь находится во втором квадранте, но центральный угол, стягиваемый полухордой, снова равен сорока пяти градусам. То же самое мы видим в третьем и четвертом квадрантах. Угол поворота продолжает увеличиваться по мере того, как мы перемещаем точку P против часовой стрелки по окружности круга, но центральный угол, образуемый полухордой в каждом квадранте, никогда не превышает девяноста градусов.
Тригонометрические функции синуса и косинуса могут быть определены в терминах точки, лежащей на окружности единичного круга. Эта точка — это точка, в которой полухорда касается окружности единичного круга (точка P на диаграммах, показанных выше). Угол θ , которому соответствует косинус, представляет собой угол между положительной осью x и радиусом, соединяющим точку P и центр окружности O, измеренный против часовой стрелки . Косинус этого угла определяется как x -координата точки P. Мы можем выразить это просто как:
cos ( θ ) = x
Как и функция синуса, функция косинуса имеет значения в диапазоне один от до минус один (от 1 до -1). В первом и четвертом квадрантах (квадранты справа от оси y ) эти значения всегда будут между нулем и единицей, поскольку x всегда будет больше или равно нулю. Во втором и третьем квадрантах (два квадранта от слева от оси y ) значения всегда будут между нулем и минус один , поскольку x всегда будет меньше или равно нуль. Косинусы углов ноль градусов (0°), девяносто градусов (90°), сто восемьдесят градусов (180°) и двести семьдесят градусов (270°) будет один (1), нуль (0), минус один (-1) и ноль (0) соответственно.
Косинусы углов ноль градусов (0°), девяносто градусов (90°), сто восемьдесят градусов (180°) и двести семьдесят градусов (270°) будет один (1), нуль (0), минус один (-1) и ноль (0) соответственно.
Выше мы видели, что в терминах единичного круга координаты x и y любой точки P на окружности задаются косинусом и синусом соответственно угла между положительными x — ось и отрезок, соединяющий центр окружности с точкой P, измеренный против часовой стрелки. Как мы видели, этот отрезок образует гипотенузу прямоугольного треугольника, для которого косинус дает длину горизонтального катета (иногда называемого отрезком ), а синус дает длину вертикальная ножка (иногда называемая подъемом ). Касательная функция , о которой мы говорим в другом месте, дает наклон (то есть частное подъема и разбега).
Говорят, что функции синуса и косинуса являются периодическими функциями с периодом триста шестьдесят градусов (360°) или 2π, потому что значения, возвращаемые каждой функцией, будут повторяться после каждого полного цикла. Это означает, что мы можем найти синус или косинус любого угла, независимо от того, насколько он велик. Поворот на два с половиной оборота , например, эквивалентен углу девятьсот градусов (900°). Синус и косинус будут иметь вид:
sin (900°) = sin (900 (mod 360)°) = sin (180°) = 0
cos (900°) = cos (900 (mod 360)°) = cos (180°) = -1
Используемый здесь оператор по модулю является сокращением от по модулю и дает остаток , полученный при делении одного числа на другое. В используемом здесь примере мы делим девятьсот на триста шестьдесят , что дает остаток сто восемьдесят . Периодический характер функций синуса и косинуса можно продемонстрировать графически, построив график этих функций в зависимости от диапазона углов, как показано ниже. Как и функция синуса, функция косинуса часто используется для моделирования поведения циклических явлений. Косинусоидальная волна представляет собой плавное повторяющееся колебание точно так же, как и синусоидальная волна, за исключением того, что (с точки зрения единичного круга) это график того, как значение x меняется со временем, а не y .
Периодический характер функций синуса и косинуса можно продемонстрировать графически, построив график этих функций в зависимости от диапазона углов, как показано ниже. Как и функция синуса, функция косинуса часто используется для моделирования поведения циклических явлений. Косинусоидальная волна представляет собой плавное повторяющееся колебание точно так же, как и синусоидальная волна, за исключением того, что (с точки зрения единичного круга) это график того, как значение x меняется со временем, а не y .
График значений синуса и косинуса в зависимости от углов от 0° до 720°
Из графика видно, что функции синуса и косинуса проходят полный цикл с интервалом в триста шестьдесят градусов. Вы также можете заметить, что косинусоидальная волна на девяносто градусов (90°) 90 721 опережает 90 722 синусоиды. Таким образом, косинусоидальная волна равна опережает синусоиду на девяносто градусов. Помимо этого очевидного отличия, косинусоидальная волна по форме идентична синусоидальной волне и, как и синусоидальная волна, часто используется для моделирования поведения циклических явлений. В своей основной форме косинусоидальная волна представляет собой функцию времени, которая описывается формулой:
Помимо этого очевидного отличия, косинусоидальная волна по форме идентична синусоидальной волне и, как и синусоидальная волна, часто используется для моделирования поведения циклических явлений. В своей основной форме косинусоидальная волна представляет собой функцию времени, которая описывается формулой:
x ( t ) = A · cos ( ωt + φ )
куда:
A = the amplitude of the function (the maximum absolute value of y )
ω = the angular frequency (usually measured in in radians per second )
t = the прошедшее время
φ = фаза , то есть угол (в радианах), когда t = 0
История функции косинуса тесно связана с историей функции синуса. Индийские математики разработали функцию косинуса к пятому веку нашей эры, которую они использовали вместе с функцией синуса в контексте выполнения астрономических расчетов. Их знания функций синуса и косинуса, наряду с остальными астрономическими и математическими знаниями, впоследствии были приобретены арабскими учеными по мере расширения исламской империи. Большая часть работ этих арабских ученых, переведенных на латынь и сопровождаемых обширными тригонометрическими таблицами, которые они составили, попала в Европу к двенадцатому веку нашей эры.
Их знания функций синуса и косинуса, наряду с остальными астрономическими и математическими знаниями, впоследствии были приобретены арабскими учеными по мере расширения исламской империи. Большая часть работ этих арабских ученых, переведенных на латынь и сопровождаемых обширными тригонометрическими таблицами, которые они составили, попала в Европу к двенадцатому веку нашей эры.
К концу шестнадцатого века нашей эры европейские ученые создали тригонометрические таблицы, которые были достаточно точными, чтобы их можно было использовать для астрономических расчетов даже в начале двадцатого века. Несколько более поздние разработки включают разработку различных представлений тригонометрических функций в виде бесконечного ряда . Не слишком останавливаясь на деталях, достаточно сказать, что значения синуса или косинуса многих углов нельзя вычислить с помощью простых алгебраических формул. Как и функция синуса, функция косинуса угла может быть точно выражена только в результате сложения бесконечного числа членов. Одно такое представление дает косинус угла x (выражено в радианах) как:
Одно такое представление дает косинус угла x (выражено в радианах) как:
| cos ( x ) = 1 — | x 2 | + | x 4 | — | x 6 | + · · · |
| 2! | 4! | 6! |
Очевидно, что нецелесообразно или даже невозможно выполнять вычисления с использованием бесконечного числа терминов. Количество фактически используемых терминов будет в значительной степени зависеть от доступных вычислительных ресурсов и от степени точности, требуемой для значения косинуса.
Правило косинусов (закон косинусов)
Патрик Энгельманн, Алекс Г, Мэй Ли, а также
способствовал
Содержимое
- Формулировка и доказательство теоремы
- Нахождение недостающих длин сторон и углов
- Приложения к задачам пеленга и курса
- Векторная форма правила косинуса
- Вывод других законов с помощью правила косинусов
- Решение проблем
- Смотрите также
Дана сторона-угол-сторона:
В треугольнике ABC ABCABC имеем ∠BAC=π4,∣BC‾∣=5 \angle BAC = \frac {\pi}{4}, \lvert \overline{BC} \rvert = \sqrt{5}∠BAC= 4π,∣BC∣=5 и ∣AB‾∣=3 \lvert \overline{AB} \rvert = 3∣AB∣=3.
2 — 3 \sqrt{2} \lvert \overline{AC} \rvert + 4 &=0 \\ \left(\lvert \overline{AC} \rvert-\sqrt{2}\right)\left(\lvert \overline{AC} \rvert-2\sqrt{2}\right)&=0. \end{выровнено}∣AB∣2+∣AC∣2−2∣AB∣⋅∣AC∣⋅cos4π∣AC∣2−32∣AC∣+4(∣AC∣−2)(∣AC∣ −22)=∣BC∣2=0=0.
Следовательно, ∣AC‾∣=2 или 22 \lvert \overline{AC} \rvert=\sqrt{2} \text{ или } 2\sqrt{2}∣AC∣=2 или 22. □ _\квадрат □
Примечание. Это похоже на «неоднозначный случай» правила синусов, поскольку мы имеем 3sinπ4<5<3 3 \sin \frac {\pi}{4} < \sqrt{5} < 33sin4π<5 <3, что является условием csinα
7\кв{7}7
555 272\кв{7}27 92?АВ2?
Дано бок-бок-бок:
В треугольнике ABCABCABC AB‾=6−2,AC‾=22,\overline{AB} = \sqrt{6} — \sqrt{2}, \overline{AC} = 2\sqrt{2},AB=6 −2,AC=22 и BC‾=23.
2 — 2\cdot 2\sqrt3 \cdot \big(\sqrt{6} — \sqrt{2}\big) \cdot \cos {\angle ABC}\\\\ 8 &= 6 — 4\sqrt{3} + 2 + 12 — \big(12\sqrt{2} — 4\sqrt{6}\big)\cos{\angle ABC}\\\\ -12 +4\sqrt{3} &= (-12\sqrt{2}+4\sqrt{6})\cos{\угол ABC}\\\\ \cos{\угол ABC} &=\dfrac{-12 +4\sqrt{3}}{-12\sqrt{2}+4\sqrt{6}} \\\\ &=\dfrac{1}{\sqrt2} \cdot \dfrac {-12 +4\sqrt{3}}{-12+4\sqrt{3}} =\dfrac{\sqrt2}{2}\\\\ \стрелка вправо \угол ABC &= \dfrac{\pi}{4}.\ _\квадрат \end{выровнено}AC2(22)28−12+43cos∠ABC⇒∠ABC=AB2+BC2−2⋅AB⋅BC⋅cos∠ABC=(6−2)2+(23 )2−2⋅23⋅(6−2)⋅cos∠ABC=6−43+2+12−(122−46)cos∠ABC=(−122+46)cos∠ ABC=−122+46−12+43=211−12+43−12+43=22=4π. □
Попробуйте решить следующую задачу:
Муравей заблудился в квадрате, и его расстояния до вершин квадрата равны 7, 35, 49 и x.x.x. Найдите х.х.х.
Примечание. Изображение выполнено не в масштабе.
Когда дело доходит до применения закона косинусов, у него есть свои приложения к векторным величинам (а не к качествам). 2.c2=a2+b2−2abcosγ=a2+b2−2abcos2π=a2+b2−0=a2+b2.
92\большой).м2).
2.c2=a2+b2−2abcosγ=a2+b2−2abcos2π=a2+b2−0=a2+b2.
92\большой).м2).
Один большой и один малый круг находятся в одном центре ООО.
Затем строится △ABC\треугольник ABC△ABC так, что точки AAA и BBB лежат на большой окружности, а точка CCC — на меньшей. ABABAB пересекает меньший круг в DDD и EEE, а ACACAC проходит через FFF и OOO, как показано выше.
Если AF=3AF = 3AF=3 (красный сегмент), DE=6DE = 6DE=6 (синий сегмент) и BC=11BC = 11BC=11 (зеленая сторона), каков радиус меньшего оранжевого круга? ?
Подшипник — Word Проблемы
Доказательство тригонометрических тождеств
Процитировать как: Правило косинусов (закон косинусов). Brilliant.org . Извлекаются из https://brilliant.org/wiki/cosine-rule/
Что такое правило косинуса? (с картинками)
`;
Г.
 Визен
Визен Правило косинуса — это формула, обычно используемая в тригонометрии для определения некоторых аспектов непрямоугольного треугольника, когда другие ключевые части этого треугольника известны или могут быть определены иным образом. Это эффективное расширение теоремы Пифагора, которая обычно работает только с прямоугольными треугольниками и утверждает, что квадрат гипотенузы треугольника равен квадратам двух других сторон при сложении (c 2 =a 2 +b 2 ). Правило косинусов является расширением этого математического принципа, которое делает его эффективным для непрямоугольных треугольников и утверждает, что относительно определенного угла квадрат стороны треугольника, противоположной этому углу, равен квадратам двух других сторон. суммируются, минус два умножения обеих этих сторон на косинус этого угла (c 2 =a 2 +b 2 -2ab cosC, где C — угол, противоположный стороне c).
суммируются, минус два умножения обеих этих сторон на косинус этого угла (c 2 =a 2 +b 2 -2ab cosC, где C — угол, противоположный стороне c).
Хотя многие современные математические источники отдают должное мусульманскому математику по имени аль-Каши за создание правила косинуса, есть также некоторые свидетельства того, что древнегреческий математик Евклид разработал аналогичный принцип. Большая часть современной алгебры и тригонометрии возникла благодаря усилиям мусульман во времена средневековья в Европе, и примерно в 15 веке аль-Каши кодифицировал формулу таким образом, что ее понимают до сих пор. Во Франции правило даже упоминается как Le theorème d’Al-Kashi или «теорема аль-Каши».
Во Франции правило даже упоминается как Le theorème d’Al-Kashi или «теорема аль-Каши».
В общем, правило косинусов используется в триангуляции и ряде других практических применений тригонометрии. Это особенно полезно в системах, где длины всех трех сторон известны или могут быть установлены, и необходимо определить меру углов внутри треугольника. Правило косинуса также можно использовать для определения длины одной стороны треугольника, если известны длины двух других сторон, а также угол, противолежащий этой стороне.
Поскольку правило косинусов имеет дело с треугольниками, состоящими из трех прямых сторон и их углов, оно обычно работает только в области евклидовой геометрии.