| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |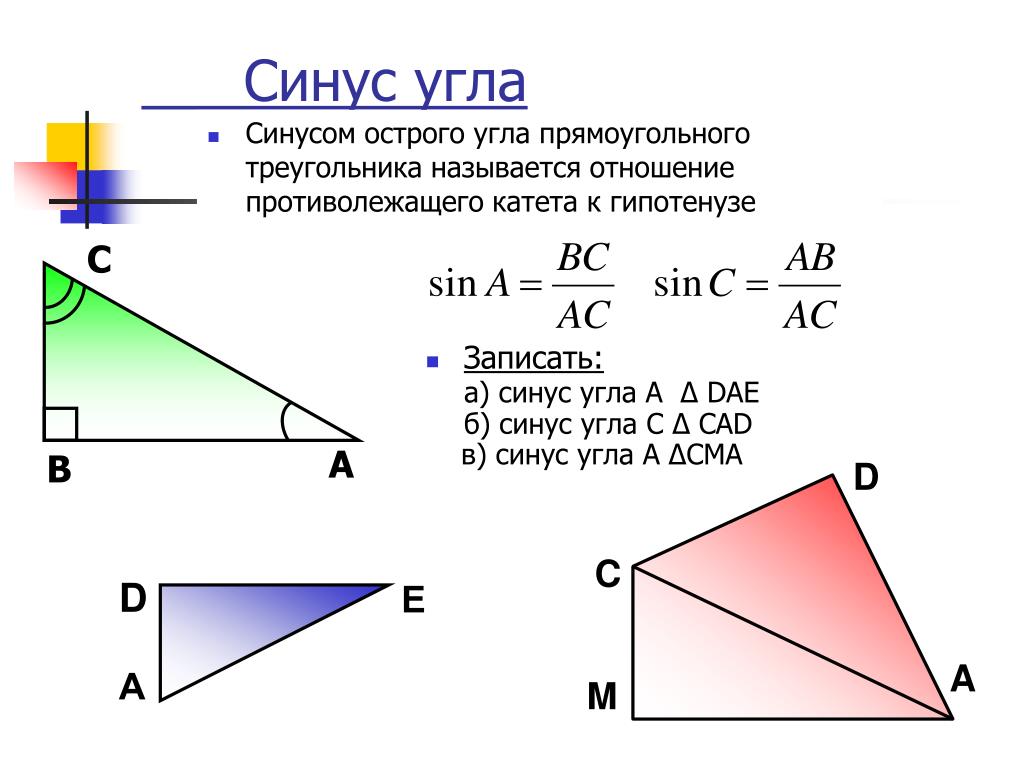
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |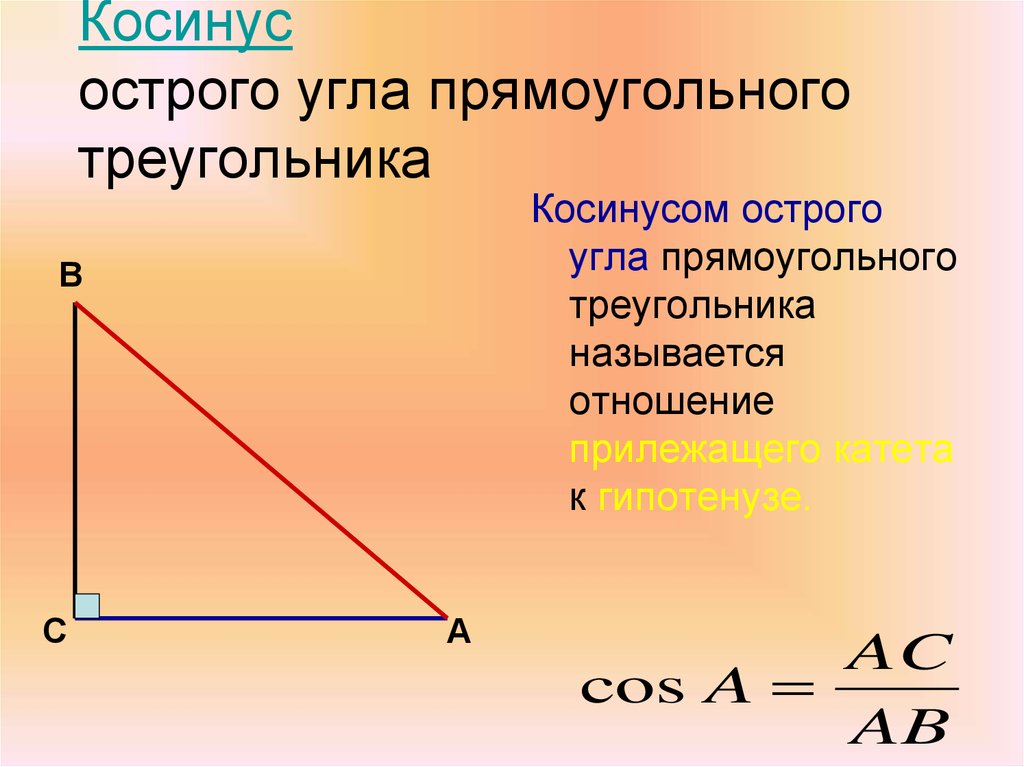
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |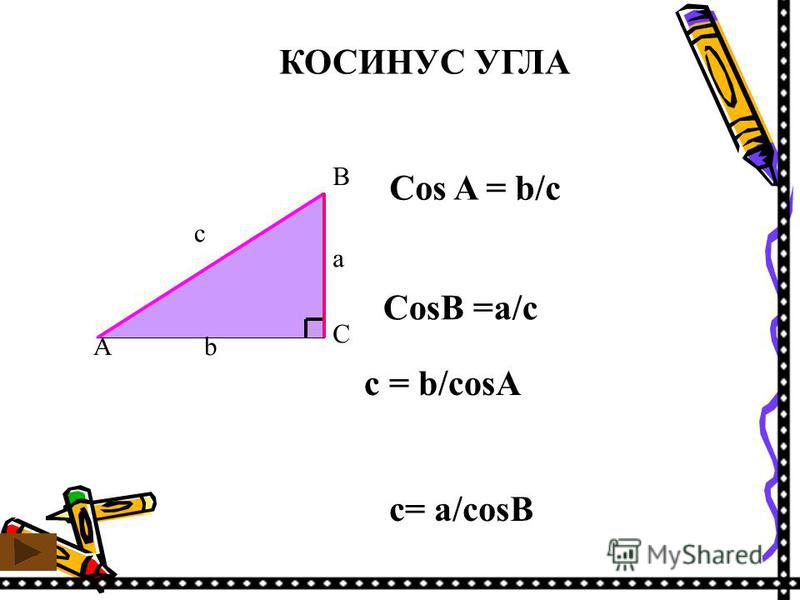
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |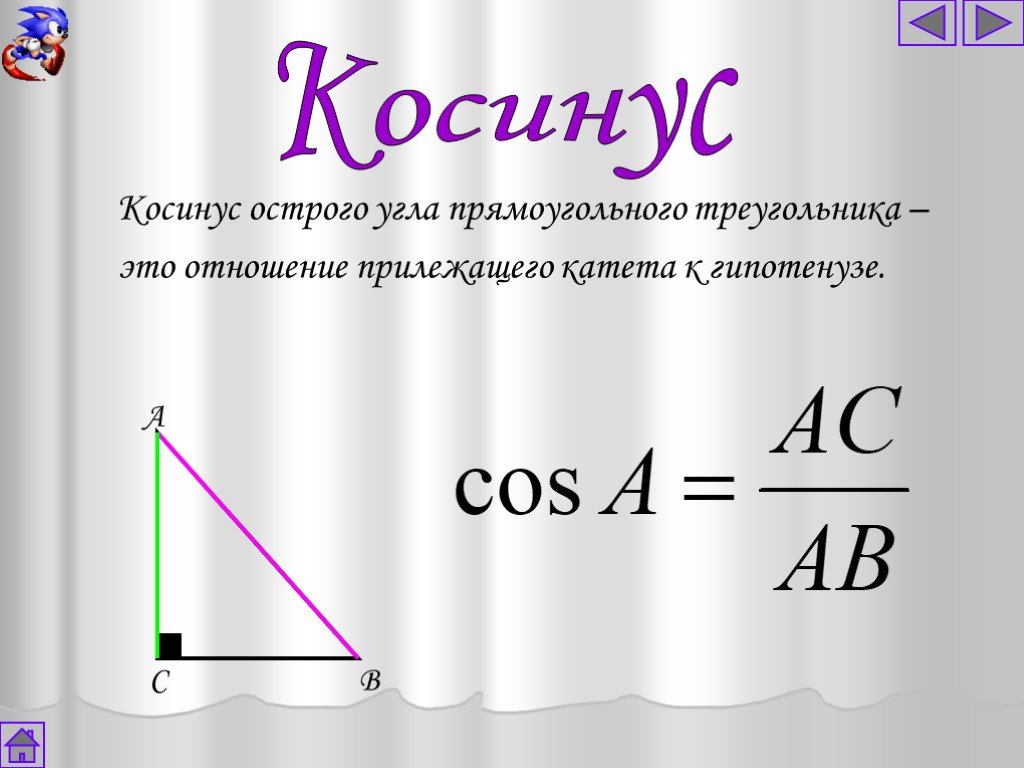
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
1. * ************ Abc **** C ***** 900, Sin A=7/25. ******* Cos A, Tga
В6. 1. В треугольнике 0 ABC угол C равен 90 , sin A=7/25. Найдите cos A, tgA, sin B, cos B, tg B. Найдем чему равняется cos A. sin2A+cos2A=1 cos A=√(1- sin2A)= √(1- (7/25)2) cos A=√ (1-49/625)= √(576/625) cos A=±24/25 Косинус угла меньше нуля в случае, если угол тупой (больше 900).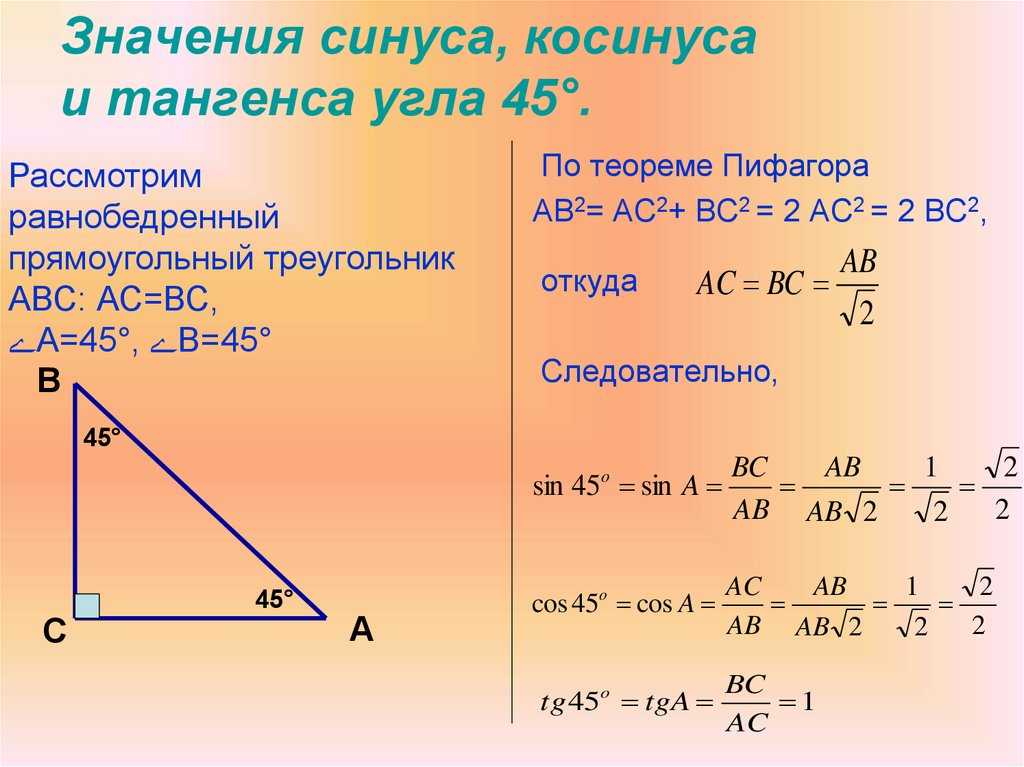
Однако, это невозможно в прямоугольном треугольнике. Следовательно, cos A=24/25. Тангенс угла равен отношению синус tg A=sin A/cos A=(7/25)/(24/25)=7/24 Следовательно, тангенс угла А равен 7/24. Теперь найдем чему равняется sin B, cos B, tg B. Итак, сумма всех углов треугольника равна 1800: А+В+С=1800 Поскольку, угол С прямой, то А+В=900 В=900-А Воспользовавшись формулами приведения, sin B=sin (900-А)=cos A=24/25 cos B=cos(900-А)=sin A=7/24 Тангенс угла В равен tg B=sinB/cosB=(24/25)/(7/25)=24/7 Следовательно, синус угла В равен 24/25, косинус равен 7/25, а тангенс 24/7.
2. В треугольнике 0 ABC угол C равен 90 , tg A=2. Найдите sinA, cos A, sinB, cosB, tg B.
Вспомним определение тангенса угла tg A=sin A/cos A=2 Но тогда, tg2 A=(sin A/cos A)2=22 sin2 A/cos2 A=4 Воспользовавшись основным тригонометрическим тождеством, запишем: (1-cos2 A)/cos2 A=4 1/cos2 A-1=4 1/cos2 A=5 cos A=±√(1/5) В прямоугольном треугольнике не может быть тупого угла, следовательно А — острый угол. Следовательно, его косинус равен 1/√5.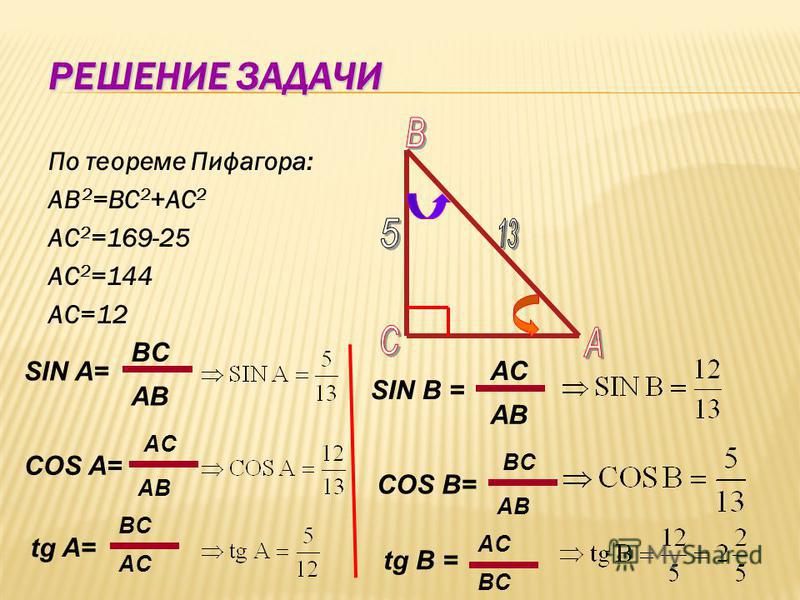
Найдите AC.
катет АС может быть найден как: АС=АВ∙ cos A Найдем чему равен косинус угла А tg A=sin A/cos A=4√(33)/33 Но тогда, tg2 A=(sin A/cos A)2=(4√(33)/33)2 sin2 A/cos2 A=16/33 Воспользовавшись основным тригонометрическим тождеством, запишем: (1-cos2 A)/cos2 A=16/33 1/cos2 A-1=16/33 1/cos2 A=49/33 cos A=±√(33/49) cos A=√(33)/7 (поскольку угол острый, косинус угла положителен) Следовательно, АС=АВ∙ cos A=7∙√(33)/7=√33 ответ : катет прямоугольного треугольника равен √33
5.В треугольник е ABC угол C равен 900, СН- высота, AB=27, cosA=2/3. Найдите AH.
Рассмотрим прямоугольный треугольник АСН. Гипотенузу АН можно найти как: AH=AC∙cos A Однако, нам неизвестна чему равняется сторона АС. Но, сторону АС можно найти из прямоугольного треугольника АВС: АС=АВ∙cos A=27∙2/3=18 Теперь из треугольника АСН можно найти АН: АН= AC∙cos A=18∙2/3=12 Следовательно, ответ к задаче: АН равняется 12.
6. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
ВС=6, АD=12, sin A=0,8 Построим высоты ВН. Очевидно, что AH=(AD-BC)/2=(12-6)/2=3 Найдем чему равняется тангенс угла А. tg A=sin A/cos A tg2 A=sin2 A/cos2 A= sin2 A/(1-sin2 A) tg2 A=0,82/(1-0,82)=0,64/0,36=16/9 tg A=4/3 (у острого угла синус, косинус, а следовательно и тангенс положительны) Рассмотрим прямоугольный треугольник АВН. Катет ВН может быть найден как: ВН=АН∙tg A=3∙4/3=4 По теореме Пифагора, гипотенуза АВ в прямоугольном треугольнике АВН равняется: АВ=√(Ah3+Bh3)= √(32+42)= √25=5 Следовательно, ответ к задаче: боковая сторона в равнобедренной трапеции, описанной в условиях задачи, равняется 5.Cos a Cos b — формула, доказательство, примеры
Cos a Cos b — это тригонометрическая формула, используемая в тригонометрии. Формула cos a cos b определяется выражением cos a cos b = (1/2) [cos (a + b) + cos (a — b)]. Мы используем формулу cos a cos b, чтобы найти значение произведения косинуса двух разных углов. формула cos a cos b может быть получена из тригонометрического тождества косинуса для суммы углов и разности углов.
Формула cos a cos b помогает решать формулы интегрирования и задачи, связанные с произведением тригонометрических отношений, таких как косинус. Давайте подробно разберемся с формулой cos a cos b и ее выводом в следующих разделах.
| 1. | Что такое Cos a Cos b в тригонометрии? |
| 2. | Вывод формулы Cos a Cos b |
| 3. | Как применять формулу cos a cos b? |
| 4. | Часто задаваемые вопросы о Cos a Cos b |
Что такое Cos a Cos b в тригонометрии?
Cos a Cos b является тригонометрическим тождеством для двух различных углов, сумма и разность которых известны. Он применяется, когда известны либо два угла a и b, либо сумма и разность углов. Его можно получить, используя тригонометрические тождества cos (a + b) и cos (a — b), которые являются одними из важных тригонометрических тождеств.
Тождество cos a cos b равно половине суммы косинусов суммы и разности углов a и b, то есть cos a cos b = (1/2)[cos(a + b) + cos(a — б)].
Получение формулы Cos a Cos b
Формула для cos a cos b может быть получена с использованием тождеств суммы и разности функции косинуса. Мы будем использовать следующие тождества косинуса, чтобы вывести формулу cos a cos b:
- cos (a + b) = cos a cos b — sin a sin b — (1)
- cos (a — b) = cos a cos b + sin a sin b — (2)
Складывая уравнения (1) и (2), имеем
cos (a + b) + cos (a — b) = (cos a cos b — sin a sin b) + (cos a cos b + sin a sin b)
⇒ cos (a + b) + cos ( a — b) = cos a cos b — sin a sin b + cos a cos b + sin a sin b
⇒ cos (a + b) + cos (a — b) = cos a cos b + cos a cos b — sin a sin b + sin a sin b
⇒ cos (a + b) + cos (a — b) = cos a cos b + cos a cos b [Термин sin a sin b был отменен из-за противоположных знаков]
⇒ cos (a + b) + cos (a — b) = 2 cos a cos b
⇒ cos a cos b = (1/2) [cos (a + b) + cos (a — b)]
Отсюда была получена формула cos a cos b.
Таким образом, cos a cos b = (1/2)[cos (a + b) + cos (a — b)]
Как применять формулу Cos a Cos b?
Теперь, когда мы знаем формулу cos a cos b, мы поймем ее применение при решении различных задач. Это тождество можно использовать для решения простых тригонометрических задач и сложных задач интегрирования. Мы можем выполнить шаги, указанные ниже, чтобы научиться применять тождество cos a cos b. Давайте рассмотрим несколько примеров, чтобы ясно понять концепцию:
Пример 1: Выразите cos 2x cos 5x как сумму функции косинуса.
Шаг 1: Мы знаем, что cos a cos b = (1/2)[cos (a + b) + cos (a — b)]
Определите a и b в данном выражении. Здесь а = 2х, b = 5х. Используя приведенную выше формулу, мы перейдем ко второму шагу.
Шаг 2: Подставьте значения a и b в формулу.
cos 2x cos 5x = (1/2)[cos (2x + 5x) + cos (2x — 5x)]
⇒ cos 2x cos 5x = (1/2)[cos (7x) + cos (-3x) )]
⇒ cos 2x cos 5x = (1/2) cos (7x) + (1/2) cos (3x) [Поскольку cos(-x) = cos x]
Следовательно, cos 2x cos 5x можно выразить как (1/2) cos (7x) + (1/2) cos (3x) как сумма функции косинуса.
Пример 2: Решите интеграл ∫ cos x cos 3x dx.
Для решения интеграла ∫ cos x cos 3x dx воспользуемся формулой cos a cos b.
Шаг 1: Мы знаем, что cos a cos b = (1/2)[cos (a + b) + cos (a — b)]
Определите a и b в данном выражении. Здесь а = х, b = 3х. Используя приведенную выше формулу, мы имеем
Шаг 2: Подставьте значения a и b в формулу и решите интеграл.
cos x cos 3x = (1/2)[cos (x + 3x) + cos (x — 3x)]
⇒ cos x cos 3x = (1/2)[cos (4x) + cos (-x) )]
⇒ cos x cos 3x = (1/2)cos (4x) + (1/2)cos (x) [Поскольку cos(-x) = cos x]
Шаг 3: Теперь замените cos x cos 3x = (1/2)cos (4x) + (1/2)cos (x) в интеграл ∫ cos x cos 3x dx. Воспользуемся интегральной формулой функции косинуса ∫ cos x dx = sin x + C
∫ cos x cos 3x dx = ∫ [(1/2) cos (4x) + (1/2) cos (x)] dx
⇒ ∫ cos x cos 3x dx = (1/2) ∫ cos ( 4x) dx + (1/2) ∫ cos (x) dx
⇒ ∫ cos x cos 3x dx = (1/2) [sin (4x)]/4 + (1/2) sin (x) + C
⇒ ∫ cos x cos 3x dx = (1/8) sin (4x) + (1/2) sin (x) + C
Следовательно, интеграл ∫ cos x cos 3x dx = (1/8) sin (4x) + (1/2) sin (x) + C по формуле cos a cos b.
Важные примечания по cos a cos b
- cos a cos b = (1/2)[cos (a + b) + cos (a — b)]
- Применяется, когда известны либо два угла a и b, либо сумма и разность углов.
- Формула cos a cos b помогает решать формулы интегрирования и задачи, связанные с произведением тригонометрических соотношений, таких как косинус
Темы, связанные с cos a cos b
- sin(a + b)
- грех 2 Пи
- потому что (а + б)
- грех (а — б)
Часто задаваемые вопросы о Cos a Cos b
Что такое
cos a cos b Формула в тригонометрии?Cos a Cos b — тригонометрическое тождество для двух разных углов, сумма и разность которых известны. Тождество cos a cos b равно половине суммы косинусов суммы и разности углов a и b, то есть cos a cos b = (1/2)[cos(a + b) + cos(a — б)].
Как получить cos a cos b Идентификацию?
cos a cos b можно получить, используя тождества суммы и разности функции косинуса.
Его можно получить, сложив формулы cos (a + b) и cos (a — b).
Какая формула для 2 cos a cos b?
Мы знаем, что cos a cos b = (1/2)[cos (a + b) + cos (a — b)]. Умножим обе части уравнения cos a cos b = (1/2)[cos (a + b) + cos (a — b)] на 2, получим 2 cos a cos b = cos (a + b) + cos (а — б)]. Следовательно, формула для 2 cos a cos b равна cos (a + b) + cos (a — b).
Какая формула для cos a cos b?
cos a cos b — одна из важных тригонометрических формул, используемых в тригонометрии. Формула для cos a cos b: cos a cos b = (1/2) [cos (a + b) + cos (a — b)].
Как доказать формулу cos a cos b?
cos a cos b можно доказать, используя тождества суммы и разности функции косинуса. Это можно доказать, добавив формулы cos (a + b) и cos (a — b).
Каковы применения формулы cos a cos b?
Формула cos a cos b помогает решать формулы интегрирования и задачи, связанные с произведением тригонометрических отношений, таких как косинус. Это тождество можно использовать для решения простых тригонометрических задач и сложных задач интегрирования.
Cos A+Cos B — формула, доказательство к формулам произведения, используемым для представления суммы функции косинуса для углов A и B в форме их произведения. Результат для Cos A + Cos B дается как 2 cos ½ (A + B) cos ½ (A — B).
Давайте разберемся в формуле Cos A + Cos B и ее доказательстве в деталях, используя решенные примеры.
| 1. | Что такое тождество Cos A + Cos B в тригонометрии? |
| 2. | Сумма Cos A + Cos B в формуле произведения |
| 3. | Доказательство формулы Cos A + Cos B |
| 4. | Как применять формулу Cos A + Cos B? |
| 5. | Часто задаваемые вопросы по Cos A + Cos B |
Что такое тождество Cos A + Cos B в тригонометрии?
Тригонометрическое тождество Cos A + Cos B используется для представления суммы косинуса углов A и B, Cos A + Cos B в виде произведения с использованием сложных углов (A + B) и (A — B).
Мы подробно изучим формулу Cos A + Cos B в следующих разделах.
Сумма Cos A + Cos B в формуле произведения
Сумма Cos A + Cos B в формуле произведения в тригонометрии для углов A и B задается как,
Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B)
Здесь A и B — углы, а (A + B) и (A — B) — их составные углы.
Доказательство формулы Cos A + Cos B
Мы можем дать доказательство тригонометрической формулы Cos A + Cos B, используя разложение формул cos(A + B) и cos(A — B). Как мы заявили в предыдущем разделе, мы пишем Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B).
Предположим, что (α + β) = A и (α — β) = B. Мы знаем, используя тригонометрические тождества,
2α = А + В
⇒ α = (А + В)/2
2β = А — В
⇒ β = (A — B)/2
½ [cos(α + β) + cos(α — β)] = cos α cos β для любых углов α и β.
[cos(α + β) + cos(α — β)] = 2 cos α cos β
⇒ Cos A + Cos B = 2 cos ½(A + B) cos ½(A — B)
Отсюда , доказано.
Как применить Cos A + Cos B?
Мы можем применить формулу Cos A + Cos B как сумму к тождеству произведения, чтобы упростить вычисления, когда трудно найти косинус заданных углов. Давайте разберемся с его применением на примере cos 60º + cos 30º. Мы решим значение данного выражения двумя способами, используя формулу и непосредственно применяя значения, и сравним результаты. Взгляните на приведенные ниже шаги.
- Сравните углы A и B с данным выражением, cos 60° + cos 30°. Здесь А = 60º, В = 30º.
- Решая с помощью расширения формулы Cos A + Cos B, заданной как, Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B), мы получаем,
Cos 60° + Cos 30° = 2 cos ½ (60° + 30°) cos ½ (60° — 30°) = 2 cos 45° cos 15° = 2 (1/√2) ((√3 + 1)/2√2) = (√ 3 + 1)/2. - Также мы знаем, что cos 60º + cos 30º = (1/2 + √3/2) = (1 + √3)/2.
Следовательно, результат проверен.
☛ Связанные темы по Cos A + Cos B:
- Тригонометрическая таблица
- грех кост загар
- Закон синусов
- Закон косинусов
- Тригонометрические функции
Давайте рассмотрим несколько примеров, чтобы лучше понять концепцию cos A + cos B.
Примеры использования идентификатора Cos A + Cos B
Пример 1: Используя значения углов из тригонометрической таблицы, решить выражение: 2 cos 52,5° cos 7,5°
Решение:
Мы можем переписать данное выражение в виде 2 cos 52,5º cos 7,5º = 2 cos ½ (105)º cos ½ (15)º
Предполагая A + B = 105º, A — B = 15º и решая для A и B, мы получаем, A = 60º и B = 45º.
⇒ 2 cos ½ (105)º cos ½ (15)º = 2 cos ½ (60º + 45º) cos ½ (60º — 45º)
Мы знаем, Cos A + Cos B = 2 cos ½ (A + B ) cos ½ (A — B)
2 cos ½ (60° + 45°) cos ½ (60° — 45°) = cos 60° + cos 45° = (1/2) + (1/√2).
Пример 2: Найдите значение cos 160° + cos 20°.
Решение:
Мы знаем, Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B)
Здесь A = 160°, B = 20°
cos 160° + cos 20° = 2 cos ½ (160° + 20°) cos ½ (160° — 20°)
= 2 cos 90° cos 70°
= 0 [ ∵ cos 90° = 0]
Пример 3: Используя cos A + cos B, докажите, что (sin A + sin B)(sin A — sin B) = — (cos A + cos B)(cos A — cos B).
Решение:
Переформулируем данное выражение.
(sin A + sin B)(sin A — sin B) = — (cos A + cos B)(cos A — cos B) можно записать как (sin A + sin B)/(cos A + cos B) = -(cos A — cos B)/(sin A — sin B)
Здесь L.H.S. = (sin A + sin B)/(cos A + cos B)
= [2 sin 1/2 (A + B) cos 1/2 (A — B)]/[2 cos 1/2 (A + B) cos 1/2 (A — B)]
= sin ½ (A + B)/cos ½ (A + B)
R.H.S. = -(cos A — cos B)/(sin A — sin B)
-[- 2 sin 1/2 (A + B) sin 1/2 (A — B)]/[2 cos 1/2 (A + B) sin 1/2 (А-В)]
= -[- sin ½ (A + B)]/[cos ½ (A + B)]
= sin ½ (A + B)/cos ½ (A + B)
⇒ L.H.S. = R.H.S.
Значит, доказано.
Пример 4: Проверьте данное выражение, используя разложение Cos A + Cos B: cos 70° + sin 70° = √2 cos 25°
Решение:
Имеем, L.H.S. = cos 70° + sin 70°
Так как sin 70° = sin(90° — 20°) = cos 20°
⇒ cos 70° + sin 70° = ⇒ cos 70° + cos 20°
Использование Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B)
⇒ cos 70° + cos 20° = 2 cos ½ (70° + 20°) cos ½ (70° — 20°)
= 2 cos 45° cos 25°
= √2 cos 25°
= R.
H.S.Следовательно, проверено.
H.S.перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по Cos A + Cos B
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Cos A + Cos B
Что такое Cos A + Cos B в тригонометрии?
Cos A + Cos B представляет собой тождество или тригонометрическую формулу, используемую для представления суммы косинусов углов A и B, Cos A + Cos B в форме произведения с использованием сложных углов (A + B) и (A — B) ). Здесь А и В — углы.
Какова формула Cos A + Cos B?
Формула Cos A + Cos B для двух углов A и B может быть представлена как Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B).
Здесь (А + В) и (А — В) — сложные углы.
Что такое расширение Cos A + Cos B в тригонометрии?
Расширение формулы Cos A + Cos B дается как Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B), где A и B — любые заданные углы.
Как доказать расширение формулы Cos A + Cos B?
Расширение Cos A + Cos B, представленное как Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B), может быть доказано с использованием тождества произведения 2 cos α cos β в тригонометрии. Нажмите здесь, чтобы проверить подробное доказательство формулы.
Как использовать формулу Cos A + Cos B?
Чтобы использовать формулу Cos A + Cos B в заданном выражении, сравните разложение Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B) с данным выражением и подставьте значения углов A и B.
Каково применение формулы Cos A + Cos B?
Формулу Cos A + Cos B можно применять для представления суммы косинуса углов A и B в виде произведения косинуса (A + B) и косинуса (A — B) по формуле Cos A + Cos B = 2 cos ½ (A + B) cos ½ (A — B).