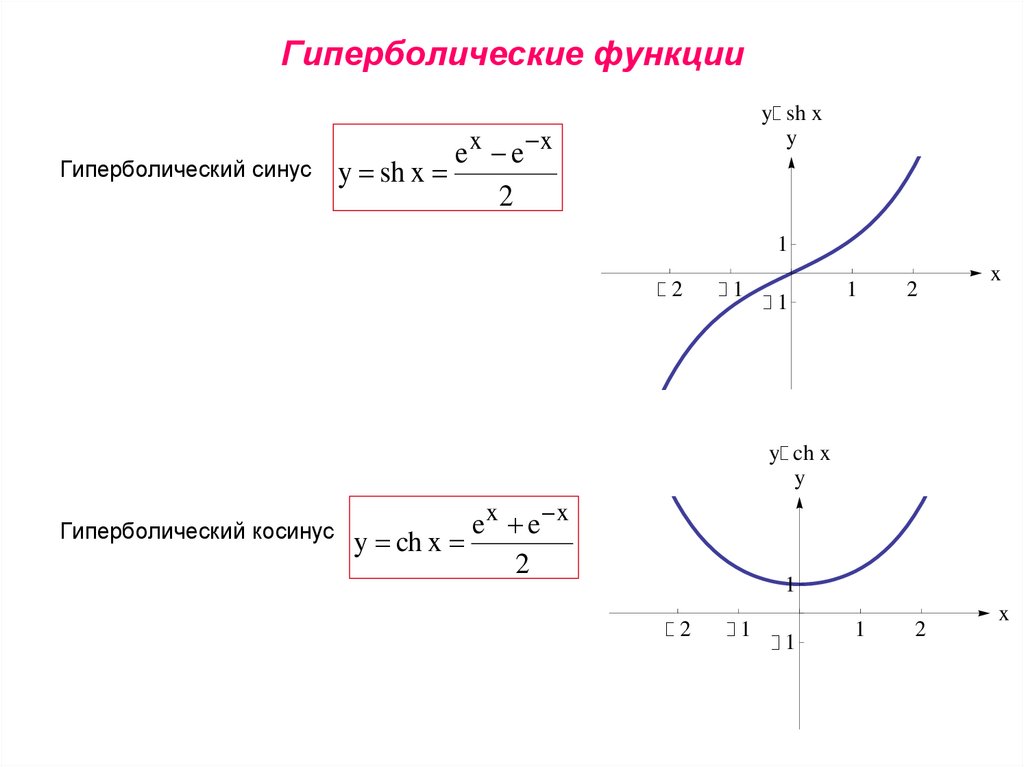
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Определение
1 Гиперболические функции. Дифференцирование и интегрирование гиперболических функций
Определение гиперболических функций через гиперболу
Гиперболические функции задаются следующими формулами:
(в англоязычной литературе обозначается )
(в англоязычной литературе обозначается )
(в англоязычной литературе обозначается )
Иногда также определяются
[править]Геометрическое определение
Параметризация гиперболического синуса (анимация).
Ввиду
соотношения
гиперболические
функции дают параметрическое
представление гиперболы
(
,
).
При этом аргумент
,
где
—
площадь криволинейного треугольника
,
взятая со знаком «+», если сектор лежит
выше оси
,
и «−» в противоположном случае. Очевидно,
что и гиперболические функции определяются
через этот параметр, например, уравнения
гиперболического синуса в параметрической
форме:
,
где
—
ордината точки гиперболы, соответствующей
площади
.
Это определение аналогично определению
тригонометрических функций через
единичную окружность, которое тоже
можно построить подобным образом.
Очевидно,
что и гиперболические функции определяются
через этот параметр, например, уравнения
гиперболического синуса в параметрической
форме:
,
где
—
ордината точки гиперболы, соответствующей
площади
.
Это определение аналогично определению
тригонометрических функций через
единичную окружность, которое тоже
можно построить подобным образом.
[править]Свойства
[править]Связь с тригонометрическими функциями
Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.
.
.
Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.
[править]Важные соотношения
(Тождество)
Чётность:
Формулы сложения:
Формулы двойного угла:
Формулы кратных углов:
Произведения
Суммы
Формулы понижения степени
Производные:
Интегралы:
2
Определение числового Ряда. Сходимость
и сумма числового ряда Числовой
ряд —
это числовая
последовательность,
рассматриваемая вместе с
другой последовательностью,
которая называется последовательностью
частичных сумм (ряда).
Сходимость
и сумма числового ряда Числовой
ряд —
это числовая
последовательность,
рассматриваемая вместе с
другой последовательностью,
которая называется последовательностью
частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
Определение
Пусть — числовая последовательность; рассмотрим наравне с данной последовательностью последовательность
каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида
Вообще, для обозначения ряда используется символ
поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.
В соответствии с этим говорится о сходимости числового ряда:
числовой ряд сходится, если сходится последовательность его частичных сумм;
числовой ряд расходится, если расходится последовательность его частичных сумм:
числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.

Если числовой ряд сходится, то предел последовательности его частичных сумм носит название суммы ряда:
Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда представляют собой либо вещественные, либокомплексные числа.
Математические функции | NumPy
Большинство математических функций NumPy являются универсальными, т.е. поддерживают множество параметров, которые позволяют оптимизировать их работу в зависимости от специфики реализуемого алгоритма.
3.1. Тригонометрические функции
-
sin(x) - Тригонометрический синус.
-
cos(x) - Тригонометрический косинус.

-
tan(x) - Тригонометрический тангенс.
-
arcsin(x) - Обратный тригонометрический синус.
-
arccos(x) - Обратный тригонометрический косинус.
-
arctan(x) - Обратный тригонометрический тангенс.
-
hypot(x1, x2) - Вычисляет длинну гипотенузы по указанным длинам катетов.

-
arctan2(x1, x2) - Обратный тригонометрический тангенс угла где x1 — противолежащий катет, x2 — прилежащий катет. В отличие от arctan (x) функция arctan2 (y, x) справедлива для всех углов и поэтому может быть использована для преобразования вектора в угол без риска деления на ноль, а также возвращает результат в правильном квадранте.
-
degrees(x) - Преобразует радианную меру угла в градусную.
-
radians(x) - Преобразует градусную меру угла в радианную.
-
unwrap(p[, discont, axis]) - Корректировка фазовых углов при переходе через значение pi.

-
deg2rad(x) - Преобразует градусную меру угла в радианную.
-
rad2deg(x) - Преобразует радианную меру угла в градусную.
3.2. Гиперболические функции
-
sinh(x) - Гиперболический синус.
-
cosh(x) - Гиперболический косинус.
-
tanh(x) - Гиперболический тангенс.

-
arcsinh(x) - Обратный гиперболический синус.
-
arccosh(x) - Обратный гиперболический косинус.
-
arctanh(x) - Обратный гиперболический тангенс.
3.3. Округление
-
around(a[, decimals, out]) - Равномерное (банковское) округление до указанной позиции к ближайшему четному числу.
-
round_(a[, decimals, out]) - Эквивалентна
around().
-
rint(x) - Округляет до ближайшего целого.
-
fix(x[, out]) - Округляет до ближайшего к нулю целого числа.
-
floor(x) - Округление к меньшему («пол»).
-
ceil(x) - Округление к большему («потолок»).
-
trunc(x) - Отбрасывает дробную часть числа.

3.4. Суммы, разности, произведения
-
prod(a[, axis, dtype, out, keepdims]) - Произведение элементов массива по заданной оси.
-
sum(a[, axis, dtype, out, keepdims]) - Сумма элементов массива по заданной оси.
-
nanprod(a[, axis, dtype, out, keepdims]) - Произведение элементов массива по заданной оси в котором элементы NaN учитываются как 1.
-
nansum(a[, axis, dtype, out, keepdims]) - Сумма элементов массива по заданной оси в котором элементы NaN учитываются как 0.

-
cumprod(a[, axis, dtype, out]) - Возвращает накопление произведения элементов по заданной оси, т.е. массив в котором каждый элемент является произведением предшествующих ему элементов по заданной оси в исходном массиве.
-
cumsum(a[, axis, dtype, out]) - Возвращает накопление суммы элементов по заданной оси, т.е. массив в котором каждый элемент является суммой предшествующих ему элементов по заданной оси в исходном массиве.
-
nancumprod(a[, axis, dtype, out]) - Возвращает накопление произведения элементов по заданной оси, т.е. массив в котором каждый элемент является произведением предшествующих ему элементов по заданной оси в исходном массиве.
 Элементы NaN в исходном массиве при произведении учитываются как 1.
Элементы NaN в исходном массиве при произведении учитываются как 1. -
nancumsum(a[, axis, dtype, out]) - Возвращает накопление суммы элементов по заданной оси, т.е. массив в котором каждый элемент является суммой предшествующих ему элементов по заданной оси в исходном массиве. Элементы NaN в исходном массиве при суммировании учитываются как 0.
-
diff(a[, n, axis]) - Возвращает n-ю разность вдоль указанной оси.
-
ediff1d(ary[, to_end, to_begin]) - Разность между последовательными элементами массива.
-
gradient(f, *varargs, **kwargs) - Дискретный градиент (конечные разности вдоль осей) массива
f.
-
cross(a, b[, axisa, axisb, axisc, axis]) - Векторное произведение двух векторов.
-
trapz(y[, x, dx, axis]) - Интегрирование массива вдоль указанной оси методом трапеций.
3.5. Экспоненцирование и логарифмирование
-
exp(x, /[, out, where, casting, order, …]) - Экспонента всех элементов массива.
-
expm1(x, /[, out, where, casting, order, …]) - Вычисляет
exp(x)-1всех элементов массива.
-
exp2(x, /[, out, where, casting, order, …]) - Вычисляет
2**xдля всех x входного массива. -
log(x, /[, out, where, casting, order, …]) - Натуральный логарифм элементов массива.
-
log10(x, /[, out, where, casting, order, …]) - Десятичный логарифм элементов массива.
-
log2(x, /[, out, where, casting, order, …]) - Логарифм элементов массива по основанию 2.
-
log1p(x, /[, out, where, casting, order, …]) - Вычисляет
log(x+1)для всех x входного массива.
-
logaddexp(x1, x2, /[, out, where, casting, …]) - Натуральный логарифм суммы экспонент элементов входных массивов.
-
logaddexp2(x1, x2, /[, out, where, casting, …]) - Двоичный логарифм от 2**x1 + 2**x2 для всех элементов входных массивов.
3.6. Другие специальные функции
-
i0(x) - Модифицированная функция Бесселя первого рода нулевого порядка.
-
sinc(x) - Вычисляет нормированный кардинальный синусс элементов массива.

3.7. Операции с плавающей точкой
-
signbit(x, /[, out, where, casting, order, …]) - Возвращает True для всех элементов массива у которых знаковый бит установлен в отрицательное значение.
-
copysign(x1, x2, /[, out, where, casting, …]) - Изменяет знак элементов из массива x1 на знак элементов из массива x2.
-
frexp(x[, out1, out2], / [, out, where, …]) - Разложение элементов массива в показатель мантиссы и двойки.
-
ldexp(x1, x2, /[, out, where, casting, …]) - Вычисляет
x1*2**x2.
-
nextafter(x1, x2, /[, out, where, casting, …]) - Возвращает значение c плавающей точкой следующее за элементом из x1 в направлении элемента из x2.
-
spacing(x, /[, out, where, casting, order, …]) - Поэлементно вычисляет расстояние между значением из массива x и ближайшим соседним числом.
3.8. Арифметические операции
-
lcm(x1, x2, /[, out, where, casting, order, …]) - Поэлементно вычисляет наименьшее общее кратное массивов x1 и x2.
-
gcd(x1, x2, /[, out, where, casting, order, …]) - Поэлементно вычисляет наибольший общий делитель массивов x1 и x2.

-
add(x1, x2, /[, out, where, casting, order, …]) - Поэлементная сумма значений массивов.
-
reciprocal(x, /[, out, where, casting, …]) - Вычисляет обратное значение (
1/x) каждого элемента массива. -
positive(x, /[, out, where, casting, order, …]) - Эквивалентно простому копированию (
numpy.copy) элементов массива, но только для массивов поддерживающих математические операции. Формально соответствует математической записиb = +a. -
negative(x, /[, out, where, casting, order, …]) - Отрицательное значение элементов массива.

-
multiply(x1, x2, /[, out, where, casting, …]) - Поэлементное умножение значений массива x1 на значения массива x2.
-
divide(x1, x2, /[, out, where, casting, …]) - Поэлементное деление значений массива x1 на значения массива x2.
-
power(x1, x2, /[, out, where, casting, …]) - Поэлементное возведение значений массива x1 в степень равную значениям из массива x2.
-
subtract(x1, x2, /[, out, where, casting, …]) - Поэлементная разность значений массива x1 и x2.

-
true_divide(x1, x2, /[, out, where, …]) - Поэлементное истинное деление значений массива x1 на значения массива x2.
-
floor_divide(x1, x2, /[, out, where, …]) - Поэлементное целочисленное деление значений массива x1 на значения массива x2.
-
float_power(x1, x2, /[, out, where, …]) - Поэлементное возведение значений массива x1 в степень равную значениям из массива x2, адаптированное для чисел с плавающей точкой.
-
fmod(x1, x2, /[, out, where, casting, …]) - Поэлементный остаток от деления значений массива x1 на значения массива x2.

-
mod(x1, x2, /[, out, where, casting, order, …]) - Поэлементно вычисляет остаток от деления значений массива x1 на значения массива x2.
-
modf(x[, out1, out2], / [, out, where, …]) - Дробная и целая часть элементов массива.
-
remainder(x1, x2, /[, out, where, casting, …]) - Элементарный остаток от деления значений массива x1 на значения массива x2.
-
divmod(x1, x2[, out1, out2], / [[, out, …]) - Результат истинного деления и остаток от деления значений массива x1 на значения массива x2.

3.9. Операции с комплексными числами
-
angle(z[, deg]) - Вычисляет угол каждого комплексного числа в массиве.
-
real(val) - Действительная часть комплексного числа.
-
imag(val) - Мнимая часть комплексного числа.
-
conj(x, /[, out, where, casting, order, …]) - Комплексно-сопряженный элемент.
3.10. Прочие математические функции
-
convolve(a, v[, mode]) - Дискретная линейная свертка.

-
clip(a, a_min, a_max[, out]) - Ограничение значений массивов указанным интервалом допустимых значений.
-
sqrt(x, /[, out, where, casting, order, …]) - Квадратный корень элементов массива.
-
cbrt(x, /[, out, where, casting, order, …]) - Кубический корень элементов массива.
-
square(x, /[, out, where, casting, order, …]) - Квадрат элементов массива.
-
absolute(x, /[, out, where, casting, order, …]) - Абсолютное значение (модуль) элементов массива.

-
fabs(x, /[, out, where, casting, order, …]) - Возвращает абсолютное значение (модуль) элементов массива в виде чисел с плавающей точкой.
-
sign(x, /[, out, where, casting, order, …]) - Элементарный указатель на знак числа.
-
heaviside(x1, x2, /[, out, where, casting, …]) - Ступенчатая функция Хевисайда.
-
maximum(x1, x2, /[, out, where, casting, …]) - Наибольшие значения после поэлементного сравнения значений массивов.

-
minimum(x1, x2, /[, out, where, casting, …]) - Наименьшие значения после поэлементного сравнения значений массивов.
-
fmax(x1, x2, /[, out, where, casting, …]) - Наибольшие значения после поэлементного сравнения значений массивов в виде чисел с плавающей точкой.
-
fmin(x1, x2, /[, out, where, casting, …]) - Наименьшие значения после поэлементного сравнения значений массивов в виде чисел с плавающей точкой.
-
nan_to_num(x[, copy]) - Заменяет nan на 0, бесконечность и минус-бесконечность заменяются на наибольшее и наименьшее доступное число с плавающей точкой соответственно.

-
real_if_close(a[, tol]) - Переводит комплексные числа в вещественные если мнимая часть комплексного числа меньше машинной эпсилон.
-
interp(x, xp, fp[, left, right, period]) - Одномерная линейная интерполяция.
→ sin()
← NumPy справочное руководство
Объясните формулу обратных гиперболических функций
В математике обратные функции гиперболических функций называются обратными гиперболическими функциями или гиперболическими функциями площади. Существует шесть обратных гиперболических функций, а именно: обратный гиперболический синус, обратный гиперболический косинус, обратный гиперболический тангенс, обратный гиперболический косеканс, обратный гиперболический секанс и обратный гиперболический котангенс. Эти функции обозначены как sinh -1 x, cosh -1 x, tanh -1 x, csch -1 x, sech -1 x, и coth -1 x. С помощью обратной гиперболической функции мы можем найти гиперболический угол соответствующей гиперболической функции.
Существует шесть обратных гиперболических функций, а именно: обратный гиперболический синус, обратный гиперболический косинус, обратный гиперболический тангенс, обратный гиперболический косеканс, обратный гиперболический секанс и обратный гиперболический котангенс. Эти функции обозначены как sinh -1 x, cosh -1 x, tanh -1 x, csch -1 x, sech -1 x, и coth -1 x. С помощью обратной гиперболической функции мы можем найти гиперболический угол соответствующей гиперболической функции.
Function name | Function | Formula | Domain | Range |
|---|---|---|---|---|
| Inverse hyperbolic sine | sinh -1 x | LN [x + √ (x 2 + 1)] | (-∞, ∞) | (-∞, ∞) | (-∞, ∞) |
cosh -1 x | ln[x + √(x 2 – 1) | [1, ∞) | [0, ∞) | |
Арктический гиперболический тангенс | tanh -1 x | ½ ln [(1 + x)/(1-x)] | (-1,1) | (-, ∞) |
Верный гиперболический космол | ||||
. CSCH -1 x | LN [(1 + √ (x 2 + 1)/x] | (-∞, ∞) | (-∞, ∞) | (-∞, ∞) | 70041
Арктический гиперболический секанс | sech -1 x | ln[(1 + √(1 – x 9)0003 2 )/x] | (0, 1] | [0, ∞) |
. [(x + 1)/(x – 1)] | (-∞, -1) или (1, ∞) | (-∞, ∞) |
sinh -1 x = ln[x + √(x 2 + 1)]
Доказательство:
Функция обратной гиперилолической косиран ch -1 x = ln[x + √(x 2 -1)]LET SINH -1 x = z, где z ∈ R
⇒ x = sinh z
Использование гиперболической функции SINE мы получаем,
⇒ x = (E z z -E -z )/2
⇒ 2x = E z -E -z
⇒ E 2Z -2xe z -1 = 0
Мы знаем, что корты уравнения ax 2 + bx + c = 0 являются x = [-b ± √(b 2 – 4ac)]/2a
Итак, e z = x ± √(x 2 + 1)
Поскольку z — действительное число, e должно быть положительным числом.
Следовательно, e z = x + √(x 2 + 1)
⇒ z = ln[x + √(x 2 + 1)]
⇒ l 0 sh3 — 900 [x + √ (x 2 + 1)]
SINH -1 X = LN [x + √ (x 2 + 1)]
Доказательство:
Обратная гиперболическая тангентная функцияLet Cosh -1 x = z, где z ∈ R
⇒ x = cosh z
Использование гиперболической функции Cosin ⇒ x = (E z + E -z )/2
⇒ 2x = E Z + E -Z
⇒ E 2Z -2xe z + 1 = 0
Мы знаем, что корнями уравнения ax 2 + bx + c = 0 являются x = [-b ± √(b 2 – 4ac)]/2a
Итак, e z = x ± √(x 2 – 1)
Поскольку z — действительное число, e должно быть положительным числом.
Следовательно, e z = x + √(x 2 – 1)
⇒ z = ln[x + √(x 2 – 1)]
⇒ l n = ln3 — 900 [x + √ (x 2 -1)]
COSH -1 x = LN [x + √ (x 2 -1)]
. Тан -1 x = ½ ln[(1 + x)/(1 – x)] = ½ [ln(1 + x) – ln(1 – x)]
Доказательство:
Let tanh -1 x = z, где z ∈ R
⇒ x = th z
С помощью касательной гиперболической функции получаем z + e -z )
x =
⇒ x = (e 2z – 1)/(e 2z + 1)
) = 1 0 4z
⇒ 3 (e 29000 2з – 1)
⇒ (x – 1) e 2z + (x + 1) = 0
⇒ e 2z = -[(x +1)/(x – 1)]
⇒ e 2z = [(x + 1)/(1 – x)]
⇒ 2z = ln [(x + 1)/(1 – x)]
⇒ z = ½ ln[(1 + x)/ (1 – x)] = ½ [ln(1 + x) – ln(1 – x)]
⇒ tanh -1 x = ½ ln[(1 + x)/(1 – x)] = ½ [ln(1 + x) – ln(1 – x)]
tanh -1 x = ½ ln[ ] = ½ [ln(1 + x) – ln(1 – x)]
Функция обратного гиперболического косеканса
CSCH -1 x = LN [(1 + √ (x 2 + 1)/x]
Доказательство:
.
∈ R
⇒ x = csch z
Используя гиперболическую функцию косеканса, получаем
⇒ x =
⇒ x = 2e z /(e 2z – 1)
⇒ x (e 2z – 1) = 2e z
⇒ xe 2z − 2e z – x = 0
Мы знаем, что корнями уравнения ax 2 + bx + c = 0 являются x = [-b ± 900(3 – 4ac)]/2a
⇒ e z = (1 + √(x 2 + 1)/x
⇒ z = ln[ ]
⇒ csch = ln
4
-1 4 = ln[1 + √(1 + x 2 )] – ln(x)csch -1 x = ln[ ] = ln[1 + √(1 + x 2 )] – пер(х)
Inverse hyperbolic secant function
sech -1 x = ln[(1 + √(1 – x 2 )/x]
Proof:
Let sech -1 x = z, где z ∈ R
⇒ x = sech z
. Используя гиперболическую функцию секущей, получаем /(e z + e -z )
⇒ x =
⇒ x = 2e z /(e 2Z + 1)
⇒ x (E 2Z +1) = 2E Z
⇒ XE 2Z — 2E Z + x = 0
Мы знаем, что Roots of Accation Ax 2 + bx + c = 0 are x = [-b ± √(b 2 – 4ac)]/2a
Таким образом, упрощая, получаем
e z =
z = ln[ ] = ln[1 + √(1 – x 2 )] – ln(x)
⇒ sech -1 x = ln[ ] = ln[1 + √(1 – x 2 )] – ln (х)
SECH -1 X = LN [ ] = LN [1 + √ (1 -x 2 )] -LN (x)
. 1 x = ½ ln[(x + 1)/(x – 1)]
1 x = ½ ln[(x + 1)/(x – 1)]
Доказательство:
Пусть coth -1 x = z, где z ∈ R
⇒ x = coth
Используя гиперболическую функцию котангенса, получаем
coth z = (e z + e -z )/(e Z -E -Z )
⇒ x = (E Z + E- Z )/(E Z -E -Z )
⇒ x =
⇒ x = x = x = x = x = x = x = x = x = x = x =. (e2z + 1)/(e 2z – 1)
⇒ x (e 2z – 1) = (e 2z + 1)
⇒ (x – 1) e2z – (x + 1) = 0
⇒ e 2z = [(x + 1)/(x – 1)]
⇒ 2z = ln [(x + 1)/(x – 1)]
⇒ z = ½ ln[ (x + 1)/(x – 1)] = ½[ln(x + 1) – ln(x – 1)]
coth -1 x = ½ ln[(x + 1)/(x – 1)] = ½ [ln(x + 1) – ln(x – 1)]
Производные обратных гиперболических функций
Inverse hyperbolic function | Derivative | |
|---|---|---|
sinh -1 x | 1/√(x 2 + 1) | |
cosh -1 х | 1/√(х 2 – 1), х>1 | |
танх -1 x | 1/(1 – x 2 ), |x| < 1 | |
csch -1 x | 1/{|x|√(1 + x 2 )}, x ≠ 0 | |
sech -1 x | -1/[x√ (1 -x 2 )], 0 | |
Coth -1 x | 1/(1 -X 2 | 1/(1 -X 20004 ), |х| > 1 |
Примеры задач
Задача 1. Если sh x = 4, то докажите, что x = log e (4 + √17).
Если sh x = 4, то докажите, что x = log e (4 + √17).
Решение:
Дано, SINH X = 4
⇒ x = SINH -1 (4)
Мы знаем, что,
SINH -1 (x) = goge [x) =. + √(x 2 + 1)]
⇒ x = log e [4 + √(4 2 + 1)] = log e (4 + √17)
Следовательно, x = log e (4 + √17)
Задача 2: Докажите, что tanh -1 (sin x) = ch -1 (sec x).
Решение:
Мы знаем, что
tanh -1 x = 1/2 ln[(1+x)/(1-x)]
9000 Теперь sin x) = 1/2 log[(1 + sin x)/(1 – sin x)]Имеем,
ch -1 x = ln(x + √[x 2 -1 ])
Сейчас, кош -1 (сек x) = ln[сек x + √(сек 2 x – 1)]
= ln[сек x + √tan 2 x] {С, сек 2 x – 1 = tan 2 x}
= ln[sec x + tan x]
= ln[1/cos x + sin x/cos x]
= ln[(1 + sin x)/cos x ]
Теперь умножьте и разделите член на 2
= 1/2 × 2 ln[(1 + sin x)/cos x]
= 1/2 ln[(1 + sin x)/cos x] 2 {так как 2 ln x = ln x 2 }
= 1/2 ln[(1 + sin x) 2 /cos 2 x]
Мы знаем, cos 2 x = 1 – sin 2 x = (1 + sin x )(1 – sin x)
Следовательно, (1 + sin x)2/cos2 x = [(1 + sin x)(1+ sin x)]/[(1 + sin x)(1 – sin x )] = (1 + sin x)/(1 – sin x)
= 1/2 ln[(1 + sin x)/(1 – sin x)]
= tanh -1 (sin x)
Следовательно, tanh -1 (sin x) = ch -1 (sec x)
Задача 3: найти значение tanh -1 (1/5).
Решение:
Мы знаем,
TANH -1 x = 1/2 LN [(1+X)/(1-x)]
⇒ Tanh — (1-x)]
⇒ TANH — (1-x)]
⇒ 1/5) = 1/2 ln[(1+(1/5))/(1 – (1/5)]
= 1/2 ln[(6/5)/(4/5)]
=1/2 ln(3/2)
Следовательно, tanh -1 (1/5) = 1/2 ln(3/2)
Задача 4. Найти значение sech -1 (3/8)
Решение:
Мы знаем,
sech -1 x = ln[(1 + √(1 – x 2 )/x]
Итак, sech -1 (3/8) =
= ln[ (8 + √(64 – 9))/3]
=
Следовательно, sech -1 (3/8) =
Задача 5. Найдите производную от [sinh -1 (5x + 1)] 2 .
Решение:
Пусть y = [sinh -1 (5x + 1)] 2
015
dy/dx = d([sinh -1 (5x + 1)] 2 )/dx
= 2[sinh -1 (5x + 1)] d/dx [sinh -1 (5x + 1)
Мы знаем d(sin -1 x)/dx = 1/√(x 2 + 1)
= 2 [sinh + 1 ) ( ] {1/√[(5x+1) 2 + 1]} d(5x+1)/dx
= 2 [sin-1 (5x + 1)] × {1/√(25×2 + 10x + 2)} × 5
= 10 sinh -1 (5x+1)/[√(25x 2 +10x+2)]
Следовательно, производная от [sinh -1 (5x+1)] = .
Видео с вопросами: Найдите ряд Маклорена для функции гиперболического косинуса
Стенограмма видео
Найдите ряд Маклорена для функция гиперболический cos двух 𝑥, который равен 𝑒 в степени двойки 𝑥 плюс 𝑒 в степени минус два 𝑥 все разделить на два.
Напомним, что для бесконечно дифференцируемая функция 𝑓 от 𝑥, ряд Маклорена от 𝑓 от 𝑥 равен 𝑓 оценивается как ноль плюс первая производная от 𝑓 оценивается как ноль, умноженная на 𝑥 плюс вторая производная от 𝑓, оцененная в нуле, деленная на два факториала умножить на 𝑥 в квадрате. И эта сумма продолжается бесконечно, что дает нам сумму от 𝑛 равной нулю до ∞ 𝑛-й производной от 𝑓, оцененной в ноль разделить на 𝑛 факториал, умноженный на 𝑥 в 𝑛-й степени.
В этот момент мы можем поддаться искушению
определить 𝑓 из 𝑥 как сумму двух 𝑥, а затем продифференцировать эту функцию и
попытайтесь найти образец для 𝑛-й производной, оцененной в нуле.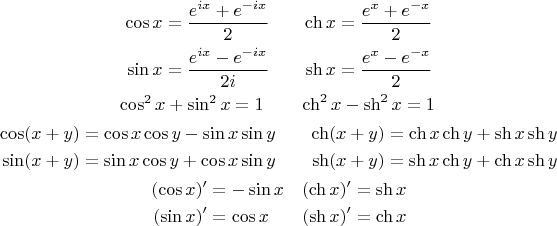 И это сработает. Однако чуть более простой способ
было бы использовать слово 𝑥, а затем заменить на 𝑥 в конце. Итак, давайте установим нашу функцию 𝑓 из 𝑥
быть равным кош 𝑥, который равен 𝑒 в степени 𝑥 плюс 𝑒 в
сила отрицательного 𝑥 все делится на два.
И это сработает. Однако чуть более простой способ
было бы использовать слово 𝑥, а затем заменить на 𝑥 в конце. Итак, давайте установим нашу функцию 𝑓 из 𝑥
быть равным кош 𝑥, который равен 𝑒 в степени 𝑥 плюс 𝑒 в
сила отрицательного 𝑥 все делится на два.
Чтобы найти первую производную нашего функция 𝑓 от 𝑥, дифференцируем каждый член отдельно. Во-первых, мы замечаем, что производная от 𝑒 в степени 𝑥, деленная на два, равна самой себе, 𝑒 в степени 𝑥 все разделить на два. Точно так же производная от 𝑒 к степень отрицательного 𝑥 все разделить на два отрицательное 𝑒 в степени отрицательного 𝑥 все разделить на два. Мы иногда называем эту функцию гиперболический грех 𝑥 или грех 𝑥.
Теперь найдем вторую производную
нашей функции 𝑓 от 𝑥 мы берем производную от нашей первой производной. Так что это производная от нашего
функция, гиперболический знак 𝑥. Производная от 𝑒 в степени
из 𝑥, деленное на два, просто равно самому себе. И когда мы различаем наши
второй член, который имеет 𝑒 в отрицательной степени 𝑥, мы получим два отрицательных
единицы, что дает нам плюс 𝑒 в степени минуса 𝑥, деленное на два. Итак, у нас есть вторая производная от
наша функция 𝑓 от 𝑥 относительно 𝑥 равна гиперболическому cos от 𝑥.
Производная от 𝑒 в степени
из 𝑥, деленное на два, просто равно самому себе. И когда мы различаем наши
второй член, который имеет 𝑒 в отрицательной степени 𝑥, мы получим два отрицательных
единицы, что дает нам плюс 𝑒 в степени минуса 𝑥, деленное на два. Итак, у нас есть вторая производная от
наша функция 𝑓 от 𝑥 относительно 𝑥 равна гиперболическому cos от 𝑥.
Таким образом, мы показали, что если
продифференцируем нашу функцию 𝑓 от 𝑥 нечетное число раз, получим
гиперболический грех 𝑥. И если мы различаем наши
функция 𝑓 от 𝑥 четное количество раз, мы получим гиперболический cos от 𝑥. Теперь мы готовы начать оценку
эти функции равны нулю. У нас есть эта наша функция 𝑓
оцененный в нуле, равен гиперболическому cos, оцененному в нуле, равен 𝑒 к
нулевая степень плюс 𝑒 в отрицательной нулевой степени, разделенная на два. А так как 𝑒 в нулевой степени
и 𝑒 в отрицательной нулевой степени просто равны единице, у нас есть только одна
плюс один все разделить на два, что равно единице.
А так как 𝑒 в нулевой степени
и 𝑒 в отрицательной нулевой степени просто равны единице, у нас есть только одна
плюс один все разделить на два, что равно единице.
Затем мы можем сделать то же самое, чтобы найти значение нашей первой производной функции, оцененное в нуле, равное гиперболический грех оценивается как ноль, который просто равен нулю. Теперь, используя тот факт, что если мы продифференцируем нашу функцию 𝑓 от 𝑥 нечетное число раз по 𝑥, мы получить гиперболический грех 𝑥. Тогда, если мы оценим это 𝑥 равно нулю, мы просто получим ноль. Точно так же, поскольку мы показали, если мы продифференцируем нашу функцию 𝑓 четное число раз, получим гиперболический cos из 𝑥. Если мы оценим это, когда 𝑥 равно нулю, мы просто получим единицу.
В частности, то, что мы показали
вот что для нечетного 𝑛 в нашем ряду Маклорена мы просто получили бы ноль в
ряд. Так что мы можем оставить их. Таким образом, используя наше определение
Серия Маклорена. У нас есть гиперболический cos 𝑥
равно сумме от 𝑛, равной нулю, до ∞ 𝑛-й производной, оцененной в нуле
разделить на 𝑛 факториал, умножить на 𝑥 в 𝑛-й степени. Мы можем разделить эту серию на две
ряд, первый дает нам все нечетные значения 𝑛, а второй дает нам
все четные значения 𝑛.
Так что мы можем оставить их. Таким образом, используя наше определение
Серия Маклорена. У нас есть гиперболический cos 𝑥
равно сумме от 𝑛, равной нулю, до ∞ 𝑛-й производной, оцененной в нуле
разделить на 𝑛 факториал, умножить на 𝑥 в 𝑛-й степени. Мы можем разделить эту серию на две
ряд, первый дает нам все нечетные значения 𝑛, а второй дает нам
все четные значения 𝑛.
Как мы уже говорили ранее, каждый коэффициент в нашем первом ряду равен нулю. Таким образом, мы можем просто удалить ряд. И во второй серии, для нашего четные значения 𝑛, мы имеем, что оценки нашей функции в нуле всегда равен единице. Давая нам серию Маклорена для гиперболический cos 𝑥 равен сумме от 𝑛 равного нулю до ∞ от 𝑥 до степень двойки 𝑛, деленная на два 𝑛 факториала.
Теперь мы хотим использовать наш Maclaurin
ряд для гиперболического cos 𝑥, чтобы найти ряд Маклорена для гиперболического
потому что два 𝑥.





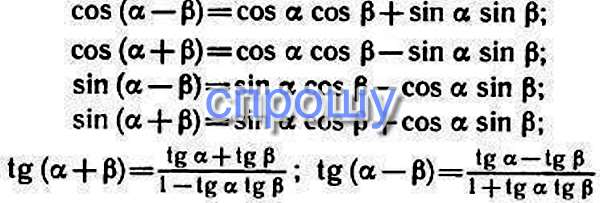


 Элементы NaN в исходном массиве при произведении учитываются как 1.
Элементы NaN в исходном массиве при произведении учитываются как 1.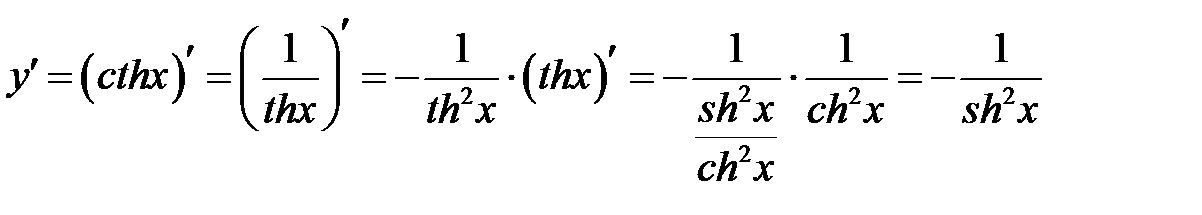







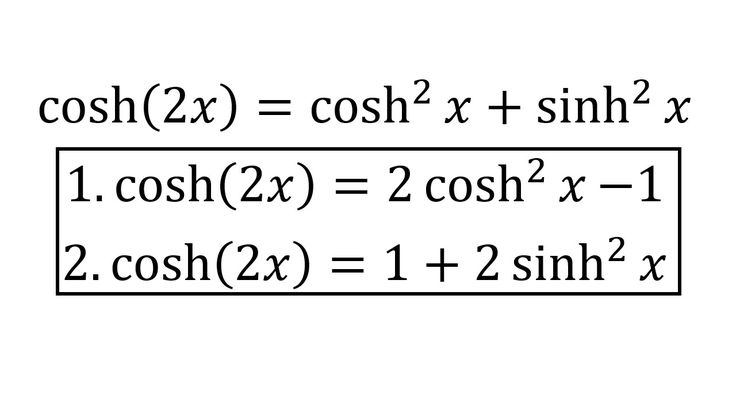




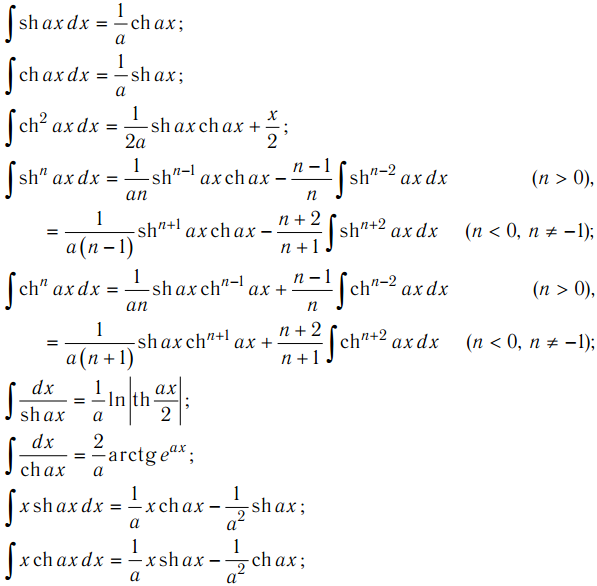 cosine
cosine
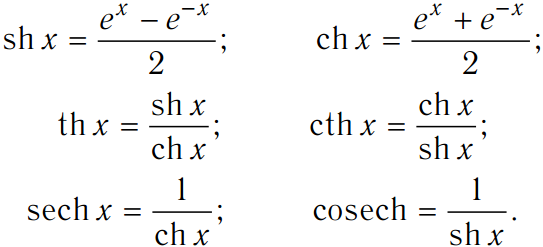 ∈ R
∈ R