Тригонометрический круг
Тригонометрический круг — это окружность с единичным радиусом и центром в начале осей координат, каждая точка которой образует треугольник с точками:- точка в начале осей координат (точка 0;0)
- точка на окружности (выбрана нами)
- точка на оси X, которая является проекцией выбранной нами точки на эту ось (перпендикуляр к оси X)
Как видно, такой треугольник является прямоугольным, так как из выбранной нами точки на ось абсцисс всегда опускается перпендикуляр. То есть сторона, соединяющая начало координат и выбранную нами точку на тригонометрическом круге ( на приведенном рисунке обозначенную как B, B1. B2, B3) всегда является гипотенузой прямоугольного треугольника, проекция выбранной точки — это катет, а сторона от точки пересечения с осью X образует второй катет.
Угол, который образуется между осью абсцисс (осью X) и гипотенузой треугольника — является углом, для которого и вычисляются значения тригонометрических функций.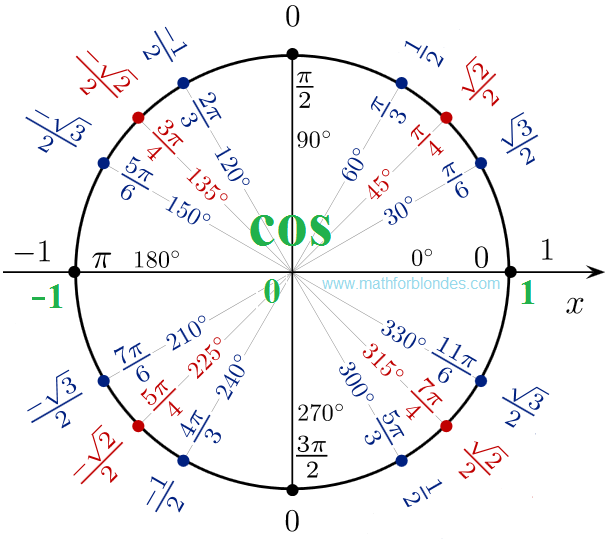
Чтобы вычислить значение тригонометрической функции для выбранного угла тригонометрического круга достаточно воспользоваться координатами точки, принадлежащей окружности тригонометрического круга. На приведенном выше рисунке, показано вычисление значения синуса для всех углов.
Например, sin α для треугольника OBC (где координаты точки B равны (x,y) ) ,будет равен: y / √ ( x2 + y2)
Свойства тригонометрического круга
Если последовательно вычислять значения тригонометрических функций для тригонометрического круга, то становится видно, что результат таких вычислений меняет свой знак в зависимости от того, в какой четверти тригонометрического круга выбрана точка. При этом знак тригонометрической функции в пределах одной и той же четверти сохраняется.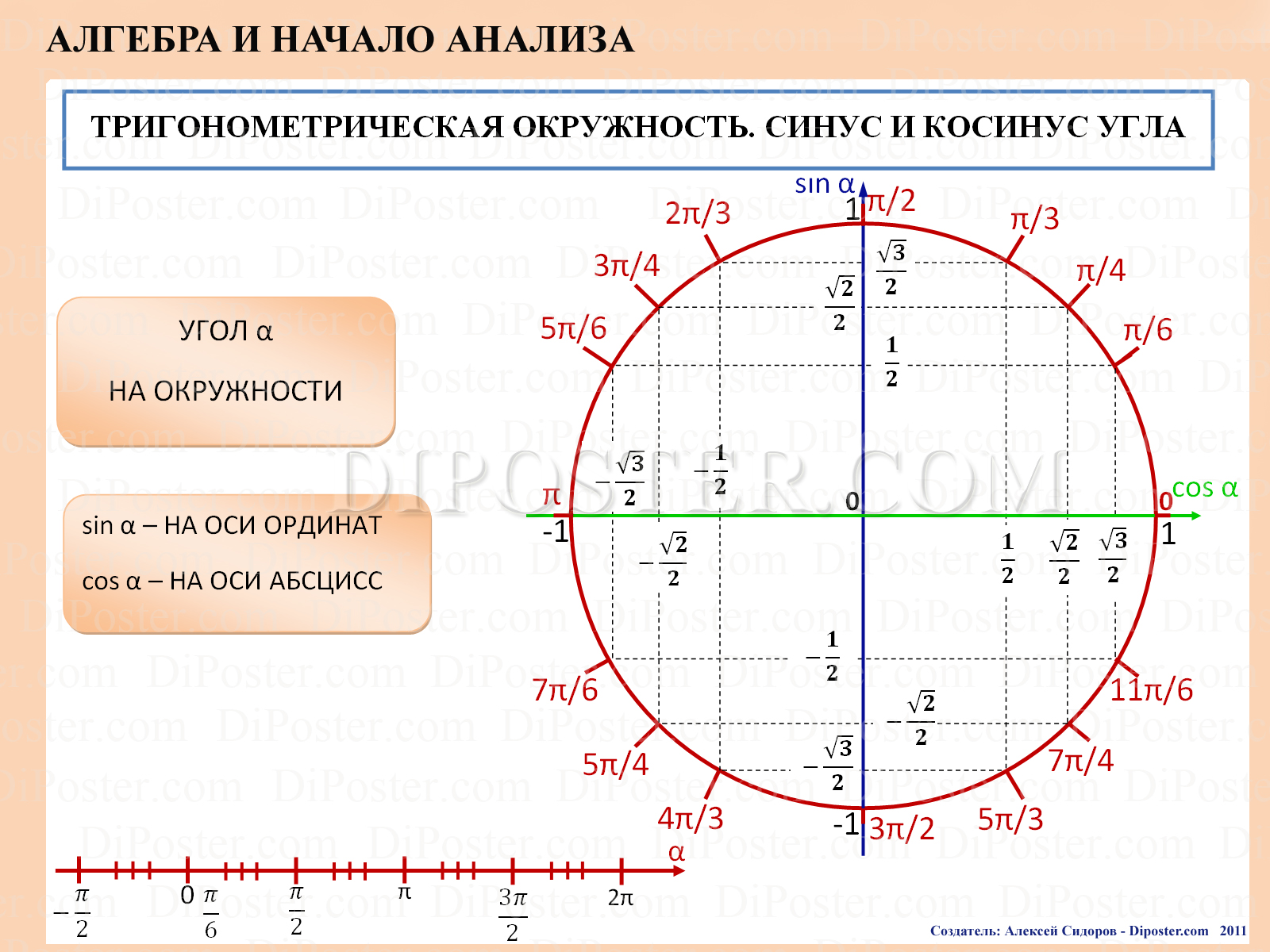
Знаки тригонометрических функций в координатных четвертях в тригонометрическом круге
Преобразование углов больше 360 градусов или 2π радиан
Как видно из картинок, после того, как значение угла превысит 360 градусов (или 2π радиан), то результат вычисления значения будет тем же самым. То есть, для того, чтобы привести значение к «нормальному» — нужно вычесть из имеющегося значения 360 градусов или 2π радиан и повторять операцию столько раз, пока результат не станет меньше 360 или 2π.
Тригонометрические соотношения в прямоугольном треугольнике | Описание курса | Радианы и градусы. Радiани i градуси
Тригонометрический круг. Основные значения тригонометрических функций
Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг:
Мы же здесь будем все подробно разбирать шаг за шагом + показать
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей.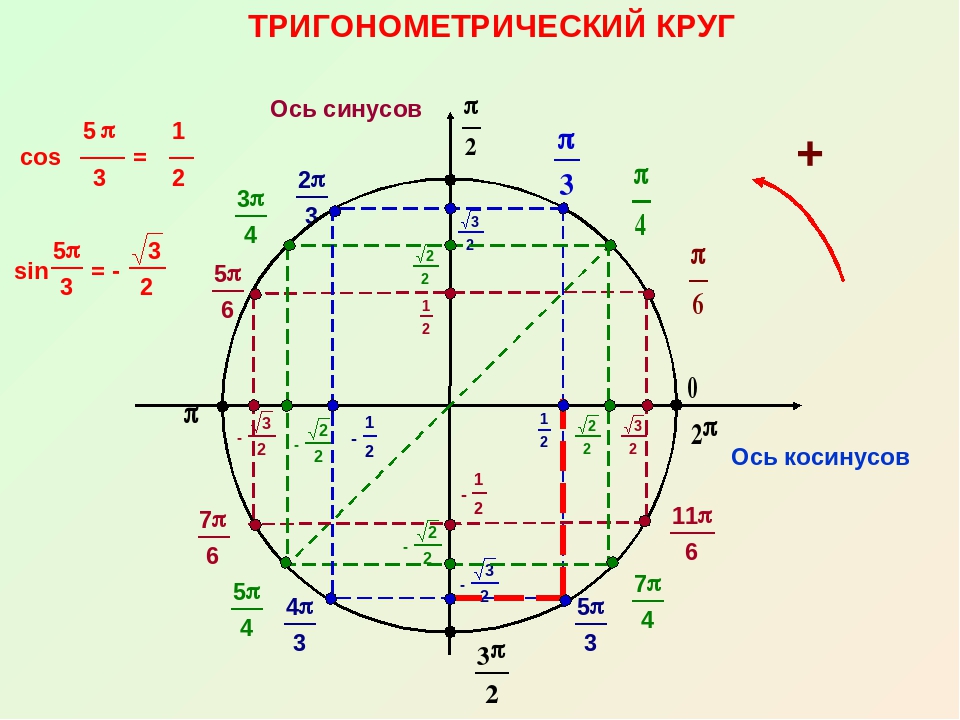 Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, градусов, или .
Никак?.. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.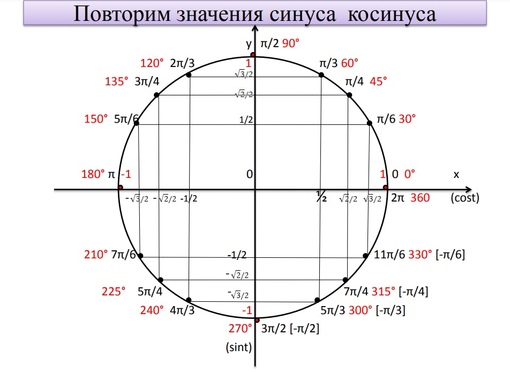
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все.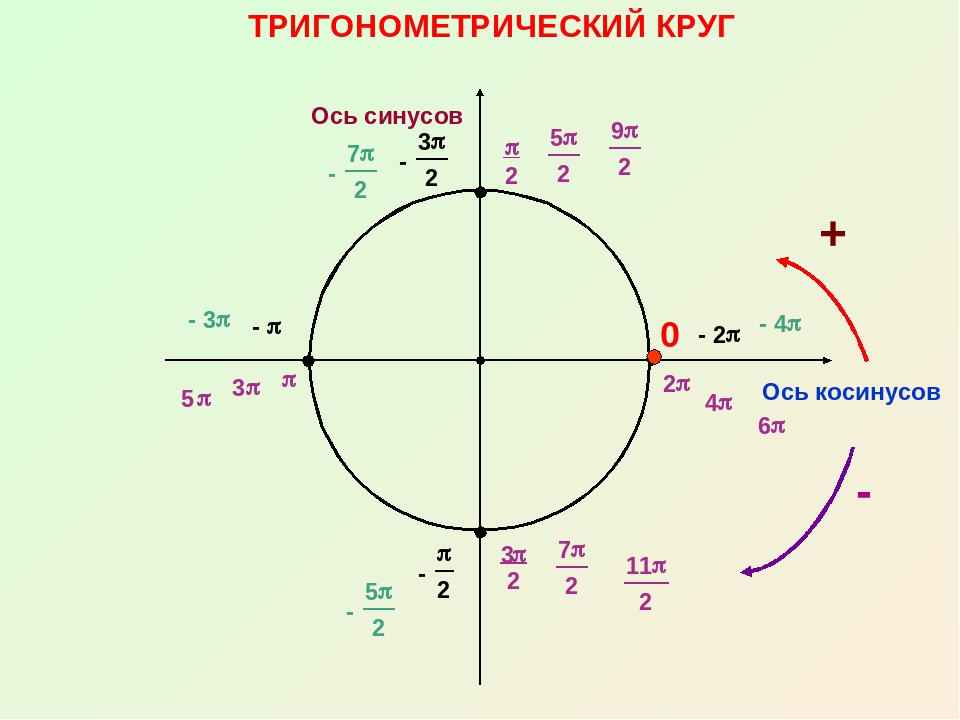 Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть ).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Наконец, что такое синус, косинус в прямоугольном треугольнике?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось (oy) – осью синусов. Про тангенс и котангенс позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.
Тригонометрический круг синус и косинус
Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.
Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)
Давайте проведем обзорную экскурсию по этому уголку математического зоопарка.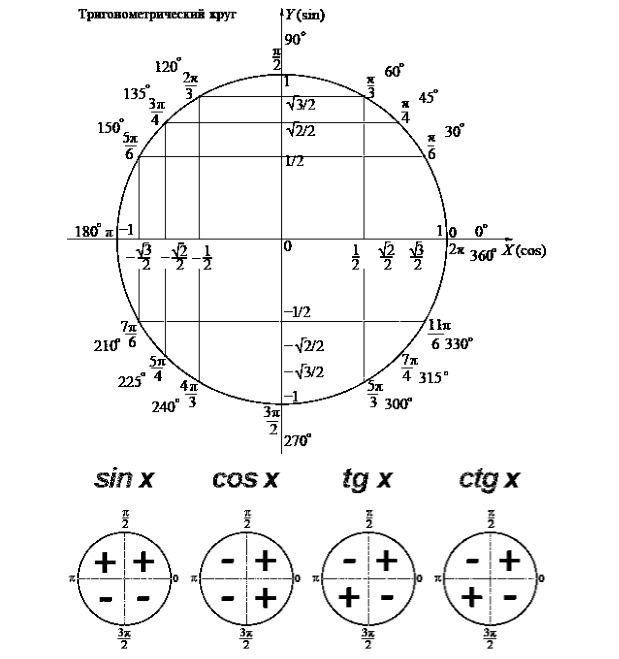 Прежде всего, нужно отметить, что здесь присутствует декартова система координат — одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая — вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы — cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы — sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы — на диване перед телевизором по горизонтали.
Прежде всего, нужно отметить, что здесь присутствует декартова система координат — одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая — вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы — cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы — sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы — на диване перед телевизором по горизонтали.
В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат — там, где в центе рисунка пересекаются
Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов.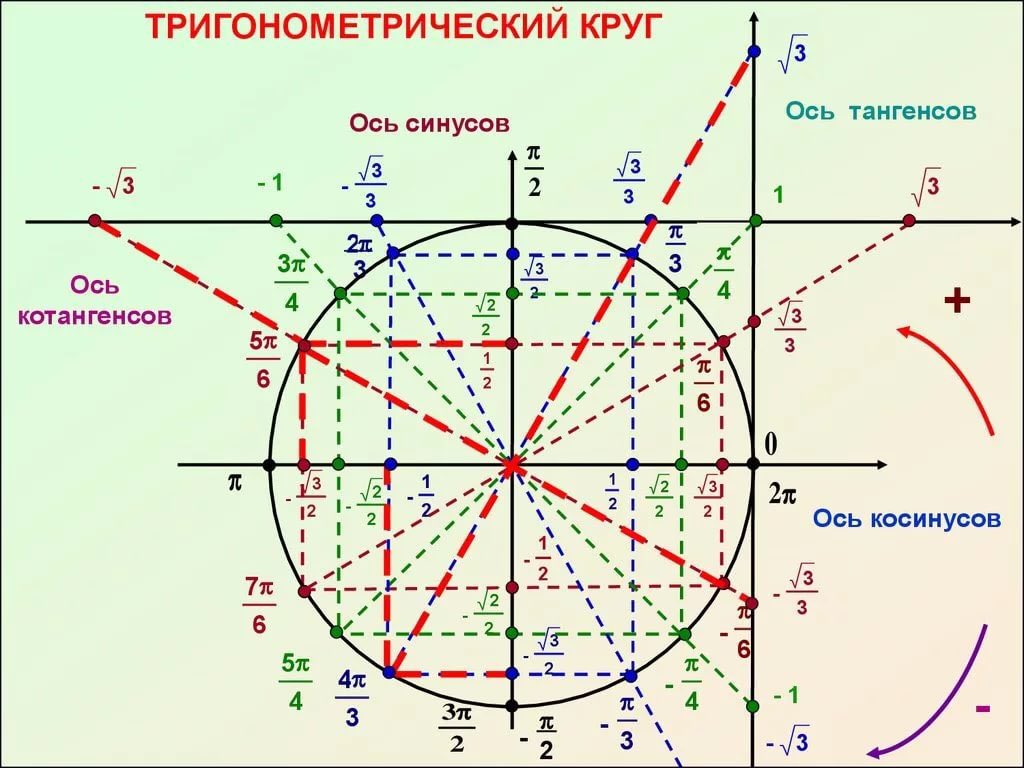 В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла.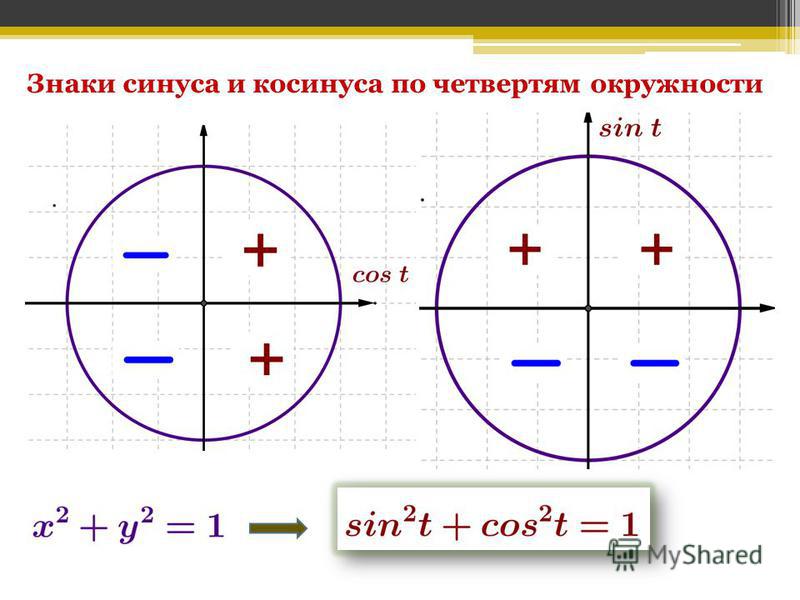 Главное, не перепутать синус с косинусом.
Главное, не перепутать синус с косинусом.
Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.
Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).
Найти решение:
Синусы и косинусы круг — здесь картинка во всей своей тригонометрической красе.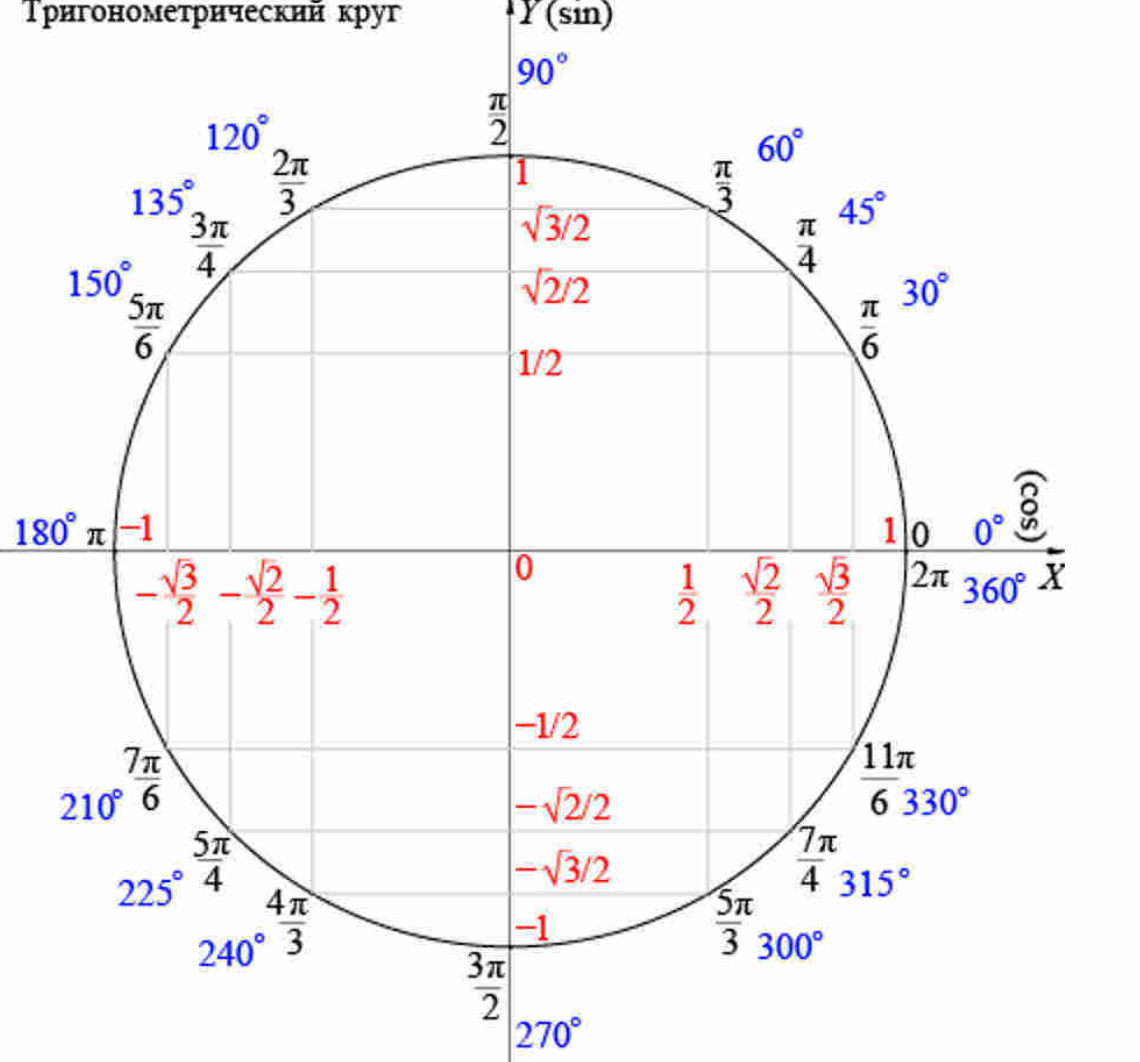
Угол 120 градусов в радианах — равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.
Значения синусов косинусов углов в радианах — на картинке есть такие, надеюсь, именно те углы, которые вы ищете.
Значение косинуса угла в 45 градусов — равно корню из двух деленному на два, можете проверить по рисунку.
Тригонометрическая окружность — я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности — вылитая тригонометрия.
Тригонометрический круг рисунок — есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию — почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников «Перед вами всемирно известное полотно «Тригонометрическая мадонна с единичным отрезком на руках» — картина гениального художника эпохи Раннего Математического Возрождения . ..» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
..» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
Круг синусов и косинусов — именно такой круг совершенно случайно оказался здесь на картинке.
Угол 9 градусов сколько это в пи — в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20
Ответ: 9 градусов = 1/20 пи.
Синус это вверх или в сторону — синус — это вверх, в сторону — это косинус.
Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.
Тригонометрические функции угла синус косинус тангенс котангенс основное тригонометрическое тождество тригонометрический круг числовая окружность
Содержание
Определение тригонометрических функций произвольного угла
Рассмотрим окружность радиуса R с центром в начале прямоугольной системой координат Oxy.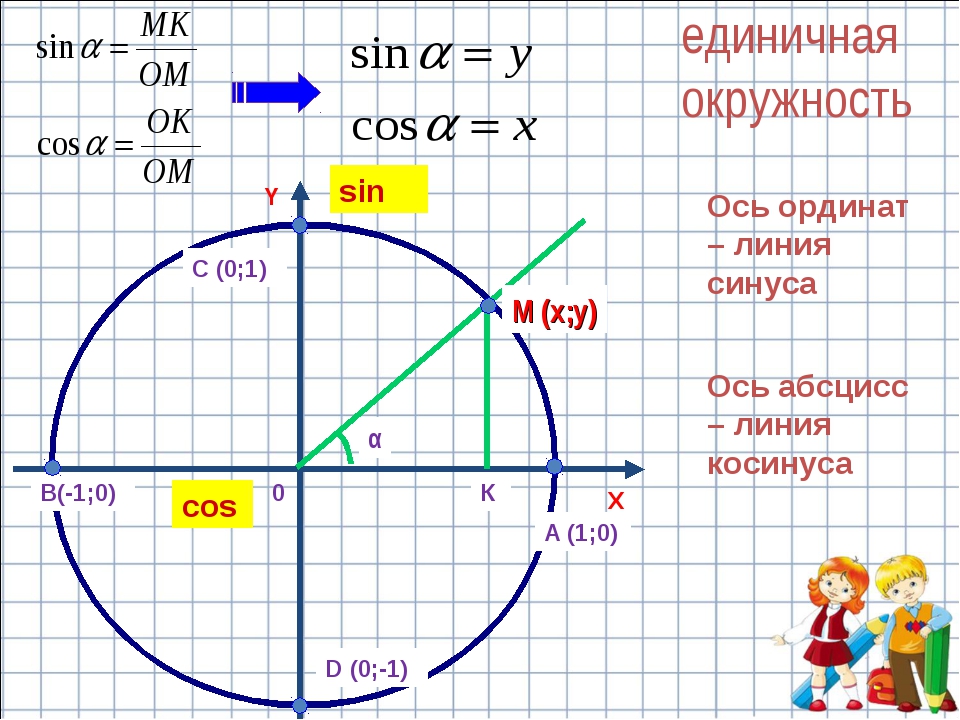
Рис.1
Положительным считается угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении движения против часовой стрелки (рис.1).
Рис.2
Отрицательным считается угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении, совпадающем с направлением движения часовой стрелки (рис. 2).
Если для координат точки M0 , лежащей на окружности радиуса R с центром в начале координат O (рис. 3),
Рис.3
ввести обозначение
M0 = ( x0 ; y0 ),
то, в силу теоремы Пифагора, будет справедливо равенство:
x02 + y02 = R2,
и можно сформулировать следующее общее определение тригонометрических функций произвольного угла.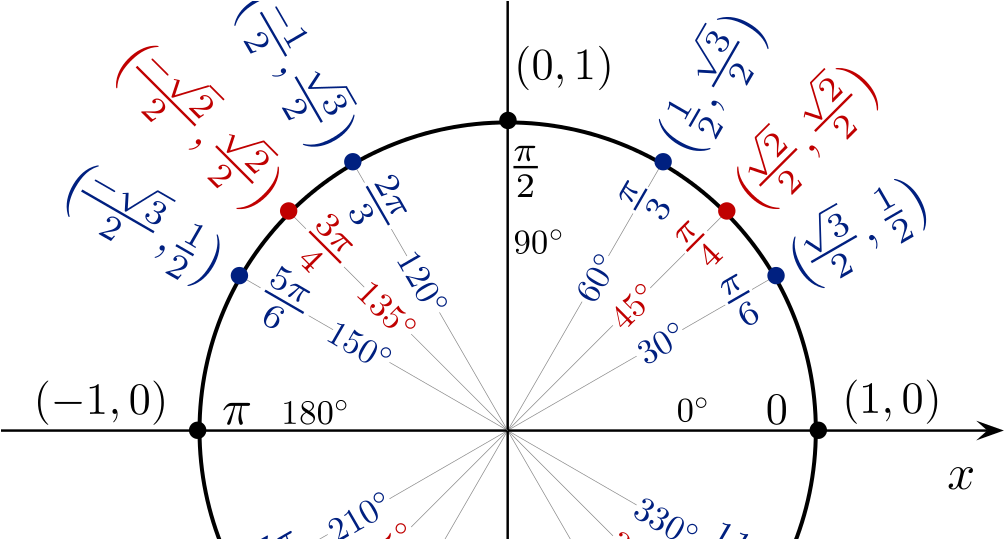
Синусом, косинусом, тангенсом и котангенсом произвольного угла α называют числа, определяемые по формулам:
ЗАМЕЧАНИЕ 1. Отметим следующее важное свойство тригонометрических функций синуса и косинуса произвольного угла:
ЗАМЕЧАНИЕ 2. Определение тригонометрических функций произвольного угла является естественным обобщением определения тригонометрических функций острого угла, данного в разделе справочника «Тригонометрические функции острого угла».
Основное тригонометрическое тождество. Тригонометрический круг
Рассмотрим окружность радиуса 1 с центром в начале координат. Если для координат точки M1 (рис. 4), лежащей на этой окружности,
Рис.4
ввести обозначение
M1 = ( x1 ; y1 ) ,
то, в силу теоремы Пифагора, будет справедливо равенство
x12 + y12 = 1 ,
а синус, косинус, тангенс и котангенс угла α будут вычисляться по формулам
Из этих формул, в частности, вытекает основное тригонометрическое тождество:
sin2α + cos2α = 1 .
Таким образом, основное тригонометрическое тождество является теоремой Пифагора, сформулированной с помощью тригонометрических функций.
Окружность радиуса 1, изображенную на рисунке 4, называют тригонометрическим кругом или числовой окружностью.
Про тригонометрию ⋆zagalina.ru
Тригонометрический круг→
Содержание:
Поговорим о тригонометрии
Вопрос:»Что такое тригонометрия?» Сразу представляю себе ответ: «Ну…., это когда синус или косинус…» «А что такое синус и косинус?» — «Ну…, отношение катетов к гипотенузе…» «То есть — геометрия?» — «???…» Нет, конечно не геометрия! Представьте себе угол в 1000° . Представили? Нет!.. А отрицательный угол? Нет таких углов!!! На 90° заканчивается прямоугольные треугольники, которые и дали определение для синусов, косинусов, тангенсов и котангенсов. На 180° заканчивается треугольник, на 360° — планиметрия.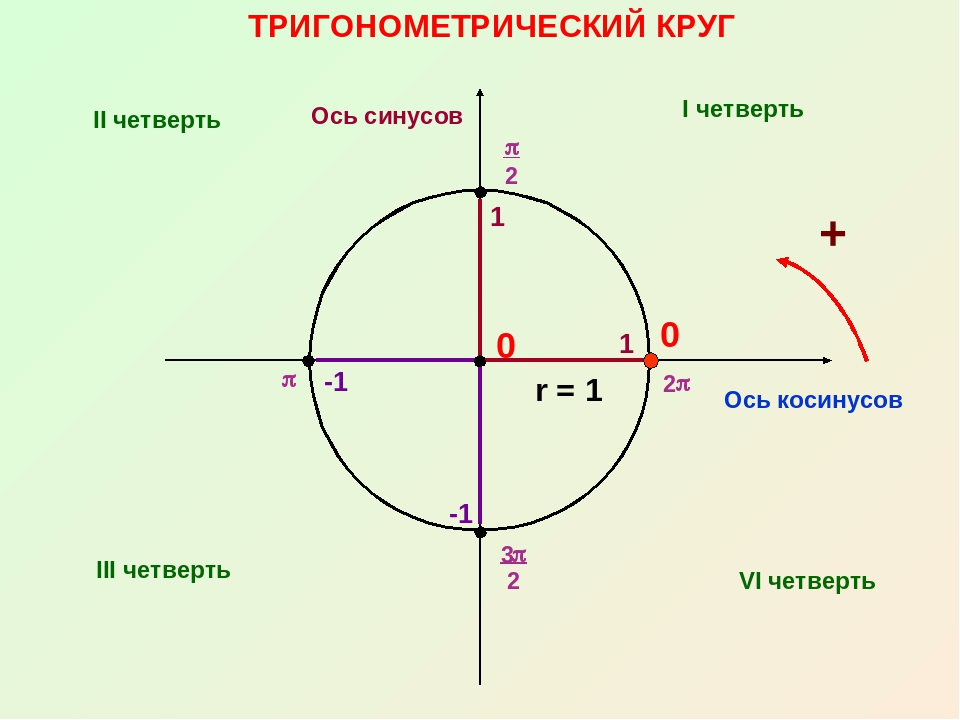 Что же тогда такое — тригонометрия? Разберемся… Начнем с двух основных понятий — синуса и косинуса. Что вы о них знаете кроме того, что это отношения катетов и гипотенузы? Вспомнили? сумма квадратов синуса и косинуса равны единице.
Что же тогда такое — тригонометрия? Разберемся… Начнем с двух основных понятий — синуса и косинуса. Что вы о них знаете кроме того, что это отношения катетов и гипотенузы? Вспомнили? сумма квадратов синуса и косинуса равны единице.
Sin²α + Cos²α = 1
А помните, как выглядит уравнение окружности с центром в начале координат, радиус которой R?
x² + y² = R²
А если радиус R = 1, то это уравнение будет выглядеть x² + y² = 1. Согласитесь, это очень похоже на основное тригонометрическое уравнение! А что особенно любят школьники, решая уравнения с неудобными выражениями? Заменять их, делать равносильную замену на какую-нибудь букву. Сделаем тоже замену двух неизвестных x² и y² на Sin²α и Cos²α, получим равносильное уравнение. Получается, что тригонометрия — это раздел математики, позволяющий решать некоторые уравнения гораздо проще, если их неизвестные удовлетворяют условиям:
Тогда неизвестную можно заменить на синус или косинус.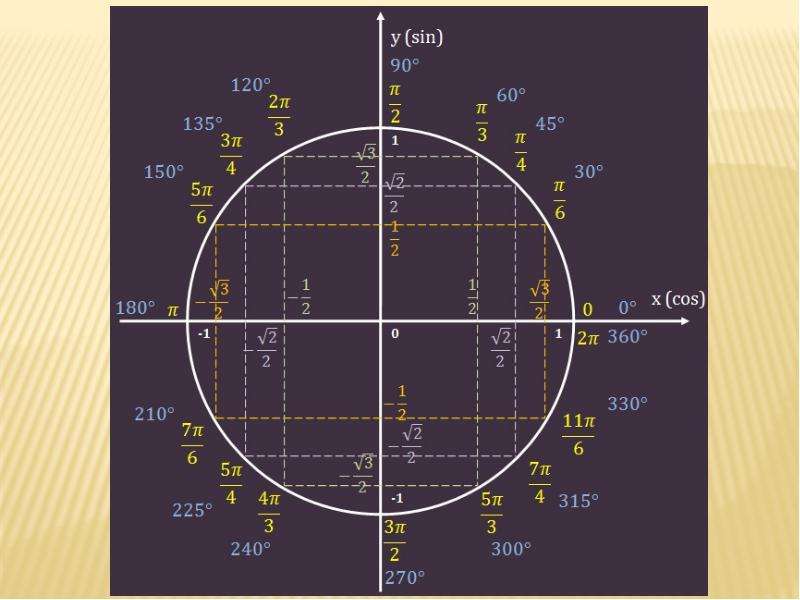
А проще потому, что в тригонометрии появляются дополнительные формулы для расчетов. Неизвестными в тригонометрии становятся уже не отдельные буквы, а тригонометрические функции: sin x, cos x, tg x, ctg x,
где , а
Вот так! Это тригонометрия!
Тригонометрические функции
Почему функции? Напомню, что же такое — функции. Функция — это отношение между двумя зависимыми друг от друга величинами, которое записывается в виде математической формулы, определяющей эту зависимость. При этом изменение одной величины ведет к изменению другой величины. Подробнее→
В случае тригонометрических функций, величина у меняется с изменением величины х, формула — это сами синус, косинус, тангенс и котангенс.
Графики этих функций приведены ниже:
| функция y(x) = sin x | |
| функция y(x) = cos x | |
| функция y(x) = tg x | |
| функция y(x) = ctg x |
Получается, что синус, косинус, тангенс и котангенс — это математические выражения, связывающие два неизвестных.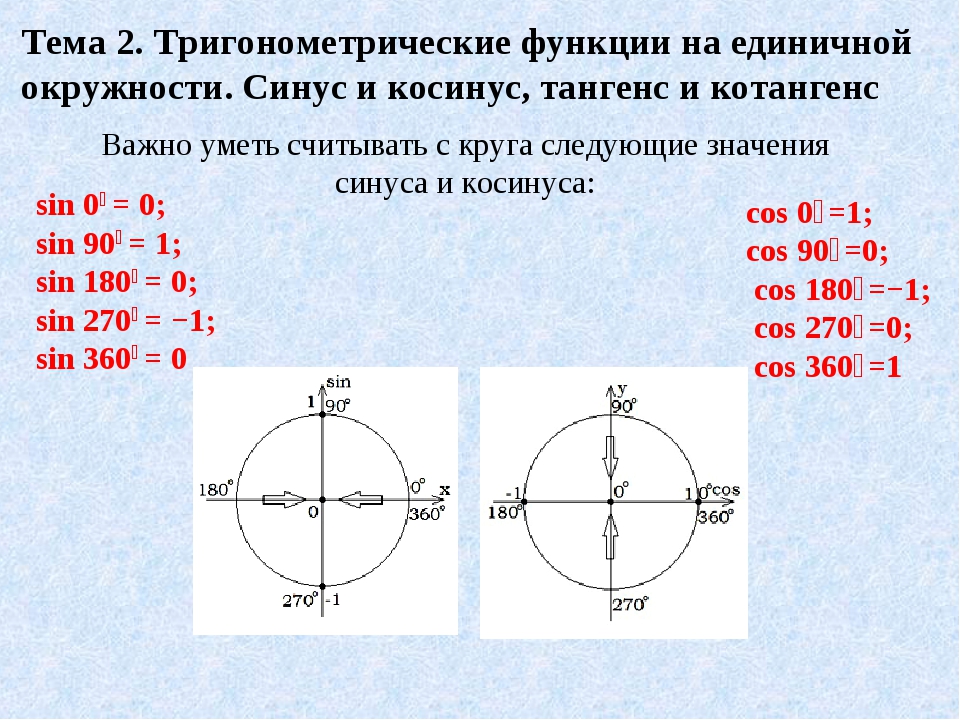 А значит, мы можем их, эти неизвестные, находить. А поможет нам в этом великолепная классическая «шпаргалка» — тригонометрический круг.
А значит, мы можем их, эти неизвестные, находить. А поможет нам в этом великолепная классическая «шпаргалка» — тригонометрический круг.
Но прежде, чем мы перейдем к тригонометрическому кругу, определимся со значениями аргумента тригонометрической функции х, который может меняться от минус бесконечности до плюс бесконечности.
x ∈ ( — ∞; + ∞).
В этом случае целесообразно отвлечься от градусной меры углов и вспомнить, что углы измеряются также радианами – просто числами, определяемыми через всем известное число π, соответствующее 180°-ному углу, и π = 3,141582….. И тогда x — это уже не углы, а числа .
Строим тригонометрический круг
Чертим на плоскости декартову систему координат, а в ней графически изображаем уравнение :
х² + у² = 1,
то есть, чертим круг радиусом, равным 1.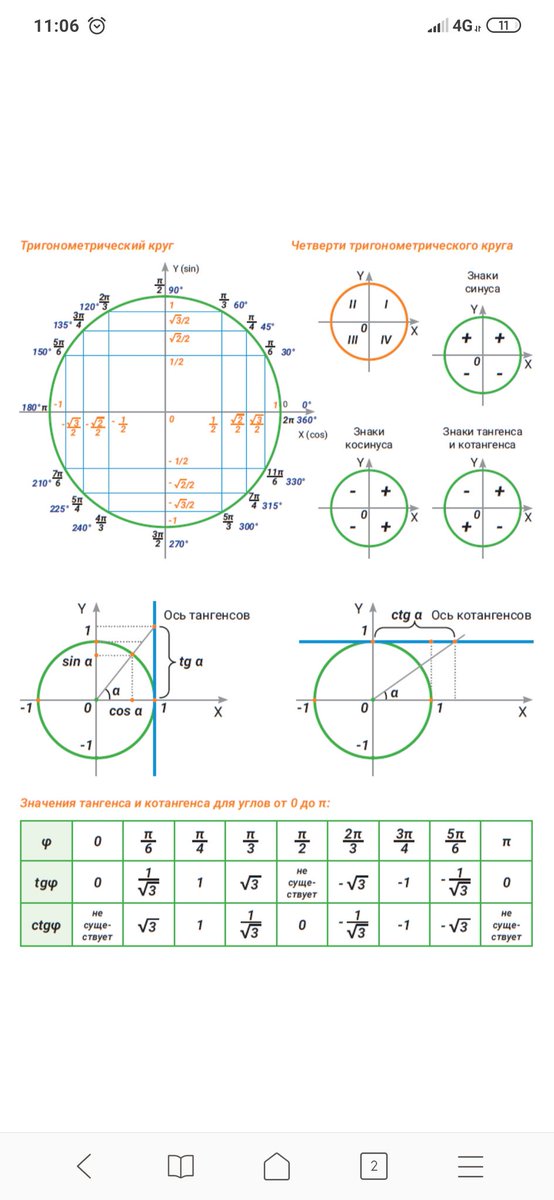
Рассмотрим точку М(хо, уо), принадлежащую первой четверти окружности, и треугольник, где хо, уо координаты точки, а 0М – радиус окружности, равный 1. Получается, что отношение уо к радиусу есть ничто иное, как синус угла α, а отношение хо к радиусу – косинус угла α. А это значит, что координаты любой точки на окружности радиусом, равным 1 – это синус и косинус угла, образованного осью 0х и радиус-вектором точки М, то есть отрезком ОМ.
Тогда наш круг можно представить следующим образом:→
Выходит, что по оси Оу получаем значения синусов аргумента, назовем ее «ось синусов», а по оси Ох — значения косинусов, получаем как бы «ось косинусов».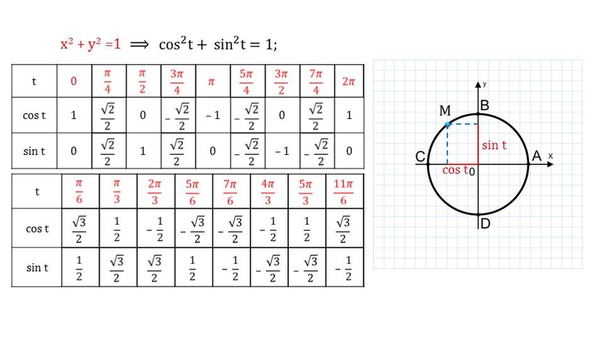 При этом, разумеется, значения синусов и косинусов не выходят за пределы круга. Просто, потому что не могут в силу своей ограниченности! Ну, а мы с вами имеем возможность определятся с синусами и косинусами уже не углов, а аргумента х ∈ ( — ∞; + ∞). Почему? А потому что тригонометрические функции — периодические, т.е. просто «вертятся» по кругу. При этом значения синусов и косинусов определяются значениями координат точек на окружности со всеми их знаками. Например, согласно рисунку, координата у точки на окружности, соответствующей углу , определяет , а координата х определяет .
При этом, разумеется, значения синусов и косинусов не выходят за пределы круга. Просто, потому что не могут в силу своей ограниченности! Ну, а мы с вами имеем возможность определятся с синусами и косинусами уже не углов, а аргумента х ∈ ( — ∞; + ∞). Почему? А потому что тригонометрические функции — периодические, т.е. просто «вертятся» по кругу. При этом значения синусов и косинусов определяются значениями координат точек на окружности со всеми их знаками. Например, согласно рисунку, координата у точки на окружности, соответствующей углу , определяет , а координата х определяет .
С синусами и косинусами разобрались. А как же тангенсы и котангенсы? С ними тоже не возникнет проблем. Тангенс определяется:
Вот и проводим «ось тангенсов» там, где cos α равен 1. Аналогично поступаем и с «осью котангенсов» В отличие от синусов и косинусов тангенсам и котангенсам прямую проводим через начало координат. То есть на круге два угла для тангенса и два угла для котангенса. Оно и понятно: период функций тангенса и котангенса составляет π, а не 2π, как у функций синуса и косинуса.
Аналогично поступаем и с «осью котангенсов» В отличие от синусов и косинусов тангенсам и котангенсам прямую проводим через начало координат. То есть на круге два угла для тангенса и два угла для котангенса. Оно и понятно: период функций тангенса и котангенса составляет π, а не 2π, как у функций синуса и косинуса.
вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Он заменяет десяток таблиц.
Сколько полезного на этом рисунке!
Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2π радиан.
Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси Х, а значение синуса — на оси Y.

И синус, и косинус принимают значения от −1 до 1.
Значение тангенса угла α тоже легко найти — поделив sin α на cos α. А чтобы найти котангенс — наоборот, косинус делим на синус.
Знаки синуса, косинуса, тангенса и котангенса.
Синус — функция нечётная, косинус — чётная.
Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен 2π.
Если вам что-то непонятно — читайте подробнее:
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна 180°.
Возьмем
треугольник и продолжим одну из его
сторон. Внешний угол при вершине А —
это угол, смежный с углом А. Если
угол А острый, то смежный с ним
угол — тупой, и наоборот.
Внешний угол при вершине А —
это угол, смежный с углом А. Если
угол А острый, то смежный с ним
угол — тупой, и наоборот.
Обратите внимание, что:
sin (180°-α) = sin α cos (180°-α) = — cos α tg (180°-α) = — tg α
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
1. В треугольнике ABC угол C равен 90°, . Найдите тангенс внешнего угла при вершине A.
Пусть — внешний угол при вершине А.
Зная cos , найдем tg по формуле
Получим:
2. В треугольнике ABC угол C равен 90°, cos A = 0,1. Найдите синус внешнего угла при вершине B.
Задача
решается за четыре секунды. Поскольку
сумма углов А и В равна 90°, sin B
= cos A = 0,1. Тогда и синус внешнего угла
при вершине В также равен 0,1.
Тогда и синус внешнего угла
при вершине В также равен 0,1.
Высота в прямоугольном треугольнике
Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.
Один из типов экзаменационных задач В6 в банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:
Высота проведена к гипотенузе АВ. Она делит треугольник АВС на два прямоугольных треугольника — АСН и СНВ. Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.
Мы помним,
что сумма двух острых углов прямоугольного
треугольника равна 90º. Значит, ∠
АСН = 90º — ∠
САН, то есть угол АСН равен углу АВС.
Аналогично, угол САВ равен углу НСВ.
Иными словами, каждый из трех углов треугольника АВС равен одному из углов треугольника АСН (и треугольника ВСН). Треугольники АВС, АСН и ВСН называются подобными. Давайте нарисуем их рядом друг с другом.
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?
Возьмем треугольники АСН и АВС. Стороны треугольника АВС длиннее, чем стороны треугольника АСН в k раз:
При решении задач нам пригодится равенство углов треугольников АВС, АСН и ВСН, а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника АВС можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.
1. В треугольнике ABC угол C равен 90°, CH — высота, ВС = 3, . Найдите AH.
Рассмотрим
треугольник АВС. В нем известны
косинус угла А и противолежащий
катет ВС. Зная синус угла А, мы могли бы
найти гипотенузу АВ. Так давайте найдем
sin A:
Так давайте найдем
sin A:
(поскольку значение синуса острого угла положительно). Тогда:
Рассмотрим прямоугольный треугольник ВСН, ∠ Н = 90°. Поскольку ∠ НСВ = ∠ А,
Отсюда
Ответ: 16.
2. В треугольнике ABC угол C равен 90º, АC = 8, sin A = 0,5. Найдите высоту CH.
Сделайте чертеж и рассмотрите прямоугольный треугольник АСН.
Ответ: 4.
3. В треугольнике ABC угол C равен 90º, АВ = 13, . К гипотенузе проведена высота CH. Найдите AH. <.
Это чуть более сложная задача. Ведь вам неизвестны катеты a и b.
Зато можно записать теорему Пифагора: a² + b² = 13².
Нам известно также, что:
Решая эту систему из двух уравнений, найдем:
;
Запишем площадь треугольника АВС двумя способами:
и найдем СН = 2,5.
Сумма углов треугольника
Сумма треугольника равна 180 градусов.
Это
легко доказать. Нарисуйте треугольник.
Через одну из его вершин проведите
прямую, параллельную противоположной
стороне, и найдите на рисунке
равные углы. Сравните с решением
в конце статьи.
Нарисуйте треугольник.
Через одну из его вершин проведите
прямую, параллельную противоположной
стороне, и найдите на рисунке
равные углы. Сравните с решением
в конце статьи.
А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85º. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85°, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение 2х + 3х = 85 и найдем х = 17. Тогда 3х = 51.
Ответ: 51.
2. Один из углов равнобедренного треугольника равен 98º. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98°?
Нет,
конечно! Ведь сумма углов треугольника
равна 180°. Значит, один из углов
треугольника равен 98°, а два других
равны .
Значит, один из углов
треугольника равен 98°, а два других
равны .
Ответ: 41.
3. На рисунке угол 1 равен 46º, угол 2 равен 30º, угол 3 равен 44º. Найдите угол 4. Ответ дайте в градусах.
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Сначала найдем угол 5. Он равен 180° — ∠1 — ∠3 = 90° Тогда ∠6 = 90° ∠7 = 180° — ∠2 — ∠6 = 60°, Угол 4, смежный с углом 7 равен 120°.
Ответ: 120.
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
4. Углы треугольника относятся как 2:3:4. Найдите меньший из них. Ответ дайте в градусах.
Пусть углы треугольника равны 2х, 3х и 4х. Запишем, чему равна сумма углов этого треугольника. 2х + 3х + 4х = 180° 9х = 180° х = 20° Тогда 2х = 40°.
Ответ: 40.
Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Пусть
прямая с пересекает параллельные
прямые а и b.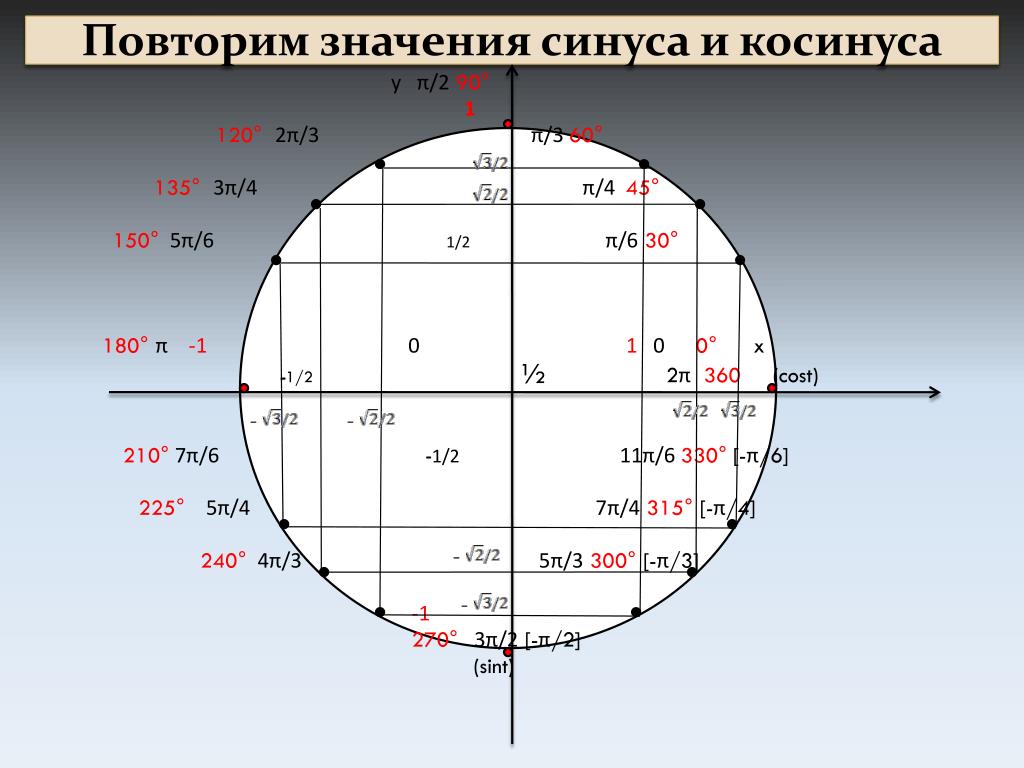 При этом образуется
восемь углов. Углы при параллельных
прямых и секущей так часто используются
в задачах, что в геометрии им даны
специальные названия.
При этом образуется
восемь углов. Углы при параллельных
прямых и секущей так часто используются
в задачах, что в геометрии им даны
специальные названия.
Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть ∠1 = ∠3, ∠2 = ∠4.
Конечно, углы 5 и 7, 6 и 8 — тоже вертикальные.
Углы 1 и 2 — смежные, это мы уже знаем. Сумма смежных углов равна 180º.
Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) — накрест лежащие. Накрест лежащие углы равны. ∠3 = ∠5, ∠1 = ∠7, ∠2 = ∠8, ∠4 = ∠6.
Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние. Сумма односторонних углов равна 180°, то есть ∠1 + ∠6 = 180°, ∠4 + ∠7 = 180°.
Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и 8) называются соответственными.
Соответственные углы равны, то есть ∠2 = ∠6, ∠3 = ∠7.
Углы
3 и 5 (а также 2 и 8, 1 и 7,
4 и 6) называют накрест
лежащими.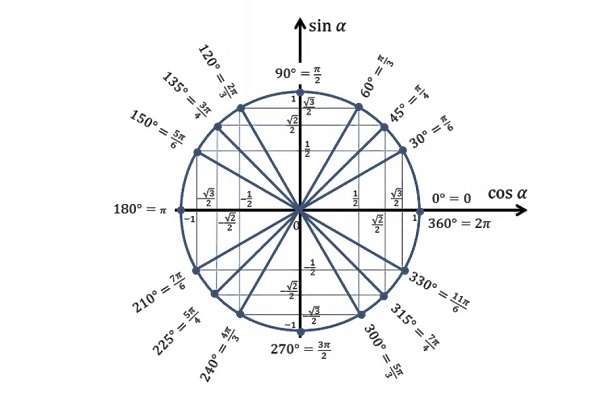
Накрест лежащие углы равны, то есть ∠3 = ∠5, ∠1 = ∠7, ∠2 = ∠8, ∠4 = ∠6.
Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.
1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.
Пусть ВМ — биссектриса тупого угла В. По условию, отрезки МD и АВ равны 3х и 4х соответственно.
Рассмотрим
углы СВМ и ВМА. Поскольку АD и ВС
параллельны, ВМ — секущая, углы СВМ
и ВМА являются накрест лежащими.
Мы знаем, что накрест лежащие углы
равны.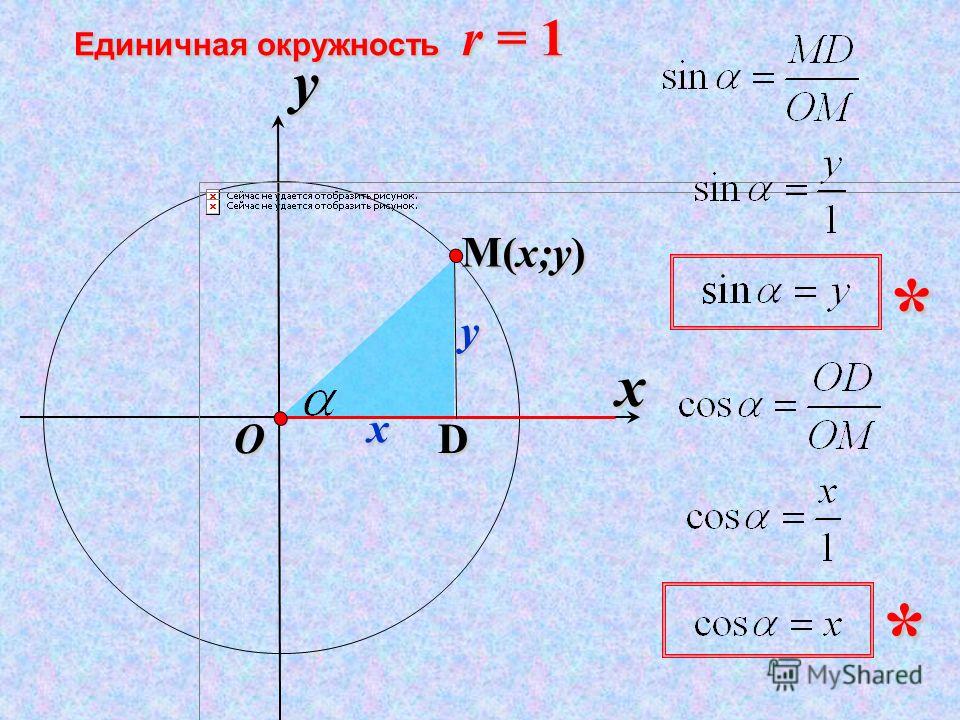 Значит, треугольник АВМ —
равнобедренный, следовательно, АВ = АМ
= 4х.
Значит, треугольник АВМ —
равнобедренный, следовательно, АВ = АМ
= 4х.
Периметр параллелограмма — это сумма всех его сторон, то есть 7х + 7х + 4х + 4х = 88. Отсюда х = 4, 7х = 28.
Ответ: 28.
2. Диагональ параллелограмма образует с двумя его сторонами углы 26º и 34º. Найдите больший угол параллелограмма. Ответ дайте в градусах.
Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: 120º.
3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50º? Ответ дайте в градусах.
Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.
Давайте посмотрим на чертеж. По условию, α — β = 50°, то есть α = β + 50°.
Углы
α и β — односторонние при
параллельных прямых и секущей,
следовательно, α + β = 180°.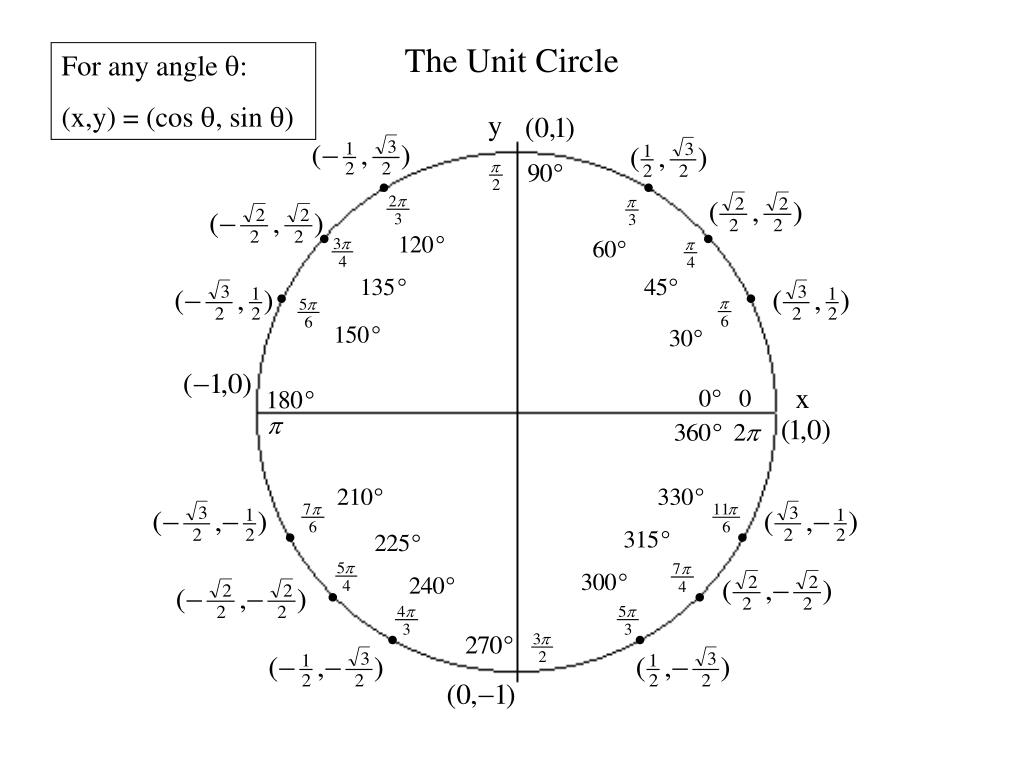
Итак, 2β + 50° = 180° β = 65°, тогда α = 115°.
Ответ: 115.
Элементы треугольника. Высоты, медианы, биссектрисы
Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии. Мы начнем с таблицы, в которой показано, что такое высоты, медианы и биссектрисы, и какими свойствами они обладают. Затем — подробные объяснения и решение задач.
Напомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
Три высоты треугольника всегда пересекаются в одной точке. Вот как это выглядит в случае остроугольного треугольника.
Попробуйте провести три высоты в тупоугольном треугольнике. Получилось? Да, редкий выпускник справляется с этим заданием. Действительно, мы не можем опустить перпендикуляр из точки А на отрезок ВС, зато можем опустить его на прямую ВС — то есть на продолжение стороны ВС.
В этом
случае в одной точке пересекаются
не сами высоты, а их продолжения.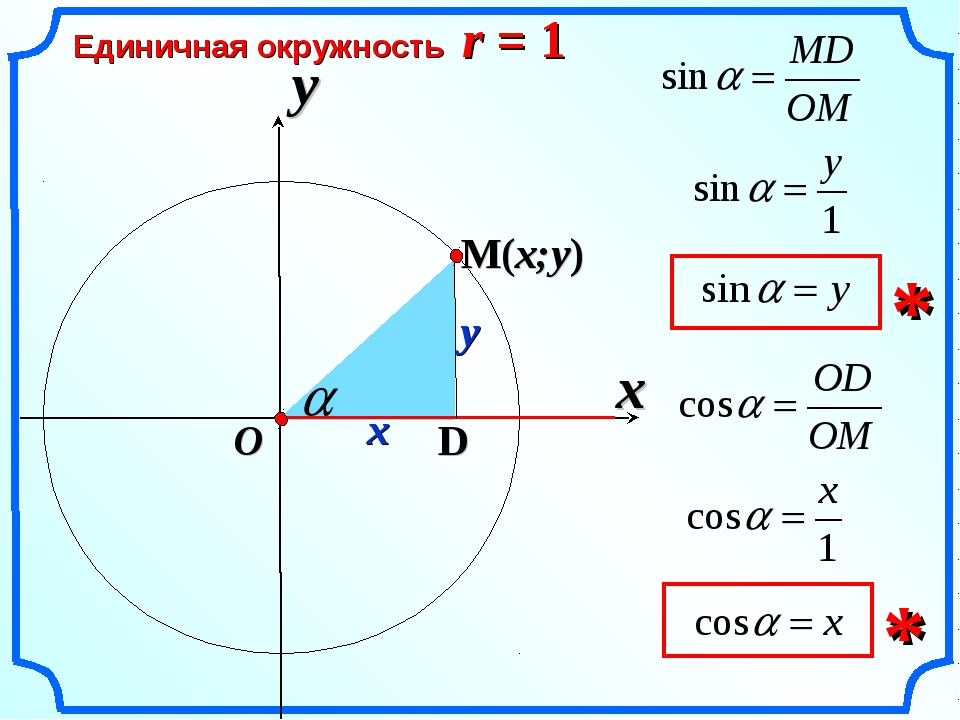
А как выглядят три высоты в прямоугольном треугольнике? В какой точке они пересекаются?
Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.
Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.
У биссектрисы угла есть замечательное свойство — точки, принадлежащие ей, равноудалены от сторон угла. Поэтому три биссектрисы треугольника пересекаются в одной точке, равноудаленной от всех сторон треугольника. Эта точка является центром окружности, вписанной в треугольник.
Еще одно свойство биссектрисы пригодится тем, кто собирается решать задачу С4. Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
Разберем
несколько задач, в которых речь идет
о высотах, медианах и биссектрисах
треугольника.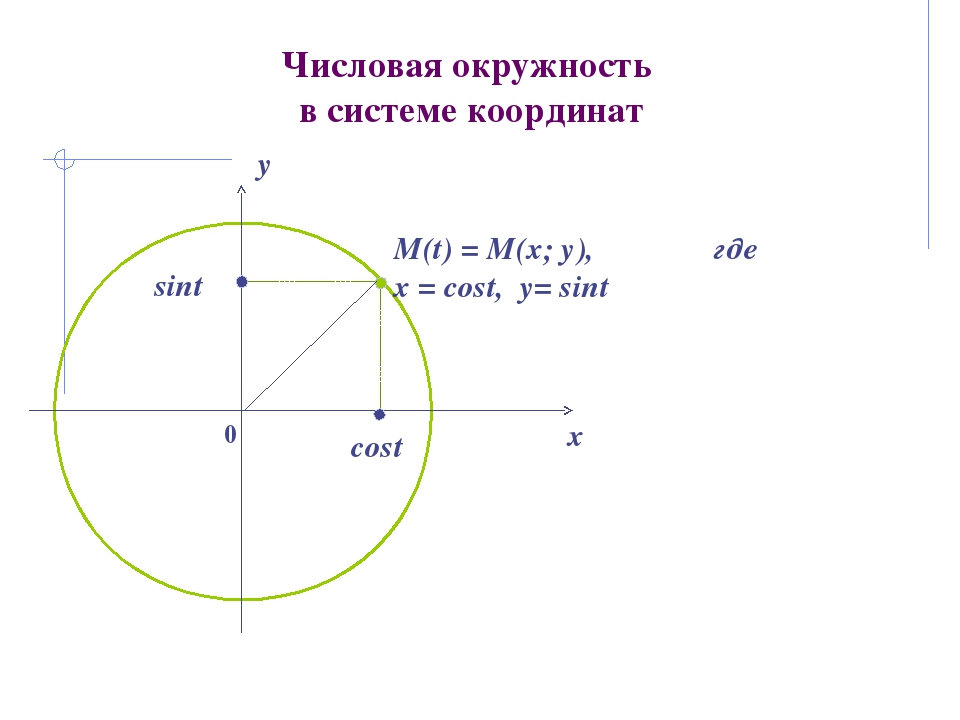 Все задачи взяты из Банка
заданий ФИПИ.
Все задачи взяты из Банка
заданий ФИПИ.
1. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Пусть биссектрисы треугольника АВС ( в котором угол С равен 90°) пересекаются в точке М.
Рассмотрим треугольник АВМ.
∠ МАВ = ∠ ВАС,
∠ АВМ = ∠ АВС, тогда ∠ АМВ = 180° — ∠ МАВ — ∠ АВМ = 180° — (∠ АВС + ∠ ВАС).
Острый угол между биссектрисами на рисунке обозначен φ.
Угол φ смежный с углом АМВ, следовательно, φ = (∠ АВС + ∠ ВАС).
Поскольку треугольник АВС — прямоугольный, то ∠ АВС + ∠ ВАС = 90°.
Тогда φ = (∠ АВС + ∠ ВАС) = 90° : 2 = 45°.
Ответ: 45.
2. Острые углы прямоугольного треугольника равны 29º и 61º. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Пусть СН — высота, проведенная из вершины прямого угла С, СК — биссектриса угла С.
Тогда
∠
АСН = ∠
АВС = 61°, ∠
АСК = 90° : 2 = 45°.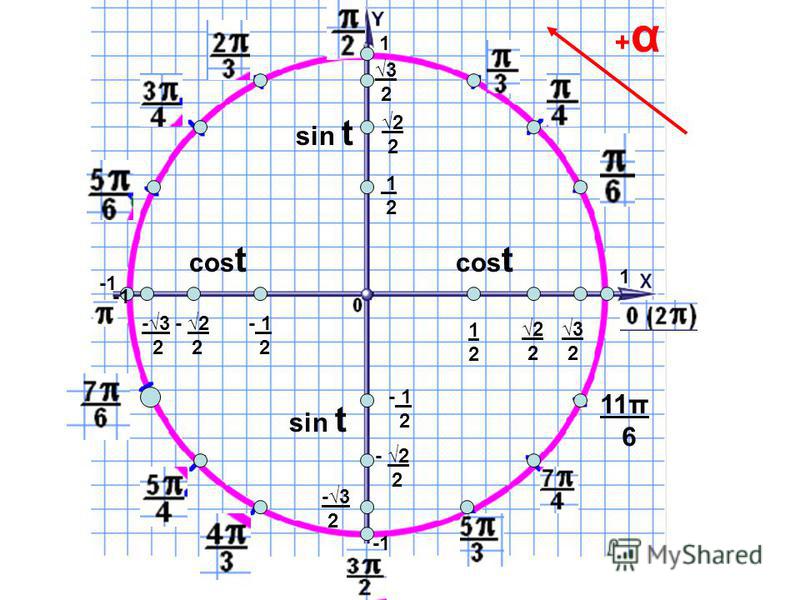
Угол между высотой и биссектрисой — это угол КСН.
∠ КСН = ∠ АСН — ∠ АСК = 61° — 45° = 16°
Ответ: 16.
3. Два угла треугольника равны 58º и 72º. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Из треугольника АВН (угол Н — прямой) найдем угол ВАН. Он равен 18°.
Из треугольника АВК (угол К — прямой) найдем угол АВК. Он равен 32°.
В треугольнике АОВ известны два угла. Найдем третий, то есть угол АОВ, который и является тупым углом между высотами треугольника АВС:
∠ АОВ = 180° — 18° — 32° = 130°.
Ответ: 130.
4. В треугольнике ABC угол C равен 58º, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
Пусть в треугольнике АВС угол ВАС равен А, угол АВС равен В.
Рассмотрим треугольник АОВ.
∠ ОАВ = ∠ А
∠ АВО
= ∠
В, тогда ∠
АОВ = 180° — (∠
А + ∠
В).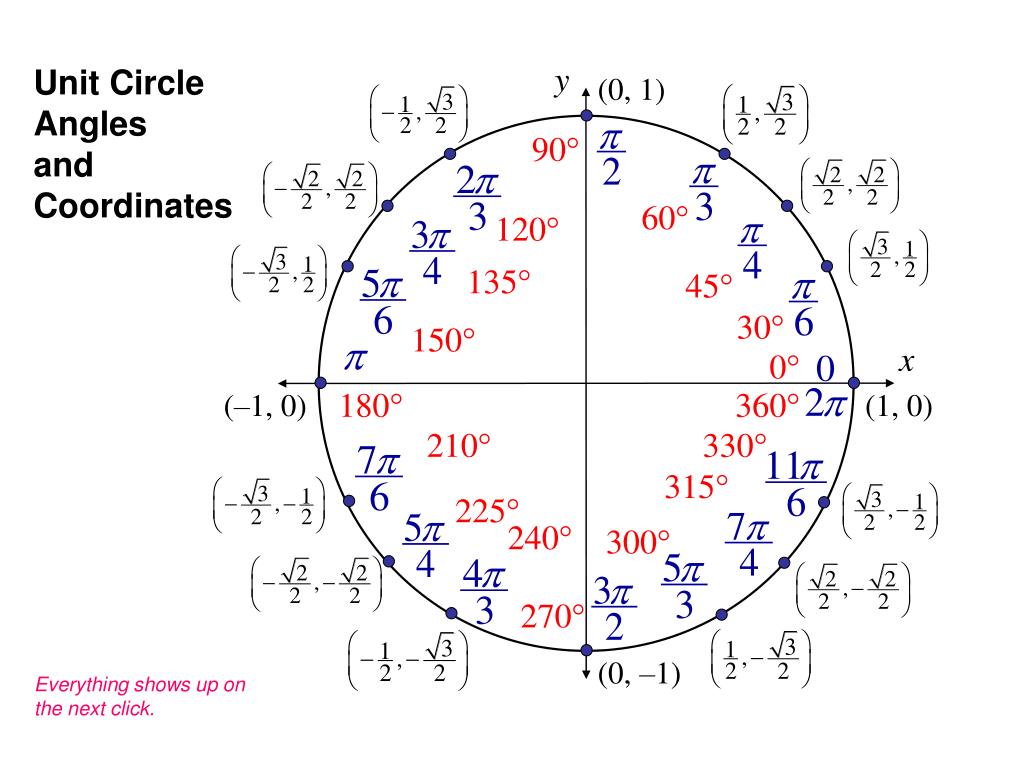 Из треугольника АВС получим,
что ∠
А + ∠
В = 180° — 58° = 122°.
Из треугольника АВС получим,
что ∠
А + ∠
В = 180° — 58° = 122°.
Тогда ∠ АОВ = 180° — (∠ А + ∠ В) = 180° — 61° = 119°.
Ответ: 119°.
5. В треугольнике ABC угол A равен 60º, угол B равен 82º. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Найдем угол АСВ. Он равен 38°.
Тогда ∠ АСF = ∠ ACB = 19°.
Из треугольника АСF найдем угол AFC. Он равен 101°.
Рассмотрим треугольник АОF.
∠ AFО = 101°, ∠ FAO = ∠ ВАС = 30°. Значит, ∠ AOF = 49°.
Ответ: 49.
6. В треугольнике АВС СD — медиана, угол ACB равен 90º, угол B равен 58º. Найдите угол ACD. Ответ дайте в градусах.
Как решать эту задачу? У медианы прямоугольного треугольника, проведенной из вершины прямого угла, есть особое свойство. Мы докажем его в теме «Прямоугольник и его свойства».
Подсказка:
Сделайте чертеж, найдите на нем
равнобедренные треугольники и докажите,
что они равнобедренные.
Правильный ответ: 22.
Четырехугольники. Сумма углов четырехугольника. Параллелограмм. Виды параллелограммов и их свойства. Ромб, прямоугольник, квадрат. Трапеция и ее свойства
В школьных задачах по геометрии мы обычно рассматриваем выпуклые четырехугольники.
В чем разница между ними? Если любые две точки выпуклого многоугольника соединить отрезком — весь отрезок будет лежать внутри многоугольника. Для невыпуклых фигур это не выполняется.
Сумма углов выпуклого четырехугольника равна 360 градусов.
Произвольные четырехугольники в задачах по геометрии встречаются редко. Намного чаще — такие, у которых есть параллельные стороны. Это параллелограмм, ромб, квадрат, прямоугольник и трапеция. Здесь в таблице собраны их определения и свойства.
| | Адрес этой страницы (вложенность) в справочнике dpva.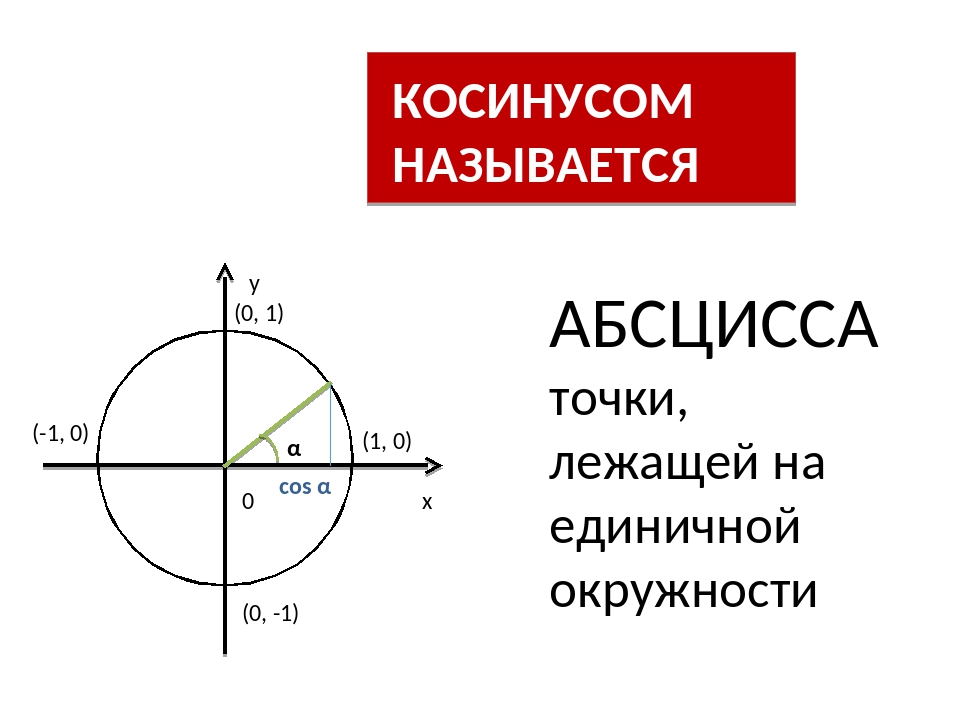 ru: главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Синус и косинус — тригонометрические функции y=sin(x), y=cos(x). Свойства, область определения, значения, четность, периоды, нули, промежутки знакопостоянства, возрастание, убывание, минимумы, максимумы, основные значения, знаки, формулы приведения ru: главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Синус и косинус — тригонометрические функции y=sin(x), y=cos(x). Свойства, область определения, значения, четность, периоды, нули, промежутки знакопостоянства, возрастание, убывание, минимумы, максимумы, основные значения, знаки, формулы приведенияПоделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 совета эксперта по использованию единичной окружности
Если вы изучаете тригонометрическую систему или математику — или готовитесь к этому — вам нужно будет познакомиться с единичным кругом. Единичная окружность — это , важный инструмент, используемый для нахождения синуса, косинуса и тангенса угла. а как это работает? И какую информацию нужно знать, чтобы ею пользоваться?
В этой статье мы объясним, что такое единичный круг и почему вы должны его знать. Мы также даем вам три совета, которые помогут вам запомнить, как использовать единичный круг.
Изображение функции: Gustavb / Wikimedia
Единичный круг: базовое введение
Единичный круг — это круг с радиусом 1. Это означает, что для любой прямой линии, проведенной от центральной точки круга к любой точке на краю круга, длина этой линии всегда будет равна 1.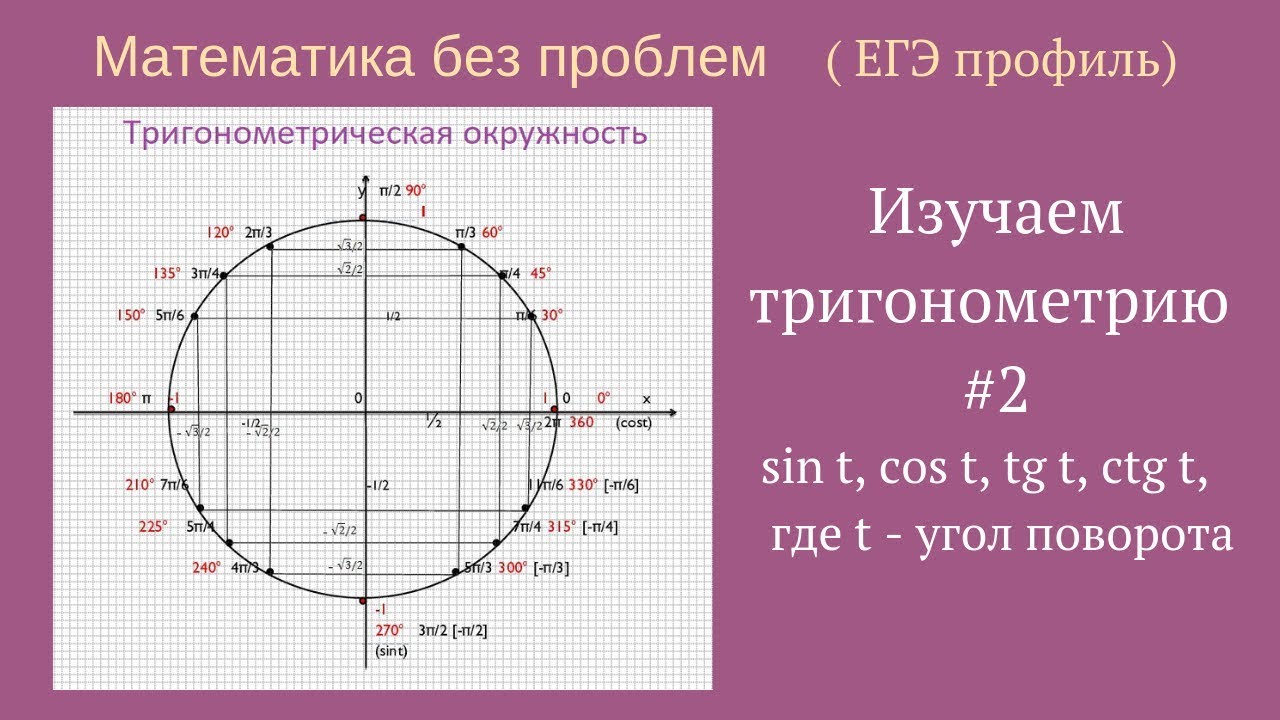 (Это также означает, что диаметр круга будет равен 2, поскольку диаметр равен удвоенной длине радиуса.)
(Это также означает, что диаметр круга будет равен 2, поскольку диаметр равен удвоенной длине радиуса.)
Как правило, центральная точка единичной окружности находится там, где пересекаются оси x и y, или в координатах (0, 0):
Единичная окружность, или триггерная окружность, как ее еще называют, полезно знать, потому что позволяет нам легко вычислить косинус, синус и тангенс любого угла между 0 ° и 360 ° (или 0 и 2π радиан).
Как вы можете видеть на приведенной выше диаграмме, нарисовав радиус под любым углом (отмечен на изображении by), вы создадите прямоугольный треугольник. На этом треугольнике косинус — это горизонтальная линия, а синус — это вертикальная линия. Другими словами, косинус = x-координата, а синус = y-координата. (Самая длинная линия треугольника, или гипотенуза, является радиусом и поэтому равна 1.)
Почему все это так важно? Помните, что вы можете найти длины сторон треугольника, используя теорему Пифагора , или $ a ^ 2 + b ^ 2 = c ^ 2 $ (где a и b — длины сторон треугольника, а c — длина гипотенузы). 2θ = 1 $$
2θ = 1 $$
Имейте в виду, что эти значения могут быть отрицательными в зависимости от образованного угла и в какой квадрант попадают координаты x и y (более подробно я объясню это позже).
Вот обзор всех основных углов в градусах и радианах на единичной окружности:
Единичный круг — градусы
Единичный круг — радианы
А что, если треугольник не образовался? Давайте посмотрим на , что происходит, когда угол равен 0 °, образуя горизонтальную прямую линию вдоль оси x:
В этой строке координата x равна 1, а координата y равна 0.Мы знаем, что косинус равен координате x, а синус равен координате y, , поэтому мы можем записать это:
Что если угол равен 90 ° и образует идеально вертикальную линию вдоль оси y?
Здесь мы видим, что координата x равна 0, а координата y равна 1. Это дает нам следующие значения для синуса и косинуса:
Это дает нам следующие значения для синуса и косинуса:
- $ \ cos90 ° = 0 $
- $ \ sin90 ° = 1 $
Этот слоган определенно подходит, если вы не любитель математики.
Почему вы должны знать единичную окружность
Как сказано выше, единичная окружность полезна, потому что позволяет нам легко найти синус, косинус или тангенс любого градуса или радиана. Особенно полезно знать круговую диаграмму единиц, если вам нужно решить определенные триггерные значения для домашнего задания по математике или если вы готовитесь к изучению математического анализа.
Но как именно знание единичного круга может вам помочь? Допустим, вам задали следующую задачу на тесте по математике, и нельзя использовать для ее решения с помощью калькулятора :
$$ \ sin30 ° $$
С чего начать? Давайте снова посмотрим на диаграмму единичного круга — на этот раз со всеми большими углами (как в градусах, так и в радианах) и их соответствующими координатами:
Джим.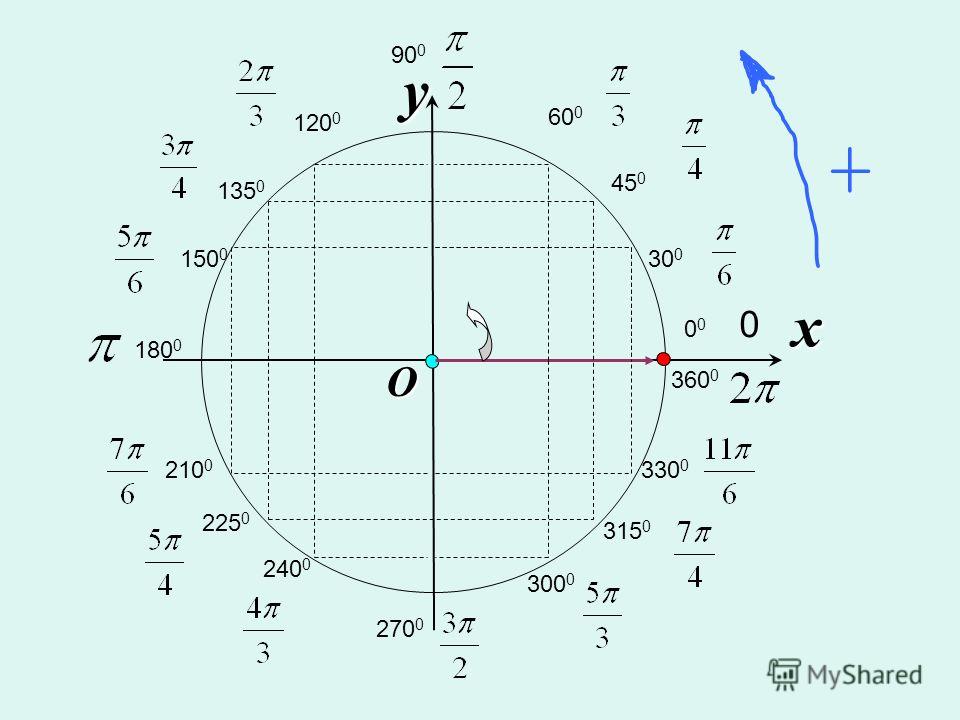 belk / Викимедиа
belk / Викимедиа
Не расстраивайтесь! Помните, все, что вам нужно, это $ \ sin30 ° $. Посмотрев на этот график, мы видим, что , координата y равна $ 1/2 $ при 30 °. А поскольку координата y равна синусу, наш ответ будет следующим:
$$ \ sin30 ° = 1/2 $$
Но что, если вы столкнетесь с проблемой, в которой вместо градусов используются радианы? Процесс ее решения остается прежним. Скажем, например, у вас возникла проблема, которая выглядит так:
$$ \ cos {{3π} / 4} $$
Опять же, используя диаграмму выше, мы можем видеть, что координата x (или косинус) для $ {3π} / 4 $ (который равен 135 °) составляет $ — {√2} / 2 $.Вот как бы тогда выглядел наш ответ на эту проблему:
$$ \ cos ({3π} / 4) = — {√2} / 2 $$
Все это довольно просто, если у вас есть приведенная выше круговая диаграмма единиц для использования в качестве справочной информации. Но в большинстве случаев (если не всегда) это не так, и вы должны будете отвечать на такие математические вопросы, используя только свой мозг.
Так как же можно запомнить единичный круг? Читайте наши главные советы!
Как запомнить единичный круг: 3 основных совета
В этом разделе мы даем вам несколько основных советов по запоминанию триггерного круга, чтобы вы могли легко использовать его для решения любой математической задачи, которая в нем требует.
Я бы не рекомендовал практиковать единичный круг с клейкими лентами, но, эй, это только начало.
# 1: Запомните общие углы и координаты
Чтобы эффективно использовать единичный круг, вам нужно запомнить наиболее распространенные углы (как в градусах, так и в радианах), а также их соответствующие координаты x и y.
Диаграмма выше представляет собой полезную диаграмму единичного круга, на которую стоит обратить внимание, поскольку она включает все основные углы в градусах и радианах в дополнение к их соответствующим координатным точкам по осям x и y.
Вот диаграмма, содержащая ту же информацию в виде таблицы:
Угол (градусы) | Угол (радианы) | Координаты точки на окружности |
0 ° / 360 ° | 0 / 2π | (1, 0) |
30 ° | $ π / 6 $ | долл. |
45 ° | $ π / 4 $ | долл. США ({√2} / 2, {√2} / 2) долл. США |
60 ° | $ π / 3 $ | долл. США (1/2, {√3} / 2) долл. США |
90 ° | $ π / 2 $ | (0, 1) |
120 ° | $ {2π} / 3 $ | долл. США (- 1/2, {√3} / 2) долл. США |
135 ° | $ {3π} / 4 $ | долл. США (- {√2} / 2, {√2} / 2) долл. США |
150 ° | $ {5π} / 6 $ | $ (- {√3} / 2, 1/2) $ |
180 ° | π | (-1, 0) |
210 ° | $ {7} / 6 $ | $ (- {√3} / 2, -1/2) $ |
225 ° | $ {5π} / 4 $ | $ (- {√2} / 2, — {√2} / 2) $ |
240 ° | $ {4π} / 3 $ | $ (- 1/2, — {√3} / 2) $ |
270 ° | $ {3π} / 2 $ | (0, -1) |
300 ° | $ {5π} / 3 $ | долл. |
315 ° | $ {7π} / 4 $ | $ ({√2} / 2, — {√2} / 2) $ |
330 ° | $ {11π} / 6 $ | долл. США ({√3} / 2, -1/2) долл. США |
Теперь, хотя вы можете попытаться запомнить все эти координаты и углы, это много, вещей, которые нужно запомнить.
К счастью, есть прием, который поможет вам запомнить самые важные части единичного круга.
Посмотрите на координаты выше, и вы заметите четкую закономерность: все точки (за исключением точек под 0 °, 90 °, 270 ° и 360 °) чередуются только между тремя значениями (положительными или отрицательными):
- $ 1/2
- $ {√2} / 2 $
- $ {√3} / 2 $
Каждому значению соответствует короткая, средняя или длинная линия для косинуса и синуса:
Вот что означают эти длины:
- Короткая горизонтальная или вертикальная линия = 1/2 доллара США
- Средняя горизонтальная или вертикальная линия = $ {√2} / 2 $
- Длинная горизонтальная или вертикальная линия = $ {√3} / 2 $
Например, если вы пытаетесь решить $ \ cos {π / 3} $, вы должны сразу знать, что этот угол (равный 60 °) указывает на короткую горизонтальную линию на единичной окружности. Следовательно, его соответствующая координата x должна равняться $ 1/2 $ (положительное значение, поскольку $ π / 3 $ создает точку в первом квадранте системы координат).
Наконец, хотя полезно запомнить все углы в таблице выше, обратите внимание, что , безусловно, самые важные углы, которые следует запомнить, следующие:
- 30 ° / $ π / 6 $
- 45 ° / $ π / 4 $
- 60 ° / $ π / 3 $
Обращайтесь со своими негативами и позитивами, как с кабелями, которые потенциально могут убить вас при неправильном подключении.
№ 2: Узнайте, что есть отрицательного и что положительного
Очень важно уметь различать положительные и отрицательные координаты x и y, чтобы вы могли найти правильное значение для триггерной проблемы. Напоминаем, что w , будет ли координата на единичной окружности положительной или отрицательной, зависит от , в какой квадрант (I, II, III или IV) попадает точка:
Вот диаграмма, показывающая, будет ли координата положительной или отрицательной в зависимости от квадранта, в котором находится конкретный угол (в градусах или радианах):
Квадрант | Координата X (косинус) | Координата Y (синус) |
Я | + | + |
II | – | + |
III | – | – |
IV | + | – |
Допустим, вам задали следующую задачу на тесте по математике:
$$ \ cos210 ° $$
Прежде чем вы даже попытаетесь ее решить, вы должны быть в состоянии распознать, что ответом будет отрицательное число , поскольку угол 210 ° попадает в квадрант III (где x-координаты всегда отрицательны).
Теперь, используя уловку, которую мы изучили в совете 1, вы можете выяснить, что угол 210 ° создает длинной горизонтальной линии. Следовательно, наш ответ таков:
$$ \ cos210 ° = — {√3} / 2 $$
# 3: Умейте находить касательную
Наконец, важно знать, как использовать всю эту информацию о триггерной окружности, синусе и косинусе, чтобы иметь возможность найти тангенс угла.
В триггере, чтобы найти тангенс угла θ (в градусах или радианах), вы просто делите синус на косинус:
$$ \ tanθ = {\ sinθ} / {\ cosθ} $$
Например, вы пытаетесь решить эту проблему:
$$ \ tan300 ° $$
Первый шаг — составить уравнение в терминах синуса и косинуса:
$$ \ tan300 ° = {\ sin300 °} / {\ cos300 °} $$
Теперь, чтобы найти касательную, нам нужно найти синус и косинус 300 °.Вы должны быстро распознать, что угол 300 ° попадает в четвертый квадрант, а это означает, что косинус или координата x будет положительным, а синус или координата y — отрицательным.
Вы также должны сразу знать, что угол 300 ° создает короткую горизонтальную линию и длинную вертикальную линию. Следовательно, косинус (горизонтальная линия) будет равен $ 1/2 $, а синус (вертикальная линия) будет равен $ — {√3} / 2 $ (отрицательное значение y, поскольку эта точка находится в квадранте IV ).
Теперь, чтобы найти касательную, все, что вам нужно сделать, это подключить и решить:
$$ \ tan300 ° = {- {√3} / 2} / {1/2} $$
$$ \ tan300 ° = -√3 $$
Пора мурлыкать по своим математическим способностям!
Набор практических вопросов «Единичный круг»
Теперь, когда вы знаете, как выглядит единичный круг и как его использовать, давайте проверим, что вы узнали, с помощью нескольких практических задач.
Вопросы
- $ \ sin45 ° $
- $ \ cos240 ° $
- $ \ cos {5π} / 3 $
- $ \ tan {2π} / 3 $
ответы
- $ {√2} / 2 долл. США
- $ -1 / 2 $
- $ 1/2
- $ -√3 $
Ответ объяснения
# 1: $ \ sin45 ° $
При этой проблеме есть два элемента информации, которые вы должны сразу определить:
- Ответ будет положительным, , поскольку угол 45 ° находится в квадранте I, а синус угла равен координате y
- Угол 45 ° образует вертикальную линию средней длины (для синуса)
Поскольку 45 ° означает положительную линию средней длины, правильный ответ: $ {√2} / 2 $.
Если вы не знаете, как это понять, нарисуйте диаграмму, которая поможет вам определить, будет ли длина линии короткой, средней или длинной.
# 2: $ \ cos240 ° $
Как и в задаче № 1 выше, есть две части информации, которую вы должны быстро понять при решении этой проблемы:
- Ответ будет отрицательным, , поскольку угол 240 ° находится в квадранте III, а косинус угла равен координате x
- Угол 240 ° образует короткую горизонтальную линию (для косинуса)
Поскольку 240 ° означает короткую отрицательную линию, правильный ответ: $ -1 / 2 $.
# 3: $ \ cos {5π} / 3 $
В отличие от задач, описанных выше, в этой задаче вместо градусов используется радиан . Хотя это может сделать проблему более сложной для решения, на самом деле здесь используются те же основные шаги, что и для двух других задач.
Во-первых, вы должны понять, что угол $ {5π} / 3 $ находится в квадранте IV, поэтому координата x или косинус будет положительным числом. Вы также должны уметь сказать, что $ {5π} / 3 $ создает короткую горизонтальную линию.
Это дает вам достаточно информации, чтобы определить, что ответ составляет $ 1/2 $.
# 4: $ \ tan {2π} / 3 $
В этой задаче используется тангенс вместо синуса или косинуса, а это значит, что с нашей стороны потребуется немного больше математических вычислений. Прежде всего, вспомните основную формулу для нахождения тангенса:
$$ \ tan θ = {\ sin θ} / {\ cos θ} $$
Теперь давайте возьмем полученную степень — $ {2π} / 3 $ — и подставим ее в это уравнение:
$$ \ tan {2π} / 3 = {\ sin {2π} / 3} / {\ cos {2π} / 3} $$
Теперь вы должны иметь возможность решать для синуса и косинуса отдельно, используя то, что вы запомнили о единичной окружности.Поскольку угол $ {2π} / 3 $ находится в квадранте II, координата x (или косинус) будет отрицательной, а координата y (или синусом) будет положительной.
Затем вы сможете определить на основе одного только угла, что горизонтальная линия — это короткая линия, , а вертикальная линия — это длинная линия. Это означает, что косинус равен $ -1 / 2 $, а синус равен $ {√3} / 2 $.
Теперь, когда мы вычислили эти значения, все, что нам нужно сделать, это вставить их в наше исходное уравнение и найти тангенс:
$$ \ tan {2π} / 3 = {{√3} / 2} / {- 1/2} $$
$$ \ tan {2π} / 3 = -√3 $$
Что дальше?
Если вы в ближайшее время будете сдавать SAT или ACT, вам нужно будет знать некоторые триггеры, чтобы вы могли преуспеть в разделе математики. Взгляните на наши экспертные руководства по тестированию SAT и ACT, чтобы вы могли точно узнать, что вам нужно знать в день теста!
Помимо запоминания единичного круга, неплохо научиться вставлять числа и ответы. Прочтите наши руководства, чтобы узнать все об этих двух полезных стратегиях, которые вы можете использовать в любом тесте по математике, включая SAT и ACT!
Файл: Circle cos sin.gif — Wikimedia Commons
Английский: У нас есть единичный круг (с радиусом = 1) зеленого цвета, расположенный в начале координат в правом нижнем углу.В середине этого круга желтым цветом представлен угол тета (θ). Этот угол представляет собой величину вращения против часовой стрелки по кругу, начиная справа по оси x, как показано на рисунке. Точная копия этого небольшого угла показана вверху справа как наглядная иллюстрация определения θ.
Под этим углом, начиная с начала координат, радиально наружу проводится (тусклая) зеленая линия. Эта линия пересекает единичный круг в одной точке, которая представляет собой зеленую точку, вращающуюся с постоянной скоростью при изменении угла θ, также с постоянной скоростью.
Вертикальное положение этой точки проецируется прямо (вдоль слабой красной линии) на график слева от круга. Это приводит к красной точке. Координата Y этой красной точки (такая же, как координата Y зеленой точки) является значением синусоидальной функции, вычисленной под углом θ, то есть:
- Координата y зеленой точки = sin θ
При изменении угла θ красная точка перемещается вверх и вниз, отслеживая красный график. Это график синусоидальной функции.Слабые вертикальные линии, проходящие слева, отмечают каждый квадрант по окружности, то есть под каждым углом 90 ° или π / 2 радиан. Обратите внимание, как синусоида идет от 1 к нулю, к -1, а затем обратно к нулю, именно на этих линиях. Это отражает тот факт, что sin (0) = 0, sin (π / 2) = 1, sin (π) = 0 и sin (3π / 2) -1.
Аналогичный процесс выполняется с координатой x зеленой точки. Однако, поскольку координата x отклонена от обычного соглашения для построения графиков (где y = f (x), с вертикальным y и x горизонтальным), была выполнена операция «untilt», чтобы повторить процесс снова в том же ориентация, а не вертикальная.Это было представлено в виде «изгиба», показанного в правом верхнем углу.
И снова зеленая точка проецируется вверх (вдоль слабой синей линии), и эта «изогнутая» проекция заканчивается у самого правого края верхнего графика, в синей точке. Координата y этой синей точки (которая из-за «изгиба» проекции совпадает с координатой x зеленой точки) — это значение функции косинуса, вычисленное под углом θ, то есть:
- x координата зеленой точки = cos θ
Единичный круг Определение функций синуса и косинуса
Единица
Круговое определение функций синуса и косинуса
Тригонометрические функции могут быть определяется в терминах единичного круга, т. е. круг радиуса один.
The sin / cos Треугольник
Если единичный круг помещен в начало прямоугольной системы координат с углом q, отсчитываемым от положительная ось x к стороне вывода, затем точка на устройстве круг, где конечная сторона пересекает единичный круг, определяется как быть (cos q, sin q), т.е. первая координата точки на устройстве круг — это cos q, а вторая координата — sin q.
The tan / sec Треугольник
Tan q и sec q определены треугольником, высота которого касается единичной окружности в точке (1, 0), гипотенуза которого находится на конечной стороне угла.
The детская кроватка / csc Triangle
Детская кроватка q и csc q определены треугольником, высота которого равна единице, а гипотенуза находится на конечная сторона уголка.
The sin / cos, tan / sec и cot / csc Треугольники
Все три треугольники, используемые для определения тригонометрических функций, показаны на рисунке ниже.
Используя sin / cos, tan / sec и cot / csc Треугольники для установления базового Тригонометрические идентификационные данные
Три одинаковых треугольника sin / cos, tan / sec и cot / csc извлекаются из рисунка.Четвертый аналогичный показан треугольник со смежными, противоположными сторонами и сторонами гипотенузы. помечены.
Определение шести
тригонометрические функции и другие полезные тождества следуют из использования
тот факт, что отношение соответствующих сторон одинаковых треугольников должно
быть равным. Результаты:
Используя sin / cos, tan / sec и cot / csc Треугольники для определения пифагорейского Идентификационные данные
Теорема Пифагора утверждает: в любом прямоугольный треугольник, сумма квадратов длин стороны, содержащие прямой угол, равны квадрату гипотенуза.Короче c 2 = a 2 + b 2 .
Применение пифагора Теорема для треугольников sin / cos, tan / sec и cot / csc дает:
Единичный круг | Purplemath
Purplemath
Когда вы работаете с углами во всех четырех квадрантах, триггерные отношения для этих углов вычисляются в терминах значений x , y и r , где r — радиус окружности, соответствующей к гипотенузе прямоугольного треугольника для вашего угла.На рисунке ниже угол заканчивается во втором квадранте, как показано диагональной линией:
MathHelp.com
Любые два прямоугольных треугольника с одинаковым углом в основании θ («тета», произносится как THAY-tuh) будут похожи в техническом смысле, имея пропорциональные стороны.Это сходство более очевидно, когда треугольники вложены друг в друга:
Сходство (и, следовательно, пропорциональность) означает, что триггерные отношения для двух вложенных треугольников, показанных выше, будут одинаковыми, как вы можете видеть из вычислений ниже для каждого из двух треугольников выше:
Триггерные отношения для угла θ одинакового размера одинаковы (как вы можете видеть выше), даже несмотря на то, что конкретные числа из наборов сторон двух треугольников различаются.Это подчеркивает, что для тригонометрических соотношений имеет значение угол θ, а не конкретный треугольник, из которого вы получили этот угол.
Для упрощения вычислений математики любят помещать угловой треугольник в круг с радиусом r = 1. Поскольку число 1 в математике называется «единицей», круг с радиусом длины 1 называется «единичным кругом». «. Как только гипотенуза имеет фиксированную длину r = 1, тогда значения триггерных отношений будут зависеть только от x и y , поскольку умножение или деление на r = 1 ничего не изменит.Только значения x и y будут иметь значение.
Единичный круг
Смысл единичного круга в том, что он упрощает и упрощает другие части математики. Например, в единичном круге для любого угла θ триггерные значения для синуса и косинуса явно не более чем sin (θ) = y и cos (θ) = x .Исходя из этого, вы можете принять тот факт, что тангенс определен как тангенс (θ) = y / x , а затем заменить x и y , чтобы легко доказать, что значение tan (θ) также должен быть равен отношению sin (θ) / cos (θ).
Еще одна вещь, которую вы можете увидеть из единичного круга, — это то, что значения синуса и косинуса никогда не будут больше 1 или меньше -1, поскольку x и y никогда не принимают значений за пределами этого интервала.Кроме того, поскольку касательная включает деление на x , и поскольку x = 0, когда вы на четверть и три четверти пути по окружности (то есть, когда вы находитесь под углом 90 ° и 270 ° ), касательная не будет определяться для этих угловых мер.
Некоторые углы имеют «хорошие» триггерные значения. Эти углы в первом квадранте (являющиеся «опорными» углами) составляют 0 °, 30 °, 45 °, 60 ° и 90 °. (Строго говоря, 0deg и 90deg не находятся «в» каком-либо квадранте, но мы будем работать с ними, как если бы они были в первом квадранте.Так проще.) Так что вы, вероятно, должны будете запомнить значения триггерных функций для этих углов. Вероятно, теперь вам также будет предоставлен круг с отмеченными углами. В первом квадранте имеем:
(Вы, возможно, заметили радикалы у 1 в приведенном выше примере. Да, они упрощаются до 1, так что вы тоже можете писать так, и вам, безусловно, следует сделать упрощение в своем окончательном ответе.Но обратите внимание, что все знаменатели равны двойкам, а числители идут вверх или вниз: 1, 2, 3. Это может быть полезно для запоминания значений триггеров.)
Вам может быть дан полный единичный круг со значениями углов в трех других квадрантах. Но вам нужно только знать значения в первом квадранте. Как только вы их узнаете, и поскольку значения повторяются (кроме знака) в других квадрантах, вы знаете все, что вам нужно знать о единичном круге.
Подтвердите, что точка (15/113, –112/113) является точкой на единичной окружности. Найдите синус и котангенс угла A, имеющего эту точку на своей конечной стороне.
Любая точка на единичной окружности будет находиться на расстоянии одной единицы от центра; это определение единичного круга. Чтобы «подтвердить», что точка, которую они мне дали, является точкой на единичной окружности, я могу применить теорему Пифагора, чтобы найти длину радиуса прямоугольного треугольника, образованного путем опускания перпендикуляра с оси x вниз. к точке.Мой перпендикуляр — ярко-синяя пунктирная линия:
Если теорема Пифагора дает мне значение радиуса 1, то я «подтверждаю», что точка находится на единичной окружности.
Тогда длина третьей стороны прямоугольного треугольника, которая также является длиной радиуса круга, равна 1. Таким образом, эта точка действительно находится на единичной окружности.
Теперь они хотят, чтобы я нашел синус и котангенс основного угла.Синус — это значение и . (Мне не нужно беспокоиться о гипотенузе, потому что она всегда равна 1 в единичной окружности.) Итак, синус нижележащего угла:
Котангенс — это величина, обратная касательной. Касательная является «противоположной по соседству» или, в данном контексте, « y над x ». Тогда котангенс обратен этому:
детская кроватка (A) = 15 / (- 112) = –15/112
В первой части этого упражнения я показал, что радиус равен 1.Остальная часть моего ручного ответа:
sin (A) = –112
детская кроватка (A) = –15/112
URL: https://www.purplemath.com/modules/unitcirc.htm
Единичный круг — Уравнение единичной окружности
Единичный круг из самого названия определяет круг с единичным радиусом.Круг — это замкнутая геометрическая фигура без сторон и углов. Единичный круг обладает всеми свойствами круга, и его уравнение также выводится из уравнения круга. Кроме того, единичный круг полезен для получения стандартных угловых значений всех тригонометрических соотношений.
Здесь мы изучим уравнение единичной окружности и поймем, как представить каждую из точек на окружности единичной окружности с помощью тригонометрических соотношений cosθ и sinθ.
Что такое единичный круг?
Единичная окружность — это окружность с радиусом в 1 единицу. Единичный круг обычно представлен в декартовой координатной плоскости. Единичный круг алгебраически представлен с помощью уравнения второй степени с двумя переменными x и y. Единичная окружность применяется в тригонометрии и помогает находить значения тригонометрических соотношений синуса, косинуса и тангенса.
Определение единичного круга
Геометрическое место точки, находящейся на расстоянии одной единицы от фиксированной точки, называется единичной окружностью.
Уравнение единичной окружности
Общее уравнение круга: (x — a) 2 + (y — b) 2 = r 2 , что представляет собой круг с центром (a, b) и радиусом r. Это уравнение круга упрощено и представляет собой уравнение единичного круга. Единичная окружность образуется с центром в точке (0, 0), которая является началом координатных осей. и радиусом 1 ед. Следовательно, уравнение единичной окружности: (x — 0) 2 + (y — 0) 2 = 1 2 .Это упрощается, чтобы получить уравнение единичной окружности.
Уравнение единичной окружности: x 2 + y 2 = 1
Здесь для единичной окружности центр лежит в точке (0,0), а радиус равен 1 единице. Вышеупомянутое уравнение удовлетворяет всем точкам, лежащим на окружности в четырех квадрантах.
Нахождение тригонометрических функций по единичной окружности
Мы можем вычислить тригонометрические функции синуса, косинуса и тангенса, используя единичную окружность.Давайте применим теорему Пифагора в единичном круге, чтобы понять тригонометрические функции. Рассмотрим прямоугольный треугольник, помещенный в единичный круг в декартовой координатной плоскости. Радиус круга представляет собой гипотенузу прямоугольного треугольника. Радиус-вектор составляет угол θ с положительной осью x, а координаты конечной точки радиус-вектора равны (x, y). Здесь значения x и y — длина основания и высота прямоугольного треугольника. Теперь у нас есть прямоугольный треугольник со сторонами 1, x, y.Применяя это в тригонометрии, мы можем найти значения тригонометрического отношения следующим образом:
- sinθ = Высота / Гипотеза = y / 1
- cosθ = База / Гипотенуза = x / 1
Теперь у нас есть sinθ = y, cosθ = x, и, используя это, мы теперь имеем tanθ = y / x. Точно так же мы можем получить значения других тригонометрических соотношений, используя прямоугольный треугольник внутри единичной окружности. Также, изменяя значения θ, мы можем получить главные значения этих тригонометрических соотношений.
Единичный круг с Sin Cos и Tan
Любая точка на единичной окружности имеет координаты (x, y), которые равны тригонометрическим тождествам (cosθ, sinθ). Для любых значений θ, образованных линией радиуса с положительной осью x, координаты конечной точки радиуса представляют собой косинус и синус значений θ. Здесь мы имеем cosθ = x и sinθ = y, и эти значения помогают вычислить другие значения тригонометрического отношения. Применяя это далее, мы имеем tanθ = sinθ / cosθ или tanθ = y / x.
Еще один важный момент, который следует понять, это то, что значения sinθ и cosθ всегда лежат между 1 и -1, а значение радиуса равно 1, и оно имеет значение -1 на отрицательной оси x. Весь круг представляет собой полный угол в 360º, а четыре квадранта круга образуют углы 90º, 180º, 270º, 360º (0º). При 90º и 270º значение cosθ равно 0 и, следовательно, значения тангенса угла наклона при этих углах не определены.
Пример: Найдите значение тангенса угла 45º, используя значения sin и cos из единичной окружности.
Решение:
Мы знаем, что tan 45 ° = sin 45 ° / cos 45 °
Используя круговую диаграмму единиц:
грех 45 ° = 1 / √2
cos 45 ° = 1 / √2
Следовательно, tan 45 ° = sin 45 ° / cos 45 °
= (1 / √2) / (1 / √2)
= 1
Ответ: Следовательно, tan 45 ° = 1
Круговая диаграмма единиц в радианах
Единичный круг представляет собой полный угол в 2π радиан. А единичный круг разделен на четыре квадранта под углами π / 2, π.3π / 2 и 2π соответственно. Далее в пределах первого квадранта под углами 0, π / 6, π / 4, π / 3, π / 2 — стандартные значения, которые применимы к тригонометрическим отношениям. Точки на единичном круге для этих углов представляют стандартные угловые значения отношений косинуса и синуса. При внимательном рассмотрении рисунка ниже значения повторяются в четырех квадрантах, но с изменением знака. Это изменение знака происходит из-за опорных осей x и y, которые положительны с одной стороны и отрицательны с другой стороны от начала координат.Теперь с помощью этого мы можем легко найти значения тригонометрических соотношений стандартных углов в четырех квадрантах единичной окружности.
Единичный круг и тригонометрические идентичности
Идентичности единичной окружности синуса, косеканса и тангенса могут быть дополнительно использованы для получения других тригонометрических идентификаторов, таких как котангенс, секанс и косеканс. Идентификаторы единичной окружности, такие как косеканс, секанс, котангенс, являются соответствующими обратными величинами синуса, косинуса и тангенса.Кроме того, мы можем получить значение tanθ, разделив sinθ на cosθ, и мы можем получить значение cotθ, разделив cosθ на sinθ.
Для прямоугольного треугольника, помещенного в единичный круг в декартовой координатной плоскости, с гипотенузой, основанием и высотой, измеряющими единицы, x, y соответственно, тождества единичного круга могут быть заданы как,
- sinθ = y / 1
- cosθ = x / 1
- tanθ = sinθ / cosθ = y / x
- с (θ = 1 / x
- csc (θ) = 1 / y
- детская кроватка (θ) = cosθ / sinθ = x / y
Единичный круг Пифагорейские тождества
Три важных пифагоровых тождества тригонометрических соотношений можно легко понять и доказать с помощью единичной окружности.Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Три пифагорова тождества в тригонометрии заключаются в следующем.
- sin 2 θ + cos 2 θ = 1
- 1 + загар 2 θ = сек 2 θ
- 1 + детская кроватка 2 θ = cosec 2 θ
Здесь мы попытаемся доказать первое тождество с помощью теоремы Пифагора.Возьмем x и y в качестве катетов прямоугольного треугольника с единицей гипотенузы 1. Применяя теорему Пифагора, мы получаем x 2 + y 2 = 1, что представляет собой уравнение единичной окружности. Также в единичном круге имеем x = cosθ и y = sinθ, и применяя это в приведенном выше утверждении теоремы Пифагора, мы имеем cos 2 θ + sin 2 θ = 1. Таким образом, мы имеем успешно доказал первое тождество с помощью теоремы Пифагора. Далее в пределах единичного круга мы также можем доказать два других тождества Пифагора.
Единичная окружность и тригонометрические значения
Различные тригонометрические тождества и их значения главных углов могут быть вычислены с помощью единичной окружности. В единичном круге косинус является координатой x, а синус — координатой y. Давайте теперь найдем их соответствующие значения для θ = 0 ° и θ = 90º.
Для θ = 0 ° координата x равна 1, а координата y равна 0. Следовательно, мы имеем cos0º = 1 и sin0º = 0.Давайте посмотрим на другой угол 90º. Здесь значение cos90º = 1 и sin90º = 1. Далее, давайте воспользуемся этой единичной окружностью и найдем важные значения тригонометрической функции θ, такие как 30º, 45º, 60º. Кроме того, мы также можем измерить эти значения θ в радианах. Мы знаем, что 360 ° = 2π радиан. Теперь мы можем преобразовать угловые меры в радианы и выразить их в радианах.
Единичный круговой стол:
Таблица единичной окружности используется для перечисления координат точек единичной окружности, соответствующих общим углам, с помощью тригонометрических соотношений.
| Угол θ | Радианы | Sinθ | Cosθ | Tanθ = Sinθ / Cosθ | Координаты |
|---|---|---|---|---|---|
| 0 ° | 0 | 0 | 1 | 0 | (1, 0) |
| 30 ° | π / 6 | 1/2 | √3 / 2 | 1 / √3 | (√3 / 2, 1/2) |
| 45 ° | π / 4 | 1 / √2 | 1 / √2 | 1 | (1 / √2, 1 / √2) |
| 60 ° | π / 3 | √3 / 2 | 1/2 | √3 | (1/2, √3 / 2) |
| 90 ° | π / 2 | 1 | 0 | undefined | (0,1) |
Мы можем найти функции секанса, косеканса и котангенса, также используя следующие формулы:
- сек θ = 1 / cosθ
- косекунд θ = 1 / sinθ
- cotθ = 1 / tanθ
Мы обсудили единичный круг для первого квадранта.Точно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Цифры 1/2, 1 / √2, √3 / 2, 0, 1 повторяются вместе со знаком во всех 4 квадрантах.
Единичный круг в сложной плоскости
Единичный круг состоит из всех комплексных чисел, абсолютное значение которых равно 1. Следовательно, оно имеет уравнение | z | = 1. Любое комплексное число z = x + \ (i \) y будет лежать на единичной окружности с уравнением, заданным как x 2 + y 2 = 1.
Единичный круг можно рассматривать как единичные комплексные числа на комплексной плоскости, т.е.е., набор комплексных чисел z, заданный формой,
z = e \ (i \) t = cos t + \ (i \) sin t = cis (t)
Приведенное выше соотношение представляет собой формулу Эйлера.
Часто задаваемые вопросы о Unit Circle
Что такое единичный круг в математике?
Единичный круг — это круг с радиусом в одну единицу. Обычно единичный круг представлен в координатной плоскости с центром в начале координат. Уравнение единичной окружности с радиусом одна единица и центром в точке (0, 0): x 2 + y 2 = 1.Кроме того, единичная окружность применяется в тригонометрии и используется для нахождения главных значений тригонометрических соотношений синуса и косинуса.
Как найти грех и разум, используя единичный круг?
Единичный круг можно использовать для определения значений sinθ и Cosθ. В единичном круге радиуса 1 единица и с центром в (0, 0), давайте возьмем радиус, наклоненный к положительной оси x под углом θ, и конечную точку радиуса как (x, y). Нарисуйте перпендикуляр от конца радиуса к оси x, и он образует прямоугольный треугольник с радиусом в качестве гипотенузы.Соседняя сторона этого треугольника — это значение x, противоположная сторона треугольника — значение y, а гипотенуза равна 1 единице. Далее, используя формулу тригонометрического отношения, имеем sinθ = Opp / Hyp = y / 1 и cosθ = Adj / Hyp = x / 1. Таким образом, sinθ = y и cosθ = x.
Что такое определение триггерных функций с помощью единичной окружности?
Тригонометрическую функцию можно вычислить для главных значений с помощью единичной окружности. Для единичного круга, имеющего центр в начале координат (0, 0), радиус 1 единицу, если радиус наклонен под углом θ и конечная точка радиус-вектора равна (x, y), то cosθ = x и sinθ = y.Кроме того, все остальные тригонометрические отношения могут быть рассчитаны на основе этих двух значений. Кроме того, основные значения можно вычислить, изменив значение θ.
Как найти конечную точку на единичной окружности?
Конечная точка на единичной окружности может быть найдена с помощью уравнения единичной окружности x 2 + y 2 = 1. Если данная точка удовлетворяет этому уравнению, то это точка, лежащая на единичной окружности. . Кроме того, конечную точку на единичном значении можно найти для значения θ, найдя значения cosθ и sinθ.
Что такое уравнение единичной окружности?
Уравнение единичной окружности: x 2 + y 2 = 1. Здесь считается, что единичная окружность имеет центр в начале (0, 0) координатных осей и имеет радиус 1. Блок. Это уравнение единичной окружности было получено с помощью формулы расстояния.
Как вывести уравнение единичной окружности?
Уравнение единичной окружности может быть вычислено с использованием формулы расстояния координатной геометрии.Для круга, имеющего центр в начале координат (0, 0), радиус 1 единицу, любая точка на окружности может быть принята как (x, y). Применяя определение круга и используя формулу расстояния, мы имеем (x — 0) 2 + (y — 0) 2 = 1, что можно упростить как x 2 + y 2 = 1
Когда загар не определяется на единичном круге?
Единичный круг, имеющий уравнение x 2 + y 2 = 1, помогает найти тригонометрические отношения sinθ = y и cosθ = x.Используя эти значения, мы можем удобно найти значение tanθ = sinθ / cosθ = y / x. Tanθ будет неопределенным для cosθ = 0, т.е. когда θ равно 90 ° и 270 °.
Какая связь между прямоугольными треугольниками и единичной окружностью?
Правые треугольники и единичная окружность однозначно связаны. Любую точку на единичном круге можно представить как прямоугольный треугольник с радиусом как гипотенузу прямоугольного треугольника и координаты точки как две другие стороны прямоугольного треугольника.Уравнение окружности x 2 + y 2 = 1 полностью удовлетворяет теореме Пифагора, относящейся к прямоугольному треугольнику. Кроме того, прямоугольный треугольник внутри единичного круга помогает получить значения тригонометрического отношения.
Для чего используется единичный круг?
Единичный круг особенно полезен в тригонометрии. Для тригонометрических соотношений sinθ, cosθ, tanθ их значения главных углов 0º, 30º, 45º, 60º, 90º могут быть легко вычислены с использованием единичной окружности.Кроме того, единичный круг полезен для представления комплексных чисел на плоскости арганда.
Каковы квадранты единичного круга?
Единичный круг состоит из четырех квадрантов, аналогичных квадрантам в системе координат. Четыре квадранта имеют равную площадь и составляют одну четвертую площади круга. Каждый из квадрантов образует угол 90 ° или прямой угол в центре круга.
Как описать единичный круг комплексными числами?
Единичный круг состоит из всех комплексных чисел с абсолютным значением как 1, таким образом, любое комплексное число z = x + \ (i \) y будет лежать на единичном круге с уравнением, заданным как x 2 + y 2 = 1 .Следовательно, уравнение единичной окружности можно представить как | z | = 1.
10 секретных триггерных функций, которым вас никогда не учили учителя математики
В понедельник The Onion сообщил, что «национальные учителя математики вводят 27 новых триггерных функций». Это забавное чтение. Гамсин, негтан и cosvnx из статьи о Луке вымышлены, но в этой статье есть доля правды: есть 10 секретных триггерных функций, о которых вы никогда не слышали, и у них есть восхитительные названия, такие как «гаверсинус» и «эксеканс».
Диаграмма с единичным кругом и большим количеством триггерных функций, чем вы можете потрясти палкой.(Хорошо известно, что вы можете встряхнуть палку максимум при 8 триггерных функциях.) Знакомые синус, косинус и тангенс выделены красным, синим и, ну, желтовато-коричневым, соответственно. Версин выделен зеленым рядом с косинусом, а эксеканс розовым справа от версина. Excosecant и coverine также присутствуют на изображении. Не изображены: веркозин, кверкозин и хавер — что угодно. Изображение: Лиманер и Стивен Джонсон, через Wikimedia Commons. Хотите ли вы мучить студентов с ними или вовлечь их в разговор, чтобы показаться эрудированным и / или невыносимым, вот определения всех «потерянных триггерных функций» , которые я нашел в своем исчерпывающем исследовании оригинальных исторических текстов Википедия рассказала я о.
Версия: версия (θ) = 1-cos (θ)
Веркозин: веркозин (θ) = 1 + cos (θ)
Coversine: охватывает (θ) = 1-sin (θ)
Covercosine: covercosine (θ) = 1 + sin (θ)
.
Гаверсин: гаверсин (θ) = версен (θ) / 2
Хаверкозин: хаверкозин (θ) = веркозин (θ) / 2
Хаковерсин: hacoversin (θ) = Coversin (θ) / 2
Гаковеркозин: гаковеркозин (θ) = кверкозин (θ) / 2
Exsecant: exsec (θ) = sec (θ) -1
Excosecant: excsc (θ) = csc (θ) -1
Должен признаться, я был немного разочарован, когда посмотрел на них.Все они представляют собой простые комбинации дорогого старого синуса и косинуса. Почему они вообще получили имена ?! Из того места и времени, когда я могу сидеть на диване и почти мгновенно находить синус любого угла с точностью до 100 десятичных знаков с помощью онлайн-калькулятора, в Версине нет необходимости. Но эти, казалось бы, лишние функции восполнили потребности в мире предварительных калькуляторов.
Numberphile недавно опубликовал видео о таблицах журналов, в котором объясняется, как люди использовали логарифмы для умножения больших чисел в темные дни, когда еще не было калькулятора.Во-первых, напомню о логарифмах. Уравнение log b x = y означает, что b y = x. Например, 10 2 = 100, поэтому log 10 100 = 2. Полезный факт о логарифмах заключается в том, что log b (c × d) = log b c + log b d. Другими словами, логарифмы превращают умножение в сложение. Если вы хотите умножить два числа вместе с помощью таблицы журнала, вы должны найти логарифм обоих чисел, а затем сложить логарифмы. Затем вы должны использовать свою таблицу журнала, чтобы узнать, какое число имеет этот логарифм, и это был ваш ответ.Сейчас это звучит громоздко, но умножение вручную требует гораздо больше операций, чем сложение. Когда каждая операция занимает нетривиальное количество времени (и подвержена нетривиальному количеству ошибок), процедура, позволяющая преобразовать умножение в сложение, в реальном времени экономит время и помогает повысить точность.
Секретные триггерные функции, такие как логарифмы, упрощают вычисления. Чаще всего использовались версин и гаверсин. Вблизи угла θ = 0 cos (θ) очень близко к 1.Если вы выполняли вычисление, в котором было 1-cos (θ), ваше вычисление могло бы быть разрушено, если в вашей таблице косинусов не было достаточно значащих цифр. Для иллюстрации косинус 5 градусов равен 0,996194698, а косинус 1 градуса равен 0,999847695. Разница cos (1 °) -cos (5 °) составляет 0,003652997. Если бы у вас было три значащих цифры в вашей таблице косинусов, вы бы получили только одну значащую цифру в своем ответе из-за ведущих нулей в разнице. А таблица только с тремя значащими цифрами точности не сможет различить углы 0 и 1 градус.Во многих случаях это не имеет значения, но может стать проблемой, если ошибки накапливаются в ходе вычислений.
Бонусные триггерные функции также имеют то преимущество, что они никогда не бывают отрицательными. Версина находится в диапазоне от 0 до 2, поэтому, если вы используете таблицы журнала для умножения на версину, вам не нужно беспокоиться о том, что логарифм не определен для отрицательных чисел. (Он также не определен для 0, но с этим легко иметь дело.) Еще одно преимущество версин и гаверсин состоит в том, что они могут удерживать вас от необходимости что-то возводить в квадрат.Немного тригонометрического волшебства (также известного как запоминание одной из бесконечного списка тригонометрических формул, которые вы выучили в старшей школе) показывает, что 1-cos (θ) = 2sin 2 (θ / 2). Таким образом, гаверсинус — это просто грех 2 (θ / 2). Точно так же гаверкозин равен cos 2 (θ / 2). Если у вас есть вычисление с использованием квадрата синуса или косинуса, вы можете использовать таблицу гаверсинусов или гаверсинусов, и вам не нужно возводить в квадрат или извлекать квадратные корни.
Диаграмма, показывающая синус, косинус и версию угла.Изображение: Qef и Стивен Дж. Джонсон, через Wikimedia Commons.Версина — это довольно очевидная триггерная функция для определения и, кажется, использовалась еще в 400 г. н.э. в Индии. Но гаверсинус мог быть более важным в более недавней истории, когда он использовался в навигации. Формула гаверсинуса — очень точный способ вычисления расстояний между двумя точками на поверхности сферы с использованием широты и долготы этих двух точек. Формула гаверсинуса — это переформулировка сферического закона косинусов, но формулировка в терминах гаверсинусов более полезна для малых углов и расстояний.(С другой стороны, формула гаверсинуса не очень хорошо справляется с углами, близкими к 90 градусам, но сферический закон косинусов справляется с этим хорошо.) Формула гаверсинуса может дать точные результаты, не требуя дорогостоящих вычислений. квадраты и квадратные корни. Еще в 1984 году любительский астрономический журнал Sky & Telescope восхвалял формулу гаверсинуса, которая полезна не только для наземной навигации, но и для астрономических расчетов.Чтобы узнать больше о формуле гаверсинуса и вычислении расстояний на сфере, ознакомьтесь с этой архивной копией страницы бюро переписи или этой статьей «Спросите доктора Матема».
У меня не так много информации об истории других триггерных функций в списке. Все они могут сделать вычисления более точными вблизи определенных углов, но я не знаю, какие из них обычно использовались, а какие назывались * аналогично другим функциям, но редко использовались на самом деле. Мне любопытно об этом, если кто-нибудь знает больше о предмете.
Когда Луковица имитирует реальную жизнь, это обычно трагично. Но в случае секретных триггерных функций суть правды в Луке меня не огорчила. Нам очень повезло, что теперь мы можем так легко умножать, возводить в квадрат и извлекать квадратные корни, а наши калькуляторы могут хранить точную информацию о синусах, косинусах и тангенсах углов, но прежде чем мы смогли это сделать, мы придумали работу -округ в виде смешного количества триггерных функций. Легко забыть, что люди, которые их определили, не были садистскими учителями математики, которые хотят, чтобы люди запоминали странные функции без всякой причины.Эти функции фактически сделали вычисления более быстрыми и менее подверженными ошибкам. Теперь, когда компьютеры стали настолько мощными, привычка к дискетам улетучилась. Но я думаю, мы все можем согласиться с тем, что он должен вернуться, хотя бы из-за «классной» шутки, которую я придумал, когда засыпал прошлой ночью: Хаверсин? Я даже не знаю!
* Я хотел бы сделать здесь небольшое отступление в мир математических префиксов, но это может быть не для всех. Вас предупредили.
В таблице секретных триггерных функций «ха» явно означает половину; Например, ценность гаверсина составляет половину стоимости версина.«Со» означает выполнение той же функции, но с дополнительным углом. (Дополнительные углы в сумме составляют 90 градусов. В прямоугольном треугольнике два непрямых угла дополняют друг друга.) Например, косинус угла также является синусом дополнительного угла. Точно так же крышка — это версия дополнительного угла, как вы можете видеть голубым цветом над одним из красных синусов на диаграмме вверху сообщения.
Одна бонусная триггерная функция, которая меня немного смущает, — это веркосинус.Если бы «со» в этом определении означало дополнительный угол, тогда веркозинус был бы таким же, как покрывающий, а это не так. Вместо этого веркосинус — это версия дополнительного угла (дополнительные углы в сумме составляют 180 градусов), а не дополнительный. В дополнение к определениям как 1-cos (θ) и 1 + cos (θ), версин и веркозин могут быть определены как versin (θ) = 2sin 2 (θ / 2) и vercos (θ) = 2cos . 2 (θ / 2). В случае версины я считаю, что определение, включающее cos (θ), старше, чем определение, включающее синус в квадрате.Я предполагаю, что веркосинус был более поздним термином, аналогом определения квадрата синуса версина с использованием вместо него косинуса. Если вы любитель истории тригонометрии и у вас есть дополнительная информация, дайте мне знать! В любом случае таблица суперсекретных триггерных функций бонусов — забавное упражнение для выяснения того, что означают префиксы.
Использование единичных окружностей для соотнесения прямоугольных треугольников с синусом и косинусом — стенограмма видео и урока
Прямоугольники и треугольник
Прямоугольники — треугольники с одним прямым углом.Все любят прямоугольные треугольники, правда? Что в них такого хорошего? Помимо прочего, они обладают уникальными тригонометрическими свойствами.
Если мы посмотрим на этот угол, тэта, ниже, мы можем обозначить стороны относительно тэты. Сторона, противоположная тэте, это … подождите … противоположная сторона. Соседняя сторона — да — соседняя сторона. И еще есть гипотенуза, самая длинная сторона.
Три основных тригонометрических функции — это синус, косинус и тангенс.Синус теты равен противоположности гипотенузы. Косинус теты равен смежному по гипотенузе. Наконец, касательная тета равна противоположной по соседнему. Мы сокращаем это до фразы SOH CAH TOA .
Но знаете ли вы, что прямоугольные треугольники соединены с окружностями? Ну, не просто круг. Я имею в виду единичный круг.
Единичная окружность
Единичная окружность — один из волшебных математических инструментов, которые облегчают вашу жизнь.Что особенно хорошо в единичном круге, так это его простота. Это просто круг с радиусом 1.
Чем он полезен? Нарисуем. Начните с базовой оси x и y . Теперь добавьте круг с центром в начале координат. Опять же, радиус круга равен 1.
Здесь немного волшебства. Но этот потрясающий ураган только начинается.
Если наша линия радиуса находится здесь (показано ниже), и мы проведем здесь еще одну линию до оси x (также показано ниже), мы получим что? Прямоугольный треугольник.
Мы будем называть угол выше тета. А гипотенуза треугольника равна 1. Теперь вернемся к нашему триггеру.
Синус и косинус
Что такое синус теты снова? Помните SOH CAH TOA . Синус противоположен гипотенузе. Итак, синус теты — это сторона гипотенузы. Но подождите — если гипотенуза равна 1, то синус теты равен любой длине.Итак, мы можем назвать эту ногу ниже синуса.
А что насчет косинуса? Косинус — это сторона, прилегающая к гипотенузе. Итак, это сторона над единицей или только эта сторона:
Это означает, что точка в желтой точке, где радиус достигает края круга, может быть идентифицирована как (cos (theta), sin (theta)). Итак, наша бабочка прямоугольного треугольника взмахнула крыльями, образуя синус и косинус.И этот ветер добрался до нашей единичной окружности, где снова появляются те же синус и косинус. Наш ураган потрясающих возможностей сейчас действительно уходит.
Треугольники единичной окружности
Давайте посмотрим на это вращение урагана (смотрите видео, начинающееся в 03:32). Независимо от того, куда мы перемещаем нашу линию радиуса, она все равно попадает в край нашего единичного круга в точке (cos (theta), sin (theta)). Когда он движется, значения косинуса тета и синус тета просто изменяются вместе с изменением теты.
Здесь тета равна 0:
Это действительно не треугольник, но принцип неизменен. Косинус-тета — это все еще расстояние от начала координат до желтой точки, поэтому косинус-тета равен 1. А как насчет синус-тета? Поскольку это похоже на треугольник, где сторона, противоположная тэте, равна 0, тогда синус тэта равен 0.
Что, если мы переместим тэту на 90 градусов? Теперь косинус тета равен 0, а синус тета равен 1.
Когда мы переходим во второй квадрант, косинус тета становится отрицательным.Почему? Наши значения x отрицательны. Синус тета остается положительным, пока мы не дойдем до квадрантов III и IV. Но в квадранте IV косинус снова становится положительным. Все это основано на наших значениях x и y .
Итак, ветер из прямоугольного треугольника всегда является частью урагана с единичным кругом. Он может дуть на север, восток, юг или запад, но все взаимосвязано.
Краткое содержание урока
В итоге нам удалось связать бабочек и ураганы с принцессой Лейей и тригонометрией.Что еще более важно, мы рассмотрели связи между прямоугольными треугольниками, единичной окружностью и синусом и косинусом.
Прямые треугольники — это треугольники с одним прямым углом. В прямоугольном треугольнике синус угла равен стороне, противоположной гипотенузе. Косинус равен стороне, прилегающей к гипотенузе.
На единичной окружности мы можем создать прямоугольный треугольник, добавив радиусную линию и соединив ее с осью x . Поскольку радиус единичного круга равен единице, гипотенуза этих треугольников также равна единице.Это означает, что синус угла, образованного радиусом и осью x , равен любой длине здесь:
И косинус равен любой длине здесь:
Результаты обучения
После этого урока вы должны уметь:
- Объяснять полезность единичного круга
- Опишите, как создать прямоугольный треугольник на единичной окружности
- Определите синус, косинус и тангенс с помощью единичной окружности и прямоугольного треугольника

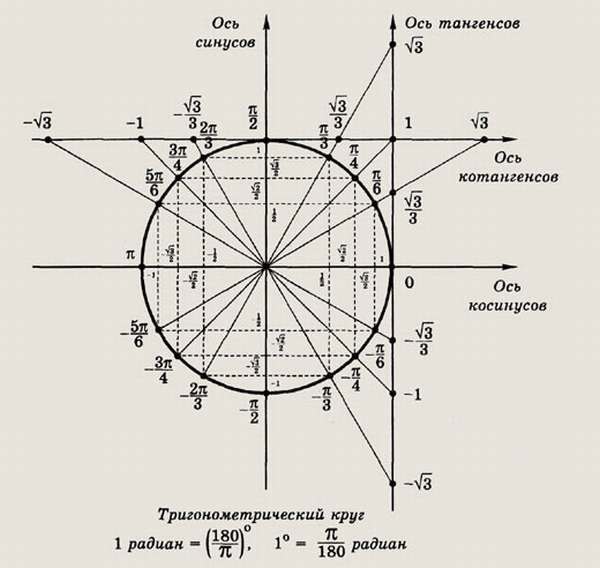

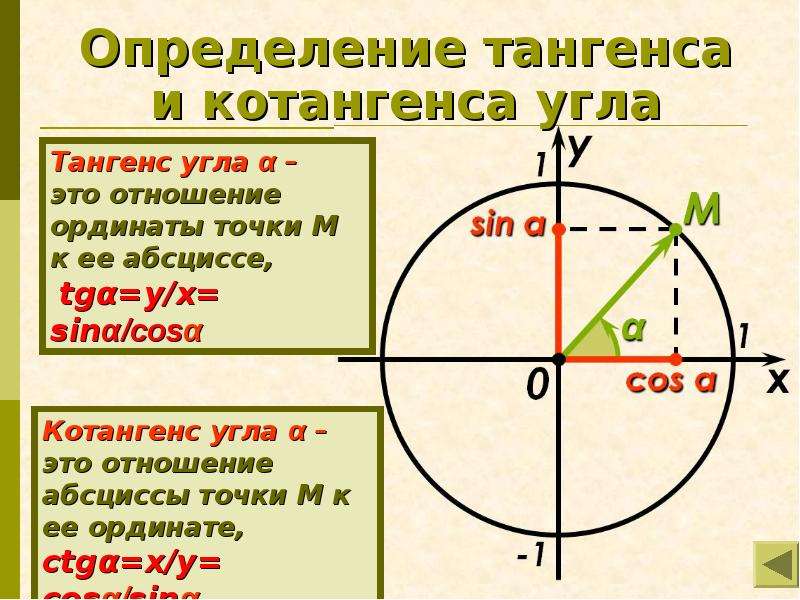 Введите свой запрос:
Введите свой запрос:
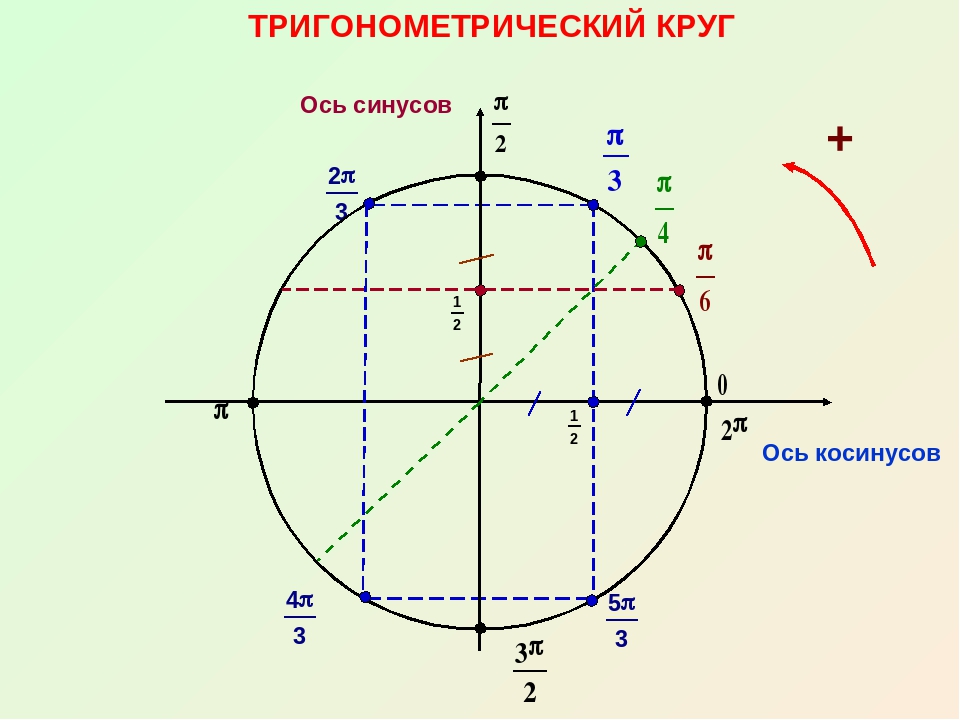 США ({√3} / 2, 1/2)
США ({√3} / 2, 1/2)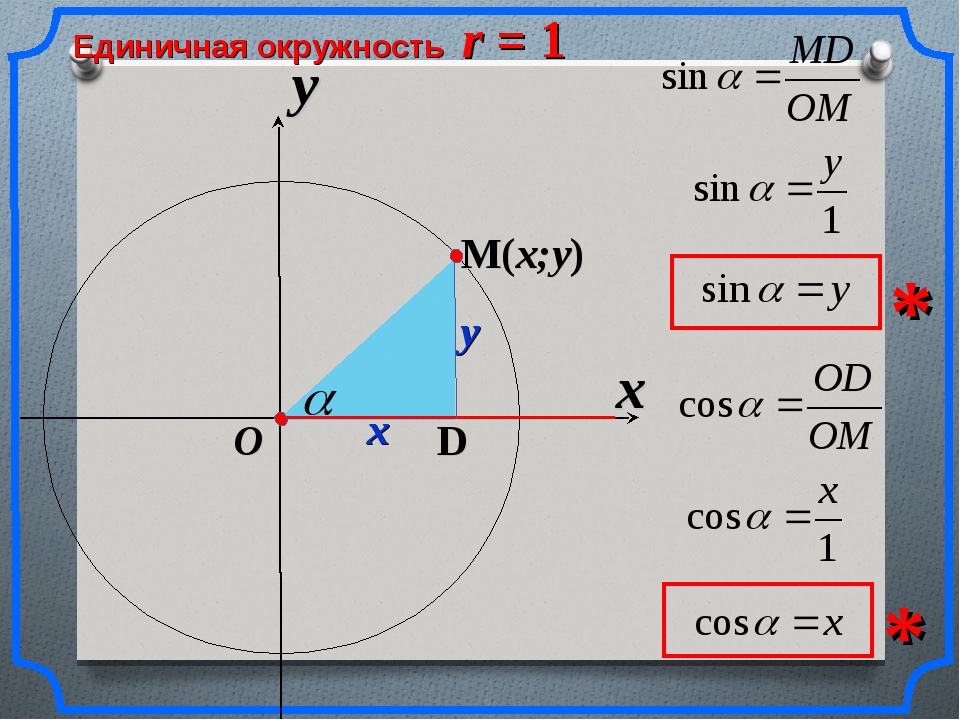 США (1/2, — {√3} / 2)
США (1/2, — {√3} / 2)