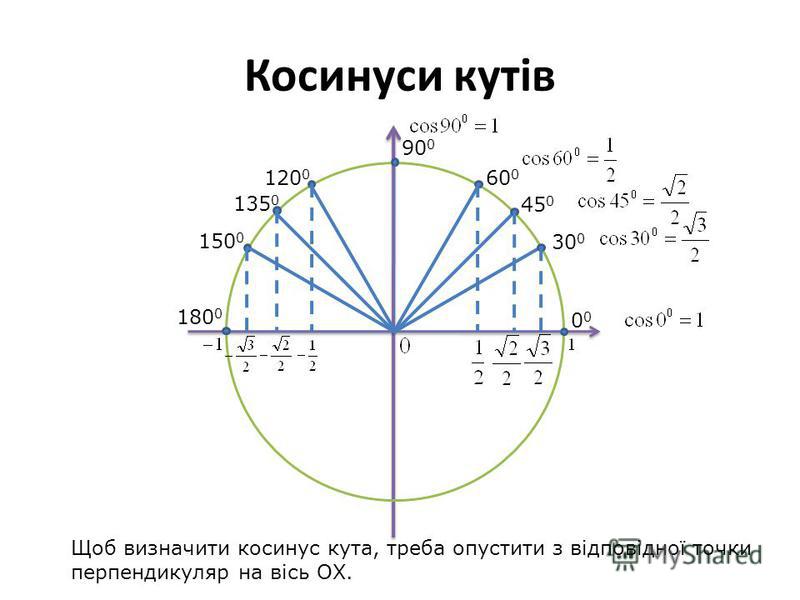
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.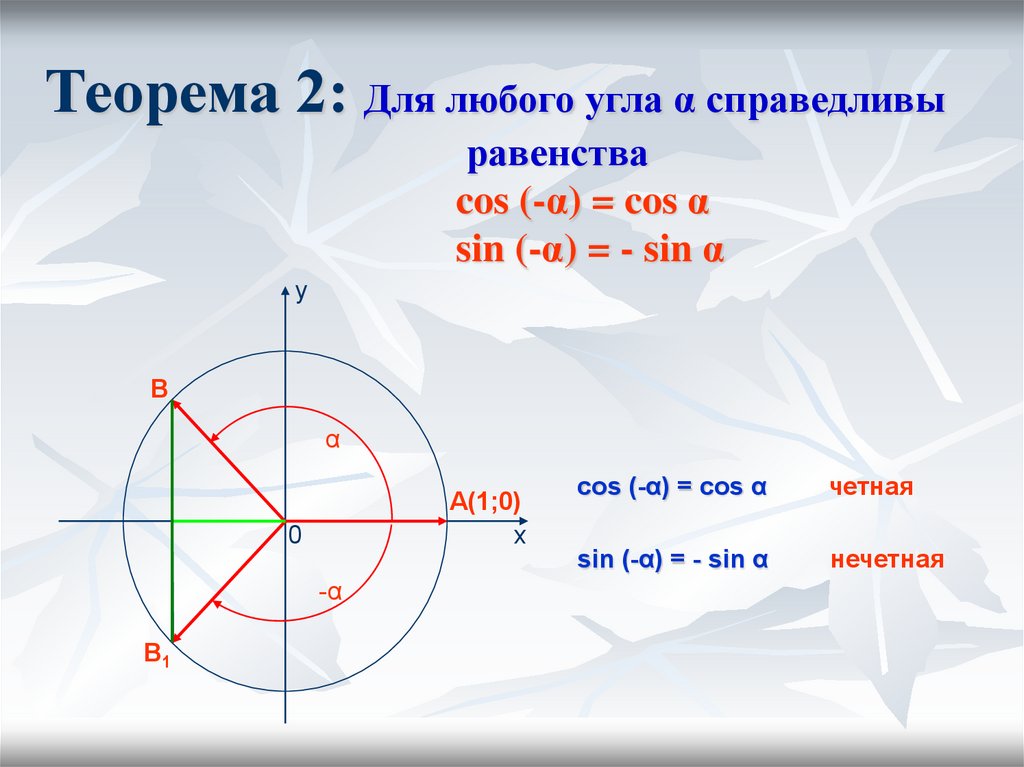 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.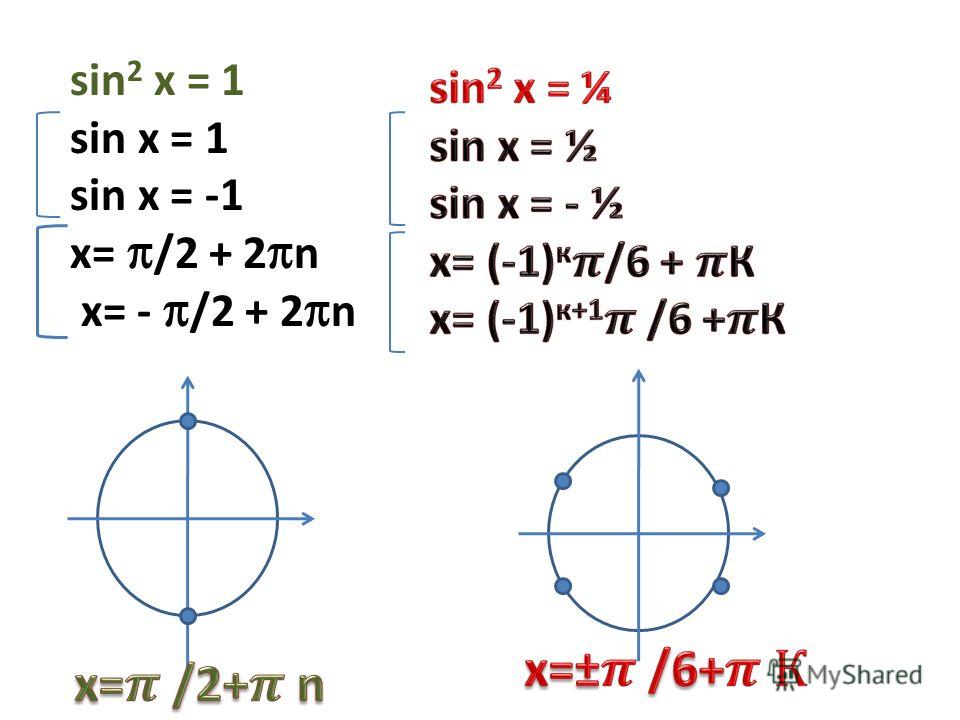 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.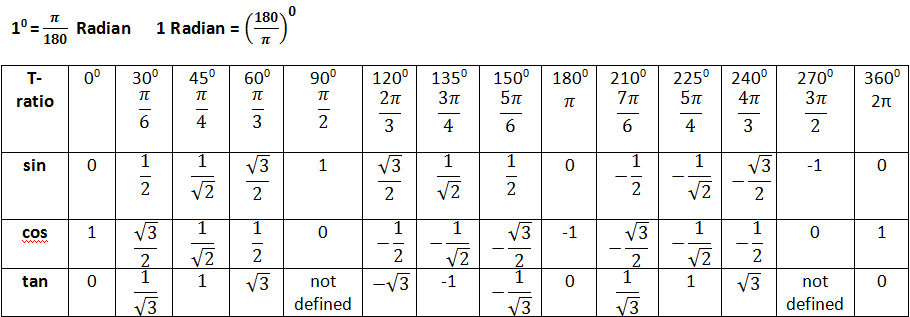 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
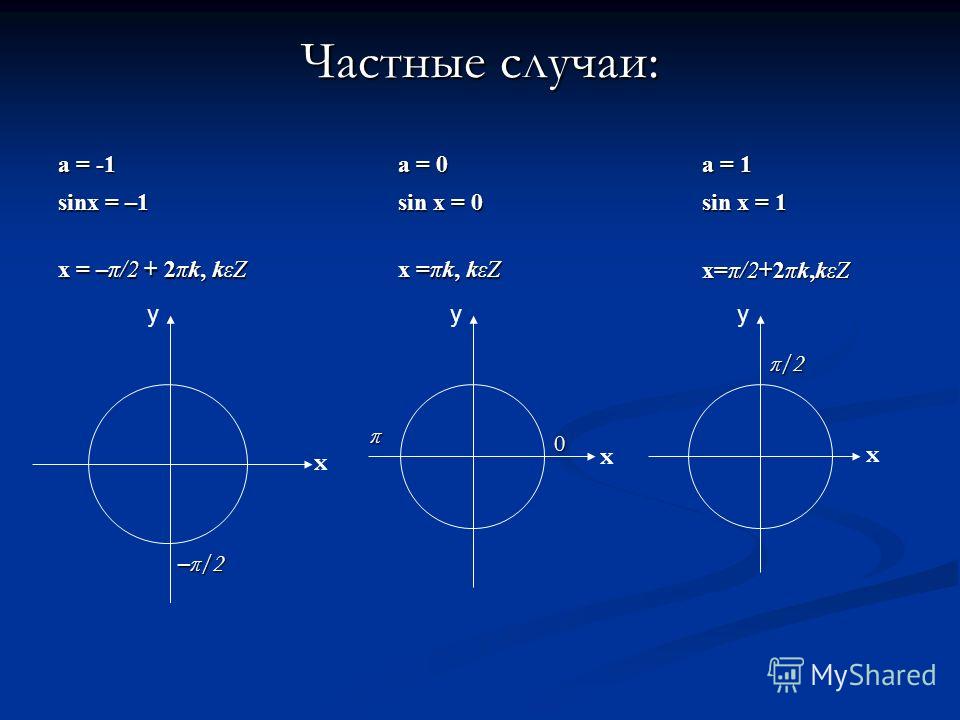
Уравнение косинус икс равен а. Тригонометрические уравнения — формулы, решения, примеры. Разложение на множители
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда.
 При любом а.
При любом а. Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.
 ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда.В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π /6.
 Полноценный ответ будет:
Полноценный ответ будет:х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.
 ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу.
 Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т.
 п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн.
Если Вам нравится этот сайт… А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Захарова Людмила Владимировна
МБОУ «Средняя общеобразовательная школа № 59» г. Барнаула
учитель математики [email protected]№1 Простейшие тригонометрические уравнения
Цель: 1. Вывести формулы решений простейших тригонометрических уравнений вида sinx =a, cosx=a, tgx=a, ctgx=a;
2. Научиться решать простейшие тригонометрические уравнения с помощью формул.
Оборудование: 1) Таблицы с графиками тригонометрических функций у= sinx, у=cosx, у=tgx, у=ctgx; 2) Таблица значений обратных тригонометрических функций; 3) Сводная таблица формул для решения простейших тригонометрических уравнений.

План урока-лекции :
1 .Вывод формул корней уравнения
а ) sinx =a,
б ) cosx=a ,
в ) tgx=a ,
г) ctgx=а .
2 . Устная фронтальная работа по закреплению полученных формул.
3 . Письменная работа по закреплению изученного материала
Ход урока.В алгебре, геометрии, физике и других предметах мы сталкиваемся с разнообразными задачами, решение которых связано с решением уравнений. Мы изучили свойства тригонометрических функций, поэтому естественно обратиться к уравнениям, в которых неизвестное содержится под знаком функций
Определение: Уравнения вида sinx = a , cosx = a , tgx = a , ctgx = а называются простейшими тригонометрическими уравнениями.
Очень важно научиться решать простейшие тригонометрические уравнения, так как все способы и приемы решения любых тригонометрических уравнений заключается в сведении их к простейшим.

Начнем с того, что выведем формулы, которые «активно» работают при решении тригонометрических уравнений.
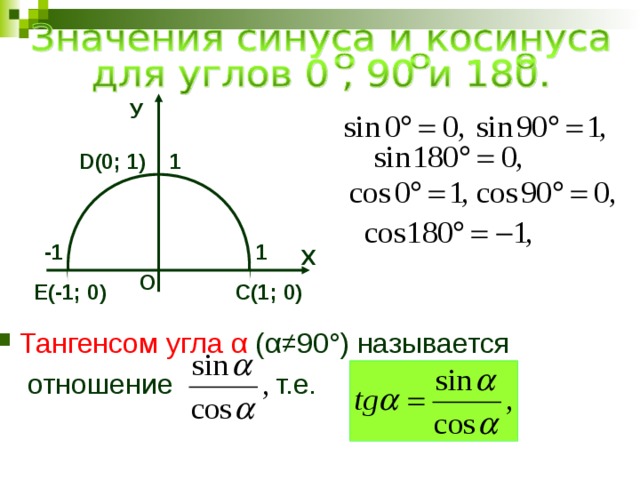
1.Уравнения вида sinx =a .
Решим уравнение sinx =a графически. Для этого в одной системе координат построим графики функций у=sinx и у=а.
1) Если а > 1 и а sin х=а не имеет решений, так как прямая и синусоида не имеют общих точек.
2) Если -1а а пересечет синусоиду бесконечно много раз. Это означает, что уравнение sinx=a имеет бесконечно много решений.
Так как период синуса равен 2, то для решения уравнения sinx=a достаточно найти все решения на любом отрезке длины 2.
Решением уравнения на [-/2; /2] по определению арксинуса х= arcsin a , а на х=-arcsin a . Учитывая периодичность функции у=sinx получим следующие выражения
х = -arcsin a +2n, n Z.
Обе серии решений можно объединить
Х = (-1) n arcsin a +n, nZ.
В следующих трех случаях предпочитают пользоваться не общей формулой, а более простыми соотношениями:
Если а =-1, то sin x =-1, х=-/2+2n
Если а =1, то sin x =1, x =/2+2n
Если а= 0, то sin x =0.
 x = n,
x = n,Пример: Решить уравнение sinx =1/2.
Составим формулы решений x=arcsin 1/2+ 2n
Х= — arcsin a+2n
Вычислим значение arcsin1/2. Подставим найденное значение в формулы решений
х= 5/6+2 n
или по общей формуле
Х= (-1) n arcsin 1/2+n,
Х= (-1) n /6+n,
2. Уравнения вида cosx=a .
Решим уравнение cosx=a также графически, построив графики функций у= cosx и у=а .
1) Если а 1, то уравнение cosx=a не имеет решений, так как графики не имеют общих точек.
2) Если -1a cosx=a имеет бесконечное множество решений.
Найдем все решения cosx=a на промежутке длины 2 так как период косинуса равен 2.
На решением уравнения по определению арккосинуса будет х= arcos a. Учитывая четность функции косинус решением уравнения на [-;0] будет х=-arcos a .
Таким образом решения уравнения cosx=a х=+ arcos a + 2 n,
В трех случаях будем пользоваться не общей формулой, а более простыми сотношениями:
Если а =-1, то cosx =-1, x =-/2+2n
Если а =1, то cosx =1, x = 2n,
Если а=0, то cosx =0.
 x =/2+n
x =/2+nПример: Решить уравнение cos x =1/2,
Составим формулы решений x=arccos 1/2+ 2n
Вычислим значение arccos1/2.
Подставим найденное значение в формулы решений
X=+ /3+ 2n, nZ.
Уравнения вида tgx=a .
Так как период тангенса равен , то для того чтобы найти все решения уравнения tgx=a , достаточно найти все решения на любом промежутке длины . По определению арктангенса решение уравнения на (-/2; /2) есть arctga . Учитывая период функции все решения уравнения можно записать в виде
х= arctg a + n, nZ.
Пример: Решите уравнение tg x = 3/3
Составим формулу для решения х= arctg 3/3 +n, nZ.
Вычислим значение арктангенса arctg 3/3= /6, тогда
Х=/6+ n, nZ.
Вывод формулы для решения уравнения с tgx = a можно предоставить учащимся.
Пример.
Решить уравнение ctg х = 1.

х = arcсtg 1 + n, nZ,
Х = /4 + n, nZ.
В результате изученного материала учащиеся могут заполнить таблицу:
«Решение тригонометрических уравнений».
уравнение
Упражнения для закрепления изученного материала.
(Устно) Какие из записанных уравнений можно решить по формулам:
а ) х= (-1) n arcsin a +n, nZ;
б ) х=+ arcos a+ 2 n?
cos x = 2/2, tg x= 1 , sin x = 1/3, ctg x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3 , cos x = 2.
Какие из перечисленных уравнений не имеют решений?
Решите уравнения:
а) sin x = 0; д) sin x = 2/2; з) sin x = 2;
б) cos x = 2/2; е) cos x = -1/2; и) cos x = 1;
г) tg x = 3; ж) ctg x = -1; к) tg x = 1/ 3.
3. Решите уравнения:
а) sin 3x = 0; д) 2cos x = 1;
б) cos x/2 =1/2; е) 3 tg 3x =1;
г) sin x/4 = 1; ж) 2cos(2x+ /5) = 3.
При решении данных уравнений полезно записать правила для решения уравнений вида sinв x =a , и с sinв x =a , | a |1.

Sinв x =a, |a|1.
в х = (-1) n arcsin a +n, nZ,
х= (-1) n 1/в arcsin a +n/в , nZ.
Подведение итогов занятия:
Сегодня на занятии мы вывели формулы для решения простейших тригонометрических уравнений.
Разобрали примеры решения простейших тригонометрических уравнений.
Заполнили таблицу, которую будем использовать для решения уравнений.
Домашнее задание.
№2 Решение тригонометрических уравнений
Цель: Изучить методы решения тригонометрических уравнений:1) приводимых к квадратным;2) приводимых к однородным тригонометрическим уравнениям.
Развивать у учащихся наблюдательность при применении различных способов решения тригонометрических уравнений.
Фронтальная работа с учащимися .
Назовите формулы корней тригонометрических уравнений cos x=a , sin x=a , tgx = a , ctg x = a .

Решите уравнения (устно):
cos x=-1, sin x=0, tgx =0, ctg x=1, cos x=1,5, sin x=0.
Найдите ошибки и подумайте о причинах ошибок.
cos x=1/2, х=+ /6+2k, kZ.
sin x= 3/2, х= /3+k, kZ.
tgx = /4, x=1+ k, kZ.
2. Изучение нового материала.
На данном занятии будут рассмотрены некоторые наиболее часто встречающиеся методы решения тригонометрических уравнений.
Тригонометрические уравнения, приводимые к квадратным.
К этому классу могут быть отнесены уравнения, в которые входят одна функция (синус или косинус) или две функции одного аргумента, но одна их них с помощью основных тригонометрических тождеств сводится ко второй.
Например, если cоsх входит в уравнение в четных степенях, то заменяем его на 1- sin 2 x, если sin 2 x, то его заменяем на 1-cos 2 x.
Пример.
Решить уравнение: 8 sin 2 x — 6sin x -5 =0.
Решение: Обозначим sin x=t, тогда 8t 2 — 6t – 5=0,
D= 196,
T 1 = -1/2, t 2 = -5/4.

Выполним обратную замену и решим следующие уравнения.
Х=(-1) к+1 /6+ k, kZ.
Так как -5/4>1, то уравнение не имеет корней.
Ответ: х=(-1) к+1 /6+ k, kZ.
Решение упражнений на закрепление.
Решить уравнение:
1) 2sin 2 x+ 3cos x = 0;
2) 5sin 2 x+ 6cos x -6 = 0;
3) 2sin 2 x+ 3cos 2 x = -2sin x;
4) 3 tg 2 x +2 tgx-1=0.
Однородные тригонометрические уравнения.
Определение: 1) Уравнение вида a sinx + b cosx =0, (а=0, в=0) называется однородным уравнением первой степени относительно sin x и cos x.
Решается данное уравнение с помощью деления обеих его частей на cosx 0. В результате получается уравнение atgx+ b=0.
2) Уравнение вида a sin 2 x + b sinx cosx + c cos 2 x =0 называется однородным уравнением второй степени, где a, b, c какие-либо числа.

Если а=0, то уравнение решаем делением обеих частей на cos 2 x 0. В результате получаем уравнение atg 2 x+ btgx+с =0.
Замечание: Уравнение вида a sin mx + b cos mx =0 или
a sin 2 mx + b sin mx cos mx + c cos 2 mx =0 также являются однородными. Для их решения обе части уравнения делят на cos mx =0 или cos 2 mx =0
3) К однородным уравнениям могут быть сведены различные уравнения, которые первоначально не являются такими. Например, sin 2 mx + b sin mx cos mx + c cos 2 mx = d , и a sinx + b cosx = d .
 Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.
Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.Упражнения на закрепление изученного материала:
1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;
2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;
3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;
4) sin 2 x -3 sinx cosx +2 cos 2 x =0
3.Подведение итогов урока. Домашнее задание.
На данном занятии в зависимости от подготовленности группы можно рассмотреть решение уравнений вида a sin mx +b cos mx=с, где а, b,с не равны нулю одновременно.
Упражнения на закрепление:
1. 3sin x + cos x=2;
2. 3sin 2x + cos 2x= 2;
3. sin x/3 + cos x/3=1;
4. 12 sin x +5 cos x+13=0.
№ 3 Решение тригонометрических уравнений
Цель: 1) Изучить метод решения тригонометрических уравнений разложением на множители; научиться решать тригонометрические уравнения с использованием различных тригонометрических формул;
2) Проконтролировать: знание учащимися формул для решения простейших тригонометрических уравнений; умение решать простейшие тригонометрические уравнения.

План занятия:
Проверка домашнего задания.
Математический диктант.
Изучение нового материала.
Самостоятельная работа.
Подведение итогов занятия. Домашнее задание.
Ход занятия:
Проверка домашнего задания (решение тригонометрических уравнений кратко записаны на доске).
Математический диктант.
В-1
1. Какие уравнения называются простейшими тригонометрическими уравнениями?
2. Как называется уравнение вида a sinx +b cosx=0? Укажите способ его решения.
3.Запишите формулу корней уравнения tgx = a (ctg x=a ).
4. Запишите формулы корней уравнений вида cosx=a , где а =1, а =0, а =-1.
5. Запишите общую формулу корней уравнения sin x=a , | a |
6. Как решаются уравнения вида a cosx=b , | b |
В-2
1.
 Запишите формулы корней уравнений
cosx=a ,| a |
Запишите формулы корней уравнений
cosx=a ,| a | 2. Запишите общую формулу корней уравнения
= a , | a |
3. Как называются уравнения вида sin x=a , tgx = a , sin x=a ?
4.Запишите формулы корней уравнения sin x=a , если а =1, а =0, а =-1.
5.Как решаются уравнения вида sin a x=b , | b |
6. Какие уравнения называются однородными уравнениями второй степени? Как они решаются?
Изучение нового материала.
Метод разложения на множители.
Одним из наиболее употребительных методов решения тригонометрических уравнений является метод разложения на множители.
Если уравнение f(x) =0 можно представить в виде f 1 (x) f 2 (x) =0 , то задача сводится к решению двух уравнений f 1 (x)=0, f 2 (x) =0.
(С учащимися полезно вспомнить правило «Произведение множителей равно нулю, если хотя бы один из множителей равен нулю, а другие при этом имеют смысл »)
Закрепление изученного материала через решение уравнений различной сложности.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(самост.)
3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;
5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2-мя способами)
7) cosx+ cos3x=0; 8) sin 3x= sin 17x;
9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x
11) sin x cos5x =sin 9x cos3x sin 2x sin 2x
12) 3 cosx sin x+ cos 2 x=0(самост.)
13) 2 cos 2 x — sin (x- /2)+ tgx tg (x+/2)=0.
Самостоятельная работа.
Вариант-1 Вариант-2
1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;
2) sin 2x – cos2x=0; 2) 3 cos x/2 — sin x/2=0;
3) 5 sin 2 x+ sin x cosx -2 cos 2 х=2; 3) 4sin 2 x- sin x cosx +7cos 2 х=5;
4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;
5) sin x+cosx=1.
 5) sin x+cosx=2.
5) sin x+cosx=2.8. Подведение итогов урока. Домашнее задание.
9 класс. Геометрия. Соотношения между сторонами и углами треугольника. Синус, косинус и тангенс угла. — Решение задач.
Комментарии преподавателяРешение задач по теме «Синус, косинус, тангенс угла»
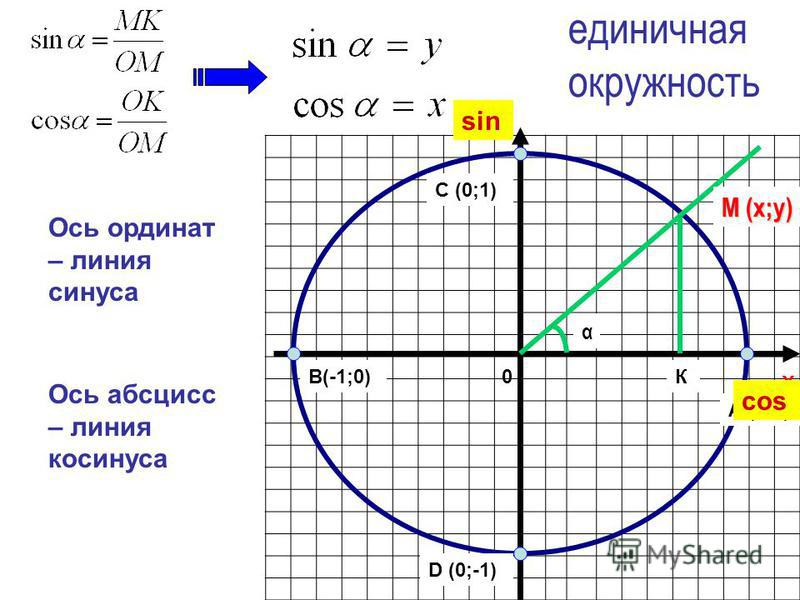
Напомним, угол определяет единственную точку М (хα; уα) на единичной полуокружности. На Рис. 1 представлена единичная полуокружность, она описывается следующим образом:
Рис. 1
, первое из этих выражений – это вся окружность, а второе ограничивает нас только верхней полуплоскостью.
Так вот, первую координату точки М (абсциссу) назвали косинусом угла. Вторую координату – ординату – назвали синусом угла.
Вот основные определения:
М = M (,).
tg α = ; ctg α =
Далее вспомним основное тригонометрическое тождество и основные формулы.
 Они здесь выписаны, проанализируем их и вспомним, откуда они получились.
Они здесь выписаны, проанализируем их и вспомним, откуда они получились., tg α · ctg α = 1 или
Во-первых, они получились из определений.
И во-вторых, из уравнения окружности.
Если есть Ð α, то ему соответствует единственная точка на окружности, и координаты этой точки назвали синусом угла и косинусом угла. Но это точка на единичной окружности, а любая точка единичной окружности подчиняется уравнению окружности ,
х – это косинус, а у – это синус, значит, для любого Ð α. Напомним, мы рассматриваем углы из отрезка [0°; 180°].
Рис. 2
Далее вспомним (Рис. 2) важные формулы для координат точки А (хА; уА)
α Î [0°; 180°].
Рис. 3
Итак, мы имеем синус, косинус, тангенс, котангенс для тупых углов в том числе, т. е. мы рассматриваем углы [0°; 180°]. Но при этом следует уметь вычислять и синус, и косинус таких углов.
 Этому помогают формулы приведения (Рис. 3). Напомним их:
Этому помогают формулы приведения (Рис. 3). Напомним их:при 0º£α £90º;
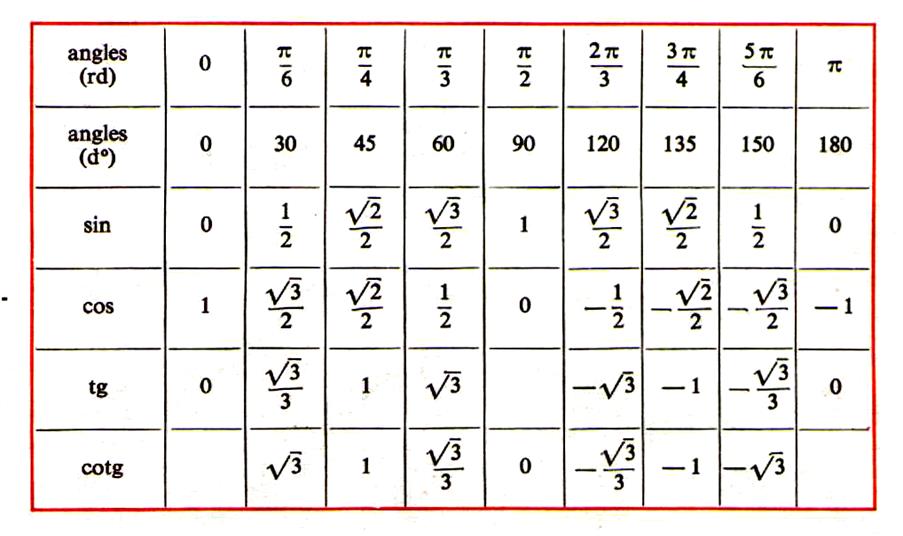
Полезно вспомнить значение тригонометрических функций основных острых углов. Почему?
Только что мы видели, что по формулам приведения к ним сводятся значения тригонометрических функций тупых углов.
30°
45°
60°
sin
½
cos
½
tg
1
ctg
1
Итак, мы вспомнили важную таблицу для тригонометрических функций острых углов.

Рассмотренная таблица и формулы приведения позволяют решать многие типовые задачи.
Найти: sin 120°, cos 120°, tg 120°, ctg 120°.
Решение: сначала формальное решение.
sin 120° = sin (180° – 60°) = sin 60° по формулам приведения, а по таблице sin 60° = .
Часть задачи решена:
cos 120° = cos (180° – 60°) = – cos 60° = – ½ .
Таким образом, мы нашли синус и косинус тупого угла 120°.
Теперь посмотрим и проиллюстрируем этот факт на графике.
Рис. 4
Строим единичную полуокружность, на ней угол 120°. Напомним, что этот угол отсчитан против часовой стрелки от положительного направления оси Ох.
Он высекает единственную точку М2 на единичной полуокружности.
Выясняется, что оставшийся угол между отрицательной полуосью Ох и лучом ОМ2 равен 60° и еще один угол 60° (между положительной полуосью Ох и лучом ОМ1). Для угла 60° синус совпадает с синусом 120°, а косинус 60° и косинус 120° – это противоположные числа.
 Таким образом, для данной типовой задачи мы нашли синус и косинус 120° и проиллюстрировали факт нахождения на чертеже.
Таким образом, для данной типовой задачи мы нашли синус и косинус 120° и проиллюстрировали факт нахождения на чертеже.Осталось найти тангенс и котангенс 120°.
Формулы известны, находим:
tg 120° = ;
ctg 120° =
Ответ:
sin 120° = , cos 120° = — ½ , tg 120° = , ctg 120° =
Задача решена.
Использованы и таблица, и формулы приведения.
Следующая типовая задача. Задана одна функция, найти другие функции или другую функцию.
Задача. Найдите , если = ¼ , α Î [0; 180°]. Сначала формальное решение. Мы имеем основное тригонометрическое тождество, которое связывает между собой и синус, и косинус: , откуда (Ответ).
Два ответа. Откуда они появились? Проиллюстрируем этот факт на чертеже (Рис. 5).
Единичная полуокружность, синус какого-то угла, неизвестно пока, какого, равна ¼. Перпендикуляр к линии синусов (оси ординат), проведенный в точке у = ¼, высвечивает две точки на единичной окружности.
 Двум точкам соответствуют два угла. Один угол α1, второй угол – α2.
Двум точкам соответствуют два угла. Один угол α1, второй угол – α2.Угол α1 имеет , Угол α2 имеет .
Сделаем такое примечание: значение = ¼ определяет два угла – α1 и α2 = 180° – α1 , причем
(синусы равны одному и тому же числу), а косинусы – разные: ,
Рис. 5
В следующей задаче, наоборот, задано значение , требуется найти значение . И понять, в чем разница между этой задачей и предыдущей.
Задача. Найдите , если = , α Î [0; 180°].
Рис. 6
Как всегда, сначала формальное решение без чертежа:
по основному тригонометрическому тождеству , откуда , два ответа, но вспоминаем, что синус меняется в пределах [0; 1], поэтому выбираем и получаем единственный ответ.
Теперь проиллюстрируем все это на чертеже (Рис. 6).
Как обычно, на рисунке – единичная полуокружность, линия косинусов (ось абсцисс), на ней точки – 1, 0, 1, а у нас абсцисса (косинус) равна .

Перпендикуляр высвечивает единственную точку на единичной окружности и единственный Ðα. Он здесь тупой. Синус тоже имеет единственное значение. Сформулируем такое примечание: значение определяет единственный ÐαÎ[0°; 180°]. Задача решена.
Формулировка следующей задачи.
Задача. Найдите угол между лучом ОА и положительной полуосью Ох, если точка А имеет координаты ( ; 1 ).
Чертеж (Рис. 7).
Рис. 7
На рисунке – точка А (; 1), и надо найти угол, который обозначим α.
Известны координаты точки А.
Используем специфику исходных данных при решении (Рис. 8). Рассмотрим треугольник АОА1.
Рис. 8
Он прямоугольный, и катеты его известны. Первый катет равен 1, второй катет длиной .
Следовательно, tg ÐАОА1 = угол ÐАОА1 = 30°, искомый угол α = 180° – 30° = 150°
Ответ получен, но мы продемонстрируем другой способ его получения.

Сначала найти длину отрезка АО, ведь координаты точки А известны и координаты точки О известны.
Далее по формулам для координат точки найти косинус угла, синус угла. В любом случае специфика конкретных исходных данных нам позволила мгновенно найти угол. Задача решена.
Итак, мы повторили теорию по теме «Синус, косинус, тангенс угла» и решили типовые задачи.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/9-klass/sinus-kosinus-i-tangens-ugla/reshenie-zadach-4
http://5klass.net/datas/algebra/Trigonometricheskie-funktsii/0007-007-Svojstva-sinusa-kosinusa-tangensa-i-kotangensa.jpg
http://lmenripacha.science/pic-reshak.ru/reshebniki/geometriya/10/wbatanasyan9/images/30.gif
http://fastform.ru/wp-content/uploads/media/%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82-%D1%83%D1%80%D0%BE%D0%BA%D0%B0-%D0%BF%D0%BE-%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8-%D0%BD%D0%B0-%D1%82%D0%B5%D0%BC%D1%83-%D0%A1%D0%B8%D0%BD%D1%83%D1%81%D0%BA%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81-%D1%82%D0%B0%D0%BD%D0%B3%D0%B5%D0%BD%D1%81-%D1%83%D0%B3%D0%BB%D0%B0/image3.
 gif
gifCos 1 частные случаи. Тригонометрические уравнения — формулы, решения, примеры
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов.
 Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения.
 Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.

Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получимtg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ: 0.
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
 n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Простейшими тригонометрическими уравнениями называют уравнения
Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a
Уравнение cos (x) = a
Объяснение и обоснование
- Корни уравнения cosx = а.
 При | a | > 1 уравнение не имеет корней, по-скольку | cosx | 1 или при а
При | a | > 1 уравнение не имеет корней, по-скольку | cosx | 1 или при а
Пусть | а |
у = cos х. На промежутке функция y = cos x убы-вает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = а имеет на этом промежутке только один корень, который по опреде-лению арккосинуса равен: x 1 = arccos а (и для этого корня cos x = а).
Косинус — четная функция, поэтому на промежутке [-п; 0] уравнение cos x = а также имеет только один корень — число, противоположное x 1 , то есть
x 2 = -arccos а.
Таким образом, на промежутке [-п; п] (длиной 2п) уравнение cos x = а при | а |
Функция y = cos x периодическая с периодом 2п, поэтому все остальные корни отличаются от найденных на 2пп (n € Z). Получаем следующую фор-мулу корней уравнения cos x = а при
x = ±arccos а + 2пп, n £ Z.
- Частные случаи решения уравнения cosx = а.
Полезно помнить специальные записи корней уравнения cos x = а при
а = 0, а = -1, а = 1, которые можно легко получить, используя как ори-ентир единичную окружность.

Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответ-ствующей точкой единичной окружности является точка A или точка B.
Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C, следовательно,
x = 2πп, k € Z.
Также cos х = —1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, х = п + 2пn,
Уравнение sin (x) = a
Объяснение и обоснование
- Корни уравнения sinx = а. При | а | > 1 уравнение не имеет корней, по-скольку | sinx | 1 или при а
тригонометрия — Почему косинус прямого угла, 90 градусов, равен нулю?
Спросил
Изменено 2 года назад
Просмотрено 23k раз
$\begingroup$
Почему косинус угла 90 градусов равен нулю?
По определению мы знаем, что: $$\text{cos} \alpha = \frac{\text{смежный}}{\text{гипотенуза}}.
 $$
$$Если мы хотим применить определение к ситуации на изображении ниже:
у нас есть это: $$\text{cos} 90° = \frac{?}{h} .$$ Как я могу сказать, что он равен $0$, если я ничего не знаю ни о двух других сторонах, ни о двух других углах?
Мне всегда удавалось найти значение, даже без единичного круга, в таких ситуациях, как $\text{csc} 90°, \text{sec} 0°$ и т. д…, но не в приведенной выше ситуации . Почему?
Пожалуйста, не могли бы вы мне что-нибудь предложить?
Итак, я делаю дополнение также на основе предоставленных предложений. Моя основная ошибка была в том, что я начал считать прямой угол, вместо этого я должен начать считать $\theta = \alpha°$, и увеличивать его до $\theta = 90°$, одна сторона становится меньше до нуля, а другая сторона становятся больше до $h$, поэтому $\text{cos} \alpha = \frac{0}{h} = 0$
- тригонометрия
$\endgroup$
3
$\begingroup$ 9{\circ}$, потому что это можно точно сделать с равнобедренным прямоугольным треугольником со стороной $1,1,\sqrt{2}$
$\endgroup$
$\begingroup$
Хотя тригонометрические функции изначально определены для углов треугольника (в радианах), они распространяются на все действительные числа и, в конечном итоге, на комплексные числа.
 Хотя их свойства, такие как законы сложения, сохраняются, они со временем теряют всякую связь с треугольниками.
Хотя их свойства, такие как законы сложения, сохраняются, они со временем теряют всякую связь с треугольниками.В приведенном вами случае ясно, что соседняя сторона становится все ближе и ближе к $0$ по мере того, как угол приближается к $\pi/2$, поэтому косинус приближается к $0,$, но вы, очевидно, не можете действительно есть треугольник с двумя прямыми углами.
$\endgroup$
$\begingroup$
В ваших рассуждениях есть изъян. При выполнении тригонометрии (классическим способом) мы рассматриваем прямоугольный треугольник. Значение $\cos(\alpha)$ обычно определяется как отношение $\frac{\text{прилежащая сторона}}{\text{гипотенуза}}.$ Это определение, однако, является неполным и не может быть найдено как это, например, в голландских школьных учебниках. В голландских школьных учебниках говорилось бы что-то вроде: $$\cos (\alpha)=\frac{\text{aanliggende $\color{red}{\text{rechthoeks}}$zijde}}{\text{hypotenusa}}.
 $$ Важным отличием здесь является то, что 9\circ)$ можно «наблюдать» только в треугольнике с двумя прямыми углами. Вы можете интерпретировать это по-разному: вырожденный треугольник с одной вершиной в бесконечно удаленной точке; предел $\lim_{h\to\infty}\frac{\text{a}}{\text{h}}$; возможно как-то иначе.
$$ Важным отличием здесь является то, что 9\circ)$ можно «наблюдать» только в треугольнике с двумя прямыми углами. Вы можете интерпретировать это по-разному: вырожденный треугольник с одной вершиной в бесконечно удаленной точке; предел $\lim_{h\to\infty}\frac{\text{a}}{\text{h}}$; возможно как-то иначе.В любом случае ключевой момент здесь вот в чем:
При выполнении классической тригонометрии в обычном случае, но определенно и в «экстремальных» случаях, вам необходимо определить смежную сторону и противоположную сторону таким образом, чтобы ни одна из них никогда не могла быть гипотенузой. 9\circ$, тогда $C$ окажется ниже $B$, а не выше, и мы считаем, что «противоположность» и «гипотенуза» отрицательны.
$\endgroup$
$\begingroup$
, потому что в точке $\cos(\pi/2)$ гипотенузой является ось y и само значение sin.
в единичном круге нет ни треугольника, ни тэты.

просто прямая. $\sin x$ — это само значение $y$, а $\cos x$ — это само значение x.
вот почему $\cos$ нуля равен 1 в единичном круге.
грех $\pi/2$ в позиции нулевого значения x также равен единице.
если тебя это ни хрена не смущает, то меня смущает.
$\sin$ в 90 градусов или $\pi/2$ не то же самое, что $\sin$ в ноль, который равен нулю.
, хотя он находится в нулевой позиции $\cos$ или $x$ на единичной окружности.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
реальный анализ — доказательство Ланга, что существует $x>0$ такое, что $\cos x=0$
$\begingroup$
В Анализе бакалавриата на с. 90 Ланг предполагает существование двух функций $f$ (синус) и $g$ (косинус), удовлетворяющих условиям $f(0)=0$, $g(0)=1$, $f’=g$ и $g’=-f$. Затем он показывает, что существует $x>0$ такое, что $\cos x=0$.
С вашей помощью я хотел бы сделать некоторые шаги его доказательства более явными.
Предположим, что такого номера не существует. Поскольку $\cos$ непрерывен, мы сделать вывод, что $\cos x$ не может быть отрицательным ни при каком значении $x>0$ (по теорема о промежуточном значении). Следовательно, $\sin$ строго возрастает для все $x>0$, и $\cos x$ строго убывает для всех $x>0$ …
Понятно, почему $\sin$ строго возрастает на интервале $(0,\infty)$. Почему $\cos$ строго убывает на отрезке $(0,\infty)$? Для этого потребуется $\sin x>0$ для всех $x\in(0,\infty)$.
 Но как я могу это показать? 9na)=0$ для всех $a>0$, но я не знаю как.
Но как я могу это показать? 9na)=0$ для всех $a>0$, но я не знаю как.- реальный анализ
- производные
- тригонометрия
- непрерывность
- доказательство-объяснение
$\endgroup$
10
$\begingroup$
К первому вопросу: если синус начинается с нуля и увеличивается, он положительный.
Значит, производная косинуса $g’=-f $ отрицательна.
Следовательно, косинус уменьшается.Добавлено 92\le 1.$
Таким образом, должно существовать $x_1>0$ с $f'(x_1)\le 0.$ А так как $f’=g$ непрерывно с $f'(0)>0$, то должен существовать $x_2\in (0,x_1]$ с $0=f'(x_2)=g(x_2).$
$\endgroup$
3
$\begingroup$
Если $\cos x>0$ для каждого $x$, то синус строго возрастает.
 Но в определении предполагается, что $\sin 0=0$. Следовательно, $\sin x>0$ при $x>0$.
Но в определении предполагается, что $\sin 0=0$. Следовательно, $\sin x>0$ при $x>0$.А теперь тот факт, что $\cos’x=-\sin x$ говорит нам о том, что косинус строго убывает по $(0,\infty)$. 92=1$.
В случае $\lim_{x\to\infty}g(x)=a>0$, то $\forall x, f'(x)\ge a$ и $\forall x\ge0, f( x)\ge ax$, что противоречит ограниченности функции $f$.
$\endgroup$
2
$\begingroup$
$n \in \mathbb{Z} \rightarrow +\infty$ можно интерпретировать как $n \in \mathbb{N} \rightarrow +\infty$.
Другими словами, когда $n$ приближается к положительной бесконечности, мы можем игнорировать отрицательные значения.
9n$, то чем больше $s$, тем меньше порог.$\endgroup$
5
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. 93-8
93-89 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 Косинус нуля — Ответы на кроссворд
Кроссворд Косинус нуля с 3 буквами в последний раз встречался на 01 января 2013 .
 Мы думаем, что наиболее вероятным ответом на эту подсказку будет ONE . Ниже приведены все возможные ответы на эту подсказку, упорядоченные по рангу. Вы можете легко улучшить поиск, указав количество букв в ответе.
Мы думаем, что наиболее вероятным ответом на эту подсказку будет ONE . Ниже приведены все возможные ответы на эту подсказку, упорядоченные по рангу. Вы можете легко улучшить поиск, указав количество букв в ответе.Ранг Слово Подсказка 94% ОДИН Косинус нуля 4% СЕКАНТ Обратное значение косинуса 3% ИНОН Нуль ___ 3% ЛЮБОВЬ Зеро в теннисе 3% НОЛЬ Нуль 3% ГУСИНОЕ ЯЙЦО Нулевой балл (США) 3% АВГУСТА Нуль 3% ОВАЛ Ноль, по сути 3% НИЧЕГО Ноль, ничего 3% НЕТОН Нуль 3% КОЭФФИЦИЕНТ Синус и косинус, например 2% НЕГ Меньше нуля: Сокращение 2% ПЕРВЫЙ МЕРИДИАН Разделительная линия на нулевой долготе 2% АРЕНА В Сиэтле находится единственный в мире завод с нулевым выбросом углерода. 
2% ЭЛЕКТРОННАЯ ПОЧТА Препятствие «Входящие ноль» 2% ЕАХНО ‘Хм . . . ноль шансов! 2% НИЛ Нулевая энергия? Источник гидроэлектроэнергии 2% МОСТЕЛЬ Ноль в фильмах 2% ТРИГФУНКЦИЯ *Синус или косинус, для краткости 2% ДИЕТРК Кола с нулевой калорийностью Уточните результаты поиска, указав количество букв.
 Если какие-то буквы уже известны, вы можете предоставить их в виде шаблона: «CA????».
Если какие-то буквы уже известны, вы можете предоставить их в виде шаблона: «CA????».- Человек, работающий в угольной шахте и работающий с землей в центре? Кроссворд
- *Генеральный прокурор Гарланд Кроссворд Подсказка
- Цели пост-колледжа, например, или намек на то, что ответы, отмеченные звездочкой, постепенно «награждаются» Подсказка кроссворда
- Парижанка в фиолетовых брюках встречается со всеми.
- Девушка делает работу по дому с веселым выражением кроссворда
- Отношения и напряженность могут сделать эту подсказку кроссворда
- Что-то сдалось как ключ к кроссворду пенальти
- Маленькая вспышка света Кроссворд
- Кроссворд первого события серии
- Позднее возвращение, получение приветствия, холод, моральный кроссворд
- Плечевая мышца, Краткая разгадка кроссворда
- Прежний; Разгадка кроссворда предков
- — Разгадка кроссворда Ланселота
- Ничтожество; Кроссворд Пугало
- Джерси, возможно, с большим капюшоном, разгадка кроссворда
- Нервный, раздражительный кроссворд
- Принятие, получение подсказки кроссворда
- Разгадка кроссворда «Камасутра»
- Способность быть идентифицированным, как видели раньше (S, а не Z) Кроссворд Подсказка
- Ноль, пики Кроссворд
- Один, чтобы носить с собой напиток? Кроссворд
- Вечер, В рекламном кроссворде
- Район за пнями, в кроссворде по крикету
- * Более разборчиво, скажи кроссворд
- Впусти в Университет Дьюка после разгадывания кроссворда на хорошую оценку
- Тряпка для носа (неофициальная) Кроссворд
- Рядовой Виктор, Отгадка кроссворда
- Духовная характеристика возрастного кроссворда
- Вставить учетную запись в папку с документами — Easy Crossword Clive
- Был занят светом, который нужно починить? Кроссворд
- Never Fit To Bat On, я забросил кроссворд
- Мать, Испанский Кроссворд
- За наградой за движущийся финальный кроссворд актера
- В Африке веселый магазин Кроссворд
- Кроссворд пользователя Python
- Наговорив слишком много, скажи кроссворд
- Побег из сюжета, вызывающий бурю негодования.
 Кроссворд.
Кроссворд. - Кроссворд Quarter Wood
- Деве нужна прохладная река вокруг части летнего кроссворда
- «Ад — нет ярости…» Кроссворд
- Ничего не положить в олово для неопрятного человека Кроссворд
- Кроссворд «Это никто — бизнес»
- Источники ночного света Кроссворд
- Кроссворд «Острые соусы»
- Серьезный человек услышал подсказку кроссворда
- Это слышно перед тем, как уйти от наказания, пойманное в заговорах с политическим кроссвордом
- Не готов отправить статью с подсказкой кроссворда Clout
- Тема некоторых кроссвордов
- *Кроссворд «Спиральные ракушки»
- *Шрифт без засечек, используемый в Absolut, Best Buy и Supreme Logos Crossword Clue
Найдено 1 решений для Косинус нуля .
 Лучшие решения определяются по популярности, рейтингу и частоте поиска. Наиболее вероятный ответ на подсказку: ОДИН .
Лучшие решения определяются по популярности, рейтингу и частоте поиска. Наиболее вероятный ответ на подсказку: ОДИН .С crossword-solver.io вы найдете 1 решения. Мы используем исторические головоломки, чтобы найти наилучшие ответы на ваш вопрос. Мы добавляем много новых подсказок на ежедневной основе.
С нашей поисковой системой для решения кроссвордов у вас есть доступ к более чем 7 миллионам подсказок. Вы можете сузить возможные ответы, указав количество букв, которые он содержит. Мы нашли более 1 отвечает для косинуса нуля.
Cos 0
Значение cos 0 равно 1.
Здесь мы обсудим значение cos 0 градусов и то, как значения получаются с использованием квадрантов единичного круга. Тригонометрические функции также известны как функция угла, которая связывает углы треугольника с длиной сторон треугольника. Тригонометрические функции являются одной из наиболее важных тем, которые используются при изучении периодических явлений, таких как звуковые и световые волны, изучении гармонических осцилляторов и нахождении средних колебаний температуры.

Три основных тригонометрических соотношения: функция синуса, функция косинуса и функция тангенса. Это обычно определяется для углов меньше прямого угла, тригонометрические функции формулируются как отношение двух сторон прямоугольного треугольника, содержащего угол, в котором значения могут быть найдены в длине различных отрезков линии вокруг единичного круга. Углы треугольника вычисляются относительно функций sin, cos и tan. Обычно градусы представляются как 0°, 30°, 45°, 60°, 90°, 180°, 270° и 360°.
Cos 0 Значение степени
Чтобы определить функцию косинуса острого угла, начните с прямоугольного треугольника ABC с интересующим углом и сторонами треугольника. Три стороны треугольника определяются следующим образом:
- Противоположная сторона определяется как сторона, противоположная углу интереса.
- Сторона гипотенузы — это сторона, противоположная прямому углу, и это самая длинная сторона прямоугольного треугольника
- Прилегающая сторона — это оставшаяся сторона, где она образует сторону как угла интереса, так и прямого угла
Функция косинуса угла равна длине прилегающей стороны, деленной на длину стороны гипотенузы, и формула имеет вид:
Cos θ = смежная сторона / сторона гипотенузы
Значение Cos 0 с использованием единичной окружности
Предположим, что единичная окружность с центром находится в начале координат осей.
 Считайте, что P (a, b) — любая точка на окружности, которая образует угол AOP = x радиан. Это означает, что длина дуги AP равна x. Таким образом, мы определяем, что cos x = a и sin x = b
Считайте, что P (a, b) — любая точка на окружности, которая образует угол AOP = x радиан. Это означает, что длина дуги AP равна x. Таким образом, мы определяем, что cos x = a и sin x = bТеперь рассмотрим треугольник OMP как прямоугольный,
Используя теорему Пифагора, мы получаем
OM 2 + MP 2 = OP 2 915 89 (или) a 915 89 2 = 1
Итак, для каждой точки единичной окружности мы определяем ее как
a 2 + b 2 = 1 (или) cos 2 x + sin 2 x = 1
Отмечается, что один полный оборот составляет угол 2π радиан в центре круга,
∠AOB=π/2,
∠AOC = π и
∠AOD =3π/2.
Поскольку все углы треугольника являются целыми кратными π/2, его обычно называют квадрантным углом. Следовательно, координаты точек A, B, C и D равны (1, 0), (0, 1), (–1, 0) и (0, –1) соответственно. Следовательно, из квадрантных углов мы можем получить значение cos 0
Cos 0° = 1
Теперь, когда мы делаем один полный оборот из точки P, он снова возвращается в ту же точку P.
 Итак, мы также наблюдаем, что значения функций синуса и косинуса не меняются, если x увеличивается или уменьшается на целое число, кратное 2π,
Итак, мы также наблюдаем, что значения функций синуса и косинуса не меняются, если x увеличивается или уменьшается на целое число, кратное 2π,cos (2nπ + x) = cos x, где n ∈ Z … Это означает, что cos x обращается в нуль, когда x является нечетным кратным π/2.
Итак, cos x = 0 подразумевает x = (2n + 1)π/2 , где n принимает любое целое значение.
Для треугольника ABC, стороны которого a, b и c противоположны углам A, B и C, определен закон косинуса.
Рассмотрим угол C, закон косинусов формулируется как
c 2 = a 2 + b 2 – 2ab cos(C)
Таким же образом мы можем получить другие значения cos градусов, такие как 30°, 45°, 60°, 90°, 180 °, 270° и 360°. Кроме того, специальные значения, такие как 0°, 30°, 45°, 60° и 90°, легко запомнить, поскольку все значения присутствуют в первом квадранте. Все функции синусов и косинусов в первом квадранте имеют вид \(\frac{\sqrt{n}}{2}\) или \(\sqrt{\frac{n}{4}}\). Как только мы найдем значения функций синуса, легко найти функции косинуса.

Sin 0 ° = \(\sqrt{\frac{0}{4}}\)
Sin 30 ° = \(\sqrt{\frac{1}{4}}\)
Sin 45 ° = \(\sqrt{\frac{2}{4}}\)
Sin 60 ° = \(\sqrt{\frac{3}{4}}\)
Sin 90 ° = \(\sqrt{\frac{4}{4}}\)
Теперь упростим все полученные значения синуса и представим в виде таблицы:
0 °
30 ° 45 ° 60 ° 90 °
Грех 0
1/2 \(\frac{1}{\sqrt{2}}\) \(\ гидроразрыва {\ sqrt {3}} {2} \) 1 По значениям синуса мы можем легко найти значения функции косинуса. Теперь, чтобы найти значения cos, заполните значения функции синуса в обратном порядке. Это означает, что
Cos 0 ° = Sin 90 °
Cos 30 ° = Sin 60 °
Cos 45 ° = sin 45 °
Cos 60 ° = sin 30 °
Cos 90 ° = sin 0 °
Таким образом, значение cos 0 градусов равно 1, поскольку cos 0 ° = sin 90°
0 °
30 ° 45 ° 60 ° 90 °
Грех 0
1/2 \(\frac{1}{\sqrt{2}}\) \(\ гидроразрыва {\ sqrt {3}} {2} \) 1
Кос 1
\(\ гидроразрыва {\ sqrt {3}} {2} \) \(\frac{1}{\sqrt{2}}\) 1/2 0
Аналогичным образом можно найти значения других степеней тригонометрических функций в зависимости от значения квадранта.
 Ниже приведена таблица тригонометрии, в которой определены все значения функции косинуса вместе с другими тригонометрическими соотношениями.
Ниже приведена таблица тригонометрии, в которой определены все значения функции косинуса вместе с другими тригонометрическими соотношениями.Таблица тригонометрических соотношений Углы (в градусах) 0 30 45 60 90 180 270 360 Углы (в радианах) 0 №/6 №/4 №/3 №/2 № 3π/2 2π грех 0 1/2 1/√2 √3/2 1 0 −1 0 потому что 1 √3/2 1/√2 1/2 0 −1 0 1 желтовато-коричневый 0 1/√3 1 √3 Не определено 0 Не определено 0 детская кроватка Не определено √3 1 1/√3 0 Не определено 0 Не определено косек Не определено 2 √2 2/√3 1 Не определено −1 Не определено сек 1 2/√3 √2 2 Не определено 9{\ circ} = \ frac {\ sqrt {3} + 1} {2 \ sqrt {2}} \) Для получения дополнительной информации о cos 0 и других тригонометрических функциях посетите сайт BYJU’S, а также посмотрите интерактивные видеоролики, чтобы прояснить сомнения.

Ссылки по теме Грех 0 Степень Тригонометрические формулы Обратный косинус Правило косинусов Как использовать функцию Numpy Cos
В этом уроке я покажу вам, как использовать функцию cos Numpy для вычисления тригонометрического косинуса в Python.
Я объясню синтаксис np.cos, как эта функция работает и как ее использовать.
Если вам нужно что-то конкретное, просто нажмите на любую из следующих ссылок.
Содержание:
- Введение в Numpy Cos
- Синтаксис np.cos
- Примеры использования Numpy cos
Но все может иметь больше смысла, если вы начнете читать весь учебник финиш. Начнем с краткого обзора функции косинуса.
Краткое введение в Numpy Cos
Функция cos Numpy очень проста. Он вычисляет тригонометрический косинус в Python, используя пакет Numpy.

Вы можете использовать функцию cos Numpy для вычисления тригонометрического косинуса одного числа, но вы также можете использовать ее для вычисления косинуса для массивов чисел.
Я покажу вам, как сделать и то, и другое, но сначала мы рассмотрим синтаксис.
Синтаксис np.cos
Синтаксис функции косинуса Numpy прост:
Помните, что этот синтаксис предполагает, что вы импортировали Numpy с псевдонимом
np(это общепринятое соглашение).Допустимые форматы для ввода
Давайте посмотрим на допустимые типы ввода для функции np.cos.
В приведенном выше объяснении синтаксиса я обозначил входное значение как «
input».Важно отметить, что это входное значение может принимать несколько возможных форм:
- число (целое или с плавающей запятой)
- Массив Numpy (заполненный числами)
- Список чисел Python или объект, подобный списку
Таким образом, функция np.
 cos будет работать с несколькими различными типами входных данных.
cos будет работать с несколькими различными типами входных данных.Вывод np.cos
Очевидно, функция cos Numpy вычисляет косинус ввода.
При этом точная структура вывода зависит от структуры ввода.
- если на входе одно число, то на выходе будет одно число (косинус входа)
- , если ввод представляет собой массив Numpy, вывод будет массивом Numpy косинусов
- , если ввод представляет собой список чисел Python или объект, подобный списку, вывод будет массивом Numpy косинусов
Дополнительные параметры
В дополнение к входному аргументу, np.cos некоторые необязательные параметры:
- out
- где
Они используются довольно редко, поэтому я не буду их здесь объяснять.
Примеры использования функции cos Numpy
Теперь, когда мы рассмотрели синтаксис np.cos, давайте рассмотрим несколько примеров вычисления косинусов в Python с использованием Numpy.
Примеры:
- Вычислить косинус 0
- Вычислить косинус π/2
- Использовать косинусную функцию Numpy на массиве Numpy .
 код: Импортируйте Numpy и настройте Plotly
код: Импортируйте Numpy и настройте PlotlyПрежде чем запускать примеры, вам нужно запустить небольшой код установки.
В частности, вам нужно импортировать Numpy, чтобы вы могли запустить функцию np.cos.
Вам также потребуется импортировать Plotly (потому что мы будем строить функцию косинуса).
Вам также может потребоваться настроить IDE для построения визуализаций из Plotly.
Импорт пакетов
Сначала мы импортируем Numpy и Plotly.
Вы можете сделать это с помощью следующего кода:
импортировать numpy как np импортировать plotly.express как px
Настройка рендеринга изображения
Далее вам может понадобиться настроить IDE для отображения визуализаций Plotly (мы собираемся использовать Plotly в примере 4).
Причина, по которой вам может понадобиться это сделать, заключается в том, что по умолчанию Plotly пытается отобразить выходные данные визуализации в окнах браузера .
Если вы используете интегрированную среду разработки (например, Spyder, PyCharm и т.
 д.), это может быть проблемой. Если вы используете IDE, вам может потребоваться настроить ее так, чтобы визуализации Plotly отображались в IDE.
д.), это может быть проблемой. Если вы используете IDE, вам может потребоваться настроить ее так, чтобы визуализации Plotly отображались в IDE.Примечание: если вы используете Jupyter, вы можете пропустить этот код !
Чтобы настроить Plotly для рендеринга графиков непосредственно в IDE в виде изображений svg, выполните следующий код:
импортировать plotly.io как pio pio.renderers.default = 'svg'
После того, как вы это сделаете, вы должны быть готовы к работе.
ПРИМЕР 1: Вычисление косинуса числа 0
Начнем с простого примера.
Здесь мы собираемся вычислить косинус 0:
np.cos(0)
ИСХОД:
1,0
Объяснение
Это очень просто.
В этом примере мы используем np.cos для вычисления косинуса 0, который равен 1.
(Обратите внимание, что выход представляет собой число с плавающей запятой, поэтому технически выход равен 1,0)
ПРИМЕР 2: Вычисление косинуса числа π/2
Теперь мы вычислим косинус числа π/2.

np.cos(np.pi/2)
ВЫХОД:
6.123233995736766e-17
Пояснение
Хорошо. Вывод выглядит странно.
Но если вы внимательно присмотритесь, то увидите, что это число представлено в экспоненциальном представлении с показателем степени .
Это очень маленькое число. Эффективно ноль. Это имеет смысл, поскольку косинус числа π/2 равен 0.
ПРИМЕР 3. Используйте функцию косинуса Numpy для массива значений Numpy
Далее мы вычислим косинус массива числовых значений.
Помните, что я упоминал в разделе о синтаксисе: косинус Numpy может работать с одним числовым значением, но он также может работать со списками, спископодобными объектами и массивами Numpy.
Создать массив Numpy
Здесь мы собираемся использовать Numpy linspace для создания массива из 300 равномерно расположенных чисел.
x_values = np.linspace (начало = -np.pi * (3/2), стоп = np.pi * (3/2), число = 300)
После запуска кода
x_values будет содержать 300 равномерно расположенных чисел от до .
Вычисление косинуса с помощью Numpy
Далее мы будем использовать этот массив значений x в качестве входных данных для косинуса Numpy; мы будем использовать np.cos для вычисления косинусов входных данных.
cosine_values = np.cos (x_values)
И мы можем взглянуть на первые 10 значений:
cosine_values[1:10]
ВЫХОД:
массив ([-0,99977921, -0,99
5, -0,99801351, -0,99646937, -0,99448523, -0,994, -0,98 9, -0,985
, -0,98216893])
Объяснение
Это довольно просто.
Здесь вводом для np.cos является массив чисел.
Результатом является поэлементный косинус каждого значения этого входного массива.
ПРИМЕР 4: Нанесите значения косинуса с помощью Plotly
Наконец, давайте нанесем на график значения косинуса, которые мы только что вычислили в примере 3.
Здесь мы будем использовать линейную функцию Plotly, px.line, для создания линейного графика.
 значений косинуса.
значений косинуса.px.line (x = x_values, y = cosine_values)
OUT:
Объяснение
Здесь мы нанесли значения косинуса, которые мы вычислили с помощью np.cos в примере 3.
Мы использовали значения, содержащиеся в
x_values в качестве входных данных по оси x для px.line.А по оси Y мы отложили значения косинуса в массиве
cosine_values , который мы вычислили с помощью np.cos.Оставьте свои другие вопросы в комментариях ниже
У вас есть другие вопросы о том, как использовать np.cos для вычисления значений косинуса в Python?
Если да, оставьте свои вопросы в разделе комментариев ниже.
Присоединяйтесь к нашему курсу, чтобы узнать больше о Numpy
В этом уроке я объяснил, как вычислить тригонометрический косинус в Python, используя Numpy cos.
Это должно помочь вам с вычислением косинусов и выполнением тригонометрических операций, но если вы действительно хотите изучить Numpy, вам предстоит еще многому научиться.


 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
 При любом а.
При любом а.  ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда. Полноценный ответ будет:
Полноценный ответ будет: ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.) Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)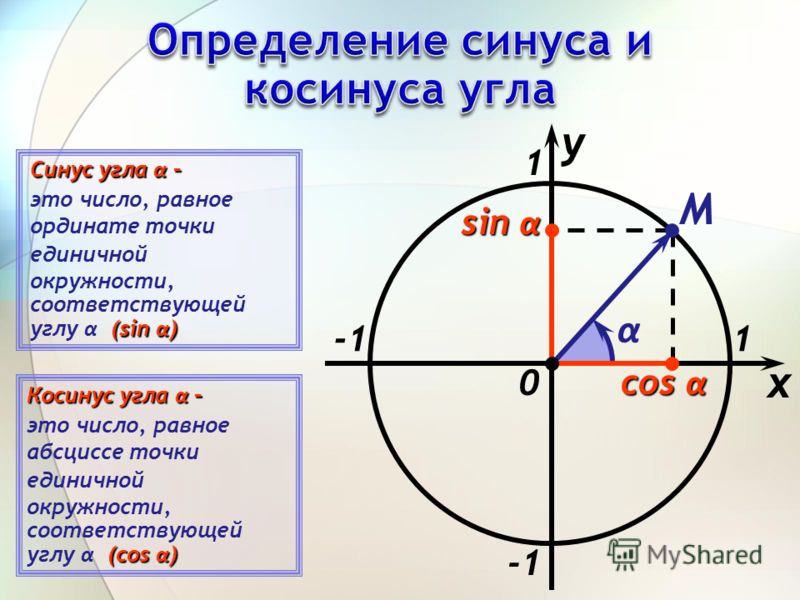 п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.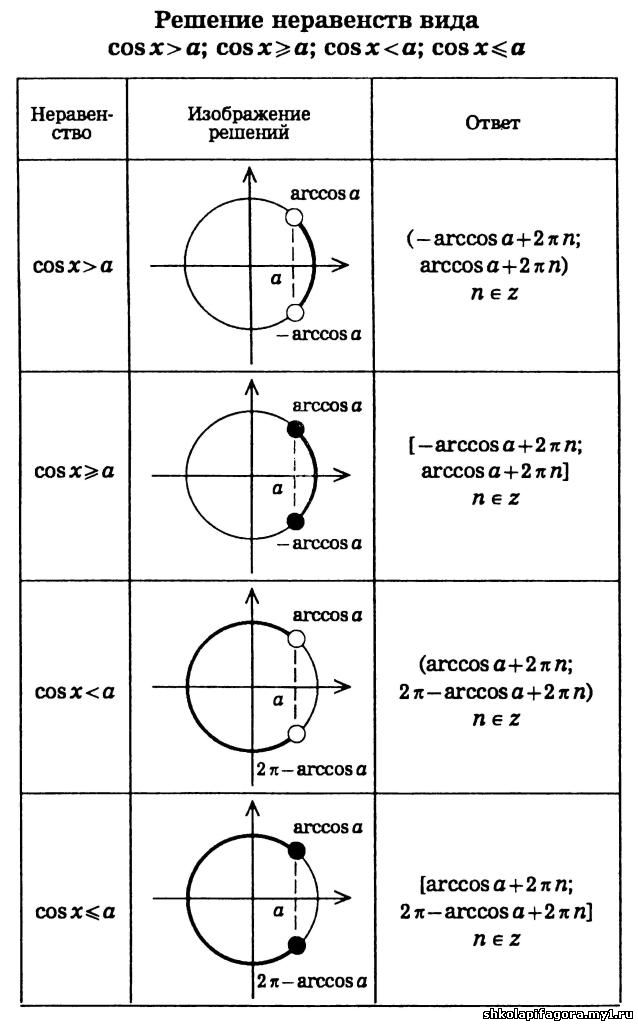 А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)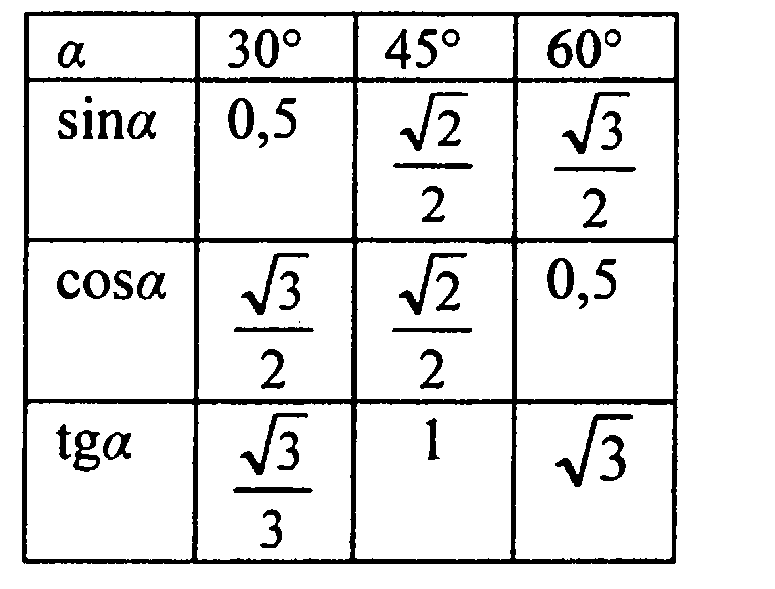

 x = n,
x = n, x =/2+n
x =/2+n



 Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.
Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.
 Запишите формулы корней уравнений
cosx=a ,| a |
Запишите формулы корней уравнений
cosx=a ,| a | 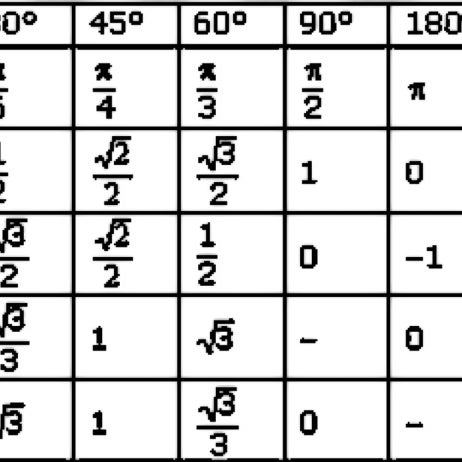
 5) sin x+cosx=2.
5) sin x+cosx=2. Они здесь выписаны, проанализируем их и вспомним, откуда они получились.
Они здесь выписаны, проанализируем их и вспомним, откуда они получились.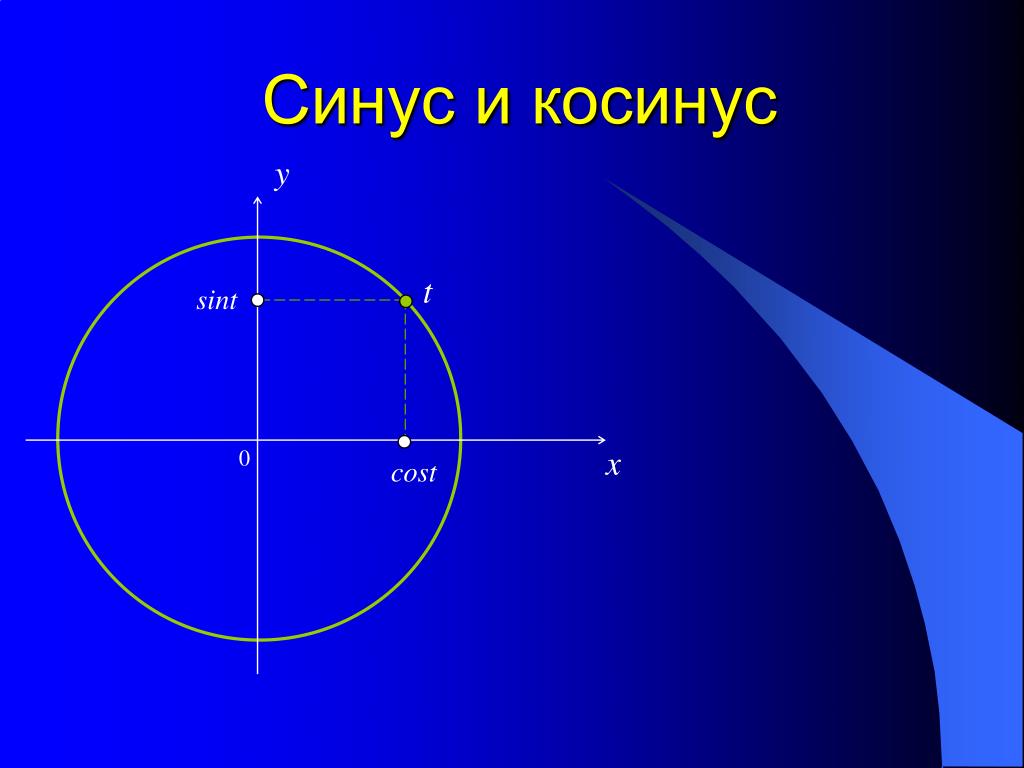 Этому помогают формулы приведения (Рис. 3). Напомним их:
Этому помогают формулы приведения (Рис. 3). Напомним их: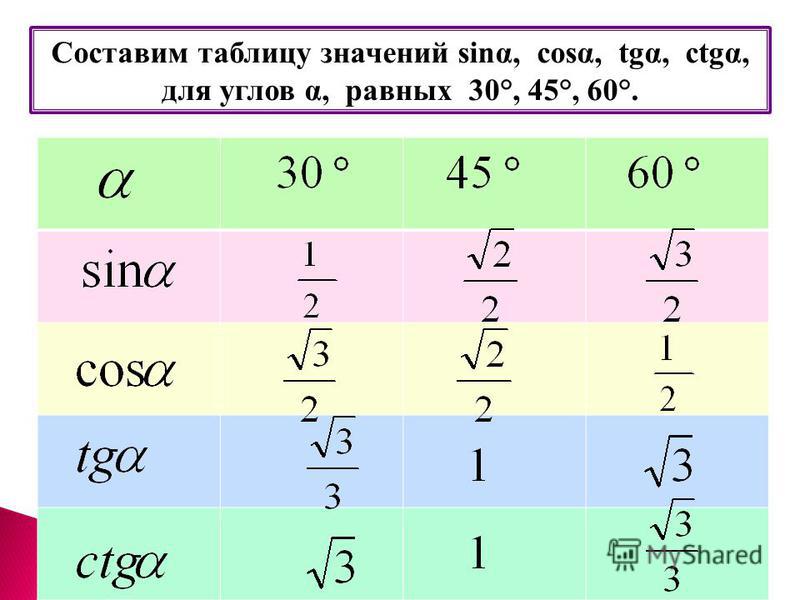
 Таким образом, для данной типовой задачи мы нашли синус и косинус 120° и проиллюстрировали факт нахождения на чертеже.
Таким образом, для данной типовой задачи мы нашли синус и косинус 120° и проиллюстрировали факт нахождения на чертеже. Двум точкам соответствуют два угла. Один угол α1, второй угол – α2.
Двум точкам соответствуют два угла. Один угол α1, второй угол – α2.

 gif
gif д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.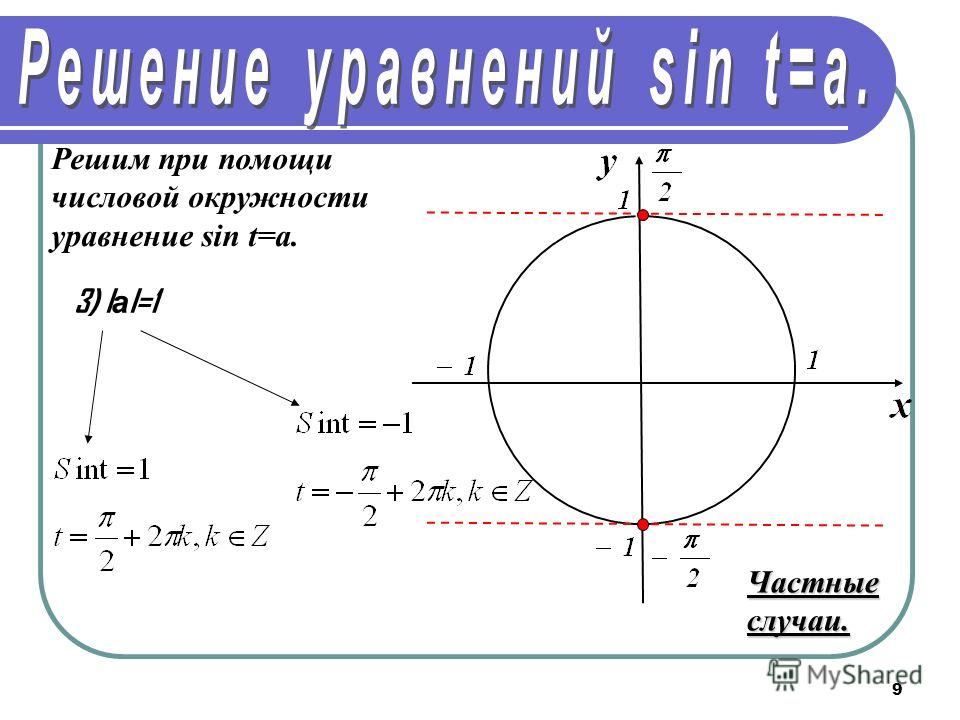 Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!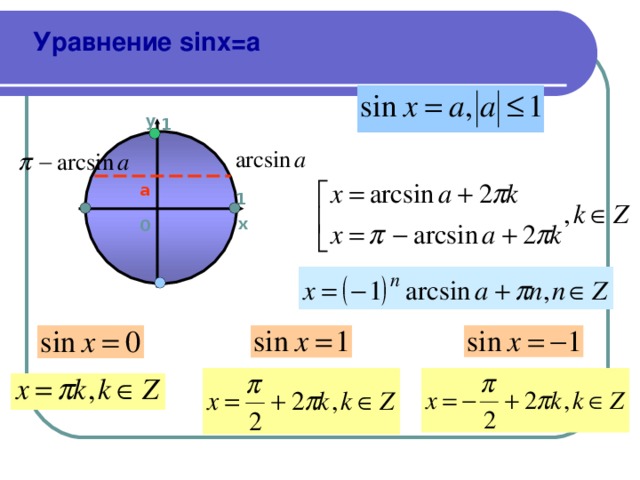 Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.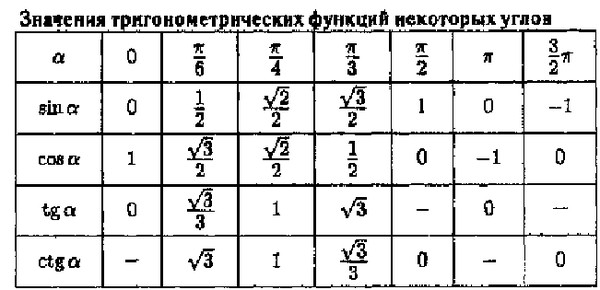
 n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z` 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`. При | a | > 1 уравнение не имеет корней, по-скольку | cosx | 1 или при а
При | a | > 1 уравнение не имеет корней, по-скольку | cosx | 1 или при а
 $$
$$ Хотя их свойства, такие как законы сложения, сохраняются, они со временем теряют всякую связь с треугольниками.
Хотя их свойства, такие как законы сложения, сохраняются, они со временем теряют всякую связь с треугольниками.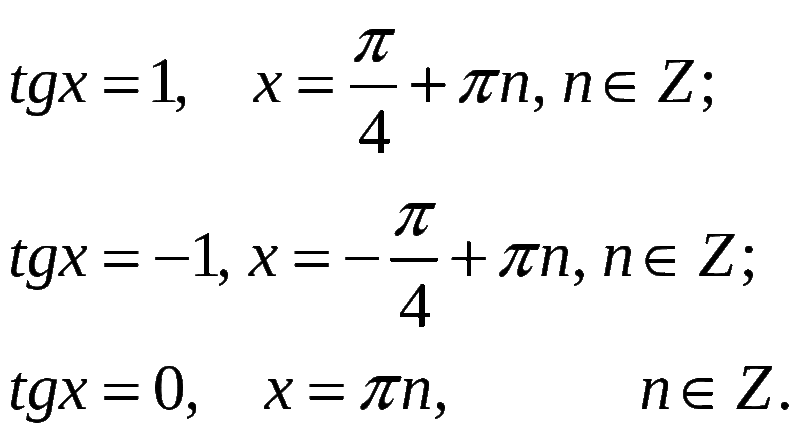 $$ Важным отличием здесь является то, что 9\circ)$ можно «наблюдать» только в треугольнике с двумя прямыми углами. Вы можете интерпретировать это по-разному: вырожденный треугольник с одной вершиной в бесконечно удаленной точке; предел $\lim_{h\to\infty}\frac{\text{a}}{\text{h}}$; возможно как-то иначе.
$$ Важным отличием здесь является то, что 9\circ)$ можно «наблюдать» только в треугольнике с двумя прямыми углами. Вы можете интерпретировать это по-разному: вырожденный треугольник с одной вершиной в бесконечно удаленной точке; предел $\lim_{h\to\infty}\frac{\text{a}}{\text{h}}$; возможно как-то иначе.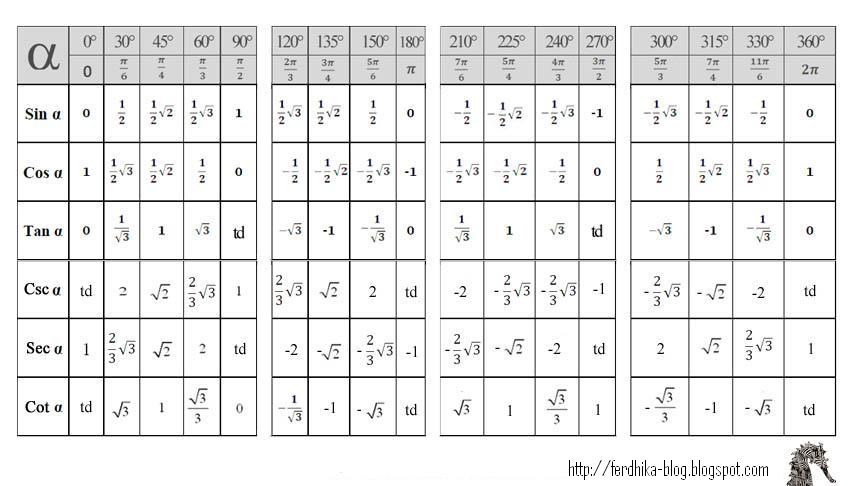
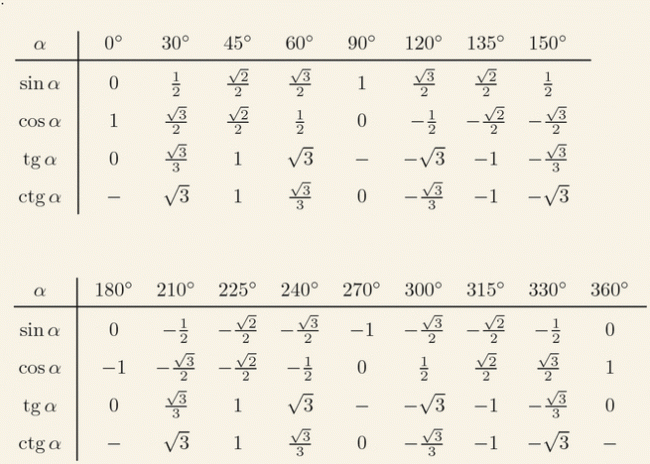
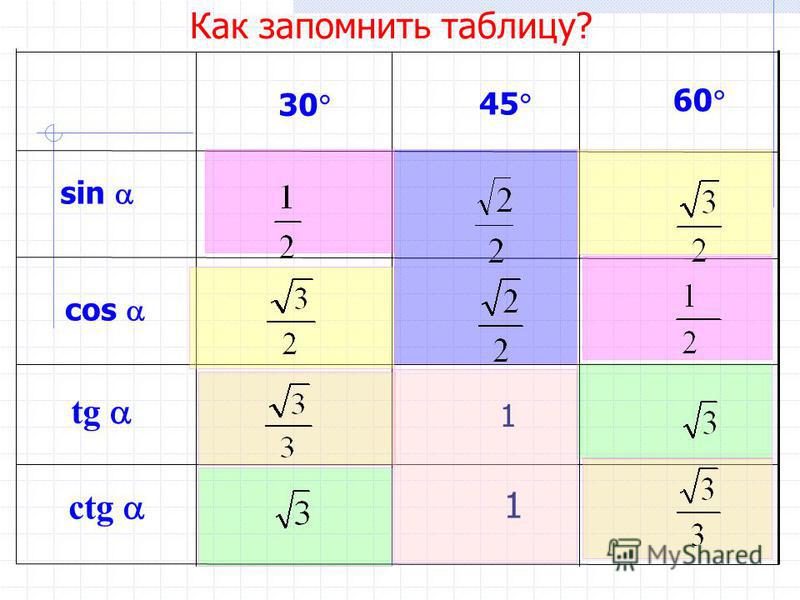 Но как я могу это показать? 9na)=0$ для всех $a>0$, но я не знаю как.
Но как я могу это показать? 9na)=0$ для всех $a>0$, но я не знаю как. Но в определении предполагается, что $\sin 0=0$. Следовательно, $\sin x>0$ при $x>0$.
Но в определении предполагается, что $\sin 0=0$. Следовательно, $\sin x>0$ при $x>0$. 93-8
93-8 Мы думаем, что наиболее вероятным ответом на эту подсказку будет ONE . Ниже приведены все возможные ответы на эту подсказку, упорядоченные по рангу. Вы можете легко улучшить поиск, указав количество букв в ответе.
Мы думаем, что наиболее вероятным ответом на эту подсказку будет ONE . Ниже приведены все возможные ответы на эту подсказку, упорядоченные по рангу. Вы можете легко улучшить поиск, указав количество букв в ответе.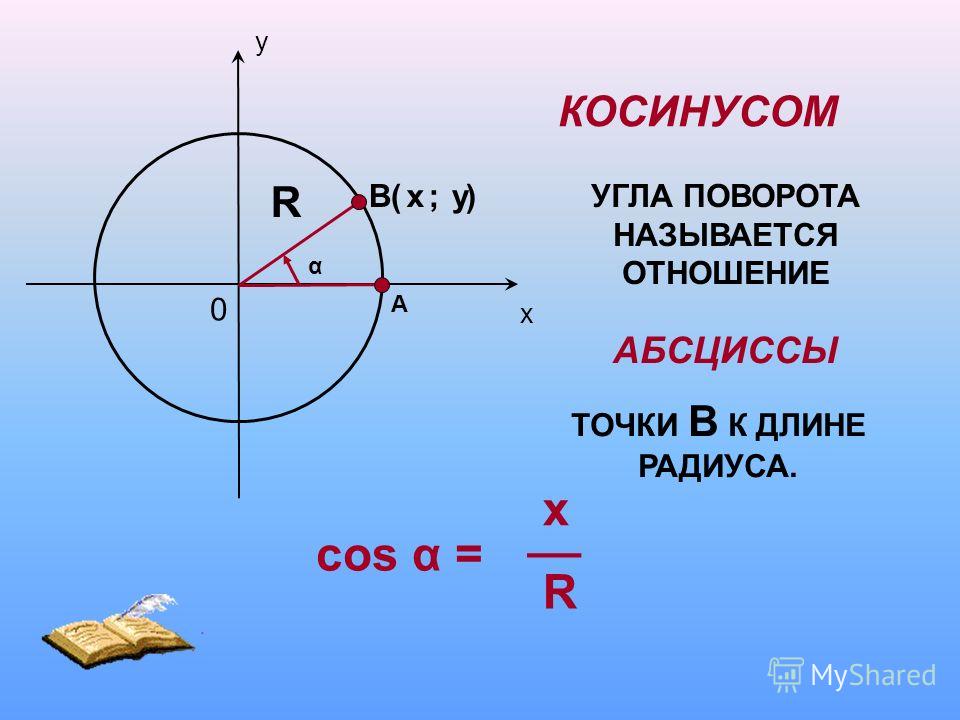
 Если какие-то буквы уже известны, вы можете предоставить их в виде шаблона: «CA????».
Если какие-то буквы уже известны, вы можете предоставить их в виде шаблона: «CA????».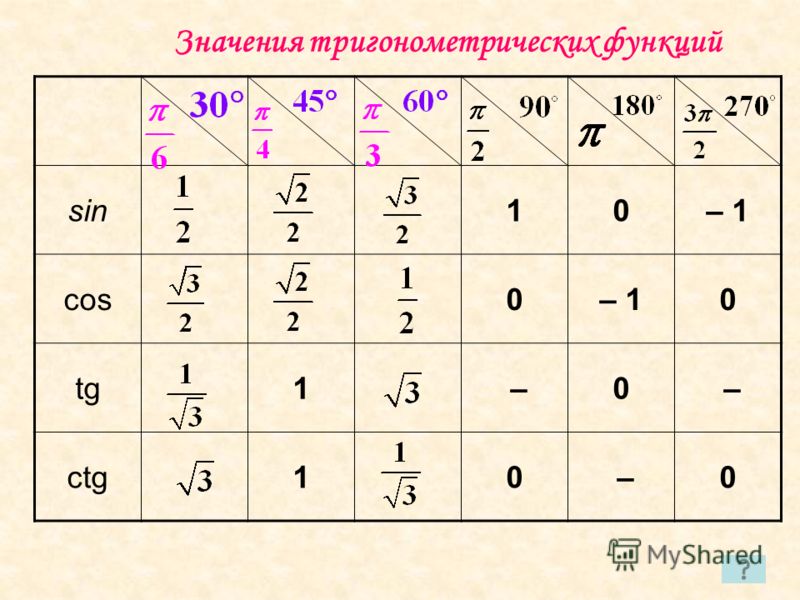 Кроссворд.
Кроссворд.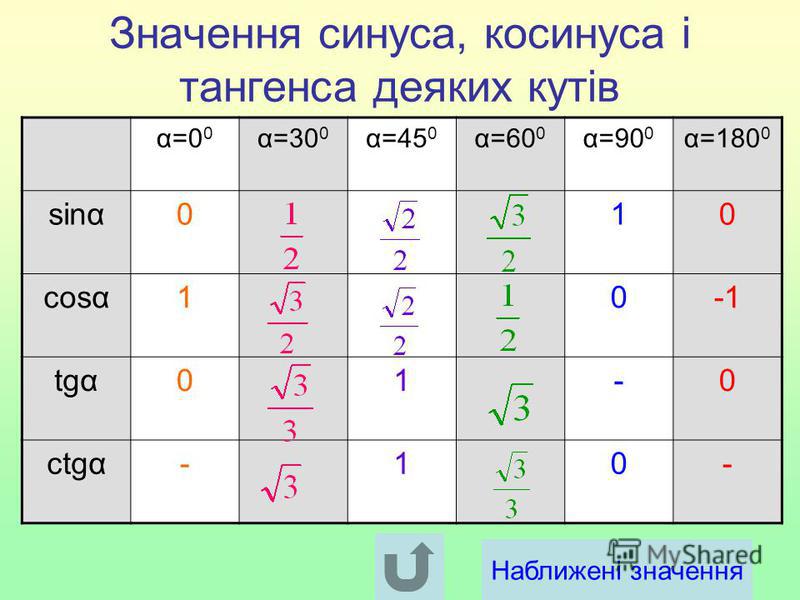 Лучшие решения определяются по популярности, рейтингу и частоте поиска. Наиболее вероятный ответ на подсказку: ОДИН .
Лучшие решения определяются по популярности, рейтингу и частоте поиска. Наиболее вероятный ответ на подсказку: ОДИН .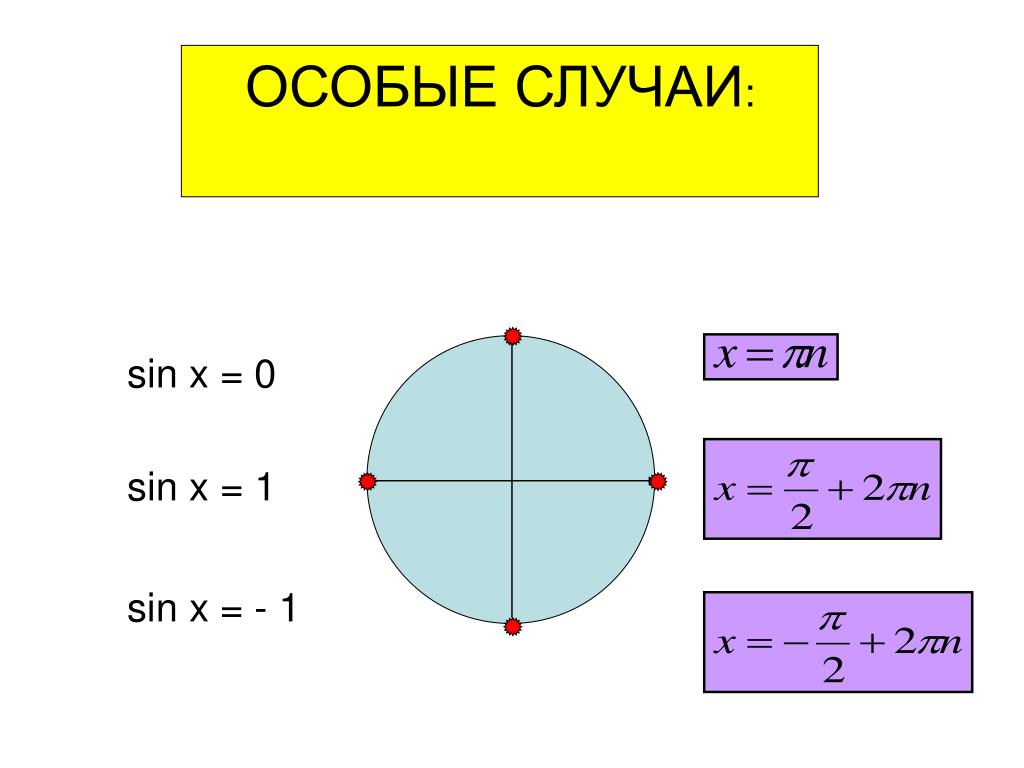
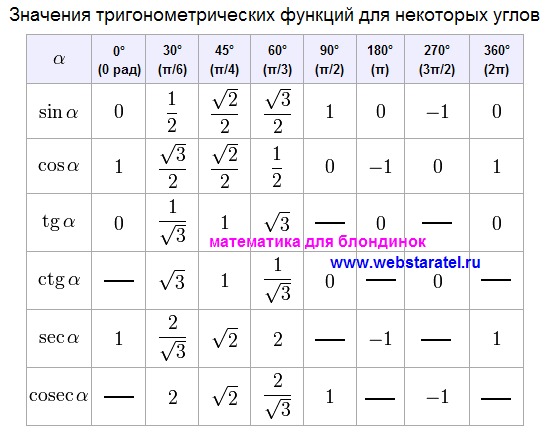 Считайте, что P (a, b) — любая точка на окружности, которая образует угол AOP = x радиан. Это означает, что длина дуги AP равна x. Таким образом, мы определяем, что cos x = a и sin x = b
Считайте, что P (a, b) — любая точка на окружности, которая образует угол AOP = x радиан. Это означает, что длина дуги AP равна x. Таким образом, мы определяем, что cos x = a и sin x = b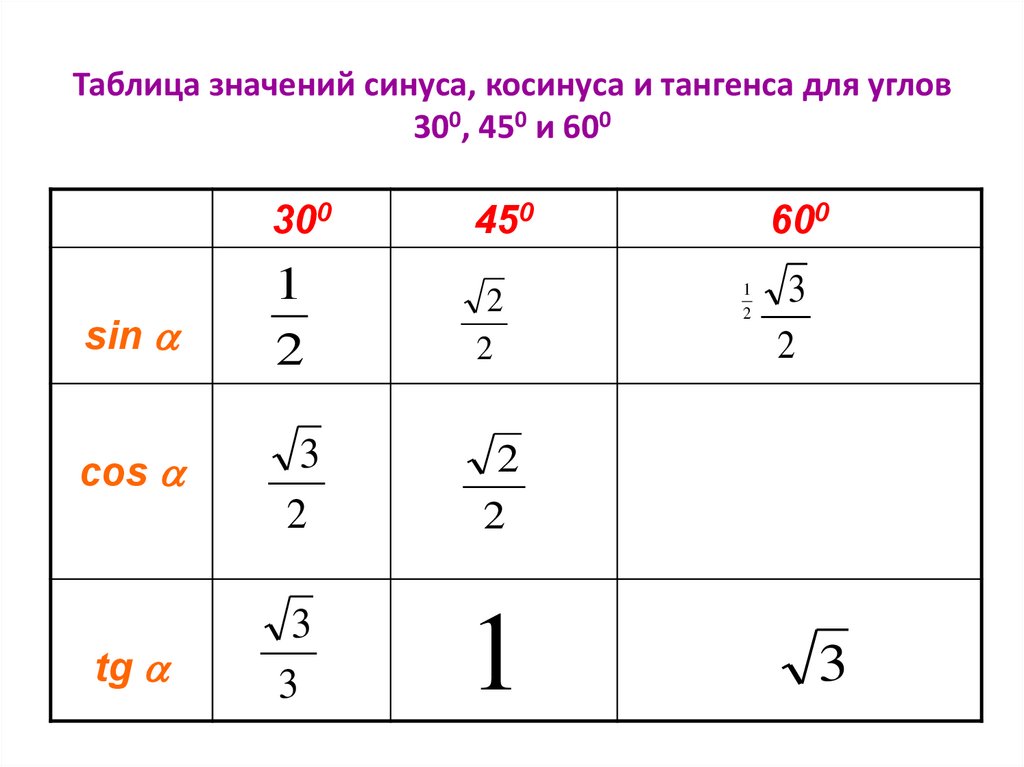 Итак, мы также наблюдаем, что значения функций синуса и косинуса не меняются, если x увеличивается или уменьшается на целое число, кратное 2π,
Итак, мы также наблюдаем, что значения функций синуса и косинуса не меняются, если x увеличивается или уменьшается на целое число, кратное 2π,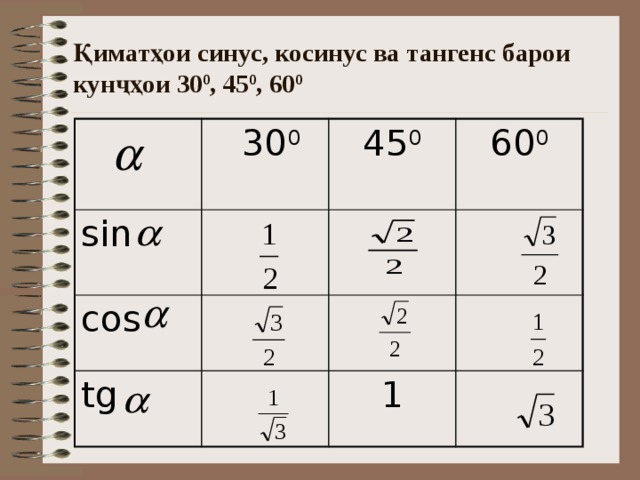
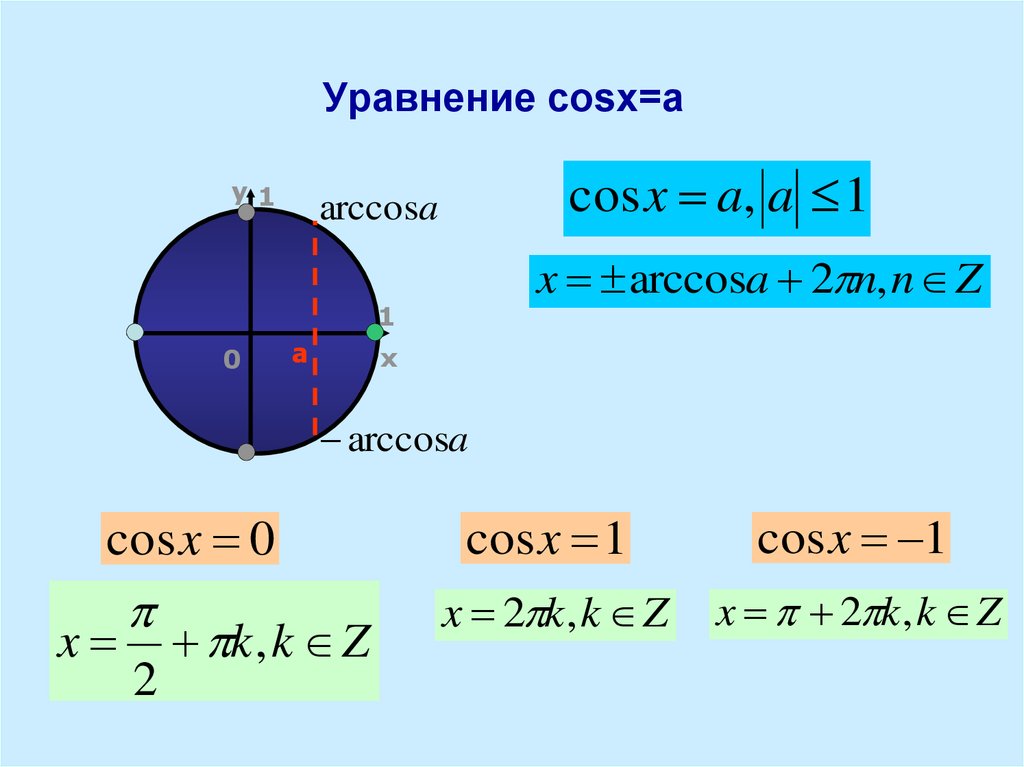 Ниже приведена таблица тригонометрии, в которой определены все значения функции косинуса вместе с другими тригонометрическими соотношениями.
Ниже приведена таблица тригонометрии, в которой определены все значения функции косинуса вместе с другими тригонометрическими соотношениями.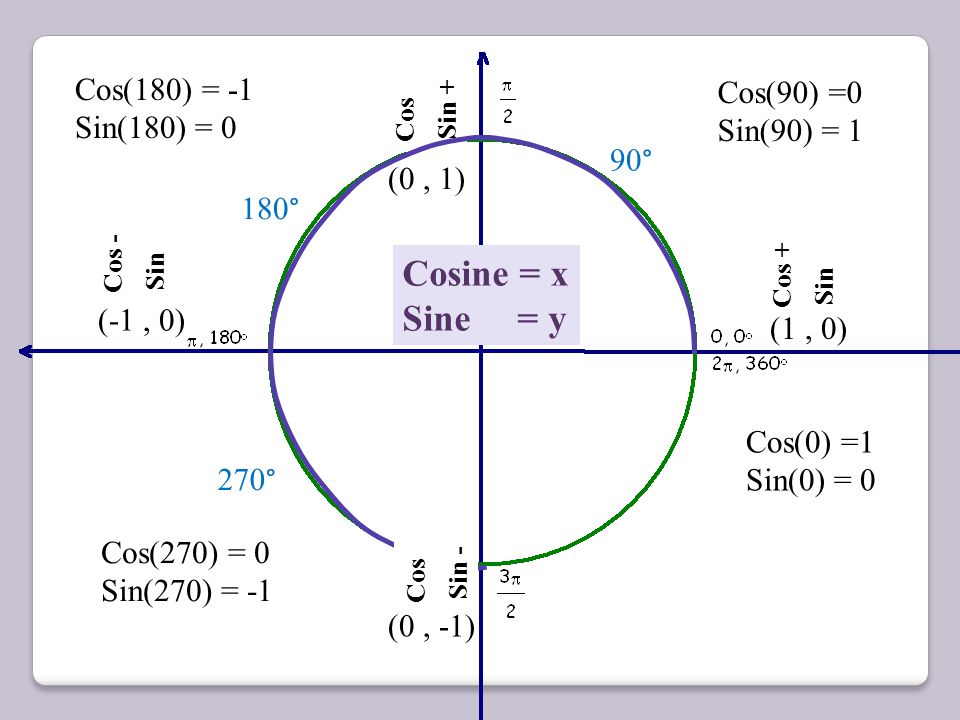

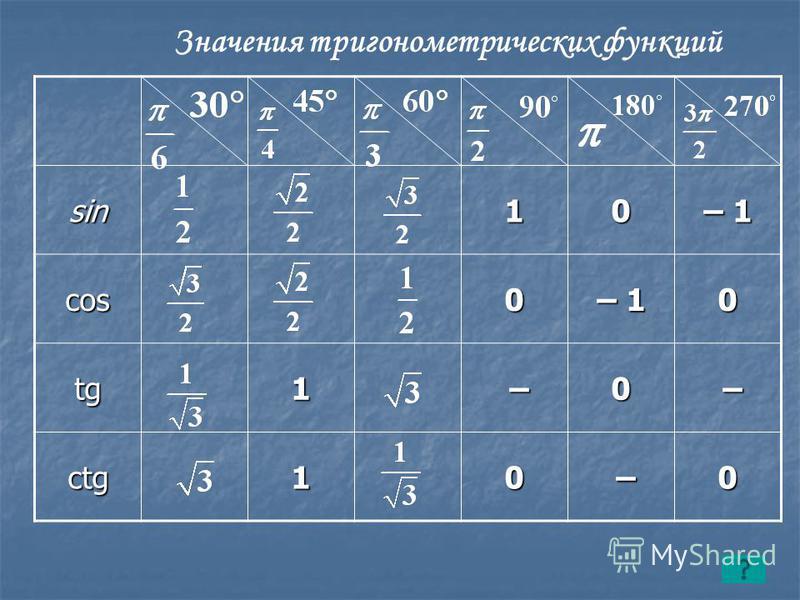 cos будет работать с несколькими различными типами входных данных.
cos будет работать с несколькими различными типами входных данных.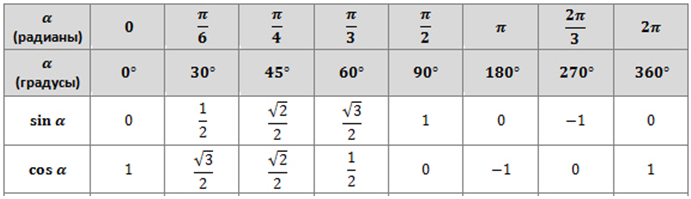 код: Импортируйте Numpy и настройте Plotly
код: Импортируйте Numpy и настройте Plotly д.), это может быть проблемой. Если вы используете IDE, вам может потребоваться настроить ее так, чтобы визуализации Plotly отображались в IDE.
д.), это может быть проблемой. Если вы используете IDE, вам может потребоваться настроить ее так, чтобы визуализации Plotly отображались в IDE.
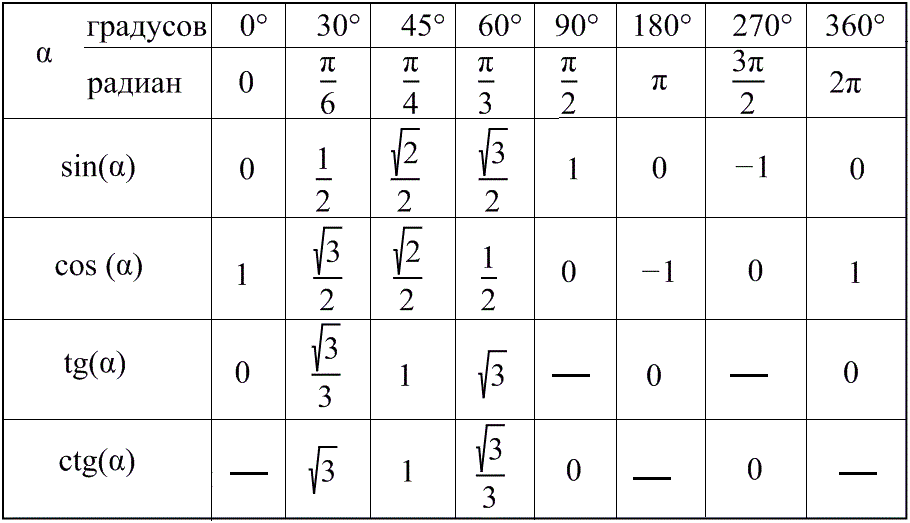
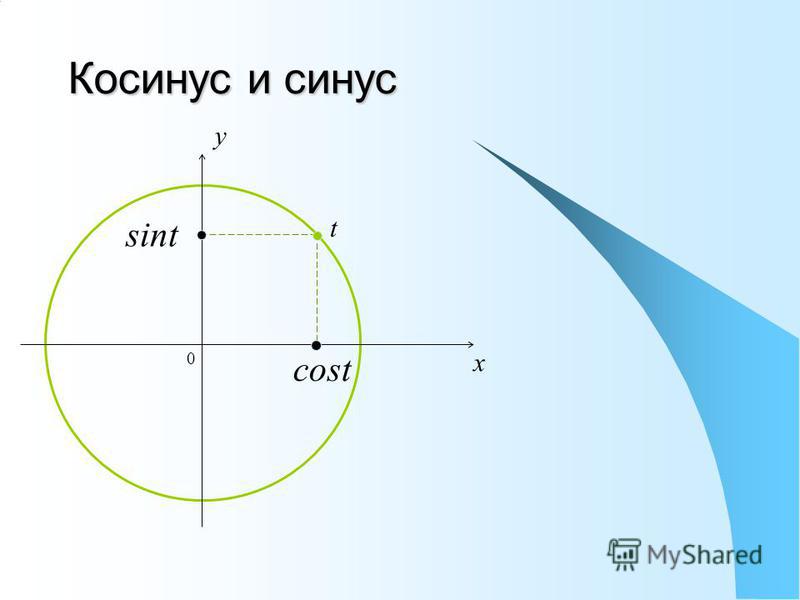 значений косинуса.
значений косинуса.