Перевод обыкновенной дроби в десятичную дробь и обратно, правила, примеры.
Зачастую дети, которые учатся в школе, интересуются, для чего в им в реальной жизни может понадобится математика, в особенности те разделы, которые уже заходят намного дальше, чем простой счет, умножение, деление, суммирование и отнимание. Многие взрослые также задаются данным вопросом, если их профессиональная деятельность очень далека от математики и разнообразных вычислений. Однако стоит понимать, что ситуации бывают всякие, и порой никак не обойтись без той самой, пресловутой школьной программы, от которой мы так пренебрежительно отказывались в детстве. К примеру, вовсе не все знают, как перевести дробь в десятичную дробь, а такие знания могут чрезвычайно пригодится, для удобства счета. Для начала, нужно полностью убедиться, что нужная вам дробь может быть преобразована в конечную десятичную. То же самое касается и процентов, которые также можно легко перевести в десятичные дроби.
Проверка обычной дроби на возможность перевода ее в десятичную
Прежде, чем что-либо считать, необходимо убедиться, что полученная в итоге десятичная дробь будет конечной, иначе она окажется бесконечной и высчитать окончательный вариант будет попросту невозможно. Причем бесконечные дроби также могут быть периодическими и простыми, но это уже тема для отдельного раздела.
Перевести обыкновенную дробь в ее конечный, десятичный вариант можно только в том случае, если ее уникальный знаменатель способен раскладываться только на множители 5 и 2 (простые множители). Причем даже в том случае, если они повторяются произвольное количество раз.
Уточним, что оба эти числа являются простыми, так в итоге разделить без остатка их можно только на самих себя, или же, на единицу. Таблицу простых чисел можно отыскать без проблем в сети интернет, это вовсе не сложно, хотя непосредственного отношения к нашему счету она и не имеет.
Рассмотрим примеры:
Дробь 7/40 поддается преобразованию из обычной дроби в ее десятичный эквивалент, потому что ее знаменатель можно без труда разложить на множители 2 и 5.
Однако, если первый вариант даст в результате конечную десятичную дробь, то, к примеру, 7/60 уже никак не даст подобного результата, так как ее знаменатель не будет уже раскладываться на искомые нами числа, а будет иметь в числе множителей знаменателя тройку.
Перевести обычную дробь в десятичную возможно несколькими способами
После того, как стало понятно, какие дроби можно переводить из обычных в десятичные, можно приступить, собственно, к самому преобразованию. На самом деле, нет ничего сверхсложного, даже для того, у кого школьная программа окончательно «выветрилась» из памяти.
Как переводить дроби в десятичные: наиболее простой метод
Этот способ перевода обычной дроби в десятичную, действительно, является наиболее простым, однако многие люди даже не догадываются о его бренном существовании, так как в школе все эти «прописные истины» кажутся ненужными и не очень-то важными. Между тем, разобраться сможет не только взрослый, но легко воспримет подобную информацию и ребенок.
Итак, чтобы преобразовать дробь в десятичную, нужно умножить числитель, равно как и знаменатель, на одно число. Однако все не так просто, так в результате, именно в знаменателе должно получиться 10, 100, 1000, 10 000, 100 000 и так далее, до бесконечности. Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.
Рассмотрим примеры:
Допустим, нам нужно провести преобразование дроби 6/20 в десятичную. Производим проверку:
После того, как мы убедились, что перевести дробь в десятичную дробь, да еще и конечную, все же, возможно, так как ее знаменатель легко раскладывается на двоечки и пятерки, следует приступить к самому переводу. Самым лучшим вариантом, по логике вещей, чтобы умножить знаменатель и получить результат 100, является 5, так как 20х5=100.
Можно рассмотреть дополнительный пример, для наглядности:
Второй и боле популярный способ
переводить дроби в десятичныеВторой вариант несколько сложнее, однако он пользуется большей популярностью, ввиду того, что он гораздо проще для понимания. Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.
Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.
Стоит запомнить
Для того, что правильно преобразовать простую, то есть обычную дробь в ее десятичный эквивалент, нужно числитель разделить на знаменатель. По сути, дробь – это и есть деление, с этим не поспоришь.
Рассмотрим действие на примере:
Итак, первым делом, чтобы перевести дробь 78/200 в десятичную, нужно ее числитель, то есть число 78, разделить на знаменатель 200. Но первым делом, что должно войти в привычку, нужно произвести проверку, о которой уже говорилось выше.
После произведения проверки, нужно вспомнить школу и делить числитель на знаменатель «уголком» или «столбиком».
Как видите, все предельно просто, и семи пядей во лбу, чтобы легко решать подобные задачки вовсе быть не требуется. Для простоты и удобства приведем также и таблицу самых популярных дробей, которые просто запомнить, и даже не прилагать усилий, чтобы их переводить.
Как перевести проценты в десятичную дробь : нет ничего прощеВот наконец дошел ход и до процентов, которые, оказывается, как гласит все та же, школьная программа, можно перевести в десятичную дробь. Причем тут все будет еще гораздо проще, и пугаться не стоит. Справятся с задачей даже те, кто не заканчивал университеты, а пятый класс школы вовсе прогулял и ничего не смыслит в математике.
Причем тут все будет еще гораздо проще, и пугаться не стоит. Справятся с задачей даже те, кто не заканчивал университеты, а пятый класс школы вовсе прогулял и ничего не смыслит в математике.
Начать, пожалуй, нужно с определения, то есть разобраться, что такое, собственно, проценты. Процент – это одна сотая часть от какого-либо числа, то есть, абсолютно произвольно. От сотни, к примеру, это будет единица и так далее.
Таким образом, чтобы перевести проценты в десятичную дробь, нужно попросту убрать значок %, а потом разделить само число на сотню.
Рассмотрим примеры:
Причем, чтобы произвести обратную «конвертацию», нужно попросту сделать все наоборот, то есть, число нужно умножить на сотню и приписать к нему значок процента. Точно таким же образом, посредством применения полученных знаний, можно также и обычную дробь перевести в проценты. Для этого достаточно будет просто сперва преобразовать обычную дробь в десятичную, а потому уже ее перевести в проценты, а также легко можно произвести и обратное действие.
Путь наименьшего сопротивления: удобные онлайн сервисы
Бывает и так, что считать совершенно не хочется, да и попросту нет времени. Именно для таких случаев, или же, особо ленивых пользователей, в сети интернет есть множество удобных и простых в применении сервисов, которые позволят перевести обычные дроби, а также проценты, в десятичные дроби. Это действительно дорога наименьшего сопротивления, потому пользоваться подобными ресурсами – одно удовольствие.
Полезный справочный портал «Калькулятор»
Для того, чтобы воспользоваться сервисом «Калькулятора», достаточно просто перейти по ссылке http://www.calc.ru/desyatichnyye-drobi.html , и ввести необходимые числа в нужные поля. Причем ресурс позволяет переводить в десятичные, как обычные, так и смешанные дроби.
После краткосрочного ожидания, приблизительно секунды в три, сервис выдаст конечный результат.
Точно таким же образом можно перевести в обычную дробь десятичную.
Онлайн-калькулятор на «Математическом ресурсе» Calcs.su
Еще одним, очень полезным сервисом можно назвать калькулятор дробей на «Математическом ресурсе. Тут также не придется ничего считать самостоятельно, просто выберите из предложенного списка то, что вам нужно и вперед, за орденами.
Далее, в отведенное специально для этого поле, нужно ввести искомое число процентов, которые и нужно преобразовать в обычную дробь. Причем если вам нужны десятичные дроби, то вы легко можете уже сами справиться с задачей перевода или же воспользоваться тем калькулятором, который для этого и предназначен.
В конечном итоге, стоит обязательно добавить, что сколько бы новомодных сервисов не было бы придумано, сколько ресурсов не предлагали бы вам свои услуги, но и голову тренировать периодически не помешает. Потому стоит обязательно применять полученные знания, тем более, что вы потом с гордостью сможете помогать делать уроки собственным детям, а затем и внукам. Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.
Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.
Дробь может быть преобразована в целое число либо в десятичную дробь. Неправильная дробь, числитель которой больше знаменателя и делится на него без остатка, переводится в целое число, например: 20/5. Делим 20 на 5 и получаем число 4. Если дробь правильная, то есть числитель меньше знаменателя, то тогда преобразовать ее в число (десятичную дробь). Больше информации о дробях вы сможете почерпнуть из нашего раздела — .
Способы преобразования дроби в число
- Первый способ, как перевести дробь в число годится для дроби, которую можно преобразовать в число, являющееся десятичной дробью. Сначала выясним, можно ли перевести заданную дробь в дробь десятичную. Для этого обратим внимание на знаменатель (цифра, которая под чертой или справа от наклонной). Если знаменатель можно разложить на множители (в нашем примере — 2 и 5), которые могут повторяться, то данную дробь реально преобразовать в конечную десятичную дробь.
 Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275
Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275 - Второй способ, как перевести дробь в число — более простой: необходимо числитель поделить на знаменатель. Для применения этого способа просто произведем деление, а полученное число и будет той искомой десятичной дробью. Например, надо перевести дробь 2/15 в число. Делим 2 на 15. Получаем 0, 1333… — бесконечная дробь. Записываем так: 0,13(3).
 Если дробь неправильная, то есть числитель больше знаменателя (например, 345/100), то в результате преобразования ее в число получится целое числовое значение или десятичная дробь с целой дробной частью. В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
Если дробь неправильная, то есть числитель больше знаменателя (например, 345/100), то в результате преобразования ее в число получится целое числовое значение или десятичная дробь с целой дробной частью. В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
Самый простой способ по переводу дроби в число — это использование калькулятора или иного вычислительного прибора. Укажем сначала числитель дроби, потом нажмем кнопку со значком «разделить» и набираем знаменатель. После нажатия клавиши «=» мы получаем искомое число.
Пытаясь решить математические задачи с дробями, школьник понимает, что ему недостаточно одного только желания решить эти задачи. Также необходимы и знания по вычислениям с дробными числами. В некоторых задачах все начальные данные подаются в условии в дробном виде.
Такие модификации помогают приводить дроби к общему знаменателю. Это нужно для того, чтобы получить возможность проводить вычитание или сложение дробных чисел. При их умножении и делении общий знаменатель не требуется. Можно рассмотреть на примере, как перевести число в дробь и потом произвести сложение двух дробных чисел. Допустим надо сложить число 12 и дробное число 3/4. Первое слагаемое (число 12) приводится к виду 12/1. Однако его знаменатель равен 1 в то время, как у второго слагаемого он равен 4.
В результате умножения получится: 12/1=48/4. Если 48 разделить на 4, то получается 12, значит дробь приведена к правильному знаменателю. Таким образом можно заодно и понять, как дробь перевести в целое число. Это касается только неправильных дробей, потому что у них числитель больше, чем знаменатель. В таком случае числитель делится на знаменатель и, если не получается остатка, будет целое число. С остатком же дробь так и остается дробью, но с выделенной целой частью. Теперь относительно приведения к общему знаменателю на рассмотренном примере. Если бы у первого слагаемого знаменатель был бы равен какому-нибудь другому числу, кроме 1, числитель и знаменатель первого числа надо бы было умножить на знаменатель второго, а числитель и знаменатель второго — на знаменатель первого.
Оба слагаемых приведены к их общему знаменателю и готовы к сложению. Получается, что в данной задаче нужно сложить два числа: 48/4 и 3/4. При сложении двух дробей с одинаковым знаменателем суммировать нужно только их верхние части, то есть числители. Знаменатель суммы останется без изменения. В этом примере должно получиться 48/4+3/4=(48+3) /4=51/4. Это и будет результат сложения. Но в математике принято неправильные дроби приводить к правильным. Выше рассматривалось, как превратить дробь в число, но в этом примере не получится целое число из дроби 51/4, так как число 51 не делится без остатка на число 4. Поэтому нужно выделить целую часть данной дроби и ее дробную часть. Целой частью будет то число, которое получается при делении нацело первого же меньшего, чем 51, числа.
То есть то, которое можно разделить на 4 без остатка. Первое число перед числом 51, которое нацело делится на 4, будет число 48. Разделив 48 на 4, получается число 12. Значит целой частью искомой дроби будет 12. Осталось только найти дробную часть числа. Знаменатель дробной части остается тем же, то есть 4 в данном случае. Чтобы найти числитель дробной части, надо от исходного числителя вычесть то число, которое делилось на знаменатель без остатка. В рассматриваемом примере требуется для этого вычесть из числа 51 число 48. То есть числитель дробной части равен 3. Результатом сложения будет 12 целых и 3/4. То же самое делается и при вычитании дробей. Допустим надо из целого числа 12 вычесть дробное число 3/4. Для этого целое число 12 переводится в дробное 12/1, а затем приводится к общему знаменателю со вторым числом — 48/4.
Осталось только найти дробную часть числа. Знаменатель дробной части остается тем же, то есть 4 в данном случае. Чтобы найти числитель дробной части, надо от исходного числителя вычесть то число, которое делилось на знаменатель без остатка. В рассматриваемом примере требуется для этого вычесть из числа 51 число 48. То есть числитель дробной части равен 3. Результатом сложения будет 12 целых и 3/4. То же самое делается и при вычитании дробей. Допустим надо из целого числа 12 вычесть дробное число 3/4. Для этого целое число 12 переводится в дробное 12/1, а затем приводится к общему знаменателю со вторым числом — 48/4.
При вычитании точно так же знаменатель обеих дробей остается без изменения, а с их числителями и проводят вычитание. То есть от числителя первой дроби вычитают числитель второй. В данном примере это будет 48/4-3/4=(48-3) /4=45/4. И опять получилась неправильная дробь, которую надо привести к правильной. Для выделения целой части определяют первое до 45 число, которое делится на 4 без остатка. Это будет 44. Если число 44 разделить на 4, получится 11. Значит целая часть итоговой дроби равна 11. В дробной части также знаменатель оставляют без изменения а из числителя исходной неправильной дроби вычитают то число, которое делилось на знаменатель без остатка. То есть надо из 45 вычесть 44. Значит числитель в дробной части равен 1 и 12-3/4=11 и 1/4.
Это будет 44. Если число 44 разделить на 4, получится 11. Значит целая часть итоговой дроби равна 11. В дробной части также знаменатель оставляют без изменения а из числителя исходной неправильной дроби вычитают то число, которое делилось на знаменатель без остатка. То есть надо из 45 вычесть 44. Значит числитель в дробной части равен 1 и 12-3/4=11 и 1/4.
Если дано одно число целое и одно дробное, но его знаменатель равен 10, то проще второе число перевести в десятичную дробь, а потом производить вычисления. Например надо сложить целое число 12 и дробное число 3/10. Если число 3/10 записать в виде десятичной дроби, получится 0,3. Теперь значительно легче к 12 прибавить 0,3 и получить 2,3, чем приводить дроби к общему знаменателю, производить вычисления, а затем выделять целую и дробную части из неправильной дроби. Даже самые простые задачки с дробными числами предполагают, что школьник (или студент) знает, как перевести целое число в дробь. Эти правила слишком просты и легко запоминаются.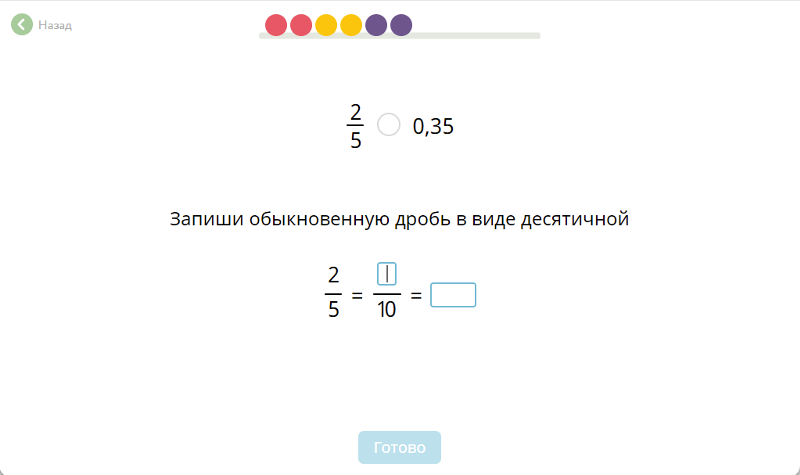
Преобразование обыкновенной дроби в десятичную
Допустим, мы хотим преобразовать обыкновенную дробь 11/4 в десятичную. Проще всего сделать это так:
2∙2∙5∙5 |
Это удалось нам потому, что в данном случае разложение знаменателя на простые множители состоит только из двоек. Мы дополнили это разложение еще двумя пятерками, воспользовались тем, что 10 = 2∙5, и получили десятичную дробь. Подобная процедура возможна, очевидно, тогда и только тогда, когда разложение знаменателя на простые множители не содержит ничего, кроме двоек и пятерок. Если в разложении знаменателя присутствует любое другое простое число, то такую дробь в десятичную преобразовать нельзя. Тем не менее, мы попробуем это сделать, но только другим способом, с которым мы познакомимся на примере всё той же дроби 11/4. Давайте поделим 11 на 4 «уголком»:
Если в разложении знаменателя присутствует любое другое простое число, то такую дробь в десятичную преобразовать нельзя. Тем не менее, мы попробуем это сделать, но только другим способом, с которым мы познакомимся на примере всё той же дроби 11/4. Давайте поделим 11 на 4 «уголком»:
В строке ответа мы получили целую часть ( 2 ), и еще у нас есть остаток ( 3 ). Раньше мы деление на этом заканчивали, но теперь мы знаем, что к делимому ( 11 ) можно приписать справа запятую и несколько нулей, что мы теперь мысленно и сделаем. Следом после запятой идет разряд десятых. Ноль, который стоит у делимого в этом разряде, припишем к полученному остатку ( 3 ):
Теперь деление можно продолжать как ни в чем не бывало. Надо только не забыть поставить в строке ответа запятую после целой части:
Теперь приписываем к остатку ( 2 ) ноль, который стоит у делимого в разряде сотых и доводим деление до конца:
В результате получаем, как и раньше,
Попробуем теперь точно таким же способом вычислить, чему равна дробь 27/11:
Мы получили в строке ответа число 2,45, а в строке остатка — число 5
. Но такой остаток нам уже раньше встречался. Поэтому мы уже сразу можем сказать, что, если мы продолжим наше деление «уголком», то следующей цифрой в строке ответа будет 4, затем пойдет цифра 5, потом — снова 4 и снова 5, и так далее, до бесконечности:
Но такой остаток нам уже раньше встречался. Поэтому мы уже сразу можем сказать, что, если мы продолжим наше деление «уголком», то следующей цифрой в строке ответа будет 4, затем пойдет цифра 5, потом — снова 4 и снова 5, и так далее, до бесконечности:
27 / 11 = 2,454545454545…
Мы получили так называемую периодическую десятичную дробь с периодом 45. Для таких дробей применяется более компактная запись, в которой период выписывается только один раз, но при этом он заключается в круглые скобки:
2,454545454545… = 2,(45).
Вообще говоря, если делить «уголком» одно натуральное число на другое, записывая ответ в виде десятичной дроби, то возможно только два исхода: (1) либо рано или поздно в строке остатка мы получим ноль, (2) либо там окажется такой остаток, который уже нам раньше встречался (набор возможных остатков ограничен, поскольку все они заведомо меньше делителя). В первом случае результатом деления является конечная десятичная дробь, во втором случае — периодическая.
Преобразование периодической десятичной дроби в обыкновенную
Пусть нам дана положительная периодическая десятичная дробь с нулевой целой частью, например:
a = 0,2(45).
Как преобразовать эту дробь обратно в обыкновенную?
Умножим ее на число 10 k , где k — это число цифр, стоящих между запятой и открывающей круглой скобкой, обозначающей начало периода. В данном случае k = 1 и 10 k = 10:
a ∙ 10 k = 2,(45).
Полученный результат умножим на 10 n , где n — «длина» периода, то есть число цифр, заключенных между круглыми скобками. В данном случае n = 2 и 10 n = 100:
a ∙ 10 k ∙ 10 n = 245,(45).
Теперь вычислим разность
a ∙ 10 k ∙ 10 n − a ∙ 10 k = 245,(45) − 2,(45).
Поскольку дробные части у уменьшаемого и вычитаемого одинаковы, то у разности дробная часть равна нулю, и мы приходим к простому уравнению относительно a :
a ∙ 10 k ∙ (10 n − 1) = 245 − 2.
Решается это уравнение с помощью следующих преобразований:
a ∙ 10 ∙ (100 − 1) = 245 − 2.
a ∙ 10 ∙ 99 = 245 − 2.
245 − 2 | ||
10 ∙ 99 |
Мы специально пока не доводим вычисления до конца, чтобы было наглядно видно, как можно сразу выписать этот результат, опуская промежуточные рассуждения. Уменьшаемое в числителе ( 245 ) — это дробная часть числа
a = 0,2(45)
если в ее записи стереть скобки. Вычитаемое в числителе ( 2
) — это непериодическая часть числа а , располагающаяся между запятой и открывающей скобкой. Первый сомножитель в знаменателе ( 10
) — это единица, к которой приписано столько нулей, сколько цифр в непериодической части (k ). Второй сомножитель в знаменателе ( 99
) — это столько девяток, сколько цифр содержит период (n ).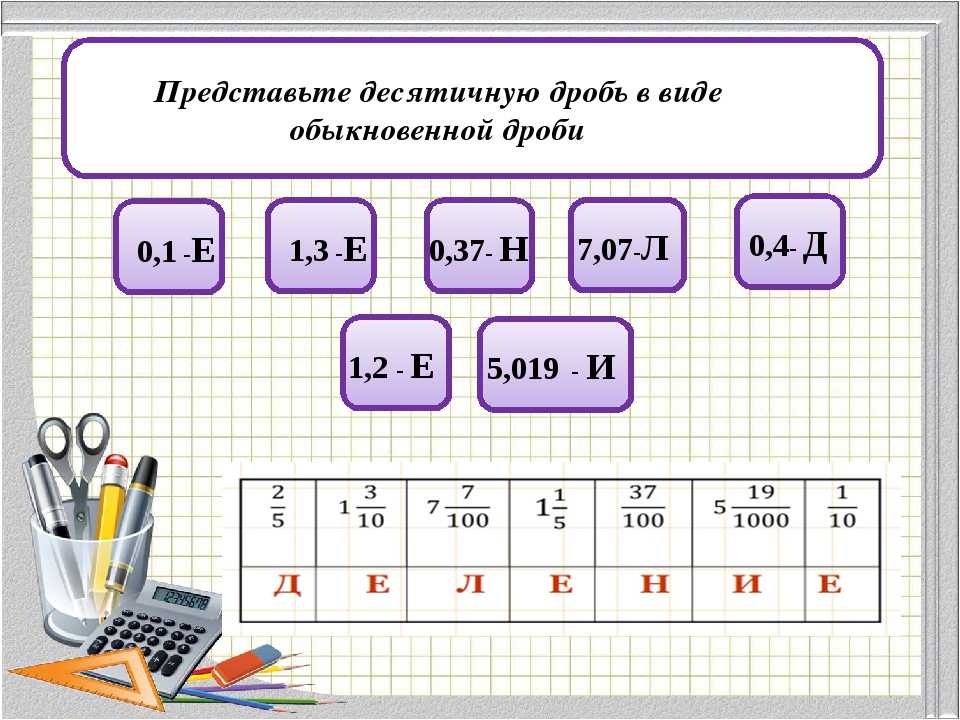
Теперь наши вычисления можно довести до конца:
Здесь в числителе стоит период, а в знаменателе — столько девяток, сколько цифр в периоде. После сокращения на 9 полученная дробь оказывается равной
Подобным же образом,
Десятичная дробь состоит из двух частей, которые разделены запятыми. Первая часть — это целая единица, вторая часть — это десятки (если число после запятой одно), сотни (два числа после запятой, как два нуля в ста), тысячные итд. Посмотрим на примеры десятичной дроби: 0, 2; 7, 54; 235,448; 5,1; 6,32; 0,5. Всё это — десятичные дроби. Как же перевести десятичную дробь в обыкновенную?
Пример первый
У нас есть дробь, к примеру, 0,5. Как уже выше писалось, она состоит из двух частей. Первое число 0, показывает, сколько целых единиц у дроби. В нашем случае их нет. Второе число показывает десятки. Дробь даже читается ноль целых пять десятых. Десятичное число перевести в дробь теперь не составит труда, пишем 5/10. Если видите, что у цифр есть общий делитель, можете сократить дробь. У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
Пример второй
Возьмем более сложную дробь — 2,25. Читается она так — две целых и двадцать пять сотых. Обратите внимание — сотых, так как чисел после запятой две. Теперь можно перевести в обыкновенную дробь. Записываем — 2 25/100. Целая часть — 2, дробная 25/100. Как и в первом примере, эту часть можно сократить. Общим делителем для цифр 25 и 100 является число 25. Заметьте, что мы всегда подбираем наибольший общий делитель. Разделив обе части дроби на НОД, получили 1/4. Итак, 2, 25 это 2 1/4.
Пример третий
И для закрепления материала возьмем десятичную дробь 4,112 — четыре целых и сто двенадцать тысячных. Почему тысячных, думаю, ясно. Записываем теперь 4 112/1000. По алгоритму находим НОД чисел 112 и 1000. В нашем случае — это число 6. Получаем 4 14/125.
Вывод
- Разбиваем дробь на целую и дробную части.
- Смотрим, сколько цифр после запятой. Если одна — это десятки, две — сотни, три -тысячные итд.

- Записываем дробь в обыкновенном виде.
- Сокращаем числитель и знаменатель дроби.
- Записываем полученную дробь.
- Выполняем проверку, делим верхнюю часть дроби на нижнюю. Если есть целая часть, прибавляем к полученной десятичной дроби. Получился исходный вариант — замечательно, значит, вы все сделали правильно.
На примерах я показала, как можно перевести десятичную дробь в обыкновенную. Как видите, сделать это очень легко и просто.
Как узнать наибольшую десятичную дробь. Сравнение конечных и бесконечных десятичных дробей: правила, примеры, решения
РАЗДЕЛ 7 ДЕСЯТИЧНЫЕ ДРОБИ И ДЕЙСТВИЯ С НИМИ
В разделе узнаете:
что такое десятичная дробь и каково его строение;
как сравнивать десятичные дроби;
какие правила сложения и вычитания десятичных дробей;
как найти произведение и частное двух десятичных дробей;
что такое округление числа и как округлять числа;
как применить изученный материал на практике
§ 29. ЧТО ТАКОЕ ДЕСЯТИЧНАЯ ДРОБЬ. СРАВНЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ
ЧТО ТАКОЕ ДЕСЯТИЧНАЯ ДРОБЬ. СРАВНЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ
Посмотрите на рисунок 220. Вы видите, что длина отрезка АВ равна 7 мм, а длина отрезка DC — 18 мм. Чтобы подать длины этих отрезков в сантиметрах, надо использовать дроби:
Вы знаете много других примеров, когда используются дроби со знаменателями 10,100, 1000 и тому подобное. Так,
Такие дроби называют десятичными. Для их записи используют более удобную форму, которую подсказывает линейка с вашего принадлежностей. Обратимся к рассматриваемому примеру.
Вы знаете, что длину отрезка DC (рис. 220) можно выразить смешанным числом
Если после целой части этого числа поставить запятую, а после нее — числитель дробной части, то получим более компактный запись: 1,8 см. Для отрезка АВ тогда получим: 0,7 см. Действительно, дробь является правильным, он меньше единицы, поэтому его целая часть равна 0. Числа 1,8 и 0,7 — примеры десятичных дробей.
Десятичная дробь 1,8 читают так: «одна целая восемь десятых» , а дробь 0,7 — «ноль целых семь десятых».
Как записать дроби в виде десятичных дробей? Для этого надо знать строение записи десятичной дроби.
В записи десятичной дроби всегда является целая и дробная части. их разделяет запятая. В целой части классы и разряды такие же, как у натуральных чисел. Вы знаете, что это — классы единиц, тысяч, миллионов и т. д., а в каждом из них по 3 разряды — единиц, десятков и сотен. В дробной части десятичной дроби классы не выделяют, а разрядов может быть сколько угодно, их названия соответствуют названиям знаменателей дробей — десятые, сотые, тысячные, десятитысячные, стотысячные, миллионные, десятимільйонні тому подобное. Разряд десятых является старейшим в дробной части десятичной дроби.
В таблице 40 вы видите названия разрядов десятичной дроби и число «сто двадцать три целых и четыре тысячи пятьсот шесть стотысячных» или
Название дробной части «стотысячных» в обыкновенной дроби определяет ее знаменатель, а в десятичной — последний разряд его дробной части. Вы видите, что в числителе дробной части числа цифр на одну меньше, чем нулей в знаменателе. Если не учесть этого, то в записи дробной части получим ошибку — вместо 4506 стотысячных запишем 4506 десятитысячных, но
Если не учесть этого, то в записи дробной части получим ошибку — вместо 4506 стотысячных запишем 4506 десятитысячных, но
Поэтому в записи данного числа десятичной дробью надо поставить 0 после запятой (в разряде десятых): 123,04506.
Обратите внимание:
в десятичной дроби после запятой должно стоять столько цифр, сколько нулей в знаменателе соответствующей обыкновенной дроби.
Можем теперь записать дроби
в виде десятичных.
Десятичные дроби можно сравнивать так же, как и натуральные числа. Если в записи десятичных дробей много цифр, то пользуются специальными правилами. Рассмотрим примеры.
Задача. Сравните дроби: 1) 96,234 и 830,123; 2) 3,574 и 3,547.
Решения. 1, Целая часть первого дроби — двухцифровое число 96, а целая часть дроби второго — трицифрове число 830, поэтому:
96,234
2. В записях дробей 3,574 и 3,547 и целые части равны. Поэтому сравниваем поразрядно их дробные части Для этого запишем данные дроби друг под другом:
Каждый из дробей имеет 5 десятых. Но в первом дроби 7 сотых, а во втором — лишь 4 сотые. Поэтому первая дробь больше второй: 3,574 > 3,547.
Но в первом дроби 7 сотых, а во втором — лишь 4 сотые. Поэтому первая дробь больше второй: 3,574 > 3,547.
Правила сравнения десятичных Дробей.
1. Из двух десятичных дробей больше то, у которого целая часть больше.
2. Если целые части десятичных дробей равны, то сравнивают их дробные части поразрядно, начиная со старшего разряда.
Как и обыкновенные дроби, десятичные дроби можно разместить на координатном луче. На рисунке 221 вы видите, что точки А, В и С имеют координаты: А(0,2), Б(0,9), С(1,6).
Узнайте больше
Десятичные дроби связаны с десятичной позиционной системой счисления. Однако их появление имеет более давнюю историю и связана с именем выдающегося математика и астронома ал-Каши (полное имя — Джемшид ибн-Масудал-Каши). В работе «Ключ к арифметике» (XV вв.) он впервые сформулировал правила действий с десятичными дробями, привел примеры выполнения действий с ними. Ничего не зная об открытии ал-Каши, вторично «открыл» десятичные дроби примерно через 150 лет фламандский математик и инженер Симон Стевін. В труде «Децималь» (1585 p
.)
С. Стевін изложил теорию десятичных дробей. Он всячески пропагандировал их, подчеркивая удобство десятичных дробей для практических вычислений.
В труде «Децималь» (1585 p
.)
С. Стевін изложил теорию десятичных дробей. Он всячески пропагандировал их, подчеркивая удобство десятичных дробей для практических вычислений.
Отделять целую часть от дробной десятичной дроби предлагали по-разному. Так, ал-Каши целую и дробную части писал разными чернилами или ставил между ними вертикальную черту. С. Стевін для отделения целой части от дробной ставил ноль в кружочке. Принятую в наше время запятую предложил известный немецкий астроном Иоганн Кеплер (1571 — 1630).
РЕШИТЕ ЗАДАЧИ
1173. Запишите в сантиметрах длину отрезка АВ, если:
1)АВ = 5мм; 2)АВ = 8мм; 3)АВ = 9мм; 4)АВ = 2мм.
1174. Прочитайте дроби:
1)12,5; 3)3,54; 5)19,345; 7)1,1254;
2)5,6; 4)12,03; 6)15,103; 8)12,1065.
Назовите: а) целую часть дроби; б) дробную часть дроби; в) разряды дроби.
1175. Приведите пример десятичной дроби, в которой после запятой стоит:
1) одна цифра; 2) две цифры; 3) три цифры.
1176. Сколько знаков после запятой имеет десятичная дробь, если знаменатель соответствующего обыкновенной дроби равна:
1)10; 2)100; 3)1000; 4) 10000?
1177. У которого из дробей больше целая часть:
У которого из дробей больше целая часть:
1) 12,5 или 115,2; 4) 789,154 или 78,4569;
2) 5,25 или 35,26; 5) 1258,00265 или 125,0333;
3) 185,25 или 56,325; 6) 1269,569 или 16,12?
1178. В числе 1256897 отделите запятой последнюю цифру и прочитайте число, которое получили. Затем последовательно переставьте запятую на одну цифру влево и называйте дроби, которые вы получили.
1179. Прочитайте дроби и запишите их в виде десятичной дроби:
1180 Прочитайте дроби и запишите их в виде десятичной дроби:
1181. Запишите обычным дробью:
1) 2,5; 4)0,5; 7)315,89; 10)45,089;
2)125,5; 5)12,12; 8)0,15; 11)258,063;
3)0,9; 6)25,36; 9) 458;,025; 12)0,026.
1182. Запишите обычным дробью:
1)4,6; 2)34,45; 3)0,05; 4)185,342.
1183. Запишите десятичной дробью:
1) 8 целых 3 десятых; 5) 145 целых 14 сотых;
2) 12 целых 5 десятых; 6) 125 целых 19 сотых;
3) 0 целых 5 десятых; 7) 0 целых 12 сотых;
4) 12 целых 34 сотых; 8) 0 целых 3 сотые.
1184. Запишите десятичной дробью:
1) нуль целых восемь тысячных;
2) двадцать целых четыре сотых;
3) тринадцать целых пять сотых;
4) сто сорок пять целых две сотых.
1185. Запишите долю в виде обыкновенной дроби, а затем в виде десятичной дроби:
1)33:100; 3)567:1000; 5)8:1000;
2)5:10; 4)56:1000; 6)5:100.
1186. Запишите в виде смешанного числа, а затем в виде десятичной дроби:
1)188:100; 3)1567:1000; 5)12548:1000;
2)25:10; 4)1326:1000; 6)15485:100.
1187. Запишите в виде смешанного числа, а затем в виде десятичной дроби:
1)1165:100; 3)2546:1000; 5)26548:1000;
2) 69: 10; 4) 1269: 1000; 6) 3569: 100.
1188. Выразите в гривнях:
1) 35 к.; 2) 6 к.; 3)12 грн 35 коп.; 4)123к.
1189. Выразите в гривнях:
1) 58 к.; 2) 2 к.; 3)56 грн 55 коп.; 4)175к.
1190. Запиши в гривнях и копейках:
1)10,34 грн; 2) 12,03 грн; 3) 0,52 грн; 4) 126,05 грн.
1191. Выразите в метрах и ответ запишите десятичной дробью: 1) 5 м 7 дм; 2) 15 м 58 см; 3) 5 м 2 мм; 4) 12 м 4 дм 3 см 2 мм.
1192. Выразите в километрах и ответ запишите десятичной дробью: 1) 3 км 175 м; 2) 45 км 47 м; 3) 15 км 2 м.
1193. Запишите в метрах и сантиметрах:
1) 12,55 м; 2) 2,06 м; 3) 0,25 м; 4) 0,08 м.
1194. Наибольшая глубина Черного моря составляет 2,211 км. Выразите глубину моря в метрах.
1195. Сравните дроби:
1) 15,5 и 16,5; 5) 4,2 и 4,3; 9) 1,4 и 1,52;
2) 12,4 и 12,5; 6) 14,5 и 15,5; 10) 4,568 и 4,569;
3)45,8 и 45,59; 7) 43,04 и 43,1; 11)78,45178,458;
4) 0,4 и 0,6; 8) 1,23 и 1,364; 12) 2,25 и 2,243.
1196. Сравните дроби:
1)78,5 и 79,5; 3) 78,3 и 78,89; 5) 25,03 и 25,3;
2) 22,3 и 22,7; 4) 0,3 и 0,8; 6) 23,569 и 23,568.
1197. Запишите в порядке возрастания десятичные дроби:
1) 15,3; 6,9; 18,1; 9,3; 12,45; 36,85; 56,45; 36,2;
2) 21,35; 21,46; 21,22; 21,56; 21,59; 21,78; 21,23; 21,55.
1198. Запишите в порядке убывания десятичные дроби:
15,6; 15,9; 15,5; 15,4; 15,45; 15,95; 15,2; 15,35.
1199. Выразите в квадратных метрах и запиши десятичной дробью:
Выразите в квадратных метрах и запиши десятичной дробью:
1) 5 дм2; 2) 15 см2; 3)5дм212см2.
1200 . Комната имеет форму прямоугольника. Ее длина составляет 90 дм, а ширина — 40 дм. Найдите площадь комнаты. Ответ запишите в квадратных метрах.
1201 . Сравните дроби:
1)0,04 и 0,06; 5) 1,003 и 1,03; 9) 120,058 и 120,051;
2) 402,0022 и 40,003; 6) 1,05 и 1,005; 10) 78,05 и 78,58;
3) 104,05 и 105,05; 7) 4,0502 и 4,0503; 11) 2,205 и 2,253;
4) 40,04 и 40,01; 8)60,4007і60,04007; 12)20,12 и 25,012.
1202. Сравните дроби:
1)0,03 и 0,3; 4) 6,4012 и 6,404;
2) 5,03 и 5,003; 5) 450,025 и 450,2054;
1203. Запишите пять десятичных дробей, которые на координатном луче находятся между дробями:
1)6,2 и 6,3; 2) 9,2 и 9,3; 3) 5,8 и 5,9; 4) 0,4 и 0,5.
1204. Запишите пять десятичных дробей, которые на координатном луче находятся между дробями: 1) 3,1 и 3,2; 2) 7,4 и 7,5.
1205. Между какими двумя соседними натуральными числами размещается десятичная дробь:
1)3,5; 2)12,45; 3)125,254; 4)125,012?
1206. Запишите пять десятичных дробей, для которых выполняется неравенство:
Запишите пять десятичных дробей, для которых выполняется неравенство:
1)3,41
2) 15,25
1207. Запишите пять десятичных дробей, для которых выполняется неравенство:
1) 3
1208. Запишите наибольшую десятичную дробь:
1) с двумя цифрами после запятой, меньше 2;
2) с одной цифрой после запятой, меньшую 3;
3) с тремя цифрами после запятой, меньше 4;
4) с четырьмя цифрами после запятой, меньше 1.
1209. Запишите наименьшую десятичную дробь:
1) с двумя цифрами после запятой, который больше 2;
2) с тремя цифрами после запятой, который больше 4.
1210. Запишите все цифры, которые можно поставить вместо звездочки, чтобы получить верное неравенство:
1) 0, *3 >0,13; 3) 3,75 > 3, *7; 5) 2,15
2) 8,5* 9,24.
1211. Какую цифру можно поставить вместо звездочки, чтобы получить верное неравенство:
1)0,*3 >0,1*; 2) 8,5* 3,*7?
1212. Запишите все десятичные дроби, целая часть которых равна 6, а дробная часть содержит три десятичные знаки, записанные цифрами 7 и 8. Запишите эти дроби в порядке их убывания.
Запишите эти дроби в порядке их убывания.
1213. Запишите шесть десятичных дробей, целая часть которых равна 45, а дробная часть — состоит из четырех различных цифр: 1, 2, 3, 4. Запишите эти дроби в порядке их возрастания.
1214. Сколько можно составить десятичных дробей, целая часть которых равна 86, а дробная часть — состоит из трех различных цифр: 1,2,3?
1215. Сколько можно составить десятичных дробей, целая часть которых равна 5, а дробная является трицифровою, записанной цифрами 6 и 7? Запишите эти дроби в порядке их убывания.
1216. Зачеркните в числе 50,004007 три нуля так, чтобы образовалось:
1) наибольшее число; 2) наименьшее число.
ПРИМЕНИТЕ НА ПРАКТИКЕ
1217. Измерьте длину и ширину своей тетради в миллиметрах и запишите ответ в дециметрах.
1218. Запишите свой рост в метрах с помощью десятичной дроби.
1219. Измерьте размеры своей комнаты и вычислите ее периметр и площадь. Ответ запишите в метрах и квадратных метрах.
ЗАДАЧИ НА ПОВТОРЕНИЕ
1220. При каких значениях х дробь является неправильным?
При каких значениях х дробь является неправильным?
1221. Решите уравнение:
1222. Магазин должен был продать 714 кг яблок. За первый день было продано всех яблок, а за второй — от того, что продали за первый день. Сколько яблок продали за 2 дня?
1223. Ребро куба уменьшили на 10 см и получили куб, объем которого равен 8 дм3. Найдите объем первого куба.
В этой статье мы рассмотрим тему «сравнение десятичных дробей ». Сначала обсудим общий принцип сравнения десятичных дробей. После этого разберемся, какие десятичные дроби являются равными, а какие – неравными. Дальше научимся определять, какая десятичная дробь больше, а какая меньше. Для этого изучим правила сравнения конечных, бесконечных периодических и бесконечных непериодических дробей. Всю теорию снабдим примерами с подробными решениями. В заключение остановимся на сравнении десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами.
Сразу скажем, что здесь мы будем говорить лишь о сравнении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях сравнение рациональных чисел и сравнение действительных чисел .
Остальные случаи разобраны в статьях сравнение рациональных чисел и сравнение действительных чисел .
Навигация по странице.
Общий принцип сравнения десятичных дробей
Исходя из этого принципа сравнения, выводятся правила сравнения десятичных дробей, позволяющие обойтись без перевода сравниваемых десятичных дробей в обыкновенные дроби. Эти правила, а также примеры их применения, мы разберем в следующих пунктах.
По схожему принципу сравниваются конечные десятичные дроби или бесконечные периодические десятичные дроби с натуральными числами , обыкновенными дробями и смешанными числами : сравниваемые числа заменяются соответствующими им обыкновенными дробями, после чего сравниваются обыкновенные дроби.
Что касается сравнения бесконечных непериодических десятичных дробей , то оно обычно сводится к сравнению конечных десятичных дробей. Для этого рассматривается такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое позволяет получить результат сравнения.
Равные и неравные десятичные дроби
Сначала введем определения равных и неравных конечных десятичных дробей .
Определение.
Две конечные десятичные дроби называются равными , если равны соответствующие им обыкновенные дроби, в противном случае эти десятичные дроби называются неравными .
На основании этого определения легко обосновать следующее утверждение: если в конце данной десятичной дроби приписать или отбросить несколько цифр 0 , то получится равная ей десятичная дробь. Например, 0,3=0,30=0,300=… , а 140,000=140,00=140,0=140 .
Действительно, дописывание или отбрасывание в конце десятичной дроби нуля справа соответствует умножению или делению на 10
числителя и знаменателя соответствующей обыкновенной дроби. А мы знаем основное свойство дроби , которое гласит, что умножение или деление числителя и знаменателя дроби на одно и то же натуральное число дает дробь, равную исходной. Этим доказано, что дописывание или отбрасывание нулей справа в дробной части десятичной дроби дает дробь, равную исходной.
Например, десятичной дроби 0,5 отвечает обыкновенная дробь 5/10 , после дописывания нуля справа получается десятичная дробь 0,50 , которой отвечает обыкновенная дробь 50/100 , а . Таким образом, 0,5=0,50 . Обратно, если в десятичной дроби 0,50 отбросить справа 0 , то мы получим дробь 0,5 , так от обыкновенной дроби 50/100 мы придем к дроби 5/10 , но . Следовательно, 0,50=0,5 .
Переходим к определению равных и неравных бесконечных периодических десятичных дробей .
Определение.
Две бесконечные периодические дроби равны , если равны отвечающие им обыкновенные дроби; если же соответствующие им обыкновенные дроби не равны, то сравниваемые периодические дроби тоже не равны .
Из данного определения следуют три вывода:
- Если записи периодических десятичных дробей полностью совпадают, то такие бесконечные периодические десятичные дроби равны. Например, периодические десятичные дроби 0,34(2987) и 0,34(2987) равны.
- Если периоды сравниваемых десятичных периодических дробей начинаются с одинаковой позиции, первая дробь имеет период 0
, вторая – период 9
, и значение разряда, предшествующего периоду 0
на единицу больше, чем значение разряда, предшествующего периоду 9
, то такие бесконечные периодические десятичные дроби равны.
 Например, периодические дроби 8,3(0)
и 8,2(9)
равны, также равны дроби 141,(0)
и 140,(9)
.
Например, периодические дроби 8,3(0)
и 8,2(9)
равны, также равны дроби 141,(0)
и 140,(9)
. - Две любые другие периодические дроби не являются равными. Приведем примеры неравных бесконечных периодических десятичных дробей: 9,0(4) и 7,(21) , 0,(12) и 0,(121) , 10,(0) и 9,8(9) .
Осталось разобраться с равными и неравными бесконечными непериодическими десятичными дробями . Как известно, такие десятичные дроби не могут быть переведены в обыкновенные дроби (такие десятичные дроби представляют иррациональные числа), поэтому сравнение бесконечных непериодических десятичных дробей нельзя свести к сравнению обыкновенных дробей.
Определение.
Две бесконечные непериодические десятичные дроби равны , если их записи полностью совпадают.
Но есть один нюанс: невозможно увидеть «законченную» запись бесконечных непериодических десятичных дробей, следовательно, невозможно убедиться и в полном совпадении их записей. Как же быть?
При сравнении бесконечных непериодических десятичных дробей рассматривают лишь конечное число знаков сравниваемых дробей, которое позволяет сделать необходимые выводы. Таким образом, сравнение бесконечных непериодических десятичных дробей сводится к сравнению конечных десятичных дробей.
Таким образом, сравнение бесконечных непериодических десятичных дробей сводится к сравнению конечных десятичных дробей.
При таком подходе можно говорить о равенстве бесконечных непериодических десятичных дробей лишь с точностью до рассматриваемого разряда. Приведем примеры. Бесконечные непериодические десятичные дроби 5,45839… и 5,45839… равны с точностью до стотысячных, так как равны конечные десятичные дроби 5,45839 и 5,45839 ; непериодические десятичные дроби 19,54… и 19,54810375… равны с точностью до сотых, так как равны дроби 19,54 и 19,54 .
Неравенство бесконечных непериодических десятичных дробей при таком подходе устанавливается вполне определенно. Например, бесконечные непериодические десятичные дроби 5,6789… и 5,67732… не равны, так как очевидны различия в их записях (не равны конечные десятичные дроби 5,6789 и 5,6773 ). Бесконечные десятичные дроби 6,49354… и 7,53789… тоже не равны.
Правила сравнения десятичных дробей, примеры, решения
После установления факта неравенства двух десятичных дробей, часто нужно узнать, какая из этих дробей больше, а какая – меньше другой. Сейчас мы разберем правила сравнения десятичных дробей, позволяющие ответить на поставленный вопрос.
Сейчас мы разберем правила сравнения десятичных дробей, позволяющие ответить на поставленный вопрос.
Во многих случаях бывает достаточно сравнить целые части сравниваемых десятичных дробей. Справедливо следующее правило сравнения десятичных дробей : больше та десятичная дробь, целая часть которой больше, и меньше та десятичная дробь, целая часть которой меньше.
Это правило относится как к конечным десятичным дробям, так и к бесконечным. Рассмотрим решения примеров.
Пример.
Сравните десятичные дроби 9,43 и 7,983023… .
Решение.
Очевидно, данные десятичные дроби не равны. Целая часть конечной десятичной дроби 9,43 равна 9 , а целая часть бесконечной непериодической дроби 7,983023… равна 7 . Так как 9>7 (смотрите сравнение натуральных чисел), то 9,43>7,983023 .
Ответ:
9,43>7,983023 .
Пример.
Какая из десятичных дробей 49,43(14) и 1 045,45029… меньше?
Решение.
Целая часть периодической дроби 49,43(14) меньше, чем целая часть бесконечной непериодической десятичной дроби 1 045,45029… , следовательно, 49,43(14)
Ответ:
49,43(14)
.
Если целые части сравниваемых десятичных дробей равны, то для выяснения, какая из них больше, а какая — меньше, приходится сравнивать дробные части. Сравнение дробных частей десятичных дробей проводится поразрядно — от разряда десятых к более младшим.
Для начала рассмотрим пример сравнения двух конечных десятичных дробей.
Пример.
Выполните сравнение конечных десятичных дробей 0,87 и 0,8521 .
Решение.
Целые части данных десятичных дробей равны (0=0 ), поэтому переходим к сравнению дробных частей. Значения разряда десятых равны (8=8 ), а значение разряда сотых дроби 0,87 больше, чем значение разряда сотых дроби 0,8521 (7>5 ). Следовательно, 0,87>0,8521 .
Ответ:
0,87>0,8521 .
Иногда, чтобы выполнить сравнение конечных десятичных дробей с разным количеством десятичных знаков, к дроби с меньшим количеством десятичных знаков приходится дописывать некоторое количество нулей справа. Достаточно удобно уравнивать количество десятичных знаков до начала сравнения конечных десятичных дробей, дописав к одной из них некоторое количество нулей справа.
Пример.
Сравните конечные десятичные дроби 18,00405 и 18,0040532 .
Решение.
Очевидно, данные дроби неравны, так как их записи отличаются, но при этом они имеют равные целые части (18=18 ).
Перед поразрядным сравнением дробных частей данных дробей уравняем количество десятичных знаков. Для этого припишем две цифры 0 в конце дроби 18,00405 , при этом получим равную ей десятичную дробь 18,0040500 .
Значения десятичных разрядов дробей 18,0040500 и 18,0040532 равны вплоть до стотысячных, а значение разряда миллионных дроби 18,0040500 меньше значения соответствующего разряда дроби 18,0040532 (0
Ответ:
18,00405
При сравнении конечной десятичной дроби с бесконечной, конечная дробь заменяется равной ей бесконечной периодической дробью с периодом 0 , после чего проводится сравнение по разрядам.
Пример.
Сравните конечную десятичную дробь 5,27 с бесконечной непериодической десятичной дробью 5,270013… .
Решение.
Целые части данных десятичных дробей равны. Значения разрядов десятых и сотых данных дробей равны, и чтобы выполнить дальнейшее сравнение, конечную десятичную дробь заменяем равной ей бесконечной периодической дробью с периодом 0 вида 5,270000… . До пятого знака после запятой значения разрядов десятичных дробей 5,270000… и 5,270013… равны, а на пятом знаке имеем 0
Ответ:
5,27
Сравнение бесконечных десятичных дробей также проводится поразрядно , и заканчивается после того, как только значения какого-то разряда оказываются разными.
Пример.
Сравните бесконечные десятичные дроби 6,23(18) и 6,25181815… .
Решение.
Целые части данных дробей равны, также равны значения разряда десятых. А значение разряда сотых периодической дроби 6,23(18) меньше разряда сотых бесконечной непериодической десятичной дроби 6,25181815… , следовательно, 6,23(18)
Ответ:
6,23(18)
Пример.
Какая из бесконечных периодических десятичных дробей 3,(73) и 3,(737) больше?
Решение.
Понятно, что 3,(73)=3,73737373… и 3,(737)=3,737737737… . На четвертом знаке после запятой поразрядное сравнение заканчивается, так как там имеем 3
Ответ:
3,(737) .
Сравнение десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами.
Получить результат сравнения десятичной дроби с натуральным числом позволяет сравнение целой части данной дроби с данным натуральным числом. При этом периодические дроби с периодами 0 или 9 нужно предварительно заменить равными им конечными десятичными дробями.
Справедливо следующее правило сравнения десятичной дроби и натурального числа : если целая часть десятичной дроби меньше данного натурального числа, то и вся дробь меньше этого натурального числа; если целая часть дроби больше или равна данному натуральному числу, то дробь больше данного натурального числа.
Рассмотрим примеры применения этого правила сравнения.
Пример.
Сравните натуральное число 7
с десятичной дробью 8,8329…
.
Решение.
Так как данное натуральное число меньше, чем целая часть данной десятичной дроби, то это число меньше данной десятичной дроби.
Ответ:
7
Пример.
Сравните натуральное число 7 и десятичную дробь 7,1 .
Отрезка АВ равна 6 см, то есть 60 мм. Так как 1 см = дм, то 6 см = дм. Значит, АВ — 0,6 дм. Так как 1 мм = дм, то 60 мм = дм. Значит, АВ = 0,60 дм.
Таким образом, АВ = 0,6 дм = 0,60 дм. Значит, десятичные дроби 0,6 и 0,60 выражают длину одного и того же отрезка в дециметрах. Эти дроби равны друг другу: 0,6 = 0,60.
Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь , равная данной.
Например,
0,87 = 0,870 = 0,8700; 141 = 141,0 = 141,00 = 141,000;
26,000 = 26,00 = 26,0 = 26; 60,00 = 60,0 = 60;
0,900 = 0,90 = 0,9.
Сравним две десятичные дроби 5,345 и 5,36. Уравняем число десятичных знаков, приписав к числу 5,36 справа нуль. Получаем дроби 5,345 и 5,360.
Запишем их в виде неправильных дробей:
У этих дробей одинаковые знаменатели. Значит, та из них больше, у которой больше числитель.
Значит, та из них больше, у которой больше числитель.
Так как 5345 а значит, 5,345 Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа .
Десятичные дроби можно изображать на координатном луче так же, как и обыкновенные дроби.
Например, чтобы изобразить на координатном луче десятичную дробь 0,4, сначала представим ее в виде обыкновенной дроби: 0,4 = Затем отложим от начала луча четыре десятых единичного отрезка. Получим точку A(0,4) (рис. 141).
Равные десятичные дроби изображаются на координатном луче одной и той же точкой.
Например, дроби 0,6 и 0,60 изображаются одной точкой В (см. рис. 141).
Меньшая десятичная дробь лежит на координатном луче левее большей, и большая — правее меньшей.
Например, 0,4
Изменится ли десятичная дробь, если в конце ее приписать нуль?
А6 нулей?
Сформулируйте правило сравнения десятичных дробей.
1172. Напишите десятичную дробь:
а) с четырьмя знаками после запятой, равную 0,87;
б) с пятью знаками после запятой, равную 0,541;
в) с тремя знаками после занятой, равную 35;
г) с двумя знаками после запятой, равную 8,40000.
1173. Приписав справа нули, уравняйте число знаков после запятой в десятичных дробях:1,8; 13,54 и 0,789.
1174. Запишите короче дроби:2,5000; 3,02000; 20,010.
85,09 и 67,99; 55,7 и 55,7000; 0,5 и 0,724; 0,908 и 0,918; 7,6431 и 7,6429; 0,0025 и 0,00247.
1176. Расставьте в порядке возрастания числа:
3,456; 3,465; 8,149; 8,079; 0,453.
0,0082; 0,037; 0,0044; 0,08; 0,0091
расставьте в порядке убывания.
а) 1,41 б) 0,1 в) 2,7
1184. Сравните величины:
а) 98,52 м и 65,39 м; д) 0,605 т и 691,3 кг;
б) 149,63 кг и 150,08 кг; е) 4,572 км и 4671,3 м;
в) 3,55°С и 3,61°С; ж) 3,835 га и 383,7 а;
г) 6,781 ч и 6,718 ч; з) 7,521 л и 7538 см3.
Можно ли сравнить 3,5 кг и 8,12 м? Приведите несколько примеров величин, которые нельзя сравнивать.
1185. Вычислите устно:
1186. Восстановите цепочку вычислений
1187. Можно ли сказать, сколько цифр после запятой в записи десятичной дроби, если ее название заканчивается словом:
а) сотых; б) десятитысячных; в) десятых; г) миллионных?
Содержание урока
конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения
рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие
Совершенствование учебников и уроковисправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей
идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
В данной теме будет рассмотрена как общая схема сравнения десятичных дробей, так и детальный разбор принципа сравнения конечных и бесконечных дробей. Теоретическую часть закрепим решением типичных задач. Также разберем на примерах сравнение десятичных дробей с натуральными или смешанными числами, и обыкновенными дробями.
Теоретическую часть закрепим решением типичных задач. Также разберем на примерах сравнение десятичных дробей с натуральными или смешанными числами, и обыкновенными дробями.
Внесем уточнение: в теории ниже будет рассмотрено сравнение только положительных десятичных дробей.
Yandex.RTB R-A-339285-1
Общий принцип сравнения десятичных дробей
Для каждой конечной десятичной и бесконечной периодической десятичной дробей существуют соответствующие им некоторые обыкновенные дроби. Следовательно, сравнение конечных и бесконечных периодических дробей возможно производить как сравнение соответствующих им обыкновенных дробей. Собственно, это утверждение и является общим принципом сравнения десятичных периодических дробей.
На основе общего принципа формулируются правила сравнения десятичных дробей, придерживаясь которых возможно не осуществлять перевод сравниваемых десятичных дробей в обыкновенные.
То же самое можно сказать и про случаи, когда происходит сравнение десятичной периодической дроби с натуральными числами или смешанными числами, обыкновенными дробями – заданные числа необходимо заменить соответствующими им обыкновенными дробями.
Если же речь идет о сравнении бесконечных непериодических дробей, то его обычно сводят к сравнению конечных десятичных дробей. Для рассмотрения берется такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое даст возможность получить результат сравнения.
Равные и неравные десятичные дроби
Определение 1
Равные десятичные дроби – это две конечные десятичные дроби, у которых равны соответствующие им обыкновенные дроби. В противном случае десятичные дроби являются неравными .
Опираясь на данное определение, просто обосновать такое утверждение: если в конце заданной десятичной дроби подписать или, наоборот, отбросить несколько цифр 0 , то получится равная ей десятичная дробь. К примеру: 0 , 5 = 0 , 50 = 0 , 500 = … . Или: 130 , 000 = 130 , 00 = 130 , 0 = 130 . По сути, дописать или отбросить нуль в конце дроби справа — значит умножить или разделить на 10 числитель и знаменатель соответствующей обыкновенной дроби. Добавим к сказанному основное свойство дробей (умножая или деля числитель и знаменатель дроби на одно и то же натуральное число, получаем дробь, равную исходной) и имеем доказательство вышеуказанного утверждения.
Добавим к сказанному основное свойство дробей (умножая или деля числитель и знаменатель дроби на одно и то же натуральное число, получаем дробь, равную исходной) и имеем доказательство вышеуказанного утверждения.
К примеру, десятичной дроби 0 , 7 соответствует обыкновенная дробь 7 10 . Дописав нуль справа, получим десятичную дробь 0 , 70 , которой соответствует обыкновенная дробь 70 100 , 7 · 70 100: 10 . Т.е.: 0 , 7 = 0 , 70 . И наоборот: отбрасывая в десятичной дроби 0 , 70 нуль справа, получаем дробь 0 , 7 – таким образом, от десятичной дроби 70 100 мы переходим к дроби 7 10 , но 7 10 = 70: 10 100: 10 Тогда: 0 , 70 = 0 , 7 .
Теперь рассмотрим содержание понятия равных и неравных бесконечных периодических десятичных дробей.
Определение 2
Равные бесконечные периодические дроби – это бесконечные периодические дроби, у которых равны отвечающие им обыкновенные дроби. Если же соответствующие им обыкновенные дроби не равны, то заданные для сравнения периодические дроби также являются неравными .
Данное определение позволяет сделать следующие выводы:
Если записи заданных периодических десятичных дробей совпадают, то такие дроби являются равными. К примеру, периодические десятичные дроби 0 , 21 (5423) и 0 , 21 (5423) равны;
Если в заданных десятичных периодических дробях периоды начинаются с одной и той же позиции, первая дробь имеет период 0 , а вторая – 9 ; значение разряда, предшествующего периоду 0 , на единицу больше, чем значение разряда, предшествующего периоду 9 , то такие бесконечные периодические десятичные дроби равны. К примеру, равными являются периодические дроби 91 , 3 (0) и 91 , 2 (9) , а также дроби: 135 , (0) и 134 , (9) ;
Две любые другие периодические дроби не являются равными. Например: 8 , 0 (3) и 6 , (32) ; 0 , (42) и 0 , (131) и т.д.
Осталось рассмотреть равные и неравные бесконечные непериодические десятичные дроби. Такие дроби представляют из себя иррациональные числа, и их невозможно перевести в обыкновенные дроби. Следовательно, сравнение бесконечных непериодических десятичных дробей не сводится к сравнению обыкновенных.
Определение 3
Равные бесконечные непериодические десятичные дроби – это непериодические десятичные дроби, записи которых полностью совпадают.
Логичным будет вопрос: как сравнить записи, если увидеть «законченную» запись таких дробей невозможно? Сравнивая бесконечные непериодические десятичные дроби, нужно рассматривать только некоторое конечное число знаков заданных для сравнения дробей так, чтобы это позволило сделать вывод. Т.е. по сути сравнение бесконечных непериодических десятичных дробей заключается в сравнении конечных десятичных дробей.
Такой подход дает возможность утверждать о равенстве бесконечных непериодических дробей только с точностью до рассматриваемого разряда. Например, дроби 6 , 73451 … и 6 , 73451 … равны с точностью до стотысячных, т.к. равными являются конечные десятичные дроби 6 , 73451 и 6 , 7345 . Дроби 20 , 47 … и 20 , 47 … равны с точностью до сотых, т.к. равными являются дроби 20 , 47 и 20 , 47 и так далее.
Неравенство бесконечных непериодических дробей устанавливается вполне конкретно при явных различиях в записях. Например, неравными являются дроби 6 , 4135 … и 6 , 4176 … или 4 , 9824 … и 7 , 1132 … и так далее.
Например, неравными являются дроби 6 , 4135 … и 6 , 4176 … или 4 , 9824 … и 7 , 1132 … и так далее.
Правила сравнения десятичных дробей. Решение примеров
Если установлен факт неравенства двух десятичных дробей, обычно также необходимо определить, какая из них больше, а какая – меньше. Рассмотрим правила сравнения десятичных дробей, которые дают возможность решить вышеуказанную задачу.
Очень часто достаточно лишь сравнить целые части заданных к сравнению десятичных дробей.
Определение 4
Та десятичная дробь, у которой целая часть больше, является бОльшей. Меньшей является та дробь, у которой целая часть меньше.
Указанное правило распространяется как на конечные десятичные дроби, так и на бесконечные.
Пример 1
Необходимо сравнить десятичные дроби: 7 , 54 и 3 , 97823 … .
Решение
Совершенно очевидно, что заданные десятичные дроби равными не являются. Целые их части равны соответственно: 7 и 3 . Т.к. 7 > 3 , то 7 , 54 > 3 , 97823 … .
Ответ: 7 , 54 > 3 , 97823 … .
В случае, когда целые части заданных к сравнению дробей равны, решение задачи сводится к сравнению дробных частей. Сравнение дробных частей производится поразрядно – от разряда десятых к более младшим.
Рассмотрим сначала случай, когда нужно сравнить конечные десятичные дроби.
Пример 2
Необходимо выполнить сравнение конечных десятичных дробей 0 , 65 и 0 , 6411 .
Решение
Очевидно, что целые части заданных дробей равны (0 = 0) . Проведем сравнение дробных частей: в разряде десятых значения равны (6 = 6) , а вот в разряде сотых значение дроби 0 , 65 больше, чем значение разряда сотых в дроби 0 , 6411 (5 > 4) . Таким образом, 0 , 65 > 0 , 6411 .
Ответ: 0 , 65 > 0 , 6411 .
В некоторых задачах на сравнение конечных десятичных дробей с разным количеством знаков после запятой необходимо к дроби с меньшим количеством десятичных знаков приписывать нужное количество нулей справа. Удобно уравнивать таким образом количество десятичных знаков в заданных дробях еще до начала сравнения.
Удобно уравнивать таким образом количество десятичных знаков в заданных дробях еще до начала сравнения.
Пример 3
Необходимо сравнить конечные десятичные дроби 67 , 0205 и 67 , 020542 .
Решение
Данные дроби очевидно не являются равными, т.к. записи их различны. При этом их целые части равны: 67 = 67 . Прежде чем приступить к поразрядному сравнению дробных частей заданных дробей, уравняем количество знаков после запятой, дописав нули справа в дроби с меньшим количеством знаков. Тогда получим для сравнения дроби: 67 , 020500 и 67 , 020542 . Проводим поразрядное сравнение и видим, что в разряде стотысячных значение в дроби 67 , 020542 больше, чем соответствующее в дроби 67 , 020500 (4 > 0) . Таким образом, 67 , 020500
Ответ: 67 , 0205
Если необходимо сравнить конечную десятичную дробь с бесконечной, то конечная дробь заменяется бесконечной, ей равной с периодом 0 . Затем производится поразрядное сравнение.
Пример 4
Необходимо сравнить конечную десятичную дробь 6 , 24 с бесконечной непериодической десятичной дробью 6 , 240012 …
Решение
Мы видим, что целые части заданных дробей равны (6 = 6) . В разрядах десятых и сотых значения обеих дробей также являются равными. Чтобы иметь возможность сделать вывод, продолжаем сравнение, заменяя конечную десятичную дробь равной ей бесконечной с периодом 0 и получаем: 6 , 240000 … . Дойдя до пятого знака после запятой, находим различие: 0
В разрядах десятых и сотых значения обеих дробей также являются равными. Чтобы иметь возможность сделать вывод, продолжаем сравнение, заменяя конечную десятичную дробь равной ей бесконечной с периодом 0 и получаем: 6 , 240000 … . Дойдя до пятого знака после запятой, находим различие: 0
Ответ: 6 , 24
Сравнивая бесконечные десятичные дроби, также применяют поразрядное сравнение, которое окончится тогда, когда значения в каком-то разряде у заданных дробей окажутся различными.
Пример 5
Необходимо сравнить бесконечные десятичные дроби 7 , 41 (15) и 7 , 42172 … .
Решение
В заданных дробях — равные целые части, значения десятых также равны, а вот в разряде сотых мы видим различие: 1
Ответ: 7 , 41 (15)
Пример 6
Необходимо сравнить бесконечные периодические дроби 4 , (13) и 4 , (131) .
Решение:
Понятными и верными являются равенства: 4 , (13) = 4 , 131313 … и 4 , (133) = 4 , 131131 … . Сравниваем целые части и поразрядно дробные, и на четвертом знаке после запятой фиксируем расхождение: 3 > 1 . Тогда: 4 , 131313 … > 4 , 131131 … , а 4 , (13) > 4 , (131) .
Сравниваем целые части и поразрядно дробные, и на четвертом знаке после запятой фиксируем расхождение: 3 > 1 . Тогда: 4 , 131313 … > 4 , 131131 … , а 4 , (13) > 4 , (131) .
Ответ: 4 , (13) > 4 , (131) .
Чтобы получить результат сравнения десятичной дроби с натуральным числом, необходимо сравнить целую часть заданной дроби с заданным натуральным числом. При этом надо учесть, что периодические дроби с периодами 0 или 9 нужно предварительно представить в виде равных им конечных десятичных дробей.
Определение 5
Если целая часть заданной десятичной дроби меньше заданного натурального числа, то и вся дробь является меньшей по отношению к заданному натуральному числу. Если целая часть заданной дроби больше или равна заданному натуральному числу, то дробь больше заданного натурального числа.
Пример 7
Необходимо сравнить натуральное число 8 и десятичную дробь 9 , 3142 … .
Решение:
Заданное натуральное число меньше, чем целая часть заданной десятичной дроби (8
Ответ: 8
Пример 8
Необходимо сравнить натуральное число 5 и десятичную дробь 5 , 6 .
Решение
Целая часть заданной дроби равна заданному натуральному числу, тогда, согласно вышеуказанному правилу, 5
Ответ: 5
Пример 9
Необходимо сравнить натуральное число 4 и периодическую десятичную дробь 3 , (9) .
Решение
Период заданной десятичной дроби равен 9 , а значит перед сравнением необходимо заменить заданную десятичную дробь равной ей конечной или натуральным числом. В данном случае: 3 , (9) = 4 . Таким, образом исходные данные равны.
Ответ: 4 = 3 , (9) .
Чтобы произвести сравнение десятичной дроби с обыкновенной дробью или смешанным числом, необходимо:
Записать обыкновенную дробь или смешанное число в виде десятичной дроби, а затем выполнить сравнение десятичных дробей или
— записать десятичную дробь в виде обыкновенной дроби (за исключением бесконечной непериодической), а затем выполнить сравнение с заданной обыкновенной дробью или смешанным числом.
Пример 10
Необходимо сравнить десятичную дробь 0 , 34 и обыкновенную дробь 1 3 .
Решение
Решим задачу двумя способами.
- Запишем заданную обыкновенную дробь 1 3 в виде равной ей периодической десятичной дроби: 0 , 33333 … . Тогда становится необходимым произвести сравнение десятичных дробей 0 , 34 и 0 , 33333 … . Получим: 0 , 34 > 0 , 33333 … , а значит 0 , 34 > 1 3 .
- Запишем заданную десятичную дробь 0 , 34 в виде равной ей обыкновенной. Т.е.: 0 , 34 = 34 100 = 17 50 . Сравним обыкновенные дроби с разными знаменателями и получим: 17 50 > 1 3 . Таким образом, 0 , 34 > 1 3 .
Ответ: 0 , 34 > 1 3 .
Пример 11
Необходимо сравнить бесконечную непериодическую десятичную дробь 4 , 5693 … и смешанное число 4 3 8 .
Решение
Бесконечную непериодическую десятичную дробь нельзя представить в виде смешанного числа, но возможно перевести смешанное число в неправильную дробь, а ее, в свою очередь, записать в виде равной ей десятичной дроби. Тогда: 4 3 8 = 35 8 и
Т. е.: 4 3 8 = 35 8 = 4 , 375 . Проведем сравнение десятичных дробей: 4 , 5693 … и 4 , 375 (4 , 5693 … > 4 , 375) и получим: 4 , 5693 … > 4 3 8 .
е.: 4 3 8 = 35 8 = 4 , 375 . Проведем сравнение десятичных дробей: 4 , 5693 … и 4 , 375 (4 , 5693 … > 4 , 375) и получим: 4 , 5693 … > 4 3 8 .
Ответ: 4 , 5693 … > 4 3 8 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Цель урока:
- создать условия для вывода правила сравнения десятичных дробей и умения его применять;
- повторить запись обыкновенных дробей в виде десятичных, округление десятичных дробей;
- развивать логическое мышление, способность к обобщению, исследовательские умения, речь.
Ход урока
Ребята давайте вспомним, чем мы занимались с вами на предыдущих уроках?
Ответ: изучали десятичные дроби, записывали обыкновенные дроби в виде десятичных и наоборот, округляли десятичные дроби.
А чем бы вы хотели сегодня заниматься?
(Ученики отвечают.)
А вот все-таки чем мы будем на уроке заниматься, вы узнаете через несколько
минут. Откройте тетради, запишите дату. К доске пойдет ученик, который будет
работать с обратной стороны доски. Я буду предлагать вам задания, которые вы
выполняете устно. Ответы записываете в тетрадь в строчку через точку с запятой.
Ученик у доски записывает в столбик.
Откройте тетради, запишите дату. К доске пойдет ученик, который будет
работать с обратной стороны доски. Я буду предлагать вам задания, которые вы
выполняете устно. Ответы записываете в тетрадь в строчку через точку с запятой.
Ученик у доски записывает в столбик.
Я читаю задания, которые заранее записаны на доске:
Проверим. У кого другие ответы? Вспомнить правила.
Получили: 1,075; 2,175; 3,275; 4,375; 5,475; 6,575; 7,675.
Установите закономерность и продолжите полученный ряд еще на 2 числа. Проверим.
Возьмите расшифровку и под каждым числом (отвечающий у доски ставит букву рядом с числом) поставьте соответствующую букву. Прочитайте слово.
Расшифровка:
Итак, чем мы будем заниматься на уроке?
Ответ: сравнением.
Сравнением! Хорошо, я, например, сейчас начну сравнивать свои руки, 2 учебника, 3 линейки. А вы что хотите сравнивать?
Ответ: десятичные дроби.
Какую тему урока запишем?
Я записываю тему урока на доске, а ученики в тетради: «Сравнение десятичных
дробей».
Задание: сравните числа (на доске записаны)
| 18,625 и 5,784 | 15,200 и 15,200 | |
| 3,0251 и 21,02 | 7,65 и 7,8 | |
| 23,0521 и 0,0521 | 0,089 и 0,0081 |
Сначала открываем левую часть. Целые части разные. Делаем вывод о сравнении десятичных дробей с разными целыми частями. Открываем правую часть. Целые части – одинаковые числа. Как сравнить?
Предложение: записать десятичные дроби в виде обыкновенных дробей и сравнить.
Записать сравнение обыкновенных дробей. Если каждую десятичную дробь
переводить в обыкновенную и сравнивать 2 дроби, то это займет много времени.
Может мы выведем правило сравнения? (Ученики предлагают. ) Я выписала правило
сравнения десятичных дробей, которое предлагает автор. Давайте сравним.
) Я выписала правило
сравнения десятичных дробей, которое предлагает автор. Давайте сравним.
На листе бумаги напечатаны 2 правила:
- Если целые части десятичных дробей различны, то та дробь больше, у которой больше целая часть.
- Если целые части десятичных дробей одинаковы, то больше та дробь, у которой больше первый из несовпавших разрядов после запятой.
Мы с вами сделали открытие. И это открытие – правило сравнения десятичных дробей. Оно у нас совпало с правилом, которое предложил автор учебника.
Я вот обратила внимание, что в правилах говорится какая из 2 дробей больше. А вы можете мне сказать какая из 2 десятичных дробей меньше.
Выполнить в тетради № 785(1, 2) на стр. 172. Задание записано на доске. Ученики комментируют, а учитель ставит знаки.
Задание: сравните
3,4208 и 3,4028
Итак, что мы научились сегодня делать? Давайте себя проверим. Работа на листочках с копиркой.
Ученики сравнивают десятичные дроби, ставя знаки >,
Самостоятельная работа.
(Проверка – ответы на обратной стороне доски.)
Сравните
148,05 и 14,805
6,44806 и 6,44863
35,601 и 35,6010
Первый, кто сделает – получает задание (выполняет с обратной стороны доски) № 786(1, 2):
Найдите закономерность и запишите следующее в последовательности число. В каких последовательностях числа расположены в порядке возрастания, в каких в порядке убывания?
Ответ:
- 0,1; 0,02; 0,003; 0,0004; 0,00005; (0,000006) – убывает
- 0,1 ; 0,11; 0,111; 0,1111; 0,11111; (0,111111) – возрастает.
После того, как последний ученик сдаст работу – проверить.
Учащиеся сравнивают свои ответы.
Те, кто все сделал правильно поставит себе отметку “5”, кто допустил 1-2 ошибки –“4”, 3 ошибки – “3”. Выяснить в каких сравнениях допущены ошибки, на какое правило.
Записать домашнее задание: № 813, № 814 (п. 4 стр. 171). Прокомментировать. Если будет время – выполнить № 786(1, 3), № 793(а).
Итог урока.
- Что вы ребята научились делать на уроке?
- Вам понравилось или не понравилось?
- Какие были затруднения?
Возьмите листочки и заполните их, указав степень вашего усвоения материала:
- усвоен полностью, могу выполнять;
- усвоен полностью, но затрудняюсь в применении;
- усвоен частично;
- не усвоен.
Спасибо за урок.
дайын үй жұмыстары Математика Абылкасымова 5 класс 2017 referatikz.com
Глава 1. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
§ 1. Запись натуральных чисел
12345678910111213
§ 2. Координатный луч
14151617181920212223242526
§ 3. Сравнение натуральных чисел
2728293031323334353637383940
§ 4. Арифметические действия е натуральными числами
4142434445464748495051525354555657585960
§ 5. Числовые и буквенные выражения.
 Упрощение выражений
Упрощение выражений61626364656667686970717273747576777879
§ 6. Уравнения
808182838485868788899091
§ 7. Формулы. Вычисления по формулам
9293949596979899100101102
§ 8. Решение текстовых задач
103104105106107108109110111112113114115116117118119
120121122
§ 9. Последовательность из натуральных чисел
123124125126127128129130131132
Глава 2. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
§ 10. Делители и кратные натуральных чисел. Простые и составные числа
133134135136137138139140141142143144145146147148149150151152153
§11. Основные свойства делимости
154155156157158159160161162163164165166167168169170
§ 12. Признаки делимости на числа 2. 3, 5, 9.
171172173174175176177178179180181182183184185186187188189190191192193194
§13.
 Степень
Степень195196197198199200201202203204205206207208209210211212
§14. Разложение натурального числа на простые множители
213214215216217218219220221222223224225226227228229230231232233
§15. Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
234235236237238239
240241242243244245246247248249250251252253254255256257258259
Глава 3. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ
§ 16. Обыкновенная дробь. Чтение и запись обыкновенных дробей
260261262263264265266267268269270271272273274275276277278279280281282283284285286
§ 17. Основное свойство обыкновенной дроби
287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325
§ 18. Правильные и неправильные обыкновенные дроби.
 Смешанные числа
Смешанные числа326327328329330331332333334335336337338339340341342343344345
§19. Перевод неправильной обыкновенной дроби в смешанное число и смешанного числа в неправильную обыкновенную дробь
346347348349350351352353354355356357358359
360361362363364
§ 20. Изображение обыкновенных дробен и смешанных чисел на координатном луче
365366367368369370371372373374375376377378379380381
§ 21. Приведение обыкновенных дробей к общему знаменателю
382383385386387388389390391392393394395396397398
§ 22. Сравнение обыкновенных дробей и смешанных чисел
399400401402403404405406407408409410411412413414415416417418419420
§ 23. Сложение и вычитание обыкновенных дробей
421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454
§ 24.
 Сложение смешанных чисел
Сложение смешанных чисел455456457458459460461462463464465466467468469470471472473474475476477478
§ 25. Вычитание смешанных чисел
479480
481482483484485486487488489490491492493494495496497498499500501502503
§ 26. Умножение обыкновенных дробей и смешанных чисел
504505506507508509510511512513514515516517518519
§ 27. Деление обыкновенных дробей и смешанных чисел
520521522523524525526527528529530531532533534535536537
§ 28. Действия с обыкновенными дробями, нулем, натуральными и смешанными числами
538539540541542543544545546547548549550551552553554555556
Глава 4. ТЕКСТОВЫЕ ЗАДАЧИ
§ 29. Нахождение дроби от числа и числа по его дроби
557558559560561562563564565566567568569570571572573574575576577578
§ 30.
 Задачи на совместную работу
Задачи на совместную работу579580581582583584585586587588589590591592593
Глава 5. ДЕСЯТИЧНЫЕ ДРОБИ II ДЕЙСТВИЯ НАД НИМИ
§ 31. Десятичная дробь. Чтение и запись десятичных дробей
594595596597598599600
601602603604606607
§ 32. Перевод десятичной дроби в обыкновенную дробь
608609610611612613614615616617
§ 33. Изображение десятичных дробей на координатном луче. Сравнение десятичных дробей
618619620621622623624625626627628629630631632633
§ 34. Сложение и вычитание десятичных дробей
634635636637638639640641642643644645646647648649650
§ 35. Умножение десятичной дроби на натуральное число
651652653654655656657658659660661662663664665666667668669
§ 36. Умножение десятичных дробей
670671672673674675676677678679680681682683684685
§ 37.
 Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число686687688689690691692693694695696697698699700701
§ 38. Деление десятичных дробей
702703704705706707708709710711712713714715716717718719720
§ 39. Умножение и деление десятичных дробей на 10. 100. 1000. … и на 0.1. 0,01, 0,001
721
722723724725726727728729730731732733734735736
§ 40. Действия с десятичными и обыкновенными дробями
737738739740741742743744745746747748749750751752753754755756757
§41. Округление чисел
758759760761762763764765
§ 42. Решение текстовых задач
766767768769770771772773774775776777778779
Глава 6. МНОЖЕСТВА
§ 43. Множество. Элементы множества. Изображение множеств
780781782783784785787
§ 44.
 Отношения между множествами. Подмножества
Отношения между множествами. Подмножества788789790791792793794795
§ 45. Объединение и пересечение множеств
796797798799800
§ 46. Решение текстовых задач
801802803804805806807808
Глава 7. ПРОЦЕНТЫ
§ 47. Процент
809810811812813815816817818819820821822823824825826828829830831
§ 48. Нахождение процентов от числа и числа по его процентам
832833834835836837838839840841842843
§ 49. Решение текстовых задач
844
845846847848849850851852853854855856857858859860861862863864865866867868869
Глава 8. УГЛЫ. МНОГОУГОЛЬНИКИ
§ 50. Угол
870871872873874875876877878880881
§ 51. Многоугольники
882883884885886887888889890
Глава 9.
 ДИАГРАММЫ
ДИАГРАММЫ§ 52. Окружность. Крут
891892893894895896897898899901902
§ 53. Диаграмма. Представление статистических данных с помощью диаграмм
903904906907908909910911912913915916917919920921
Глава 10. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР
§ 54. Прямоугольный параллелепипед (куб) и его развертка
922923924926
§ 55. Задачи на разрезание фигур. Задачи на складывание фигур
929930931932933934
Глава 11. УПРАЖНЕНИЯ ДЛЯ ПОВТОРНЕИЯ
937938939940941942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974
975976977978979980
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | знак минус | вычитание | 1 1/2 — 2/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | asterisk | multiplication | 2/3 * 3/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | times sign | multiplication | 2 /3 × 5/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | division sign | division | 1/2 : 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Преобразование десятичных дробей в дроби – пояснения и примеры Прежде чем мы научимся преобразовывать десятичные дроби в дроби, нам необходимо знать некоторые основные сведения о десятичных дробях и дробях. Дробь, с другой стороны, является частью целого числа, обычно обозначаемого как отношение двух целых чисел a/b. Два целых числа a и b называются числителем и знаменателем соответственно. Дроби бывают трех видов: правильные, неправильные и смешанные. Примеры дробей: 5/8, 7/3 и 2 1 / 5. Мы можем легко преобразовать десятичное число в дробь, выполнив простые шаги, и никаких калькуляторов не требуется. В этой статье подробно описаны все этапы преобразования десятичных дробей в дроби с некоторыми примерами. Давайте изучим эти шаги для преобразования десятичной дроби в дроби:
Давайте решим следующие примеры, чтобы лучше понять, как преобразовать десятичную дробь в дробь. Пример 1 Преобразуйте 0,7 в дробь. Решение
Пример 2 Преобразуйте 0,05 в дробь и упростите ее в низшей форме. Решение
Пример 3 Преобразуйте десятичное число 5,066 в дробь. Раствор
|

 Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275
Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275 Если дробь неправильная, то есть числитель больше знаменателя (например, 345/100), то в результате преобразования ее в число получится целое числовое значение или десятичная дробь с целой дробной частью. В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
Если дробь неправильная, то есть числитель больше знаменателя (например, 345/100), то в результате преобразования ее в число получится целое числовое значение или десятичная дробь с целой дробной частью. В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
 Например, периодические дроби 8,3(0)
и 8,2(9)
равны, также равны дроби 141,(0)
и 140,(9)
.
Например, периодические дроби 8,3(0)
и 8,2(9)
равны, также равны дроби 141,(0)
и 140,(9)
. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.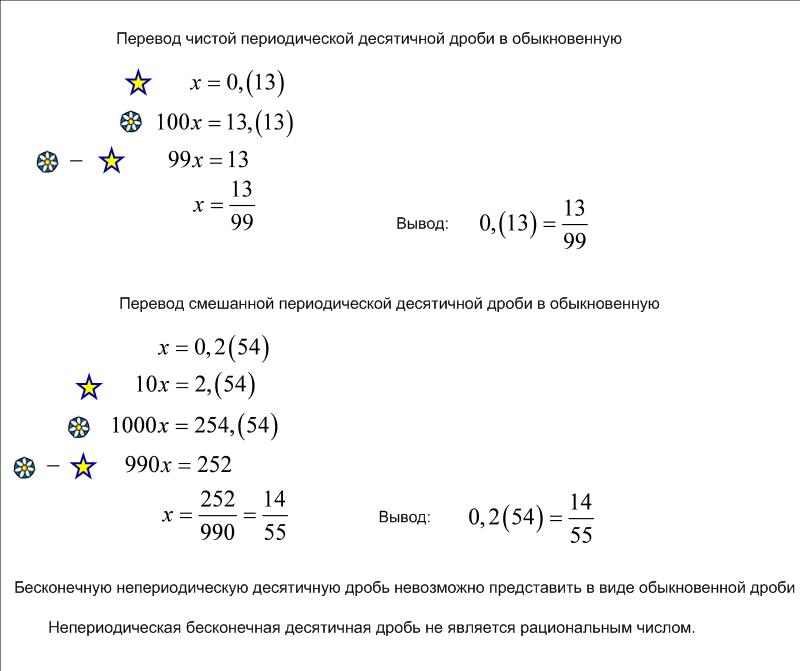 Какую часть составляют девочки?
Какую часть составляют девочки? 02+17.19
02+17.19 Начнем с того, что десятичное число — это, вероятно, число, в котором есть точка (.) между цифрами, эта точка известна как десятичная точка. По сути, десятичные числа — это просто дроби, знаменатель которых выражен в степени 10. Примеры десятичных чисел: 0,005, 3,2, 10,9, 55,1, 1,28, 9..234 и т. д.
Начнем с того, что десятичное число — это, вероятно, число, в котором есть точка (.) между цифрами, эта точка известна как десятичная точка. По сути, десятичные числа — это просто дроби, знаменатель которых выражен в степени 10. Примеры десятичных чисел: 0,005, 3,2, 10,9, 55,1, 1,28, 9..234 и т. д.


 , 0,666…, 4,2525252525…, 0,56111 и т. д.
, 0,666…, 4,2525252525…, 0,56111 и т. д. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported. . Чтобы понять, в чем разница, давайте рассмотрим несколько примеров десятичных представлений рациональных чисел:
. Чтобы понять, в чем разница, давайте рассмотрим несколько примеров десятичных представлений рациональных чисел: )
) Другими словами, в примерах, которые мы приводили ранее, мы говорили такие вещи, как «дробь 1/4 равна конечному десятичному числу 0,25» и «дробь 7/9равно повторяющейся десятичной дроби 0,7777…» и так далее. Но теперь давайте выясним, как решить эту задачу в обратном порядке, чтобы мы могли взять десятичное число, например 0,818181…, и преобразовать его в дробь с эквивалентным значением.
Другими словами, в примерах, которые мы приводили ранее, мы говорили такие вещи, как «дробь 1/4 равна конечному десятичному числу 0,25» и «дробь 7/9равно повторяющейся десятичной дроби 0,7777…» и так далее. Но теперь давайте выясним, как решить эту задачу в обратном порядке, чтобы мы могли взять десятичное число, например 0,818181…, и преобразовать его в дробь с эквивалентным значением. Не вдаваясь в подробности, основная идея состоит в том, что мы можем разделить и числитель, и знаменатель дроби 5/10 на 5, чтобы найти эквивалентное и более простое представление 1/2. Но не волнуйтесь, если сейчас все это звучит как сумасшедшая болтовня — мы скоро рассмотрим это более подробно.
Не вдаваясь в подробности, основная идея состоит в том, что мы можем разделить и числитель, и знаменатель дроби 5/10 на 5, чтобы найти эквивалентное и более простое представление 1/2. Но не волнуйтесь, если сейчас все это звучит как сумасшедшая болтовня — мы скоро рассмотрим это более подробно. И это ответ!
И это ответ! Мы можем сократить это до наименьших членов, разделив числитель и знаменатель или 4/10 на 2, чтобы получить эквивалент дроби 1 и 2/5.
Мы можем сократить это до наименьших членов, разделив числитель и знаменатель или 4/10 на 2, чтобы получить эквивалент дроби 1 и 2/5. Там, где имеется длинная серия повторяющихся цифр, над ними появляются точки первая и последняя цифры повторяющейся последовательности. Например, для повторяющегося числа 0,385385 вы увидите точки над цифрами 3 и 5.
Там, где имеется длинная серия повторяющихся цифр, над ними появляются точки первая и последняя цифры повторяющейся последовательности. Например, для повторяющегося числа 0,385385 вы увидите точки над цифрами 3 и 5. Используйте здесь несколько повторов повторяющегося десятичного знака.
Используйте здесь несколько повторов повторяющегося десятичного знака. Однако в большинстве случаев второй шаг является более сложным.
Однако в большинстве случаев второй шаг является более сложным. 8484…
8484… 322 повторяющиеся = 7 и 29/90
322 повторяющиеся = 7 и 29/90 