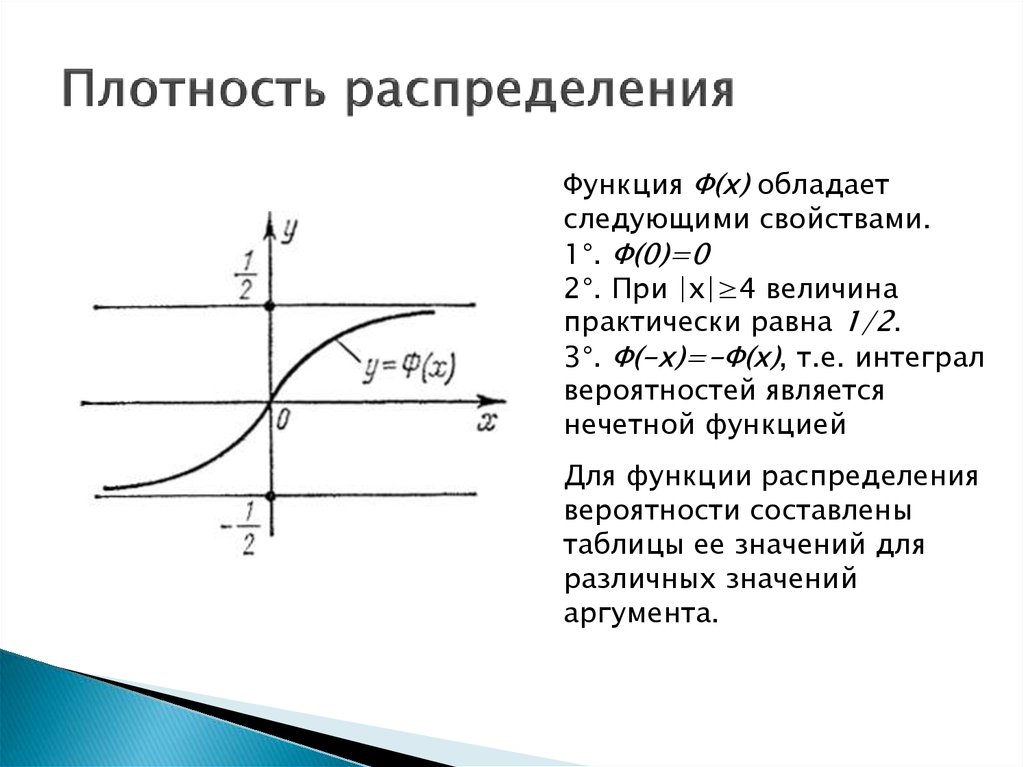
Функция ПЛОТНОСТИ распределения вероятностей
или дифференциальная функция распределения. Она представляет собой производную функции распределения: .
Примечание: для дискретной случайной величины такой функции не существует
В нашем примере:
то есть, всё очень просто – берём производную от каждого куска, и порядок.
Но настоящий порядок состоит в том, что несобственный интеграл от с пределами интегрирования от «минус» до «плюс» бесконечности:
– равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция была найдена как производная, то – не является функцией распределения (несмотря на какие бы то ни было другие признаки).
Проверим «подлинность» наших функций. Если случайная величина принимает значения из конечного
 В силу свойства аддитивности, делим интеграл на 3 части:
В силу свойства аддитивности, делим интеграл на 3 части:Совершенно понятно, что левый и правый интегралы равны нулю и нам осталось вычислить средний интеграл:
, что и требовалось проверить.
С вероятностной точки зрения это означает, что случайная величина достоверно примет одно из значений отрезка . Геометрически же это значит, что площадь между осью и графиком равна единице, и в данном случае речь идёт о площади треугольника . Сторона является фрагментом прямой и для её построения достаточно найти точку :
Ну вот, теперь всё наглядно – где бОльшая площадь, там и сконцентрированы более вероятные значения.
Так как функция плотности «собирает под собой» вероятности, то она неотрицательна и её график не может располагаться ниже оси . В общем случае функция разрывна (смотрим, где «жирные» оранжевые точки!).
Теперь разберём весьма любопытный факт: поскольку действительных чисел несчётно много, то вероятность того, что случайная величина примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадываетесь:
И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадываетесь:
(синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка ;
(красная площадь) – вероятность того, что случайная величина примет значение из отрезка .
По той причине, что отдельно взятые значения можно не принимать во внимание, с помощью этих же интегралов рассчитываются и вероятности по интервалам и полуинтервалам, в частности:
Этим же объяснятся аналогичная «вольность» с функцией
Возможно, кто-то спросит: а зачем считать интегралы, если есть функция ?
А дело в том, что во многих задачах непрерывная случайная величина ИЗНАЧАЛЬНО задана функцией плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию (с помощью тех же интегралов), после чего использовать «лёгкий способ» бросить курить отыскания вероятностей. Впрочем, об этом чуть позже:
Впрочем, об этом чуть позже:
Задача 105
Непрерывная случайная величина задана своей функцией распределения:
Найти значения и функцию . Проверить, что действительно является функцией плотности распределения. Вычислить вероятности . Построить графики .
Тренируемся самостоятельно! Если возникнут затруднения, то внимательно перечитайте вышеизложенный материал. Краткое решение и ответ в конце книги.
Вообще, типовые задачи на непрерывную случайную величину можно разделить на 2 большие группы:
1) когда дана функция , 2) когда дана функция .
В первом случае не составляет особых трудностей отыскать функцию плотности распределения – почти всегда производные не то что простЫ, а примитивны (в чём мы только что убедились). Но вот когда НСВ задана функцией , то нахождение функции распределения – есть более кропотливый процесс:
Задача 106
Непрерывная случайная величина задана функцией плотности распределения:
Найти значение и составить функцию распределения вероятностей . Вычислить .
Вычислить .
Построить графики .
Решение
В данном случае:
На практике нулевые интегралы можно опускать, а константу сразу выносить за знак интеграла:
(*)
Пользуясь чётностью подынтегральной функции, вычислим интеграл:
и подставим результат в уравнение (*):
, откуда выразим
Таким образом, функция плотности распределения:
Выполним проверку, а именно, вычислим тот же самый интеграл, но уже с известной константой. Для разнообразия я не буду пользоваться чётностью:
, отлично.
Обратите внимание, что только при и только при этом значении предложенная в условии функция является функцией плотности распределения.
Теперь начинается самое интересное. Функции распределения вероятностей – есть интеграл:
Так как состоит из трёх кусков, то решение разобьётся на 3 шага:
1) На промежутке , поэтому:
2) На интервале , и мы прицепляем следующий вагончик:
При подстановке верхнего предела интегрирования можно считать, что вместо «икс» мы подставляем «икс». Если же возник вопрос с пределом нижним, то вспоминаем график синуса либо его нечётность: .
3) И, наконец, на , и детский паровозик отправляется в путь:
Внимание! А вот в этом задании нулевые интегралы пропускать НЕ НАДО. Чтобы показать своё понимание функции распределения 😉 К тому же, они могут оказаться вовсе не нулевыми, и тогда придётся иметь дело с интегралами несобственными. И такой пример я обязательно разберу ниже.
Чтобы показать своё понимание функции распределения 😉 К тому же, они могут оказаться вовсе не нулевыми, и тогда придётся иметь дело с интегралами несобственными. И такой пример я обязательно разберу ниже.
Записываем наши достижения под единую скобку:
С высокой вероятностью всё правильно, но, тем не менее, устно возьмём производную: , а также «прозвоним» точки «стыка»:
Правильность решения можно проконтролировать и в ходе построения графика, но, во-первых, он не всегда требуется, а во-вторых, до сего момента можно успеть «наломать дров». Ибо вероятности попадания чаще находят с помощью функции распределения:
– вероятность того, что случайная величина примет значение из промежутка
Второй способ состоит в вычислении интеграла:
Выполним чертежи. График представляет собой косинусоиду, сжатую вдоль ординат в 2 раза. Тот редкий случай, когда функция плотности непрерывна:
Тот редкий случай, когда функция плотности непрерывна:
Значение численно равно заштрихованной площади – это я специально нарисовал, чтобы напомнить вероятностный смысл плотности функции распределения. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала . Заметьте, что значения по условию, невозможны.
Осталось изобразить функцию распределения. График представляет собой синусоиду, сжатую в 2 раза вдоль оси ординат и сдвинутую на вверх:
В принципе, тут можно было не заморачиваться преобразованием графиков, а найти несколько опорных точек и догадаться, как выглядит кривая (
Чертежи желательно расположить так, чтобы оси ординат (вертикальные оси) лежали ровненько одна под другой. Это будет хорошим тоном.
И я так чувствую, вам уже не терпится проверить свои силы. Как водится, пример попроще:
Задача 107
Задана плотность распределения вероятностей непрерывной случайной величины :
Требуется:
1) определить коэффициент ;
2) найти функцию распределения ;
4) найти вероятность того, что примет значение из промежутка
и задачка поинтереснее:
Задача 108
Непрерывная случайная величина задана плотностью распределения вероятностей:
Найти значение и построить график плотности распределения. Найти функцию распределения вероятностей и построить её график. Вычислить вероятность .
Дерзайте! Свериться с решением можно внизу книги.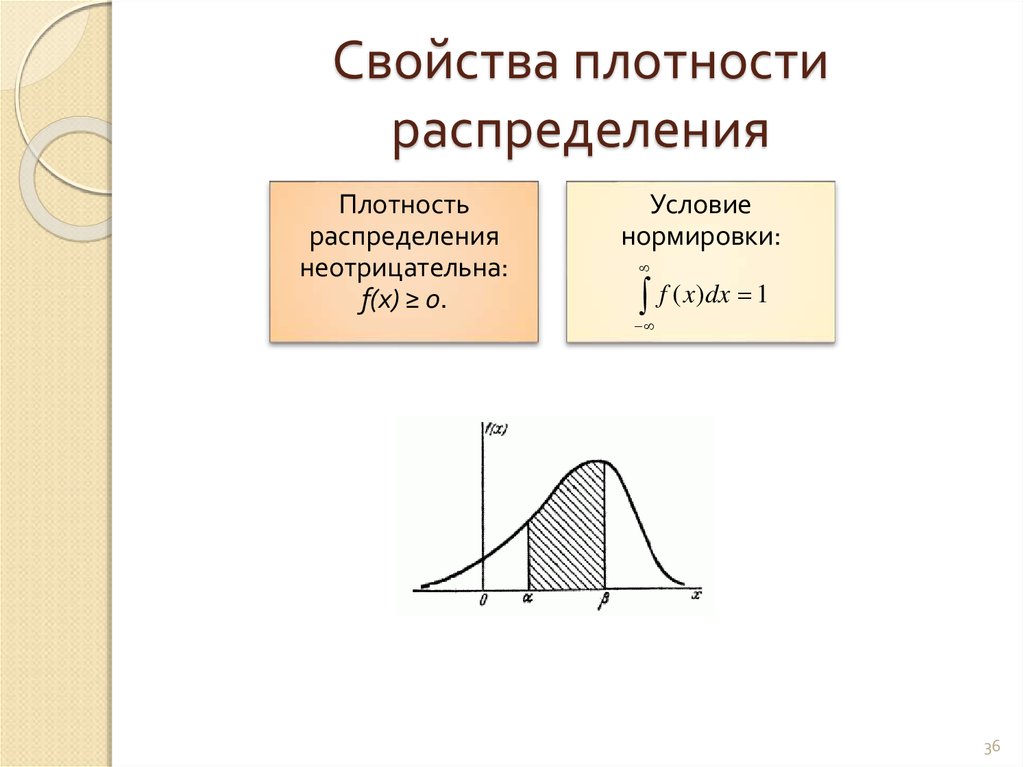
Следует отметить, что все эти задачи реально предлагают студентам-заочникам, и поэтому я не предлагаю вам ничего необычного.
И в заключение параграфа обещанные случаи с несобственными интегралами:
Задача 109
Непрерывная случайная величина задана своей плотностью распределения:
Найти коэффициент и функцию распределения . Построить графики.
Решение: по свойству функции плотности распределения:
В данной задаче состоит из 2 частей, поэтому:
Правый интеграл равен нулю, а вот левый – есть «живой» несобственный интеграл с бесконечным нижним пределом:
Таким образом, наше уравнение превратилось в готовый результат:
и функция плотности:
Функция , как нетрудно понять, отыскивается в 2 шага:
1) На промежутке , следовательно:
– вот такая вот у нас замечательная экспонента.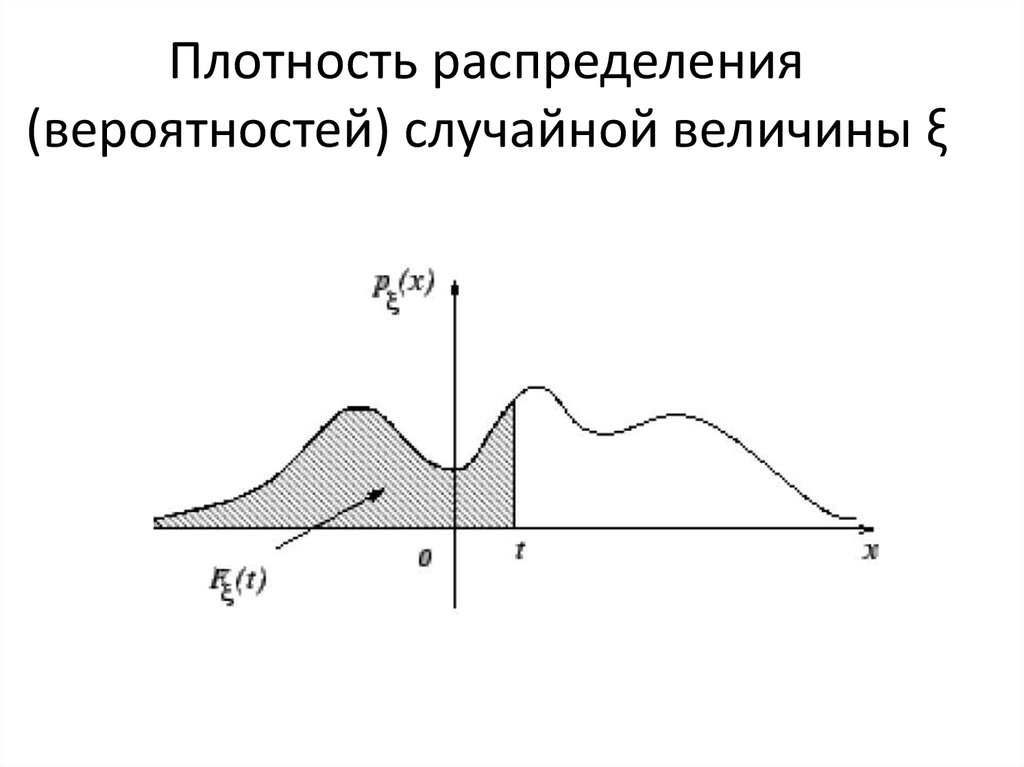 Как птица Феникс.
Как птица Феникс.
2) На интервале и:
, что и должно получиться.
Для построения графиков найдём пару опорных точек: и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:
Заметьте, что теоретически случайная величина может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при .
В соответствующей статье сайта я рассмотрел ещё более интересный пример с функцией , где случайная величина теоретически принимает вообще ВСЕ действительные значения. Но это уже несколько повышенный уровень сложности.
2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?
2.4.2. Вероятность попадания в промежуток
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.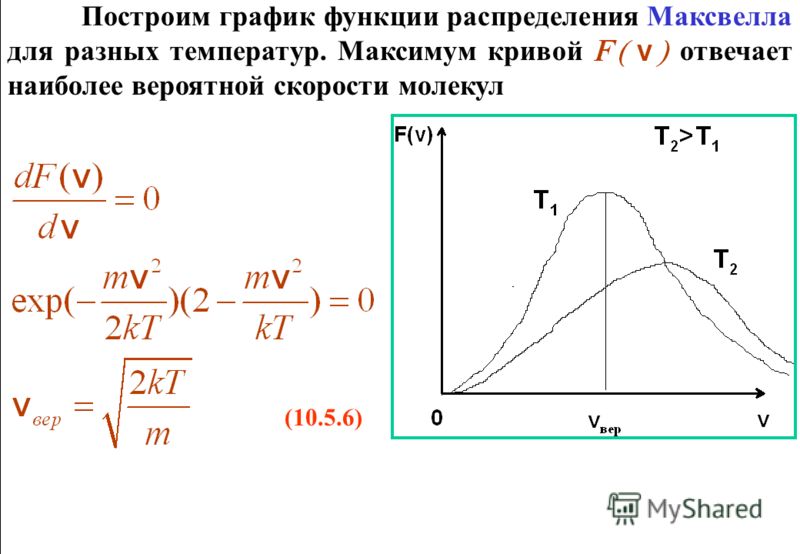
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Непрерывная случайная величина, функция распределения и плотность
- Определение непрерывной случайной величины и её связь с вероятностью
- Функция распределения непрерывной случайной величины и плотность вероятности
Случайной величиной называется переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств, и случайная величина называется непрерывной, если она может принимать любое значение из какого-либо ограниченного или неограниченного интервала. Для непрерывной случайной величины невозможно указать все возможные значения, поэтому обозначают интервалы этих значений, которые связаны с определёнными вероятностями.
Примерами непрерывных случайных величин могут служить: диаметр
детали, обтачиваемой до заданного размера, рост человека, дальность полёта снаряда и др.
Так как для непрерывных случайных величин функция F(x), в отличие от дискретных случайных величин, нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю.
Это значит, что для непрерывной случайной величины бессмысленно говорить о распределении вероятностей между её значениями: каждое из них имеет нулевую вероятность. Однако в некотором смысле среди значений непрерывной случайной величины есть «более и менее вероятные». Например, вряд ли у кого-либо возникнет сомнение, что значение случайной величины — роста наугад встреченного человека — 170 см — более вероятно, чем 220 см, хотя и одно, и другое значение могут встретиться на практике.
В качестве закона распределения, имеющего смысл только для непрерывных случайных
величин, вводится понятие плотности распределения или плотности вероятности. Подойдём к нему путём
сравнения смысла функции распределения для непрерывной случайной величины и для дискретной случайной величины.
Итак, функцией распределения случайной величины (как дискретной, так и непрерывной) или интегральной функцией называется функция , которая определяет вероятность, что значение случайной величины X меньше или равно граничному значению х.
Для дискретной случайной величины в точках её значений x1, x2, …, xi,…
сосредоточены массы вероятностей p1, p2, …, pi,…,
причём сумма всех масс равна 1. Перенесём эту интерпретацию на случай непрерывной случайной величины.
Представим себе, что масса, равная 1, не сосредоточена в отдельных точках, а непрерывно «размазана»
по оси абсцисс Оx с какой-то неравномерной плотностью. Вероятность попадания случайной величины
на любой участок Δx будет интерпретироваться как масса, приходящаяся
на этот участок, а средняя плотность на этом участке — как отношение массы к длине. Только что мы
ввели важное понятие теории вероятностей: плотность распределения.
Плотностью вероятности f(x) непрерывной случайной величины называется производная её функции распределения:
.
Зная функцию плотности, можно найти вероятность того, что значение непрерывной случайной величины принадлежит закрытому интервалу [a; b]:
вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала [a; b], равна определённому интегралу от её плотности вероятности в пределах от a до b:
или
.
При этом общая формула функции F(x) распределения вероятностей непрерывной случайной величины, которой можно пользоваться, если известна функция плотности f(x):
.
График плотности вероятности непрерывной случайной величины
называется её кривой распределения (рис.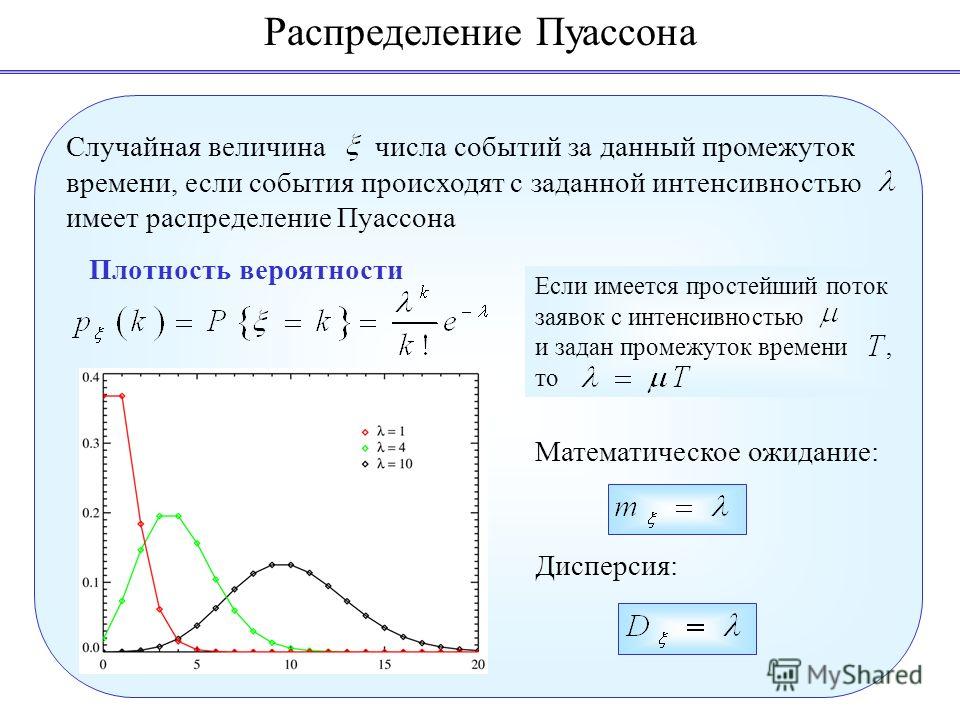 ниже).
ниже).
Площадь фигуры (на рисунке заштрихована), ограниченной кривой, прямыми, проведёнными из точек a и b перпендикулярно оси абсцисс, и осью Ох, графически отображает вероятность того, что значение непрерывной случайной величины Х находится в пределах от a до b.
Свойства функции плотности вероятности непрерывной случайной величины
1. Вероятность того, что случайная величина примет какое-либо значение из интервала (и площадь фигуры, которую ограничивают график функции f(x) и ось Ох) равна единице:
2. Функция плотности вероятности не может принимать отрицательные значения:
,
а за пределами существования распределения её значение равно нулю
Плотность распределения f(x), как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции
распределения, она не универсальна: плотность распределения существует только для непрерывных
случайных величин.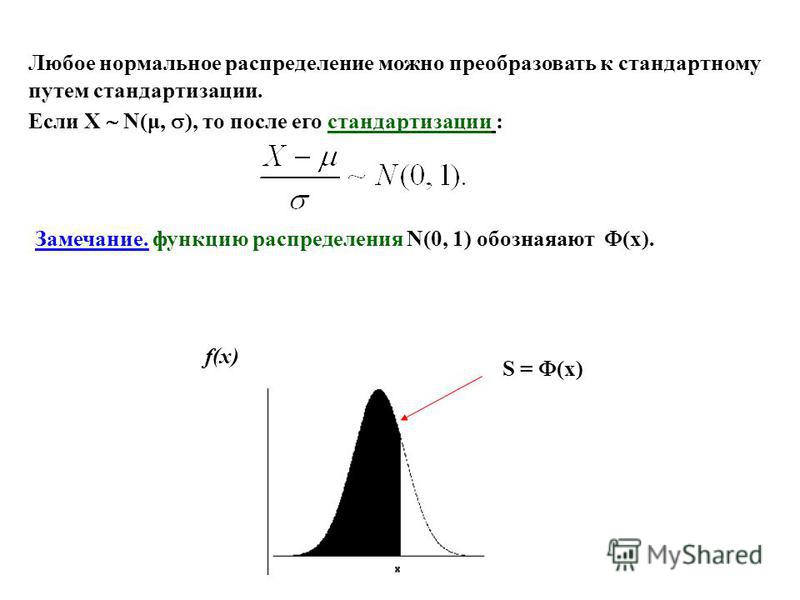
Упомянем о двух важнейших в практике видах распределения непрерывной случайной величины.
Если функция плотности распределения f(x) непрерывной случайной величины в некотором конечном интервале [a; b] принимает постоянное значение C, а за пределами интервала принимает значение, равное нулю, то такое распределение называется равномерным.
Если график функции плотности распределения симметричен относительно центра, средние значения сосредоточены вблизи центра, а при отдалении от центра собираются более отличающиеся от средних (график функции напоминает разрез колокола), то такое распределение называется нормальным.
Пример 1. Известна функция распределения вероятностей непрерывной случайной величины:
Найти функцию f(x) плотности
вероятности непрерывной случайной величины.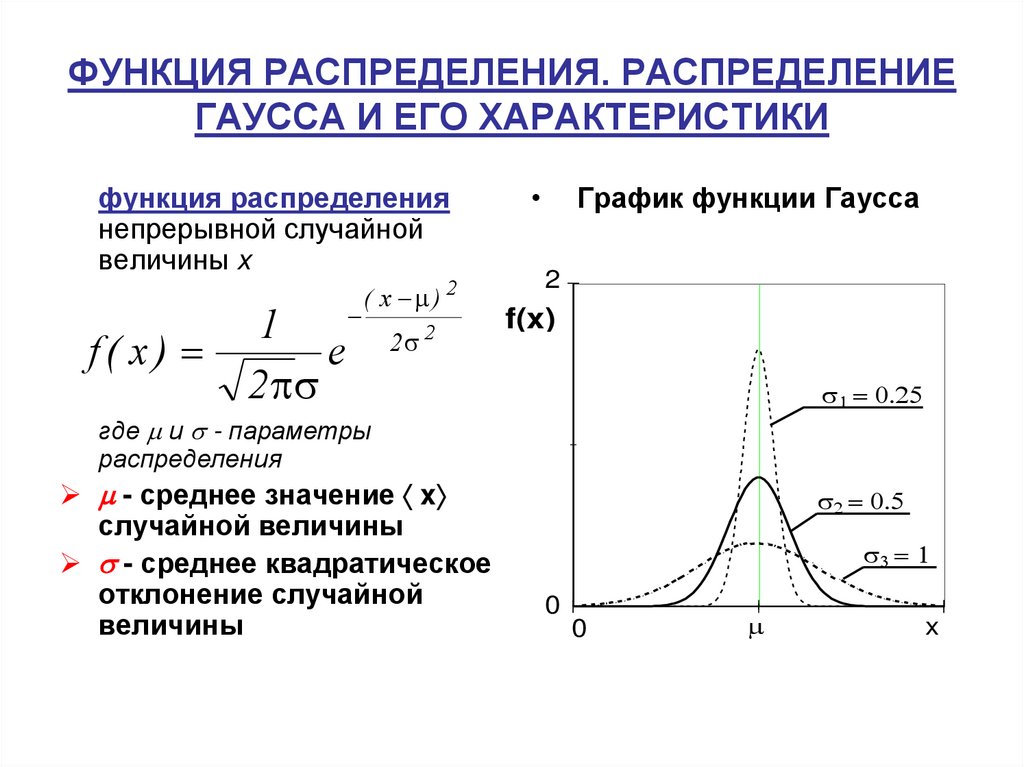 Построить графики обеих функций. Найти вероятность того, что
непрерывная случайная величина примет какое-либо значение в интервале от 4 до 8:
.
Построить графики обеих функций. Найти вероятность того, что
непрерывная случайная величина примет какое-либо значение в интервале от 4 до 8:
.
Решение. Функцию плотности вероятности получаем, находя производную функции распределения вероятностей:
График функции F(x) — парабола:
График функции f(x) — прямая:
Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 4 до 8:
.
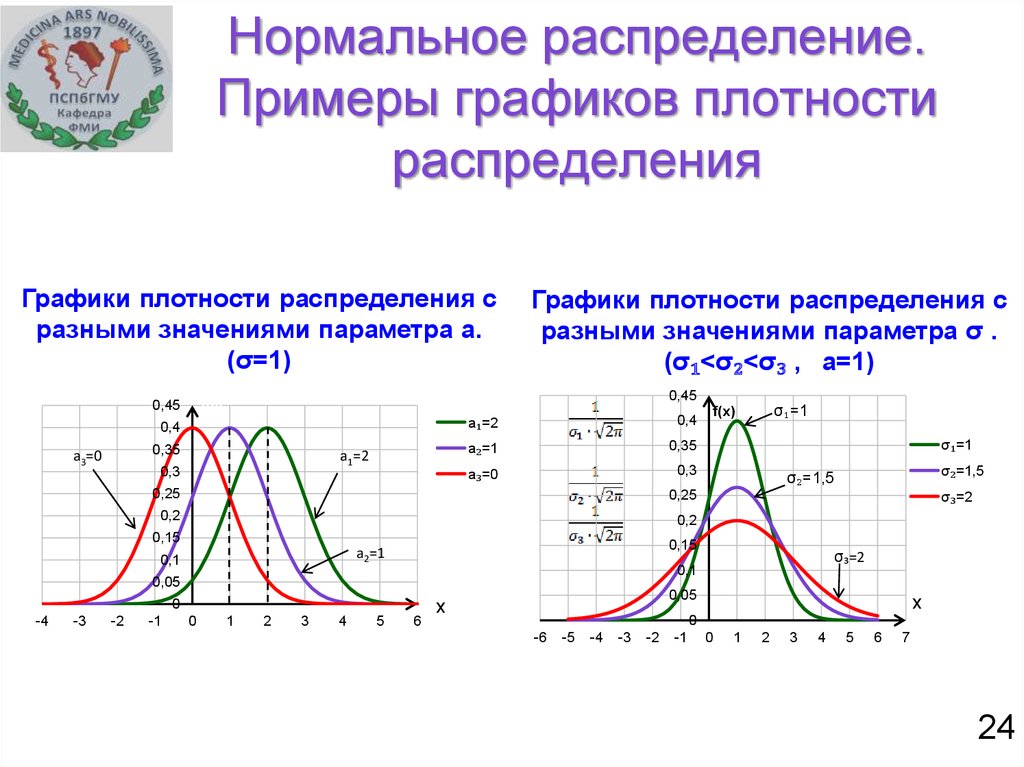
Пример 2. Функция плотности вероятности непрерывной случайной величины дана в виде:
Вычислить коэффициент C. Найти функцию F(x)
распределения вероятностей непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что
непрерывная случайная величина примет какое-либо значение в интервале от 0 до 5:
.
Решение. Коэффициент C найдём, пользуясь свойством 1 функции плотности вероятности:
Таким образом, функция плотности вероятности непрерывной случайной величины:
Интегрируя, найдём функцию F(x) распределения вероятностей. Если x < 0, то F(x) = 0. Если 0 < x < 10, то
.
x > 10, то F(x) = 1.
Таким образом, полная запись функции распределения вероятностей:
График функции f(x):
График функции F(x):
Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 0 до 5:
.
Пример 3. Плотность вероятности непрерывной
случайной величины X задана равенством
,
при этом . Найти коэффициент А, вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[, функцию распределения
непрерывной случайной величины X.
Найти коэффициент А, вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[, функцию распределения
непрерывной случайной величины X.
Решение. По условию приходим к равенству
.
Но
Следовательно, , откуда . Итак,
.
Теперь находим вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[:
Теперь получим функцию распределения данной случайной величины:
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Пример 4. Найти плотность вероятности непрерывной случайной величины X, которая принимает только неотрицательные значения, а её функция распределения .
Решение.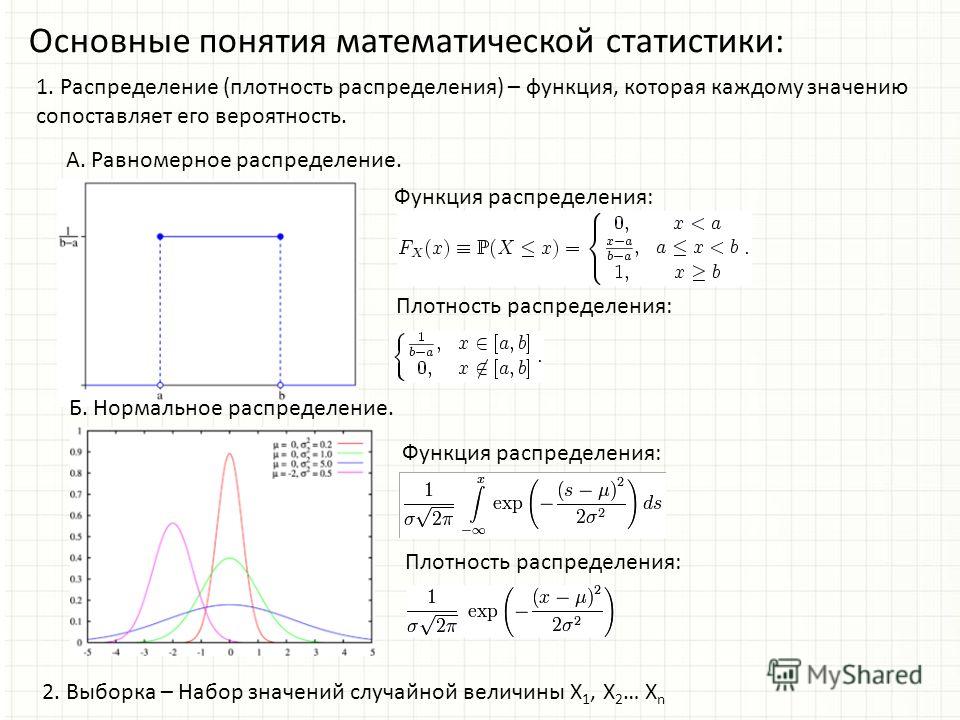 По определению плотности вероятности получаем
По определению плотности вероятности получаем
при и при , поскольку F(x) для этих значений x постоянна (равна нулю).
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Пройти тест по теме Теория вероятностей и математическая статистика
Пример 5. Плотность распределения непрерывной случайной величины задана формулой:
(при x > 0)
(a — положительный коэффициент).
1) найти функцию распределения непрерывной случайной величины;
2) найти вероятность того, что непрерывная случайная величина примет значение, лежащее между 1 и 2.
Решение.
1) При x < 0 f(x) = 0, значит . При x > 0 . Первый интеграл равен нулю. Второй . Итак, функция распределения данной непрерывной случайной величины имеет вид:
2) вероятность попадания непрерывной случайной величины на участок между 1 и 2 вычислим как приращение функции распределения на этом участке:
Пример 6. Непрерывная случайная величина
имеет плотность
Непрерывная случайная величина
имеет плотность
при .
1) найти вероятность попадания непрерывной случайной величины на участок от 0 до π/4;
2) функцию распределения непрерывной случайной величины.
Решение.
1) находим вероятность:
.
2) находим функцию распределения непрерывной случайной величины:
Пример 7. Плотность распределения непрерывной случайной величины задана формулой
.
Найти вероятность попадания непрерывной случайной величины на участок (-1; +1)
Решение.
.
| Назад | Листать | Вперёд>>> |
Пройти тест по теме Теория вероятностей и математическая статистика
К началу страницы
Начало темы «Теория вероятностей»
Действия над вероятностями
Различные задачи на сложение и умножение вероятностей
Формула полной вероятности
Формула Байеса
Независимые испытания и формула Бернулли
Распределение вероятностей дискретной случайной величины
Математическое ожидание и дисперсия случайной величины
Биномиальное распределение дискретной случайной величины
Распределение Пуассона дискретной случайной величины
Равномерное распределение непрерывной случайной величины
Нормальное распределение непрерывной случайной величины
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Теория вероятностей. Математическая статистика. Комбинаторика. / / Функция распределения плотности вероятностей и ее свойства. Функция плотности вероятности. Поделиться:
| |||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ | Энциклопедия Кругосвет
Содержание статьи- Примеры.
- Броуновское движение.
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ – плотность вероятности распределения частиц макроскопической системы по координатам, импульсам или квантовым состояниям. Функция распределения является основной характеристикой самых разнообразных (не только физических) систем, которым свойственно случайное поведение, т. е. случайное изменение состояния системы и, соответственно, ее параметров. Даже в стационарных внешних условиях само состояние системы может быть таким, что результат измерения некоторого его параметра является случайной величиной. Функция распределения в подавляющем большинстве случаев содержит в себе всю возможную и потому исчерпывающую информацию о свойствах таких систем.
е. случайное изменение состояния системы и, соответственно, ее параметров. Даже в стационарных внешних условиях само состояние системы может быть таким, что результат измерения некоторого его параметра является случайной величиной. Функция распределения в подавляющем большинстве случаев содержит в себе всю возможную и потому исчерпывающую информацию о свойствах таких систем.
В математической теории вероятностей и математической статистике функция распределения и плотность вероятности отличаются друг от друга, но однозначно связаны между собой. Ниже речь пойдет почти исключительно о плотности вероятности, которую (согласно принятой в физике давней традиции) называют плотностью распределения вероятности или функцией распределения, ставя знак равенства между этими двумя терминами.
Случайное поведение в той или иной мере характерно для всех квантовомеханических систем: элементарные частицы, атомы молекулы и т.п. Однако случайное поведение – это не специфическая черта только квантовомеханических систем, многие чисто классические системы обладают этим свойством.
Примеры.
При бросании монеты на твердую горизонтальную поверхность, неясно, как она ляжет: цифрой вверх или гербом. Известно, что вероятности этих событий, при определенных условиях, равны 1/2. При бросании игральной кости нельзя с уверенностью сказать, какая из шести цифр окажется на верхней грани. Вероятность выпадения каждой из цифр при определенных предположениях (кость – однородный куб без сколотых ребер и вершин падает на твердую, гладкую горизонтальную поверхность) равна 1/6.
Хаотичность движения молекул в наибольшей степени проявляется в газе. Даже в стационарных внешних условиях, флуктуируют (меняются случайным образом) точные значения макроскопических параметров, и только их средние значения при этом постоянны. Описание макроскопических систем на языке средних значений макропараметров и составляет суть термодинамического описания (см. статью ТЕРМОДИНАМИКА).
Пусть есть идеальный одноатомный газ и три его (еще не усредненных) макроскопических параметра: N – число атомов, движущихся внутри сосуда, занятого газом; P –давление газа на стенку сосуда и – внутренняя энергия газа. Газ идеальный и одноатомный, поэтому его внутренняя энергия есть просто сумма кинетических энергий поступательного движения атомов газа.
Газ идеальный и одноатомный, поэтому его внутренняя энергия есть просто сумма кинетических энергий поступательного движения атомов газа.
Число N флуктуирует, по крайней мере, из-за процесса сорбции (прилипания к стенке сосуда при соударении с ней) и десорбции (процесса отлипания, когда молекула отрывается от стенки сама по себе или в результате удара по ней другой молекулы), наконец, процесса образования кластеров – короткоживущих комплексов из нескольких молекул. Если бы Можно было измерять N мгновенно и точно, то полученная зависимость N(t) была бы похожей на изображенную на рисунке.
Размах флуктуаций на рисунке для наглядности сильно завышен, но при небольшом среднем значении (бN с ~ 102) числа частиц в газе он примерно таким и будет.
Если выбрать маленькую площадку на стенке сосуда измерять силу, действующую на эту площадку в результате ударов молекул газа, находящегося в сосуде, то отношение среднего значения нормальной к площадке компоненты этой силы к площади площадки и принято называть давлением. В разные моменты времени к площадке будет подлетать разное количество молекул, причем с разными скоростями. В результате, если бы можно было измерять эту силу мгновенно и точно, была бы картина, подобная изображенной на рисунке, нужно только изменить обозначения по вертикальной оси:
В разные моменты времени к площадке будет подлетать разное количество молекул, причем с разными скоростями. В результате, если бы можно было измерять эту силу мгновенно и точно, была бы картина, подобная изображенной на рисунке, нужно только изменить обозначения по вертикальной оси:
N(t) Ю P(t) и бN(t)с Ю бP(t)с.
Практически все то же справедливо и для внутренней энергии газа, только процессы, приводящие к случайным изменениям данной суммы другие. Например, подлетая к стенке сосуда, молекула газа сталкивается не с абстрактной абсолютно упруго и зеркально отражающей стенкой, а с одной из частиц, составляющих материал этой стенки. Пусть стенка стальная, тогда это ионы железа, колеблющиеся около положений равновесия – узлов кристаллической решетки. Если молекула газа подлетает к стенке на той фазе колебаний иона, когда он движется ей навстречу, то в результате соударения молекула отлетит от стенки со скоростью большей чем подлетала. Вместе с энергией этой молекулы увеличится и внутренняя энергия газа E. Если молекула сталкивается с ионом, движущемся в том же направлении, что и она, то отлетит эта молекула со скоростью меньшей, чем та, с которой она полетала. Наконец, молекула может попасть в междуузелье (пустое место между соседними узлами кристаллической решетки) и застрять там, так, что даже сильным нагревом ее не извлечь оттуда. В последних двух случаях внутренняя энергия газа E уменьшится. Следовательно, E(t) – также случайная функция времени и – среднее значение этой функции.
Вместе с энергией этой молекулы увеличится и внутренняя энергия газа E. Если молекула сталкивается с ионом, движущемся в том же направлении, что и она, то отлетит эта молекула со скоростью меньшей, чем та, с которой она полетала. Наконец, молекула может попасть в междуузелье (пустое место между соседними узлами кристаллической решетки) и застрять там, так, что даже сильным нагревом ее не извлечь оттуда. В последних двух случаях внутренняя энергия газа E уменьшится. Следовательно, E(t) – также случайная функция времени и – среднее значение этой функции.
Броуновское движение.
Определив положение броуновской частицы в некоторый момент времени t1, можно точно предсказать только то, что ее положение в последующий момент времени t2 не превышает (t2 – t1)·c, где c – скорость света в вакууме.
Различают случаи дискретного и непрерывного спектра состояний и, соответственно, переменной x. Под спектром значений некоторой переменной понимается вся совокупность возможных ее значений.
Под спектром значений некоторой переменной понимается вся совокупность возможных ее значений.
В случае дискретного спектра состояний для задания распределения вероятностей нужно, во-первых, указать полный набор возможных значений случайной переменной
x1, x2, x3,… xk,… (1)
и, во-вторых, их вероятности:
W1, W2, W3,… Wk,… (2)
Сумма вероятностей всех возможных событий должна быть равна единице (условие нормировки)
(3)
Описание распределения вероятностей соотношениями (1) – (3) невозможно в случае непрерывного спектра состояний и, соответственно, непрерывного спектра возможных значений переменной x. Пусть x принимает все возможные действительные значения в интервале
x О [a, b] (4)
где a и b необязательно конечны. Например, для модуля вектора скорости молекулы газа V О [0, Ґ), а для проекции вектора скорости на направление, скажем, оси OZ: VzО (–Ґ, +Ґ)1 (рассматривается случай нерелятивистской теории, когда скорости частиц не ограничены сверху скоростью движения света в вакууме С).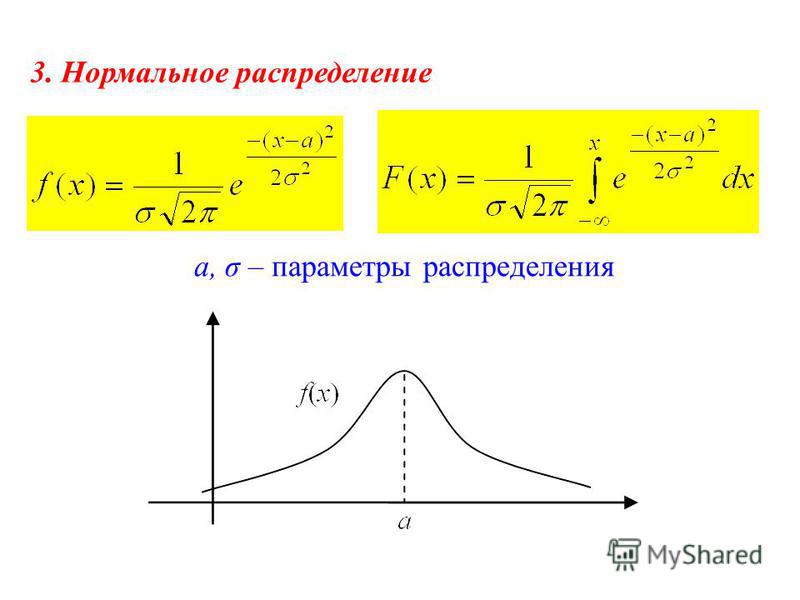
Пусть есть событие (результат измерения x) – значение переменной x принадлежит интервалу [x, x + Dx], лежащему внутри всего интервала возможных значений, т.е. x О [x, x + Dx] О [a, b] (5)
Тогда вероятность DW(x, Dx) попадания x в интервал (5) равна
(6)
Здесь N – полное число измерений x, а Dn(x, Dx) – число результатов, попавших в интервал (5).
Вероятность DW естественно зависит от двух аргументов: x – положения интервала внутри [a, b] и Dx – его длины (предполагается, хотя это совершенно необязательно, что Dx > 0). Например, вероятность получения точного значения x, другими словами, вероятность попадания x в интервал нулевой длины есть вероятность невозможного события и потому равна нулю: DW(x, 0) = 0
С другой стороны, вероятность получить значение x где-то (все равно где) внутри всего интервала [a, b] есть вероятность достоверного события (уж что-нибудь всегда получается) и потому равна единице (принимается, что b > a): DW(a, b – a) = 1.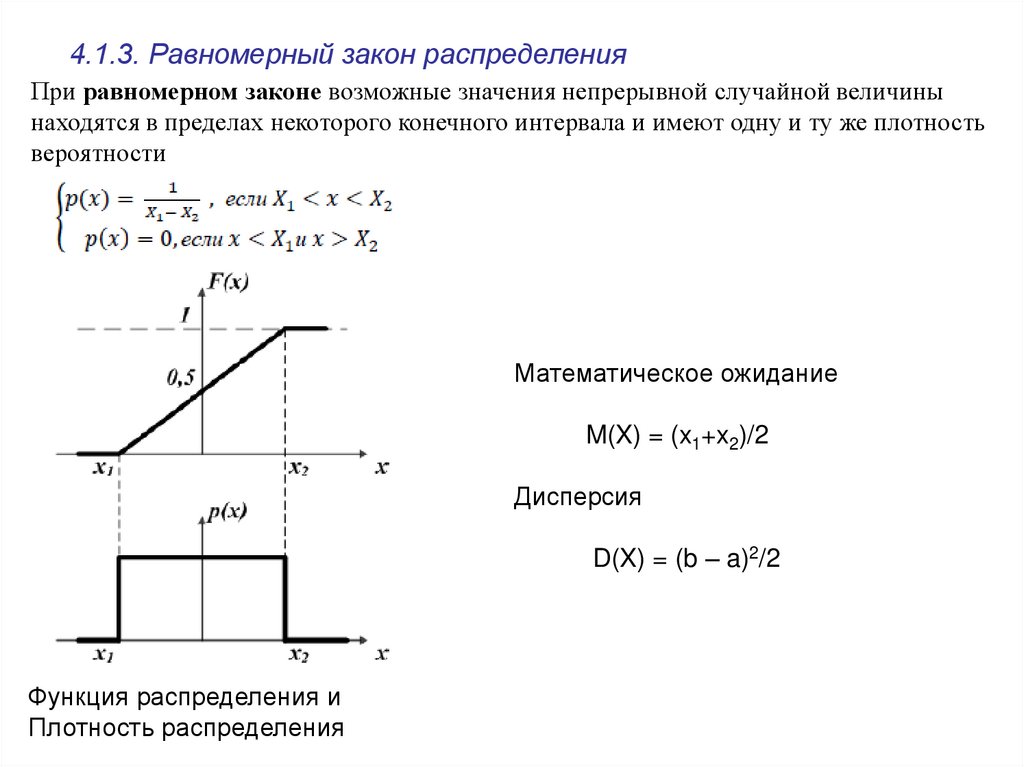
Пусть Dx мало. Критерий достаточной малости зависит от конкретных свойств системы, которую описывает распределение вероятностей DW(x, Dx). Если Dx мало, то функцию DW(x, Dx) можно разложить в ряд по степеням Dx:
(7)
Если нарисовать график зависимости DW(x, Dx) от второго аргумента Dx, то замена точной зависимости приближенным выражением (7) означает замену (на небольшом участке) точной кривой куском параболы (7).
В (7) первое слагаемое равно нулю точно, третье и последующие слагаемые при достаточной малости Dx можно опустить. Введение обозначения
дает важный результат DW(x, Dx) » r(x)·Dx (8)
Соотношение (8), выполняемое тем точнее, чем меньше Dx означает, что при малой длине интервала, вероятность попадания в этот интервал пропорциональна его длине.
Можно еще перейти от малого, но конечного Dx к формально бесконечно малому dx, с одновременной заменой DW(x, Dx) на dW(x). Тогда приближенное равенство (8) превращается в точное dW(x) = r(x)·dx (9)
Тогда приближенное равенство (8) превращается в точное dW(x) = r(x)·dx (9)
Коэффициент пропорциональности r(x) имеет простой смысл. Как видно из (8) и (9), r(x) численно равно вероятности попадания x в интервал единичной длины. Поэтому одно из названий функции r(x) – плотность распределения вероятностей для переменной x.
Функция r(x) содержит в себе всю информацию о том, как вероятность dW(x) попадания x в интервал заданной длины dx зависит от местоположения этого интервала, т.е. она показывает, как вероятность распределена по x. Поэтому функцию r(x) принято называть функцией распределения для переменной x и, тем самым, функцией распределения для той физической системы, ради описания спектра состояний которой была введена переменная x. Термины «плотность распределения вероятностей» и «функция распределения» в статистической физике используются как эквивалентные.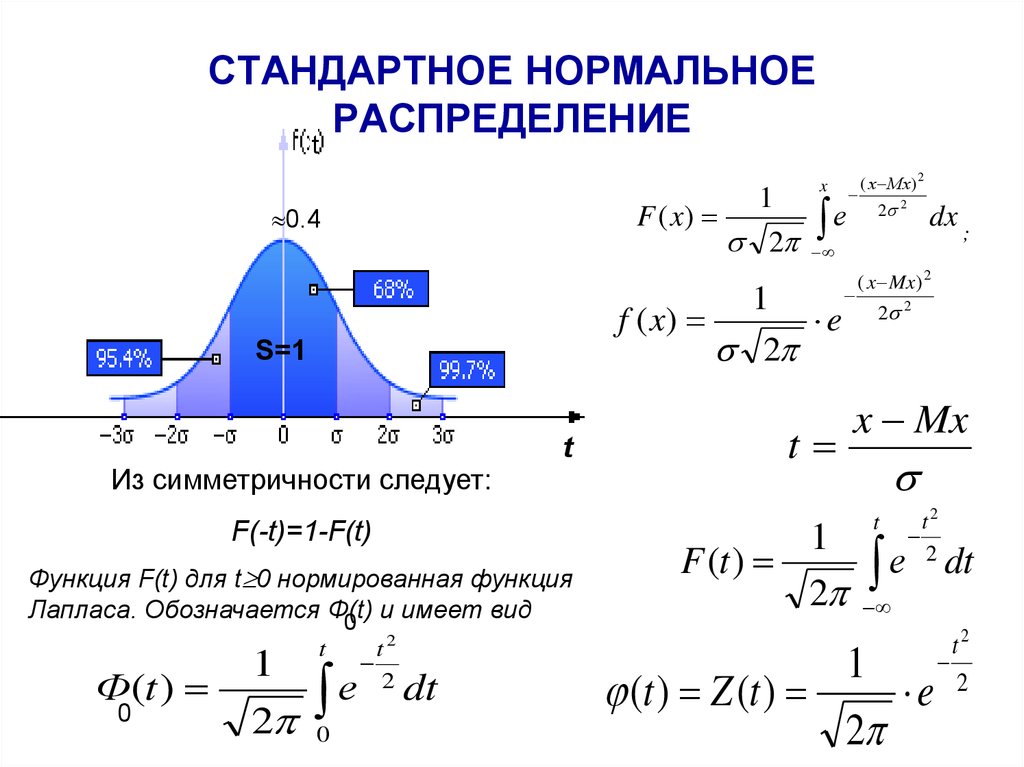
Можно рассмотреть обобщение определения вероятности (6) и функции распределения (9) на случай, к примеру, трех переменных. Обобщение на случай произвольно большого числа переменных выполняется точно также.
Пусть случайно меняющееся во времени состояние физической системы определяется значениями трех переменных x, y и z с непрерывным спектром:
x О [a, b]
y О [c, d]
z О [e, f] (10)
где a, b,…, f, как и ранее, не обязательно конечны. Переменные x, y и z могут быть, например, координатами центра масс молекулы газа, компонентами вектора ее скорости x Ю Vx, y Ю Vy и z Ю Vz или импульса и т.д. Под событием понимается одновременное попадание всех трех переменных в интервалы длины Dx, Dy и Dz соответственно, т. е.:
е.:
x О [x, x + Dx]
y О [y, y + Dy]
z О [z, z + Dz] (11)
Вероятность события (11) можно определить аналогично (6)
(12)
с тем отличием, что теперь Dn – число измерений x, y и z, результаты которых одновременно удовлетворяют соотношениям (11). Использование разложения в ряд, аналогичного (7), дает
dW(x, y, z) = r(x, y, z)·dx dy dz (13)
где r(x, y, z) – функция распределения сразу для трех переменных x, y и z.
В математической теории вероятностей термин «функция распределения» используется для обозначения величины отличающейся от r(x), а именно: пусть x – некоторое значение случайной переменной x. Функция Ф(x), дающая вероятность того, что x примет значение не большее, чем x и называется функцией распределения. Функции r и Ф имеют разный смысл, но они связаны между собой. Использование теоремы сложения вероятностей дает (здесь а – левый конец интервала возможных значений x (см. ВЕРОЯТНОСТЕЙ ТЕОРИЯ): , (14) откуда
Функции r и Ф имеют разный смысл, но они связаны между собой. Использование теоремы сложения вероятностей дает (здесь а – левый конец интервала возможных значений x (см. ВЕРОЯТНОСТЕЙ ТЕОРИЯ): , (14) откуда
(15)
Вероятность попадания в интервал произвольной длины [x, x + Dx] можно записать как
(16)
Использование приближенного соотношения (8) дает DW(x, Dx) » r(x)·Dx.
Сравнение с точным выражением (15) показывает, что использование (8) эквивалентно замене интеграла, входящего в (16), произведением подынтегральной функции r(x) на длину промежутка интегрирования Dx:
(17)
Соотношение (17) будет точным, если r = const, следовательно, ошибка при замене (16) на (17) будет невелика, когда подынтегральная функция слабо меняется на длине промежутка интегрирования Dx.
Можно ввести Dxэфф – длину интервала, на котором функция распределения r(x) меняется существенно, т. е. на величину порядка самой функции, или величина Drэфф по модулю порядка r. Используя формулу Лагранжа, можно написать:
е. на величину порядка самой функции, или величина Drэфф по модулю порядка r. Используя формулу Лагранжа, можно написать:
, (18)
откуда следует, что Dxэфф для любой функции r
(19)
Функцию распределения можно считать «почти постоянной» на некотором промежутке изменения аргумента, если ее приращение |Dr| на этом промежутке по модулю много меньше самой функции в точках этого промежутка. Требование |Dr| эфф| ~ r (функция распределения r і 0) дает
Dx xэфф (20)
длина промежутка интегрирования должна быть мала по сравнению с той, на которой подынтегральная функция меняется существенно. Иллюстрацией служит рис. 1.
Интеграл в левой части (17) равен площади под кривой. Произведение в правой части (17) – площадь заштрихованного на рис. 1 столбика. Критерием малости отличия соответствующих площадей является выполнение неравенства (20). В этом можно убедиться, подставляя в интеграл (17) первые члены разложения функции r(x) в ряд по степеням
(21)
Требование малости поправки (второго слагаемого в правой части (21) по сравнению с первым и дает неравенство (20) с Dxэфф из (19).
Примеры ряда функций распределения, играющих важную роль в статистической физике.
Распределение Максвелла для проекции вектора скорости молекулы на заданное направление (для примера, это направление оси OX).
(22)
Здесь m – масса молекулы газа, T – его температура, k – постоянная Больцмана.
Распределение Максвелла для модуля вектора скорости:
(23)
Распределение Максвелла для энергии поступательного движения молекул e = mV2/2
(24)
Распределение Больцмана, точнее, так называемая барометрическая формула, которая определяет распределение концентрации молекул или давления воздуха по высоте h от некоторого «нулевого уровня» в предположении, что температура воздуха от высоты не зависит (модель изотермической атмосферы). В действительности температура в нижних слоях атмосферы заметно падает с ростом высоты.
(25)
Здесь g – ускорение свободного падения.
Зависимости (22) – (25) показаны на рис. 2–5.
2–5.
, где .
Увеличение a означает увеличение массы молекул газа или уменьшение (во столько же раз) температуры газа.
При произвольном физическом (или совсем нефизическом) смысле переменных Vx = x – x0 и распределение принято называть распределением Гаусса или нормальным распределением. Распределение Гаусса широко применяется в самых различных областях науки, техники, промышленности и т.п. В последней формуле x0 – наиболее вероятное значение переменной x. Ввиду четности функции относительно разности x – x0 величина x0 совпадает со средним значением переменной x. Параметр s называется дисперсией и характеризует ширину (и высоту) максимума кривой распределения. Чем меньше дисперсия s, тем уже и выше максимум кривой распределения (рис. 2). Если под x понимать такие характеристики человеческого организма как рост, вес, способность к интеллектуальной деятельности (которую удается приближенно измерить с помощью различных тестов) и т.п., то кривые на рис. 2 качественно показывают различие биологических ролей мужчин и женщин. Высокая и узкая (относительно малая дисперсия) пунктирная кривая на рис. 2 – женская, широкая и низкая (относительно большая дисперсия) сплошная кривая на том же рисунке – мужская. Видно, что в среднем женщины заметно совершеннее мужчин. Биологическая задача женщины – сохранить в своих генах оптимальные в данной обстановке качества и передать их потомству. Задача мужчины – определить эти качества.
2 качественно показывают различие биологических ролей мужчин и женщин. Высокая и узкая (относительно малая дисперсия) пунктирная кривая на рис. 2 – женская, широкая и низкая (относительно большая дисперсия) сплошная кривая на том же рисунке – мужская. Видно, что в среднем женщины заметно совершеннее мужчин. Биологическая задача женщины – сохранить в своих генах оптимальные в данной обстановке качества и передать их потомству. Задача мужчины – определить эти качества.
, где .
Увеличение a означает увеличение массы молекул газа или уменьшение (во столько же раз) температуры газа.
, где .
Увеличение a означает увеличение массы молекул газа или уменьшение (во столько же раз) температуры газа.
p(h) = p0·exp(–g·h), где .
Увеличение g означает увеличение массы молекул газа или уменьшение (во столько же раз) температуры газа, p0 – давление на уровне h = 0, переход к формуле (25) осуществляется с помощью уравнения состояния идеального газа p = nkT.
Приведенные выше статистические распределения могут быть получены как частные случаи из наиболее общего большого канонического распределения Гиббса, которое (опять таки как частные случаи) содержит в себе квантовые распределения а) Ферми – Дирака для идеального газа фермионов – частиц с полуцелым спином и 2) Бозе – Эйнштейна для идеального бозонов – частиц с целым спином.
Валериан Гервидс
5.4. Плотность распределения кратко Теория вероятностей. Математическая…
Привет, Вы узнаете про плотность распределения, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое плотность распределения , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Пусть имеется непрерывная случайная величина с функцией распределения , которую мы предположим непрерывной и дифференцируемой.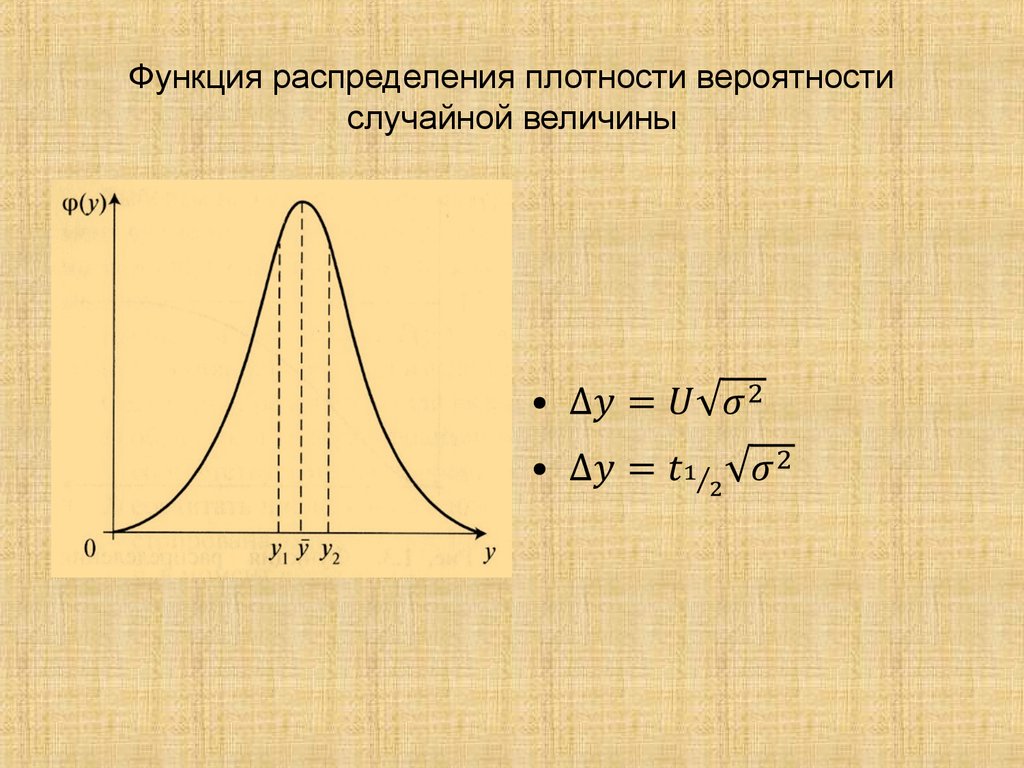 Вычислим вероятность попадания этой случайной величины на участок от до :
Вычислим вероятность попадания этой случайной величины на участок от до :
,
т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать к нулю. В пределе получим производную от функции распределения:
. (5.4.1)
Введем обозначение:
. (5.4.2)
Функция — производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины .
Термины «
плотность распределения », «плотность вероятности» становятся особенно наглядными при пользовании механической интерпретацией распределения; в этой интерпретации функция буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»). Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 5.4.1).
Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 5.4.1).
Рис. 5.4.1.
Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.
Рассмотрим непрерывную случайную величину с плотностью распределения и элементарный участок , примыкающий к точке (рис. 5.4.2). Вероятность попадания случайной величины на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна . Величина называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок (рис. 5.4.2).
Рис. 5.4.2.
Выразим вероятность попадания величины на отрезок от до (рис 5.4.3) через плотность распределения . Об этом говорит сайт https://intellect.icu . Очевидно, она равна сумме элементов вероятности на всем этом участке, т.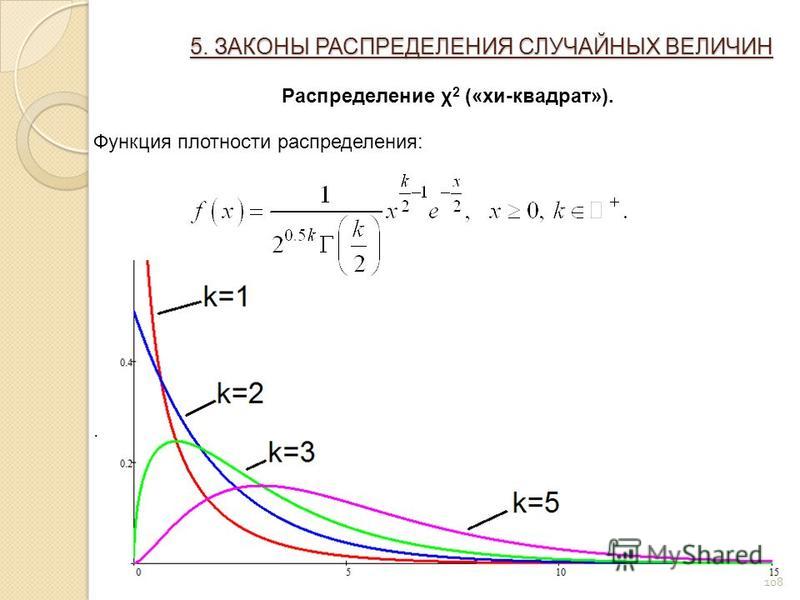 е. интегралу:
е. интегралу:
(5.4.3)
*) Так как вероятность любого отдельного значения непрерывной случайной величины равна нулю, то можно рассматривать здесь отрезок , не включая в него левый конец, т.е. отбрасывая знак равенства в .
Геометрически вероятность попадания величины на участок равна площади кривой распределения, опирающейся на этот участок (рис. 5.4.3.).
Рис. 5.4.3.
Формула (5.4.2.) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению
,
откуда по формуле (5.4.3) имеем:
. (5.4.4)
Геометрически есть не что иное, как площадь кривой распределения, лежащая левее точки (рис. 5.4.4).
Рис. 5.4.4.
Укажем основные свойства плотности распределения.
1. Плотность распределения есть неотрицательная функция:
.
Это свойство непосредственно вытекает из того, что функция распределения есть неубывающая функция.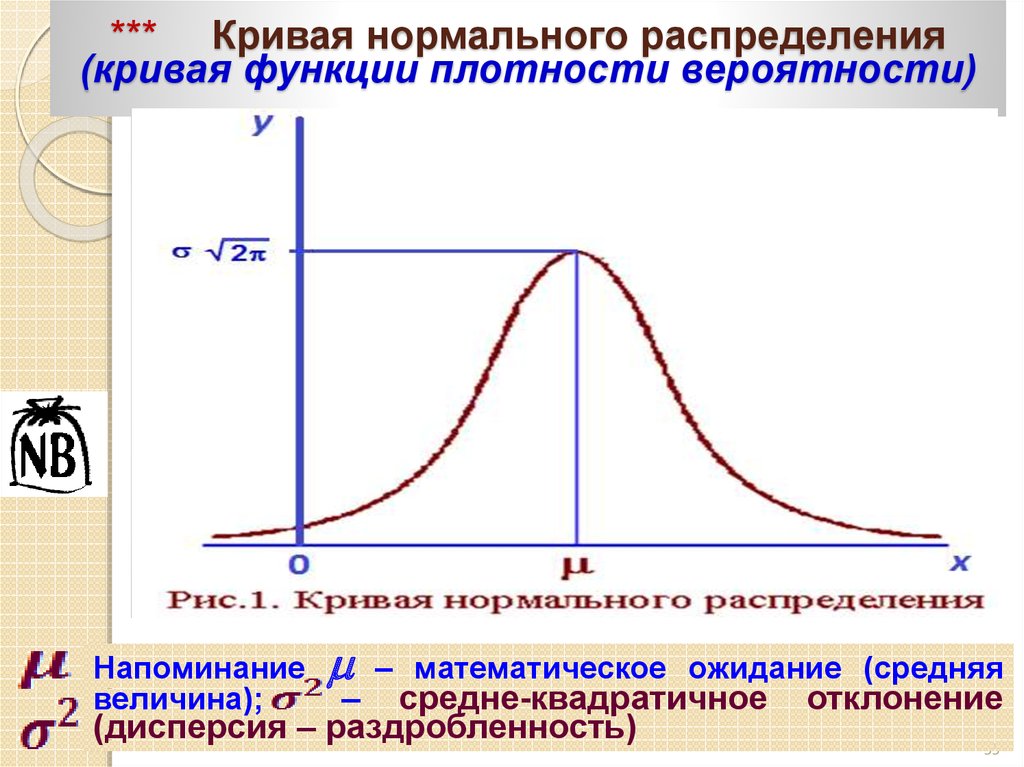
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
.
Это следует из формулы (5.4.4) и из того, что .
Геометрически основные свойства плотности распределения означают, что:
1) вся кривая распределения лежит не ниже оси абсцисс;
2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Выясним размерность основных характеристик случайной величины – функции распределения и плотности распределения. Функция распределения , как всякая вероятность, есть величина безразмерная. Размерность плотности распределения , как видно из формулы (5.4.1), обратна размерности случайной величины.
Пример 1. Функция распределения непрерывной случайной величины Х задана выражением
а) Найти коэффициент а.
б) Найти плотность распределения .
в) Найти вероятность попадания величины на участок от 0,25 до 0,5.
Решение. а) Так как функция распределения величины непрерывна, то при , откуда .
б) Плотность распределения величины выражается формулой
в) По формуле (5.3.1) имеем:
.
Пример 2. Случайная величина подчинена закону распределения с плотностью:
при
при или .
а) Найти коэффициент а.
б) Построить график плотности распределения .
в) Найти функцию распределения и построить ее график.
г) Найти вероятность попадания величины на участок от 0 до .
Решение. а) Для определения коэффициента а воспользуемся свойством плотности распределения:
,
откуда .
б) График плотности представлен на рис. 5.4.5.
Рис. 5.4.5.
в) По формуле (5.4.4) получаем выражение функции распределения:
График функции изображен на рис. 5.4.6.
Рис. 5.4.6.
г) По формуле (5.3.1) имеем:
.
Тот же результат, но несколько более сложным путем, можно получить по формуле (5.4.3).
Пример 3. Плотность распределения случайной величины задана формулой:
.
а) Построить график плотности .
б) Найти вероятность того, что величина попадет на участок (-1, +1).
Решение. а) График плотности дан на рис. 5.4.7.
Рис. 5.4.7.
б) По формуле (5.4.3) имеем:
.
Плотность нормального распределения
•Куполообразное, симметричное распределение
•Задается двумя параметрами: среднее (µ) и стандартное отклонение (σ). Параметры идеального распределения пишутся греческими буквами, как и параметры генеральной совокупности
•
Кривые плотности вероятности
•Описывают общую картину распределения. Площадь под кривой в некотором интервале отражает долю от всех наблюдений, попадающих в этот интервал
•Находится всегда выше горизонтальной оси или на ней
•Имеет площадь под ней, равную 1
Среднее и медиана в контексте кривых плотности вероятности
•Медиана делит площадь под кривой плотности вероятности на две равные части по 0. 5
5
•Среднее является «точкой баланса» кривой. Стремится располагаться у более вытянутого хвоста
Надеюсь, эта статья про плотность распределения, была вам полезна,счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое плотность распределения и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Функция, плотность распределения
2.1. Функция распределения.
Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений.
Однако, такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал.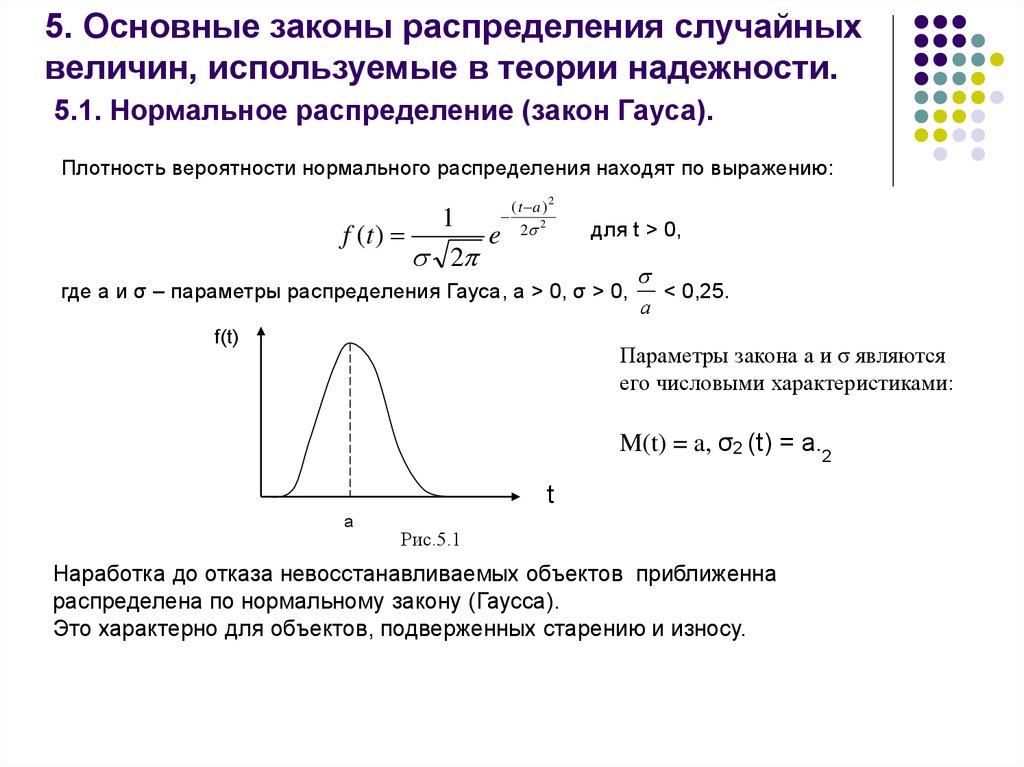 Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?
Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. Х < x, обозначим через F(x).
Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.
Функцию распределения также называют интегральной функцией.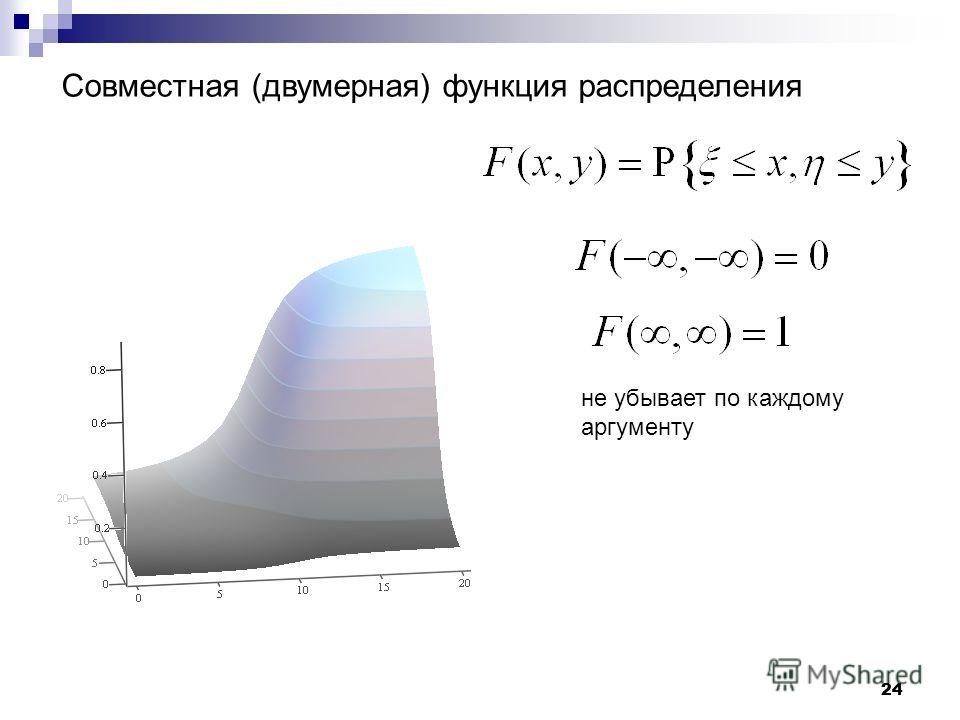
Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет вид:
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение хi.
Так для примера, рассмотренного выше, функция распределения будет иметь вид:
Свойства функции распределения:
1) значения функции распределения принадлежат отрезку [0, 1].
2) F(x) – неубывающая функция.
при
3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале.
4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.
5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.
Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.
2.2. Плотность распределения.
Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.
Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.
Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением( может быть, конечного числа точек.
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.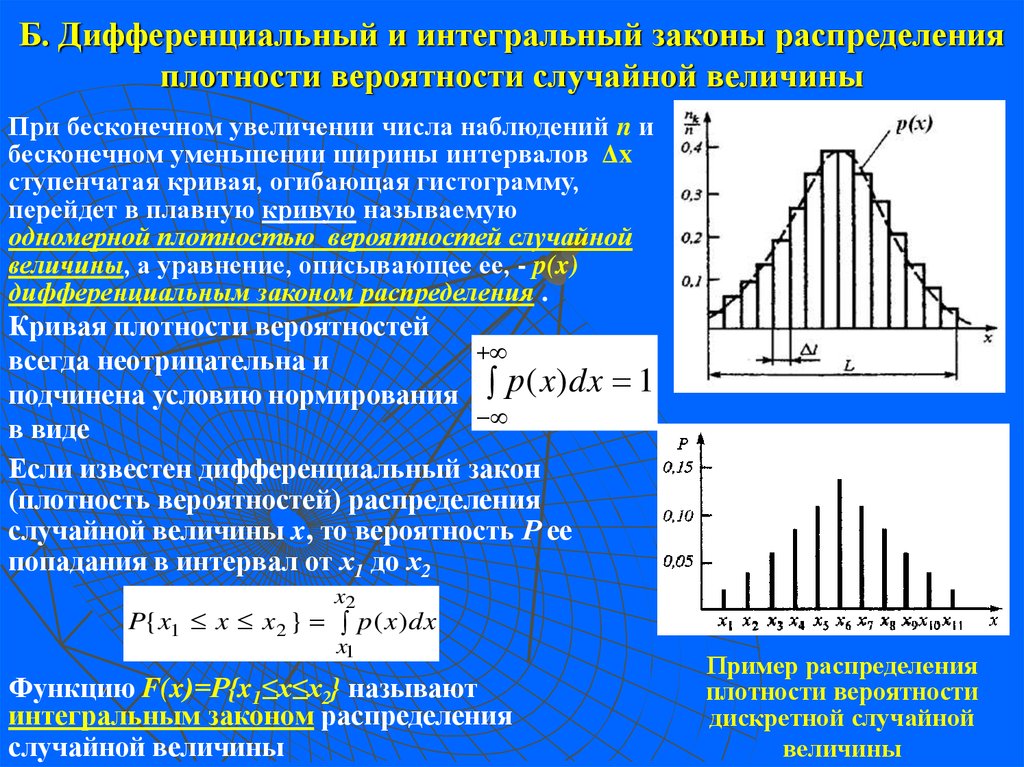
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше.
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.
Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
Свойства плотности распределения:
1) Плотность распределения – неотрицательная функция:
2) Несобственный интеграл от плотности распределения в пределах от — ¥ до ¥ равен единице:
Пример. Случайная величина подчинена закону распределения с плотностью:
Случайная величина подчинена закону распределения с плотностью:
Требуется найти коэффициент а, построить график функции плотности распределения, определить вероятность того, что случайная величина попадет в интервал от 0 до .
Построим график плотности распределения:
Для нахождения коэффициента а воспользуемся свойством .
Находим вероятность попадания случайной величины в заданный интервал.
Пример. Задана непрерывная случайная величина х своей функцией распределения f(x).
Требуется определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал .
Найдем коэффициент А.
Найдем функцию распределения:
1) На участке :
2) На участке
3) На участке
Итого:
Построим график плотности распределения:
f(x)
Построим график функции распределения:
F(x)
Найдем вероятность попадания случайной величины в интервал .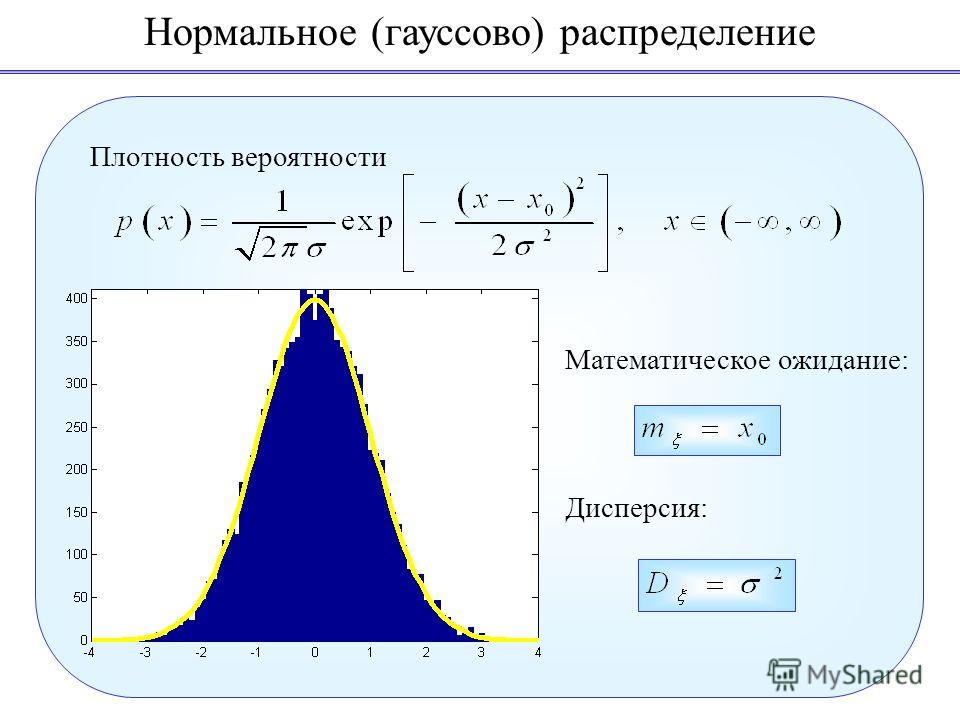
Ту же самую вероятность можно искать и другим способом:
Дата добавления: 2019-12-09; просмотров: 292; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
14.1 — Функции плотности вероятности
Непрерывная случайная величина принимает несчетно бесконечное число возможных значений. Для дискретной случайной величины \(X\), которая принимает конечное или счетно бесконечное число возможных значений, мы определили \(P(X=x)\) для всех возможных значений \(X\) и назвали это функция массы вероятности («pmf»). Для непрерывных случайных величин, как мы вскоре увидим, вероятность того, что \(X\) примет любое конкретное значение \(x\), равна 0. То есть нахождение \(P(X=x)\) для непрерывного случайного переменная \(X\) не будет работать. Вместо этого нам нужно найти вероятность того, что \(X\) попадает в некоторый интервал \((a, b)\), то есть нам нужно найти \(P(a
Несмотря на то, что сеть ресторанов быстрого питания может рекламировать гамбургер весом в четверть фунта, вы можете себе представить, что это не совсем 0,25 фунта. Один случайно выбранный гамбургер может весить 0,23 фунта, а другой — 0,27 фунта. Какова вероятность того, что случайно выбранный гамбургер весит от 0,20 до 0,30 фунта? То есть, если мы позволим \(X\) обозначить вес случайно выбранного гамбургера в четверть фунта в фунтах, что будет \(P(0,20 На самом деле, я не особенно заинтересован в использовании этого примера просто для того, чтобы вы знали, обманули вас или нет, когда в следующий раз будете заказывать гамбургер! Вместо этого мне интересно использовать пример, чтобы проиллюстрировать идею функции плотности вероятности. Теперь вы можете представить случайный выбор, скажем, 100 гамбургеров, рекламируемых весом в четверть фунта. Если вы взвесите 100 гамбургеров и создадите гистограмму плотности полученных весов, возможно, гистограмма будет выглядеть примерно так: В этом случае гистограмма показывает, что вес большинства отобранных гамбургеров действительно приближается к 0,25 фунта, но некоторые из них немного больше, а некоторые немного меньше. А что, если мы продвинемся дальше и еще больше уменьшим интервалы? Вы можете себе представить, что интервалы в конечном итоге станут настолько малы, что мы сможем представить распределение вероятностей \(X\) не в виде гистограммы плотности, а скорее в виде кривой (соединив «точки» на вершинах крошечных крошечных крошечные прямоугольники), что в данном случае могло бы выглядеть так: Такая кривая обозначается \(f(x)\) и называется (непрерывной) функцией плотности вероятности . Теперь вы можете вспомнить, что гистограмма плотности определяется так, что площадь каждого прямоугольника равна относительной частоте соответствующего класса, а площадь всей гистограммы равна 1. Это предполагает, что нахождение вероятности того, что непрерывная случайная переменная \(X\) попадает в некоторый интервал значений, включает в себя нахождение площади под кривой \(f(x)\), зажатой концами интервала. Решение
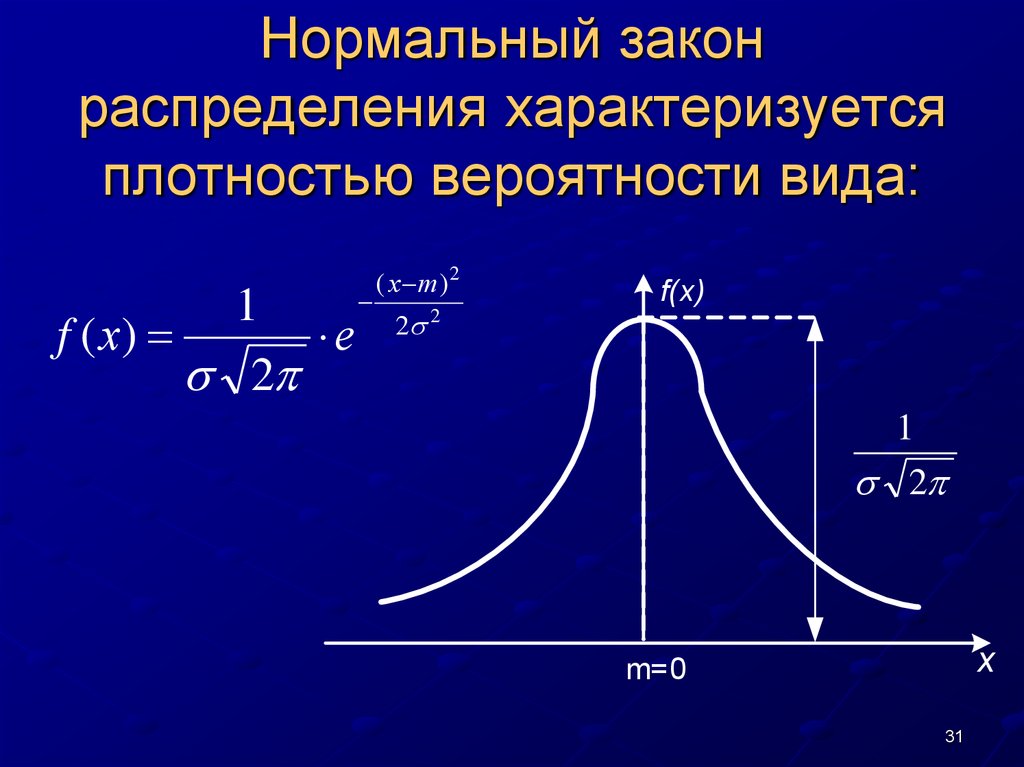 А что, если мы уменьшим длину интервала класса на этой гистограмме плотности? Тогда гистограмма плотности будет выглядеть примерно так:
А что, если мы уменьшим длину интервала класса на этой гистограмме плотности? Тогда гистограмма плотности будет выглядеть примерно так: В этом примере вероятность того, что случайно выбранный гамбургер весит от 0,20 до 0,30 фунта, равна следующей площади:
В этом примере вероятность того, что случайно выбранный гамбургер весит от 0,20 до 0,30 фунта, равна следующей площади:
- Функция плотности вероятности («p.d.f.»)
Функция плотности вероятности (« p.d.f. «) непрерывной случайной величины \(X\) с носителем \(S\) является интегрируемой функцией \(f(x)\), удовлетворяющей следующему:
\(f(x)\) положительно всюду в носителе \(S\), т. е. \(f(x)>0\), для всех \(x\) в \(S\)
Площадь под кривой \(f(x)\) в опоре \(S\) равна 1, то есть:
\(\int_S f(x)dx=1\)
Если \(f(x)\) является п.ф.п. от \(x\), то вероятность того, что \(x\) принадлежит \(A\), где \(A\) — некоторый интервал, определяется интегралом от \(f(x)\) по этому интервал, то есть:
\(P(X\in A)=\int_A f(x)dx\)
Как видите, определение файла p. Теперь давайте сначала проверим, что \(f(x)\) является допустимой функцией плотности вероятности. Какова вероятность того, что \(X\) находится между \(\frac{1}{2}\) и 1? То есть что такое \(P\left(\frac{1}{2} Вообще говоря, если \(X\ ) непрерывна, вероятность того, что \(X\) принимает какое-либо конкретное значение \(x\), равна 0. То есть, когда \(X\) непрерывно, \(P(X=x)=0\) для все \(x\) в носителе. Следствием того факта, что \(P(X=x)=0\) для всех \(x\), когда \(X\) является непрерывным, является то, что вы можете не заботиться о концах интервалов при нахождении вероятностей непрерывные случайные величины. То есть: \(P(a\le X\le b)=P(a для интервала \(0 Для дискретного распределения плотность вероятности — это вероятность того, что
переменная принимает значение x. \( f(x) = Pr[X = x] \) Ниже приведен график нормальной функции плотности вероятности. Ниже приведен график нормального кумулятивного распределения.
функция. Горизонтальная ось представляет собой допустимую область для данного
функция вероятности. Поскольку вертикальная ось — это вероятность,
он должен находиться между нулем и единицей. Увеличивается от нуля до единицы
как мы идем слева направо по горизонтальной оси. \( Pr[X \le G(\alpha)] = \alpha \) или альтернативно \( х = G(\альфа) = G(F(x)) \) Ниже приведен график нормальной процентной функции. Поскольку горизонтальная ось — это вероятность, она идет от нуля до единицы.
Вертикальная ось идет от наименьшего к наибольшему значению
кумулятивная функция распределения. \( h(x) = \frac {f(x)} {S(x)} = \frac {f(x)} {1 — F(x)} \) Ниже приведен график функции опасности нормального распределения. Графики опасностей чаще всего используются в приложениях для обеспечения надежности.
Обратите внимание, что Джонсон,
Коц и Балакришнан называют это условным провалом.
функция плотности, а не функция опасности. Альтернативно это может быть выражено как \( Н(х) = -\ln {(1 — F(х))} \) Ниже приведен график нормальной кумулятивной функции опасности. Кумулятивные графики опасностей чаще всего используются для оценки надежности.
Приложения. Обратите внимание, что
Джонсон, Коц и др.
Балакришнан ссылается
к этому как функция опасности, а не кумулятивная опасность
функция. \( S(x) = Pr[X > x] = 1 — F(x) \) Ниже приведен график выживания нормального распределения.
функция. Для функции выживания значение y на графике начинается с 1 и
монотонно убывает до нуля. Функция выживания должна быть
по сравнению с кумулятивной функцией распределения. \( Z(\альфа) = G(1 — \альфа) \) Ниже приведен график обратного выживания нормального распределения.
функция. Как и в случае с функцией процента, горизонтальная ось представляет собой
вероятность. Поэтому горизонтальная ось идет от 0 до 1
независимо от конкретного дистрибутива. Появление
аналогична функции процента. Однако вместо
переходя от наименьшего к наибольшему значению по вертикальной оси,
он идет от наибольшего к наименьшему значению. Введение: В этой статье мы будем изучать различные типы функций распределения вероятностей. В терминах статистики функция распределения — это математическое выражение, описывающее вероятность различных возможных исходов эксперимента. Обозначается как Переменная ~ Тип (Характеристики) Допустим, мы проводим эксперимент по подбрасыванию правильной монеты. Возможные события: Голова , Решка . И, например, если мы используем X для обозначения событий, распределение вероятности X будет принимать значение 0,5 для X=орла и 0,5 для X=решки. На более высоком уровне у нас есть качественные и количественные данные. А в количественных данных у нас есть типы данных Continuous и Discrete . Непрерывные данные измеряются и могут принимать любое количество значений в заданном конечном или бесконечном диапазоне. Его можно представить в десятичном формате. А случайная величина, которая содержит непрерывные значения, называется Непрерывной случайной величиной . Примеров: Рост человека, время, расстояние и т. д. Дискретные данные подсчитываются и могут принимать только ограниченное число значений. Пример: Количество учащихся в классе, количество работников в компании и т. д. В зависимости от типов данных, с которыми мы имеем дело, у нас есть два типа функций распределения. Для дискретных данных у нас есть дискретные распределения; а для непрерывных данных у нас есть непрерывные распределения. Прежде чем углубляться в типы распределений, важно пересмотреть основные понятия, такие как Функция плотности вероятности (PDF), Функция массы вероятности (PMF) и Функция кумулятивной плотности (CDF). Это статистический термин, описывающий распределение вероятностей непрерывной случайной величины. Вероятность, связанная с одним значением, всегда равна нулю. Ниже приведена формула для PDF. Формула для PDF. Источник Это статистический термин, описывающий распределение вероятностей дискретной случайной величины. Это еще один метод описания распределения случайной величины (непрерывной или дискретной). Начнем с самого простого — Равномерного распределения. Обозначается как X ~ U (a, b) . И читается как X — дискретная случайная величина, которая следует равномерному распределению в диапазоне от a до b. Равномерное распределение — это когда все возможные события равновероятны. Например, рассмотрим эксперимент с бросанием игральной кости. У нас есть шесть возможных событий X = {1, 2, 3, 4, 5, 6}, каждое из которых имеет вероятность P(X) = 1/6. График PMF приведенного выше эксперимента: Формула для PMF, CDF функции равномерного распределения: Среднее значение и дисперсия равномерного распределения: Среднее = (а+b)/2 Дисперсия = (n 2 -1)/12 Обозначается как X ~ B(n, p) . И читается как X — дискретная случайная величина, которая следует биномиальному распределению с параметрами n, p. Биномиальное распределение — это дискретное распределение вероятностей числа успешных попыток в последовательности «n» независимых экспериментов. Обычно исход успех обозначается как 1, , а связанная с ним вероятность равна p . И Отказ обозначается как 0 , и связанная с ним вероятность равна q = 1-p . Формула для PMF, CDF биномиального распределения: Источник K в приведенной выше формуле — это количество успехов. Среднее значение и дисперсия биномиального распределения задаются как: Среднее = np Дисперсия = npq Теперь рассмотрим, мы провели биномиальный эксперимент 10 раз, и вероятность успеха = 0,25. Ниже показано, как выглядит PMF, CDF. Изображение автора PMF, CDF для биномиального эксперимента с вероятностью успеха = вероятность неудачи, как показано ниже. Обозначается как X ~ Bern(p) . Бернулли можно представить как биномиальный эксперимент с одним испытанием. X ~ Берн(р) -> X ~ В(1, р) Формула для PMF, CDF распределения Бернулли: Среднее значение и дисперсия распределения Бернулли задаются как: Среднее = p Дисперсия = p(1-p) = pq Пример: Рассмотрим пример подбрасывания ярмарки. Возможны два исхода: орел, решка. Вероятность (p), связанная с каждым из них, равна 1/2. Если мы возьмем нечестную монету, вероятность, связанная с каждой из них, не обязательно должна быть 1/2. Орел может иметь вероятность p = 0,8·, тогда вероятность выпадения решки q = 1-p = 1-0,8 = 0,2· Событие Бернулли предполагает, какой результат можно ожидать для одного испытания. Обозначается как X ~ P o ( λ ). И читается как X — дискретная случайная величина, соответствующая распределению Пуассона с параметром λ . Распределение Пуассона — это дискретная функция распределения вероятностей, которая выражает вероятность того, что заданное число событий произойдет в фиксированный интервал времени. Примеры: Формула для PMF, CDF распределения яда: Среднее значение и дисперсия распределения Пуассона задаются как: Среднее значение = дисперсия = λ Распределение Пуассона с λ = 5 выглядит следующим образом: Обозначается как X ~ N (μ, σ 2 ). Нормальное распределение — это непрерывное распределение, описывающее вероятность того, что непрерывная случайная величина принимает действительные значения. Примеры: Рост людей, результаты экзаменов студентов, баллы IQ и т. д. подчиняются нормальному распределению. Свойства нормального распределения: Нормальное распределение с различными средними значениями, стандартные отклонения выглядят следующим образом: Источник Нормальное распределение следует правилу 68-95-99,7. Это правило также известно как эмпирическое правило. Согласно ему, 68 % данных лежат в первом диапазоне стандартных отклонений, 95 % данных — во втором диапазоне стандартных отклонений и 99,7 % данных — в третьем диапазоне стандартных отклонений. Формула для PDF, CDF нормального распределения: Среднее значение и дисперсия нормального распределения задаются как: Среднее значение = мк Отклонение = σ 2 Предположим, у нас есть распределение роста со средним значением = 25, стандартным отклонением = 2,48. Ниже показано, как выглядит график. Обозначается как Z ~ N(0, 1). Это преобразование нормального распределения таким образом, что среднее значение = 0, а стандартное отклонение 1. Преобразование — это способ изменения каждого элемента распределения для получения нового распределения с аналогичными характеристиками. Всем свойствам нормального распределения соответствует стандартное нормальное распределение. Источник Кроме того, существует таблица, в которой приведены наиболее часто используемые значения CDF стандартного нормального распределения. Эта таблица известна как таблица Z-показателей . Формула стандартизации Z = (X-μ)/σ Формула для PDF, CDF стандартного нормального распределения дается как: Среднее значение и дисперсия стандартного нормального распределения: Среднее = 0 Разница = 1 Нормальное распределение со средним значением 0 и дисперсией 1 (SND) выглядит следующим образом: Обозначается как X ~ t(k). Т-распределение Стьюдента представляет собой небольшую выборку, приближенную к нормальному распределению. По мере увеличения степеней свободы t-распределение имеет тенденцию становиться стандартным нормальным распределением. Источник Формула для PDF, CDF t-распределения: (v в формулах выше — степени свободы) t-распределение можно использовать при проверке гипотез (чтобы проверить, есть ли какие-либо существенные различия между двумя средними выборками), расчет доверительных интервалов со стандартным отклонением населения неизвестен. Как и стандартное нормальное распределение, t-распределение также имеет собственную таблицу. Эта таблица известна как t-таблица . Среднее значение и дисперсия распределения Т Стьюдента: Среднее = 0 дисперсия = k/(k-2) Распределение Стьюдента со степенями свободы = 25 выглядит следующим образом: Обозначается как X~χ 2 (к). Используется при проверке гипотез, вычислении доверительных интервалов и для проверки соответствия. Это преобразование t-распределения. Нахождение t-распределения в степени 2 дает распределение хи-квадрат, а нахождение квадратного корня из хи-квадрата распределения дает нам t-распределение. хи-квадрат имеет таблицу хи-квадрат . Формула для PDF, CDF распределения хи-квадрат: Источник Среднее значение и дисперсия распределения хи-квадрат: Среднее = k Дисперсия = 2k Распределение хи-квадрат со степенями свободы = 5 выглядит следующим образом. Спасибо, что дочитали до конца. К концу этой статьи мы познакомились с различными вероятностными распределениями, которые часто используются в статистике. Я надеюсь, что эта статья будет информативной. Не стесняйтесь поделиться им со своими товарищами по учебе. Распределение участков онлайн Не стесняйтесь проверять другие мои сообщения в блоге из моего профиля Analytics Vidhya. Вы можете найти меня в LinkedIn, Twitter, если захотите связаться. Я был бы рад связаться с вами. Для немедленного обмена мнениями, пожалуйста, напишите мне на [email protected]. Материалы, показанные в этой статье, не принадлежат Analytics Vidhya и используются по усмотрению Автора. Поскольку общий вид функций вероятности может быть
выражается в стандарте
распределение, все последующие формулы в этом разделе
дано для стандартной формы функции. Ниже приведен график стандартной нормальной плотности вероятности.
функция. Заметим, что этот интеграл не существует в простой замкнутой формуле. это
вычисляется численно. Ниже приведен график нормального кумулятивного распределения.
функция. Ниже приведен график нормальной процентной функции. \( ч (х) = \ гидроразрыва {\ фи (х)} {\ фи (-х)} \) где \(\Phi\) — кумулятивная функция распределения стандартного
нормальное распределение и \(\phi\) — вероятность
функция плотности стандартной нормали
распределение. Ниже приведен график нормальной функции опасности. Ниже приведен график нормальной кумулятивной функции опасности. Ниже приведен график нормальной функции выживания. Ниже приведен график нормальной обратной функции выживания. Центральная предельная теорема в основном утверждает, что, поскольку выборка
размер ( N ) становится большим, происходит следующее: Неотъемлемой частью статистики является кумулятивная функция распределения, которая помогает найти вероятность случайной величины в определенном диапазоне. Этот учебник научит вас основам кумулятивной функции распределения и тому, как реализовать ее в Python. Кумулятивная функция распределения используется для описания распределения вероятностей случайных величин. Функция плотности вероятности — это функция, которая дает нам распределение вероятностей случайной величины для любого ее значения. Чтобы получить распределение вероятностей в точке, вам нужно только решить функцию плотности вероятности для этой точки. Кумулятивная функция распределения случайной величины, вычисляемая в точке x, представлена как Fx(X). Это вероятность того, что случайная величина X примет значение, меньшее или равное x. Рассмотрим диаграмму, показанную ниже. На диаграмме показана функция плотности вероятности f(x), которая при построении дает нам прямоугольник между точками (a, b). f(x) имеет значение 1/(b-a). Рисунок 1. Функция плотности вероятности Теперь рассмотрим точку c на оси x. Это точка, в которой вам нужно найти кумулятивную функцию распределения. Рисунок 2: Расчет CDF Вы можете сделать это, умножив длину и ширину прямоугольника. Ширина — это расстояние между a и c, полученное путем их вычитания, а длина — это функция плотности вероятности. В итоге вы получите CDF как: Рисунок 3: CDF Поскольку кумулятивная функция распределения является функцией плотности полной вероятности до некоторой точки x, ее можно представить как вероятность того, что случайная величина X меньше или равна x. Рисунок 4: Представление CDF Поскольку вам нужно получить общую сумму PDF между двумя точками, вы также можете представить CDF как интеграцию PDF между точками, в которых он был рассчитан. Формула, изображенная ниже, показывает кумулятивную функцию распределения, рассчитанную между точками (a, b) для PDF Fx(x). Рисунок 5: CDF как интеграция PDF В этом тематическом исследовании вы будете рассматривать набор данных Iris, который содержит информацию о длине чашелистиков, ширине чашелистиков, длине лепестков и ширине лепестков трех разных видов Iris: Рисунок 6: Набор данных Iris Все значения указаны в сантиметрах. Набор данных содержит 50 точек данных по каждому из разных видов. Вам нужно найти надежную меру, с помощью которой мы сможем отличить разные виды друг от друга. Теперь постройте каждую функцию нашего набора данных с помощью гистограммы. Вы рисуете функции разными цветами для каждого цветка, чтобы увидеть, как они перекрываются друг с другом. Это способ найти PDF-файл данных. Рисунок 7: Набор данных Iris PDF Графики выше расположены сверху слева направо и снизу: Отсюда можно сделать вывод, что длина лепестков – лучший показатель для дифференциации видов ирисов. Затем добавьте PDF-файл и постройте результирующий график, чтобы увидеть CDF для наших данных по радужной оболочке. Рисунок 8: Набор данных Iris PDF и CDF На приведенном выше графике вы можете заметить три вещи: Теперь посмотрим, как можно реализовать кумулятивную функцию распределения в Python. Рисунок 9: Импорт необходимых модулей Далее прочитайте наш набор данных радужной оболочки. Рис. 10. Импорт набора данных Iris Вы можете найти среднее значение и медиану данных и посмотреть, как они различаются в зависимости от вида. Рисунок 11. Нахождение среднего и медианы Как видите, среднее и медиана не сильно отличаются. Это означает, что нет большой разницы в средней длине и ширине чашелистиков, а также в длине и ширине лепестков для разных видов. То же самое можно сказать и о медиане, а медианы сопоставимы для разных видов. Теперь найдите стандартное отклонение данных. Рисунок 12: Нахождение стандартного отклонения Данные имеют минимальное значение стандартного отклонения для каждого признака по разным видам. Это означает, что он не распространяет наши данные и не сильно отличается. Кроме того, выбросы далеко и мало. Теперь постройте график для скрипки, чтобы увидеть, как различные функции сравниваются друг с другом. Рисунок 13: Построение скрипичных сюжетов Рисунок 14: Графики для скрипки Скрипичные графики отображают диапазон значений в нашем наборе данных по оси x и показывают, как распределить данные по ширине. Приведенные выше графики показывают, что длина лепестка имеет самые узкие скрипки и, следовательно, наименьшее количество выбросов. Их диапазон значений также имеет наименьшее пересечение, в чем можно убедиться, сравнив высоты скрипок. Если бы вам нужно было выбрать два признака для сравнения цветов, какие бы они были? Это можно найти, построив парные графики ваших данных. Парные графики отображают каждую функцию по сравнению с другими в виде диаграммы рассеяния, чтобы увидеть, какая пара работает лучше всего. Рисунок 15: Построение парных графиков При запуске приведенного выше кода вы получаете следующие графики: Рисунок 16: Графики Iris Pair Приведенные выше графики показывают значение по оси X в крайнем левом углу и значение по оси Y в нижней части. Теперь постройте PDF вместе с гистограммой для данных радужной оболочки. Рисунок 17: построение графика PDF Рисунок 18: Графики в формате PDF для набора данных Iris Приведенные выше графики показывают, что характеристика длина лепестка имеет наименьшее перекрытие между данными по разным видам ирисов. Кривая в форме колокола, которую вы видите во всех наших функциях, представляет собой распределение вероятностей, называемое нормальным распределением. Колоколообразная кривая дляpetal_leanght также более гладкая, чем колоколообразная кривая дляpetal_width. Теперь, используя приведенные выше данные, постройте кумулятивную функцию распределения. Сначала вы разделяете данные на три набора в зависимости от вида цветка. Рисунок 19: Разделение наших наборов данных Затем вы наносите PDF и CDF вместе на один и тот же график. Чтобы получить PDF, вы подсчитываете количество точек данных в каждой ячейке гистограммы и делите количество на количество точек данных в этой ячейке. CDF — это не что иное, как кумулятивная сумма или общая сумма PDF до определенного момента. Чтобы получить кумулятивную функцию распределения для каждого бина, вы добавляете PDF всех предыдущих бинов. Рисунок 20: График PDF и CDF набора данных Iris Запустив приведенный выше код, вы получите наш график, как показано ниже. Вы можете видеть, что вид setosa имеет свой уникальный диапазон значений лепестка_длины, который составляет чуть меньше 2 см. Рисунок 21: PDF и CDF набора данных Iris На приведенной выше диаграмме можно сказать, что для разных видов ирисов можно определить разные диапазоны длины лепестка. Диапазоны: В этом руководстве по кумулятивной функции распределения вы впервые поняли концепцию CDF и способы ее расчета с помощью PDF. Мы надеемся, что эта статья помогла вам понять, как найти кумулятивную функцию распределения случайной величины. Чтобы узнать больше о python и статистике, а также о том, как статистику можно использовать в анализе данных, ознакомьтесь с сертификационной программой Simplilearn по анализу данных. С другой стороны, если вам нужны какие-либо разъяснения или у вас есть какие-либо сомнения, поделитесь ими с нами, прокомментировав их ниже в разделе комментариев на этой странице, и наши эксперты немедленно ответят на них! Приятного обучения! Функция плотности вероятности (PDF) – это статистическое выражение, определяющее распределение вероятности (вероятность исхода) для дискретной случайной переменной (например, акции или ETF) в отличие от непрерывной случайной величины. Нормальное распределение является распространенным примером PDF, образующим хорошо известную форму кривой колокола. В финансах трейдеры и инвесторы используют PDF-файлы, чтобы понять, как распределяется ценовая доходность, чтобы оценить свой профиль риска и ожидаемой доходности. PDF-файлы используются в финансах для оценки риска конкретной ценной бумаги, такой как отдельная акция или ETF. Обычно они изображаются на графике, где нормальная колоколообразная кривая указывает на нейтральный рыночный риск, а колокольчики на обоих концах указывают на больший или меньший риск/вознаграждение. Когда PDF изображается графически, область под кривой будет указывать интервал, в который попадает переменная. Суммарная площадь на этом интервале графика равна вероятности появления дискретной случайной величины. Точнее, поскольку абсолютная вероятность того, что непрерывная случайная величина примет любое конкретное значение, равна нулю из-за бесконечного множества доступных возможных значений, значение PDF можно использовать для определения вероятности попадания случайной величины в определенный диапазон. ценностей. Изображение Джули Бэнг © Investopedia 2020 Распределение, смещенное в правую сторону кривой, предполагает более высокую прибыль, в то время как распределение, смещенное влево, указывает на больший риск падения для трейдеров. Распределения вероятностей также можно использовать для создания кумулятивных функций распределения (CDF), которые суммируют вероятность событий кумулятивно и всегда начинаются с нуля и заканчиваются на 100%. Инвесторы должны использовать PDF-файлы как один из многих инструментов для расчета общего соотношения риск/прибыль в своих портфелях. PDF-файлы могут описывать как дискретные, так и непрерывные данные. Разница в том, что дискретные переменные могут принимать только определенные значения, такие как целые числа, да или нет, время суток и т. д. Непрерывная переменная, напротив, содержит все значения вдоль кривой, включая очень маленькие дроби или десятичные дроби до теоретически бесконечного числа разрядов. Изображение Джули Бэнг © Investopedia 2020 PDF часто характеризуются средним значением, стандартным отклонением, эксцессом и асимметрией. Вычисление PDF и его графическое отображение могут включать сложные вычисления, в которых используются дифференциальные уравнения или интегральное исчисление. На практике для расчета функции распределения вероятностей требуются графические калькуляторы или пакеты статистического программного обеспечения. В качестве примера, вычисление PDF нормального распределения выглядит следующим образом: ф ( Икс ) знак равно 1 о 2 π е − 1 2 ( Икс − мю о ) 2 куда: Икс знак равно Значение проверяемой переменной или данных мю знак равно Иметь в виду о знак равно Стандартное отклонение \begin{aligned}&f(x) = \frac{ 1 }{ \sigma \sqrt{ 2 \pi }} e ^ { — \frac{ 1 }{ 2 } ( \frac { x — \mu }{ \sigma } ) ^ 2 } \\&\textbf{где:} \\&x = \text{Значение исследуемой переменной или данных} \\&\mu = \text{Среднее значение} \\&\sigma = \text{ Стандартное отклонение} \\\end{выровнено}
f(x)=σ2π1e−21(σx−µ)2где:x=значение переменной или исследуемых данныхµ=среднее σ=стандартное отклонение Нормальное распределение всегда имеет асимметрию = 0 и эксцесс = 3,0. Хотя нормальное распределение часто является наиболее цитируемым и известным, существует несколько других PDF-файлов. Самым простым и популярным распределением является равномерное распределение, при котором все исходы имеют равные шансы. Шестигранный кубик имеет равномерное распределение. Каждый исход имеет вероятность около 16,67% (1/6). Изображение Джули Бэнг © Investopedia 2020 Биномиальное распределение представляет данные, которые могут принимать только одно из двух значений, таких как подбрасывание монеты (орел или решка) или логические выражения, которые принимают форму да/нет, вкл/выкл и т. д. Логнормальное распределение важно в финансах, потому что оно лучше описывает фактическую доходность цен на активы, чем стандартное нормальное распределение. Изображение Джули Бэнг © Investopedia 2020 Распределение Пуассона — это PDF-файл, который используется для описания переменных подсчета или вероятностей того, что произойдет определенное количество событий. Например, сколько яблок находится на яблонях, сколько пчел живет в улье с течением времени или за сколько торговых дней портфель потеряет 5% или более. Изображение Джули Бэнг © Investopedia 2020 Бета-распределение — это общий тип PDF, который может принимать различные формы и характеристики, определяемые всего двумя параметрами: альфа и бета. Он часто используется в финансах для оценки уровня возмещения дефолта по облигациям или уровня смертности в страховании. В качестве простого примера распределения вероятностей рассмотрим число, наблюдаемое при броске двух стандартных шестигранных игральных костей. Семь — самый распространенный результат (1+6, 6+1, 5+2, 2+5, 3+4, 4+3). С другой стороны, два и двенадцать гораздо менее вероятны (1+1 и 6+6). Изображение Сабрины Цзян © Investopedia, 2020 Функция плотности вероятности (PDF) описывает, насколько вероятно наблюдать некоторый результат, являющийся результатом процесса генерации данных. Например, насколько вероятно, что подброшенная монета выпадет орлом (50%). Или на роль кубика выпадет 6 (1/6 = 16,7%). PDF может сказать нам, какие значения, таким образом, появятся с наибольшей вероятностью по сравнению с менее вероятными результатами. Это будет меняться в зависимости от формы и характеристик PDF. Центральная предельная теорема (ЦПТ) утверждает, что распределение случайной величины в выборке начинает приближаться к нормальному распределению по мере увеличения размера выборки, независимо от истинной формы распределения. Функция плотности вероятности (PDF) объясняет, какие значения могут появиться в процессе генерации данных в любой момент времени или для любого заданного розыгрыша. Кумулятивная функция распределения (CDF) вместо этого показывает, как складываются эти предельные вероятности, достигая в конечном итоге 100% (или 1,0) возможных результатов. Используя CDF, мы можем увидеть, насколько вероятно, что результат переменной будет меньше или равен некоторому предсказанному значению.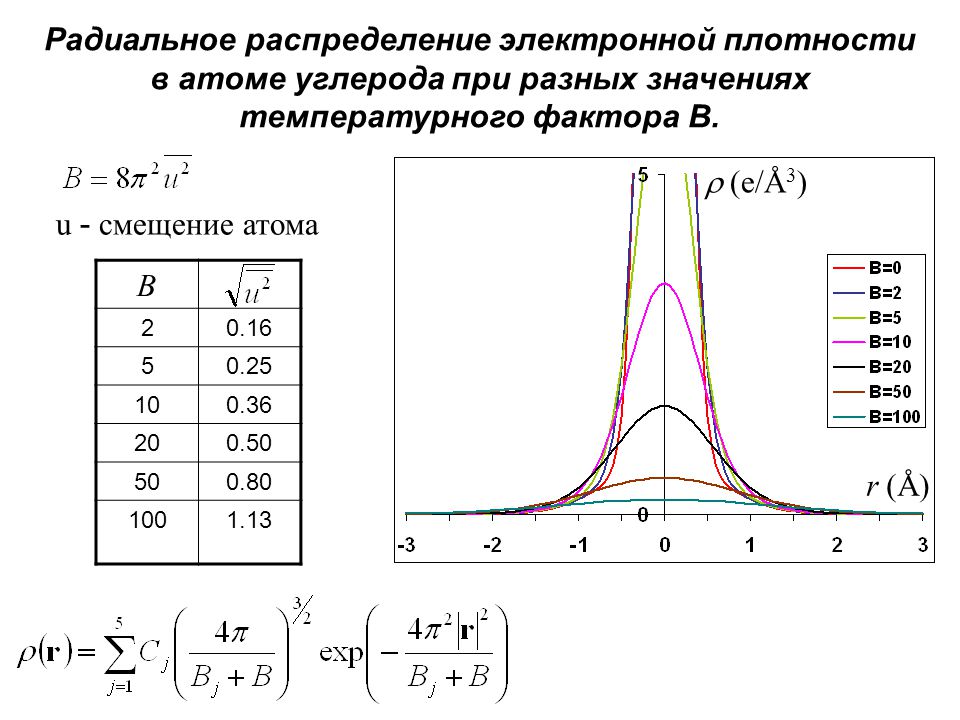 2, \qquad 0
2, \qquad 0 Решение

Раствор
1.3.6.2. Родственные дистрибутивы
1.3.6.2. Родственные дистрибутивы 1.
Исследовательский анализ данных
1.3.
Методы ЭДА
1.3.6.
Распределения вероятностей
1.
 3.6.2.
3.6.2. Связанные дистрибутивы
Распределения вероятностей обычно определяются в терминах
функция плотности вероятности. Однако существует ряд
функции вероятности, используемые в приложениях. Функция плотности вероятности Для непрерывной функции функция плотности вероятности (PDF) равна
вероятность того, что переменная имеет значение x. Так как для непрерывного
распределений вероятность в одной точке равна нулю, это
часто выражается через интеграл между двумя точками.
9{b} {f(x) dx} = Pr[a \le X \le b] \) Кумулятивная функция распределения Кумулятивная функция распределения (cdf) — это вероятность того, что
переменная принимает значение меньше или равное x.  То есть
9{х} {е(я)} \)
То есть
9{х} {е(я)} \) Функция процентной точки Функция процентного пункта (ppf) является обратной кумулятивной
функция распределения. По этой причине процентная функция
также обычно называют обратной функцией распределения.
То есть для функции распределения мы вычисляем вероятность
что переменная меньше или равна x для данного x. Для
функция процентной точки, мы начинаем с вероятности и вычисляем
соответствующий x для кумулятивного распределения. Математически,
это можно выразить как 
Функция опасности Функция опасности представляет собой отношение функции плотности вероятности
к функции выживания, S (х). Кумулятивная функция опасности Кумулятивная функция опасности представляет собой интеграл опасности
функция. 9{х} {ч(\мю) д\мю} \) 
Функция выживания Функции выживания чаще всего используются в надежности и
родственные поля. Функция выживания – это вероятность того, что
variate принимает значение больше x. Обратная функция выживания Точно так же, как процентная функция является обратной кумулятивной
функция распределения, функция выживания также имеет обратную
функция.  Обратная функция выживания может быть определена в терминах
функция процентного пункта.
Обратная функция выживания может быть определена в терминах
функция процентного пункта. Изучение различных типов функции распределения вероятностей!
Что такое функция распределения?

Типы данных
 Это не имеет смысла при записи в десятичном формате. А случайная величина, содержащая дискретные данные, называется Дискретная случайная величина .
Это не имеет смысла при записи в десятичном формате. А случайная величина, содержащая дискретные данные, называется Дискретная случайная величина . Типы функций распределения:
Дискретные Распределения Непрерывное Распределение Равномерное распределение Нормальное распределение Биномиальное распределение Стандартный Стандартный распространение Бернулли распространение Студенческая Т раздача Пуассона распределение Хи-квадрат распределение 
Дискретные распределения
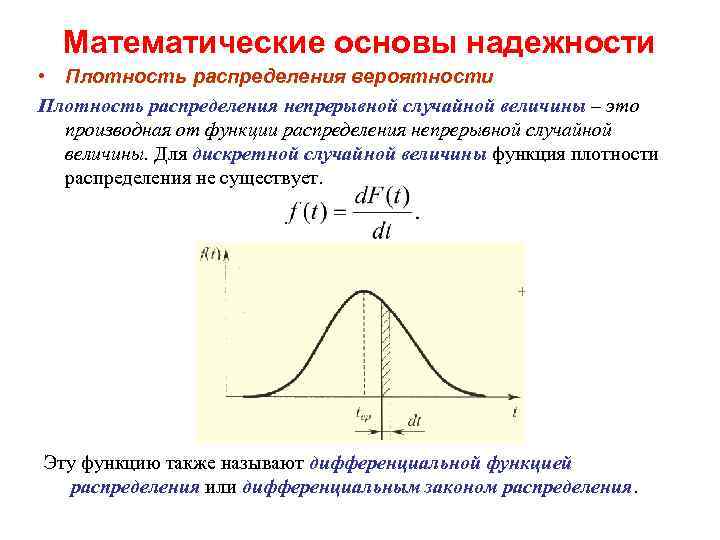
Биномиальное распределение (B):
Где n — номер. испытаний, а p — вероятность успеха для каждого испытания. Двумя исходами биномиального испытания могут быть: успех/неудача, успех/неудача/, победа/проигрыш и т. д.
Двумя исходами биномиального испытания могут быть: успех/неудача, успех/неудача/, победа/проигрыш и т. д.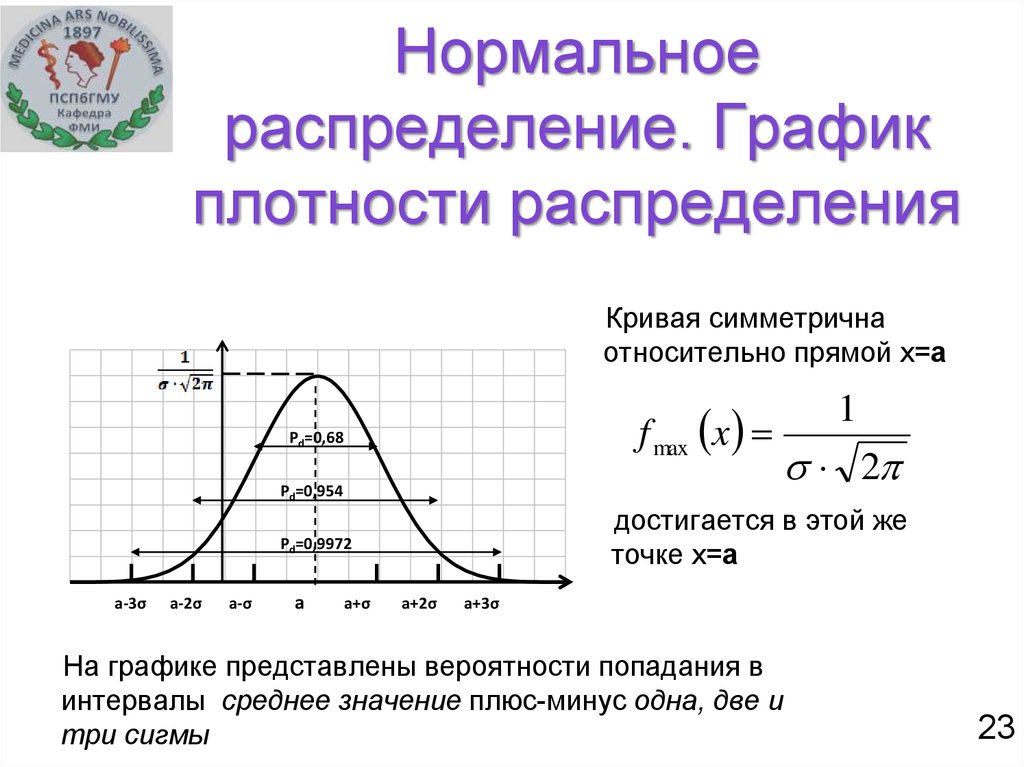 И читается как X — дискретная случайная величина, которая следует распределению Бернулли с параметром p.
И читается как X — дискретная случайная величина, которая следует распределению Бернулли с параметром p.
Где p — вероятность успеха. Принимая во внимание, что биномиальное событие предполагает нет. раз можно ожидать определенного результата.
Принимая во внимание, что биномиальное событие предполагает нет. раз можно ожидать определенного результата.
Где λ – ожидаемая частота возникновения. Непрерывное распределение
Нормальное или гауссово распределение (N) 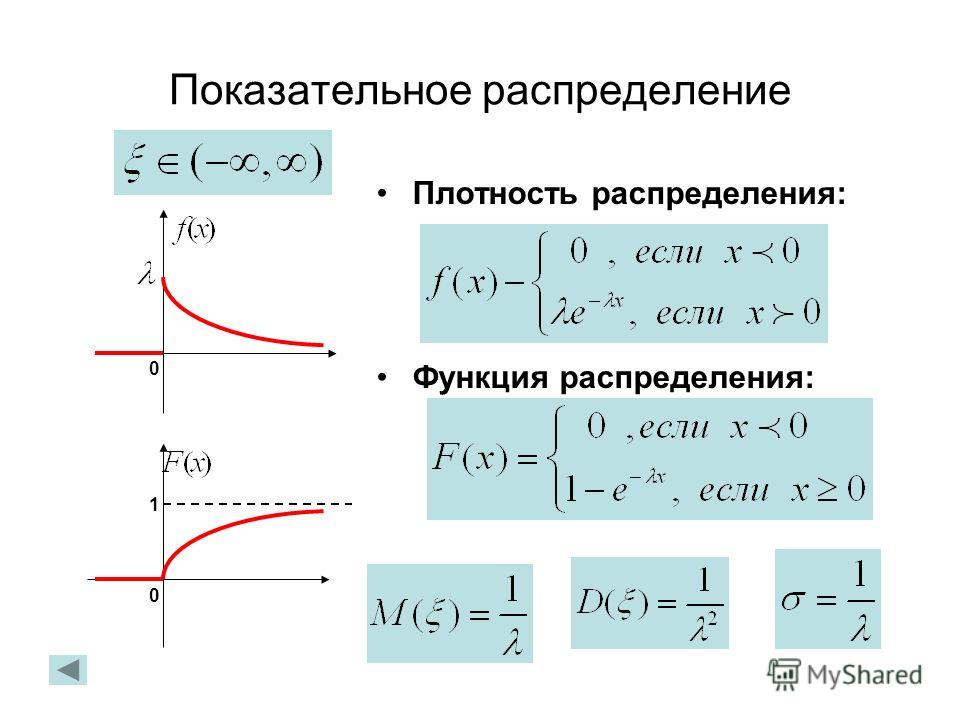 И читается как X — непрерывная случайная величина, которая следует нормальному распределению с параметрами μ, σ 2 .
И читается как X — непрерывная случайная величина, которая следует нормальному распределению с параметрами μ, σ 2 .
Где μ — среднее значение, а σ 2 — дисперсия. Имейте в виду, что дисперсия вместе говорит о статистике формы. е. среднее = медиана = мода
е. среднее = медиана = мода И читается как X — непрерывная случайная величина, которая соответствует нормальному распределению со средним значением 0 и дисперсией 1.
И читается как X — непрерывная случайная величина, которая соответствует нормальному распределению со средним значением 0 и дисперсией 1. И читается как X — непрерывная случайная величина, которая соответствует распределению T Стьюдента с параметром k.
И читается как X — непрерывная случайная величина, которая соответствует распределению T Стьюдента с параметром k.
где k — количество степеней свободы. Если размер выборки равен n, то k = n-1.  И читается как X — непрерывная случайная величина, которая следует распределению хи-квадрат с k степенями свободы.
И читается как X — непрерывная случайная величина, которая следует распределению хи-квадрат с k степенями свободы. Конец Примечания:

Каталожные номера:
Другие сообщения в моем блоге
1.3.6.6.1. Нормальное распределение
1.3.6.6.1. Нормальное распределение 1.
Исследовательский анализ данных
1.3.
Методы ЭДА
1.3.6.
Распределения вероятностей
1.3.6.6.
Галерея дистрибутивов
1.
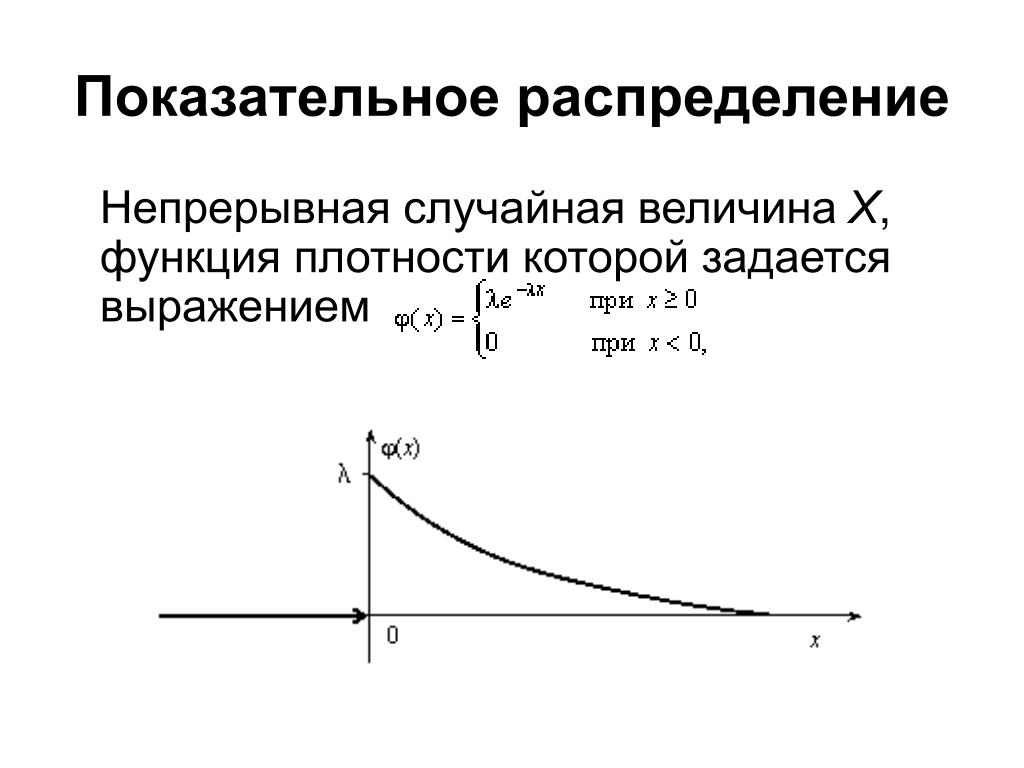 3.6.6.1.
3.6.6.1. Нормальное распределение 9{2}/2}} {\ sqrt {2 \ pi}} \)
Кумулятивная функция распределения Формула кумулятивной функции распределения эталона
нормальное распределение
9{2}/2}} {\ sqrt {2 \ pi}} \) Функция процентной точки Формула процентного пункта
функция нормального распределения не существует в
простая замкнутая формула.  Он вычисляется численно.
Он вычисляется численно. Функция опасности Формула опасности
функция нормального распределения Кумулятивная функция опасности Нормальная кумулятивная функция опасности
можно вычислить по нормальной кумулятивной функции распределения. Функция выживания Нормальная функция выживания
можно вычислить по нормальной кумулятивной функции распределения. 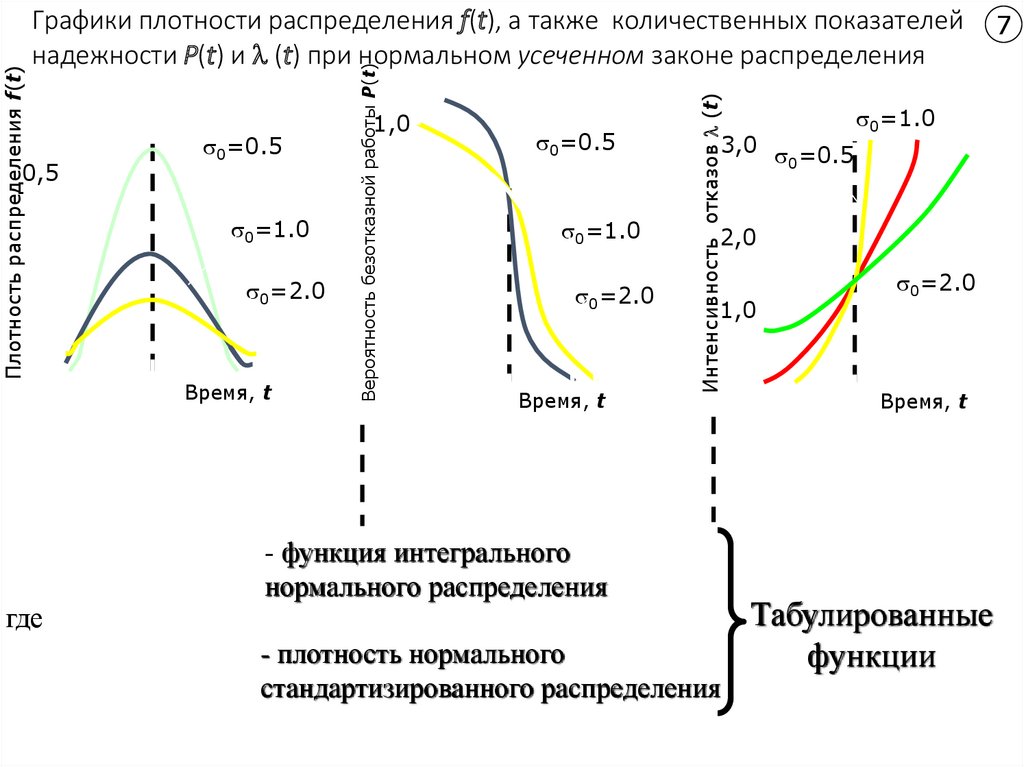
Обратная функция выживания Нормальная обратная выживаемость
функция может быть вычислена из обычной процентной функции. Общая статистика Иметь в виду Параметр местоположения μ . медиана Параметр местоположения μ . Режим Параметр местоположения μ . Диапазон \(-\infty\) в \(\infty\). 
Стандартное отклонение Параметр масштаба σ . Коэффициент вариации σ / μ асимметрия 0 эксцесс 3 Оценка параметра Параметры положения и масштаба нормального распределения могут
быть оценено с выборочным средним и выборочным
стандартное отклонение соответственно. Комментарии Как по теоретическим, так и по практическим причинам нормальное распределение
вероятно, самое важное распределение в статистике.  Например,
Например, Теоретическое обоснование — центральная предельная теорема Широко используется нормальное распределение. Часть апелляции
что он хорошо себя ведет и математически податлив. Однако,
центральная предельная теорема дает теоретическое обоснование того, почему
имеет широкое применение. 
Программного обеспечения Большинство статистических программ общего назначения поддерживают как минимум
некоторые функции вероятности для нормального распределения. Что такое кумулятивная функция распределения и функция плотности
Что такое кумулятивная функция распределения?
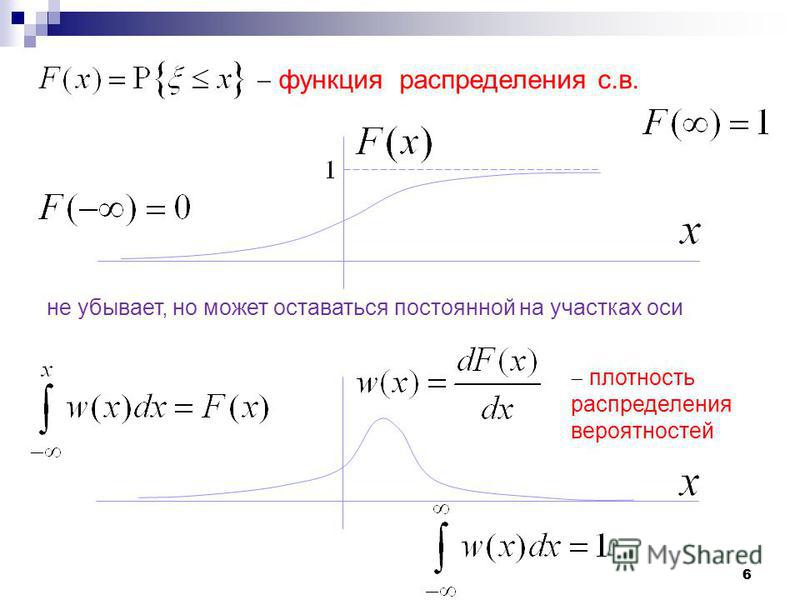 Его можно использовать для описания вероятности дискретной, непрерывной или смешанной переменной. Он получается путем суммирования функции плотности вероятности и получения кумулятивной вероятности для случайной величины.
Его можно использовать для описания вероятности дискретной, непрерывной или смешанной переменной. Он получается путем суммирования функции плотности вероятности и получения кумулятивной вероятности для случайной величины.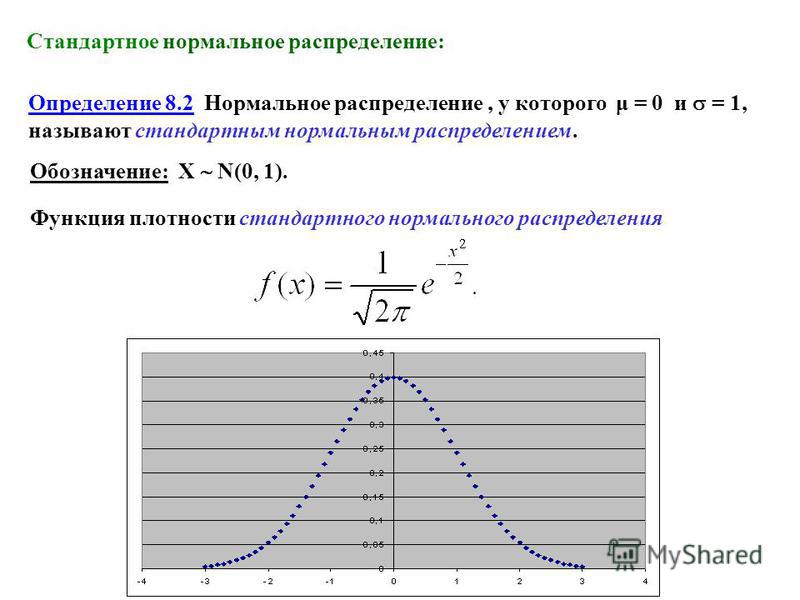 Согласно определению, нужно найти функцию плотности полной вероятности до точки c. Это означает, что вам нужно найти площадь прямоугольника между точками а и с.
Согласно определению, нужно найти функцию плотности полной вероятности до точки c. Это означает, что вам нужно найти площадь прямоугольника между точками а и с.
Понимание кумулятивной функции распределения с помощью набора данных IRIS
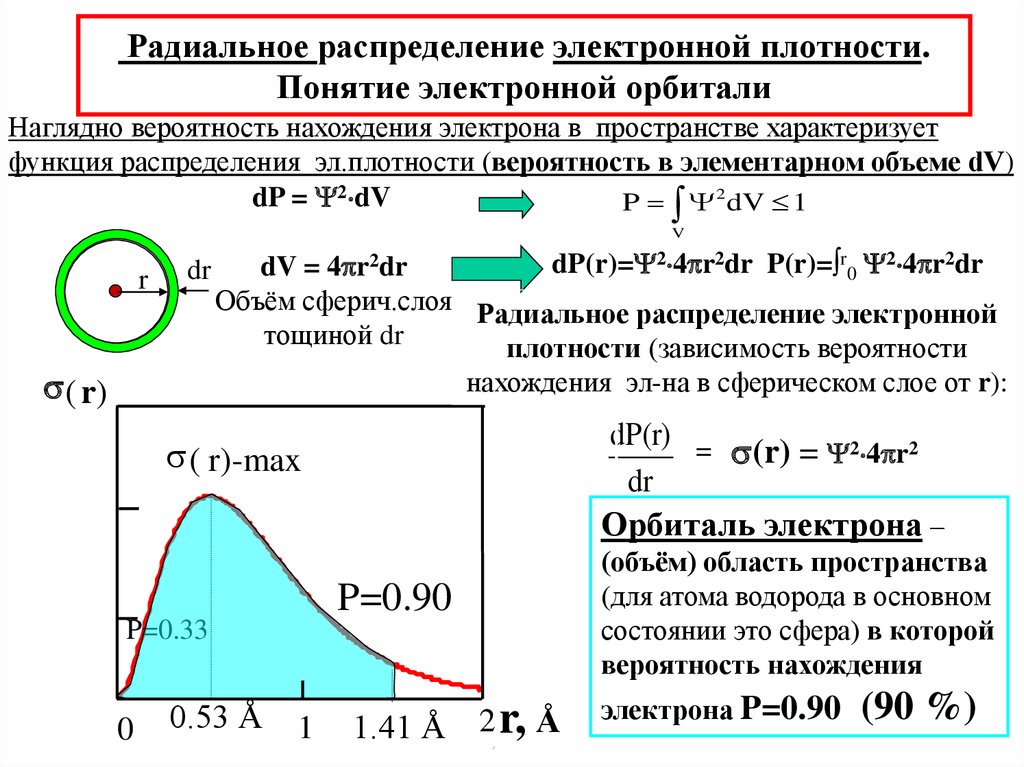 Следовательно, становится сложно установить параметры или диапазоны, которые вы можете использовать, чтобы различать наши цветы.
Следовательно, становится сложно установить параметры или диапазоны, которые вы можете использовать, чтобы различать наши цветы.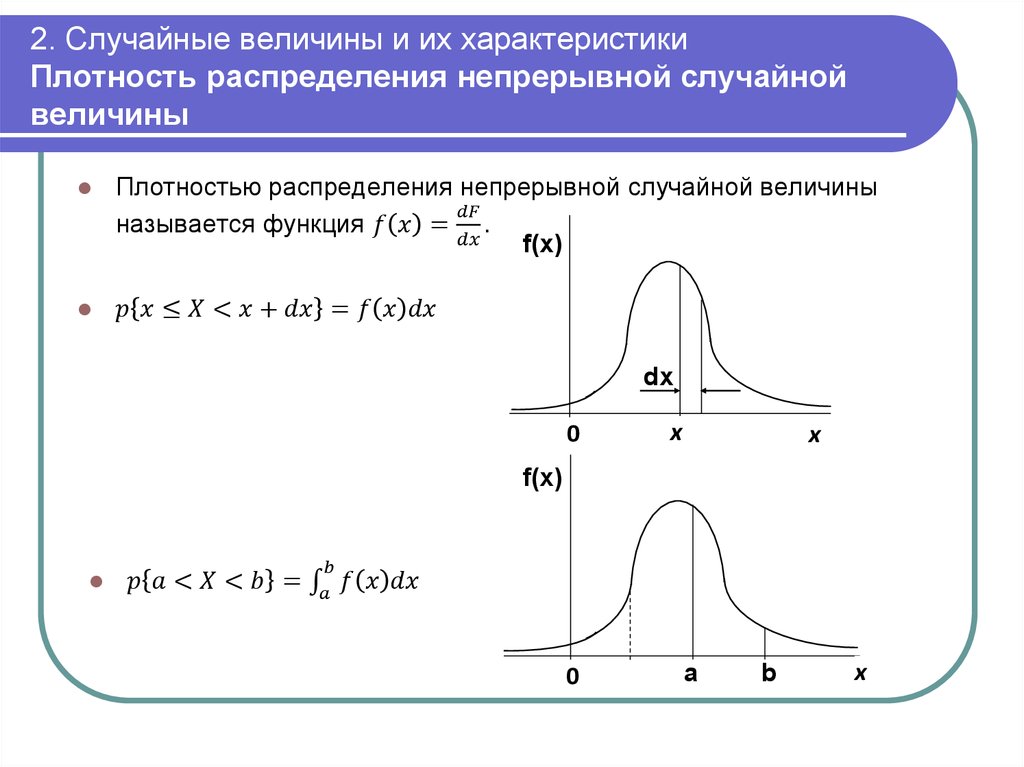
Реализация кумулятивной функции распределения с помощью Python
 Начнем с импорта необходимых библиотек.
Начнем с импорта необходимых библиотек.
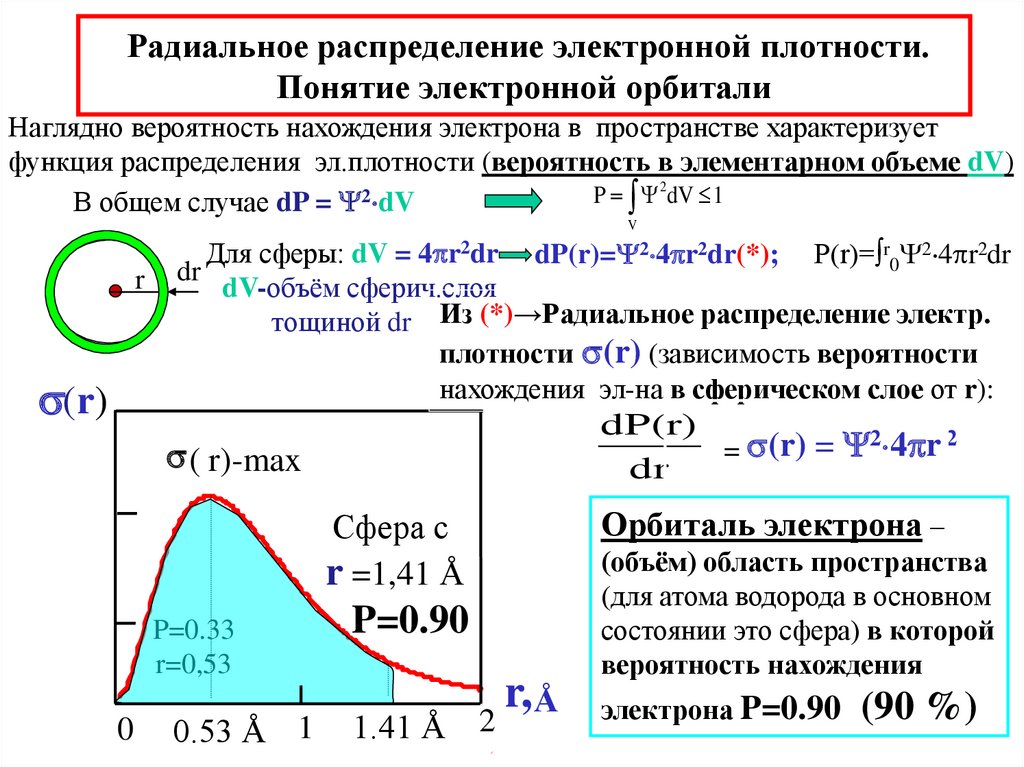 Когда вы наносите два одинаковых объекта друг на друга, вы получаете PDF-файл этого объекта. Из приведенных выше графиков можно сказать, что длина лепестка и ширина лепестка были бы лучшими функциями для совместного использования, поскольку точечная диаграмма этих двух функций имеет наименьшее перекрытие как по оси x, так и по оси y. Используя их, вы можете четко определить уникальные диапазоны для разных цветов.
Когда вы наносите два одинаковых объекта друг на друга, вы получаете PDF-файл этого объекта. Из приведенных выше графиков можно сказать, что длина лепестка и ширина лепестка были бы лучшими функциями для совместного использования, поскольку точечная диаграмма этих двух функций имеет наименьшее перекрытие как по оси x, так и по оси y. Используя их, вы можете четко определить уникальные диапазоны для разных цветов. В целом, длина лепестка — лучший признак для классификации наших данных.
В целом, длина лепестка — лучший признак для классификации наших данных.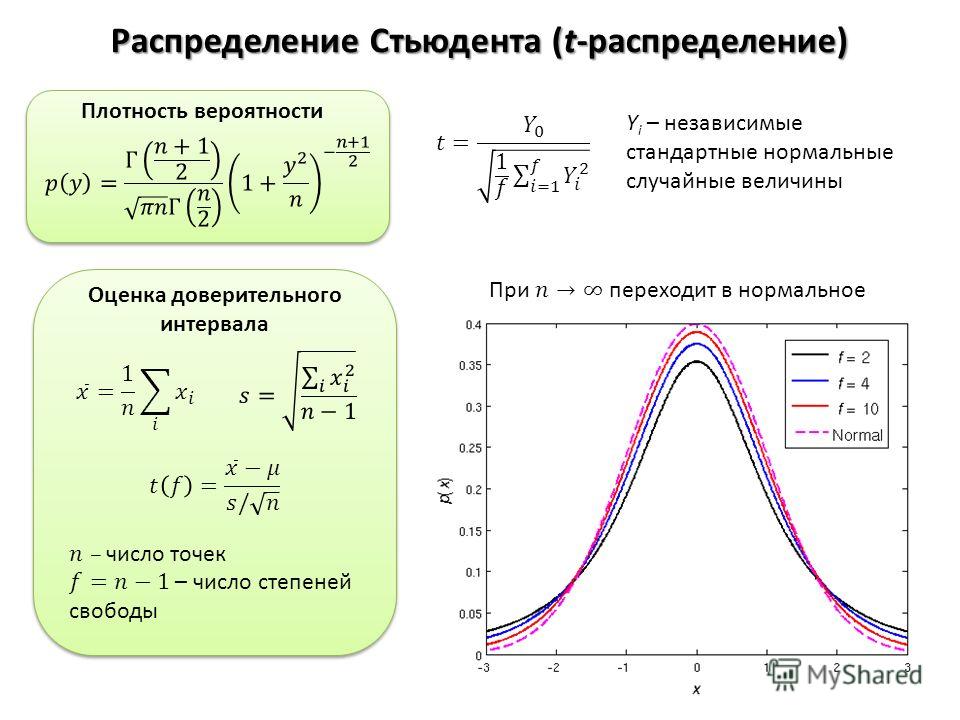 Для Вирджиники и Версиколора есть некоторое совпадение. Но большинство цветов этих двух видов попадают в их уникальный диапазон. Таким образом, точность предсказания не сильно страдает.
Для Вирджиники и Версиколора есть некоторое совпадение. Но большинство цветов этих двух видов попадают в их уникальный диапазон. Таким образом, точность предсказания не сильно страдает. Планируете карьеру в области анализа данных? Ознакомьтесь с учебным курсом по аналитике данных и пройдите сертификацию уже сегодня.
Заключение
 Затем вы провели тематическое исследование набора данных об ирисах и нашли диапазоны, позволяющие различать разные виды ирисов в зависимости от длины их лепестков. Наконец, вы использовали Python для реализации тематического исследования и получения его результатов.
Затем вы провели тематическое исследование набора данных об ирисах и нашли диапазоны, позволяющие различать разные виды ирисов в зависимости от длины их лепестков. Наконец, вы использовали Python для реализации тематического исследования и получения его результатов. Функция плотности вероятности (PDF)
Что такое функция плотности вероятности (PDF)?
 Отличие дискретной случайной величины в том, что можно определить точное значение переменной.
Отличие дискретной случайной величины в том, что можно определить точное значение переменной. Основные выводы

Понимание функций плотности вероятности (PDF)

Дискретные и непрерывные функции распределения вероятностей
Расчет функции распределения вероятностей
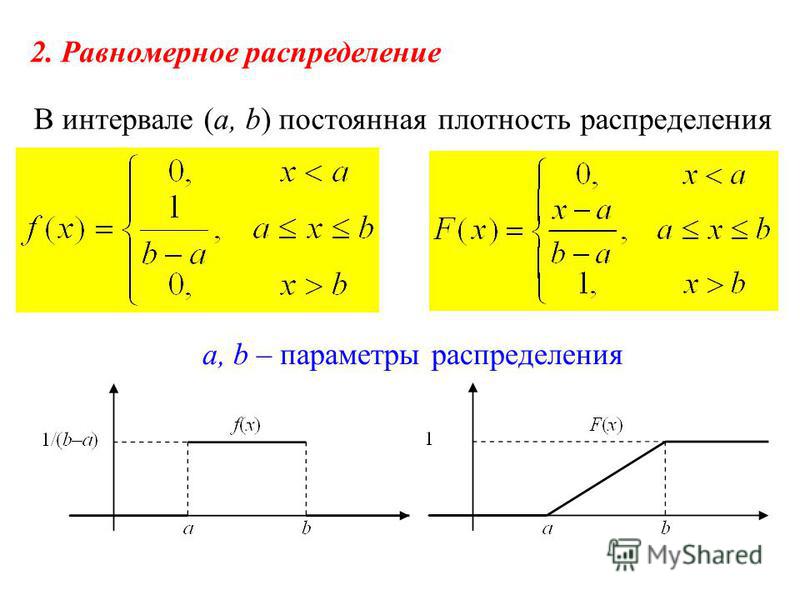
Нормальное распределение

Другие функции распределения вероятностей
Равномерное распределение
Биномиальное распределение
Логнормальное распределение
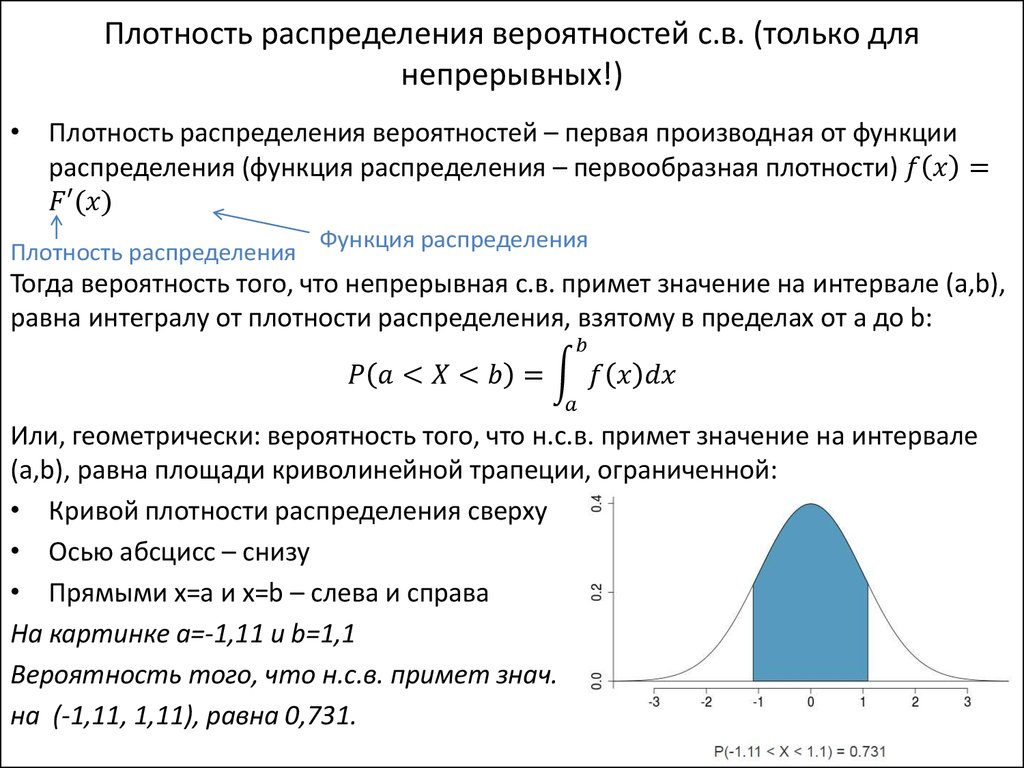 Этот PDF имеет положительную (правую) асимметрию и более высокий эксцесс.
Этот PDF имеет положительную (правую) асимметрию и более высокий эксцесс. Распределение Пуассона
Бета-версия
Пример функции плотности вероятности
 Каждая кость имеет вероятность 1/6 выпадения любого числа, от одного до шести, но сумма двух игральных костей сформирует распределение вероятностей, изображенное на изображении ниже.
Каждая кость имеет вероятность 1/6 выпадения любого числа, от одного до шести, но сумма двух игральных костей сформирует распределение вероятностей, изображенное на изображении ниже. Что говорит нам функция плотности вероятности (PDF)?
Что такое Центральная предельная теорема (ЦПТ) и как она связана с PDF-файлами?
 Итак, мы знаем, что подбрасывание монеты — это бинарный процесс, описываемый биномиальным распределением (орел или решка). Однако, если мы рассмотрим несколько подбрасываний монеты, шансы получить ту или иную комбинацию орла и решки начинают различаться. Например, если бы мы подбрасывали монету десять раз, шансы выпадения 5 из каждого были бы наиболее вероятными, но выпадение десяти орлов подряд крайне редко. Представьте себе 1000 подбрасываний монеты, и распределение приближается к нормальной колоколообразной кривой.
Итак, мы знаем, что подбрасывание монеты — это бинарный процесс, описываемый биномиальным распределением (орел или решка). Однако, если мы рассмотрим несколько подбрасываний монеты, шансы получить ту или иную комбинацию орла и решки начинают различаться. Например, если бы мы подбрасывали монету десять раз, шансы выпадения 5 из каждого были бы наиболее вероятными, но выпадение десяти орлов подряд крайне редко. Представьте себе 1000 подбрасываний монеты, и распределение приближается к нормальной колоколообразной кривой. Чем отличается PDF от CDF?
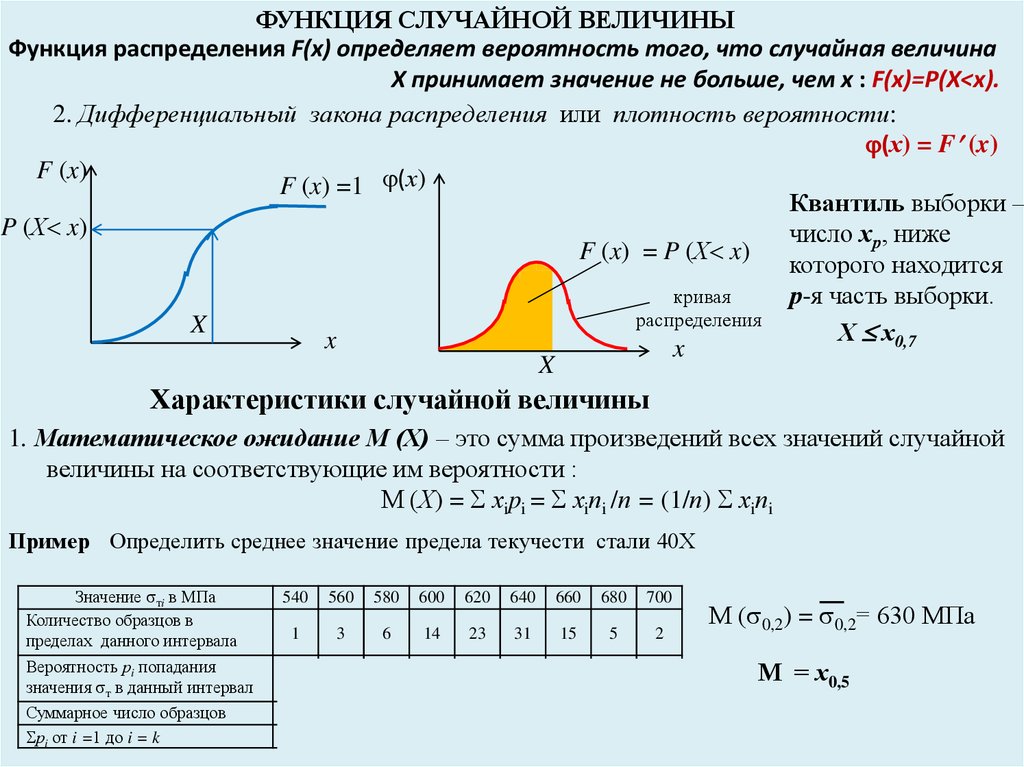

 Функция плотности вероятности. Функция плотности. Подробно.
Функция плотности вероятности. Функция плотности. Подробно.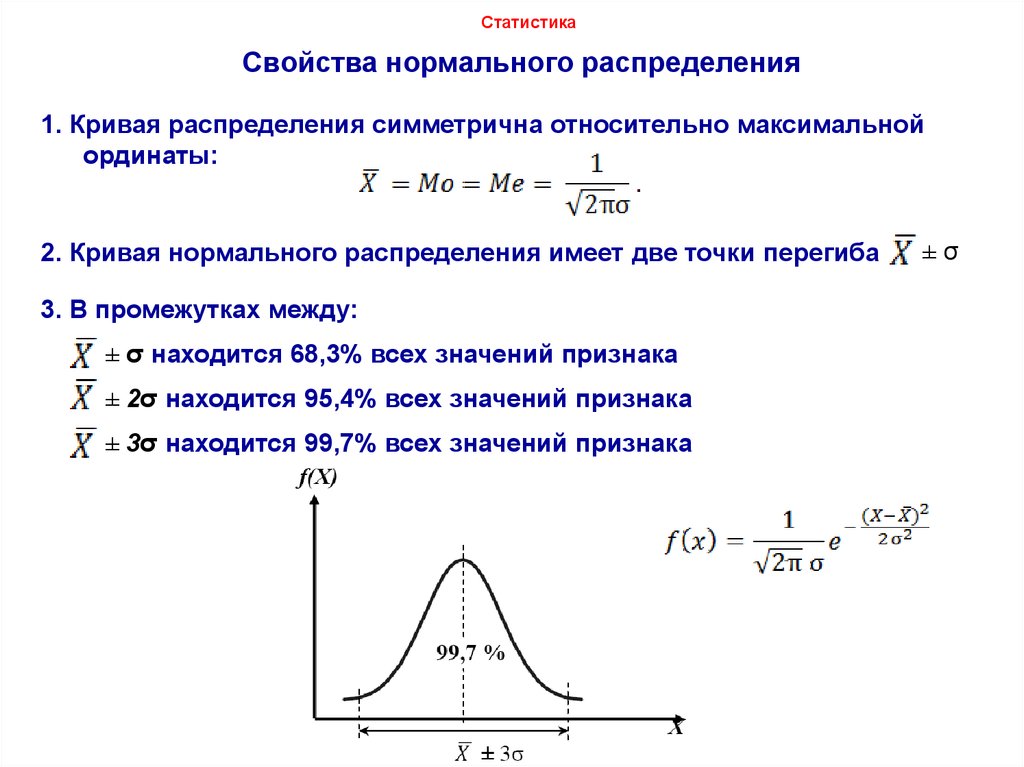 Функция плотности. Подробно.
Функция плотности. Подробно.
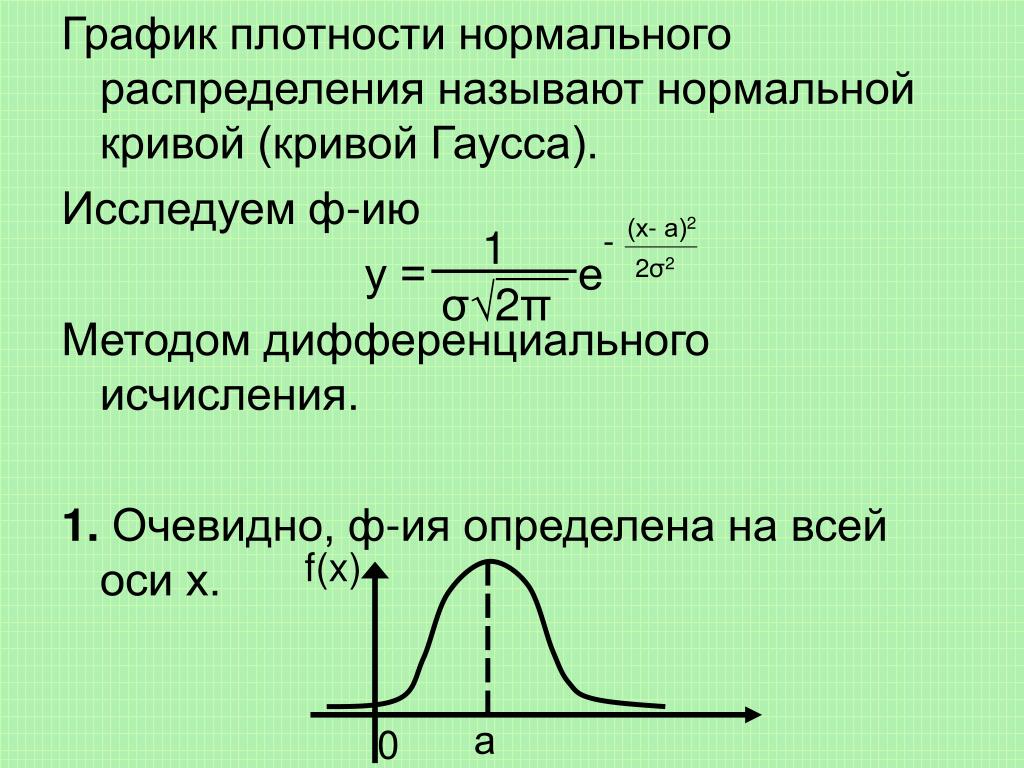
 Вероятность попадания случайной величины в интервал [Α ; Β] численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (заштрихованная на рисунке область). Площадь всей криволинейной трапеции, заключенной между осью 0Х и графиком плотности распределения, всегда равна единице. Любая функция, удовлетворяющая перечисленным выше свойствам, может быть плотностью распределения некоторой непрерывной случайной величины.
Вероятность попадания случайной величины в интервал [Α ; Β] численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (заштрихованная на рисунке область). Площадь всей криволинейной трапеции, заключенной между осью 0Х и графиком плотности распределения, всегда равна единице. Любая функция, удовлетворяющая перечисленным выше свойствам, может быть плотностью распределения некоторой непрерывной случайной величины.