Косинус синус формулы приведения: Формулы приведения

Формула приведения для синуса и косинуса. Формулы приведения

Для использования формул приведения существует два правила.

1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.

Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет.

2. Правило «каким ты был, таким ты и остался».

Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».

На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.

Вычислить Sin(150˚)

Воспользуемся формулами приведения:

Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен +.

Значит у приведенной функции тоже будет знак «плюс». Это мы применили второе правило.

Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.

При желании все формулы приведения можно свести в одну таблицу. Но все же легче запомнить эти два правила и пользоваться ими.

Тригонометрия.Формулы приведения.

Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!

Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.

Разберем в каждой четверти функции sin(a) и cos(a).

Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.

В первой четверти видно, что функция sin(a)>0
И функция cos(a)>0
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).

Во второй четверти видно, что функция sin(a)>0 , потому что ось Y положительна в этой четверти.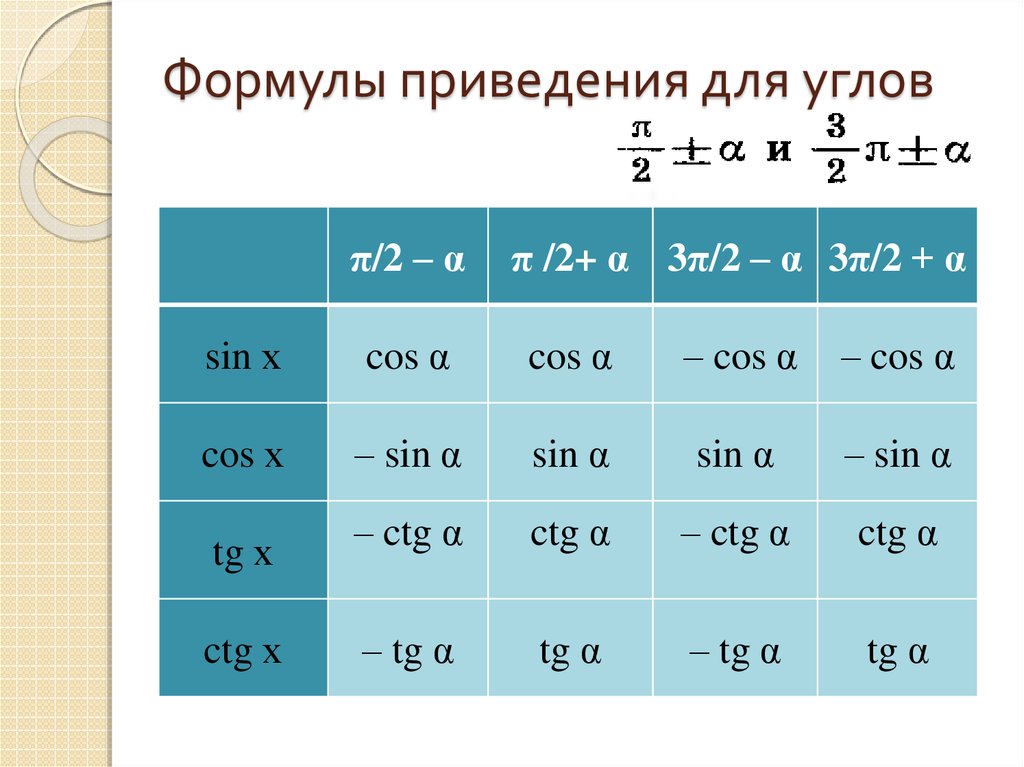
А функция cos(a) , потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).

В третьей четверти видно, что функции sin(a) Третья четверть можно описать через градусную меру, как (180+α) или (270-α).

В четвертой четверти видно, что функция sin(a) , потому что ось Y отрицательна в этой четверти.
А функция cos(a)>0 , потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).

Теперь рассмотрим сами формулы приведения.

Запомним простой алгоритм :
1. Четверть.

(Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется .

И так начнем разбирать по четвертям данный алгоритм.

Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.

Будет cos(90-α) = sin(α)

Выясни чему будет равно выражение sin(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.

Будет sin(90-α) = cos(α)

Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.

Будет cos(360+α) = cos(α)

Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:

1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)

Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.

3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)

Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.

3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)

Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.

Будет cos(180-α) = cos(α)

Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)

Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Тема урока

• Изменение синуса, косинуса и тангенса при возрастании угла.

Цели урока

• Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
• Познакомится с закономерностью изменений значений синуса косинуса и тангенса при возрастании угла.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока

• Проверить знания учащихся.

План урока

1. Повторение ранее изученного материала.
2. Задачи на повторение.
3. Изменение синуса, косинуса и тангенса при возрастании угла.
4. Практическое применение.

Повторение ранее изученного материала

Начнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.

Тригонометрия — это такое сложное греческое слово: тригонон — треугольник, метро — мерять. Стало быть по-гречески это означает: мерятся треугольниками.

Предмети > Математика > Математика 8 класс

И еще одна задача B11 на ту же тему — из реального ЕГЭ по математике.

Задача. Найдите значение выражения:

В этом коротком видеоуроке мы узнаем, как применять формулы приведения для решения реальных задач B11 из ЕГЭ по математике. Как вы видите, перед нами — два тригонометрических выражения, каждое из которых содержит синусы и косинусы, а также довольно зверские числовые аргументы.

Прежде чем решать эти задачи, давайте вспомним, что такое формулы приведения. Итак, если у нас есть выражения вида:

То мы можем избавиться от первого слагаемого (вида k · π/2) по специальным правилам. Начертим тригонометрическую окружность, отметим на ней основные точки: 0, π/2; π; 3π/2 и 2π. Затем смотрим на первое слагаемое под знаком тригонометрической функции. Имеем:

1. Если интересующее нас слагаемое лежит на вертикальной оси тригонометрического круга (например: 3π/2; π/2 и т.д.), то исходная функция заменяется на ко-функцию: синус заменяется косинусом, а косинус — наоборот, синусом.
2. Если же наше слагаемое лежит на горизонтальной оси, то исходная функция не меняется. Просто убираем первое слагаемое в выражении — и все.

Таким образом, мы получим тригонометрическую функцию, не содержащую слагаемых вида k · π/2. Однако на этом работа с формулами приведения не заканчивается. Дело в том, что перед нашей новой функцией, полученной после «отбрасывания» первого слагаемого, может стоять знак плюс или минус. Как определить этот знак? Вот сейчас и узнаем.

Представим, что угол α, оставшийся внутри тригонометрической функции после преобразований, имеет очень малую градусную меру. Но что значит «малая мера»? Допустим, α ∈ (0; 30°) — этого вполне достаточно.

Рассмотрим для примера функцию:

Тогда, следуя нашим предположениям, что α ∈ (0; 30°), заключаем, что угол 3π/2 − α лежит в третьей координатной четверти, т.е. 3π/2 − α ∈ (π; 3π/2). Вспоминаем знак исходной функции, т.е. y = sin x на этом интервале. Очевидно, что синус в третьей координатной четверти отрицателен, поскольку по определению синус — это ордината конца подвижного радиуса (короче синус — это координата y ). Ну, а координата y в нижней полуплоскости всегда принимает отрицательные значения. Значит, и в третьей четверти y тоже отрицателен.

На основании этих размышлений мы можем записать окончательное выражение:

Задача B11 — 1 вариант

Вот эти же самые приемы вполне подходят для решения задачи B11 из ЕГЭ по математике. Разница лишь в том, что во многих реальных задачах B11 вместо радианной меры (т.е. чисел π, π/2, 2π и т.д.) используется градусная мера (т.е. 90°, 180°, 270° и т.д.). Давайте посмотрим на первую задачу:

Сначала разберемся с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем сделать с ним. Пока так и оставим.

Теперь смотрим на знаменатель:

sin 131° = sin (90° + 41°) = cos 41°

Очевидно, что перед нами формула приведения, поэтому синус заменился на косинус. Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y = sin x там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).

Осталось разобраться с последним элементом:

cos 240° = cos (180° + 60°) = −cos 60° = −0,5

Здесь мы видим, что 180° — это горизонтальная ось. Следовательно, сама функция не поменяется: был косинус — и останется тоже косинус. Но вновь возникает вопрос: плюс или минус будет стоять перед полученным выражением cos 60°? Заметим, что 180° — это третья координатная четверть.

Косинус там отрицательный, следовательно, перед косинусом в итоге будет стоять знак «минус». Итого, получаем конструкцию −cos 60° = −0,5 — это табличное значение, поэтому все легко считается.

Теперь подставляем полученные числа в исходную формулу и получаем:

Как видим, число cos 41° в числителе и знаменателе дроби легко сокращается, и остается обычное выражение, которое равно −10. При этом минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений. Ответ в любом случае получится −10. Все, задача B11 решена!

Задача B14 — 2 вариант

Переходим ко второй задаче. Перед нами снова дробь:

Ну, 27° у нас лежит в первой координатной четверти, поэтому здесь ничего менять не будем. А вот sin 117° надо расписать (пока без всякого квадрата):

sin 117° = sin (90° + 27°) = cos 27°

Очевидно, перед нами снова формула приведения : 90° — это вертикальная ось, следовательно, синус поменяется на косинус. Кроме того, угол α = 117° = 90° + 27° лежит во второй координатной четверти. Исходная функция y = sin x там положительна, следовательно, перед косинусом после всех преобразований все равно остается знак «плюс». Другими словами, там ничего не добавляется — так и оставляем: cos 27°.

Возвращаемся к исходному выражению, которое требуется вычислить:

Как видим, в знаменателе после преобразований возникло основное тригонометрическое тождество: sin 2 27° + cos 2 27° = 1. Итого −4: 1 = −4 — вот мы и нашли ответ ко второй задаче B11.

Как видите, с помощью формул приведения такие задачи из ЕГЭ по математике решаются буквально в пару строчек. Никаких синусов суммы и косинусов разности. Все, что нам нужно помнить — это только тригонометрический круг.

С центром в точке A .
α — угол, выраженный в радианах.

Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

;
;
.

;
;
.

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2 π .

Четность

Функция синус — нечетная. Функция косинус — четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

	y = sin x	y = cos x
Область определения и непрерывность	— ∞	— ∞
Область значений	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = -1
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы

Сумма квадратов синуса и косинуса

Формулы синуса и косинуса от суммы и разности

;
;

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражение синуса через косинус

;
;
;
.

Выражение косинуса через синус

;
;
;
.

Выражение через тангенс

; .

При , имеем:
; .

При :
; .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

Выражения через комплексные переменные

;

Формула Эйлера

Выражения через гиперболические функции

;
;

Производные

; . Вывод формул > > >

Производные n-го порядка:
{ -∞

Секанс, косеканс

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.

Арксинус, arcsin

Арккосинус, arccos

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Формулы приведения

Формулы приведения предполагают, что уже известны Sin(α) и Cos(α).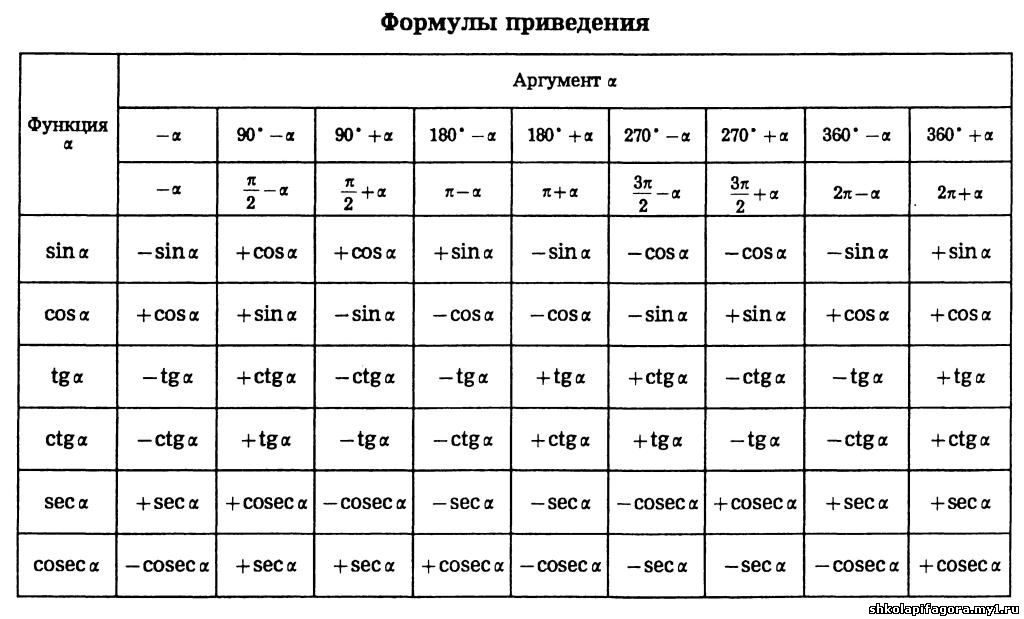 И через эти две величины – Sin(α) и Cos(α) нужно выразить синусы и косинусы углов (90° + α), (90° – α), (180° + α), (180° – α), (270° + α), (270° – α). Помните: формулы приведения запомнить очень трудно, и лучше уметь их выводить, и вот как это делается.

Выберем угол α в первой координатной четверти с таким расчетом чтобы синус и косинус отличались. Косинус длинный большой, а синус маленький короткий.

И вот этот треугольник повернём вокруг начала координат на 90° – и гипотенуза укажет на угол 90° + α. У этой точки (90° + α) абсцисса и ордината равны косинусу и синусу угла 90° + α. А в то же время эти абсцисса и ордината равны прежним катетам прежнего треугольника (катеты только поменялись местами и направление изменили). И вот так получается, что:

Абсцисса (90° + α) = Cos(90° + α) = –Sin(α)

Ордината (90° + α) = Sin(90° + α) = +Cos(α)

Ещё раз повернём изначальный треугольник, и гипотенуза укажет на угол 180° + α. У точки (180° + α) абсцисса и ордината равны косинусу и синусу угла 180° + α. А в то же время эти абсцисса и ордината равны прежним катетам прежнего треугольника (теперь оба катета поменяли направление). И вот так получается, что

Абсцисса (180° + α) = Cos(180° + α) = –Cos(α)

Ордината (180° + α) = Sin(180° + α) = -Sin(α)

Ещё раз повернём изначальный треугольник, и гипотенуза укажет на угол 270° + α. У точки (270° + α) абсцисса и ордината равны косинусу и синусу угла 270° + α. А в то же время эти абсцисса и ордината равны прежним катетам прежнего треугольника (теперь катеты опять поменялись местами и изменили направления). И вот так получается, что

Абсцисса (270° + α) = Cos(270° + α) = +Sin(α)

Ордината (270° + α) = Sin(270° + α) = -Cos(α)

Теперь изначальный треугольник отразим сверху-вниз: гипотенуза укажет на угол –α. У точки (–α) абсцисса и ордината равны косинусу и синусу угла –α. А в то же время эти абсцисса и ордината равны прежним катетам прежнего треугольника (только синус изменил направление). И вот так получается, что

Абсцисса (–α) = Cos(–α) = +Cos(α)

Ордината (–α) = Sin(–α) = –Sin(α)

Теперь отражённый треугольник повернём на угол 90°: гипотенуза укажет на угол 90° – α. У точки (90° – α) абсцисса и ордината равны косинусу и синусу угла (90° – α). А в то же время эти абсцисса и ордината равны прежним катетам прежнего треугольника (теперь синус с косинусом поменялись). И вот так получается, что

Абсцисса (90° – α) = Cos(90° – α) = +Sin(α)

Ордината (90° – α) = Sin(90° – α) = +Cos(α)

Теперь отражённый треугольник ещё повернём на угол 90°: гипотенуза укажет на угол 180° – α. У точки (180° – α) абсцисса и ордината равны косинусу и синусу угла (180° – α). А в то же время эти абсцисса и ордината равны прежним катетам прежнего треугольника (только косинус поменял направление). И вот так получается, что

Абсцисса (180° – α) = Cos(180° – α) = –Cos(α)

Ордината (180° – α) = Sin(180° – α) = +Sin(α)

Теперь отражённый треугольник ещё повернём на угол 90°: гипотенуза укажет на угол 270° – α. У точки (270° – α) абсцисса и ордината равны косинусу и синусу угла (270° – α). А в то же время эти абсцисса и ордината равны прежним катетам прежнего треугольника (теперь косинус с синусом поменялись и к тому же поменяли направление). И вот так получается, что

Абсцисса (270° – α) = Cos(270° – α) = –Sin(α)

Ордината (270° – α) = Sin(270° – α) = –Cos(α)

Формул приведения можно придумать ещё очень много. Поэтому я рекомендую их не запоминать а уметь выводить.

← Предыдущий урок

Оглавление

Формулы приведения — Mathonline

Формулы приведения

Сложить Содержание Формулы приведения Пример 1 Пример 2

Иногда нам может быть интересно вывести формулу приведения для интеграла или общее тождество для кажущегося сложным интеграла. В приведенном ниже списке представлены наиболее распространенные формулы приведения:

• Формула приведения для синуса: 9{n — 2} x \: dx$

  Если не указано иное, содержимое этой страницы находится под лицензией Creative Commons Attribution-ShareAlike 3.0 License

  формула редукции косинуса для интегрирования.

  9{n-2}x~dx} }\)

  Рекомендуемые книги на Amazon (партнерские ссылки)

  Это последнее уравнение представляет собой формулу преобразования косинуса. Теперь давайте поработаем над некоторыми практическими задачами.

  Огромная книга задач по арифметике

  Практика

  Если не указано иное, оцените эти интегралы напрямую, а затем проверьте свой ответ, используя формулу редукции.

  • 92 x ~dx }\) напрямую, используя тождества триггеров, затем проверьте свой ответ, используя формулу приведения.

    Решение

    Органическая химическая репетитор — 2578 Видеореал

    Видео на The Organic Chemistry Tutor

    В журнале.

    • 93 x ~dx }\) непосредственно с использованием триггерных тождеств, затем проверьте свой ответ с помощью формулы приведения.

      Решение

      Органическая химическая репетитор — 2579 Видеореал

      Видео на The Organic Chemistry Tutor

      В журнале.

      интеграция триггера 17calculus плейлист youtube

      Действительно ПОНИМАТЬ исчисление

      Войдите, чтобы оценить эту страницу и увидеть ее текущий рейтинг.

      Темы.

      базовые идентификаторы триггеров

      92\тета\)

      \(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\)   | \(\displaystyle{\cot\theta=\frac{\cos\theta}{\sin\theta}}\)

      \(\displaystyle{\sec\theta=\frac{1}{\cos\theta}}\)   | \(\displaystyle{\csc\theta=\frac{1}{\sin\theta}}\)

      формулы уменьшения мощности (половина угла) 92\тета\)

      ссылки

      список тригонометрических тождеств — wikipedia

      триггерных листа — заметки Пауля онлайн

      17 формул тригонометрического исчисления — полный список

      Триггерные производные и интегралы

      (t) }\)

      \(\displaystyle{ \frac{d[\sec(t)]}{dt} = }\) \(\sec(t)\tan(t) \ )		\(\displaystyle{ \frac{d[\csc(t)]}{dt} = }\) \( -\csc(t)\cot(t) \)
      базовый триггер интегралы
      \(\int{\sin(x)~dx} = -\cos(x)+C\)
      \(\int{\cos(x)~dx } = \sin(x)+C\)
      \(\int{\tan(x)~dx} = -\ln\abs{\cos(x)}+C\)
      \(\int{\cot(x) ~dx} = \ln\abs{\sin(x)}+C\)
      \(\int{\sec(x)~dx} = \ln\abs{\sec(x)+ \tan(x)}+C\)
      \(\int{\csc(x)~dx} = -\ln\abs{\csc(x)+\cot(x)}+C \)
      формулы приведения
      формулы приведения ( n — натуральное число) 9{n-2}x~dx}}\)
      links
      17calculus trig formulas — full list

      Related Topics and Links

      related topics on other pages
      basic trig integration 100263
      Википедия — список идентификаторов триггеров

      Чтобы добавить эту страницу в закладки и практиковать задачи, войдите в свою учетную запись или создайте бесплатную учетную запись.

      No related posts.